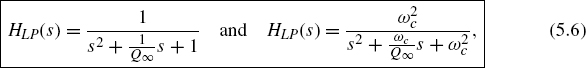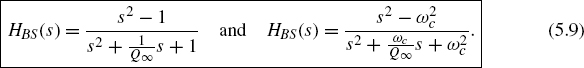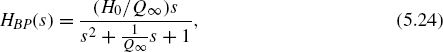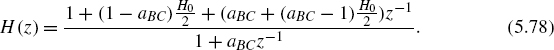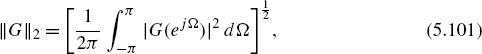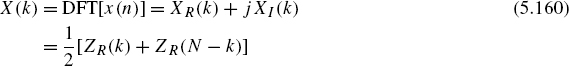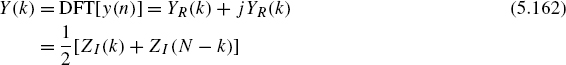Chapter 5
Equalizers
Spectral sound equalization is one of the most important methods for processing audio signals. Equalizers are found in various forms in the transmission of audio signals from a sound studio to the listener. The more complex filter functions are used in sound studios. But in almost every consumer product like car radios, hifi amplifiers, simple filter functions are used for sound equalization. We first discuss basic filter types followed by the design and implementation of recursive audio filters. In Sections 5.3 and 5.4 linear phase nonrecursive filter structures and their implementation are introduced.
5.1 Basics
For filtering of audio signals the following filter types are used:
- Low-pass and high-pass filters with cutoff frequency fc (3 dB cutoff frequency) are shown with their magnitude response in Fig. 5.1. They have a pass-band in the lower and higher frequency range, respectively.
- Band-pass and band-stop filters (magnitude responses in Fig. 5.1) have a center frequency fc and a lower and upper fl und fu cutoff frequency. They have a passand stop-band in the middle of the frequency range. For the bandwidth of a band-pass or a band-stop filter we have
Band-pass filters with a constant relative bandwidth fb/fc are very important for audio applications [Cre03]. The bandwidth is proportional to the center frequency, which is given by
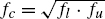 (see Fig. 5.2).
(see Fig. 5.2). - Octave filters are band-pass filters with special cutoff frequencies given by
A spectral decomposition of the audio frequency range with octave filters is shown in Fig. 5.3. At the lower and upper cutoff frequency an attenuation of −3 dB occurs.
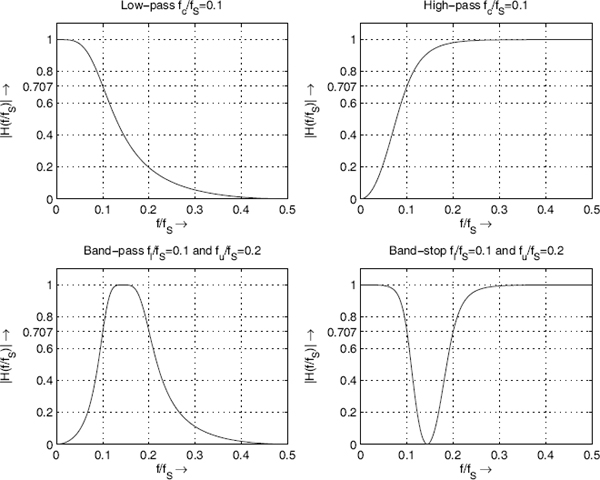
Figure 5.1 Linear magnitude responses of low-pass, high-pass, band-pass, and band-stop filters.
The upper octave band is represented as a high-pass. A parallel connection of octave filters can be used for a spectral analysis of the audio signal in octave frequency bands. This decomposition is used for the signal power distribution across the octave bands. For the center frequencies of octave bands we get fci = 2 · fci−1. The weighting of octave bands with gain factors Ai and summation of the weighted octave bands represents an octave equalizer for sound processing (see Fig. 5.4). For this application the lower and upper cutoff frequencies need an attenuation of −6 dB, such that a sinusoid at the crossover frequency has gain of 0 dB. The attenuation of −6 dB is achieved through a series connection of two octave filters with −3 dB attenuation.
- One-third octave filters are band-pass filters (see Fig. 5.3) with cutoff frequencies given by
The attenuation at the lower and upper cutoff frequency is −3 dB. One-third octave filters split an octave into three frequency bands (see Fig. 5.3).

Figure 5.2 Logarithmic magnitude responses of band-pass filters with constant relative bandwidth.

Figure 5.3 Linear magnitude responses of octave filters and decomposition of an octave band by three one-third octave filters.
- Shelving filters and peak filters are special weighting filters, which are based on low-pass/high-pass/band-pass filters and a direct path (see Section 5.2.2). They have no stop-band compared to low-pass/high-pass/band-pass filters. They are used in a series connection of shelving and peak filters as shown in Fig. 5.5. The lower frequency range is equalized by low-pass shelving filters and the higher frequencies are modified by high-pass shelving filters. Both filter types allow the adjustment of cutoff frequency and gain factor. For the mid-frequency range a series connection of peak filters with variable center frequency, bandwidth, and gain factor are used. These shelving and peak filters can also be applied for octave and one-third octave equalizers in a series connection.
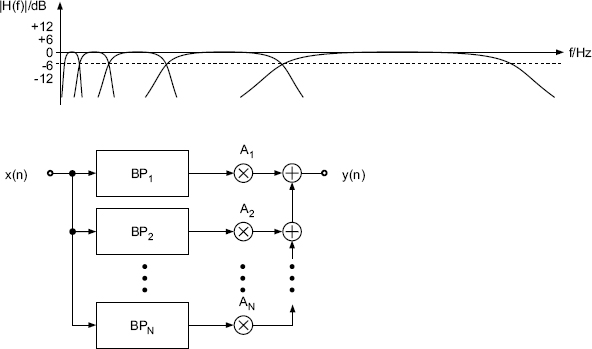
Figure 5.4 Parallel connection of band-pass filters (BP) for octave/one-third octave equalizers with gain factors (Ai for octave or one-third octave band).

Figure 5.5 Series connection of shelving and peak filters (low-frequency LF, high-frequency HF).
- Weighting filters are used for signal level and noise measurement applications. The signal from a device under test is first passed through the weighting filter and then a root mean square or peak value measurement is performed. The two most often used filters are the A-weighting filter and the CCIR-468 weighting filter (see Fig. 5.6). Both weighting filters take the increased sensitivity of the human perception in the 1–6 kHz frequency range into account. The 0 dB of the magnitude response of both filters is crossed at 1 kHz. The CCIR-468 weighting filter has a gain of 12 dB at 6 kHz. A variant of the CCIR-468 filter is the ITU-ARM 2 kHz weighting filter, which is a 5.6 dB down tilted version of the CCIR-468 filters and passes the 0 dB at 2 kHz.

Figure 5.6 Magnitude responses of weighting filters for root mean square and peak value measurements.
5.2 Recursive Audio Filters
5.2.1 Design
A certain filter response can be approximated by two kinds of transfer function. On the one hand, the combination of poles and zeros leads to a very low-order transfer function H(z) in fractional form, which solves the given approximation problem. The digital implementation of this transfer function needs recursive procedures owing to its poles. On the other hand, the approximation problem can be solved by placing only zeros in the z-plane. This transfer function H(z) has, besides its zeros, a corresponding number of poles at the origin of the z-plane. The order of this transfer function, for the same approximation conditions, is substantially higher than for transfer functions consisting of poles and zeros. In view of an economical implementation of a filter algorithm in terms of computational complexity, recursive filters achieve shorter computing time owing to their lower order. For a sampling rate of 48 kHz, the algorithm has 20.83 µs processing time available. With the DSPs presently available it is easy to implement recursive digital filters for audio applications within this sampling period using only one DSP. To design the typical audio equalizers we will start with filter designs in the S-domain. These filters will then be mapped to the Z-domain by the bilinear transformation.
Low-pass/High-pass Filters. In order to limit the audio spectrum, low-pass and high-pass filters with Butterworth response are used in analog mixers. They offer a monotonic pass-band and a monotonically decreasing stop-band attenuation per octave (n · 6 dB/oct.) that is determined by the filter order. Low-pass filters of the second and fourth order are commonly used. The normalized and denormalized second-order low-pass transfer functions are given by
where Ωc is the cutoff frequency and Q∞ is the pole quality factor. The Q-factor Q∞ of a Butterworth approximation is equal to ![]() . The denormalization of a transfer function is obtained by replacing the Laplace variable s by s/Ωg in the normalized transfer function.
. The denormalization of a transfer function is obtained by replacing the Laplace variable s by s/Ωg in the normalized transfer function.
The corresponding second-order high-pass transfer functions
are obtained by a low-pass to high-pass transformation. Figure 5.7 shows the pole-zero locations in the s-plane. The amplitude frequency response of a high-pass filter with a 3 dB cutoff frequency of 50 Hz and a low-pass filter with a 3 dB cutoff frequency of 5000 Hz are shown in Fig. 5.8. Second- and fourth-order filters are shown.

Figure 5.7 Pole-zero location for (a) second-order low-pass and (b) second-order high-pass.

Figure 5.8 Frequency response of low-pass and high-pass filters – high-pass fc = 50 Hz (second/fourth order), low-pass fc = 5000 Hz (second/fourth order).
Table 5.1 summarizes the transfer functions of low-pass and high-pass filters with Butterworth response.
Table 5.1 Transfer functions of low-pass and high-pass filters.

Band-pass and band-stop filters. The normalized and denormalized band-pass transfer functions of second order are
and the band-stop transfer functions are given by
The relative bandwidth can be expressed by the Q-factor
which is the ratio of center frequency fc and the 3 dB bandwidth given by fb. The magnitude responses of band-pass filters with constant relative bandwidth are shown in Fig. 5.2. Such filters are also called constant-Q filters. The geometric symmetric behavior of the frequency response regarding the center frequency fc is clearly noticeable (symmetry regarding the center frequency using a logarithmic frequency axis).
Shelving Filters. Besides the purely band-limiting filters like low-pass and high-pass filters, shelving filters are used to perform weighting of certain frequencies. A simple approach for a first-order low-pass shelving filter is given by
It consists of a first-order low-pass filter with dc amplification of H0 connected in parallel with an all-pass system of transfer function equal to 1. Equation (5.11) can be written as
where V0 determines the amplification at Ω = 0. By changing the parameter V0, any desired boost (V0> 1) and cut (V0< 1) level can be adjusted. Figure 5.9 shows the frequency responses for fc = 100 Hz. For V0< 1, the cutoff frequency is dependent on V0 and is moved toward lower frequencies.
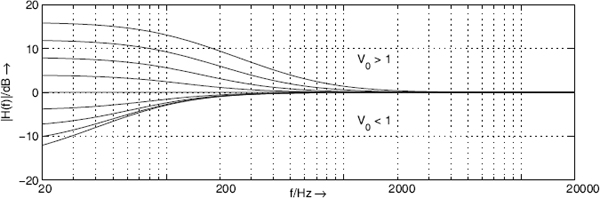
Figure 5.9 Frequency response of transfer function (5.12) with varying V0 and cutoff frequency fc = 100 Hz.
In order to obtain a symmetrical frequency response with respect to the zero decibel line without changing the cutoff frequency, it is necessary to invert the transfer function (5.12) in the case of cut (V0< 1). This has the effect of swapping poles with zeros and leads to the transfer function
for the cut case. Figure 5.10 shows the corresponding frequency responses for varying V0.
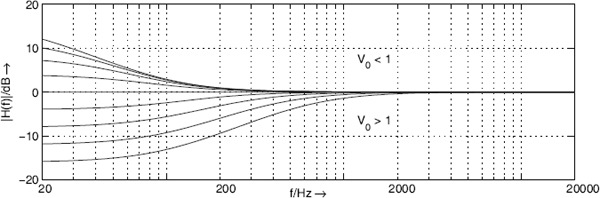
Figure 5.10 Frequency responses of transfer function (5.13) with varying V0 and cutoff frequency fc = 100 Hz.
Finally, Figure 5.11 shows the locations of poles and zeros for both the boost and the cut case. By moving zeros and poles on the negative σ-axis, boost and cut can be adjusted.
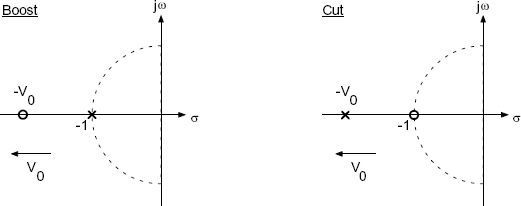
Figure 5.11 Pole-zero locations of a first-order low-frequency shelving filter.
The equivalent shelving filter for high frequencies can be obtained by
which is a parallel connection of a first-order high-pass with gain H0 and a system with transfer function equal to 1. In the boost case the transfer function can written with V0 = H0 + 1 as
and for cut we get
The parameter V0 determines the value of the transfer function H(s) at Ω = ∞ for high-frequency shelving filters.
In order to increase the slope of the filter response in the transition band, a general second-order transfer function
is considered, in which complex zeros are added to the complex poles. The calculation of poles leads to
If the complex zeros
are moved on a straight line with the help of the parameter V0 (see Fig. 5.12), the transfer function
of a second-order low-frequency shelving filter is obtained. The parameter V0 determines the boost for low frequencies. The cut case can be achieved by inversion of (5.20).
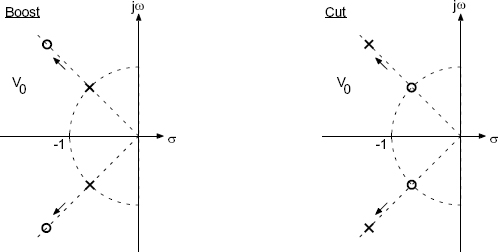
Figure 5.12 Pole-zero locations of a second-order low-frequency shelving filter.
A low-pass to high-pass transformation of (5.20) provides the transfer function
of a second-order high-frequency shelving filter. The zeros
are moved on a straight line toward the origin with increasing V0 (see Fig. 5.13). The cut case is obtained by inverting the transfer function (5.21). Figure 5.14 shows the amplitude frequency response of a second-order low-frequency shelving filter with cutoff frequency 100 Hz and a second-order high-frequency shelving filter with cutoff frequency 5000 Hz (parameter V0).
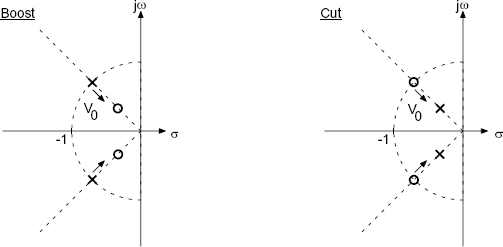
Figure 5.13 Pole-zero locations of second-order high-frequency shelving filter.
Peak Filter. Another equalizer used for boosting or cutting any desired frequency is the peak filter. A peak filter can be obtained by a parallel connection of a direct path and a band-pass according to
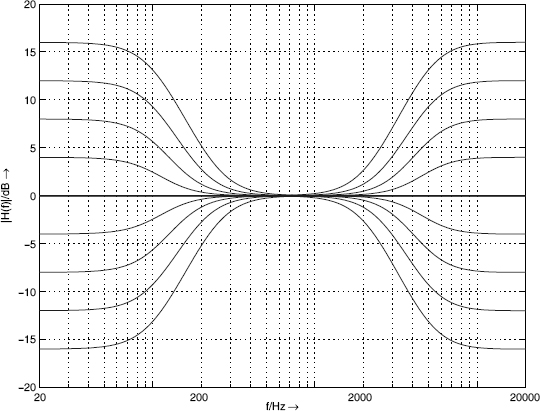
Figure 5.14 Frequency responses of second-order low-/high-frequency shelving filters – low-frequency shelving filter fc = 100 Hz (parameter V0), high-frequency shelving filter fc = 5000 Hz (parameter V0).
With the help of a second-order band-pass transfer function
the transfer function
of a peak filter can be derived. It can be shown that the maximum of the amplitude frequency response at the center frequency is determined by the parameter V0. The relative bandwidth is fixed by the Q-factor. The geometrical symmetry of the frequency response relative to the center frequency remains constant for the transfer function of a peak filter (5.25). The poles and zeros lie on the unit circle. By adjusting the parameter V0, the complex zeros are moved with respect to the complex poles. Figure 5.15 shows this for the boost and cut cases. With increasing Q-factor, the complex poles move toward the jΩ-axis on the unit circle.
Figure 5.16 shows the amplitude frequency response of a peak filter by changing the parameter V0 at a center frequency of 500 Hz and a Q-factor of 1.25. Figure 5.17 shows the variation of the Q-factor Q∞ at a center frequency of 500 Hz, a boost/cut of ±16 dB and Q-factor of 1.25. Finally, the variation of the center frequency with boost and cut of ±16 dB and a Q-factor 1.25 is shown in Fig. 5.18.
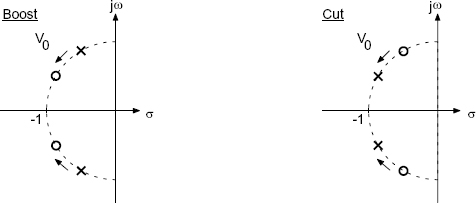
Figure 5.15 Pole-zero locations of a second-order peak filter.

Figure 5.16 Frequency response of a peak filter – fc = 500 Hz, Q∞ = 1.25, cut parameter V0.
Mapping to Z-domain. In order to implement a digital filter, the filter designed in the S-domain with transfer function H(s) is converted to the Z-domain with the help of a suitable transformation to obtain the transfer function H(z). The impulse-invariant transformation is not suitable as it leads to overlapping effects if the transfer function H(s) is not band-limited to half the sampling rate. An independent mapping of poles and zeros from the S-domain into poles and zeros in the Z-domain is possible with help of the bilinear transformation given by
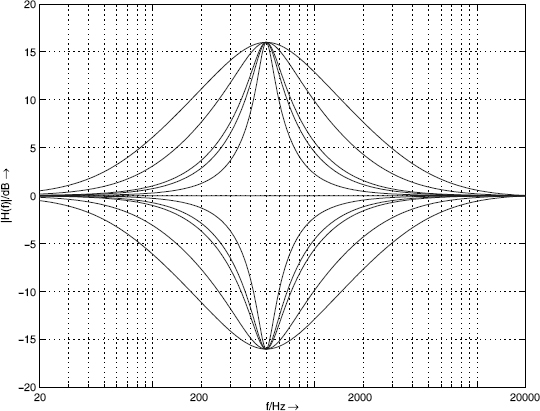
Figure 5.17 Frequency responses of peak filters – fc = 500 Hz, boost/cut ±16 dB, Q∞ = 0.707, 1.25, 2.5, 3, 5.
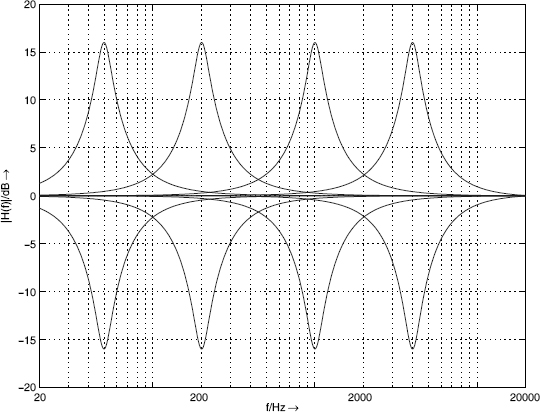
Figure 5.18 Frequency responses of peak filters – boost/cut ±16 dB, Q∞ = 1.25, fc = 50, 200, 1000, 4000 Hz.
Tables 5.2–5.5 contain the coefficients of the second-order transfer function
which are determined by the bilinear transformation and the auxiliary variable K = tan(ΩcT/2) for all audio filter types discussed. Further filter designs of peak and shelving filters are discussed in [Moo83, Whi86, Sha92, Bri94, Orf96a, Dat97, Cla00]. A method for reducing the warping effect of the bilinear transform is proposed in [Orf96b]. Strategies for time-variant switching of audio filters can be found in [Rab88, Mou90, Zöl93, Din95, Väl98].
Table 5.2 Low-pass/high-pass/band-pass filter design.

5.2.2 Parametric Filter Structures
Parametric filter structures allow direct access to the parameters of the transfer function, like center/cutoff frequency, bandwidth and gain, via control of associated coefficients. To modify one of these parameters, it is therefore not necessary to compute a complete set of coefficients for a second-order transfer function, but instead only one coefficient in the filter structure is calculated.
Independent control of gain, cutoff/center frequency and bandwidth for shelving and peak filters is achieved by a feed forward (FF) structure for boost and a feed backward (FB) structure for cut as shown in Fig. 5.19. The corresponding transfer functions are:

Table 5.4 Low-frequency shelving filter design.

Table 5.5 High-frequency shelving filter design.


Figure 5.19 Filter structure for implementing boost and cut filters.
The boost/cut factor is V0 = 1 + H0. For digital filter implementations, it is necessary for the FB case that the inner transfer function be of the form H(z) = z−1H1(z) to ensure causality. A parametric filter structure proposed by Harris [Har93] is based on the FF/FB technique, but the frequency response shows slight deviations near z = 1 and z = −1 from that desired. This is due to the z−1 in the FF/FB branch. Delay-free loops inside filter computations can be solved by the methods presented in [Här98, Fon01, Fon03]. Higher-order parametric filter designs have been introduced in [Kei04, Orf05, Hol06a, Hol06b, Hol06c, Hol06d]. It is possible to implement typical audio filters with only an FF structure. The complete decoupling of the control parameters is possible for the boost case, but there remains a coupling between bandwidth and gain factor for the cut case. In the following, two approaches for parametric audio filter structures based on an all-pass decomposition of the transfer function will be discussed.
Regalia Filter [Reg87]. The denormalized transfer function of a first-order shelving filter is given by
with
![]()
A decomposition of (5.30) leads to
The low-pass and high-pass transfer functions in (5.31) can be expressed by an all-pass decomposition of the form
With the all-pass transfer function
for boost, (5.30) can be rewritten as
The bilinear transformation
![]()
leads to
with
and the frequency parameter
A filter structure for direct implementation of (5.36) is presented in Fig. 5.20a. Other possible structures can be seen in Fig. 5.20b, c. For the cut case V0< 1, the cutoff frequency of the filter moves toward lower frequencies [Reg87].

Figure 5.20 Filter structures by Regalia.
In order to retain the cutoff frequency for the cut case [Zöl95], the denormalized transfer function of a first-order shelving filter (cut)
![]()
can be decomposed as
With the all-pass decompositions
and the all-pass transfer function
for cut, (5.39) can be rewritten as
The bilinear transformation leads to
with
and the frequency parameter
Due to (5.45) and (5.36), boost and cut can be implemented with the same filter structure (see Fig. 5.20). However, it has to be noted that the frequency parameter aC as in (5.47) for cut depends on the cutoff frequency and gain.
A second-order peak filter is obtained by a low-pass to band-pass transformation according to
For an all-pass as given in (5.37) and (5.46), the second-order all-pass is given by
with parameters (cut as in [Zöl95])
The center frequency fc is fixed by the parameter d, the bandwidth fb by the parameters aB and aC, and gain by the parameter V0.
Simplified All-pass Decomposition [Zöl95]. The transfer function of a first-order low-frequency shelving filter can be decomposed as
with
The transfer function (5.55) is composed of a direct branch and a low-pass filter. The first-order low-pass filter is again implemented by an all-pass decomposition. Applying the bilinear transformation to (5.55) leads to
with
For cut, the following decomposition can be derived:
The bilinear transformation applied to (5.63) again gives (5.59). The filter structure is identical for boost and cut. The frequency parameter aB for boost and aC for cut can be calculated as
The transfer function of a first-order low-frequency shelving filter can be calculated as
With A1(z) = −A(z) the signal flow chart in Fig. 5.21 shows a first-order low-pass filter and a first-order low-frequency shelving filter.

Figure 5.21 Low-frequency shelving filter and first-order low-pass filter.
The decomposition of a denormalized transfer function of a first-order high-frequency shelving filter can be given in the form
where
The transfer function results by adding a high-pass filter to a constant. Applying the bilinear transformation to (5.68) gives
For cut, the decomposition can be given by
which in turn results in (5.71) after a bilinear transformation. The boost and cut parameters can be calculated as
The transfer function of a first-order high-frequency shelving filter can then be written as
With A1(z) = −A(z) the signal flow chart in Fig. 5.22 shows a first-order high-pass filter and a high-frequency shelving filter.
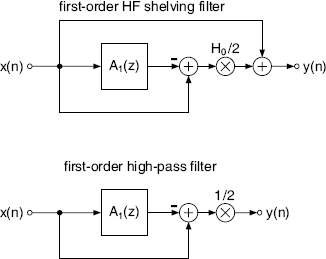
Figure 5.22 First-order high-frequency shelving and high-pass filters.
The implementation of a second-order peak filter can be carried out with a low-pass to band-pass transformation of a first-order shelving filter. But the addition of a second-order band-pass filter to a constant branch also results in a peak filter. With the help of an all-pass implementation of a band-pass filter as given by
and
a second-order peak filter can be expressed as
The bandwidth parameters aB and aC for boost and cut are given
The center frequency parameter d and the coefficient H0 are given by
The transfer function of a second-order peak filter results in
The signal flow charts for a second-order peak filter and a second-order band-pass filter are shown in Fig. 5.23.

Figure 5.23 Second-order peak filter and band-pass filter.
The frequency responses for high-frequency shelving, low-frequency shelving and peak filters are shown in Figs 5.24, 5.25 and 5.26.

Figure 5.24 Low-frequency first-order shelving filter (G = ±18 dB, fc = 20, 50, 100, 1000 Hz).

Figure 5.25 First-order high-frequency shelving filter (G = ±18 dB, fc = 1, 3, 5, 10, 16 kHz).

Figure 5.26 Second-order peak filter (G = ±18 dB, fc = 50, 100, 1000, 3000, 10000 Hz, fb = 100 Hz).
5.2.3 Quantization Effects
The limited word-length for digital recursive filters leads to two different types of quantization error. The quantization of the coefficients of a digital filter results in linear distortion which can be observed as a deviation from the ideal frequency response. The quantization of the signal inside a filter structure is responsible for the maximum dynamic range and determines the noise behavior of the filter. Owing to rounding operations in a filter structure, roundoff noise is produced. Another effect of the signal quantization is limit cycles. These can be classified as overflow limit cycles, small-scale limit cycles and limit cycles correlated with the input signal. Limit cycles are very disturbing owing to their small-band (sinusoidal) nature. The overflow limit cycles can be avoided by suitable scaling of the input signal. The effects of other errors mentioned above can be reduced by increasing the word-lengths of the coefficient and the state variables of the filter structure.
The noise behavior and coefficient sensitivity of a filter structure depend on the topology and the cutoff frequency (position of the poles in the Z-domain) of the filter. Since common audio filters operate between 20 Hz and 20 kHz at a sampling rate of 48 kHz, the filter structures are subjected to specially strict criteria with respect to error behavior. The frequency range for equalizers is between 20 Hz and 4–6 kHz because the human voice and many musical instruments have their formants in that frequency region. For given coefficient and signal word-lengths (as in a digital signal processor), a filter structure with low roundoff noise for audio application can lead to a suitable solution. For this, the following second-order filter structures are compared.
The basis of the following considerations is the relationship between the coefficient sensitivity and roundoff noise. This was first stated by Fettweis [Fet72]. By increasing the pole density in a certain region of the z-plane, the coefficient sensitivity and the roundoff noise of the filter structure are reduced. Owing to these improvements, the coefficient word-length as well as signal word-length can be reduced. Work in designing digital filters with minimum word-length for coefficients and state variables was first carried out by Avenhaus [Ave71].
Typical audio filters like high-/low-pass, peak/shelving filters can be described by the second-order transfer function
The recursive part of the difference equation which can be derived from the transfer function (5.88) is considered more closely, since it plays a major role in affecting the error behavior. Owing to the quantization of the coefficients in the denominator in (5.88), the distribution of poles in the z-plane is restricted (see Fig. 5.27 for 6-bit quantization of coefficients). The pole distribution in the second quadrant of the z-plane is the mirror image of the first quadrant. Figure 5.28 shows a block diagram of the recursive part. Another equivalent representation of the denominator is given by
Here r is the radius and φ the corresponding phase of the complex poles. By quantizing these parameters, the pole distribution is altered, in contrast to the case where b1 and b2 are quantized as in (5.88).
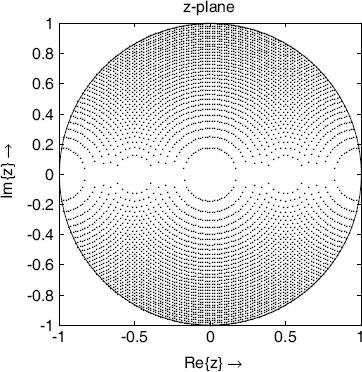
Figure 5.27 Direct-form structure – pole distribution (6-bit quantization).

Figure 5.28 Direct-form structure – block diagram of recursive part.
The state variable structure [Mul76, Bom85] is based on the approach by Gold and Rader [Gol67], which is given by
The possible pole locations are shown in Fig. 5.29 for 6-bit quantization (a block diagram of the recursive part is shown in Fig. 5.30). Owing to the quantization of real and imaginary parts, a uniform grid of different pole locations results. In contrast to direct quantization of the coefficients b1 and b2 in the denominator, the quantization of the real and imaginary parts leads to an increase in the pole density at z = 1. The possible pole locations in the second quadrant in the z-plane are the mirror images of the ones in the first quadrant.

Figure 5.29 Gold and Rader – pole distribution (6-bit quantization).
In [Kin72] a filter structure is suggested which has a pole distribution as shown in Fig. 5.31 (for a block diagram of the recursive part, see Fig. 5.32).

Figure 5.30 Gold and Rader – block diagram of recursive part.
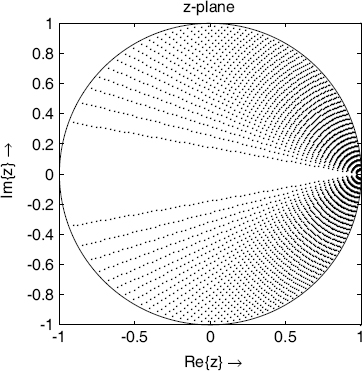
Figure 5.31 Kingsbury – pole distribution (6-bit quantization).

Figure 5.32 Kingsbury – block diagram of recursive part.
The corresponding transfer function,
shows that in this case the coefficients b1 and b2 can be obtained by a linear combination of the quantized coefficients k1 and k2. The distance d of the pole from the point z = 1 determines the coefficients
as illustrated in Fig. 5.33.
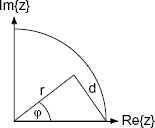
Figure 5.33 Geometric interpretation.
The filter structures under consideration showed that by a suitable linear combination of quantized coefficients, any desired pole distribution can be obtained. An increase of the pole density at z = 1 can be achieved by influencing the linear relationship between the coefficient k1 and the distance d from z = 1 [Zöl89, Zöl90]. The nonlinear relationship of the new coefficients gives the following structure with the transfer function
and coefficients
with
The pole distribution of this structure is shown in Fig. 5.34. The block diagram of the recursive part is illustrated in Fig. 5.35. The increase in the pole density at z = 1, in contrast to previous pole distributions is observed. The pole distributions of the Kingsbury and Zölzer structures show a decrease in the pole density for higher frequencies. For the pole density, a symmetry with respect to the imaginary axis as in the case of the direct-form structure and the Gold and Rader structure is not possible. But changing the sign in the recursive part of the difference equation results in a mirror image of the pole density. The mirror image can be achieved through a change of sign in the denominator polynomial. The denominator polynomial
shows that the real part depends on the coefficient of z−1.

Figure 5.34 Zölzer – pole distribution (6-bit quantization).
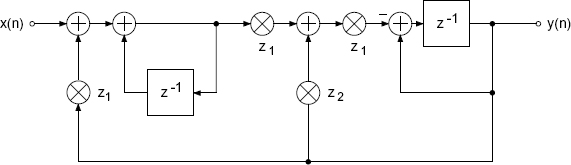
Figure 5.35 Zölzer – block diagram of recursive part.
Analytical Comparison of Noise Behavior of Different Filter Structures
In this section, recursive filter structures are analyzed in terms of their noise behavior in fixed-point arithmetic [Zöl89, Zöl90, Zöl94]. The block diagrams provide the basis for an analytical calculation of noise power owing to the quantization of state variables. First of all, the general case is considered in which quantization is performed after multiplication. For this purpose, the transfer function Gi(z) of every multiplier output to the output of the filter structure is determined.
For this error analysis it is assumed that the signal within the filter structure covers the whole dynamic range so that the quantization error ei(n) is not correlated with the signal. Consecutive quantization error samples are not correlated with each other so that a uniform power density spectrum results [Sri77]. It can also be assumed that different quantization errors ei(n) are uncorrelated within the filter structure. Owing to the uniform distribution of the quantization error, the variance can be given by
The quantization error is added at every point of quantization and is filtered by the corresponding transfer function G(z) to the output of the filter. The variance of the output quantization noise (due to the noise source e(n)) is given by
Exact solutions for the ring integral (5.100) can be found in [Jur64] for transfer functions up to the fourth order. With the L2 norm of a periodic function
the superposition of the noise variances leads to the total output noise variance
The signal-to-noise ratio for a full-range sinusoid can be written as
The ring integral
is given in [Jur64] for first-order systems by
and for second-order systems by
In the following, an analysis of the noise behavior for different recursive filter structures is presented. The noise transfer functions of individual recursive parts are responsible for noise shaping.

Figure 5.36 Direct form with additive error signal.
Table 5.6 Direct form – (a) noise transfer function, (b) quadratic L2 norm and (c) output noise variance in the case of quantization after every multiplication.

The error transfer function of a second-order direct-form structure (see Fig. 5.36) has only complex poles (see Table 5.6).
The implementation of poles near the unit circle leads to high amplification of the quantization error. The effect of the pole radius on the noise variance can be observed in the equation for output noise variance. The coefficient b2 = r2 approaches 1, which leads to a huge increase in the output noise variance.
The Gold and Rader filter structure (Fig. 5.37) has an output noise variance that depends on the pole radius (see Table 5.7) and is independent of the pole phase. The latter fact is because of the uniform grid of the pole distribution. An additional zero on the real axis (z = r cos ![]() ) directly beneath the poles reduces the effect of the complex poles.
) directly beneath the poles reduces the effect of the complex poles.
The Kingsbury filter (Fig. 5.38 and Table 5.8) and the Zölzer filter (Fig. 5.39 and Table 5.9), which is derived from it, show that the noise variance depends on the pole radius. The noise transfer functions have a zero at z = 1 in addition to the complex poles. This zero reduces the amplifying effect of the pole near the unit circle at z = 1.
Figure 5.40 shows the signal-to-noise ratio versus the cutoff frequency for the four filter structures presented above. The signals are quantized to 16 bits. Here, the poles move with increasing cutoff frequency on the curve characterized by the Q-factor Q∞ = 0.7071 in the z-plane. For very small cutoff frequencies, the Zölzer filter shows an improvement of 3 dB in terms of signal-to-noise ratio compared with the Kingsbury filter and an improvement of 6 dB compared with the Gold and Rader filter. Up to 5 kHz, the Zölzer filter yields better results (see Fig. 5.41). From 6 kHz onwards, the reduction of pole density in this filter leads to a decrease in the signal-to-noise ratio (see Fig. 5.41).

Figure 5.37 Gold and Rader structure with additive error signals.
Table 5.7 Gold and Rader – (a) noise transfer function, (b) quadratic L2 norm and (c) output noise variance in the case of quantization after every multiplication.


Figure 5.38 Kingsbury structure with additive error signals.
Table 5.8 Kingsbury – (a) noise transfer function, (b) quadratic L2 norm and (c) output noise variance in the case of quantization after every multiplication.

Table 5.9 Zölzer – (a) noise transfer function, (b) quadratic L2 norm and (c) output noise variance in the case of quantization after every multiplication.


Figure 5.39 Zölzer structure with additive error signals.
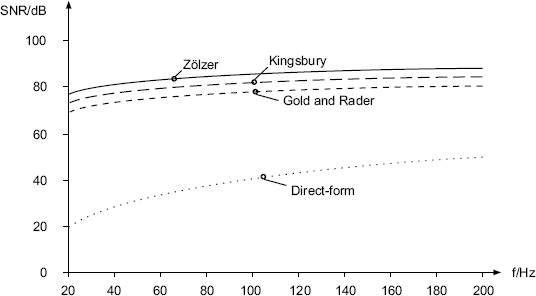
Figure 5.40 SNR vs. cutoff frequency – quantization of products (fc < 200 Hz).

Figure 5.41 SNR vs. cutoff frequency – quantization of products (fc > 2 kHz).
With regard to the implementation of the these filters with digital signal processors, a quantization after every multiplication is not necessary. Quantization takes place when the accumulator has to be stored in memory. This can be seen in Figs 5.42–5.45 by introducing quantizers where they really occur. The resulting output noise variances are also shown. The signal-to-noise ratio is plotted versus the cutoff frequency in Figs 5.46 and 5.47. In the case of direct-form and Gold and Rader filters, the signal-to-noise ratio increases by 3 dB whereas the output noise variance for the Kingsbury filter remains unchanged. The Kingsbury filter and the Gold and Rader filters exhibit similar results up to a frequency of 200 kHz (see Fig. 5.46). The Zölzer filter demonstrates an improvement of 3 dB compared with these structures. For frequencies of up to 2 kHz (see Fig. 5.47) it is seen that the increased pole density leads to an improvement of the signal-to-noise ratio as well as a reduced effect due to coefficient quantization.
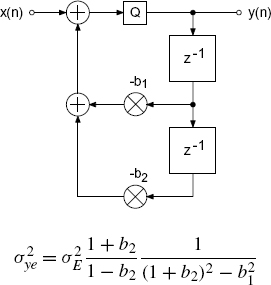
Figure 5.42 Direct-form filter – quantization after accumulator.

Figure 5.43 Gold and Rader filter – quantization after accumulator.

Figure 5.44 Kingsbury filter – quantization after accumulator.

Figure 5.45 Zölzer filter – quantization after accumulator.

Figure 5.46 SNR vs. cutoff frequency – quantization after accumulator (fc < 200 Hz).
Noise Shaping in Recursive Filters
The analysis of the noise transfer function of different structures shows that for three structures with low roundoff noise a zero at z = 1 occurs in the transfer functions G(z) of the error signals in addition to the complex poles. This zero near the poles reduces the amplifying effect of the pole. If it is now possible to introduce another zero into the noise transfer function then the effect of the poles is compensated for to a larger extent. The procedure of feeding back the quantization error as shown in Chapter 2 produces an additional zero in the noise transfer function [Tra77, Cha78, Abu79, Bar82, Zöl89]. The feedback of the quantization error is first demonstrated with the help of the direct-form structure as shown in Fig. 5.48. This generates a zero at z = 1 in the noise transfer function given by

Figure 5.47 SNR vs. cutoff frequency – quantization after accumulator (fc > 2 kHz).
The resulting variance σ2 of the quantization error at the output of the filter is presented in Fig. 5.48. In order to produce two zeros at z = 1, the quantization error is fed back over two delays weighted 2 and −1 (see Fig. 5.48b). The noise transfer function is, hence, given by
The signal-to-noise ratio of the direct-form is plotted versus the cutoff frequency in Fig. 5.49. Even a single zero significantly improves the signal-to-noise ratio in the direct form. The coefficients b1 and b2 approach −2 and 1 respectively with the decrease of the cutoff frequency. With this, the error is filtered with a second-order high-pass. The introduction of the additional zeros in the noise transfer function only affects the noise signal of the filter. The input signal is only affected by the transfer function H(z). If the feedback coefficients are chosen equal to the coefficients b1 and b2 in the denominator polynomial, complex zeros are produced that are identical to the complex poles. The noise transfer function G(z) is then reduced to unity. The choice of complex zeros directly at the location of the complex poles corresponds to double-precision arithmetic.
In [Abu79] an improvement of noise behavior for the direct form in any desired location of the z-plane is achieved by placing additional simple-to-implement complex zeros near the poles. For implementing filter algorithms with digital signal processors, these kinds of suboptimal zero are easily realized. Since the Gold and Rader, Kingsbury, and Zölzer filter structures already have zeros in their respective noise transfer functions, it is sufficient to use a simple feedback for the quantization error. By virtue of this extension, the block diagrams in Figs 5.50, 5.51 and 5.52 are obtained.

Figure 5.48 Direct form with noise shaping.

Figure 5.49 SNR – Noise shaping in direct-form filter structures.
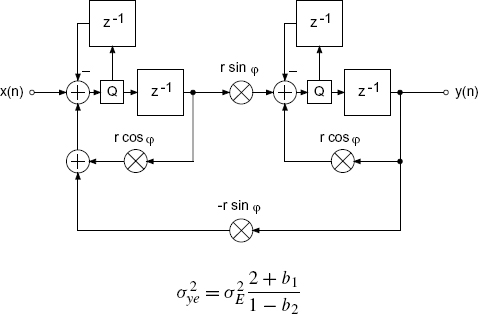
Figure 5.50 Gold and Rader filter with noise shaping.

Figure 5.51 Kingsbury filter with noise shaping.
The effect of noise shaping on signal-to-noise ratio is shown in Figs 5.53 and 5.54. The almost ideal noise behavior of all filter structures for 16-bit quantization and very small cutoff frequencies can be observed. The effect of this noise shaping for increasing cutoff frequencies is shown in Fig. 5.54. The compensating effect of the two zeros at z = 1 is reduced.

Figure 5.52 Zölzer filter with noise shaping.

Figure 5.53 SNR – noise shaping (20–200 Hz).
Scaling
In a fixed-point implementation of a digital filter, a transfer function from the input of the filter to a junction within the filter has to be determined, as well as the transfer function from the input to the output. By scaling the input signal, it has to be guaranteed that the signals remain within the number range at each junction and at the output.
In order to calculate scaling coefficients, different criteria can be used. The Lp norm is defined as
and an expression for the L∞ norm follows for p = ∞:

Figure 5.54 SNR – noise shaping (200 – 12000 Hz).
The L∞ norm represents the maximum of the amplitude frequency response. In general, the modulus of the output is
with
For the L1, L2 and L∞ norms the explanations in Table 5.10 can be used.
Table 5.10 Commonly used scaling.

With
the L∞ norm is given by
For a sinusoidal input signal of amplitude 1 we get ![]() X(ejΩ)
X(ejΩ)![]() 1 = 1. For |yi(n)| ≤ 1 to be valid, the scaling factor must be chosen as
1 = 1. For |yi(n)| ≤ 1 to be valid, the scaling factor must be chosen as
The scaling of the input signal is carried out with the maximum of the amplitude frequency response with the goal that for |x(n)| ≤ 1, |yi(n)| ≤ 1. As a scaling coefficient for the input signal the highest scaling factor Si is chosen. To determine the maximum of the transfer function
of a second-order system
![]()
the maximum value can be calculated as
With x = cos (Ω) it follows that
The solution of (5.124) leads to x = cos(Ωmax/min) which must be real (−1 ≤ x ≤ 1) for the maximum/minimum to occur at a real frequency. For a single solution (repeated roots) of the above quadratic equation, the discriminant must be D = (p/2)2 − q = 0(x2 +px + q = 0). It follows that
and
The solution of (5.126) gives two solutions for S2. The solution with the larger value is chosen. If the discriminant D is not greater than zero, the maximum lies at x = 1 (z = 1) or x = −1 (z = −1) as given by
or
Limit Cycles
Limit cycles are periodic processes in a filter which can be measured as sinusoidal signals. They arise owing to the quantization of state variables. The different types of limit cycle and the methods necessary to prevent them are briefly listed below:
- overflow limit cycles
- → saturation curve
- → scaling
- limit cycles for vanishing input
- → noise shaping
- → dithering
- limit cycles correlated with the input signal
- →noise shaping
- →dithering.
5.3 Nonrecursive Audio Filters
To implement linear phase audio filters, nonrecursive filters are used. The basis of an efficient implementation is the fast convolution
where the convolution in the time domain is performed by transforming the signal and the impulse response into the frequency domain, multiplying the corresponding Fourier transforms and inverse Fourier transform of the product into the time domain signal (see Fig. 5.55). The transform is carried out by a discrete Fourier transform of length N, such that N = N1 + N2 − 1 is valid and time-domain aliasing is avoided. First we discuss the basics. We then introduce the convolution of long sequences followed by a filter design for linear phase filters.

Figure 5.55 Fast convolution of signal x(n) of length N1 and impulse response h(n) of length N2 delivers the convolution result y(n) = x(n)*h(n) of length N1 + N2 − 1.
5.3.1 Basics of Fast Convolution
IDFT Implementation with DFT Algorithm. The discrete Fourier transformation (DFT) is described by
and the inverse discrete Fourier transformation (IDFT) by
Suppressing the scaling factor 1/N, we write
so that the following symmetrical transformation algorithms hold:
The IDFT differs from the DFT only by the sign in the exponential term.
An alternative approach for calculating the IDFT with the help of a DFT is described as follows [Cad87, Duh88]. We will make use of the relationships
Conjugating (5.133) gives
The multiplication of (5.138) by j leads to
Conjugating and multiplying (5.139) by j results in
An interpretation of (5.137) and (5.140) suggests the following way of performing the IDFT with the DFT algorithm:
- Exchange the real with the imaginary part of the spectral sequence

- Transform with DFT algorithm

- Exchange the real with the imaginary part of the time sequence

For implementation on a digital signal processor, the use of DFT saves memory for IDFT.
Discrete Fourier Transformation of Two Real Sequences. In many applications, stereo signals that consist of a left and right channel are processed. With the help of the DFT, both channels can be transformed simultaneously into the frequency domain [Sor87, Ell82].
For a real sequence x(n) we obtain
For a discrete Fourier transformation of two real sequences x(n) and y(n), a complex sequence is first formed according to
The Fourier transformation gives
where
Since x(n) and y(n) are real sequences, it follows from (5.142) that
Considering the real part of Z(k), adding (5.148) and (5.151) gives
and subtraction of (5.151) from (5.148) results in
Considering the imaginary part of Z(k), adding (5.148) and (5.151) gives
and subtraction of (5.151) from (5.148) results in
Hence, the spectral functions are given by
and
Fast Convolution if Spectral Functions are Known. The spectral functions X(k), Y(k) and H(k) are known. With the help of (5.148), the spectral sequence can be formed by
Filtering is done by multiplication in the frequency domain:
The inverse transformation gives
so that the filtered output sequence is given by
The filtering of a stereo signal can hence be done by transformation into the frequency domain, multiplication of the spectral functions and inverse transformation of left and right channels.
5.3.2 Fast Convolution of Long Sequences
The fast convolution of two real input sequences xl(n) and xl+1(n) of length N1 with the impulse response h(n) of length N2 leads to the output sequences
of length N1 + N2 − 1. The implementation of a nonrecursive filter with fast convolution becomes more efficient than the direct implementation of an FIR filter for filter lengths N > 30. Therefore the following procedure will be performed:
- Formation of a complex sequence
- Fourier transformation of the impulse response h(n) that is padded with zeros to a length N ≥ N1 + N2 − 1,
- Fourier transformation of the sequence z(n) that is padded with zeros to a length N ≥ N1 + N2 − 1,
- Formation of a complex output sequence
- Formation of a real output sequence

Figure 5.56 Fast convolution with partitioning of the input signal x(n) into blocks of length L.
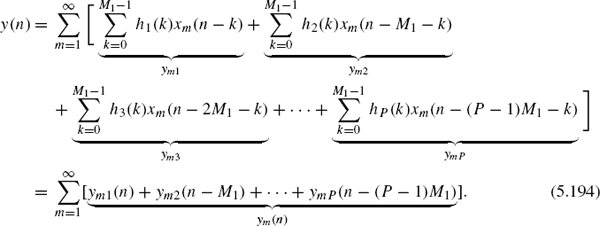
For the convolution of an infinite-length input sequence (see Fig. 5.56) with an impulse response h(n), the input sequence is partitioned into sequences xm(n) of length L:
The input sequence is given by superposition of finite-length sequences according to
The convolution of the input sequence with the impulse response h(n) of length M gives
The term in brackets corresponds to the convolution of a finite-length sequence xm(n) of length L with the impulse response of length M. The output signal can be given as superposition of convolution products of length L +M − 1. With these partial convolution products
the output signal can be written as
![]()
Figure 5.57 Partitioning of the impulse response h(n).
If the length M of the impulse response is very long, it can be similarly partitioned into P parts each of length M/P (see Fig. 5.57). With
it follows that
With Mp = pM/P and (5.189) the following partitioning can be done:
This can be rewritten as
An example of partitioning the impulse response into P = 4 parts is graphically shown in Fig. 5.58. This leads to

Figure 5.58 Scheme for a fast convolution with P = 4.
The procedure of a fast convolution by partitioning the input sequence x(n) as well as the impulse response h(n) is given in the following for the example in Fig. 5.58.
- Decomposition of the impulse response h(n) of length 4M:
- Zero-padding of partial impulse responses up to a length 2M:
- Calculating and storing
- Decomposition of the input sequence x(n) into partial sequences xl(n) of length M:
- Nesting partial sequences:
- Zero-padding of complex sequence zm(n) up to a length 2M:
- Fourier transformation of the complex sequences zm(n):
- Multiplication in the frequency domain:
- Inverse transformation:
- Determination of partial convolutions:
- Overlap-add of partial sequences, increment l = l + 2 and m = m + 1, and back to step 5.
Based on the partitioning of the input signal and the impulse response and the following Fourier transform, the result of each single convolution is only available after a delay of one block of samples. Different methods to reduce computational complexity or overcome the block delay have been proposed [Soo90, Gar95, Ege96, Mül99, Mül01, Garc02]. These methods make use of a hybrid approach where the first part of the impulse response is used for time-domain convolution and the other parts are used for fast convolution in the frequency domain. Figure 5.59a, b demonstrates a simple derivation of the hybrid convolution scheme, which can be described by the decomposition of the transfer function as
where the impulse response has length M · N and M is the number of smaller partitions of length N. Figure 5.59c, d shows two different signal flow graphs for the decomposition given by (5.226) of the entire transfer function. In particular, Fig. 5.59d highlights (with gray background) that in each branch i = 1,…, M − 1 a delay of i · N occurs and each filter Hi(z) has the same length and makes use of the same state variables. This means that they can be computed in parallel in the frequency domain with 2N-FFTs/IFFTs and the outputs have to be delayed according to (i − 1) · N, as shown in Fig. 5.59e. A further simplification shown in Fig. 5.59f leads to one input 2N-FFT and block delays z−1 for the frequency vectors. Then, parallel multiplications with Hi(k) of length 2N and the summation of all intermediate products are performed before one output 2N-IFFT for the overlap-add operation in the time domain is used. The first part of the impulse response represented by H0(z) is performed by direct convolution in the time domain. The frequency and time domain parts are then overlapped and added. An alternative realization for fast convolution is based on the overlap and save operation.
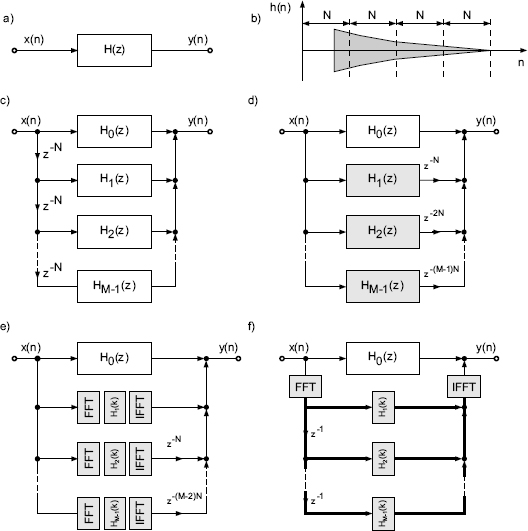
Figure 5.59 Hybrid fast convolution.
5.3.3 Filter Design by Frequency Sampling
Audio filter design for nonrecursive filter realizations by fast convolution can be carried out by the frequency sampling method. For linear phase systems we obtain
where A(ejΩ) is a real-valued amplitude response and NF is the length of the impulse response. The magnitude |H(ejΩ)| is calculated by sampling in the frequency domain at equidistant places
according to
Hence, a filter can be designed by fulfilling conditions in the frequency domain. The linear phase is determined as
Owing to the real transfer function H(z) for an even filter length, we have to fulfill
This has to be taken into consideration while designing filters of even length NF. The impulse response h(n) is obtained through an NF -point IDFT of the spectral sequence H(k). This impulse response is extended with zero-padding to the length N and then transformed by an N-point DFT resulting in the spectral sequence H(k) of the filter.
Example: For NF = 8, |H(k)| = 1 (k = 0, 1, 2, …, 7) and |H(4)| = 0, the group delay is tG = 3.5. Figure 5.60 shows the amplitude, real part and imaginary part of the transfer function and the impulse response h(n).
5.4 Multi-complementary Filter Bank
The subband processing of audio signals is mainly used in source coding applications for efficient transmission and storing. The basis for the subband decomposition is critically sampled filter banks [Vai93, Fli00]. These filter banks allow a perfect reconstruction of the input provided there is no processing within the subbands. They consist of an analysis filter bank for decomposing the signal in critically sampled subbands and a synthesis filter bank for reconstructing the broad-band output. The aliasing in the subbands is eliminated by the synthesis filter bank. Nonlinear methods are used for coding the subband signals. The reconstruction error of the filter bank is negligible compared with the errors due to the coding/decoding process. Using a critically sampled filter bank as a multi-band equalizer, multi-band dynamic range control or multi-band room simulation, the processing in the subbands leads to aliasing at the output. In order to avoid aliasing, a multi-complementary filter bank [Fli92, Zöl92, Fli00] is presented which enables an aliasing-free processing in the subbands and leads to a perfect reconstruction of the output. It allows a decomposition into octave frequency bands which are matched to the human ear.
5.4.1 Principles
Figure 5.61 shows an octave-band filter bank with critical sampling. It performs a successive low-pass/high-pass decomposition into half-bands followed by downsampling by a factor 2. The decomposition leads to the subbands Y1 to YN (see Fig. 5.62). The transition frequencies of this decomposition are given by
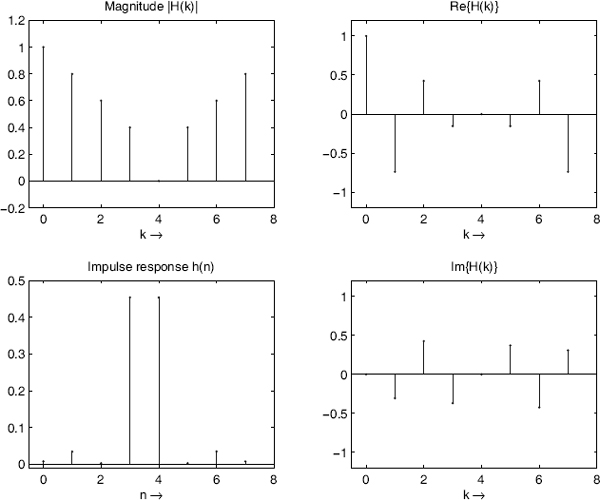
Figure 5.60 Filter design by frequency sampling (NF even).
In order to avoid aliasing in subbands, a modified octave-band filter bank is considered which is shown in Fig. 5.63 for a two-band decomposition. The cutoff frequency of the modified filter bank is moved from ![]() to a lower frequency. This means that in downsampling the low-pass branch, no aliasing occurs in the transition band (e.g. cutoff frequency
to a lower frequency. This means that in downsampling the low-pass branch, no aliasing occurs in the transition band (e.g. cutoff frequency ![]() ). The broader high-pass branch cannot be downsampled. A continuation of the two-band decomposition described leads to the modified octave-band filter bank shown in Fig. 5.64. The frequency bands are depicted in Fig. 5.65 showing that besides the cutoff frequencies
). The broader high-pass branch cannot be downsampled. A continuation of the two-band decomposition described leads to the modified octave-band filter bank shown in Fig. 5.64. The frequency bands are depicted in Fig. 5.65 showing that besides the cutoff frequencies
the bandwidth of the subbands is reduced by a factor 2. The high-pass subband Y1 is an exception.
The special low-pass/high-pass decomposition is carried out by a two-band complementary filter bank as shown in Fig. 5.66. The frequency responses of a decimation filter HD(z), interpolation filter HI(z) and kernel filter HK(z) are shown in Fig. 5.67.
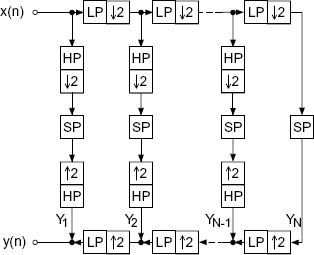
Figure 5.61 Octave-band QMF filter bank (SP = signal processing, LP = low-pass, HP = high-pass).

Figure 5.62 Octave-frequency bands.

Figure 5.63 Two-band decomposition.
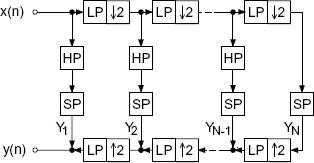
Figure 5.64 Modified octave-band filter bank.
The low-pass filtering of a signal x1(n) is done with the help of a decimation filter HD(z), the downsampler of factor 2 and the kernel filter HK(z) and leads to y2(2n). The Z-transform of y2(2n) is given by

Figure 5.65 Modified octave decomposition.
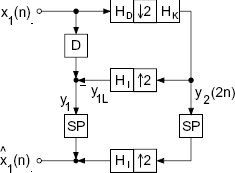
Figure 5.66 Two-band complementary filter bank.
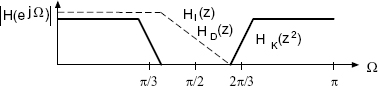
Figure 5.67 Design of HD(z), HI(z) and HK(z).
The interpolated low-pass signal y1L(n) is generated by upsampling by a factor 2 and filtering with the interpolation filter HI(z). The Z-transform of y1L(n) is given by
The high-pass signal y1(n) is obtained by subtracting the interpolated low-pass signal y1L(n) from the delayed input signal x1(n − D). The Z-transform of the high-pass signal is given by
The low-pass and high-pass signals are processed individually. The output signal ![]() is formed by adding the high-pass signal to the upsampled and filtered low-pass signal. With (5.237) and (5.239) the Z-transform of
is formed by adding the high-pass signal to the upsampled and filtered low-pass signal. With (5.237) and (5.239) the Z-transform of ![]() can be written as
can be written as
Equation (5.240) shows the perfect reconstruction of the input signal which is delayed by D sampling units.
The extension to N subbands and performing the kernel filter using complementary techniques [Ram88, Ram90] leads to the multi-complementary filter bank as shown in Fig. 5.68. Delays are integrated in the high-pass (Y1) and band-pass subbands (Y2 to YN−2) in order to compensate the group delay. The filter structure consists of N horizontal stages. The kernel filter is implemented as a complementary filter in S vertical stages. The design of the latter will be discussed later. The vertical delays in the extended kernel filters (EKF1 to EKFN−1) compensate group delays caused by forming the complementary component. At the end of each of these vertical stages is the kernel filter HK. With
the signals ![]() can be written as a function of the signals Xk(zk) as
can be written as a function of the signals Xk(zk) as
with
![]()
and with k = N − l the delays are given by
Perfect reconstruction of the input signal can be achieved if the horizontal delays DHk are given by
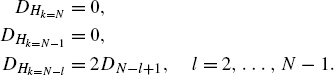
The implementation of the extended vertical kernel filters is done by calculating complementary components as shown in Fig. 5.69. After upsampling, interpolating with a high-pass HP (Fig. 5.69b) and forming the complementary component, the kernel filter HK with frequency response as in Fig. 5.69a becomes low-pass with frequency response as illustrated in Fig. 5.69c. The slope of the filter characteristic remains constant whereas the cutoff frequency is doubled. A subsequent upsampling with an interpolation high-pass (Fig. 5.69d) and complement filtering leads to the frequency response in Fig. 5.69e. With the help of this technique, the kernel filter is implemented at a reduced sampling rate. The cutoff frequency is moved to a desired cutoff frequency by using decimation/interpolation stages with complement filtering.
Computational Complexity. For an N-band multi-complementary filter bank with N − 1 decomposition filters where each is implemented by a kernel filter with S stages, the horizontal complexity is given by

Figure 5.68 Multi-complementary filter bank.
HC1 denotes the number of operations that are carried out at the input sampling rate. These operations occur in the horizontal stage HS1 (see Fig. 5.68). HC2 denotes the number of operations (horizontal stage HS2) that are performed at half of the sampling rate. The number of operations in the stages from HS2 to HSN are approximately identical but are calculated at sampling rates that are successively halved.
The complexities VC1 to VCN−1 of the vertical kernel filters EKF1 to EKFN−1 are calculated as
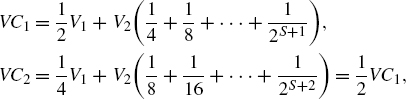

Figure 5.69 Multirate complementary filter.

where V1 depicts the complexity of the first stage VS1 and V2 is the complexity of the second stage VS2 (see Fig. 5.68). It can be seen that the total vertical complexity is given by
The upper bound of the total complexity results is the sum of horizontal and vertical complexities and can be written as
The total complexity Ctot is independent of the number of frequency bands N and vertical stages S. This means that for real-time implementation with finite computation power, any desired number of subbands with arbitrarily narrow transition bands can be implemented!
5.4.2 Example: Eight-band Multi-complementary Filter Bank
In order to implement the frequency decomposition into the eight bands shown in Fig. 5.70, the multirate filter structure of Fig. 5.71 is employed. The individual parts of the system provide means of downsampling (D = decimation), upsampling (I = interpolation), kernel filtering (K), signal processing (SP), delays (N1 = Delay 1, N2 = Delay 2) and group delay compensation Mi in the ith band. The frequency decomposition is carried out successively from the highest to the lowest frequency band. In the two lowest frequency bands, a compensation for group delay is not required. The slope of the filter response can be adjusted with the kernel complementary filter structure shown in Fig. 5.72 which consists of one stage. The specifications of an eight-band equalizer are listed in Table 5.11. The stop-band attenuation of the subband filters is chosen to be 100 dB.

Figure 5.70 Modified octave decomposition of the frequency band.
Table 5.11 Transition frequencies fCi and transition bandwidths TB in an eight-band equalizer.

Filter Design
The design of different decimation and interpolation filters is mainly determined by the transition bandwidth and the stop-band attenuation for the lower frequency band. As an example, a design is made for an eight-band equalizer. The kernel complementary filter structure for both lower frequency bands is illustrated in Fig. 5.72. The design specifications for the kernel low-pass, decimation and interpolation filters are presented in Fig. 5.73.
Kernel Filter Design. The transition bandwidth of the kernel filter is known if the transition bandwidth is given for the lower frequency band. This kernel filter must be designed for a sampling rate of ![]() . For a given transition bandwidth fTB at a frequency
. For a given transition bandwidth fTB at a frequency ![]() , the normalized pass-band frequency is
, the normalized pass-band frequency is
and the normalized stop-band frequency

Figure 5.71 Linear phase eight-band equalizer.

Figure 5.72 Kernel complementary filter structure.
With the help of these parameters the filter can be designed. Making use of the Parks – McClellan program, the frequency response shown in Fig. 5.74 is obtained for a transition bandwidth of fTB = 20 Hz. The necessary filter length for a stop-band attenuation of 100 dB is 53 taps.
Decimation and Interpolation High-pass Filter. These filters are designed for a sampling rate of ![]() and are half-band filters as illustrated in Fig. 5.73. First a low-pass filter is designed, followed by a high-pass to low-pass transformation. For a given transition bandwidth fTB, the normalized pass-band frequency is
and are half-band filters as illustrated in Fig. 5.73. First a low-pass filter is designed, followed by a high-pass to low-pass transformation. For a given transition bandwidth fTB, the normalized pass-band frequency is
and the normalized stop-band frequency is given by
With these parameters the design of a half-band filter is carried out. Figure 5.75 shows the frequency response. The necessary filter length for a stop-band attenuation of 100 dB is 55 taps.
Decimation and Interpolation Low-pass Filter. These filters are designed for a sampling rate of fS = 44100/(26) and are also half-band filters. For a given transition bandwidth fTB, the normalized pass-band frequency is
and the normalized stop-band frequency is given by

Figure 5.73 Decimation and interpolation filters.
With these parameters the design of a half-band filter is carried out. Figure 5.76 shows the frequency response. The necessary filter length for a stop-band attenuation of 100 dB is 43 taps. These filter designs are used in every decomposition stage so that the transition frequencies and bandwidths are obtained as listed in Table 5.11.
Memory Requirements and Latency Time. The memory requirements depend directly on the transition bandwidth and the stop-band attenuation. Here, the memory operations for the actual kernel, decimation and interpolation filters have to be differentiated from the group delay compensations in the frequency bands. The compensating group delay N1 for decimation and interpolation high-pass filters of order ODHP/IHP is calculated with the help of the kernel filter order OKF according to

Figure 5.74 Kernel low-pass filter with a transition bandwidth of 20 Hz.
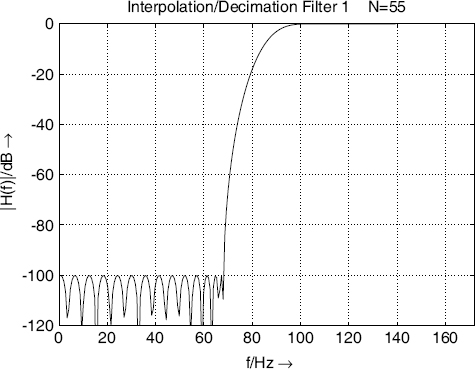
Figure 5.75 Decimation and interpolation high-pass filter.
The group delay compensation N2 for the decimation and interpolation low-pass filters of order ODLP/ILP is given by

Figure 5.76 Decimation and interpolation low-pass filter.
The delays M3,…, M8 in the individual frequency bands are calculated recursively starting from the two lowest frequency bands:
![]()
The memory requirements per decomposition stage are listed in Table 5.12. The memory for the delays can be computed by σi Mi = 240N2. The latency time (delay) is given by tD = (M8/44100)103 ms (tD = 725 ms).
Table 5.12 Memory requirements.
| Kernel filter | OKF |
| DHP/IHP | 2 · ODHP/IHP |
| DLP/ILP | 3 · ODLP/ILP |
| N1 | OKF + ODHP/IHP |
| N2 | 2 · N1 + ODLP/ILP |
5.5 Java Applet – Audio Filters
The applet shown in Fig. 5.77 demonstrates audio filters. It is designed for a first insight into the perceptual effect of filtering an audio signal. Besides the different filter types and their acoustical effect, the applet offers a first insight into the logarithmic behavior of loudness and frequency resolution of our human acoustical perception.
The following filter functions can be selected on the lower right of the graphical user interface:
- Low-/high-pass filter (LP/HP) with control parameter
- – cutoff frequency fc in hertz (lower horizontal slider)
- – all frequencies above (LP) or below (HP) the cutoff frequency are attenuated according to the shown frequency response.
- Low/high-frequency shelving filter (LFS/HFS) with control parameters
- – cutoff frequency fc in hertz (lower horizontal slider)
- – boost/cut in dB (left vertical slider with + for boost or − for cut)
- – all frequencies below (LFS) or above (HFS) the cutoff frequency are boosted/cut according to the selected boost/cut.
- Peak filter with control parameters
- – center frequency fc in hertz (lower horizontal slider)
- – boost/cut in dB (left vertical slider with + for boost or − for cut)
- – Q-factor Q = fc/fb (right vertical slider), which controls the bandwidth fb of the boost/cut around the adjusted center frequency fc. Lower Q-factor means wider bandwidth.
- – the peak filter boosts/cuts the center frequency with a bandwidth adjusted by the Q-factor.
The center window shows the frequency response (filter gain versus frequency) of the selected filter functions. You can choose between a linear and a logarithmic frequency axis.
You can choose between two predefined audio files from our web server (audio1.wav or audio2.wav) or your own local wav file to be processed [Gui05].
5.6 Exercises
1. Design of Recursive Audio Filters
- How can we design a low-frequency shelving filter? Which parameters define the filter? Explain the control parameters.
- How can we derive a high-frequency shelving filter? Which parameters define the filter?
- What is the difference between first- and second-order shelving filters.
- How can we design a peak filter? Which parameters define the filter? What is the filter order? Explain the control parameters. Explain the Q-factor.
- How do we derive the digital transfer function?
- Derive the digital transfer functions for the first-order shelving filters.

Figure 5.77 Java applet – audio filters.
2. Parametric Audio Filters
- What is the basic idea of parametric filters?
- What is the difference between the Regalia and the Zölzer filter structures? Count the number of multiplications and additions for both filter structures.
- Derive a signal flow graph for first- and second-order parametric Zölzer filters with a direct-form implementation of the all-pass filters.
- Is there a complete decoupling of all control parameters for boost and cut? Which parameters are decoupled?
3. Shelving Filter: Direct Form
Derive a first-order low shelving filter from a purely band-limiting first-order low-pass filter. Use a bilinear transform and give the transfer function of the low shelving filter.
- Write down what you know about the filter coefficients and calculate the poles/zeros as functions of V0 and T. What gain factor do you have if z = ±1?
- What is the difference between purely band-limiting filters and the shelving filter?
- How can you describe the boost and cut effect related to poles/zeros of the filter?
- How do we get a transfer function for the boost case from the cut case?
- How do we go from a low shelving filter to a high shelving filter?
4. Shelving Filter: All-pass Form
Implement a first-order high shelving filter for the boost and cut cases with the sampling rate fS = 44.1 kHz, cutoff frequency fc = 10 kHz and gain G = 12 dB.
- Define the all-pass parameters and coefficients for the boost and cut cases.
- Derive from the all-pass decomposition the complete transfer function of the shelving filter.
- Using Matlab, give the magnitude frequency response for boost and cut. Show the result for the case where a boost and cut filter are in a series connection.
- If the input signal to the system is a unit impulse, give the spectrum of the input and out signal for the boost and cut cases. What result do you expect in this case when boost and cut are again cascaded?
5. Quantization of Filter Coefficients
For the quantization of the filter coefficients different methods have been proposed: direct form, Gold and Rader, Kingsbury and Zölzer.
- What is the motivation behind this?
- Plot a pole distribution using the quantized polar representation of a second-order IIR filter

6. Signal Quantization inside the Audio Filter
Now we combine coefficient and signal quantization.
- Design a digital high-pass filter (second-order IIR), with a cutoff frequency fc = 50 Hz. (Use the Butterworth, Chebyshev or elliptic design methods implemented in Matlab.)
- Quantize the signal only when it leaves the accumulator (i.e. before it is saved in any state variable).
- Now quantize the coefficients (direct form), too.
- Extend your quantization to every arithmetic operation (i.e. after each addition/multiplication).
7. Quantization Effects in Recursive Audio Filters
- Why is the quantization of signals inside a recursive filter of special interest?
- Derive the noise transfer function of the second-order direct-form filter. Apply a firstand second-order noise shaping to the quantizer inside the direct-form structure and discuss its influence. What is the difference between second-order noise shaping and double-precision arithmetic?
- Write a Matlab implementation of a second-order filter structure for quantization and noise shaping.
8. Fast Convolution
For an input sequence x(n) of length N1 = 500 and the impulse response h(n) of length N2 = 31, perform the discrete-time convolution.
- Give the discrete-time convolution sum formula.
- Using Matlab, define x(n) as a sum of two sinusoids and derive h(n) with Matlab function
remez (..). - Realize the filter operation with Matlab using:
- the function
conv (x, h) - the sample-by-sample convolution sum method
- the FFT method
- the FFT with overlap-add method.
- the function
- Describe FIR filtering with the fast convolution technique. What conditions do the input signal and the impulse responses have to fulfill if convolution is performed by equivalent frequency-domain processing?
- What happens if input signal and impulse response are as long as the FFT transform length?
- How can we perform the IFFT by the FFT algorithm?
- Explain the processing steps
- for a segmentation of the input signal into blocks and fast convolution;
- for a stereo signal by the fast convolution technique;
- for the segmentation of the impulse response.
- What is the processing delay of the fast convolution technique?
- Write a Matlab program for fast convolution.
- How does quantization of the signal influence the roundoff noise behavior of an FIR filter?
9. FIR Filter Design by Frequency Sampling
- Why is frequency sampling an important design method for audio equalizers? How do we sample magnitude and phase response?
- What is the linear phase frequency response of a system? What is the effect on an input signal passing through such a system?
- Explain the derivation of the magnitude and phase response for a linear phase FIR filter.
- What is the condition for a real-valued impulse response of even length N? What is the group delay?
- Write a Matlab program for the design of an FIR filter and verify the example in the book.
- If the desired frequency response is an ideal low-pass filter of length NF = 31 with cutoff frequency Ωc = π/2, derive the impulse response of this system. What will the result be for NF = 32 and Ωc = π?
10. Multi-complementary Filter Bank
- What is an octave-spaced frequency splitting and how can we design a filter bank for that task?
- How can we perform aliasing-free subband processing? How can we achieve narrow transition bands for a filter bank? What is the computational complexity of an octave-spaced filter bank?
References
[Abu79] A. I. Abu-El-Haija, A. M. Peterson: An Approach to Eliminate Roundoff Errors in Digital Filters, IEEE Trans. ASSP, Vol. 3, pp. 195–198, April 1979.
[Ave71] E. Avenhaus: Zum Entwurf digitaler Filter mit minimaler Speicherwortlänge für Koeffizienten und Zustandsgrössen, Ausgewählte Arbeiten über Nachrichtensysteme, No. 13, Prof. Dr.-Ing. W. Schüssler, Ed., Erlangen 1971.
[Bar82] C. W. Barnes: Error Feedback in Normal Realizations of Recursive Digital Filters, IEEE Trans. Circuits and Systems, pp. 72–75, January 1982.
[Bom85] B. W. Bomar: New Second-Order State-Space Structures for Realizing Low Roundoff Noise Digital Filters, IEEE Trans. ASSP, Vol. 33, pp. 106–110, Feb. 1985.
[Bri94] R. Bristow-Johnson: The Equivalence of Various Methods of Computing Biquad Coefficients for Audio Parametric Equalizers, Proc. 97th AES Convention, Preprint No. 3906, San Francisco, November 1994.
[Cad87] J. A. Cadzow: Foundations of Digital Signal Processing and Data Analysis, New York: Macmillan, 1987.
[Cha78] T. L. Chang: A Low Roundoff Noise Digital Filter Structure, Proc. Int. Symp. on Circuits and Systems, pp. 1004–1008, May 1978.
[Cla00] R. J. Clark, E. C. Ifeachor, G. M. Rogers, P. W. J. Van Eetvelt: Techniques for Generating Digital Equalizer Coefficients, J. Audio Eng. Soc., Vol. 48, pp. 281–298, April 2000.
[Cre03] L. Cremer, M. Möser: Technische Akustik, Springer-Verlag, Berlin, 2003.
[Dat97] J. Dattorro: Effect Design – Part 1: Reverberator and Other Filters, J. Audio Eng. Soc., Vol. 45, pp. 660–684, September 1997.
[Din95] Yinong Ding, D. Rossum: Filter Morphing of Parametric Equalizers and Shelving Filters for Audio Signal Processing, J. Audio Eng. Soc., Vol. 43, pp. 821–826, October 1995.
[Duh88] P. Duhamel, B. Piron, J. Etcheto: On Computing the Inverse DFT, IEEE Trans. Acoust., Speech, Signal Processing, Vol. 36, pp. 285–286, February 1988.
[Ege96] G. P. M. Egelmeers, P. C. W. Sommen: A New Method for Efficient Convolution in Frequency Domain by Nonuniform Partitioning for Adaptive Filtering, IEEE Trans. Signal Processing, Vol. 44, pp. 3123–3192, December 1996.
[Ell82] D. F. Elliott, K. R. Rao: Fast Transforms: Algorithms, Analyses, Applications, Academic Press, New York, 1982.
[Fet72] A. Fettweis: On the Connection Between Multiplier Wordlength Limitation and Roundoff Noise in Digital Filters, IEEE Trans. Circuit Theory, pp. 486–491, September 1972.
[Fli92] N. J. Fliege, U. Zölzer: Multi-complementary Filter Bank: A New Concept with Aliasing-Free Subband Signal Processing and Perfect Reconstruction, Proc. EUSIPCO-92, pp. 207–210, Brussels, August 1992.
[Fli93a] N.J. Fliege, U. Zölzer: Multi-complementary Filter Bank, Proc. ICASSP-93, pp. 193–196, Minneapolis, April 1993.
[Fli00] N. Fliege: Multirate Digital Signal Processing, John Wiley & Sons, Ltd, Chichester, 2000.
[Fon01] F. Fontana, M. Karjalainen: Magnitude-Complementary Filters for Dynamic Equalization, Proc. of the DAFX-01, Limerick, pp. 97–101, December 2001.
[Fon03] F. Fontana, M. Karjalainen: A Digital Bandpass/Bandstop Complementary Equalization Filter with Independent Tuning Characteristics, IEEE Signal Processing Letters, Vol. 10, No. 4, pp. 119–122, April 2003.
[Gar95] W. G. Gardner: Efficient Convolution Without Input-Output Delay, J. Audio Eng. Soc., Vol. 43, pp. 127–136, 1995.
[Garc02] G. Garcia: Optimal Filter Partition for Efficient Convolution with Short Input/Output Delay, Proc. 113th AES Convention, Preprint No. 5660, Los Angeles, October 2002.
[Gol67] B. Gold, C. M. Rader: Effects of Parameter Quantization on the Poles of a Digital Filter, Proc. IEEE, Vol. 55, pp. 688–689, May 1967.
[Gui05] M. Guillemard, C. Ruwwe, U. Zölzer: J-DAFx – Digital Audio Effects in Java, Proc. 8th Int. Conference on Digital Audio Effects (DAFx-05), pp. 161–166, Madrid, 2005.
[Har93] F. J. Harris, E. Brooking: A Versatile Parametric Filter Using an Imbedded All-Pass Sub-filter to Independently Adjust Bandwidth, Center Frequency and Boost or Cut, Proc. 95th AES Convention, Preprint No. 3757, San Francisco, 1993.
[Här98] A. Härmä: Implementation of Recursive Filters Having Delay Free Loops, Proc. IEEE Int. Conf. Acoustics, Speech, and Signal Processing (ICASSP'98), Vol. 3, pp. 1261–1264, Seattle, 1998.
[Hol06a] M. Holters, U. Zölzer: Parametric Recursive Higher-Order Shelving Filters, Jahrestagung Akustik DAGA, Braunschweig, March 2006.
[Hol06b] M. Holters, U. Zölzer: Parametric Recursive Higher-Order Shelving Filters, Proc. 120th Conv. Audio Eng. Soc., Preprint No. 6722, Paris, 2006.
[Hol06c] M. Holters, U. Zölzer: Parametric Higher-Order Shelving Filters, Proc. EUSIPCO-06, Florence, 2006.
[Hol06d] M. Holters, U. Zölzer: Graphic Equalizer Design Using Higher-Order Recursive Filters, Proc. of the 9th Int. Conference on Digital Audio Effects (DAFx-06), pp. 37–40, Montreal, September 2006.
[Jur64] E. I. Jury: Theory and Application of the z-Transform Method, John Wiley & Sons, Inc., New York, 1964.
[Kei04] F. Keiler, U. Zölzer, Parametric Second- and Fourth-Order Shelving Filters for Audio Applications, Proc. of IEEE 6th International Workshop on Multimedia Signal Processing, Siena, September–October 2004.
[Kin72] N. G. Kingsbury: Second-Order Recursive Digital Filter Element for Poles Near the Unit Circle and the Real z-Axis, Electronic Letters, Vol. 8, pp. 155–156, March 1972.
[Moo83] J. A. Moorer: The Manifold Joys of Conformal Mapping, J. Audio Eng. Soc., Vol. 31, pp. 826–841, 1983.
[Mou90] J. N. Mourjopoulos, E. D. Kyriakis-Bitzaros, C. E. Goutis: Theory and Real-Time Implementation of Time-Varying Digital Audio Filters, J. Audio Eng. Soc., Vol. 38, pp. 523–536, July/August 1990.
[Mul76] C. T. Mullis, R. A. Roberts: Synthesis of Minimum Roundoff Noise Fixed Point Digital Filters, IEEE Trans. Circuits and Systems, pp. 551–562, September 1976.
[Mül99] C. Müller-Tomfelde: Low Latency Convolution for Real-time Application, In Proc. of the AES 16th International Conference: Spatial Sound Reproduction, pp. 454–460, Rovaniemi, Finland, April 1999.
[Mül01] C. Müller-Tomfelde: Time-Varying Filter in Non-uniform Block Convolution, Proc. of the COST G-6 Conference on Digital Audio Effects (DAFX-01), Limerick, December 2001.
[Orf96a] S. J. Orfanidis: Introduction to Signal Processing, Prentice Hall, Englewood Cliffs, NJ, 1996.
[Orf96b] S. J. Orfanidis: Digital Parametric Equalizer Design with Prescribed Nyquist-Frequency Gain, Proc. 101st AES Convention, Preprint No. 4361, Los Angeles, November 1996.
[Orf05] S. J. Orfanidis: High-Order Digital Parametric Equalizer Design, J. Audio Eng. Soc., Vol. 53, pp. 1026–1046, 2005.
[Rab88] R. Rabenstein: Minimization of Transient Signals in Recursive Time-Varying Digital Filters, Circuits, Systems, and Signal Processing, Vol. 7, No. 3, pp. 345–359, 1988.
[Ram88] T. A. Ramstad, T. Saramäki: Efficient Multirate Realization for Narrow Transition-Band FIR Filters, Proc. IEEE Int. Symp. on Circuits and Syst., pp. 2019–2022, Espoo, Finland, June 1988.
[Ram90] T. A. Ramstad, T. Saramäki: Multistage, Multirate FIR Filter Structures for Narrow Transition-Band Filters, Proc. IEEE Int. Symp. on Circuits and Syst., pp. 2017–2021, New Orleans, May 1990.
[Reg87] P. A. Regalia, S. K. Mitra: Tunable Digital Frequency Response Equalization Filters, IEEE Transactions on Acoustics, Speech, and Signal Processing, Vol. 35, No. 1, pp. 118–120, January 1987.
[Sha92] D. J. Shpak: Analytical Design of Biquadratic Filter Sections for Parametric Filters, J. Audio Eng. Soc., Vol. 40, pp. 876–885, November 1992.
[Soo90] J. S. Soo, K. K. Pang: Multidelay Block Frequency Domain Adaptive Filter, IEEE Transactions on Acoustics, Speech, and Signal Processing, Vol. 38, No. 2, pp. 373–376, February 1990.
[Sor87] H. V. Sorensen, D. J. Jones, M. T. Heideman, C. S. Burrus: Real-Valued Fast Fourier Transform Algorithms, IEEE Trans. ASSP, Vol. 35, No. 6, pp. 849–863, June 1987.
[Sri77] A. B. Sripad, D. L. Snyder: A Necessary and Sufficient Condition for Quantization Errors to be Uniform and White, IEEE Trans. ASSP, Vol. 25, pp. 442–448, October 1977.
[Tra77] Tran-Thong, B. Liu: Error Spectrum Shaping in Narrow Band Recursive Filters, IEEE Trans. ASSP, pp. 200–203, April 1977.
[Vai93] P. P. Vaidyanathan: Multirate Systems and Filter Banks, Prentice Hall, Englewood Cliffs, NJ, 1993.
[Väl98] V. Välimäki, T. I. Laakso: Suppression of Transients in Time-Varying Recursive Filters for Audio Signals, Proc. IEEE Int. Conf. Acoustics, Speech, and Signal Processing (ICASSP'98), Vol. 6, pp. 3569–3572, Seattle, 1998.
[Whi86] S. A. White: Design of a Digital Biquadratic Peaking or Notch Filter for Digital Audio Equalization, J. Audio Eng. Soc., Vol. 34, pp. 479–483, 1986.
[Zöl89] U. Zölzer: Entwurf digitaler Filter für die Anwendung im Tonstudiobereich, Wissenschaftliche Beiträge zur Nachrichtentechnik und Signalverarbeitung, TU Hamburg-Harburg, June 1989.
[Zöl90] U. Zölzer: A Low Roundoff Noise Digital Audio Filter, Proc. EUSIPCO-90, pp. 529–532, Barcelona, 1990.
[Zöl92] U. Zölzer, N. Fliege: Logarithmic Spaced Analysis Filter Bank for Multiple Loudspeaker Channels, Proc. 93rd AES Convention, Preprint No. 3453, San Francisco, 1992.
[Zöl93] U. Zölzer, B. Redmer, J. Bucholtz: Strategies for Switching Digital Audio Filters, Proc. 95th AES Convention, Preprint No. 3714, New York, October 1993.
[Zöl94] U. Zölzer: Roundoff Error Analysis of Digital Filters, J. Audio Eng. Soc., Vol. 42, pp. 232–244, April 1994.
[Zöl95] U. Zölzer, T. Boltze: Parametric Digital Filter Structures, Proc. 99th AES Convention, Preprint No. 4099, New York, October 1995.