Chapter 19
More of a Good Thing: Multiple Regression
In This Chapter
Understanding what multiple regression is
Preparing your data for a multiple regression and interpreting the output
Understanding how synergy and collinearity affect regression analysis
Estimating the number of subjects you need for a multiple regression analysis
Chapter 17 introduces the general concepts of correlation and regression, two related techniques for detecting and characterizing the relationship between two or more variables. Chapter 18 describes the simplest kind of regression — fitting a straight line to a set of data consisting of one independent variable (the predictor) and one dependent variable (the outcome). The model (the formula relating the predictor to the outcome) is of the form Y = a + bX, where Y is the outcome, X is the predictor, and a and b are parameters (also called regression coefficients). This kind of regression is usually the only one you encounter in an introductory statistics course, but it’s just the tip of the regression iceberg.
This chapter extends simple straight-line regression to more than one predictor — to what’s called the ordinary multiple linear regression model (or multiple regression, to say it simply).
Understanding the Basics of Multiple Regression
In Chapter 18, I outline the derivation of the formulas for determining the parameters (slope and intercept) of a straight line so that the line comes as close as possible to all the data points. The term as close as possible, in the least-squares sense, means that the sum of the squares of vertical distances of each point from the fitted line is smaller for the least-squares line than for any other line you could possibly draw.
The same idea can be extended to multiple regression models containing more than one predictor (and more than two parameters). For two predictor variables, you’re fitting a plane (a flat sheet) to a set of points in three dimensions; for more than two predictors, you’re fitting a “hyperplane” to points in four-or-more-dimensional space. Hyperplanes in multidimensional space may sound mind-blowing, but the formulas are just simple algebraic extensions of the straight-line formulas.
The most compact way to describe these formulas is by using matrix notation, but because you'll never have to do the calculations yourself (thanks to the software packages that I describe in Chapter 4), I'll spare you the pain of looking at a bunch of matrix formulas. If you really want to see the formulas, you can find them in almost any statistics text or in the Wikipedia article on regression analysis: http://en.wikipedia.org/wiki/Regression_analysis.
In the following sections, I define some basic terms related to multiple regression and explain when you should use it.
Defining a few important terms
Multiple regression is formally known as the ordinary multiple linear regression model. What a mouthful! The terms mean:
Ordinary: The outcome variable is a continuous numerical variable whose random fluctuations are normally distributed (see Chapter 25 for more about normal distributions).
Multiple: The model has more than two predictor variables.
Linear: Each predictor variable is multiplied by a parameter, and these products are added together to give the predicted value of the outcome variable. You can also have one more parameter thrown in that isn’t multiplied by anything — it’s called the constant term or the Intercept. The following are some linear functions:
• Y = a + bX (the simple straight-line model; X is the predictor variable, Y is the outcome, and a and b are parameters)
• Y = a + bX + cX2 + dX3 (the variables can be squared or cubed, but as long as they’re multiplied by a coefficient and added together, the function is still considered linear in the parameters)
• Y = a + bX + cZ + dXZ (the XZ term, often written as X*Z, is called an interaction)
In textbooks and published articles, you may see regression models written in various ways:
A collection of predictor variables may be designated by a subscripted variable and the corresponding coefficients by another subscripted variable, like this: Y = b0 + b1X1 + b2X2.
In practical research work, the variables are often given meaningful names, like Age, Gender, Height, Weight, SystolicBP, and so on.
Linear models may be represented in a shorthand notation that shows only the variables, and not the parameters, like this:
Y = X + Z + X * Z instead of Y = a + bX + cZ + dX * Z
or Y = 0 + X + Z + X * Z to specify that the model has no intercept.
And sometimes you’ll see a “~” instead of the “=”; read the “~” as “is a function of,” or “is predicted by.”
Knowing when to use multiple regression
Chapter 17 lists a number of reasons for doing regression analysis — testing for significant association, getting a compact representation of the data, making predictions and prognoses, performing mathematical operations on the data (finding the minimum, maximum, slope, or area of a curve), preparing calibration curves, testing theoretical models, and obtaining values of parameters that have physical or biological meaning. All these reasons apply to multiple regression.
Being aware of how the calculations work
Basically, fitting a linear multiple regression model involves creating a set of simultaneous equations, one for each parameter in the model. The equations involve the parameters from the model and the sums of various products of the dependent and independent variables, just as the simultaneous equations for the straight-line regression in Chapter 18 involve the slope and intercept of the straight line and the sums of X, Y, X2, and XY. You then solve these simultaneous equations to get the parameter values, just as you do for the straight line, except now you have more equations to solve. As part of this process you can also get the information you need to estimate the standard errors of the parameters, using a very clever application of the law of propagation of errors (which I describe in Chapter 11).
As the number of predictors increases, the computations get much more laborious, but the computer is doing all the work, so who cares? Personal computers can easily fit a model with 100 predictor variables to data from 10,000 subjects in less than a second!
Running Multiple Regression Software
With so many programs available that can do multiple regression, you’ll never have to run this procedure by hand, but you may need to do a little prep work on your data first. In the following sections, I explain how to handle categorical variables (if you have them) and make a few charts before you run a multiple regression.
Preparing categorical variables
The predictors in a multiple regression model can be either numerical or categorical. (For more info, flip to Chapter 7, which deals with different kinds of data.) The different categories that a variable can have are called levels. If a variable, like Gender, can have only two levels, like Male or Female, then it’s called a dichotomous or a binary categorical variable; if it can have more than two levels, I call it a multilevel variable.
Using categorical predictors in a multiple regression model is never a no-brainer. You have to set things up the right way or you’ll get results that are either wrong or difficult to interpret properly. Here are two important things to be aware of.
Having enough cases in each level of each categorical variable
Before using a categorical variable in a multiple regression model, you (or, better yet, your computer) should tabulate how many cases are in each level. You should have at least two cases (and preferably more) in each level. Usually, the more evenly distributed the cases are spread across all the levels, the more precise and reliable the results will be. If a level doesn’t contain enough cases, the program may ignore that level, halt with a warning message, produce incorrect results, or crash.
So if you tally a Race variable and get: White: 73, Black: 35, Asian: 1, and Other: 10, you may want to create another variable in which Asian is lumped together with Other (which would then have 11 subjects). Or you may want to create a binary variable with the levels: White: 73 and Non-White: 46 (or perhaps Black: 35 and Non-Black: 84, depending on the focus of your research).
Similarly, if your model has two categorical variables with an interaction term (like Gender + Race + Gender * Race), prepare a two-way cross-tabulation of Gender by Race first. You should have at least two subjects (and preferably many more) in each distinct combination of Gender and Race. (See Chapter 13 for details about cross-tabulations.)
Choosing the reference level wisely
For each categorical variable in a multiple regression model, the program considers one of the categories to be the reference level, and evaluates how each of the other levels affects the outcome, relative to that reference level. Some software lets you specify the reference level for a categorical variable; other software chooses it for you, sometimes in a way you may not like (like the level whose description comes first in the alphabet).
Choose your reference level wisely, or the results won’t be very meaningful or useful.
For a variable representing the presence or absence of some condition (like a risk factor), the reference level should represent the absence of the condition.
For a variable representing treatment groups, the reference level should be the placebo, or the standard treatment, or whatever treatment you want to compare the other treatments to.
For a variable representing a subject characteristic, like Gender or Race, the reference level is arbitrary. Sometimes the appropriate choice may be implicit in the objectives of the study (one group may be of special interest). If there’s no compelling reason to select one level over the others, you can choose the level with the most cases (which in the preceding Race example would be White, with 73 subjects).
Recoding categorical variables as numerical
If your statistics software lets you enter categorical variables as character data (like Gender coded as Male or Female), then you don’t have to read this section; you just have to make sure that, for each categorical variable, you have enough cases in each level, and that you’ve chosen the reference level wisely (and told the software what that level was). But if your regression program accepts only numerical variables as predictors, then you have to recode your categorical variables from descriptive text to numeric codes.
Binary categorical predictors can be recoded to numbers very simply; just recode the reference level to 0, and the other level to 1.
For categorical variables with more than two levels, it’s more complicated. You can’t just code the different categories as different numbers, like 0, 1, 2, 3, and so on, because then the computer will think that it’s a numerical (quantitative) variable, and give completely wrong answers. Instead, you have to split up the one multilevel variable into a set of binary dummy variables — one for each level in the original variable. For example, a variable called Race, with the levels White, Black, Asian, and Other, would be split up into four dummy variables, which could be called WhiteRace, BlackRace, AsianRace, and OtherRace. Each dummy variable would be coded as 1 if the subject is of that race or as 0 if the subject isn’t of that race, as shown in Table 19-1.
Then instead of including the variable Race in the model, you’d include the dummy variables for all levels of Race except the reference level. So if the reference level for Race was White, you’d include BlackRace, AsianRace, and OtherRace into the regression, but would not include WhiteRace.
Leave the reference-level dummy variable out of the regression.
Creating scatter plots before you jump into your multiple regression
One common mistake many researchers make is immediately running a regression (or some other statistical analysis) before taking a look at their data. As soon as you put your data into a computer file, you should run certain error-checks and generate summaries and histograms for each variable to assess the way the values of the variables are distributed, as I describe in Chapters 8 and 9. And if you plan to analyze your data by multiple regression, you also should do some other things first. Namely, you should chart the relationship between each predictor variable and the outcome variable, and also the relationships between the predictor variables themselves.
Table 19-2 shows a small data file that I use throughout the remainder of this chapter. It contains the age, weight, and systolic blood pressure of 16 subjects from a small clinical study. You might be interested in whether systolic blood pressure is associated with age or body weight (or both). Research questions involving the association between numerical variables are often handled by regression methods.
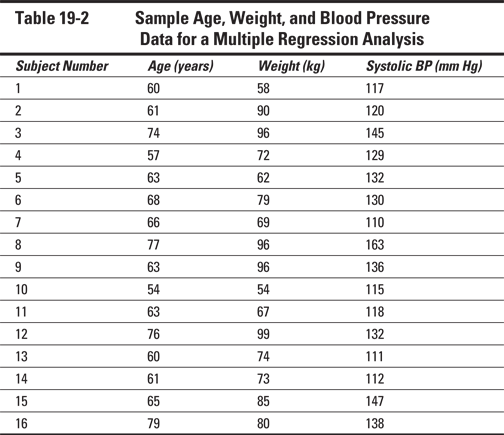
If you’re planning to run a regression model like this: SystolicBP ~ Age + Weight (in the shorthand notation described in the earlier section Defining a few important terms), you should first prepare several scatter charts: one of SystolicBP (outcome) versus Age (predictor), one of SystolicBP versus Weight (predictor), and one of Age versus Weight. For regression models involving many predictors, that can be a lot of scatter charts, but fortunately many statistics programs can automatically prepare a set of small “thumbnail” scatter charts for all possible pairings between a set of variables, arranged in a matrix like Figure 19-1.
These charts can give you an idea of what variables are associated with what others, how strongly they’re associated, and whether your data has outliers. The scatter charts in Figure 19-1 indicate that there are no extreme outliers in the data. Each scatter chart also shows some degree of positive correlation (as described in Chapter 17). In fact, referring to Figure 17-1, you may guess that the charts in Figure 19-1 correspond to correlation coefficients between 0.5 and 0.8. You can have your software calculate correlation coefficients (r values) between each pair of variables, and you’d get values of r = 0.654 for Age versus Weight, r = 0.661 for Age versus SystolicBP, and r = 0.646 for Weight versus SystolicBP.
Illustration by Wiley, Composition Services Graphics
Figure 19-1: A scatterchart matrix for a set of variables prior to multiple regression.
Taking a few steps with your software
The exact steps you take to run a multiple regression depend on your software, but here’s the general approach:
1. Assemble your data into a file with one row per subject and one column for each variable you want in the model.
2. Tell the software which variable is the outcome and which are the predictors.
3. If the software lets you, specify certain optional output — graphs, summaries of the residuals (observed minus predicted outcome values), and other useful results.
Some programs, like SPSS (see Chapter 4), may offer to create new variables in the data file for the predicted outcome or the residuals.
4. Press the Go button (or whatever it takes to start the calculations).
You should see your answers almost instantly.
Interpreting the Output of a Multiple Regression
The output from a multiple regression run is usually laid out much like the output from the simple straight-line regression run in Chapter 18.
Examining typical output from most programs
Figure 19-2 shows the output from a multiple regression run on the data in Table 19-2, using the R statistical software that I describe in Chapter 4. (Other software would produce generally similar output, but arranged and formatted differently.)
Illustration by Wiley, Composition Services Graphics
Figure 19-2: Output from a multiple regression on the data from Table 19-2.
The components of the output are
A description of the model to be fitted: In Figure 19-2, this description is SystolicBP ~ Age + Weight.
A summary of the residuals (observed minus predicted values of the outcome variable): For this example, the Max and Min Residuals indicate that one observed systolic BP value was 17.8 mmHg greater than predicted by the model, and one was 15.4 mmHg smaller than predicted.
The regression table, or coefficients table, with a row for each parameter in the model, and columns for the following:
• The estimated value of the parameter, which tells you how much the outcome variable changes when the corresponding variable increases by exactly 1.0 units, holding all the other variables constant. For example, the model predicts that every additional year of age increases systolic BP by 0.84 mmHg, holding weight constant (as in a group of people who all weigh the same).
• The standard error (precision) of that estimate. So the estimate of the Age coefficient (0.84 mmHg per year) is uncertain by about ± 0.52 mmHg per year.
• The t value (value of the parameter divided by its SE). For Age, the t value is 0.8446/0.5163, or 1.636.
• The p value, designated “Pr(>|t|)” in this output, indicating whether the parameter is significantly different from zero. If p < 0.05, then the predictor variable is significantly associated with the outcome after compensating for the effects of all the other predictors in the model. In this example, neither the Age coefficient nor the Weight coefficient is significantly different from zero.
Several numbers that describe the overall ability of the model to fit the data:
• The residual standard error, which, in this example, indicates that the observed-minus-predicted residuals have a standard deviation of 11.23 mmHg.
• The multiple R-squared is the square of an overall correlation coefficient for the multivariate fit.
• The F statistic and associated p value indicate whether the model predicts the outcome significantly better than a null model, which has only the intercept term and no predictor variables at all. The highly significant p value (0.0088) indicates that age and weight together predict SystolicBP better than the null model.
Checking out optional output available from some programs
Depending on your software, you may also be able to get several other useful results from the regression:
Predicted values for the dependent variable (one value for each subject), either as a listing or as a new variable placed into your data file.
Residuals (observed minus predicted value, for each subject), either as a listing or as a new variable placed into your data file.
The parameter error-correlations matrix, which is important if two parameters from the same regression run will be used to calculate some other quantity (this comes up frequently in pharmacokinetic analysis). The Propagation of Errors web page (http://StatPages.info/erpropgt.html) asks for an error-correlation coefficient when calculating how measurement errors propagate through an expression involving two variables.
Deciding whether your data is suitable for regression analysis
Before drawing conclusions from any statistical analysis, make sure that your data fulfilled assumptions on which that analysis was based. Two assumptions of ordinary linear regression include the following:
The amount of variability in the residuals is fairly constant and not dependent on the value of the dependent variable.
The residuals are approximately normally distributed.
Figure 19-3 shows two kinds of optional diagnostic graphs that help you determine whether these assumptions were met.
Figure 19-3a provides a visual indication of variability of the residuals. The important thing is whether the points seem to scatter evenly above and below the line, and whether the amount of scatter seems to be the same at the left, middle, and right parts of the graph. That seems to be the case in this figure.
Figure 19-3b provides a visual indication of the normality of the residuals. The important thing is whether the points appear to lie along the dotted line or are noticeably “curved.” In this figure, most of the points are reasonably consistent with a straight line, except perhaps in the lower-left part of the graph.
Illustration by Wiley, Composition Services Graphics
Figure 19-3: Diagnostic graphs from a regression.
Determining how well the model fits the data
Several numbers in the standard regression output relate to how closely the model fits your data:
The residual standard error is the average scatter of the observed points from the fitted model (about ± 11 mm Hg in the example from Figure 19-2); the smaller that number is, the better.
The larger the multiple R2 value is, the better the fit (it’s 0.44 in this example, indicating a moderately good fit).
A significant F statistic indicates that the model predicts the outcome significantly better than the null model (p = 0.009 in this example).
Figure 19-4 shows another way to judge how well the model predicts the outcome. It’s a graph of observed and predicted values of the outcome variable, with a superimposed identity line (Observed = Predicted). Your program may offer this “Observed versus Predicted” graph, or you can generate it from the observed and predicted values of the dependent variable. For a perfect prediction model, the points would lie exactly on the identity line. The correlation coefficient of these points is the multiple R value for the regression.
Illustration by Wiley, Composition Services Graphics
Figure 19-4: Observed versus predicted outcomes for the model SystolicBP ~ Age + Weight, for the data in Table 19-2.
Watching Out for Special Situations that Arise in Multiple Regression
Here I describe two topics that come up in multiple regression: interactions (both synergistic and anti-synergistic) and collinearity. Both relate to how the simultaneous behavior of two predictors can influence an outcome.
Synergy and anti-synergy
It sometimes happens that two predictor variables exert a synergistic effect on an outcome. That is, if both predictors were to increase by one unit, the outcome would change by more than simply the sum of the two increases you’d expect from changing each value individually by one unit. You can test for synergy between two predictors on an outcome by fitting a model that contains an interaction term (the product of those two variables):
SystolicBP = Age + Weight + Age * Weight
In some software, if you include the Age*Weight term, you don’t have to include the separate Age and Weight terms; the program will do that for you.
If the interaction coefficient has a significant p value (p < 0.05), then the two variables have significant synergy between them. The sign of the coefficient indicates whether the synergy is positive or negative (anti-synergy).
Collinearity and the mystery of the disappearing significance
After you get into multiple regression analysis, it won’t be long before you encounter the puzzling/disturbing/exasperating phenomenon of “disappearing significance.” It happens this way: First you run a bunch of simple straight-line regressions on each predictor separately versus the outcome, as a first look at your data. You may find that several predictors are each significantly associated with the outcome. Then you run a multiple regression, using all the predictors, only to find (to your shock and dismay) that one or more (maybe even all) of the formerly significant variables have lost their significance!
In the example from Table 19-2, there’s a significant association between Age and SystolicBP (p = 0.005), and between Weight and Systolic BP (p = 0.007). (You can run straight-line regressions, with the help of Chapter 18, on the data in that table if you don’t believe me.) But the multiple regression output in Figure 19-2 shows that neither Age nor Weight has regression coefficients that are significantly different from zero! What happened?
You’ve just been visited by the collinearity fairy. In the regression world, the term collinearity (also called multicollinearity) refers to a strong correlation between two or more of the predictor variables. And, sure enough, if you run a straight-line regression on Age versus Weight, you’ll find that they’re significantly correlated with each other (p = 0.006).
The good news is that collinearity doesn’t make the model any worse at predicting outcomes. The bad news is that collinearity between two variables can make it hard to tell which variable was really influencing the outcome and which one was getting a free ride (was associated with the outcome only because it was associated with another variable that was really influencing the outcome). This problem isn’t trivial — it can be difficult, if not impossible, to discern the true cause-and-effect relationships (if there are any) among a set of associated variables. The nearby sidebar Model building describes a technique that may be helpful.
There's a good discussion of multicollinearity (what it is, what its consequences are, how to detect it, and what to do about it) in the Wikipedia article at http://en.wikipedia.org/wiki/Multicollinearity.
Figuring How Many Subjects You Need
Every good experiment should have a large enough sample to ensure that you get a significant result in the test of your primary research hypothesis when the effect you’re testing in that hypothesis is large enough to be of clinical importance. So if the main hypothesis of your study is going to be tested by a multiple regression, you should do some kind of power calculation, specifically designed for multiple regressions, to determine the sample size you need.
Unfortunately, you probably won’t be able to do that. Programs are available for estimating sample-size requirements for multiple regression (both PS and GPower, described in Chapter 4, can handle some simple multivariate models), but they’re going to ask you for input that you almost certainly can’t provide.
If you plow through enough textbooks, you’ll find many rules of thumb for multiple regression, including the following:
You need 4 subjects for every predictor variable in your model.
You need 10 subjects for every predictor variable in your model.
You need 100 subjects, plus one more for every predictor variable.
100 is adequate; 200 is good; 400 or more is great.
These rules don’t even remotely agree with each other, and they have no real theoretical justification, so they’re probably no better than the obvious advice that “more subjects give more statistical power.”
For practical purposes, you can probably make do with a simple, sample-size estimate based on what you consider to be a clinically meaningful correlation coefficient between the most important predictor and the outcome. The simple formula from Chapter 26 — N = 8/r2, where N is the number of observations (subjects you need) and r is the clinically meaningful correlation coefficient — is probably as good as anything else.