Chapter 8

Summarizing and Graphing Your Data

In This Chapter

Representing categorical data

Characterizing numerical variables

Putting numerical summaries into tables

Displaying numerical variables with bars and graphs

A large study can involve thousands of subjects, hundreds of different variables, and millions of individual pieces of data. Even a small research project normally generates much more data than you can (or would want to) put into a publication or report. Instead, you need to boil the individual values for each variable down to a few numbers, called summary statistics, that give readers an idea of what the whole collection of numbers looks like — that is, how they’re distributed.

When presenting your results, you may want to arrange these summary statistics into tables that describe how the variables change over time or differ between treatments, or how two or more variables are related to each other. And, because a picture really is worth a thousand words, you probably want to display these distributions, changes, differences, and relationships graphically.

In this chapter, I show you how to summarize and graph two types of data: categorical and numerical. Note: This chapter doesn’t cover time-to-event (survival) data. That topic is so important, and the methods for summarizing and charting survival data are so specialized, that I describe them in a chapter all their own — Chapter 22.

Summarizing and Graphing Categorical Data

A categorical variable is summarized in a fairly straightforward way. You just tally the number of subjects in each category and express this number as a count — and perhaps also as a percentage of the total number of subjects in all categories combined. So, for example, a sample of 422 subjects can be summarized by race, as shown in Table 8-1.

Table 8-1 Study Subjects Categorized by Race

Race	Count	Percent of Total
White	128	30.3%
Black	141	33.4%
Asian	70	16.6%
Other	83	19.7%
Total	422	100%

The joint distribution of subjects between two categorical variables (such as Race by Gender), is summarized by a cross-tabulation (“cross-tab”), as shown in Table 8-2.

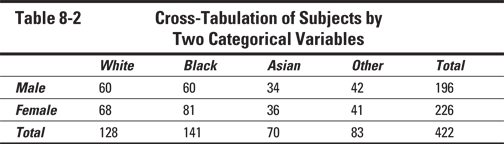
A cross-tab can get very cluttered if you try to include percentages. And there are three different kinds of percentage for each count in a cross-tab. For example, the 60 white males in Table 8-2 comprise 46.9 percent of all white subjects, 30.6 percent of all males, and 14.2 percent of all subjects.

Categorical data is usually displayed graphically as frequency bar charts and as pie charts:

Frequency bar charts: Displaying the spread of subjects across the different categories of a variable is most easily done by a bar chart (see Figure 8-1a). To create a bar chart manually from a tally of subjects in each category, you draw a graph containing one vertical bar for each category, making the height proportional to the number of subjects in that category. But almost all statistical programs will prepare bar charts for you; you simply select the options you want, such as which categorical variable you want to display and whether you want the vertical axis to show counts or percent of total.

Pie charts: Pie charts indicate the relative number of subjects in each category by the angle of a circular wedge (a piece of the pie). To create a pie chart manually, you multiply the percent of subjects in each category by 360 (the number of degrees of arc in a full circle), and then divide by 100. You draw a circle with a compass and then split it up into wedges using a protractor (remember those drawing tools from high school?). Much better to have the computer make a pie chart for you — it’s no more difficult than having a program make a bar chart.

But comparing the relative magnitude of the different sections of a pie chart is more difficult than comparing bar heights. Can you tell at a glance from Figure 8-1b whether there are more whites or blacks? Or more Asians than “others”? You can make those distinctions immediately from Figure 8-1a. Pie charts are often used to present data to the public (perhaps because the “piece of the pie” metaphor is so intuitive), but they’re frowned upon in technical publications.

Many programs let you generate so-called “3D” charts. However, these charts are often drawn with a slanting perspective that renders them almost impossible to interpret, so avoid 3D charts when presenting your data.

Illustration by Wiley, Composition Services Graphics

Figure 8-1: A simple bar chart (a) and pie chart (b).

Summarizing Numerical Data

Summarizing a numerical variable isn’t as simple as summarizing a categorical variable. The summary statistics for a numerical variable should convey, in a concise and meaningful way, how the individual values of that variable are distributed across your sample of subjects, and should give you some idea of the shape of the true distribution of that variable in the population from which you draw your sample. That true distribution can have almost any shape, including the typical shapes shown in Figure 8-2: normal, skewed, pointy-topped, and bimodal (two-peaked).

Illustration by Wiley, Composition Services Graphics

Figure 8-2: Four different shapes of distributions: normal (a), skewed (b), pointy-topped (c), and bimodal (two-peaked) (d).

How can you convey a general picture of what the true distribution may be using just a few summary numbers? Frequency distributions have some important characteristics, including:

Center: Where do the numbers tend to center?

Dispersion: How much do the numbers spread out?

Symmetry: Is the distribution shaped the same on the left and right sides, or does it have a wider tail on one side than the other?

Shape: Is the top of the distribution nicely rounded, or pointier or flatter?

You need to come up with numbers that measure each of these four characteristics; the following sections give you the scoop. (I explain how to graph numerical data later in this chapter.)

Locating the center of your data

Perhaps the most important single thing you want to know about a set of numbers is what value they tend to center around. This characteristic is called, intuitively enough, central tendency. Many statistical textbooks describe three measures of central tendency: mean, median, and mode. These measures don’t make a particularly good “top-three” list when it comes to describing experimental data because such a list omits several measures that are quite useful and important, and includes one that’s pretty lousy, as I explain in the following sections.

Arithmetic mean

The arithmetic mean, also commonly called the mean, or the average, is the most familiar and most often quoted measure of central tendency. Throughout this book, whenever I use the two-word term the mean, I’m referring to the arithmetic mean. (There are several other kinds of means, besides the arithmetic mean, and I describe them later in this chapter.)

The mean of a sample is often denoted by the symbol m or by placing a horizontal bar over the name of the variable, like . The mean is obtained by adding up the values and dividing by how many there are. Here’s a small sample of numbers — the IQ values of seven subjects, arranged in increasing numerical order: 84, 84, 89, 91, 110, 114, and 116. For the IQ sample:

Arithmetic Mean = ( 84 + 84 + 89 + 91 + 110 + 114 + 116 )/7 = 688/7 = 98.3 (approximately)

You can write the general formula for the arithmetic mean of N number of values contained in the variable X in several ways:

See Chapter 2 for a refresher on mathematical notation and formulas, including how to interpret the various forms of the summation symbol Σ (the Greek capital sigma). In the rest of this chapter, I use the simplest form (without the i subscripts that refer to specific elements of an array) whenever possible.

Median

Like the mean (see the preceding section), the median is a common measure of central tendency (and, in fact, is the only one that really takes the word central seriously).

The median of a sample is the middle value in the sorted (ordered) set of numbers. Half the numbers are smaller than the median, and half of them are larger. The median of a population frequency distribution function (like the curves shown in Figure 8-2) divides the total area under the curve into two equal parts: half of the area under the curve (AUC) lies to the left of the median, and half lies to the right.

The median of the IQ sample from the preceding section (84, 84, 89, 91, 110, 114, and 116) is the fourth of the seven sorted values, which is 91. Three IQs in the sample are smaller than 91, and three are larger than 91. If you have an even number of values, the median is the average of the two middle values.

The median is much less strongly influenced by extreme outliers than the mean. For example, if the largest value in the IQ example had been 150 instead of 116, the mean would have jumped from 98.3 to 103.1, but the median would have remained unchanged at 91. Here’s an even more extreme example: If a multibillionaire were to move into a certain state, the mean family net worth in that state might rise by hundreds of dollars, but the median family net worth would probably rise by only a few cents (if it were to rise at all).

Mode

The mode of a sample of numbers is the most frequently occurring value in the sample. The mode is, quite frankly, of very little use for summarizing observed values for continuous numerical variables, for several reasons:

If the data were truly continuous (and recorded to many decimal places), there would probably be no exact duplicates, and there would be no mode for the sample.

Even when dealing with data that’s rounded off to fairly coarse intervals, the mode may not be anywhere near the “center” of the data. In the IQ example, the only value that occurs more than once happens to be the lowest value (84), which is a terrible indicator of central tendency.

There could be several different values in your data that occur multiple times, and therefore several modes.

So the mode is not a good summary statistic for sampled data. But it’s very useful for characterizing a population distribution. It’s the place where the peak of the distribution function occurs. Some distribution functions can have two peaks (a bimodal distribution), as shown in Figure 8-3d, which often indicates two distinct subpopulations, such as the distribution of a sex hormone in a mixed population of males and females. Some variables can have a distribution with three or even more peaks in certain populations.

Considering some other “means” to measure central tendency

Several other kinds of means are useful measures of central tendency in certain circumstances. They’re called means because they all involve the same “add them up and divide by how many” process as the arithmetic mean (which I describe earlier in this chapter), but each one adds a slightly different twist to the basic process.

Inner mean

The inner mean (also called the trimmed mean) of N numbers is calculated by removing the lowest value and the highest value and calculating the arithmetic mean of the remaining N – 2 “inner” values. For the IQ example that I use earlier in this chapter (84, 84, 89, 91, 110, 114, and 116), the inner mean equals (84 + 89 + 91 + 110 + 114)/5 = 488/5 = 97.6.

An even “inner-er” mean can be calculated by dropping the two (or more) highest and two (or more) lowest values from the data and then calculating the arithmetic mean of the remaining values. In the interest of fairness, you should always chop the same number of values from the low end as from the high end.

Like the median (which I discuss earlier in this chapter), the inner mean is more resistant to outliers than the arithmetic mean. And, if you think about it, if you chop off enough numbers from both ends of the sorted set of values, you’ll eventually be left with only the middle one or two values — this ­“inner-est” mean would actually be the median!

Geometric mean

The geometric mean (often abbreviated GM) can be defined by two different-looking formulas that produce exactly the same value. The basic definition has this formula:

I describe the product symbol Π (the Greek capital pi) in Chapter 2. This formula is telling you to multiply the values of the N observations together, and then take the Nth root of the product. The IQ example (84, 84, 89, 91, 110, 114, and 116) looks like this:

This formula can be difficult to evaluate; even computers can run into trouble with the very large product that calculating the GM of a lot of numbers can generate. By using logarithms (which turn multiplications into additions and roots into divisions), you get a “numerically stable” alternative formula:

This formula may look complicated, but it really just says, “The geometric mean is the antilog of the mean of the logs of the numbers.” You take the log of each number, average all those logs the usual way, and then take the antilog of the average. You can use natural or common logarithms; just be sure to use the same type of antilog. (Flip to Chapter 2 for the basics of logarithms.)

Root-mean-square

The root-mean-square (RMS) of a bunch of numbers is defined this way:

You square each number, average all those squares the usual way, and then take the square root of the average. For example, the RMS of the two numbers 10 and 20 is . The RMS is useful for summarizing the size of random fluctuations, as you see in the later section Standard deviation, variance, and coefficient of variation.

Describing the spread of your data

After central tendency (see the previous sections), the second most important thing you can say about a set of numbers is how tightly or loosely they tend to cluster around a central value; that is, how narrowly or widely they’re dispersed. There are several common measures of dispersion, as you find out in the following sections.

Standard deviation, variance, and coefficient of variation

The standard deviation (usually abbreviated SD, sd, or just s) of a bunch of numbers tells you how much the individual numbers tend to differ (in either direction) from the mean (which I discuss earlier in this chapter). It’s calculated as follows:

This formula is saying that you calculate the standard deviation of a set of N numbers (Xi) by subtracting the mean from each value to get the deviation (di) of each value from the mean, squaring each of these deviations, adding up the terms, dividing by N – 1, and then taking the square root.

This is almost the formula for the root-mean-square deviation of the points from the mean, except that it has N – 1 in the denominator instead of N. This difference occurs because the sample mean is used as an approximation of the true population mean (which you don’t know). If the true mean were available to use, the denominator would be N.

When talking about population distributions, the SD describes the width of the distribution curve. Figure 8-3 shows three normal distributions. They all have a mean of zero, but they have different standard deviations and, therefore, different widths. Each distribution curve has a total area of exactly 1.0, so the peak height is smaller when the SD is larger.

Illustration by Wiley, Composition Services Graphics

Figure 8-3: Three distributions with the same mean but different standard deviations.

For the IQ example that I use earlier in this chapter (84, 84, 89, 91, 110, 114, and 116) where the mean is 98.3, you calculate the SD as follows:

Standard deviations are very sensitive to extreme values (outliers) in the data. For example, if the highest value in the IQ dataset had been 150 instead of 116, the SD would have gone up from 14.4 to 23.9.

Several other useful measures of dispersion are related to the SD:

Variance: The variance is just the square of the SD. For the IQ example, the variance = 14.42 = 207.36.

Coefficient of variation: The coefficient of variation (CV) is the SD divided by the mean. For the IQ example, CV = 14.4/98.3 = 0.1465, or 14.65 percent.

Range

The range of a set of values is the difference between the smallest value (the minimum value) and the largest value (the maximum value):

Range = maximum value – minimum value

So for the IQ example in the preceding section (84, 84, 89, 91, 110, 114, and 116), the minimum value is 84, the maximum value is 116, and the range is 32 (equal to 116 – 84).

The range is extremely sensitive to outliers. If the largest IQ were 150 instead of 116, the range would increase from 32 to 66 (equal to 150 – 84).

Outside of its formal definition in statistics, the term range can also refer to two numbers marking the limits of some interval of interest. For example, suppose that a clinical trial protocol (see Chapter 5) specifies that you’re to enroll only subjects having glucose values within the range 150 to 250 milligrams per deciliter. You may ask whether a subject with a value of exactly 250 falls “within” that range. This possible ambiguity is usually avoided by using the term inclusive or exclusive to specify whether a person who is exactly at the limit of a range is considered within it or not. Some ranges can be inclusive at one end and exclusive at the other end.

Centiles

The basic idea of the median (that half of your numbers are less than the median) can be extended to other fractions besides ¹⁄₂.

A centile is a value that a certain percentage of the values are less than. For example, ¹⁄₄ of the values are less than the 25th centile (and ³⁄₄ of the values are greater). The median is just the 50th centile. Some centiles have common nicknames:

The 25th, 50th, and 75th centiles are called the first, second, and third quartiles, respectively.

The 20th, 40th, 60th, and 80th centiles are called quintiles.

The 10th, 20th, 30th, and so on, up to the 90th centile, are called deciles.

Other Latin-based nicknames include tertiles, sextiles, and so forth.

As I explain in the earlier section Median, if the sorted sequence has no middle value, you have to calculate the median as the average of the two middle numbers. The same situation comes up in calculating centiles, but it’s not as simple as just averaging the two closest numbers; there are at least eight different formulas for estimating centiles. Your statistical software may pick one of the formulas (and may not tell you which one it picked), or it may let you choose the formula you prefer. Fortunately, the different formulas usually give nearly the same result.

The inter-quartile range (or IQR) is the difference between the 25th and 75th centiles (the first and third quartiles). When summarizing data from strangely shaped distributions, the median and IQR are often used instead of the mean and SD.

Showing the symmetry and shape of the distribution

In the following sections, I discuss two summary statistical measures that are used to describe certain aspects of the symmetry and shape of the distribution of numbers.

Skewness

Skewness refers to whether the distribution has left-right symmetry (as shown in Figures Figure 8-2a and Figure 8-2c) or whether it has a longer tail on one side or the other (as shown in Figures Figure 8-2b and Figure 8-2d). Many different skewness coefficients have been proposed over the years; the most common one, often represented by the Greek letter γ (lowercase gamma), is calculated by averaging the cubes (third powers) of the deviations of each point from the mean and scaling by the standard deviation. Its value can be positive, negative, or zero.

A negative skewness coefficient (γ) indicates left-skewed data (long left tail); a zero γ indicates unskewed data; and a positive γ indicates right-skewed data (long right tail), as shown in Figure 8-4.

Illustration by Wiley, Composition Services Graphics

Figure 8-4: Distributions can be left-skewed (a), symmetric (b), or right-skewed (c).

Of course, the skewness coefficient for any set of real data almost never comes out to exactly zero because of random sampling fluctuations. So how large does γ have to be before you suspect real skewness in your data? A very rough rule of thumb for large samples is that if γ is greater than , your data is probably skewed.

Kurtosis

The three distributions shown in Figure 8-5 happen to have the same mean and the same standard deviation, and all three have perfect left-right symmetry (that is, they are unskewed). But their shapes are still very different. Kurtosis is a way of quantifying these differences in shape.

If you think of a typical distribution function curve as having a “head” (near the center), “shoulders” (on either side of the head), and “tails” (out at the ends), the term kurtosis refers to whether the distribution curve tends to have

A pointy head, fat tails, and no shoulders (leptokurtic, κ < 3, as shown in Figure 8-5a)

Normal appearance (κ = 3; see Figure 8-5b)

Broad shoulders, small tails, and not much of a head (platykurtic, κ > 3, as shown in Figure 8-5c)

The Pearson kurtosis index, often represented by the Greek letter κ (lowercase kappa), is calculated by averaging the fourth powers of the deviations of each point from the mean and scaling by the standard deviation. Its value can range from 1 to infinity and is equal to 3.0 for a normal distribution. The excess kurtosis is the amount by which κ exceeds (or falls short of) 3. A very rough rule of thumb for large samples is that if κ differs from 3 by more than , your data probably has abnormal kurtosis.

Illustration by Wiley, Composition Services Graphics

Figure 8-5: Three distributions: leptokurtic (a), normal (b), and platykurtic (c).

Structuring Numerical Summaries into Descriptive Tables

Now you know how to calculate the basic summary statistics that convey a general idea of how a set of numbers is distributed. So what do you do with those summary numbers? Generally, when presenting your results, you pick a few of the most useful summary statistics and arrange them in a concise way. Many biostatistical reports select N, mean, SD, median, minimum, and maximum, and arrange them something like this:

mean ± SD (N)

median (minimum – maximum)

For the IQ example that I use earlier in this chapter (84, 84, 89, 91, 110, 114, and 116), the preceding arrangement looks like this:

98.3 ± 14.4 (7)

91 (84 – 116)

The real utility of this kind of compact summary is that you can place it in each cell of a table to show changes over time and between groups. For example, systolic blood pressure measurements, before and after treatment with a hypertension drug or a placebo, can be summarized very concisely, as shown in Table 8-3.

Table 8-3 Systolic Blood Pressure Treatment Results

	Drug	Placebo
Before Treatment	138.7 ± 10.3 (40)139.5 (117 – 161)	141.0 ± 10.8 (40)143.5 (111 – 160)
After Treatment	121.1 ± 13.9 (40)121.5 (85 – 154)	141.0 ± 15.4 (40)142.5 (100 – 166)
Change	–17.6 ± 8.0 (40)–17.5 (–34 – 4)	–0.1 ± 9.9 (40)1.5 (–25 – 18)

This table shows that the drug tended to lower blood pressure by about 18 millimeters of mercury (mmHg), from 139 to 121, whereas the placebo produced no noticeable change in blood pressure (it stayed around 141 mmHg). All that’s missing are some p values to indicate the significance of the changes over time within each group and of the differences between the groups. I show you how to calculate those in Chapter 12.

Graphing Numerical Data

Displaying information graphically is a central part of interpreting and communicating the results of scientific research. You can easily spot subtle features in a graph of your data that you’d never notice in a table of numbers. Entire books have been written about graphing numerical data, so I can only give a brief summary of some of the more important points here.

Showing the distribution with histograms

Histograms are bar charts that show what fraction of the subjects have values falling within specified intervals. The main purpose of a histogram is to show you how the values of a numerical value are distributed. This distribution is an approximation of the true population frequency distribution for that variable, as shown in Figure 8-6.

The smooth curve in Figure 8-6a shows how IQ values are distributed in an infinitely large population. The height of the curve at any IQ value is proportional to the fraction of the population in the immediate vicinity of that IQ. This curve has the typical “bell” shape of a normal distribution. In the following sections, I explain how histograms are useful when dealing with several types of non-normal distributions.

Illustration by Wiley, Composition Services Graphics

Figure 8-6: Population distribution of IQ scores (a) and distribution of a sample from that population (b).

The histogram in Figure 8-6b indicates how the IQs of 60 subjects randomly sampled from the population might be distributed. Each bar represents an interval of IQ values with a width of ten IQ points, and the height of each bar is proportional to the number of subjects in the sample whose IQ fell within that interval.

Log-normal distributions

Because a sample is only an imperfect representation the population, determining the precise shape of a distribution can be difficult unless your sample size is very large. Nevertheless, a histogram usually helps you spot skewed data, as shown in Figure 8-7a. This kind of shape is typical of a log-normal distribution, which occurs very often in biological work (see Chapter 25). It’s called log-normal because if you take the logarithm of each data value (it doesn’t matter what kind of logarithm you take), the resulting logs will have a normal distribution, as shown in Figure 8-7b.

So it’s good practice to prepare a histogram for every numerical variable you plan to analyze, to see whether it’s noticeably skewed and, if so, whether a logarithmic “transformation” makes the distribution more nearly normal.

Other abnormal distributions

Log-normality isn’t the only kind of non-normality that can arise in real-world data. Depending on the underlying process that gives rise to the data, the numbers can be distributed in other ways. For example, event counts often behave according to the Poisson distribution (see Chapter 25) and can be, at least approximately, normalized by taking the square root of each count (instead of the logarithm, as you do for log-normal data). Still other processes can give rise to left-skewed data or to data with two (or more) peaks.

Illustration by Wiley, Composition Services Graphics

Figure 8-7: Log-normal data is skewed (a), but the logarithms are normally distributed (b).

What if neither the log-normal nor the square-root transformation normalizes your skewed data? One approach is to use the Box-Cox transformation, which has this general formula: Transformed X = (XA – 1)/A, where A is an adjustable parameter that you can vary from negative to positive values. Depending on the value of A, this transformation can often make left-skewed or right-skewed data more symmetrical (and more normally distributed). Figure 8-8 shows how the Box-Cox transformation can help normalize skewed data. Some software lets you vary A through a range of positive or negative values using a slider on the screen that you can move with your mouse. As you slide the A value back and forth, you see the histogram change its shape from left-skewed to symmetrical to right-skewed. In Figure 8-8, using A = 0.12 normalizes the data quite well.

When A is exactly 0, the Box-Cox formula becomes 0/0, which is indeterminate. But it can be shown that as A approaches 0 (either from the positive or negative side), the Box-Cox formula becomes the same as the logarithm function. So the logarithmic transformation is just a special case of the more general Box-Cox transformation.

Illustration by Wiley, Composition Services Graphics

Figure 8-8: Box-Cox transformations of a skewed ­distribution.

If you can’t find any transformation that makes your data look even approximately normal, then you have to analyze your data using nonparametric methods, which don’t assume that your data is normally distributed. I describe these methods in Chapter 12.

Summarizing grouped data with bars, boxes, and whiskers

Sometimes you want to show how a variable varies from one group of subjects to another. For example, blood levels of some enzymes vary among the different races. Two types of graphs are commonly used for this purpose: bar charts and box-and-whiskers plots.

Bar charts

One simple way to display and compare the means of several groups of data is with a bar chart, like the one shown in Figure 8-9a, where the bar height for each race equals the mean (or median, or geometric mean) value of the enzyme level for that race. And the bar chart becomes even more informative if you indicate the spread of values for each race by placing lines representing one standard deviation above and below the tops of the bars, as shown in Figure 8-9b. These lines are always referred to as error bars (an unfortunate choice of words that can cause confusion when error bars are added to a bar chart).

But even with error bars, a bar chart still doesn’t give a very good picture of the distribution of enzyme levels within each group. Are the values skewed? Are there outliers? The mean and SD may not be very informative if the values are distributed log-normally or in another unusual way. Ideally, you want to show a histogram for each group of subjects (I discuss histograms earlier in this chapter), but that may take up way too much space. What should you do? Keep reading to find out.

Illustration by Wiley, Composition Services Graphics

Figure 8-9: Bar charts showing mean values (a) and standard deviations (b).

Box-and-whiskers charts

Fortunately, another kind of graph called a box-and-whiskers plot (or B&W, or just Box plot) shows — in very little space — a lot of information about the distribution of numbers in one or more groups of subjects. A simple B&W plot of the same enzyme data illustrated with a bar chart in Figure 8-9 is shown in Figure 8-10a.

The B&W figure for each group usually has the following parts:

A box spanning the interquartile range (IQR), extending from the first quartile (25th centile) to the third quartile (75th centile) of the data (see the earlier section Centiles for more about this range), and therefore encompassing the middle 50 percent of the data

A thick horizontal line, drawn at the median (50th centile), which usually puts it at or near the middle of the box

Dashed lines (whiskers) extending out to the farthest data point that’s not more than 1.5 times the IQR away from the box

Individual points lying outside the whiskers, considered outliers

B&W plots provide a useful summary of the distribution. A median that’s not located near the middle of the box indicates a skewed distribution.

Some software draws the different parts of a B&W plot according to different rules (the horizontal line may be at the mean instead of the median; the box may represent the mean ± 1 standard deviation; the whiskers may extend out to the farthest outliers; and so on). Always check the software’s documentation and provide the description of the parts whenever you present a B&W plot.

Some software provides various enhancements to the basic B&W plot. Figure 8-10b illustrates two such embellishments you may consider using:

Variable width: The widths of the bars can be scaled to indicate the relative size of each group. You can see that there are considerably fewer Asians and “others” than whites or blacks.

Notches: The box can have notches that indicate the uncertainty in the estimation of the median. If two groups have non-overlapping notches, they probably have significantly different medians. Whites and “others” have similar median enzyme levels, whereas Asians have significantly higher levels and blacks have significantly lower levels.

Illustration by Wiley, Composition Services Graphics

Figure 8-10: Box-and-whiskers charts: no-frills (a) and with variable width and notches (b).

Depicting the relationships between numerical variables with other graphs

One of the most important uses for graphs in scientific publications is to show the relationship between two or more numerical variables, such as the associations described in these example questions:

Is there an association between Hemoglobin A1c (an indicator of diabetes) and Body Mass Index (an indicator of obesity)?

Is the reduction in blood pressure associated with the administered dose of an antihypertensive drug (in other words, is there a dose-response effect)?

These questions are usually answered with the help of regression analysis, which I describe in Part IV and Chapter 24. In these chapters, I cover the appropriate graphical techniques for showing relationships between variables.