Chapter 14

The Man Who Counted Everything Except Calories

We have just witnessed Frank Knight’s determination to elevate uncertainty to a central role in the analysis of risk and decision-making and the energy and eloquence with which Keynes mounted his attack on the assumptions of the classical economists. Yet faith in the reality of rational behavior and in the power of measurement in risk management persisted throughout all the turmoil of the Depression and the Second World War. Theories on these matters now began to move along sharply divergent paths, one traveled by the followers of Keynes (“We simply do not know”) and the other by the followers of Jevons (“Pleasure, pain, labour, utility, value, wealth, money, capital, etc. are all notions admitting of quantity.”)

During the quarter-century that followed the publication of Keynes’s General Theory, an important advance in the understanding of risk and uncertainty appeared in the guise of the theory of games of strategy. This was a practical paradigm rooted in the Victorian conviction that measurement is indispensable in interpreting human behavior. The theory focuses on decision-making, but bears little resemblance to the many other theories that originated in games of chance.

Despite its nineteenth-century forebears, game theory represents a dramatic break from earlier efforts to incorporate mathematical inevitability into decision-making. In the utility theories of both Daniel Bernoulli and Jevons, the individual makes choices in isolation, unaware of what others might be doing. In game theory, however, two or more people try to maximize their utility simultaneously, each aware of what the others are about.

Game theory brings a new meaning to uncertainty. Earlier theories accepted uncertainty as a fact of life and did little to identify its source. Game theory says that the true source of uncertainty lies in the intentions of others.

From the perspective of game theory, almost every decision we make is the result of a series of negotiations in which we try to reduce uncertainty by trading off what other people want in return for what we want ourselves. Like poker and chess, real life is a game of strategy, combined with contracts and handshakes to protect us from cheaters.

But unlike poker and chess, we can seldom expect to be a “winner” in these games. Choosing the alternative that we judge will bring us the highest payoff tends to be the riskiest decision, because it may provoke the strongest defense from players who stand to lose if we have our way. So we usually settle for compromise alternatives, which may require us to make the best of a bad bargain; game theory uses terms like “maximin” and “minimax” to describe such decisions. Think of seller-buyer, landlord-tenant, husband-wife, lender-borrower, GM-Ford, parent-child, President-Congress, driver-pedestrian, boss-employee, pitcher-batter, soloist-accompanist.

Game theory was invented by John von Neumann (1903–1957), a physicist of immense intellectual accomplishment.1 Von Neumann was instrumental in the discovery of quantum mechanics in Berlin during the 1920s, and he played a major role in the creation of the first American atomic bomb and, later, the hydrogen bomb. He also invented the digital computer, was an accomplished meteorologist and mathematician, could multiply eight digits by eight digits in his head, and loved telling ribald jokes and reciting off-color limericks. In his work with the military, he preferred admirals to generals because admirals were the heavier drinkers. His biographer Norman Macrae describes him as “excessively polite to everybody except . . . two long-suffering wives,” one of whom once remarked, “He can count everything except calories.”2

A colleague interested in probability analysis once asked von Neumann to define certainty. Von Neumann said first design a house and make sure the living-room floor will not give way. To do that, he suggested, “Calculate the weight of a grand piano with six men huddling over it to sing. Then triple that weight.” That will guarantee certainty.

Von Neumann was born in Budapest to a well-to-do, cultured, jolly family. Budapest “at the time was the sixth-largest city in Europe, prosperous and growing, with the world’s first underground subway. Its literacy rate was over 90%. More than 25% of the population was Jewish, including the von Neumanns, although John von Neumann paid little attention to his Jewishness except as a source of jokes.

He was by no means the only famous product of pre-World War I Budapest. Among his contemporaries were famous physicists like himself—Leo Szilard and Edward Teller—as well as celebrities from the world of entertainment—George Solti, Paul Lukas, Leslie Howard (born Lazlo Steiner), Adolph Zukor, Alexander Korda, and, perhaps most famous of all, ZsaZsa Gabor.

Von Neumann studied in Berlin at a leading scientific institution that had considered Einstein unqualified for a research grant.3 He went on to Göttingen, where he met such distinguished scientists as Werner Heisenberg, Enrico Fermi, and Robert Oppenheimer. During his first visit to the United States, in 1929, von Neumann fell in love with the country and spent most of his subsequent career, except for extended periods working for the U.S. government, at the Institute for Advanced Study in Princeton. His starting salary at the Institute in 1937 was $10,000, the equivalent of over $100,000 in current purchasing power. When Einstein joined the Institute in 1933, he had asked for a salary of $3,000; he received $16,000.

Von Neumann first presented his theory of games of strategy in a paper that he delivered in 1926, at the age of 23, to the Mathematical Society at the University of Göttingen; the paper appeared in print two years later. Robert Leonard of the University of Quebec, a leading historian of game theory, has surmised that this paper was not so much the product of a “detached moment of inspiration” as an effort by von Neumann to focus his restless fancy on a subject that had been attracting the attention of German and Hungarian mathematicians for some time. Apparently the stimulus for the work was primarily mathematical, with little or nothing to do with decision-making as such.

Although the subject matter of the paper appears to be trivial at first glance, it is highly complex and mathematical. The subject is a rational strategy for playing a childhood game called match-penny. Each of two players turns up a coin at the same moment as the other. If both coins are heads or if both are tails, player A wins. If different sides come up, player B wins. When I was a boy, we played a variation of this game in which my opponent and I took turns shouting either “Odds!” or “Evens!” as, at an agreed call, we opened our fists to show either one finger or two.

According to von Neumann, the trick in playing match-penny against “an at least moderately intelligent opponent” lies not in trying to guess the intentions of the opponent so much as in not revealing your own intentions. Certain defeat results from any strategy whose aim is to win rather than to avoid losing. (Note that dealing with the possibility of losing appears here for the first time as an integral part of risk management.) So you should, play heads and tails in random fashion, simulating a machine that would systematically reveal each side of the coin with a probability of 50%. You cannot expect to win by employing this strategy, but neither can you expect to lose.

If you try to win by showing heads six times out of every ten plays, your opponent will catch on to your game plan and will win an easy victory. She will play tails six times out of every ten plays if she wins when the pennies fail to match; she will play heads six times out of every ten plays if she wins when the pennies do match.

So the only rational decision for both players is to show heads and tails in random fashion. Then, over the long run, the pennies will match half the time and will fail to match half the time. Fun for a little while, but then boring.

The mathematical contribution von Neumann made with this demonstration was the proof that this was the only outcome that could emerge from rational decision-making by the two players. It is not the laws of probability that decree the 50–50 payoff in this game. Rather, it is the players themselves who cause that result. Von Neumann’s paper is explicit about this point:

. . . [E]ven if the rules of the game do not contain any elements of “hazard” (i.e., no draws from urns) . . . dependence on . . . the statistical element is such an intrinsic part of the game itself (if not of the world) that there is no need to introduce it artificially.4

The attention von Neumann’s paper attracted suggests that he had something of mathematical importance to convey. It was only later that he realized that more than mathematics was involved in the theory of games.

In 1938, while he was at the Institute for Advanced Study socializing with Einstein and his friends, von Neumann met the German-born economist Oskar Morgenstern. Morgenstern became an instant acolyte. He took to game theory immediately and told von Neumann he wanted to write an article about it. Though Morgenstern’s capability in mathematics was evidently not up to the task, he persuaded von Neumann to collaborate with him on a paper, a collaboration that extended into the war years. The results of their joint efforts was Theory of Games and Economic Behavior, the classic work in both game theory and its application to decision-making in economics and business. They completed the 650 pages of their book in 1944, but the wartime paper shortage made Princeton University Press hesitant to publish it. At last a member of the Rockefeller family personally subsidized the publication of the book in 1953.

The economic subject matter was not entirely new to von Neumann. He had had some interest in economics earlier, when he was trying to see how far he could go in using mathematics to develop a model of economic growth. Always the physicist as well as the mathematician, his primary focus was on the notion of equilibrium. “As [economics] deals throughout with quantities,” he wrote, “it must be a mathematical science in matter if not in language . . . a close analogy to the science of statical mechanics.”

Morgenstern was born in Germany in 1902 but grew up and was educated in Vienna. By 1931, he had attained sufficient distinction as an economist to succeed Friedrich von Hayek as director of the prestigious Viennese Institute for Business Cycle Research. Though he was a Christian with a touch of anti-Semitism, he left for the United States in 1938, following the German invasion of Austria, and soon found a position on the economics faculty at Princeton.5

Morgenstern did not believe that economics could be used for predicting business activity. Consumers, business managers, and policymakers, he argued, all take such predictions into consideration and alter their decisions and actions accordingly. This response causes the forecasters to change their forecast, prompting the public to react once again. Morgenstern compared this constant feedback to the game played by Sherlock Holmes and Dr. Moriarty in their attempts to outguess each other.-Hence, statistical methods in economics are useless except for descriptive purposes, “but the diehards don’t seem to be aware of this.”6

Morgenstern was impatient with the assumption of perfect foresight that dominated nineteenth-century economic theory. No one, he insisted, can know what everybody else is going to do at any given moment: “Unlimited foresight and economic equilibrium are thus irreconcilable with each other.”7 This conclusion drew high praise from Frank Knight and an offer by Knight to translate this paper by Morgenstern from German into English.

Morgenstern appears to have been short on charm. Nobel Laureate Paul Samuelson, the author of the long-run best-selling textbook in economics, once described him as “Napoleonic. . . . [A]lways invoking the authority of some physical scientists or other.”a8 Another contemporary recalls that the Princeton economics department “just hated Oskar.”9 Morgenstern himself complained about the lack of attention his beloved masterpiece received from others. After visiting Harvard in 1945 he noted “none of them” had any interest in game theory.10 He reported in 1947 that a fellow economist named Röpke said that game theory “was Viennese coffeehouse gossip.”b When he visited a group of distinguished economists in Rotterdam in 1950, he discovered that they “wanted to know nothing about [game theory] because it disturbs them.”

Although an enthusiast for the uses of mathematics in economic analysis—he despised Keynes’s nonrigorous treatment of expectations and described The General Theory as “simply horrible”—Morgenstern complained constantly about his problems with the advanced material into which von Neumann had lured him.11 Throughout their collaboration Morgenstern held von Neumann in awe. “He is a mysterious man,” Morgenstern wrote on one occasion. “The moment he touches something scientific, he is totally enthusiastic, clear, alive, then he sinks, dreams, talks superficially in a strange mixture. . . . One is presented with the incomprehensible.”

The combination of the cool mathematics of game theory and the tensions of economics seemed a natural fit for a mathematician with an enthusiasm for economics and an economist with an enthusiasm for mathematics. But the stimulus to combine the two arose in part from a shared sense that, to use Morgenstern’s words, the application of mathematics to economics was “in a lamentable condition.”12

An imperial motivation was also there—the aspiration to make mathematics the triumphant master in the analysis of society as well as in the analysis of the natural sciences. While that approach would be welcomed by many social scientists today, it was probably the main source of the resistance that game theory encountered when it was first broadly introduced in the late 1940s. Keynes ruled the academic roost at the time, and he rejected any sort of mathematical description of human behavior.

The Theory of Games and Economic Behavior loses no time in advocating the use of the mathematics in economic decision-making. Von Neumann and Morgenstern dismiss as “utterly mistaken” the view that the human and psychological elements of economics stand in the way of mathematical analysis. Recalling the lack of mathematical treatment in physics before the sixteenth century or in chemistry and biology before the eighteenth century, they claim that the outlook for mathematical applications in those fields “at these early periods can hardly have been better than that in economics—mutatis mutandis—at present.”13

Von Neumann and Morgenstern reject the objection that their rigidly mathematical procedures and their emphasis on numerical quantities are unrealistic simply because “the common individual. . . conducts his economic activities in a sphere of considerable haziness.”14 After all, people respond hazily to light and heat, too:

[I]n order to build a science of physics, these phenomena [heat and light] had to be measured. And subsequently, the individual has come to use the results of such measurements—directly or indirectly—even in his everyday life. The same may obtain in economics at a future date. Once a fuller understanding of human behavior has been achieved with the aid of a theory that makes use of [measurement], the life of the individual may be materially affected. It is, therefore, not an unnecessary digression to study these problems.15

The analysis in The Theory of Games and Economic Behavior begins with the simple case of an individual who faces a choice between two alternatives, as in the choice between heads and tails in match-penny. But this time von Neumann and Morgenstern go more deeply into the nature of the decision, with the individual making a choice between two combinations of events instead of between two single possibilities.

They take as an example a man who prefers coffee to tea and tea to milk.16 We ask him this question: “Do you prefer a cup of coffee to a glass that has a 50–50 chance of being filled with tea or milk?” He prefers the cup of coffee.

What happens when we reorder the preferences but ask the same question? This time the man prefers milk over both coffee and tea but still prefers coffee to tea. Now the decision between coffee for certain and a 50–50 chance of getting tea or milk has become less obvious than it was the first time, because now the uncertain outcome contains something he really likes (milk) as well as something he could just as well do without (tea). By varying the probabilities of finding tea or milk and by asking at what point the man is indifferent between the coffee for certain and the 50–50 gamble, we can develop a quantitative estimate—a hard number—to measure by how much he prefers milk to coffee and coffee to tea.

The example becomes more realistic when we translate it into a technique for measuring the utility—the degree of satisfaction—of possessing $1 compared to the utility of possessing a second dollar, for a total of $2. This man’s favored outcome must now be $2, which takes the place of milk in the above example; no money takes the place of tea, the least favored outcome, and $1 becomes the middle choice and takes the place of coffee.

Once again we ask our subject to choose between a sure thing and a gamble. But in this case the choice is between $1 versus a gamble that pays either $2 or nothing. We set the odds in the gamble at a 50% chance of $2 and a 50% chance of nothing, giving it a mathematical expectancy of $1. If the man declares that he is indifferent between the $1 certain and the gamble, then he is neutral on the subject of risk at this low level of the gamble. According to the formula proposed by von Neumann and Morgenstern, the probability on the favorite possibility—in this case the $2 outcome—defines how much the subject prefers $1 over zero compared with how much he prefers $2 over zero. Here 50% means that his preference for $1 over zero is half as great as his preference for $2 over zero. Under these circumstances, the utility of $2 is double the utility of $1.

The response might well differ with other people or under other circumstances. Let us see what happens when we increase the amount of money involved and change the probabilities in the gamble. Assume now that this man is indifferent between $100 certain and a gamble with a 67% probability of paying $200 and a 33% probability of coming up zero. The mathematical expectancy of this gamble is $133; in other words, the man’s preference for the certain outcome—$100—is now larger than it was when only a couple of dollars were involved. The 67% probability on $200 means that his preference for $100 over zero is two-thirds as great as his preference for $200 over zero: the utility of the first $100 is larger than the utility of the second $100. The utility of the larger sum diminishes as the amount of money at risk increases from single digits to triple digits.

If all this sounds familiar, it is. The reasoning here is precisely the same as in the calculation of the “certainty equivalent,” which we derived from Bernoulli’s fundamental principle that the utility of increases in wealth will be inversely related to the amount of wealth already possessed (page 105). This is the essence of risk aversion—that is, how far we are willing to go in making decisions that may provoke others to make decisions that will have adverse consequences for us. This line of analysis puts von Neumann and Morgenstern strictly in the classical mode of rationality, for rational people always understand their preferences clearly, apply them consistently, and lay them out in the fashion described here.

Alan Blinder, a long-time member of the Princeton economics faculty, co-author of a popular economics textbook, and Vice Chairman of the Federal Reserve Board from 1994 to 1996, has provided an interesting example of game theory.17 The example appeared in a paper published in 1982. The subject was whether coordination is possible, or even desirable, between monetary policy, which involves the control of short-term interest rates and the supply of money, and fiscal policy, which involves the balance between federal government spending and tax revenue.

The players in this game are the monetary authorities of the Federal Reserve System and the politicians who determine the mix between government spending and tax revenues. The Federal Reserve authorities perceive control of inflation as their primary responsibility, which makes them favor economic contraction over economic expansion. They serve long terms—fourteen years for members of the Board, and until retirement age for presidents of the Federal Reserve Banks—so they can act with a good deal of independence from political pressures. The politicians, on the other hand, have to run regularly for election, which leads them to favor economic expansion over economic contraction.

The object of the game is for one player to force the other to make the unpleasant decisions. The Fed would prefer to have tax revenues exceed spending rather than to have the government suffer a budget deficit. A budget surplus would tend to hold inflation in check, thereby protecting the members of the Fed from being seen as the bad guys. The politicians, who worry about being elected, would prefer the Fed to keep interest rates low and the money supply ample. That policy would stimulate business activity and employment and would relieve Congress and the President of the need to incur a budget deficit. Neither side wants to do what the other side wants to do.

Blinder sets up a matrix that shows the preferences of each side in regard to each of three decisions by the other: contract, do nothing, or expand. The numbers above the diagonal in each square represent the order of preference of the members of the Fed; the numbers below the diagonals represent the order of preference of the politicians.

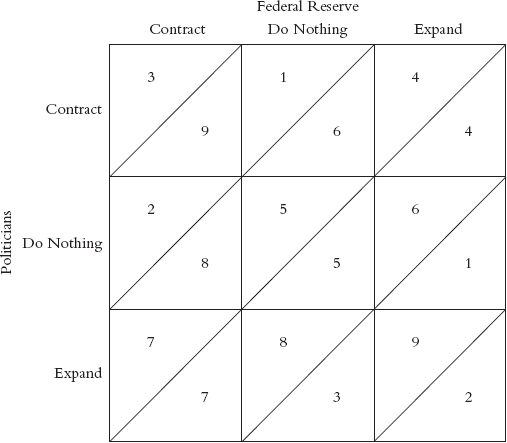
The highest-ranked preferences of the Fed (1, 2, and 3) appear in the upper left-hand corner of the matrix, where at least one side is contractionary while the other is either supportive or does nothing to rock the boat. The members of the Fed clearly prefer to have the politicians do their job for them. The three highest-ranked preferences of the politicians appear in the lower right-hand corner, where at least one side is expansionary while the other is either supportive or does nothing to rock the boat. The politicians clearly prefer to have the Fed adopt expansionary policies and for the politicians to do nothing. The lowest-ranked preferences of the politicians appear in the left-hand column, while the lowest-ranked preferences of the Fed appear in the bottom row. This is hardly a situation in which much accommodation is likely.

How will the game end? Assuming that the relationship between the Fed and the politicians is such that collaboration and coordination are impossible, the game will end in the lower left-hand corner where monetary policy is contractionary and fiscal policy is expansionary. This is precisely the outcome that emerged in the early Reagan years, when Blinder wrote this paper.

Why this outcome and no other? First, both sides are displaying their character here—an austere Fed and generous politicians. Under our assumption that the Fed cannot persuade the politicians to run a budget surplus and-that the politicians cannot persuade the Fed to lower interest rates, neither side has any desire to alter its preferences nor can either dare to be simply neutral.

Look upward and to the right from those two 7s. Note that there is no number below the diagonal (the politicians’ preference) looking upward on the left-hand vertical that is lower than 7; there is no number above the diagonal (the Fed’s preference) looking horizontally to the right that is lower than 7. As long as the Fed is contractionary and the politicians are expansionary, both sides are making the best of a bad bargain.

That is not the case in the upper right-hand corner, where the Fed’s monetary policy is less tight and a budget surplus emerges. Looking left horizontally and above the diagonals, we note that both the choices rank higher than 4: the Fed would rather do nothing or even be contractionary as compared to contributing to a business expansion that might end up in an inflationary situation. The opposite view would prevail among the politicians. Looking downward vertically, we find that both the choices rank higher than 4: the politicians would rather do nothing or run a deficit than follow a policy that cost them their jobs if their constituents lose their jobs as a result.

This outcome is known as a Nash Equilibrium, named after John Nash, another Princetonian and one of the 1994 winners of the Nobel Prize for his contributions to game theory.18 Under the Nash Equilibrium the outcome, though stable, is less than optimal. Both sides would obviously prefer almost anything to this one. Yet they cannot reach a better bargain unless they drop their adversarial positions and work together on a common policy that would give each a supportive, or at least a neutral, role that would keep them from getting into each other’s way. An example of that radically different state of affairs arose in 1994, when Fed policy was contractionary and the politicians were uncharacteristically willing to stand by without interfering.

Blinder’s game reveals a keen insight into the way contesting powers in Washington behave toward one another. But it can be generalized into many other situations: Drop the bomb, do nothing, or sue for peace. Cut prices, do nothing, or raise prices. Bet your poker hand on the basis of the probabilities, fold, or bluff.

In Blinder’s example, the players know each other’s intentions, which is seldom the case. It also fails to include the preferences of consumers, employees, and business managers, all of whom are very much involved in the outcome. When we change the rules by expanding the number of players or by restricting the information available to the players, we have no choice but to resort to higher mathematics. As von Neumann and Morgenstern remarked, “. . . what a complexity of theoretical forms must be expected in social theory.”

In August 1993, the Federal Communications Commission decided to auction off wireless communications rights. Two licenses would be issued for each of 51 zones around the country; no bidder could acquire more than one license in any zone. The usual procedure in such auctions is to call for sealed bids and to award the contract to the highest bidders. This time, acting on the advice of Paul Milgrom, a Stanford University professor, the FCC chose to conduct the auction according to game theory, calling it a “Spectrum Auction.”

First, all bids would be open, so that each contestant would always know what all the others were doing. Second, there would be successive rounds of bidding until no contestant wanted to raise its bid any higher. Third, between rounds, contestants could switch their bid from one zone to another or could bid simultaneously for licenses in adjoining zones; since there is an economic advantage in having licenses in adjoining zones, a particular license might be worth more to one party than it would be to another. In short, each decision would be based on the known decisions of the other players.

The contestants found that making decisions was no easy matter. Each of them had to guess about the intentions of the others, studying their reputation for aggressiveness, their financial capacity, and their existing licensing structures. On occasion, a properly placed bid by one contestant would clearly signal its intentions to the others, thereby avoiding a cycle of competitive bidding for some particular license. Pacific Telesis, which hired Milgrom as their consultant in the auction, went so far as to take out full-page ads in cities where potential competitors were located to make clear their determination to win no matter what. Some contestants joined together to prevent costly bidding for the same license.

The auction went on for 112 rounds over three months and brought the government $7-7 billion. Although some argued that the government could have raised more money if the FCC had prohibited the alliances, the allocation of licenses in the end probably turned out to be more efficient in terms of the economies of building franchises than it would have been under the traditional procedure.

The motivation to avoid destructive bidding competitions is understandable. The highest bidder in an auction of this kind often suffers what is known as the Winner’s Curse—overpaying out of a determination to win. The Winner’s Curse does not need a fancy auction—the same curse may be visited on an investor in a hurry to buy a stock on which someone has provided a hot tip. To avoid the curse, trading sometimes takes place on computer screens in a manner that closely resembles the spectrum auction. The players—usually large financial institutions like pension funds or mutual funds—are anonymous, but all bids and offers are displayed on the screen together with reservation prices above which the investor will not buy and below which the seller will not sell.

In January 1995, the publication Pensions and Investments reported on another application of game theory in making investments. ANB Investment Management & Trust in Chicago had introduced a strategy explicitly designed to avoid the Winner’s Curse. The chief investment officer, Neil Wright, saying he had based the strategy on the Nash Equilibrium, claimed that the Winner’s Curse is usually associated with stocks that have abnormally wide price ranges, which “means there is a lot of uncertainty about how the company will do.” A wide price range also indicates limited liquidity, which means that a relatively small volume of buying or selling will have a significant impact on the price of the stock. Wright accordingly planned to select his portfolio from stocks with narrow trading ranges, an indication that they are priced around consensus views, with sellers and buyers more or less evenly matched. The assumption is that such stocks can be bought for little more than their consensus valuation.

Von Neumann and Morgenstern based The Theory of Games and Economic Behavior on one essential element of behavior: the winnings that will accrue to an individual who maximizes his utility—makes the best of the available tradeoffs within the constraints set by the game theory—will depend upon how much he “can get if he behaves ‘rationally.’ This ‘can get’ [the winnings he can expect] is, of course, presumed to be a minimum; he may get more if others make mistakes (behave irrationally).”19

This stipulation has posed a major problem for critics, including distinguished behavioral psychologists like Daniel Ellsberg and Richard Thaler, whom we will meet later. In a highly critical paper published in 1991, the historian Philip Mirowski asserted, “All is not well in the House of Game Theory—in every dreamhouse a heartache—and signs of pathology can no longer be ignored.”20 He cites criticisms by Nobel Prize winners Henry Simon, Kenneth Arrow, and Paul Samuelson. He claims that game theory would never have amounted to anything had von Neumann not sold it to the military; he even goes so far as to speculate, “Some laid the blame for the escalation of nuclear weaponry directly at the door of game theory.”21 Indeed, Mirowski claims that Morgenstern was a “godsend” to von Neumann because he proposed economists as an audience for game theory when no one else was interested. Mirowski is scathing about the naiveté and oversimplification of their definitions of “that sadly abused word,” rationality, which he describes as “a strangepotage.”22

Yet, game theory’s assumption of rational behavior, and von Neumann and Morgenstern’s dream that such behavior can be measured and expressed in numbers, has unleashed a flood of exciting theories and practical applications. As the examples I have offered make clear, its influence has reached far beyond the military.

During the 1950s and 1960s efforts were renewed to broaden the study of rationality, particularly in economics and finance. Some of the ideas advanced then seem lacking in substance today; in Chapters 16 and 17 we will subject those ideas to critical analysis. But we must understand that, up to about 1970, much of the enthusiasm for rationality, for measurement, and for the use of mathematics in forecasting emerged from the optimism that accompanied the great victories of the Second World War.

The return of peacetime was heralded as an opportunity to apply the lessons learned so painfully during the long years of depression and war. Perhaps the dreams of the Enlightenment and the Victorian age might at last come true for all members of the human race. Keynesian economics was enlisted as a means of controlling the business cycle and promoting full employment. The aim of the Bretton Woods Agreements was to recapture the stability of the nineteenth-century gold standard. The International Monetary Fund and the World Bank were set up to nourish economic progress among disadvantaged people around the world. Meanwhile, the United Nations would keep peace among nations.

In this environment, the Victorian concept of rational behavior regained its former popularity. Measurement always dominates intuition: rational people make choices on the basis of information rather than on the basis of whim, emotion, or habit. Once they have analyzed all the available information, they make decisions in accord with well-defined preferences. They prefer more wealth to less and strive to maximize utility. But they are also risk-averse in the Bernoullian sense that the utility of additional wealth is inversely related to the amount already possessed.

With the concept of rationality so well defined and so broadly accepted in intellectual circles, its transformation into rules for governing risk and maximizing utility was bound to influence the world of investing and managing wealth. The setting was perfect.

The achievements that followed brought Nobel prizes to gifted scholars, and the definitions of risk and the practical applications that emerged from those achievements revolutionized investment management, the structure of markets, the instruments used by investors, and the behavior of the millions of people who keep the system working.

a The feeling appears to have been mutual. Morgenstern took a dim view of Samuelson’s knowledge of mathematics. Complaining that “[von Neumann] says [Samuelson] has murky ideas about stability,” he predicted that “even in thirty yean he won’t absorb game theory!” See Leonard, 1994, p. 494n.

b Röpke, also a Christian, was far more emphatic than Morgenstern had been about his reasons for leaving Hitler’s Germany.

Notes

1. Most of the background material and much of the detail about von Neumann is from Macrae, 1992.

2. Ibid., p. 20.

3. Ibid., p. 87.

4. Quoted in Leonard, 1995, p. 7.

5. Re Morgenstern’s anti-Semitism, see Leonard, 1995, Section III. 1.

6. Ibid., p. 16.

7. Ibid.

8. Leonard, 1994, footnote 3.

9. Ibid., footnote 4.

10. This and the subsequent quotations in this paragraph are from Mirowski, 1991, p. 239.

11. Leonard, 1995, p. 22n.

12. Ibid., p. 22.

13. von Neumann, 1944, p. 3.

14. Ibid., p. 9.

15. Ibid., p. 20.

16. This example is adapted from von Neumann, 1944, Chapter I, Section 3.3, pp. 17–20.

17. Blinder, 1982, esp. pp. 22–24.

18. For an interesting biography of Nash and his contribution to game theory, see Nasar, 1994.

19. von Neumann, 1944, p. 33.

20. Mirowski, 1991, p. 234.

21. Ibid., p. 229.

22. Ibid., pp. 231 and 237.