Chapter 2

As Easy as I, II, III

Without numbers, there are no odds and no probabilities; without odds and probabilities, the only way to deal with risk is to appeal to the gods and the fates. Without numbers, risk is wholly a matter of gut.

We live in a world of numbers and calculations, from the clock we squint at when we wake up, to the television channel we switch off at bedtime. As the day proceeds, we count the measures of coffee we put into the coffeemaker, pay the housekeeper, consult yesterday’s stock prices, dial a friend’s telephone number, check the amount of gas in the car and the speed on the speedometer, press the elevator button in our office building, and open the office door with our number on it. And the day has hardly started!

It is hard for us to imagine a time without numbers. Yet if we were able to spirit a well-educated man from the year 1000 to the present, he probably would not recognize the number zero and would surely flunk third-grade arithmetic; few people from the year 1500 would fare much better.

The story of numbers in the West begins in 1202, when the cathedral of Chartres was nearing completion and King John was finishing his third year on the throne of England. In that year, a book titled Liber Abaci, or Book of the Abacus, appeared in Italy. The fifteen chapters of the book were entirely handwritten; almost three hundred years would pass before the invention of printing. The author, Leonardo Pisano, was only 27 years old but a very lucky man: his book would receive the endorsement of the Holy Roman Emperor, Frederick II. No author could have done much better than that.1

Leonardo Pisano was known for most of his life as Fibonacci, the name by which he is known today. His father’s first name was Bonacio, and Fibonacci is a contraction of son-of-Bonacio. Bonacio means “simpleton” and Fibonacci means “blockhead.” Bonacio must have been something less than-a simpleton, however, for he represented Pisa as consul in a number of different cities, and his son Leonardo was certainly no blockhead.

Fibonacci was inspired to write Liber Abaci on a visit to Bugia, a thriving Algerian city where his father was serving as Pisan consul. While Fibonacci was there, an Arab mathematician revealed to him the wonders of the Hindu-Arabic numbering system that Arab mathematicians had introduced to the West during the Crusades to the Holy Land. When Fibonacci saw all the calculations that this system made possible—calculations that could not possibly be managed with Roman letter-numerals—he set about learning everything he could about it. To study with the leading Arab mathematicians living around the Mediterranean, he set off on a trip that took him to Egypt, Syria, Greece, Sicily, and Provence.

The result was a book that is extraordinary by any standard. Liber Abaci made people aware of a whole new world in which numbers could be substituted for the Hebrew, Greek, and Roman systems that used letters for counting and calculating. The book rapidly attracted a following among mathematicians, both in Italy and across Europe.

Liber Abaci is far more than a primer for reading and writing with the new numerals. Fibonacci begins with instructions on how to determine from the number of digits in a numeral whether it is a unit, or a multiple of ten, or a multiple of 100, and so on. Later chapters exhibit a higher level of sophistication. There we find calculations using whole numbers and fractions, rules of proportion, extraction of square roots and roots of higher orders, and even solutions for linear and quadratic equations.

Ingenious and original as Fibonacci’s exercises were, if the book had dealt only with theory it would probably not have attracted much attention beyond a small circle of mathematical cognoscenti. It commanded an enthusiastic following, however, because Fibonacci filled it with practical applications. For example, he described and illustrated many innovations that the new numbers made possible in commercial bookkeeping, such as figuring profit margins, money-changing, conversions of weights and measures, and—though usury was still prohibited in many places—he even included calculations of interest payments.

Liber Abaci provided just the kind of stimulation that a man as brilliant and creative as the Emperor Frederick would be sure to enjoy. Though Frederick, who ruled from 1211 to 1250, exhibited cruelty and an obsession with earthly power, he was genuinely interested in science, the arts, and the philosophy of government. In Sicily, he destroyed all the private garrisons and feudal castles, taxed the clergy, and banned them from civil office. He also set up an expert bureaucracy, abolished internal tolls, removed all regulations inhibiting imports, and shut down the state monopolies.

Frederick tolerated no rivals. Unlike his grandfather, Frederick Barbarossa, who was humbled by the Pope at the Battle of Legnano in 1176, this Frederick reveled in his endless battles with the papacy. His intransigence brought him not just one excommunication, but two. On the second occasion, Pope Gregory IX called for Frederick to be deposed, characterizing him as a heretic, rake, and anti-Christ. Frederick responded with a savage attack on papal territory; meanwhile his fleet captured a large delegation of prelates on their way to Rome to join the synod that had been called to remove him from power.

Frederick surrounded himself with the leading intellectuals of his age, inviting many of them to join him in Palermo. He built some of Sicily’s most beautiful castles, and in 1224 he founded a university to train public servants—the first European university to enjoy a royal charter.

Frederick was fascinated with Liber Abaci. Some time in the 1220s, while on a visit to Pisa, he invited Fibonacci to appear before him. In the course of the interview, Fibonacci solved problems in algebra and cubic equations put to him by one of Frederick’s many scientists-in-residence. Fibonacci subsequently wrote a book prompted by this meeting, Liber Quadratorum, or The Book of Squares, which he dedicated to the Emperor.

Fibonacci is best known for a short passage in Liber Abaci that led to something of a mathematical miracle. The passage concerns the problem of how many rabbits will be born in the course of a year from an original pair of rabbits, assuming that every month each pair produces another pair and that rabbits begin to breed when they are two months old. Fibonacci discovered that the original pair of rabbits would have spawned a total of 233 pairs of offspring in the course of a year.

He discovered something else, much more interesting. He had assumed that the original pair would not breed until the second month and then would produce another pair every month. By the fourth month, their first two offspring would begin breeding. After the process got started, the total number of pairs of rabbits at the end of each month would be as follows: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233. Each successive number is-the sum of the two preceding numbers. If the rabbits kept going for a hundred months, the total number pairs would be 354,224,848,179,261,915,075.

The Fibonacci series is a lot more than a source of amusement. Divide any of the Fibonacci numbers by the next higher number. After 3, the answer is always 0.625. After 89, the answer is always 0.618; after higher numbers, more decimal places can be filled in.a Divide any number by its preceding number. After 2, the answer is always 1.6. After 144, the answer is always 1.618.

The Greeks knew this proportion and called it “the golden mean.” The golden mean defines the proportions of the Parthenon, the shape of playing cards and credit cards, and the proportions of the General Assembly Building at the United Nations in New York. The horizontal member of most Christian crosses separates the vertical member by just about the same ratio: the length above the crosspiece is 61.8% of the length below it. The golden mean also appears throughout nature—in flower patterns, the leaves of an artichoke, and the leaf stubs on a palm tree. It is also the ratio of the length of the human body above the navel to its length below the navel (in normally proportioned people, that is). The length of each successive bone in our fingers, from tip to hand, also bears this ratio.b

In one of its more romantic manifestations, the Fibonacci ratio defines the proportions and shape of a beautiful spiral. The accompanying illustrations demonstrate how the spiral develops from a series of squares whose successive relative dimensions are determined by the Fibonacci series. The process begins with two small squares of equal size. It then progresses to an adjacent square twice the size of the first two, then to a square three times the size of the first two, then to five times, and so on. Note that the sequence produces a series of rectangles with the proportions of the golden mean. Then quarter-circle arcs connect the opposite corners of the squares, starting with the smallest squares and proceeding in sequence.

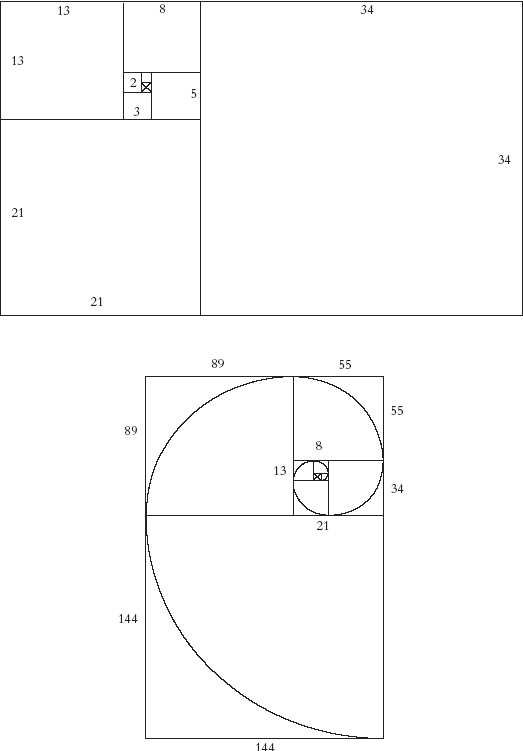
This familiar-looking spiral appears in the shape of certain galaxies, in a ram’s horn, in many seashells, and in the coil of the ocean waves that surfers ride. The structure maintains its form without change as it is made larger and larger and regardless of the size of the initial square with which the process is launched: form is independent of growth. The journalist William Hoffer has remarked, “The great golden spiral seems to be nature’s way of building quantity without sacrificing quality.”2

Some people believe that the Fibonacci numbers can be used to make a wide variety of predictions, especially predictions about the stock market; such predictions work just often enough to keep the enthusiasm going. The Fibonacci sequence is so fascinating that there is even an American Fibonacci Association, located at Santa Clara University in California, which has published thousands of pages of research on the subject since 1962.

Fibonacci’s Liber Abaci was a spectacular first step in making measurement the key factor in the taming of risk. But society was not yet prepared to attach numbers to risk. In Fibonacci’s day, most people still thought that risk stemmed from the capriciousness of nature. People would have to learn to recognize man-made risks and acquire the courage to do battle with the fates before they would accept the techniques of taming risk. That acceptance was still at least two hundred years in the future.

We can appreciate the full measure of Fibonacci’s achievement only by looking back to the era before he explained how to tell the difference between 10 and 100. Yet even there we shall discover some remarkable innovators.

Primitive people like the Neanderthals knew how to tally, but they had few things that required tallying. They marked the passage of days on a stone or a log and kept track of the number of animals they killed. The sun kept time for them, and five minutes or a half-hour either way hardly mattered.

The first systematic efforts to measure and count were undertaken some ten thousand years before the birth of Christ.3 It was then that humans settled down to grow food in the valleys washed by such great rivers as the Tigris and the Euphrates, the Nile, the Indus, the Yangtse, the Mississippi, and the Amazon. The rivers soon became highways for trade and travel, eventually leading the more venturesome people to the oceans and seas into which the rivers emptied. To travelers ranging over longer and longer distances, calendar time, navigation, and geography mattered a great deal and these factors required ever more precise computations.

Priests were the first astronomers, and from astronomy came mathematics. When people recognized that nicks on stones and sticks no longer sufficed, they began to group numbers into tens or twenties, which were easy to count on fingers and toes.

Although the Egyptians became experts in astronomy and in predicting the times when the Nile would flood or withdraw, managing or influencing the future probably never entered their minds. Change was not part of their mental processes, which were dominated by habit, seasonality, and respect for the past.

About 450 BC, the Greeks devised an alphabetic numbering system that used the 24 letters of the Greek alphabet and three letters that subsequently became obsolete. Each number from 1 to 9 had its own letter, and the multiples of ten each had a letter. For example, the symbol “pi” comes from the first letter of the Greek word “penta,” which represented 5; delta, the first letter of “deca,” the word for 10, represented 10; alpha, the first letter of the alphabet, represented 1, and rho represented 100. Thus, 115 was written rho–deca–penta, or ρδπ. The Hebrews, although Bemitic rather than Indo-European, used the same kind of cipher-alphabet system.4

Handy as these letter–numbers were in helping people to build stronger structures, travel longer distances, and keep more accurate time, the system had serious limitations. You could use letters only with great difficulty—and almost never in your head—for adding or subtracting or multiplying or dividing. These substitutes for numbers provided nothing more than a means of recording the results of calculations performed by other methods, most often on a counting frame or abacus. The abacus—the oldest counting device in history—ruled the world of mathematics until the Hindu-Arabic numbering system arrived on the scene between about 1000 and 1200 AD.

The abacus works by specifying an upper limit for the number of counters in each column; in adding, as the furthest right column fills up, the excess counters move one column to the left, and so on. Our concepts of “borrow one” or “carry over three” date back to the abacus.5

Despite the limitations of these early forms of mathematics, they made possible great advances in knowledge, particularly in geometry—the language of shape—and its many applications in astronomy, navigation, and mechanics. Here the most impressive advances were made by the Greeks and by their colleagues in Alexandria. Only the Bible has appeared in more editions and printings than Euclid’s most famous book, Elements.

Still, the greatest contribution of the Greeks was not in scientific innovation. After all, the temple priests of Egypt and Babylonia had learned a good bit about geometry long before Euclid came along. Even the famous theorem of Pythagoras—the square of the hypotenuse of a right triangle is equal to the sum of the square of the other two sides—was in use in the Tigris-Euphrates valley as early as 2000 BC.

The unique quality of the Greek spirit was the insistence on proof. “Why?” mattered more to them than “What?” The Greeks were able to reframe the ultimate questions because theirs was the first civilization in history to be free of the intellectual straitjacket imposed by an all-powerful priesthood. This same set of attitudes led the Greeks to become the world’s first tourists and colonizers as they made the Mediterranean basin their private preserve.

More worldly as a consequence, the Greeks refused to accept at face value the rules of thumb that older societies passed on to them. They were not interested in samples; their goal was to find concepts that would apply everywhere, in every case. For example, mere measurement would confirm that the square of the hypotenuse of a right triangle is equal to the sum of the squares of the other two sides. But the Greeks asked why that should be so, in all right triangles, great and small, without a single exception to the rule. Proof is what Euclidean geometry is all about. And proof, not calculation, would dominate the theory of mathematics forever after.

This radical break with the analytical methodologies of other civilizations makes us wonder again why it was that the Greeks failed to discover the laws of probability, and calculus, and even simple algebra. Perhaps, despite all they achieved, it was because they had to depend on a clumsy numbering system based on their alphabet. The Romans suffered from the same handicap. As simple a number as 9 required two letters: IX. The Romans could not write 32 as III II, because people would have no way of knowing whether it meant 32, 302, 3020, or some larger combination of 3, 2, and 0. Calculations based on such a system were impossible.

But the discovery of a superior numbering system would not occur until about 500 AD, when the Hindus developed the numbering system we use today. Who contrived this miraculous invention, and what circumstances led to its spread throughout the Indian subcontinent, remain mysteries. The Arabs encountered the new numbers for the first time some ninety years after Mohammed established Islam as a proselytizing religion in 622 and his followers, united into a powerful nation, swept into India and beyond.

The new system of numbering had a galvanizing effect on intellectual activity in lands to the west. Baghdad, already a great center of learning, emerged as a hub of mathematical research and activity, and the Caliph retained Jewish scholars to translate the works of such pioneers of mathematics as Ptolemy and Euclid. The major works of mathematics were soon circulating throughout the Arab empire and by the ninth and tenth centuries were in use as far west as Spain.

Actually, one westerner had suggested a numbering system at least two centuries earlier than the Hindus. About 250 AD, an Alexandrian mathematician named Diophantus wrote a treatise setting forth the advantages of a system of true numbers to replace letters substituting for numbers.6

Not much is known about Diophantus, but the little we do know is amusing. According to Herbert Warren Turnbull, a historian of mathematics, a Greek epigram about Diophantus states that “his boyhood lasted l/6th of his life; his beard grew after l/12th more; he married after l/7th more, and his son was born five years later; the son lived to half his father’s age, and the father died four years after his son.” How old was Diophantus when he died?7 Algebra enthusiasts will find the answer at the end of this chapter.

Diophantus carried the idea of symbolic algebra—the use of symbols to stand for numbers—a long way, but he could not quite make it all the way. He comments on “the impossible solution of the absurd equation 4 = 4x + 20. “8 Impossible? Absurd? The equation requires x to be a negative number: −4. Without the concept of zero, which Diophantus lacked, a negative number is a logical impossibility.

Diophantus’s remarkable innovations seem to have been ignored. Almost a millennium and a half passed before anyone took note of his work. At last his achievements received their due: his treatise played a central role in the flowering of algebra in the seventeenth century. The algebraic equations we are all familiar with today—equations like a + bx = c—are known as Diophantine equations.

The centerpiece of the Hindu-Arabic system was the invention of zero—sunya as the Indians called it, and cifr as it became in Arabic.9 The term has come down to us as “cipher,” which means empty and refers to the empty column in the abacus or counting frame.c

The concept of zero was difficult to grasp for people who had used counting only to keep track of the number of animals killed or the number of days passed or the number of units traveled. Zero had nothing to do with what counting was for in that sense. As the twentieth-century English philosopher Alfred North Whitehead put it,

The point about zero is that we do not need to use it in the operations of daily life. No one goes out to buy zero fish. It is in a way the most civilized of all the cardinals, and its use is only forced on us by the needs of cultivated modes of thought.10

Whitehead’s phrase “cultivated modes of thought” suggests that the concept of zero unleashed something more profound than just an enhanced method of counting and calculating. As Diophantus had sensed, a proper numbering system would enable mathematics to develop into a science of the abstract as well as a technique for measurement. Zero blew out the limits to ideas and to progress.

Zero revolutionized the old numbering system in two ways. First, it meant that people could use only ten digits, from zero to nine, to perform every conceivable calculation and to write any conceivable number. Second, it meant that a sequence of numbers like 1, 10, 100 would indicate that the next number in the sequence would be 1000. Zero makes the whole structure of the numbering system immediately visible and clear. Try that with the Roman numerals I, X, and C, or with V, L, and D—what is the next number in those sequences?

The earliest known work in Arabic arithmetic was written by al-Khowârizmî, a mathematician who lived around 825, some four hundred years before Fibonacci.11 Although few beneficiaries of his work are likely to have heard of him, most of us know of him indirectly. Try saying “al-Khowârizmî” fast. That’s where we get the word “algorithm,” which means rules for computing.12 It was al-Khowârizmî who was the first mathematician to establish rules for adding, subtracting, multiplying, and dividing with the new Hindu numerals. In another treatise, Hisâb al-jabr w’ almuqâbalah, or “Science of transposition and cancellation,” he specifies the process for manipulating algebraic equations. The word al-jabr thus gives us our word algebra, the science of equations.13

One of the most important, surely the most famous, early mathematician was Omar Khayyam, who lived from about 1050 to about 1130 and was the author of the collection of poems known as the Rubaiyat.14 His haunting sequence of 75 four-line poems (the word Rubaiyat defines the poetic form) was translated in Victorian times by the English poet Edward Fitzgerald. This slim volume has more to do with the delights of drinking wine and taking advantage of the transitory nature of life than with science or mathematics. Indeed, in number XXVII, Omar Khayyam writes:

Myself when young did eagerly frequent

Doctor and Saint, and heard great Argument

About it and about; but evermore

Came out by the same Door as in I went.

According to Fitzgerald, Omar Khayyam was educated along with two friends, both as bright as he: Nizam al Mulk and Hasan al Sabbah. One day Hasan proposed that, since at least one of the three would attain wealth and power, they should vow that “to whomsoever this fortune falls, he shall share it equally with the rest, and preserve no preeminence for himself.” They all took the oath, and in time Nizam became vizier to the sultan. His two friends sought him out and claimed their due, which he granted as promised.

Hasan demanded and received a place in the government, but, dissatisfied with his advancement, left to become head of a sect of fanatics who spread terror throughout the Mohammedan world. Many years later, Hasan would end up assassinating his old friend Nizam.

Omar Khayyam asked for neither title nor office. “The greatest boon you can confer on me,” he said to Nizam, “is to let me live in a corner under the shadow of your fortune, to spread wide the advantages of science and pray for your long life and prosperity.” Although the sultan loved Omar Khayyam and showered favors on him, “Omar’s epicurean audacity of thought and speech caused him to be regarded askance in his own time and country.”

Omar Khayyam used the new numbering system to develop a language of calculation that went beyond the efforts of al-Khowârizmî and served as a basis for the more complicated language of algebra. In addition, Omar Khayyam used technical mathematical observations to reform the calendar and to devise a triangular rearrangement of numbers that facilitated the figuring of squares, cubes, and higher powers of mathematics; this triangle formed the basis of concepts developed by the seventeenth-century French mathematician Blaise Pascal, one of the fathers of the theory of choice, chance, and probability.

The impressive achievements of the Arabs suggest once again that an idea can go so far and still stop short of a logical conclusion. Why, given their advanced mathematical ideas, did the Arabs not proceed to probability theory and risk management? The answer, I believe, has to do with their view of life. Who determines our future: the fates, the gods, or ourselves? The idea of risk management emerges only when people believe that they are to some degree free agents. Like the Greeks and the early Christians, the fatalistic Muslims were not yet ready to take the leap.

By the year 1000, the new numbering system was being popularized by Moorish universities in Spain and elsewhere and by the Saracens in Sicily. A Sicilian coin, issued by the Normans and dated “1134 Annoy Domini,” is the first known example of the system in actual use. Still, the new numbers were not widely used until the thirteenth century.

Despite Emperor Frederick’s patronage of Fibonacci’s book and the book’s widespread distribution across Europe, introduction of the Hindu-Arabic numbering system provoked intense and bitter resistance up to the early 1500s. Here, for once, we can explain the delay. Two factors were at work.

Part of the resistance stemmed from the inertial forces that oppose any change in matters hallowed by centuries of use. Learning radically new methods never finds an easy welcome.

The second factor was based on more solid ground: it was easier to commit fraud with the new numbers than with the old. Turning a 0 into a 6 or a 9 was temptingly easy, and a 1 could be readily converted into a 4, 6, 7, or 9 (one reason Europeans write 7 as 7). Although the new numbers had gained their first foothold in Italy, where education levels were high, Florence issued an edict in 1229 that forbade bankers from using the “infidel” symbols. As a result, many people who wanted to learn the new system had to disguise themselves as Moslems in order to do so.15

The invention of printing with movable type in the middle of the fifteenth century was the catalyst that finally overcame opposition to the full use of the new numbers. Now the fraudulent alterations were no longer possible. Now the ridiculous complications of using Roman numerals became clear to everyone. The breakthrough gave a great lift to commercial transactions. Now al-Khowârizmî’s multiplication tables became something that all school children have had to learn forever after. Finally, with the first inklings of the laws of probability, gambling took on a whole new dimension.

The algebraic solution to the epigram about Diophantus is as follows. If x was his age when he died, then:

Diophantus lived to be 84 years old.

a One of chose odd quirks that numbers can produce reveals that you can derive 0.618 if you take the square root of 5, which is 2.24, subtract 1, and then divide by 2; this result is the algebraic proof of Fibonacci’s sequence of numbers.

b In technical terms, the formula for the Fibonacci ratio is as follows: the ratio of the smaller part to the larger part equals the ratio of the larger part to the whole.

c The Arabic term survives even in Russian, where it appears as tsifra, which is the word for number.

Notes

1. Most of the background and biographical material on Fibonacci comes from the Encyclopedia Brittanica; Eves, 1983, p. 161; Hogben, 1968, p. 250; and Garland, 1987.

2. Two stimulating commentaries on the Fibonacci numbers are Garland, 1987, and Hoffer, 1975. The examples here are drawn from those two sources.

3. The background material presented here comes primarily from Hogben, 1968, Chapter I.

4. See Hogben, 1968, p. 35; also Eves, 1983, Chapter I.

5. See Hogben, 1968, p. 36 and pp. 246–250.

6. The background material on Diophantus is from Turnbull, 1951, p. 113.

7. Ibid., p. 110.

8. Ibid., p. 111.

9. See Hogben, 1968, pp. 244–246.

10. From Newman, 1988a, p. 433.

11. The background material on al-Khowârizmî is primarily from Muir, 1961, and Hogben, 1968.

12. Hogben, 1968, p. 243.

13. See Hogben, 1968, Chapter VI, for an extended and stimulating discussion of the development of algebra and the uses of zero.

14. The background material on Omar Khayyam is from Fitzgerald.

15. Hogben, 1968, p. 245.