![]()
Puzzle Statistics and More Puzzles
According to Wikipedia, the total number of possible solved Sudokus is a staggering 6,670,903,752,021,072,936,960 (http://en.wikipedia.org/wiki/Sudoku, accessed on February 6, 2015). Moreover, it is possible to create many different puzzles resulting in each one of the 6.67 sextillions of solved Sudokus. Therefore, you might be disappointed that the Generator as described in the previous chapter can only produce up to 2,147,483,648 different puzzles because that is the number of different pseudorandom seeds you can choose from.
Although more than two billion puzzles seem enough for any practical purpose, in this chapter, besides statistically analyzing the puzzles that the Generator creates, I will also tell you how to modify the Generator to produce even more puzzles.
If you configure the Generator with
#define N_SET_QUADS 5
#define N_SET_PAIRS 10
#define ADDITIONAL_CELLS TRUE
the maximum number of clues of the puzzles it generates is 41. This is because the Generator only looks for possible puzzles when it removes individual cells. By then, it has already removed N_SET_QUADS * 4 + N_SET_PAIRS * 2 = 40 numbers, out of 81 of a solved Sudoku.
I plotted the number of clues for the first 30,000 seeds, from 0 to 29,999 (see Figure 16-1).
It looks like the lower half of a normal distribution with a mean of 41. For those of you who are not familiar with statistics and the normal distribution, I will just say that they are the bell-shaped curves that often appear when you count random events. In practical terms, it means that puzzles with a particular number of clues become less and less likely as the number of clues differs more and more from the mean. The distribution in Figure 16-1 isn’t exactly normal, because its “tail” decreases more rapidly than that of a perfectly normal distribution. Not that it really matters, though.

Figure 16-1. Distribution of the number of clues—1
Figure 16-2 shows what a puzzle with 41 clues looks like (seed 2928).
Obviously, it is perfectly symmetrical, because you obtain 41 clues when the Generator removes all the clues in quadruplets and pairs. But it does look a bit crowded. Figure 16-3 shows one of the ten puzzles the Generator made with 26 clues (seed 28288).
It looks more interesting, but much of the symmetry has disappeared, because 15 clues were removed individually.
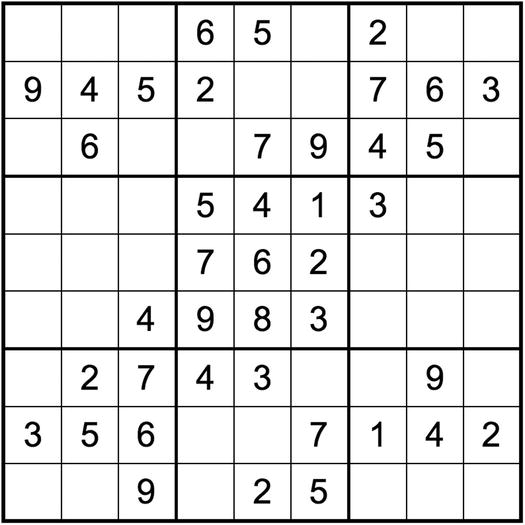
Figure 16-2. A puzzle with 41 clues

Figure 16-3. A puzzle with 26 clues
Incidentally, although it is true that puzzles with fewer clues are in general more difficult, this is not true for the puzzles in Figures 16-2 and 16-3. To complete the puzzle with 41 clues, the Solver needed to use rectangle, while for the puzzle with 26 clues it only needed the naked-pair strategy. Also, you will recall from Chapter 13 that you can solve most of the minimum Sudokus with unique, although they only include 17 clues.
To make puzzles with fewer clues, you can change the parameters of the Generator as follows (for example):
#define N_SET_QUADS 6
#define N_SET_PAIRS 13
By doing so, you reduce the maximum number of clues to 31. Figure 16-4 shows the new distribution of the number of clues, based on 1,000 puzzles.
Figure 16-4. Distribution of the number of clues—2
For those who are interested, this matches almost perfectly the left tail of a normal distribution. Not that one can deduct anything interesting from it . . .
As the Generator removes the clues at random, on average, no number appears more often than any others. In each individual puzzle, though, it is a different story: the number of clues with a particular number can be anything between 0 and 9. For example, in the two puzzles in Figures 16-2 and 16-3, the distribution of the numbers is as follows:
Number: 1 2 3 4 5 6 7 8 9 Total
Figure 16-2: 2 6 5 6 6 5 5 1 5 41
Figure 16-3: 3 3 3 2 5 2 2 4 2 26
An interesting question is: are there puzzles in which a number is missing or in which a number is completely solved? It turns out that a number is missing in 521 of the 30,000 puzzles I checked, and a number is completely solved in 114 puzzles. Here is an example in which the 7 is missing:
Number: 1 2 3 4 5 6 7 8 9 Total
2 5 3 3 3 3 0 5 4 28
and here is an example in which the number 7 is completely solved:
Number: 1 2 3 4 5 6 7 8 9 Total
5 3 3 7 5 2 9 3 1 38
Note that there cannot ever be puzzles in which two numbers are missing, because then the solution wouldn’t be unique: you could swap the two numbers and obtain two distinct and valid solutions.
Among the 30,000 puzzles, there was none with two or more numbers completely solved, but there were eight that had one number missing and one completely solved. Figure 16-5 shows one of them, in which the 6 is completely solved and the 9 is absent.
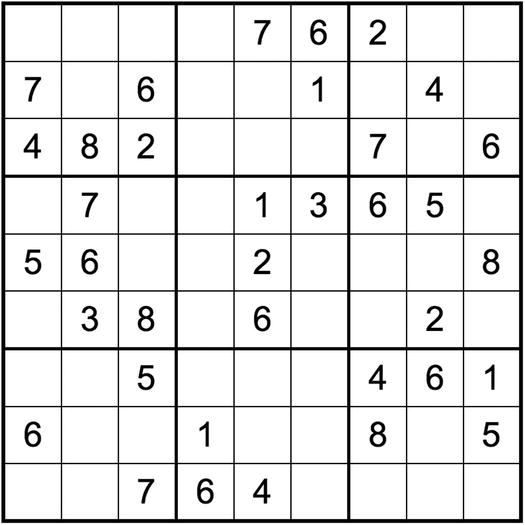
Figure 16-5. Completely solved 6 and absent 9
Before completing the Generator, I was very curious to find out how difficult the generated puzzles would be. As it turned out, most of them are very easy, some are easy, a sizable number are of intermediate difficulty, and a few are hard.
One big issue concerning Sudokus is the grading of their difficulty. It would be nice if there were a universally accepted method for measuring how difficult a Sudoku puzzle is, but, unfortunately, this is not the case. If you look at magazines and newspapers, you will be hard pressed to find two compatible classifications.
Ultimately, how difficult a puzzle is depends on the strategies that you need to apply in order to solve it. In Chapter 2, I grouped the strategies in five categories of increasing complexity, from 0 to 4. Clearly, if you need to apply level 3 strategies like XY-chain and rectangle, you should consider a puzzle more difficult than one you can solve with, say, unique and naked pair. The length of the series of strategies you need to apply also plays a role: if you need to use several strategies one after the other, it is fair to say that the puzzle is more difficult than one for which you only need to use a single strategy.
Table 16-1 shows how many times the Solver used the various strategies to complete 30,000 puzzles.
To better understand the figures, you need to know that in 24,374 cases the Solver completed the puzzle by doing the initial cleanup before applying any strategy. Therefore, the strategies counted in Table 16-1 refer to the remaining 5,626 puzzles.
Table 16-1. Usage of Strategies

Table 16-1 also shows the percentages of occurrence of the strategies, and I added a column with the percentages calculated from Table 14-1 for the minimum Sudokus.
Several strategies occur in both groups in less than 0.1% (i.e., 1 in 1,000) of the puzzles: naked triple, hidden triple, naked quad, lines-3, and lines-4. In particular, naked quad and lines-4 never occur.
The generated puzzles require unique-loop much more often than the minimum Sudokus, while the minimum Sudokus require backtrack more than twice as often as the generated puzzles. This is not surprising, considering that puzzles with fewer clues often are more difficult.
Obviously, I cannot claim that this statistical analysis applies to all puzzles. Nevertheless, if you want to participate in Sudoku championships, where speed is of the essence, you might like to practice rectangle, XY-chain, and Y-wing more than the lines strategies!
It is interesting to compare the percentages of the strategies of levels 1 to 3, as shown graphically in Figure 16-6. Notice that the minimum puzzles, when compared with the generated ones, rely much more on level 1 strategies and much less on the strategies of levels 2 and 3.
These results have no practical impact on generating and solving Sudokus, but I find them intriguing. Obviously, you could do much more. For example, you could see how the usage of strategies changes when you modify the Generator’s parameters to answer questions such as the following: are more symmetrical puzzles easier or more difficult?
If you do use the Generator and the Solver to study the Sudoku puzzles, I would love to hear from you!

Figure 16-6. Comparison of strategy occurrences
I was pleased to see that the Solver needed backtrack in only 37 cases (of 30,000). To be honest, the Solver might have not needed backtrack at all if I had programmed additional strategies into the Solver. But I wanted to keep the Solver close to what a human being can hope to achieve in a real-life situation. Recognizing the pattern required to apply strategies like rectangle and XY-chain is at the limit of what normal (whatever that means) people like you and me can achieve. To clarify what I mean, I would like to show you a partially solved puzzle (see Figure 16-7).
I have listed all candidates to help you, but can you see where you can apply lines-4? Don’t feel too bad if you don’t and my sincere congratulations if you do!
Figure 16-7. The Solver applies lines-4
Let’s see: to apply lines-4, you have to find four rows or four columns with the same four numbers in pairs, although not all numbers need to be in all four lines. The following is what the Solver logs:
lines(4): the rows 1 3 4 7 let us eliminate 2 from the columns 3 5 6 7
lines: removed 2 from (6,3)
lines: removed 2 from (8,3)
lines: removed 2 from (2,5)
lines: removed 2 from (0,7)
The four rows 1, 3, 4, and 7 contain pairs of candidates for 1, 2, 7, and 9. The candidate for 2 is in columns 3 (rows 3 and 7), 5 (rows 1 and 3), 6 (rows 4 and 7), and 7 (rows 1 and 4). Clearly, there cannot be 2s in those columns of any other row. That’s why the Solver removes 2s from (6,3), (8,3), (2,5), and (0,7).
I don’t think that the Solver needs to know strategies more complicated than the jellyfish (as lines-4 is often called). Do you?
The Solver is very quick and goes through thousands of puzzles in well below a minute. It certainly takes more time to log the results than to solve a puzzle.
But the Generator, at least on my aging Mac, takes a non-negligible amount of time to create puzzles. It spent approximately 11 hours creating the 30,000 puzzles with N_SET_QUADS set to 5, N_SET_PAIRS set to 10, and ADDITIONAL_CELLS set to TRUE. This means that each puzzle required 1.32 seconds to be generated.
The amount of time the Generator needs to create a puzzle grows as you decrease the maximum number of clues. For example, it took almost three and a half hours to generate 1,000 puzzles with N_SET_QUADS set to 6, N_SET_PAIRS set to 13, and ADDITIONAL_CELLS set to TRUE, or 12.38 seconds per puzzle.
I tried to generate a puzzle with 21 clues by setting N_SET_QUADS to 7 and N_SET_PAIRS set to 16 but, after longer than half an hour, the Generator had not yet managed to create it. The same happened when I tried to generate a puzzle with 23 clues by setting N_SET_QUADS to 7 and N_SET_PAIRS to 15.
I thought that perhaps puzzles with so few clues couldn’t be very symmetric. It was just a wild and unconfirmed hypothesis (well possibly wrong), but, in an attempt to generate a puzzle with not more than 21 clues, I configured the Generator to remove 60 individual clues instead of quadruplets and pairs. Unfortunately, once more, no valid puzzle was produced after longer than half an hour.
I tried removing 58 individual clues to generate a puzzle with not more than 23 clues. Checking the log, I noticed that on some occasions it attempted to remove more than 58 clues. I was not surprised, because that is how the algorithm works, but it made me realize that, by seeking to remove further clues, the program might “throw away” possible solutions. Therefore, I restarted the Generator after removing the code that attempts to minimize the number of clues. In other words, I configured the Generator to find a puzzle with exactly 23 clues, rather than 23 or less. It succeeded after 31 minutes. This obviously doesn’t confirm my conjecture that puzzles with fewer clues are less symmetric, but it was encouraging. I changed the seed from 0 to 62416598 and tried again. This time, I stopped the Generator after one hour of unsuccessful attempts.
I configured the Generator to create a puzzle with exactly 24 clues by removing individual clues. With seed set to 0, it was still trying after a quarter of an hour; with seed set to 123456789, it succeeded after 1 minute. I then tried with seed set to 333333 and it succeeded after 11 minutes. Clearly the variability is too high to make some sense out of it with unsystematic tests.
In order to make more reliable projections, I made several runs of the Generator, each producing ten puzzles and removing only individual clues. I started by removing 41 clues (to obtain puzzles with 40 clues) and went up to 56 (to obtain puzzles with 25 clues), using as seeds, for no particular reason, the prime numbers (2, 3, 5, 7, etc.) and noting every time how long it took. Figure 16-8 shows the combined results of two batches of tests.
As you can see, and as was expected, the Generator takes longer and longer to create a puzzle as the number of removed clues increases. The interpolated line fits the measured points reasonably well. Therefore, I felt I could extend it to make estimates of timing outside the range of the measurements. Notice that the scale of the time axis is logarithmic. This means that a straight line in the plot represents an exponential function. As a result of this exponential behavior, the Generator can create a puzzle with 40 clues in approximately 0.1 seconds, but to create one with 26 clues, it needs 100 seconds or more.
The formula that expresses the best-fit line is
seconds_per_puzzle = 3*10-11*exp(0.5256*clues_removed)
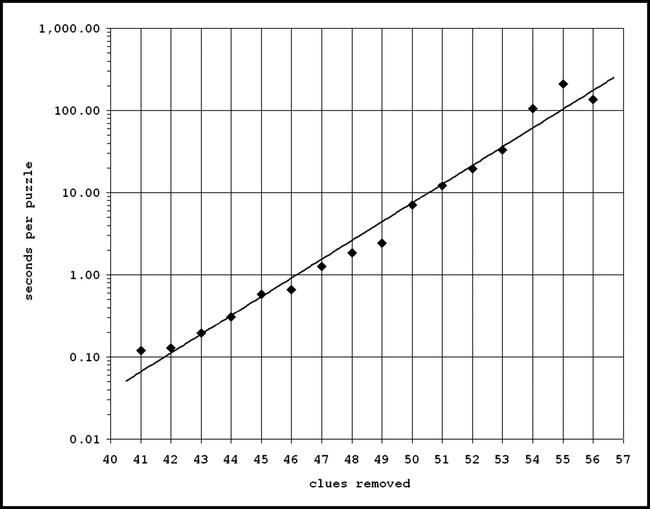
Figure 16-8. Time profile of puzzle generation
Obviously, this interpolation is only valid for my computer, but the behavior with newer and faster computers should be the same. You can easily repeat my analysis with your system.
Generating More Puzzles
There are several ways of generating more puzzles. I shall start with the simplest one and then move on to more complex methods.
As long as all numbers are present in each row, column, and box, the rules of Sudoku only apply to individual numbers. This means that you can swap numbers without invalidating the puzzle. As each permutation of the numbers results in a different puzzle, by swapping pairs of numbers, you can generate 9! - 1 = 362,879 new puzzles from each puzzle you have, although most of them will only differ by some numbers,
You can also add a value to each number and take modulo 9 of the result (i.e., divide the result by 9 and use the remainder). In this way, considering that you can add any value between 1 and 8, you can create eight new puzzles from the original one. But the advantage of this method is that you don’t leave any number in its original place. Figure 16-9 shows a puzzle you generate by adding 2 modulo 9 to the puzzle of Figure 16-3.
Figure 16-10 shows how you shift the numbers.
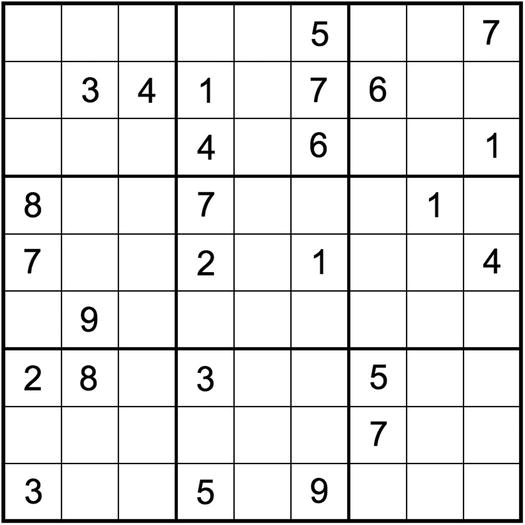
Figure 16-9. Puzzle of Figure 16-3 with shifted numbers
The puzzle is for all practical purposes identical to the original one, but it looks different.
There are other methods to create sets of puzzles in which all numbers move to different places, but I am no mathematician expert in group theory, and one method is sufficient for our purposes.
You might find swapping and shifting numbers trivial and uninteresting, but I might change your mind in the next section.
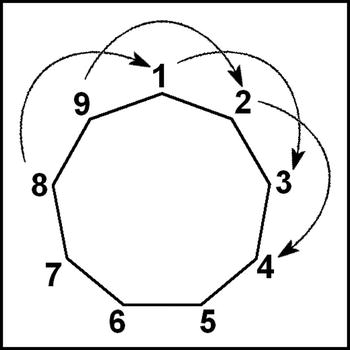
Figure 16-10. Shifting numbers
Rotating, Flipping, and Mirroring
Figure 16-11 shows you the same puzzle of Figure 16-3 after a rotation of 180o and Figure 16-12 shows you the same puzzle again after flipping (i.e., up-down mirroring).
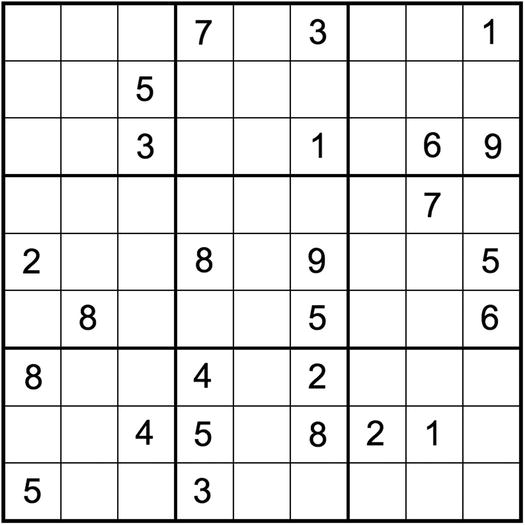
Figure 16-11. Puzzle of Figure 16-3 rotated 180°

Figure 16-12. Puzzle of Figure 16-3 flipped
You will agree with me that only a Sudoku champion would perhaps recognize that the two new puzzles are equivalent to the original one.
The rotations and reflections of a square (including a Sudoku grid) form a group that the mathematicians call D4. In practical terms, it means that you can obtain a new puzzle by doing one of the following seven operations: vertical flip (around a line in the middle of row 4, what I used to generate the puzzle of Figure 16-11), horizontal mirroring (around a line in the middle of column 4), clockwise rotation by 90o, rotation by 180o (what I used to generate the puzzle of Figure 16-10), counterclockwise rotation by 90o, diagonal flip (around the line through the bottom-left and top-right corners), and counter-diagonal flip (around the line through the top-left and bottom-right corners).
All in all, if you combine the eight possibilities you have by shifting numbers and the seven possibilities you have through rotation and flipping, you can generate 56 puzzles from the original one. Note that if you apply more than one operation, you don’t necessarily obtain more puzzles. For example, a rotation by 180o followed by a vertical flip has the same result as a horizontal mirroring.
Swapping Lines and Triplets of Lines
Question: if you swap two lines (either two rows or two columns), is the resulting puzzle still valid? The answer is yes, but only if you swap lines within the same blocks.
For example, if you swap rows 0 and 1 of the puzzle of Figure 16-3, you obtain the puzzle shown in Figure 16-13.

Figure 16-13. Puzzle of Figure 16-3 with the top two rows swapped
The new puzzle must be valid and have the same solution as the puzzle shown in Figure 16-3 but with the top two rows swapped. To convince yourself that this is the case, consider that there are two broad types of strategies: those that involve individual units, like the naked and hidden strategies, and those that involve alignment of cells across units, like box-line and rectangle, to name two. Clearly, the strategies based on single units are unaffected by the swapping. And as the content of the boxes remains unchanged, all alignments and chains of lines and cells will also be maintained. For example, a rectangle might become narrower or broader, but, when applicable before the swap, it will remain applicable after it.
There are six possible orderings of the three lines that cross the same three boxes (e.g., 012, 021, 102, 120, 201, and 210), and six triples of aligned boxes whose lines can be swapped in any order (boxes 012, 345, 678 horizontally, and 036, 147, and 258 vertically). This means that you can generate 36 different puzzles from each one that you directly create with the Generator. That said, be aware that the Generator might (but it is not said) generate these puzzles directly with a particular choice of pseudorandom seed. Given the number of possible puzzles, this eventuality is certainly rare, but you cannot rely on the fact that all puzzles you generate (or even directly create with the Generator) are unique. If you select a number of puzzles for a book or a web site, you have to check that they really are different from each other!
The considerations about swapping individual lines also apply to triplets of lines. For example, the puzzle shown in Figure 16-4 is the puzzle of Figure 16-3 but with boxes 1, 4, and 7 (i.e., the three central columns) swapped with boxes 2, 5, and 8 (i.e., the three rightmost columns) (see Figure 16-14).

Figure 16-14. Puzzle of Figure 16-3 with the central and rightmost column-triples swapped
As there are six triples of aligned boxes, you can generate 36 different puzzles, by arranging the horizontal triples (Top-Center-Bottom, TBC, CTB, CBT, BTC, BCT) and then the vertical ones (Left-Middle-Right, LRM, MLR, MRL, RLM, RML) in any order you like.
You can apply as many swaps as you like of either type and in any order. Note that the operations described in the section “Rotating, flipping, and mirroring” are a subset of the swapping operations. That is, you can rotate, flip, and mirror a puzzle by applying swapping, but not vice versa. For example, if you swap the row-triples TCB -> BCT and the row swaps 012 -> 210, 345 -> 543, and 678 -> 876, you obtain the same puzzle you would have obtained by a vertical flip of the original one.
Removing Different Numbers of Clues
To make the statistical analysis of puzzles and solutions, I first generated 30,000 puzzles with N_SET_QUADS == 5 and N_SET_PAIRS == 10. That is, I left N_SET_CELLS set to zero. If you had set N_SET_PAIRS == 9 (i.e., 1 less) and N_SET_CELLS set to 2 (i.e., 2 more), the puzzles generated with the same seed in the two cases would have been completely different.
Every time you change one, two, or all three of the N_SET_ parameters, the Generator produces different puzzles because it uses the pseudorandom number generator in different ways. If you want to remove a total of between, say, 40 and 56 cells (to obtain puzzles with a maximum of between 41 and 25 clues), you have 2,845 different combinations of the N_SET_ parameters, and the Generator produces 2,845 * 2,147,483,648 = 6,109,590,978,560 different puzzles. That said, to be 100% correct, some of the parameter combinations will generate identical puzzles. But this is true for every generator based on random numbers.
Listing 16-1 shows the algorithm to calculate the number of combinations.
Listing 16-1. Calculating the Number of Parameter Combinations
int kount = 0;
for (int n = 40; n <= 56; n++) {
int mq = n / 4;
for (int nq = 0; nq <= mq; nq++) {
int mp = (n - nq * 4) / 2;
for (int np = 0; np <= mp; np++) {
kount++;
}
}
}
printf("kount=%d ", kount);
Did you think I had used some combinatorial analysis? It would certainly be possible to do so but, as I said in Chapter 1, this is a practical book, not a scientific treaty, even if sometimes I get a bit (pun intended!) carried away by my fondness for statistics.
Summary
After reading this chapter, you know what puzzles you can create with the Generator and how you can multiply their number by a factor of thousands. Next, you will learn how to make fancy Sudokus that you never see in newspapers and seldom in bookstores.
