![]()
Implementing “Backtrack”
As I have already explained in Chapter 2, backtracking is a nice way of saying “guessing.” When you exhaust all strategies you know, you can only pick a cell that you haven’t yet solved and try out one of its candidates. If you reach a contradiction, you need to revert the Sudoku grid back to what it was before your arbitrary choice and try another candidate—hence the “back” of backtracking.
The Solver program with the analytical strategies illustrated in the previous chapters solved 99.85% of the 30,000 generated puzzles (see Chapters 14–16 for more details), but for the remaining 0.15%, backtracking was the only way of solving the puzzles. In 38 puzzles of 30,000, the Solver had to guess once. In six of the remaining puzzles, it had to guess twice.
Gordon Royle of the University of Western Australia maintains a web site dedicated to minimum Sudokus (http://staffhome.ecm.uwa.edu.au/~00013890/sudokumin.php)—that is, puzzles that contain exactly 17 clues. From the site you can download 49,151 minimum Sudokus (as of February 4, 2015) guaranteed to have unique solutions. Not surprisingly, many of them are quite difficult, and the Solver had to resort to backtracking in 1,918 cases. The most difficult of all (see Figure 13-1) needed eight guesses.
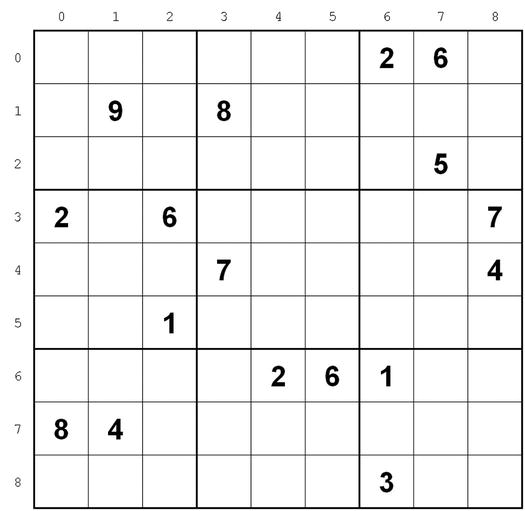
Figure 13-1. The hardest Sudoku
Among the list of minimum Sudokus, you will also find what could be the most difficult puzzle that can still be solved analytically, without guessing (see Figure 13-2). To find the solution, the Solver applied a sequence of 32 strategies (not in sequence and ignoring cleanup and naked single): 2 x naked pair, 3 x pointing line, 4 x unique-loop, 5 x box-line, 3 x pointing line, and 15 x XY-chain.

Figure 13-2. The hardest analytical Sudoku
Listing 13-1 shows how you can implement the backtrack strategy.
Listing 13-1. backtrack.c–Not Optimized
/* backtrack.c
*
* Copyright (C) 2015 Giulio Zambon - http://zambon.com.au/
*
*/
#include <stdio.h>
#include <stdlib.h>
#include "backtrack.h"
#include "cleanup_around.h"
#include "count_solved.h"
#include "def.h"
#include "display_strats_in_clear.h"
#include "solve.h"
#define MAX_DEPTH 10
int backtrack(int depth) {
#ifdef LOG_IN_OUT
printf("--- backtrack (%d) >>> ", depth);
#endif
int result = FALSE;
char grid_backup[9][9][10];
int done = FALSE;
// Select the cell
for (int k = 0; k < 9 && !done; k++) {
for (int j = 0; j < 9 && !done; j++) {
if (grid[k][j][0] > 1) {
// Process the cell
char *elem = grid[k][j];
if (!silent) {
for (int kd = 0; kd < depth; kd++) {
printf(" ");
}
printf("backtrack (%d): (%d,%d) has candidates", depth, k, j);
for (int i = 1; i <= 9; i++) {
if (elem[i]) printf(" %d", i);
}
printf(" ");
} // if (!silent..
int n_candidates = elem[0];
int n_failures = 0;
for (int i = 1; i <= 9 && !done; i++) {
if (elem[i]) {
// Save the current state of the grid
for (int k1 = 0; k1 < 9; k1++) {
for (int j1 = 0; j1 < 9; j1++) {
for (int i1 = 0; i1 <= 9; i1++) {
grid_backup[k1][j1][i1] = grid[k1][j1][i1];
}
} // for (int j1..
} // for (int k1..
// Force a solution
for (int i1 = 1; i1 <= 9; i1++) {
elem[i1] = FALSE;
}
elem[i] = TRUE;
elem[0] = 1;
int orig_silent = silent;
silent = TRUE;
cleanup_around(k, j);
// Attempt to solve the puzzle
solve();
silent = orig_silent;
// Check the result
int do_restore = FALSE;
if (problem_found) {
problem_found = FALSE;
do_restore = TRUE;
n_failures++;
if (!silent) {
for (int kd = 0; kd < depth; kd++) (" ");
printf("backtrack (%d): %d unsuccessful ", depth, i);
}
} // if (problem_found..
else {
if (!silent) {
for (int kd = 0; kd < depth; kd++) printf(" ");
printf("backtrack (%d): %d successful (%d solved) ",
depth, i, count_solved()
);
for (int kd = 0; kd < depth; kd++) printf(" ");
printf("backtrack (%d) strategies:", depth);
display_strats_in_clear();
printf(" ");
}
if (count_solved() == 81) {
strats_used[n_strats_used] = 40+depth;
n_strats_used++;
done = TRUE;
result = TRUE;
}
else {
int success = (depth < MAX_DEPTH)
? backtrack(depth + 1)
: TRUE
;
if (success) {
done = TRUE;
result = TRUE;
}
else {
do_restore = TRUE;
n_failures++;
}
}
} // if (problem_found.. else..
// If unsuccessful, restore the grid to
// its original content
if (do_restore) {
for (int k1 = 0; k1 < 9; k1++) {
for (int j1 = 0; j1 < 9; j1++) {
for (int i1 = 0; i1 <= 9; i1++) {
grid[k1][j1][i1] =
grid_backup[k1][j1][i1];
}
} // for (int j1..
} // for (int k1..
} // if (do_restore..
} // if (elem[i]..
} // for (int i..
// When all candidates fail, go back
if (n_failures == n_candidates) done = TRUE;
} // if (grid[k][j][0]..
} // for (int j..
} // for (int k..
#ifdef LOG_IN_OUT
printf("<<< backtrack (%d) --- ", depth);
#endif
return result;
}
The first two for-loops and the if-statement immediately inside them scan the Sudoku grid from the top-left corner and select the first unsolved cell. Then, the for-loop with control variable i and the if-statement that follows try out the candidates one by one.
To try a candidate out, backtrack() performs three steps: set the current candidate (i.e., the one identified by i) to solve its cell; attempt to solve the altered puzzle by executing solve(); and check whether solve() succeeds in finding the solution. If not, it sets i to the next candidate and tries again. Obviously, you must save the grid before each attempt and restore it after each failed attempt.
display_strats_in_clear() is a small function described in the next section. The name says it all.
To find out whether solve() is successful, backtrack() checks that the global variable problem_found has remained set to FALSE and that the number of solved cells has become 81.
You only set problem_found to TRUE within remove_candidate() (see Listing 3-10). This occurs when remove_candidate() removes the last candidate from a cell. Clearly, if a cell cannot contain any candidate, it means that the puzzle is impossible. That is, it means that backtrack() has chosen the wrong i.
If problem_found remains FALSE but the number of solved cells is less than 81, it means that one guess is not enough, and backtrack() must execute itself recursively on the partially solved puzzle. This happens in the following lines of code:
int success = (depth < MAX_DEPTH)
? backtrack(depth + 1)
: TRUE
;
if (success) {
done = TRUE;
result = TRUE;
}
else {
do_restore = TRUE;
n_failures++;
}
The limit of ten recursive calls is purely arbitrary. In fact, as I said at the beginning of this chapter about the hardest Sudoku, the highest value of depth I have ever seen is 8.
This is a straightforward utility function used only by backtrack() that converts the strategy codes of strategies from levels 0–3 into strategy names in clear (see Listing 13-2).
Listing 13-2. display_strats_in_clear.c
/* display_strats_in_clear.c
*
* Copyright (C) 2015 Giulio Zambon - http://zambon.com.au/
*
*/
#include <stdio.h>
#include <stdlib.h>
#include "def.h"
#include "display_strats_in_clear.h"
void display_strats_in_clear() {
for (int k = 0; k < n_strats_used; k++) {
int level = strats_used[k] / 10;
int k_strat = strats_used[k] - level * 10;
printf(" '%s'", strat_all_names[level][k_strat]);
}
printf(" ");
}
You might feel that choosing to begin backtracking with the first cell that has more than one candidate is not the most efficient choice.
Why not choose a cell with only two candidates? Then, either one of them must be correct. This is true, but consider that the amount of information you get when choosing between two alternatives is definitely less than what you get when the alternatives are more. That is, choosing between two candidates of a pair is more likely to leave some parts of the puzzle unsolved, which would force you to do further backtracking. Moreover, there might not be any pair in the puzzle. Therefore, backtrack() would need to be able to look for cells with three candidates when it doesn’t find any pair, for cells with four candidates if there are no cells with triples, and so on. This would make the function more complicated than it already is.
In view of the aforementioned considerations, you are probably better off when backtrack() starts from a cell with the maximum number of candidates. To do so, you need to replace or remove the lines of code highlighted in bold in Listing 13-1. The optimized version is shown in Listing 13-3, where the new lines are in bold.
Listing 13-3. backtrack.c–Optimized
/* backtrack.c
*
* Copyright (C) 2015 Giulio Zambon - http://zambon.com.au/
*
*/
#include <stdio.h>
#include <stdlib.h>
#include "backtrack.h"
#include "cleanup_around.h"
#include "count_solved.h"
#include "def.h"
#include "display_strats_in_clear.h"
#include "solve.h"
#define MAX_DEPTH 10
int backtrack(int depth) {
#ifdef LOG_IN_OUT
printf("--- backtrack (%d) >>> ", depth);
#endif
int result = FALSE;
char grid_backup[9][9][10];
// Select the cell
int k;
int j;
{
int max_i = -1;
int row_max_i;
int col_max_i;
for (k = 0; k < 9 && max_i < 9; k++) {
for (j = 0; j < 9 && max_i < 9; j++) {
if (grid[k][j][0] > max_i) {
max_i = grid[k][j][0];
row_max_i = k;
col_max_i = j;
}
}
}
k = row_max_i;
j = col_max_i;
}
// Process the cell
char *elem = grid[k][j];
if (!silent) {
for (int kd = 0; kd < depth; kd++) printf(" ");
printf("backtrack (%d): (%d,%d) has candidates", depth, k, j);
for (int i = 1; i <= 9; i++) {
if (elem[i]) printf(" %d", i);
}
printf(" ");
} // if (!silent..
for (int i = 1; i <= 9 && !result; i++) {
if (elem[i]) {
// Save the current state of the grid
for (int k1 = 0; k1 < 9; k1++) {
for (int j1 = 0; j1 < 9; j1++) {
for (int i1 = 0; i1 <= 9; i1++) {
grid_backup[k1][j1][i1] = grid[k1][j1][i1];
}
} // for (int j1..
} // for (int k1..
// Force a solution
for (int i1 = 1; i1 <= 9; i1++) {
elem[i1] = FALSE;
}
elem[i] = TRUE;
elem[0] = 1;
int orig_silent = silent;
silent = TRUE;
cleanup_around(k, j);
// Attempt to solve the puzzle
solve();
silent = orig_silent;
// Check the result
if (problem_found) {
problem_found = FALSE;
if (!silent) {
for (int kd = 0; kd < depth; kd++) (" ");
printf("backtrack (%d): %d unsuccessful ", depth, i);
}
} // if (problem_found..
else {
if (!silent) {
for (int kd = 0; kd < depth; kd++) {
printf(" ");
}
printf("backtrack (%d): %d successful (%d solved) ",
depth, i, count_solved()
);
for (int kd = 0; kd < depth; kd++) printf(" ");
printf("backtrack (%d) strategies:", depth);
display_strats_in_clear();
printf(" ");
}
if (count_solved() == 81) {
strats_used[n_strats_used] = 40 + depth;
n_strats_used++;
result = TRUE;
}
else if (depth < MAX_DEPTH) {
result = backtrack(depth + 1);
}
} // if (problem_found.. else..
// If unsuccessful, restore the grid to its
// original content
if (!result) {
for (int k1 = 0; k1 < 9; k1++) {
for (int j1 = 0; j1 < 9; j1++) {
for (int i1 = 0; i1 <= 9; i1++) {
grid[k1][j1][i1] = grid_backup[k1][j1][i1];
}
} // for (int j1..
} // for (int k1..
} // if (do_restore..
} // if (elem[i]..
} // for (int i..
#ifdef LOG_IN_OUT
printf("<<< backtrack (%d) --- ", depth);
#endif
return result;
}
As you can see, the function has become simpler, with fewer loops and fewer control variables. It is also more efficient.
Notice that backtrack() doesn’t solely rely on “brute force” to find a solution. Instead, it exploits solve(), which uses the analytical strategies. A 100% brute-force approach would try all possible numbers in a cell, all possible numbers in another cell, and so on, until a solution finally turned up. You could implement such a strategy very simply, but it would be very inefficient and would require a long time to find the solution. Moreover, it wouldn’t give you any indication of the comparative difficulty of the puzzles.
An Example
As an example, I want to show you a Sudoku that required the Solver to backtrack five times (i.e., to a maximum depth of 4).
The partially solved puzzle, after the analytical strategies have done their bit, is shown in Figure 13-3, with 24 cells solved.

Figure 13-3. A hard Sudoku—1
Listing 13-4 shows the backtracking log.
Listing 13-4. A Backtracking Log
backtrack (0): (6,3) has candidates 2 4 5 7 8 9
backtrack (0): 2 successful (27 solved)
backtrack (0) strategies:none
backtrack (1): (4,7) has candidates 3 4 5 6 7
backtrack (1): 3 unsuccessful
backtrack (1): 4 successful (30 solved)
backtrack (1) strategies:none
backtrack (2): (7,5) has candidates 3 5 6 8 9
backtrack (2): 3 successful (31 solved)
backtrack (2) strategies:none
backtrack (3): (8,1) has candidates 2 5 6 8 9
backtrack (3): 2 unsuccessful
backtrack (3): 5 successful (34 solved)
backtrack (3) strategies:none
backtrack (4): (0,2) has candidates 2 4 6 8
backtrack (4): 2 unsuccessful
backtrack (4): 4 unsuccessful
backtrack (4): 6 unsuccessful
backtrack (4): 8 unsuccessful
backtrack (3): 6 unsuccessful
backtrack (3): 8 unsuccessful
backtrack (3): 9 unsuccessful
backtrack (2): 5 unsuccessful
backtrack (2): 6 unsuccessful
backtrack (2): 8 unsuccessful
backtrack (2): 9 unsuccessful
backtrack (1): 5 unsuccessful
backtrack (1): 6 unsuccessful
backtrack (1): 7 unsuccessful
backtrack (0): 4 successful (26 solved)
backtrack (0) strategies:none
backtrack (1): (7,5) has candidates 2 3 5 6 8 9
backtrack (1): 2 unsuccessful
backtrack (1): 3 successful (27 solved)
backtrack (1) strategies:none
backtrack (2): (8,5) has candidates 1 2 5 6 8 9
backtrack (2): 1 successful (36 solved)
backtrack (2) strategies:none
backtrack (3): (4,7) has candidates 3 4 5 6 7
backtrack (3): 3 unsuccessful
backtrack (3): 4 unsuccessful
backtrack (3): 5 unsuccessful
backtrack (3): 6 unsuccessful
backtrack (3): 7 unsuccessful
backtrack (2): 2 unsuccessful
backtrack (2): 5 unsuccessful
backtrack (2): 6 unsuccessful
backtrack (2): 8 successful (32 solved)
backtrack (2) strategies:none
backtrack (3): (5,3) has candidates 1 2 5 7 9
backtrack (3): 1 unsuccessful
backtrack (3): 2 unsuccessful
backtrack (3): 5 unsuccessful
backtrack (3): 7 unsuccessful
backtrack (3): 9 unsuccessful
backtrack (2): 9 unsuccessful
backtrack (1): 5 successful (81 solved)
backtrack (1) strategies:none
sudoku: the final grid contains 81 solved cells
Let’s follow the first iterations. backtrack() chooses (6,3) to start doing its job because it is the first cell it finds with the maximum number of candidates (six). In an attempt to solve the cell, backtrack() sets it to 2, which is the lowest candidate in the cell (there is no reason to choose another candidate. The log reports that solve() removes some candidates by cleaning up around (6,3) but is not able to apply any other strategy (hence the strategy:none). This leaves the puzzle with 27 cells solved, as shown in Figure 13-4, where the updates are marked in gray.
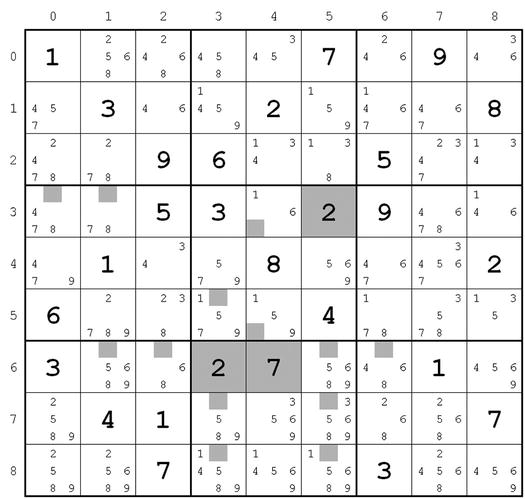
Figure 13-4. A hard Sudoku—2
As the number of solved cells is less than 81, backtrack() executes itself recursively. There are no more cells with six candidates, and the first one with five candidates is (4,7). The first possible number is 3, but it is unsuccessful. To see how this comes about, you can insert two lines into backtrack.c, which you will then remove after executing the Solver.
The first line is
if (depth == 1 && i == 3 && k == 4 && j == 7) silent = FALSE;
and you should insert it before the statement
solve();
It will cause the strategies to generate log entries during backtracking, which is not normally the case.
The second line aborts the Solver
if (depth == 1 && i == 3 && k == 4 && j == 7) exit(0);
and should go immediately before the comment
// If unsuccessful, restore the grid to its original content
What you get is a log the relevant parts of which are shown in Listing 13-5. The two lines in bold are those also highlighted in Listing 13-4.
Listing 13-5. The Log of a Wrong Choice When Backtracking
backtrack (1): (4,7) has candidates 3 4 5 6 7
unique_unit: 2 in (2,7) is unique within the row
unique_unit: removed 4 from (2,7)
unique_unit: removed 7 from (2,7)
cleanup_unit [column of (2,7)]: removed 2 from (7,7)
cleanup_unit [column of (2,7)]: removed 2 from (8,7)
unique_unit: 2 in (5,1) is unique within the box
unique_unit: removed 7 from (5,1)
unique_unit: removed 8 from (5,1)
unique_unit: removed 9 from (5,1)
cleanup_unit [column of (5,1)]: removed 2 from (8,1)
unique_unit: 2 in (7,6) is unique within the column
unique_unit: removed 6 from (7,6)
unique_unit: removed 8 from (7,6)
cleanup_unit [row of (7,6)]: removed 2 from (7,0)
unique_unit: 2 in (8,0) is unique within the box
unique_unit: removed 5 from (8,0)
unique_unit: removed 9 from (8,0)
unique_unit: 9 in (4,0) is unique within the box
unique_unit: removed 7 from (4,0)
cleanup_unit [row of (4,0)]: removed 9 from (4,3)
cleanup_unit [row of (4,0)]: removed 9 from (4,5)
cleanup_unit [column of (4,0)]: removed 9 from (7,0)
cleanup_unit [row of (7,0)]: removed 5 from (7,3)
cleanup_unit [row of (7,0)]: removed 5 from (7,4)
cleanup_unit [row of (7,0)]: removed 5 from (7,5)
cleanup_unit [row of (7,0)]: removed 5 from (7,7)
cleanup_unit [column of (7,0)]: removed 5 from (1,0)
cleanup_unit [box of (7,0)]: removed 5 from (6,1)
cleanup_unit [box of (7,0)]: removed 5 from (8,1)
unique_unit: 8 in (5,6) is unique within the column
unique_unit: removed 1 from (5,6)
unique_unit: removed 7 from (5,6)
cleanup_unit [row of (5,6)]: removed 8 from (5,7)
cleanup_unit [box of (5,6)]: removed 8 from (3,7)
unique_unit: 5 in (0,1) is unique within the box
unique_unit: removed 8 from (0,1)
cleanup_unit [row of (0,1)]: removed 5 from (0,3)
cleanup_unit [row of (0,1)]: removed 5 from (0,4)
unique_unit: 1 in (1,6) is unique within the column
unique_unit: removed 4 from (1,6)
unique_unit: removed 7 from (1,6)
cleanup_unit [row of (1,6)]: removed 1 from (1,3)
cleanup_unit [row of (1,6)]: removed 1 from (1,5)
cleanup_unit [box of (1,6)]: removed 1 from (2,8)
unique_unit: 8 in (0,3) is unique within the row
unique_unit: removed 4 from (0,3)
cleanup_unit [column of (0,3)]: removed 8 from (7,3)
cleanup_unit [row of (7,3)]: removed 9 from (7,4)
cleanup_unit [row of (7,3)]: removed 9 from (7,5)
cleanup_unit [column of (7,3)]: removed 9 from (1,3)
cleanup_unit [column of (7,3)]: removed 9 from (5,3)
cleanup_unit [column of (7,3)]: removed 9 from (8,3)
cleanup_unit [box of (7,3)]: removed 9 from (6,5)
cleanup_unit [box of (7,3)]: removed 9 from (8,4)
cleanup_unit [box of (7,3)]: removed 9 from (8,5)
cleanup_unit [column of (0,3)]: removed 8 from (8,3)
cleanup_unit [box of (0,3)]: removed 8 from (2,5)
unique_unit: 9 in (1,5) is unique within the row
unique_unit: removed 5 from (1,5)
unique_unit: 5 in (1,3) is unique within the box
unique_unit: removed 4 from (1,3)
cleanup_unit [column of (1,3)]: removed 5 from (4,3)
cleanup_unit [row of (4,3)]: removed 7 from (4,6)
cleanup_unit [row of (4,6)]: removed 6 from (4,5)
cleanup_unit [column of (4,5)]: removed 5 from (6,5)
cleanup_unit [row of (6,5)]: removed 6 from (6,1)
cleanup_unit [row of (6,1)]: removed 9 from (6,8)
cleanup_unit [column of (6,1)]: removed 9 from (8,1)
cleanup_unit [row of (8,1)]: removed 6 from (8,4)
cleanup_unit [row of (8,1)]: removed 6 from (8,5)
cleanup_unit [row of (8,1)]: removed 6 from (8,7)
cleanup_unit [row of (8,1)]: removed 6 from (8,8)
cleanup_unit [row of (6,5)]: removed 6 from (6,6)
cleanup_unit [row of (6,6)]: removed 4 from (6,8)
cleanup_unit [column of (6,6)]: removed 4 from (0,6)
cleanup_unit [row of (0,6)]: removed 6 from (0,8)
cleanup_unit [column of (0,6)]: removed 6 from (4,6)
*** No candidates left in (4,6)
strategy: after 'unique-loop' the grid contains 53 solved cells
backtrack (1): 3 unsuccessful
When remove_candidate() logs “no candidates left in (4,6),” it also sets the variable problem_found to TRUE. This causes backtrack() to log that 3 was unsuccessful and to try 4. This happens at depth 1. When depth 4 is reached, all four candidates of cell (0,2) fail. This means that the Sudoku is unsolvable and backtrack() must go back to depth 3 and try the next available candidate. When all candidates of depth 3, 2, and 1 also fail to provide a solution, backtrack() goes back to depth 0 and tries the second candidate (i.e., a 4) of cell (6,3). When backtrack() reaches depth 3, it discovers that all candidates in (4,7) fail. It keeps going up and down in depth until it manages to solve all 81 cells.
It turns out that the Solver only needs two guesses to solve the puzzle, as shown in Table 13-1.
Table 13-1. The Solving Guesses
|
Depth |
cell |
number |
|---|---|---|
|
0 |
(6,3) |
4 |
|
1 |
(7,5) |
5 |
Summary
This chapter has told you how to solve analytically unsolvable puzzles. You now know how a computer program can solve all puzzles, even if it needs to resort to guessing. In Chapter 14, you will learn what to do when you have thousands (or more) of puzzles to solve.
