![]()
The Strategies
Not all strategies are created equal. When solving a Sudoku puzzle manually it makes sense to use simpler strategies as long as they result in candidate removals and cell solutions, and only then move to more complex strategies. Obviously, there is no reason for making the same distinction when writing a computer program to solve Sudokus. And yet, that is precisely how I structured my Sudoku-solving program. The reason is that I want to use the Sudoku Solver to estimate the difficulty of Sudoku puzzles. If the program applied more complex strategies before achieving what is possible with simple ones, it would be impossible to know whether the complex strategies were needed at all.
Let’s go about this systematically.
I group Sudoku-solving strategies in five levels of increasing complexity, which I number from 0 to 4.
Level 0 Strategies
Level 0 strategies are those that every Sudoku beginner knows and applies. They are naked single, unique, and cleanup (my naming convention).
The Strategy Naked Single
If a cell only has a single candidate, that candidate solves the cell. This is obvious: if there are no other possible candidates in a cell, the only one present must be it. I hesitated before including this strategy in the list because it is trivial. But I then decided to mention it because if you decided to modify the Solver or the Generator, perhaps to make them more efficient, you might choose to flag solved cells in a special way. By flagging the cell, you would effectively be implementing naked single. Being aware of it could help you to structure the software more consistently.
If you find a candidate for a particular number in a single cell of a unit, the candidate must solve the cell. For example, suppose that looking at all cells of box 4 you find out that the only candidate 2 of the box is in (5,3). As there must be a 2 in every box, it means that the 2 in (5,3) must be the 2 for that box, and you can remove all other candidates from that cell.
When you solve a cell, the number that solves it cannot be a candidate anywhere else in any of the units to which the cell belongs. For example, if (0,4) solves to a 3, you can remove the candidate 3s from all the cells of row 0, column 4, and box 1.
When removing a candidate from a cell, it could be that it was one of only two candidates in that cell. If that is the case, by removing it, you leave the cell with a single candidate, which means that the naked single strategy applies. For example, if (2,7) contains two candidates, 1 and 3, and you remove the 3, it is clear that 1 must solve the cell.
It could also be that the candidate you have removed was one of only two candidates for a particular number in a unit. In that case, the unique strategy applies to the remaining candidate. For example, if you remove a 3 from cell (2,7), it could be that only one candidate 3 is left in column 7, say, in (8,7). In that case, 3 must solve (8,7), otherwise there wouldn’t be any 3 at all in column 7.
Obviously, you must do a cleanup whenever you solve a cell. Otherwise, there is a good chance that you keep considering as possible some candidates that are not.
All in all, it makes sense to apply naked single and unique whenever you remove a candidate, followed by a cleanup if naked single or unique solves a cell. This often results in a chain of removals that can completely solve easy Sudokus. (See, for example, Figure 2-1).

Figure 2-1. An easy Sudoku
And following is the beginning of the Solver’s log:
unique_unit: 5 in (4,0) is unique within the column
unique_unit: removed 3 from (4,0)
unique_unit: removed 6 from (4,0)
unique_unit: removed 8 from (4,0)
unique_unit: removed 9 from (4,0)
cleanup_unit [row of (4,0)]: removed 5 in (4,3)
cleanup_unit [row of (4,0)]: removed 5 in (4,4)
cleanup_unit [row of (4,0)]: removed 5 in (4,5)
unique_unit: 4 in (2,1) is unique within the box
unique_unit: removed 1 from (2,1)
unique_unit: removed 8 from (2,1)
cleanup_unit [row of (2,1)]: removed 4 in (2,4)
...
I don’t show the whole log because it is 158 lines long. But you get the idea: the functions unique_unit() and cleanup_unit() keep executing until all candidates have been removed, without any need of more complex strategies. The log doesn’t show any entry marked “naked single” because when a single candidate remains in a cell, besides “cleaning up” around it, the program doesn’t need to execute any additional function.
Level 1 Strategies
Level 1 strategies are those that most Sudoku players easily discover on their own. They are naked pair, hidden pair, box-line, and pointing line.
If two cells in the same unit only contain the same two candidates, it means that one of those candidates will solve one of the two cells, and the other candidate will solve the other cell. Therefore, you can remove the same candidates from all other cells of the unit.
For example, suppose that box 3 has reached the point shown in Figure 2-2.

Figure 2-2. A naked pair
The two cells (4,0) and (4,2) contain the naked pair 8 and 9. If 8 solves (4,0), then 9 must solve (4,2). On the other hand, if 8 solves (4,2), then 9 must solve (4,0). In either case, both 8 and 9 are used. Therefore, you can remove the 8s in cells (5,0), (5,1), and (5,2) as well as the 9s in cells (3,1) and (3,2).
If two candidates only appear in two cells of a unit, it means that one of those candidates will solve one of the two cells, and the other candidate the other cell. Therefore, you can remove all other candidates in the two cells.
Consider for example the row shown in Figure 2-3.

Figure 2-3. A hidden pair
Notice that the candidates 2 and 3 only appear in column 0 and 5. Either the 2 is in 0 and the 3 in 5 or vice versa. In either case, cell 0 cannot contain either 1 or 8, and cell 5 cannot contain either 5 or 8. It means that you can “strip” the 2–3 pairs in columns 0 and 5 and leave them naked. The name “hidden” comes from the fact that the two candidates of the pair are hidden among other candidates.
When a specific candidate within a row or a column only occurs in a single box, one of those occurrences must be a solution. Therefore, you can remove the same candidate from all other cells of the same box.
To understand how this strategy works, refer to the partial Sudoku shown in Figure 2-4.

Figure 2-4. A box-line configuration
All 5s of row 7 are within box 6. Therefore, 5 must solve either (7,0) or (7,2). Otherwise, there would be no 5 in row 7. As a result, you can remove the 5s from (6,0) and (8,0).
This strategy is often named pointing pair, but I prefer to call it pointing line because the action of pointing might actually be done by a triple instead of a pair. It works as follows: when all the cells containing a particular candidate within a box belong to the same line (row or column), you can remove the candidates for the same number that appear in the line but outside that box. I know, it sounds complicated. Let’s look at the example shown in Figure 2-5.

Figure 2-5. A pointing line configuration
All 5s of box 6 are within row 7. Therefore, 5 must solve either (7,0) or (7,2). Otherwise, there would be no 5 in box 6. As a result, you can remove the 5s from (7,7) and (7,8) because there cannot be more than one 5 in row 7, and you know that either (7,0) or (7,2) is a 5.
This strategy is in a sense symmetrical to the box-line strategy that I described in the previous section. Both strategies rely on a candidate that appears in the three-cell intersection of a box with a line, but box-line lets you remove some candidates from the box when the candidates do not appear anywhere else in the intersecting line, while pointing line lets you remove some candidates from the line when the candidates do not appear anywhere else in the intersecting box.
Level 2 Strategies
Level 2 strategies are more complex than level 1 strategies. The patterns of candidates that let you apply the strategies are not easy to identify. The strategies are naked triple, hidden triple, lines-2, naked quad, and Y-wing.
The Strategies Naked Triple and Naked Quad
These are extensions of the naked pair strategy to triplets and quadruplets of candidates.
Naked triple: if three cells in the same unit only contain the same three candidates, it means that one of those candidates will solve one of the three cells, another candidate will solve a second cell, and the third candidate will solve the remaining cell. Therefore, you can remove the same candidates from all other cells of the unit.
Naked quad: if four cells in the same unit only contain the same four candidates, it means that one of those candidates will solve one of the four cells, another candidate will solve a second cell, yet another candidate will solve a third cell, and the fourth candidate will solve the remaining cell. Therefore, you can remove the same candidates from all other cells of the unit.
Now, theoretically, you could have a naked strategy with more than four cells, but they are so unlikely that it isn’t worth considering them.
This is an extension of the hidden pair strategy to triplets of candidates. If three candidates only appear in three cells of a unit, it means that one of those candidates will solve one of the three cells, another candidate will solve a second cell, and the third candidate will solve the remaining cell. Therefore, you can remove all other candidates in the three cells.
It sounds very similar to naked triple, but hidden triple lets you remove candidates from the cells that contain the triplets of candidates, while naked triple lets you remove candidates from the cells of the unit that do not contain the triplets.
The situations in which you can apply this strategy are very unlikely—so unlikely, that it would be unreasonable to consider a hidden quad strategy.
You might argue that, unlike us humans, a program wouldn’t mind scanning a Sudoku for very unlikely strategies. Sooner or later, it might be the only way of solving a difficult Sudoku without having to guess. Perhaps, but I don’t like the idea of programming strategies that a human being would never apply. In one of the next chapters, you will see the code for hidden pair and hidden triple. I’ll leave it up to you to write hidden quad, if you feel like it.
The Strategy Lines-2
This strategy is also called X-wing. If you find a particular candidate in the same two rows (i.e., positions) within two columns, you can remove that candidate from the other cells of those two rows. (See Figure 2-6 for an example.)

Figure 2-6. Lines-2 (columns)
Notice that in columns 0 and 8 all candidates for 4 are in the two rows 2 and 5. That is, there are candidates for 4 in the four cells (2,0), (2,8), (5,0), and (5,8). If the 4 of column 0 is in (2,0), it means that there cannot be a 4 in either (2,8) or (5,0). Therefore, there must be a 4 in (5,8). If, on the other hand, the 4 of column 0 is in (5,0), it means that the 4 of column 8 is in (2,8). In either case, you have identified cells in row 2 and row 5 whose solution must be a 4. As a result, you can remove all the candidates for 4 in rows 2 and 5 that are not in columns 0 and 8. These are the grayed cells in Figure 2-6. To be completely clear, you can remove the 4 from (2,7), (5,2), and (5,6).
Obviously, the same applies if you swap rows and columns: if in two rows all the cells that contain a particular candidate are in the same two columns, you can remove that candidate from the other cells of those two columns.
On the web there are many explanations of the Y-wing strategy, but none seems to go to the core of the issue. The only clear statement I found was that Y-wing doesn’t solve cells but only eliminates possible candidates. Correct, but not of much help.
To apply the Y-wing strategy you need to look for cells that contain only two candidates each. Among those cells, you need to find three cells that satisfy the following two conditions:
- The arrangement of candidates in the cells is AB, AC, and BC. That is, no two cells have the same pair of candidates.
- The cells are in two intersecting units. This is equivalent to say that the two wing cells cannot share any unit, and it can only happen in two ways: row+column (one of the cells shares the row with one of the other two cells and the column with the third one) and line+box, where “line” stands for either “column” or “row” (one of the cells shares the line (row or column) with one of the other two cells and the box with the third one).
In other words, you can apply Y-wing when you find a chain of three cells containing all possible different pairs that can be formed with three candidates, whereby two cells are said to be “chained” when they belong to the same unit and one (and only one) of their two candidates is identical.
You will see in the next section of this chapter that if the chain of cells is longer than three, Y-wing becomes the more general strategy XY-chain.
When both conditions are satisfied, you have one of the two configurations shown in Figures 2-7 and 2-8.

Figure 2-7. Y-wing row+column

Figure 2-8. Y-wing line+box
The four boxes shown in Figure 2-7 can be adjacent to each other or not. Regardless of what numeric candidates correspond to A, B, and C, one of the candidates appears in both of the two “wings.” In the example, it is C. If, at a later stage, you find out that the solution for the intersection cell (i.e., the cell that, at this stage, contains the candidates A and B) is A, C must be in the bottom-left cell. If, on the other hand, the intersection cell turns out to solve into B, C must be in the top-right cell. In either case, the grayed cell cannot contain C.
In the example in Figure 2-8, the line containing one of the pairs is in the top row of a box, and the box is the left one. But the row could be in the middle or at the bottom of the box, and the box could be on the right. Also, you could rotate the diagram by 90 degrees and have column-box configurations. You can easily verify that regardless of whether the intersection cell turns out to solve into A or B, the grayed cells cannot contain a C.
Level 3 Strategies
Level 3 strategies are complex, and only clever Sudoku solvers can discover them on their own. They are XY-chain, rectangle, lines-3, and lines-4.
As I already mentioned, X Y-chain is a generalization of Y-wing. Essentially, instead of looking for a chain of three pairs, you look for longer chains in which the intersection cell of the Y-wing is expanded to a chain. The chain can be surprisingly long, as shown in Figures 2-9 to 2-11.

Figure 2-9. XY-chain 1

Figure 2-10. XY-chain 2

Figure 2-11. XY-chain 3
In Figure 2-9, the cells highlighted in gray are the cells from which you can remove candidates for 1. If cell (4,4) contains a 1, the grayed cells cannot contain 1s. If, on the other hand, cell (4,4) contains a 2, it means that cell (4,7) must contain a 3, (1,7) a 4, ..., and (6,4) a 1. Therefore, again, the grayed cells cannot contain 1s. Without knowing whether the 1 of column 4 is in row 4 or in row 6, you can safely remove all 1s from the grayed cells.
In Figure 2-10, you can only exclude the presence of a 1 in cell (4,7). But notice that the chain consists of 14 cells. Also note that some of the cells contain the same pair. In fact, it is possible for most of the cells of a chain to contain the same candidates. The fact that the chain is so long shouldn’t deter you from attempting to apply this method. You only need to ignore all cells that contain more than two candidates (and, obviously, the cells that are already solved); start from the top-left cell, see whether you can chain it to another cell with two candidates, and keep going until you hit a cell of which the second candidate is identical to the first one of the first cell of the chain.
Obviously, it will often happen that you don’t manage to build a chain. If so, look at the next cell with exactly two candidates and try again.
Figure 2-11 shows another example.
Notice that most pairs are identical. I have only written them alternatively as 23 and 32 to highlight the chain.
There is still one thing I would like to tell you about chains: they are not always unique. Look, for example, at Figure 2-12.
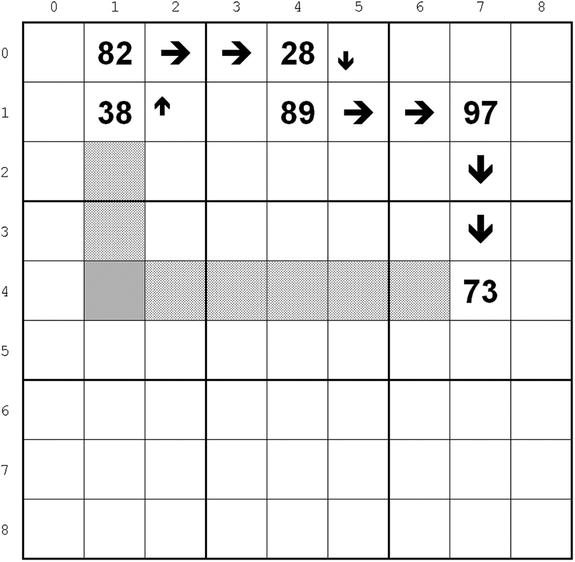
Figure 2-12. Chain with redundant cells
To connect (1,1) with (4,7), there was no need to go from (1,1) to (0,1), (0,4), and (1,4). The chain could have gone directly from (1,1) to (1,4). So, why take the detour? There is no reason. It might be argued that the alternate chain, being shorter, is “nicer,” but either chain is perfectly valid.
If the cells containing a particular candidate outline a rectangle with its vertices in four different boxes, the vertices cannot contain the candidate. For example, consider the configuration shown in Figure 2-13 (only the candidates for 5 are shown).

Figure 2-13. The rectangle strategy
If (1,0) contains a 5, then (1,4) cannot. Therefore, (2,5) must. Then, in box 7 there can only be a 5 in (7,4), and in box 6 there can only be a 5 in (6,0). But, as column 0 would end up with two 5s (one in row 6 and the initial one in row 1), your premise must be wrong, and (1,0) cannot contain a 5. Similarly, (7,0) cannot contain a 5 either.
Notice that there can be many more 5 candidates, but, for the strategy to apply, it seems that the candidates in the four boxes with the vertices of the rectangle must be on the edge of the rectangle, as highlighted in Figure 2-14. But that is actually not always true, as shown in the example in Figure 2-15.

Figure 2-14. A full rectangle
Figure 2-15 is almost identical to Figure 2-13. I only moved the candidate from (6,0) to (6,1), but the candidate for 5 in (7,0) can still be removed although (6,1) is inside the rectangle. There is a difference, though: the candidate in (1,0) can no longer be removed.
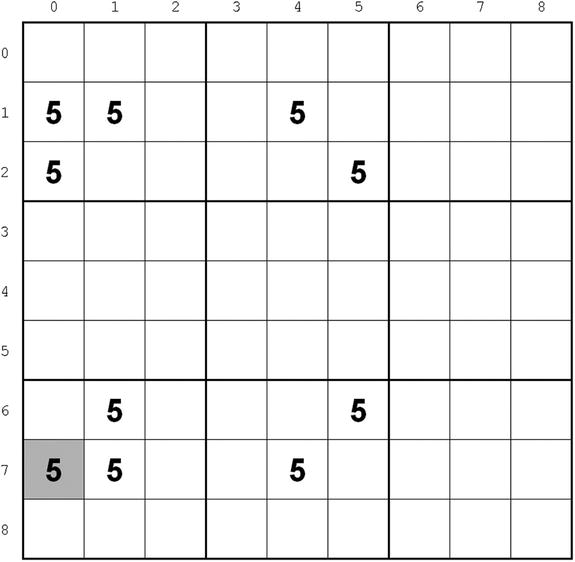
Figure 2-15. A not-hollow rectangle
To complete the section on the rectangle strategy, I would like to show you that there are some cases in which a candidate can be outside the rectangle without invalidating the strategy, as shown in Figure 2-16.
The candidate in (7,1) can be removed although there are nine candidates outside the rectangle: (0,1), (0,5), (6,0), (6,5), (7,0), (8,0), (8,1), (8,2), and (8,5).

Figure 2-16. A rectangle with something more
The Strategies Lines-3 and Lines-4
These two strategies are generalizations of the level 2 strategy lines-2. Lines-3, which is also known as Swordfish, applies to three lines what lines-2 applies to two. If you find all the cells with a particular candidate in the same three rows (or columns) of three columns (or rows), you can remove that candidate from the other cells of those three rows (columns). See Figure 2-17 for an example, this time with rows instead of columns.
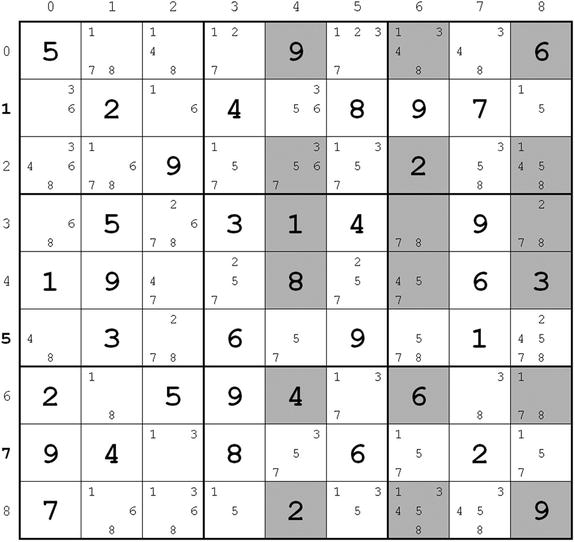
Figure 2-17. Lines-3 (rows)
Notice that in rows 1, 5, and 7 the candidates for 5 are in the three columns 4, 6, and 8. You can examine all possibilities by building a small table in which you list the column IDs of the 5s for each one of the three rows (see Table 2-1, where A, B, C, and D are arbitrary names to identify the possibilities).
Table 2-1. Lines-3 Possibilities

As you can see, regardless of how you choose the columns in which to place the 5s in the three rows (e.g., in case A, you choose to place the 5s in column 4 of row 3, column 6 of row 5, and column 8 of row 7), there is always a 5 in column 4, one in column 6, and one in column 8. How could it be otherwise? You need a 5 in each row and you have exactly three columns to choose from! Notice that in row 1 the 5 can only be in two of the three columns, but that is OK. The important thing is that the 5s of each row are confined to the same three columns. It doesn’t matter that one or more of them are missing.
I am going into so much detail because this strategy is not easy to visualize. In any case, as you know that the columns 4, 6, and 8 already have a 5 in one of the rows 1, 5, and 7, you can remove the 5s from all the other cells of columns 4, 6, and 8 (grayed in Figure 2-17) —that is, from (2,4), (2,8), (4,6), and (8,6).
Lines-4 is like lines-2 and lines-3 but with four rows (or columns). If you find four rows (or columns), each with two, three, or four candidates for a particular number and all the candidates are in the same four columns (rows), you can remove the candidates for the same number from all other cells of the same columns (rows).
Level 4 Strategies
There is only one level 4 strategy, and that is backtrack. Backtrack is nothing more and nothing less than trial and error, and it is the last resort when everything else fails. It is not so satisfying to resort to random choices and see whether they lead to a solution, but—brace yourself—there are Sudokus that cannot be solved with any combination of the strategies I listed in the previous sections. Perhaps they could be solved with strategies of which I am not aware. If you discover or hear of a strategy that I have not included, I would like to know about it.
You might have read about coloring as a strategy for solving Sudokus. But coloring is only a way of making the discovery of chains easier. That’s why I haven’t introduced it as a separate strategy.
The only reason for dividing strategies into levels of complexity is to select them separately when solving a puzzle. As you will see, the Sudoku Solver keeps trying all strategies of one level before attempting any individual strategy of a higher level. That is, it only attempts a strategy of a certain level of complexity when no strategy of a lower level succeeds in removing a single candidate (let alone solving a cell). This ensures that the Solver only attempts more complex strategies when strictly necessary.
Summary
In this chapter, I described the strategies that the Sudoku Solver applies and explained how they work. In Chapter 3, I’ll talk about the Solver’s main program and general utility functions.
