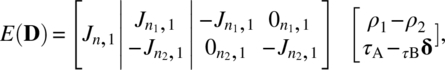Chapter 7
Two-Period Cross-Over Designs with Residual Effects
7.1 INTRODUCTION
Two-period CODWR using two treatments introduced by Grizzle were extensively used in pharmaceutical studies until the early 1970s. These designs consist of using two sequences of treatments (A, B) and (B, A) on n1 and n2 experimental units.
This design has an intuitive appeal to the clinicians in that each patient acts as his or her own control, resulting in
- Elimination of between-patient variation
- Reduction in sample size
- Reduction in cost due to fewer patients
However, several anomalies and controversies surround these designs. These designs are severely criticized for not accounting for the interaction between the periods and sequences of treatments used in the experiment or the carryover effect. The carryover effect may exist due to an inadequate washout period. In the presence of a carryover effect, the estimated treatment effect may be biased. However, if we can assume the carryover effect to be negligible in size, then one can proceed using this design (Huitson et al., 1982; Jones and Kenward, 2003). Brown (1980), Hills and Armitage (1979) and Grizzle (1965) recommend that if carryover effects are not negligible, a parallel design should be used, or if a cross-over design has been used, then the analysis should only be based on the first-period data. However, (Willan and Pater, 1986) disagree with this advice. Their view is that ‘the amount of carryover effect required to make a parallel group design worthwhile is substantial.’
In Grizzle’s (1965) procedure, a preliminary test of the hypothesis of equal carryover effects is tested at a higher level of significance. If the null hypothesis is rejected, the first-period data alone are used for treatment comparison. If the null hypothesis is not rejected, data from both periods are used for testing the hypothesis of equal treatment effects. Several authors have commented about the preliminary test. They feel that there may be inadequate power for testing the hypothesis of no difference in carryover effects, especially in small sample sizes (see Armitage and Hills, 1982; Brown, 1980; Kenward and Jones, 1987; Willan and Pater, 1986). Jones and Kenward (2003), Patel (1983) and Hills and Armitage (1979) have shown that this power can be improved through the use of baseline measurements or covariates.
For further discussion on these issues, the interested reader is referred to Brown (1978, 1980), Dubey (1986), Senn (1992, ), and Jones and Kenward (2003).
Ignoring the controversy, the design has interesting statistical problems, and they will be discussed in this chapter. The parametric and nonparametric methods of analysis for these designs will be discussed in Sections 7.2 and 7.3. Balaam’s designs will be provided in Section 7.4, and numerical examples will be given in Section 7.5.
7.2 Two-Period, Two-Treatment CODWR Analysis: Parametric Methods
Let n = n1 + n2 and let (A, B) and (B, A) be called sequences 1 and 2, respectively. Let Yiju be the observation in the uth period on the jth experimental unit in the ith sequence and let
where d(u, i) is the treatment applied in the uth period in the ith sequence, μ is the general mean, ρu is the uth period effect, γij is the jth unit effect receiving the ith sequence of treatments, τd(u,i) is the direct effect of the treatment d(u, i), δd(u–1,i) is the first-order residual effect of the treatment d(u - 1, i), and eiju are random errors distributed IIN (0, σ2), u=1, 2; j=1, 2, …, ni; i=1, 2. We take d(0, i) to be empty and δd(0, i) to be 0. Without loss of generality, for the purpose of analysis, assume that the first n1 units receive the treatment sequence 1 so that the matrices L, M, L*, M*, and S of Section 6.2 become
If the experimental units are not randomly selected from a population and are fixed effects, the analysis will be performed as discussed in Section 6.2, and we obtain
thereby implying that no parametric function of τ’s and δ’s is estimable. This can be verified in another way. Let  and let
and let
where ![]() and
and

Numbering the columns of X as X1, X2, X3, X4, …, Xn + 3, Xn + 4, Xn + 5, Xn + 6, Xn + 7, we note that
and that ρ1 – ρ2 is nonestimable, because column condition (7.2.5) is violated when X is augmented by
This result is true for any CODWR as indicated in Chapter 6. Again, we note that
and τA - τB is nonestimable because the condition (7.2.7) is violated when X is augmented by
For a similar reason, δA – δB is also nonestimable.
However, if the experimental units are randomly selected, γij are distributed IIN(0, ![]() ), and assuming γij and eij are independent, the model (7.2.4) reduces to
), and assuming γij and eij are independent, the model (7.2.4) reduces to
where β*′ = (μ, ρ1, ρ2, τA, τB, δA, δB) and
Using the design matrix X*, it can be easily verified that ρ1 - ρ2 is sill nonestimable, while the contrasts τA - τB and δA - δB are both estimable.
Interestingly, Grizzle (1965) showed that τA - τB and δA - δB are estimable even when γij are fixed effects but satisfy the conditions ![]() and
and ![]() . These two conditions on γij do not appear to be the consequence of reparameterization of the model (7.2.1), and hence, their validity is questionable. The authors feel that the units must be randomly selected in these two-period, two-treatment, two-sequence CODWR.
. These two conditions on γij do not appear to be the consequence of reparameterization of the model (7.2.1), and hence, their validity is questionable. The authors feel that the units must be randomly selected in these two-period, two-treatment, two-sequence CODWR.
7.2.1 Analysis of the design based on the model (7.2.9)
Clearly,
where
Put ![]() ,
, ![]() ,
, ![]() , and
, and ![]() By taking the parametric relations
By taking the parametric relations ![]() , τA + τB = 0, n1δA + n2δB = 0, and using the notation of Section 6.2 for the model (7.2.9), we get the normal equations (7.2.13):
, τA + τB = 0, n1δA + n2δB = 0, and using the notation of Section 6.2 for the model (7.2.9), we get the normal equations (7.2.13):
where G is the overall total, P′ = (P1, P2), T′ = (TA, TB), R′ = (RA, RB), Pi(i = 1, 2) is the ith period total, Tg(g = A, B) is the gth treatment total, and Rh(h = A, B) is the response total in the succeeding period of the period in which the hth treatment is used.
After some tedious algebra, we get the b.l.u.e. of τA - τB and δA - δB from the normal equations (7.2.13), and they are
and
The variances of the estimators given in Equations (7.2.14) and (7.2.15) are, respectively,
and
We can estimate ![]() as the pooled variance of the sample data {Y1j1} and {Y2j1} and is
as the pooled variance of the sample data {Y1j1} and {Y2j1} and is
Using the b.l.u.e. of Equation (7.2.14) and the estimated variance obtained from Equations (7.2.16) and (7.2.18), we can construct a t-test to test the null hypothesis
against the one- or two-sided alternatives.
Let
Assuming δA=δB, we estimate ![]() as the pooled variance of the data {s1j} and {s2j} and is
as the pooled variance of the data {s1j} and {s2j} and is
where ![]() , i=1, 2.
, i=1, 2.
Using the b.l.u.e. of Equation (7.2.15) and the estimated variance given by Equations (7.2.17) and (7.2.21), we can construct a t-test to test the null hypothesis
against the one- or two-sided alternatives. We can also construct confidence intervals for the contrasts τA - τB and δA - δB by standard methods.
Surprisingly, the estimators (Eqs. 7.2.14 and 7.2.15) are free of the nuisance parameters σ2and ![]() . Further, the estimator of τA - τB is not using the cross-over nature of the design, defeating the purpose of introducing cross-over designs. In Subsection 7.2.3, an estimator of τA - τB using the cross-over nature of the design is provided.
. Further, the estimator of τA - τB is not using the cross-over nature of the design, defeating the purpose of introducing cross-over designs. In Subsection 7.2.3, an estimator of τA - τB using the cross-over nature of the design is provided.
7.2.2 Decomposition of the model (7.2.9) into intra- and interunit components
Consider the model (7.2.9) and put sij as in Equation (7.2.20) and
Here, ![]() and Var(dij)=2σ2. Let
and Var(dij)=2σ2. Let ![]() and
and ![]() .
.
Based on the model (7.2.9), and using the parametric constraints given in Subsection (7.2.1), we have
which can be called as an interunit model, and
which can be called as an intraunit model. By using R in the subscripts of the least squares estimators of interunit model (7.2.24) and a subscript F for intraunit model (7.2.25), we can verify that
and that
It can be easily seen that ρ1 - ρ2, τA - τB, and δA - δB are not estimable from intraunit model (7.2.25), while δA - δB is estimable from interunit model (7.2.24), but τA - τB and δA - δB are nonestimable.
It is interesting to observe that ![]() and the function, τA - τB, which is nonestimable in intra- and interunit model, becomes estimable in the general model (7.2.9). The results in this subsection are based on the work of Mercado (1976) and Khatri, Raghavarao, and Mercado (1981).
and the function, τA - τB, which is nonestimable in intra- and interunit model, becomes estimable in the general model (7.2.9). The results in this subsection are based on the work of Mercado (1976) and Khatri, Raghavarao, and Mercado (1981).
7.2.3 Estimating direct effects contrast using cross-over nature of the treatments
If δA – δB = 0, then ![]() can be estimated by
can be estimated by ![]() given in Equation (7.2.28):
given in Equation (7.2.28):
with variance
The estimator (7.2.28) clearly uses the cross-over nature of the experiment, subject to the severe condition that both treatments produce equal amounts of residual effects. We estimate σ2 as the pooled variance of the samples {d1j}, j=1, 2, …, n1, and {d2j}, j=1, 2, …, n2.
Cox (1958) and Grizzle (1965) advocate the use of Equation (7.2.28) if there are no significant residual effects of the treatments. Further, Grizzle advices of testing δA– δB = 0 at a significance level higher than usual (say, α = 0.1), and if no significant residual effects hypothesis is tenable, then use the estimate (7.2.28) rather than using Equation (7.2.14). The interested reader is referred to Brown (1978, 1980) and Hills and Armitage (1979) for further discussion on this topic. It is recommended to use washout period between the two treatments’ application so that the residual effects disappear.
7.2.4 Modified two-period, two-treatment design
A good use of the cross-over nature of the treatments can be made in a four-sequence, two-period, two-treatment designs. Let the four sequences of treatments {A, B}, {B, A}, {A, A}, and {B, B} be used, respectively, on randomly selected n1, n2, n3, and n4 experimental units. Let Yiju be the observation in the uth period on the jth unit of the ith sequence and let ![]() Then,
Then,
These designs have the disadvantage of requiring more units in experimentation at the cost of not making any assumption to use the cross-over nature of the design to estimate τA - τB.
7.2.5 Cost analysis
In this subsection, the cost analysis of a cross-over design is made in relation to a CRD. Let S0 be the cost of obtaining a new patient and let S1 be the cost of taking an observation in one period on a unit. Let 2n patients be used in a cross-over design and 2m patients be used in an equally efficient CRD using equal replications of the sequences or treatment. Let SC0 and SCR be the respective costs of running a cross-over design and a CRD. Then,
and
Since the design under discussion is a cross-over design, the estimator ![]() of Equation (7.2.28) will be considered for τA – τB and the usual estimators of τA – τB will be considered for a CRD. To get equal precision from cross-over design and CRD in estimating τA – τB, the sample sizes 2m and 2n must satisfy
of Equation (7.2.28) will be considered for τA – τB and the usual estimators of τA – τB will be considered for a CRD. To get equal precision from cross-over design and CRD in estimating τA – τB, the sample sizes 2m and 2n must satisfy
The efficiency of cross-over design compared with CRD is
If S1/S0 is small and ![]() is large, then R is large and CRD is inferior compared to a cross-over design. In Table 7.2.1, R is given for selected values of
is large, then R is large and CRD is inferior compared to a cross-over design. In Table 7.2.1, R is given for selected values of ![]() and S1/S0.
and S1/S0.
Table 7.2.1 R for selected S1/S0 and σu2/σ2
| |
|||||
| S1/S0 | 0.0005 | 0.025 | 0.5 | 2.5 | 5 |
| 0.01 | 0.50 | 0.51 | 0.74 | 1.73 | 2.97 |
| 0.05 | 0.48 | 0.49 | 0.72 | 1.67 | 2.86 |
| 1 | 0.33 | 0.34 | 0.50 | 1.17 | 2.00 |
| 5 | 0.27 | 0.28 | 0.41 | 0.95 | 1.64 |
| 10 | 0.26 | 0.27 | 0.39 | 0.92 | 1.57 |
Brown (1980) points out that the cost analysis unfairly shows the superiority of cross-over designs. He argues that the cost of recruitment of a subject in the experiment is more for a cross-over design compared to a CRD and that since more dropouts may result in a cross-over design, more patients have to be added to the cross-over design study, violating the premise of the cost analysis.
7.3 Two-Period, Two-Treatment CODWR Analysis: NonParametric Methods
Though parametric methods were discussed throughout this monograph, due to the wider application of the two-period, two-treatment CODWR, nonparametric method analysis of such designs will be discussed in this section. The results of this section are mainly due to Koch (1972).
The model of (7.2.1) will still be considered subject to the interpretation of the symbols given there. However, the eiju will no longer be considered to follow IIN (0, σ2). Instead eiju’s will be assumed to have a symmetrical distribution so that Wilcoxon two-sample rank sum (or Mann–Whitney) test will be used to make the required inferences.
Clearly,
where δ1=δA and δ2=δB.
Under the null hypothesis
the distribution of the sample {S1j}, j=1, 2, …, n1, is the same as the sample {S2j}, j=1, 2, …, n2, and Wilcoxon two-sample rank sum test can be used, as described in standard statistics methods or nonparametric textbooks (Desu and Raghavarao, 2004), to test H0 of (7.3.2).
To test the null hypothesis
we use
The two samples {d1j}, j=1, 2, …, n1, and {d2j}, j=1, 2, …, n2, have identical distribution under H0 if (7.3.3) is valid, and once again, Wilcoxon two-sample rank sum test can be used to test H0 if (7.3.2) is not rejected. Otherwise, we test the null hypothesis
without assumptions, using the two samples {Y1j1}, j=1, 2, …, n1, and {Y2j1}, j=1, 2, …, n2, representing the data of the first periods, by the Wilcoxon two-sample rank sum test.
Koch (1972) discussed the use of bivariate Wilcoxon test for testing the null hypothesis
However, parametric tests for hypotheses given in Equation (7.3.6) are not usually given in literature.
When the response to the treatments is a 0 or 1 variable, Gart (1969) proposed the analysis based on the logistic model. The tests obtained are formally equivalent to Fisher’s exact test for the usual two-by-two contingency table. (Also, see Bennett, 1971, and George and Desu, 1973).
7.4 Two-Period t Treatment Cross-Over Design
Balaam (1968) discussed a two-period design in t treatments on t2 experimental units. His design consists of using all possible t2 sequences of pairs of treatments, whether identical or not, and he analyzed the design using a treatment × periods interaction term and ignoring residual effects term. A closer look of the model reveals that this interaction term is really the residual effect of the treatments term, and hence, it is a CODWR. A particular case of the design with t=2 was discussed in Subsection 7.2.4. Since this design is a CODWR, the general analysis discussed in Section 6.2 is applicable when the unit effects are fixed. Without loss of generality, using 1,2, …, t as treatments, we can write the design as
| Units | |||||||||||||
| Periods | 1 | 2 | … | t | t + 1 | t + 2 | … | 2t | … | (t - 1)t + 1 | (t - 1)t + 2 | … | t2 |
| 1 | 1 | 1 | … | 1 | 2 | 2 | … | 2 | … | t | t | … | t |
| 2 | 1 | 2 | … | t | 1 | 2 | … | t | … | 1 | 2 | … | t |
We easily verify that

Putting
to denote the vectors of adjusted treatment and residual treatment totals, the solutions of the normal equations are given by
The variances of direct and residual treatment effects contrasts are clearly
Table 6.2.1 in this case can be written as Table 7.4.1.
Table 7.4.1 ANOVA for Balaam’s design
| Source | d.f. | S.S | M.S. | F |
| Periods | 1 | |
||
| Units | t 2 - 1 |  |
||
| Direct effects (ig residual effects) | t - 1 |  TC′TC TC′TC |
||
| Residual effects (el direct effects) | t - 1 | |
MSr | MSr/MSe |
| Direct effects (el residual effects) | t - 1 | |
MSt | MSt/MSe |
| Error | (t - 1)2 | SSe | MSe |
SSe=![]() -
- ![]() -
-  -
-  TC′ TC -
TC′ TC - ![]() Q′δ|ρ,γ,τ Qδ|ρ,γ,τ.
Q′δ|ρ,γ,τ Qδ|ρ,γ,τ.
While researchers usually test the significance of direct effects and/or residual effects separately, it is interesting to note that the effectiveness of a treatment depends on the sum of direct and residual effects. To this end, one likes to test
and Balaam’s cross-over designs provide a suitable test. Let sij be the column sums with i in the first period and j in the second period, and ![]() . Then, assuming subject effects are random and uncorrelated with error,
. Then, assuming subject effects are random and uncorrelated with error, ![]() for i=1, 2, …, t have the same mean under the null hypothesis (7.4.12). Let
for i=1, 2, …, t have the same mean under the null hypothesis (7.4.12). Let ![]() . We will test the null hypothesis (7.4.12) with the t-statistic
. We will test the null hypothesis (7.4.12) with the t-statistic
with t - 1 degrees of freedom. We will illustrate this in Example 7.5.2.
For other optimality results on two-period designs, the reader is referred to Carriere and Reinsel (1993), Hedayat and Zhou (1990), and Kunert (1983). See Patel (1983) for the use of baseline measurements in cross-over designs and Patel and Hearne (1980) for the use of multivariate analysis in this context.
7.5 Numerical Examples
Parametric and nonparametric methods will now be discussed for two treatments in Example 7.5.1 and parametric analysis for t=3 in Example 7.5.2.
Table 7.5.1 Artificial data on cholesterol change
| Volunteer | Period 1 | Period 2 | sij | dij |
| 1 | A (−10) | B (−5) | −15 | −5 |
| 2 | A (−8) | B (−10) | −18 | 2 |
| 3 | A (5) | B (−3) | 2 | 8 |
| 4 | A (−15) | B (−10) | −25 | −5 |
| 5 | A (10) | B (5) | 15 | 5 |
| 6 | B (−5) | A (−5) | −10 | 0 |
| 7 | B (3) | A (5) | 8 | −2 |
| 8 | B (−4) | A (0) | −4 | −4 |
| 9 | B (5) | A (5) | 10 | 0 |
| 10 | B (10) | A (−5) | 5 | 15 |
The programming lines and output are given as follows:
data a;input seq period1 period2 @@; cards;
1 -10 −5 1 −8 −10 1 5 −3 1 −15 −10 1 10 5 2 −5 −5 2 3 5 2 −4 0 2 5 5 2 10 −5
;
data b;set a;sum=period1+period2;diff=period1-period2;
proc ttest;var sum diff; class seq;run;
proc npar1way wilcoxon; var sum diff; class seq;run;The TTEST Procedure
Variable: sum
| seq | N | Mean | Std Dev | Std Err | Minimum | Maximum |
| 1 | 5 | −8.2000 | 16.3310 | 7.3034 | −25.0000 | 15.0000 |
| 2 | 5 | 1.8000 | 8.4971 | 3.8000 | −10.0000 | 10.0000 |
| Diff (1−2) | −10.0000 | 13.0173 | 8.2329 |
| seq | Method | Mean | 95% CL Mean | Std Dev | 95% CL Std Dev | ||
| 1 | −8.2000 | −28.4776 | 12.0776 | 16.3310 | 9.7844 | 46.9279 | |
| 2 | 1.8000 | −8.7505 | 12.3505 | 8.4971 | 5.0909 | 24.4168 | |
| Diff (1−2) | Pooled | −10.0000 | −28.9850 | 8.9850 | 13.0173 | 8.7926 | 24.9382 |
| Diff (1−2) | Satterthwaite | −10.0000 | −30.1306 | 10.1306 | |||
| Method | Variances | DF | t Value | Pr > |t|! |
| Pooled | Equal | 8 | −1.21 | 0.2591 (a2) |
| Satterthwaite | Unequal | 6.0178 | −1.21 | 0.2700 (a3) |
| Equality of Variances | |||||||
| Method Num DF Den DF F Value Pr > F | |||||||
| Folded F 4 4 3.69 0.2336 (a1) |
Variable: diff
| seq | N | Mean | Std Dev | Std Err | Minimum | Maximum |
| 1 | 5 | 1.0000 | 5.8737 | 2.6268 | −5.0000 | 8.0000 |
| 2 | 5 | 1.8000 | 7.5631 | 3.3823 | −4.0000 | 15.0000 |
| Diff (1−2) | −0.8000 | 6.7713 | 4.2825 |
| seq | Method | Mean | 95% CL Mean | Std Dev | 95% CL Std Dev | ||
| 1 | 1.0000 | −6.2931 | 8.2931 | 5.8737 | 3.5191 | 16.8783 | |
| 2 | 1.8000 | −7.5908 | 11.1908 | 7.5631 | 4.5313 | 21.7329 | |
| Diff (1−2) | Pooled | −0.8000 | −10.6755 | 9.0755 | 6.7713 | 4.5737 | 12.9722 |
| Diff (1−2) | Satterthwaite | −0.8000 | −10.7819 | 9.1819 | |||
| Method | Variances | DF | t Value | Pr > |t| |
| Pooled | Equal | 8 | −0.19 | 0.8565 (a5) |
| Satterthwaite | Unequal | 7.5381 | −0.19 | 0.8567 (a6) |
The TTEST Procedure
Variable: diff
Equality of Variances
| Method | Num DF | Den DF | F Value | Pr > F |
| Folded F | 4 | 4 | 1.66 | 0.6363 (a4) |
The NPAR1WAY Procedure
Wilcoxon Scores (Rank Sums) for Variable sum
Classified by Variable seq
| Sum of | Expected | Std Dev | Mean | ||
| seq | N | Scores | Under H0 | Under H0 | Score |
| 1 | 5 | 22.0 | 27.50 | 4.787136 | 4.40 |
| 2 | 5 | 33.0 | 27.50 | 4.787136 | 6.60 |
Wilcoxon Two-Sample Test
Statistic 22.0000
| Normal Approximation | |
| Z | −1.0445 |
| One-Sided Pr < Z | 0.1481 |
| Two-Sided Pr > |Z| | 0.2963 (a7) |
| t Approximation | |
| One-Sided Pr < Z | 0.1618 |
| Two-Sided Pr > |Z| | 0.3235 |
Z includes a continuity correction of 0.5.
| Kruskal-Wallis Test | |
| Chi-Square | 1.3200 |
| DF | 1 |
| Pr > Chi-Square | 0.2506 |
The NPAR1WAY Procedure
Wilcoxon Scores (Rank Sums) for Variable diff
Classified by Variable seq
| Sum of | Expected | Std Dev | Mean | ||
| seq | N | Scores | Under H0 | Under H0 | Score |
| 1 | 5 | 27.0 | 27.50 | 4.758034 | 5.40 |
| 2 | 5 | 28.0 | 27.50 | 4.758034 | 5.60 |
Average scores were used for ties.
Wilcoxon Two-Sample Test
| Statistic | 27.0000 |
| Normal Approximation | |
| Z | 0.0000 |
| One-Sided Pr < Z | 0.5000 (a8) |
| Two-Sided Pr > |Z| | 1.0000 (a9) |
| t Approximation | |
| One-Sided Pr < Z | 0.5000 |
| Two-Sided Pr > |Z| | 1.0000 |
Z includes a continuity correction of 0.5.
| Kruskal-Wallis Test | |
| Chi-Square | 0.0110 |
| DF | 1 |
| Pr > Chi-Square | 0.9163 |
Assuming normal distribution for the response variable, the p-value for testing the equality of variances for the sums is given at (a1) and for differences at (a4). If these p-values are not significant, we can use the t-test with the usual degrees of freedom for the sums and differences. If any of the p-values at (a1) or (a4) is significant, Satterthwaite’s degrees of freedom will be used, with the p-values given at (a3) and (a6). In our example, the p-values at (a1) and (a4) are not significant. Hence, the p-value at (a2) is used, and we will not reject the null hypothesis that the residual effects are the same. Using the p-value at (a5), the null hypothesis that the direct effects of the treatments are the same is not rejected.
If we do not assume that the data are normally distributed, the Wilcoxon test will be used. The p-value at (a7) is used to test the residual effects of the treatments, and in our case, it is not significant and we will not reject the null hypothesis that the residual effects are the same. The p-values at (a8) and (a9) are used to test the significance of the direct effects for one-sided or two-sided alternatives. The hypothesis of the equality of the direct effects is not rejected in our example.
Table 7.5.2 Artificial data on coffee brand elevation
| First | A (8) | B (5) | C (7) | A (9) | A (8) | B (7) | B (6) | C (5) | C (6) |
| Second | A (7) | B (6) | C (7) | B (6) | C (9) | C (7) | A (8) | A (6) | B (7) |
data a;input unit trt1$ resp1 trt2$ resp2 @@;
cards;
1 A 8 A 7 2 B 5 B 6 3 C 7 C 7 4 A 9 B 6
5 A 8 C 9 6 B 7 C 7 7 B 6 A 8 8 C 5 A 6 9 C 6 B 7
;
data b;set a;
if trt1=trt2 then trtcnt=2;else trtcnt=1;
resp=resp1+resp2;
if trt1='A' then trt11sum=resp1;
if trt2='A' then trt12sum=resp2;
trt1total=sum(trt11sum,trt12sum);
if trt1='B' then trt21sum=resp1;
if trt2='B' then trt22sum=resp2;
trt2total=sum(trt21sum,trt22sum);
if trt1='C' then trt31sum=resp1
;if trt2='C' then trt32sum=resp2;
trt3total=sum(trt31sum,trt32sum);
if trt1='A' then r1=resp2;
if trt1='B' then r2=resp2;
if trt1='C' then r3=resp2;
if trt1='A' or trt2='A' then tarespa=resp/2*trtcnt;
if trt1='B' or trt2='B' then tarespb=resp/2*trtcnt;
if trt1='C' or trt2='C' then tarespc=resp/2*trtcnt;
if trt1='A' then rarespa=resp/2;
if trt1='B' then rarespb=resp/2;
if trt1='C' then rarespc=resp/2;
proc sort;by unit;run;
proc univariate noprint data=b;
var resp1 resp2 trt1total trt2total trt3total r1 r2 r3 tarespa tarespb tarespc rarespa rarespb rarespc;
output out=outg sum=grand1 grand2 trt1 trt2 trt3 r1 r2 r3 tac tbc tcc rac rbc rcc;
proc univariate noprint data=b;var resp;by unit;output out=outu sum= c;
data grand;set outg;
grand=grand1+grand2;
p1=grand1;p2=grand2;
drop grand1 grand2;a=1;proc sort;by a;
data unit;set outu;proc transpose out=unitt;var c;
data unit;set unitt;
c1=col1; c2= col2; c3=col3; c4=col4; c5=col5; c6=col6; c7=col7; c8=col8; c9=col9;
drop _name_ _label_ col1 col2 col3 col4 col5 col6 col7 col8 col9;
a=1;proc sort;by a;
data final;merge unit grand;by a;
tacnew=trt1-tac;
tbcnew=trt2-tbc;
tccnew=trt3-tcc;
racnew=r1-rac;
rbcnew=r2-rbc;
rccnew=r3-rcc;
t=3;*number of treatments;
tsq=t**2;
sse=grand**2;
dferror=(t−1)**2;
mse=sse/dferror;a=1;
proc sort;by a;
data period;set final;
source='Periods ';
df=1;
ss=((p1**2+p2**2)/tsq)-(grand**2/(2*tsq));
keep source df ss ms f ;
data unit;set final;
source='Units';df=tsq−1;
ss=((c1**2+c2**2+c3**2+c4**2+c5**2+c6**2+c7**2+c8**2+c9**2)/2)-(grand**2/(2*tsq));
keep source df ss ms f;
data dirigreseff;set final;
source='Dir eff(ig res eff)';df=t−1;ss=(tacnew**2+tbcnew**2+tccnew**2)/t;
keep source df ss ms f;
data reseffeldireff;set final;
source='Res eff(el dir eff)';df=t−1;
adjrta=tacnew/2+racnew+((grand−2*p2)/(2*t));
adjrtb=tbcnew/2+rbcnew+((grand−2*p2)/(2*t));
adjrtc=tccnew/2+rbcnew+((grand−2*p2)/(2*t));
ss=(adjrta**2+adjrtb**2+adjrtc**2)*(4/t);ms=ss/df;f=ms/mse;
keep source df ss ms f;
data direffelreseff;set final;source='Dir eff(el res eff)';df=t−1;
adjdta=tacnew+racnew+((grand−2*p2)/(2*t));
adjdtb=tbcnew+rbcnew+((grand−2*p2)/(2*t));
adjdtc=tccnew+rbcnew+((grand−2*p2)/(2*t));
ss=(adjdta**2+adjdtb**2+adjdtc**2)/(2/t);
ms=ss/df;
f=ms/mse;a=1;
keep source df ss ms f adjdta adjdtb adjdtc a;
proc sort;by a;
data total;set a;resp1sq=resp1*resp1;resp2sq=resp2*resp2;
proc univariate noprint data=total;var resp1sq resp2sq resp1 resp2;
output out=total sum=resp1sqsum resp2sqsum grand1 grand2;
data total1;set total;
t=3;tsq=t**2;
respsq=(resp1sqsum+resp2sqsum)-((grand1+grand2)**2)/(2*tsq);a=1;
data total2;set total1;source='Total';ss=respsq;keep source ss;
data ss;set period unit dirigreseff reseffeldireff;
proc univariate noprint data=ss;var ss df;
output out=out2 sum=ss df;
data ss;set out2;a=1;proc sort;by a;
data error;merge total1 ss final;by a;
ss=respsq-ss;
source='Error';
df=(t−1)**2;
ms=ss/df;keep source ss df ms;
data mse;set error;a=1;
mse=ms;
errordf=df;
keep mse a errordf;proc sort;by a;
data final1;set period unit dirigreseff reseffeldireff direffelreseff error ;
a=1;proc sort;by a;
data final2;merge final1 mse;by a;
f=ms/mse;
if source='Error' then f= .;
pvalue=1-probf(f,df,errordf);
proc print;var source df ss ms f pvalue;run;The following is the necessary output:
| Obs | source | df | ss | ms | f | pvalue |
| 1 | Periods | 1 | 0.2222 | . | . | . |
| 2 | Units | 8 | 14.7778 | . | . | . |
| 3 | Direff(ig res eff) | 2 | 3.5000 | . | . | . |
| 4 | Res eff(el dir eff) | 2 | 1.6111 | 0.80556 | 0.87879 | 0.48266(b2) |
| 5 | Dir eff(el res eff) | 2 | 2.3750 | 1.18750 | 1.29545 | 0.36832(b1) |
| 6 | Error | 4 | 3.6667 | 0.91667 | . | . |
The p-value given at (b1) is used to test the equality of direct effects, and the p-value given at (b2) is used to test the residual effects of the treatments. In our example, these are not significant.
The following addition to the program provides the least squares estimates of direct treatment effects and the standard error for the mean difference:
data final2;merge direffelreseff mse;by a;
t=3;trta=adjdta*(2/t);trtb=adjdtb*(2/t);
trtc=adjdtc*(2/t);semeandiff=mse*(4/t);
proc print;var trta trtb trtc semeandiff;run;| trta | trtb | trtc | semeandiff |
| 0.44444 (b3) | −0.55556 (b4) | 0.44444 (b5) | 1.22222 (b6) |
The least squares estimates direct effects of the treatments A, B, and C are given at (b3), (b4), and (b5), respectively. The standard error of the estimated elementary contrasts of the direct treatment effects is given at (b6).
The following programming lines will be used to test the null hypothesis 7.4.12:
data a;input unit trt1$ resp1 trt2$ resp2 @@;
cards;
1 A 8 A 7 2 B 5 B 6 3 C 7 C 7 4 A 9 B 6
5 A 8 C 9 6 B 7 C 7 7 B 6 A 8 8 C 5 A 6 9 C 6 B 7
;
data b;set a;
response=resp1+resp2;if trt1='A' then trt1total=response;
if trt1='B' then trt2total=response;if trt1='C' then trt3total=response;
proc univariate noprint data=b;var trt1total ;output out=out1 sum=mean;
proc univariate noprint data=b;var trt2total ;output out=out2 sum=mean;
proc univariate noprint data=b;var trt3total ;output out=out3 sum=mean;
data final;set out1 out2 out3;proc univariate;var mean;run;***
Tests for Location: Mu0 = 0
| Test | -Statistic- | -----p Value------ | ||
| Student's t | t | 14.5131 | Pr > |t| | 0.0047(c1) |
| Sign | M | 1.5 | Pr > = |M| | 0.2500 |
| Signed Rank | S | 3 | Pr > = |S| | 0.2500 |
The p-value given at (c1) is significant, implying that the sum of direct and residual effects of the treatment are different.
References
- Armitage P, Hills M. The two-period crossover trial. The Statistician 1982;31:119–131.
- Balaam LN. A two-period design with t2 experimental units. Biometrics 1968;24:61–73.
- Bennett BM.On tests for order and treatment differences in a matched 2 × 2. Biometrical J 1971;3:95–99.
- Brown Jr, BW. Statistical controversies in the design of clinical trials. Technical Report #37. Stanford, CA: Division of Biostatistics, Stanford University; 1978.
- Brown Jr, BW. The crossover experiment for clinical trials. Biometrics 1980;36:69–79.
- Carriere KC, Reinsel GC. Optimal two-period repeated measurements designs with two or more treatments. Biometrika 1993;80:924–929.
- Cox DR. Planning of Experiments. New York: Wiley; 1958.
- Desu MM, Raghavarao D. Nonparametric Statistical Methods for Complete and Censored Data. Boca Raton: Chapman and Hall/CRC; 2004.
- Dubey SD Current thoughts on crossover designs. Clin Res Pract Drug Reg Aff 1986;4:127–142.
- Gart JJ. An exact test for comparing matched proportions in crossover designs, Biometrika 1969;56:75–80.
- George SL, Desu MM. Testing for order effects in a crossover design. Biometrical J 1973;15:113–116.
- Grizzle JE. The two-period change over design and its use in clinical trials. Biometrics 1965;21:467–480.
- Hedayat A, Zhou W. Optimal two-period repeated measurements designs. Ann Math Statist 1990;18:1805–1816.
- Hills M, Armitage P. The two-period crossover clinical trial. Br J Clin Pharmacol 1979;8:7–20.
- Huitson A, Poloniecki J, Hews R, Barker N. A review of cross-over trials. The Statistician 1982;31:71–80.
- Jones B, Kenward MG. Design and Analysis of Cross-Over Trials. 2nd edition. London: Chapman & Hall; 2003.
- Kenward MG, Jones B. The analysis of data from 2 × 2 cross-over trials with baseline measurements. Stats Med 1987;6:911–926.
- Khatri CG, Raghavarao D, Mercado R. On the estimation of fixed effects in a mixed model. Gujarat Statist Rev 1981;8:1–6.
- Koch GG. The use of non-parametric methods in the statistical analysis of the two-period change-over design. Biometrics 1972;28:577–584.
- Kunert J. Optimal design and refinement of the linear model with applications to repeated measurements designs. Ann Math Statist 1983;11:247–257.
- Mercado R. Generalized residual effects designs [Unpublished Ph.D. dissertation]. Philadelphia, PA: Temple University; 1976.
- Patel HI. Use of baseline measurements in the two-period cross-over designs. Comm Statist—Theor Meth 1983;12:2693–2712.
- Patel HI, Hearne EM. Multivariate analysis for the two-period repeated measures cross-over design with applications to clinical trials. Comm Statist—Theor Meth 1980;9:1919–1929.
- Senn SJ. Is the simple carry-over modes useful? Statist Med 1992;11:715–726.
- Senn SJ. Crossover Trials in Clinical Research. Chichester: Wiley & Sons; 1993.
- Senn SJ. Cross-over trials at the crossroads? Appl Clin Trials 1995;4:24–31.
- Willan AR, Pater JL. Carryover and the two-period crossover clinical trial. Biometrics 1986;42:593–599.