CHAPTER 7

GAME THEORETIC APPROACHES FOR RESOURCE MANAGEMENT IN MULTI-TIER NETWORKS

Game theory is a set of mathematical tools used to analyze the interactions among independent rational entities. Recently, game theory has found many applications in wireless communications and networking [1]. Game theory can be used in the decision making process of multiple rational entities, so that the wireless systems can operate efficiently and meet the users’ QoS requirements. In a multi-tier cellular wireless network such as a two-tier macrocell–femtocell network, there are many decision problems involving multiple entities (e.g., macro base stations, femto access points, macro and femto users). These entities can be rational and self-interested to maximize their own benefits (or minimize their own costs).

In this chapter, we discuss the applications of game theory for resource management in two-tier macrocell–femtocell networks. Game theory is a suitable tool to model the interactions among different entities in these networks. We provide an introduction to game theory and discuss different types of game models. Then, we provide a review of the game theoretic models for resource allocation in two-tier networks. We first discuss the game formulations for power control and sub-channel allocation in an orthogonal frequency-division multiple access (OFDMA)-based two-tier (macrocell–femtocell) network. Then, we review the game formulations for resource management with pricing. Based on economic models, the pricing schemes can be used to reduce interference and enhance the efficiency of spectrum sharing. Then, we present the game theoretic models for access control. Users in a two-tier macrocell–femtocell network can choose to join either a femtocell or a macrocell based on their utility. Also, the femtocell and macrocell can control the data transmission of the users. Different game models can be developed for access control in a two-tier network. To this end, we outline some future research directions.

7.1 INTRODUCTION TO GAME THEORY

Game theory, developed as one of the fields in mathematics, has many applications in economics and social sciences. Recently, game theory has been applied to solve various issues in wireless communication networks including small cell networks such as femtocell networks. In this section, we will provide an introduction to game theory. To give a background for understanding and using game theory in small cell networks, we will first discuss the motivations of using game theory. Then, we will briefly review different types of game models before discussing the design considerations to use game theory to model and analyze the resource management problems in small cell networks.

7.1.1 Motivations of Using Game Theory

The motivations of using game theory for the resource management in multi-tier and small cell networks can be summarized as follows:

• Self-interested players: In small cell networks, there are multiple entities which may not belong to or be controlled by a single provider or controller. For example, in two-tier macrocell–femtocell networks, multiple femto access points (i.e., SBSs) can be deployed in the service area of a macrocell. The femto access points can be operated by different owners which could also be different from the provider of the macro base station. Likewise, the macro users and femto users may subscribe to the different providers, and they have different subscription plans. In this situation, the entities in the femtocell network are independent and make decisions on resource management in such a way that they achieve the highest benefit (e.g., optimal performance) or the lowest cost. This is referred to as the self-interest or rational behavior. These entities can be considered as players in a game, in which their strategies are chosen based on the individual payoff rather than the system-wide objective.
• Distributed environment: Distributed architecture will be common for multi-tier networks such as femtocell networks. This is due to the limited communication capability of backhaul among macro base stations and femto access points. Therefore, without complete information and full control, distributed resource management algorithms for the small cell networks will be highly desirable. Game theory can be used to design and develop distributed resource management algorithms with minimum information exchange and control. A game theory framework allows different entities to collect the network state and wireless channel status to make a decision locally and intelligently. This can be referred to as the self-organizing capability. Distributed algorithms can be designed to achieve the optimal or near optimal solution. In addition, the distributed algorithms will be highly scalable to accommodate a large number of femto access points and users.

Game theory provides a rich set of mathematical and analytical tools to investigate the behaviors (e.g., convergence) and solutions (e.g., equilibrium) of game-theoretic resource management algorithms in multi-tier and small cell networks providing the opportunity to improve users’ satisfaction and system’s efficiency.

7.1.2 Types of Games

In general, a game model is defined by a set of players, a set of actions and strategies, and payoffs. The players are the decision makers who plan their strategies and accordingly choose actions to optimize their payoffs. The payoff, which represents the motivation of a player, is generally defined as a utility function. A brief introduction to the different types of game models typically used to model and analyze radio resource management (RRM) problems is provided in the following.

• Noncooperative game: In a noncooperative game, the players could have fully or partially conflicting interests in the decision making process. In particular, an action of one player (i.e., strategy) will impact the payoffs of other players. For example, in the transmission power control game [2], femto users (i.e., players) choose transmission power (i.e., strategy) to transmit data. The payoff of the femto user is defined as the utility in terms of transmission rate. The transmission rate is derived as a function of the signal-to-interference-plus-noise ratio (SINR). Therefore, the utility is a function of transmission powers of all femto users in the network. If one femto user increases its transmission power, this user can achieve a higher transmission rate due to higher SINR. However, other femto users will suffer from stronger interference from the transmitted signal of this femto user. This situation can be modeled as a noncooperative game since the femto users will choose their transmission powers to maximize their utilities, without concerning about the interference caused to other users. Given a set of players, a set of strategies, and payoff functions, the solution of the noncooperative game in terms of an equilibrium can be obtained. In the literature, there are a few common equilibrium solution concepts for the noncooperative game. The most widely used solution concept is a Nash equilibrium. The Nash equilibrium ensures that none of the players can increase his payoff by unilaterally changing his strategy. Other solution concepts, such as correlated equilibrium [3] and dominant-strategy equilibrium [4], can also be used.
• Cooperative game: A cooperative game can be applied to the situation where players in a group (i.e., coalition) can enforce cooperation among each other to achieve a common objective of the group. A cooperative game can be either a bargaining game or a coalitional game. While the bargaining game is based on a bargaining process among the players, the coalitional game focuses on players acting as groups. The coalitional game can be classified into two categories: canonical game and coalition formation game [5]. In the canonical coalitional game, all players aim to form and stabilize a grand coalition (i.e., coalition of all players in the game). A common approach is to divide the value of coalitions (i.e., payoff of the coalition) among the players such that none of the players has any incentive to leave the grand coalition. The most commonly used solution is a core which ensures that no other coalition exists such that any player can achieve a higher payoff. However, the core could be empty, and if exists, it is usually not unique. Therefore, alternative solution concepts such as Shapley value [6] can be applied. In the coalition formation game, the players are rational in forming coalitions. A common approach is to allow players to join and split from an existing coalition based on their received payoffs. The common solution of the coalition formation game is the Nash stable coalition, which is similar to the Nash equilibrium. That is, the players inside or outside the Nash stable coalition cannot improve their individual payoffs by unilaterally splitting or joining the coalition, respectively.
• Static and dynamic games: A game can be either static or dynamic. In a static game, all players choose their strategies and perform actions at the same time. The players do not have information or knowledge of the strategies to be used by other players. Also, the strategy and the outcome are determined regardless of time. On the other hand, in a dynamic game, there is an implication of time in choosing the strategy and determining the outcome. A dynamic game can be a repeated game, in which the players play the static game multiple times. In this case, the players may have the knowledge about the strategies used by the other players and can adjust their strategies to be used in the current and future time based on the obtained knowledge. Alternatively, a dynamic game can be a differential game. In the differential game, an optimal control method is applied in which the payoff is a function of not only the time but also the state of the system.
• Hierarchical Game: In a hierarchical game, also widely known as a Stackelberg game, some players (i.e., leaders) can make decisions before other players (i.e., followers). In this case, the followers can observe the strategies used by the leaders and the followers optimize their strategies accordingly (i.e., to maximize the payoffs). Based on the knowledge that the followers will act according to the strategies of the leaders, the leaders can choose the strategies that maximize their payoffs. In general, the payoffs of the leaders are not less than those in a non-hierarchical game. This is called the first move advantage. A hierarchical game can be used for resource management in femtocell networks. The typical leaders are the macrocell entities such as a macro base station or a macro user. The followers are the femtocell entities such as the femto access points or femto users. The solution is defined in terms of a Stackelberg equilibrium which is a strategy profile such that the leaders maximize their payoffs, while the followers achieve the highest possible payoffs (i.e., best response) given the strategies of the leaders. A common approach to obtain the Stackelberg equilibrium is to use backward induction. In the backward induction method, the optimization models are formulated for the leaders and the followers. The optimization model for the followers is solved first. Next, the optimal solution of the followers is used to obtain the optimal solution of the leaders.

Note that the detail of each type of game can be found in the standard game theory books [7, 8]. In addition, the details of game models formulated for solving RRM problems in wireless communications and networking can be found in [1].

7.1.3 Noncooperative Game

A noncooperative game in strategic or normal form is a triplet defined as follows: , where

• is the finite set of players.
• is the set of strategies of player .
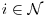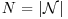• ui is the payoff function of player , which is defined as a function of for where 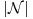is the Cardinality of the set .

In the strategic game, a strategy profile is defined as , where and are the vectors of strategies of player i and all other players, respectively. The player in the strategic game chooses the strategy to optimize her payoff function. If the players deterministically choose strategies (i.e., the strategies are chosen with probability of one), then it is called pure strategy. On the other hand, if the players choose their strategies based on probability distributions, then it is called a mixed strategy.

A strategy is dominant for player i if

(7.1)

for all and for all . In other words, the dominant strategy is the best strategy of that player. In particular, the dominant strategy will yield the highest payoff for the player regardless of the strategies of other players. The dominant strategy is useful to define the solution of a strategic game, since if the dominant strategy exists for the player, the rational player has no incentive and will not deviate from the dominant strategy. As a result, if every player has the dominant strategy, then all players will choose their dominant strategies rationally. The solution concept derived from the dominant strategy is called dominant-strategy equilibrium. The equilibrium is the strategy profile, which is composed of the dominant strategies of all players.

Conversely, we can define the strictly dominated strategy. is the strictly dominated strategy of player i by a strategy si if

(7.2)

for all . In other words, if the strategy is strictly dominated, there will be another better strategy (i.e., yielding higher payoff) regardless of the strategies of other players. A rational player will avoid choosing all the strictly dominated strategies. The elimination of a strictly dominated strategy is called iterated strict dominance, which could help in reducing the strategy set to be chosen toward the equilibrium solution. One important property of the iterated strict dominance is that the order of strategy elimination does not affect the outcome of a game. Therefore, regardless of which strictly dominated strategy is removed from the game first, the final remaining strategy set will be the same.

A similar concept is weakly dominated strategy. The strategy of player i is said to be weakly dominated by strategy if

(7.3)

for all . Again, the concept of weakly dominated strategy can be used to reduce a strategy set of a player, by eliminating the strategy which will result in a lower payoff. Similarly, this concept is called iterated weak dominance. However, it is important to highlight that unlike iterated strict dominance, the iterated weak dominance may not lead to a unique final outcome. In other words, the order of strategy elimination will affect the final outcome.

Although the concepts of dominant and dominated strategies are useful, in some game, such strategies may not exist and hence the corresponding equilibrium cannot be obtained. The most widely used solution concept for a noncooperative game is called the Nash equilibrium. The intuition of the Nash equilibrium solution is that none of the players has an incentive to deviate from the equilibrium if other players keep their strategies unchanged. The Nash equilibrium strategy profile (, ) is defined as follows:

(7.4)

for all and for all . At the Nash equilibrium, no player can unilaterally change her strategy, given that other players’ strategies are fixed. If , then the Nash equilibrium is said to be strict. The Nash equilibrium has a nice property that once the game reaches the equilibrium, if the players are rational, the strategy profile will not change, implying that the game has reached the stable point.

The typical approach to solve for the Nash equilibrium of a noncooperative game is through the use of a best response function. The best response function for player i can be defined as bi(s−i), which is a set of strategies for that player such that

(7.5)

In other words, the best response function is defined by . The best response ensures that the player will achieve the highest payoff given the fixed strategies of other players. Then, the Nash equilibrium can be defined based on the best response function. In this case, the strategy profile is a Nash equilibrium if and only if every player’s strategy is a best response to the other players’ strategies, that is,

(7.6)

for all players i. To solve for the Nash equilibrium, first the best response functions will need to be obtained, for example, by using standard optimization methods. Then, the strategy profile which satisfies the condition of a Nash equilibrium is identified.

There are some issues related to the Nash equilibrium. Firstly, with a pure strategy, the noncooperative game may possess zero, one, or many Nash equilibria. Secondly, the Nash equilibrium may not be the optimal solution. In other words, the Nash equilibrium may not yield the highest payoff for all players in the game. It is important to analyze the property of a Nash equilibrium in a game. In the following, the sketches of the widely used proofs for existence and uniqueness of the Nash equilibrium in a noncooperative game are given.

• Existence: The most commonly used approach for proving the existence of a Nash equilibrium is through showing that the game is a concave game [9]. A concave game is defined as a game in which player i chooses strategy si so that where is a closed bounded convex set. Also, the payoff function ui(s) of player i should be continuous and twice differentiable in and concave in . The concavity of a payoff function can be proved through checking the Hessian matrix. In particular, if the Hessian matrix is negative definite, then the payoff function is concave.
• Uniqueness: The uniqueness of a Nash equilibrium in a noncooperative game can be proved by showing that the best response function is a standard function. Let . The standard function possesses three properties: (i) positivity, where b(s)>0, (ii) monotonicity, where if , then , and (iii) scalability, where for all , . Note that the vector inequality is a strict inequality in all elements. Alternatively, the uniqueness of the Nash equilibrium can be verified through that the game is diagonally strictly concave on its strategy space [10]. Another approach is to prove that a noncooperative game is a potential game [11]. In the potential game, any changes in the payoff function of any player are also correspondingly reflected in a potential function due to a unilateral deviation by the player, that is, , where is a potential function.

It is also important to analyze the efficiency or optimality of a Nash equilibrium of a noncooperative game. One important measure of efficiency is the Pareto optimality. The strategy profile is Pareto superior to another strategy profile if, for every player ,

(7.7)

with at least one player where

(7.8)

Then, the strategy profile is Pareto optimal if there exists no other strategy profile that is Pareto superior to . In other words, if a strategy profile is Pareto optimal, there is no other strategy profile that results in a higher payoff for one player without lowering the payoff of at least one other player. With the Pareto optimality, every player can gain the highest payoff without hurting other players. Therefore, it is desirable to find the Nash equilibrium which is also Pareto optimal.

An alternative efficiency measure of a Nash equilibrium is the price of anarchy. The price of anarchy is defined as a ratio of the maximum social welfare to the social welfare achieved at the worst-case equilibrium. The maximum social welfare or the total utility (or sum of payoffs of all the players in a game) is achieved by a centralized or a genie-aided solution. The social welfare at the worst-case Nash equilibrium is defined as follows:

(7.9)

where is the Nash equilibrium strategy space. The maximum social welfare from the centralized solution can be obtained from

(7.10)

Then, the price of anarchy is defined as follows:

(7.11)

7.1.4 Cooperative Game

While a noncooperative game models the rational and self-interest behavior of the individual players, a cooperative game focuses on the players cooperating and acting as a group. In the cooperative game, the players are allowed to make agreements among themselves. The agreements will influence the strategies to be used by the players and their payoffs. The cooperative game can be divided into two categories: bargaining game and coalitional game. The bargaining game analyzes the bargaining process among players, while the coalitional game focuses on the formation of coalitions.

Bargaining game: Bargaining refers to a situation where two or more players can mutually benefit from reaching a certain agreement, mostly in terms of resource sharing. Although in the bargaining game literature, there are different approaches and solution concepts proposed, the most commonly used model is the Nash bargaining solution. The Nash bargaining solution considers the bargaining outcome at the final agreement, but not intermediate bargaining process. For a two player bargaining game (i.e., ), the payoff space (i.e., set of all possible payoffs that two players can achieve) can be defined as follows:

(7.12)

In addition, the disagreement point is defined as the payoffs that the players will receive if the agreement of the bargaining game cannot be reached. The disagreement point is defined as d=(d1, d2). In this case, is a convex and compact set. There exists some such that u>d. The Nash bargaining solution is obtained from

(7.13)

for and . Let a bargaining problem be denoted by . Then, the bargaining solution is a function f that determines a unique outcome for every bargaining problem . In other words, is the payoff of player i in the bargaining outcome, where is an element of . The Nash bargaining solution satisfies the following properties.

• Pareto optimality: The bargaining solution is Pareto optimal if there does not exist such that 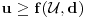and for some i.
• Symmetry: If the bargaining game is such that u1=u2 and d1=d2, then .
• Invariance to equivalent payoff representation: If a bargaining problem is transformed into another bargaining problem in such a way that and , then .
• Independent of irrelevant alternatives: With two bargaining problems denoted by and such that , if , then .

While the above description of the Nash bargaining solution is for two players, the generalized Nash bargaining solution for an N player bargaining game can be obtained as a solution of the optimization problem defined as follows:

(7.14)

where ρ is the bargaining power of a player i for . In other words, the bargaining power is the weight for the negotiation capability of each player. The player with higher bargaining power will have an advantage in getting a higher payoff from the bargaining solution.

Coalitional game: A coalitional game is a branch of a cooperative game to model cooperative behavior of players. A coalitional game defines a set of players whose objectives are to participate in the game as groups. The coalition is a group with an agreement among the players to act as a single entity. The coalition has a value , which determines the worth of the coalition. Therefore, in general, a coalition game is defined as a pair , where v is the value or mapping, which quantifies the payoffs that the players receive in the game. The coalitional game can have transferable utility (TU) or non-transferable utility (NTU). In the TU coalitional game, the values of coalitions can be apportioned and allocated to the players arbitrarily. On the other hand, in an NTU coalitional game, there are restrictions on the payoff distributions among players.

The coalitional game can be either a canonical coalitional game or a coalition formation game.

Canonical coalitional game: In a canonical coalitional game, players benefit from forming big coalitions. In particular, it is assumed that the payoffs when the players are in coalitions are always higher than or equal to that of when the players are in smaller coalitions. This is referred to as the superadditivity property, which is formally defined as follows for two coalitions and :

(7.15)

Since the canonical coalitional game has the superadditivity property, the aim is to divide and allocate the value among players in a grand coalition (i.e., a coalition of all the players). The payoff allocation should be done to ensure that none of the players has incentive to deviate from the grand coalition. One of the most commonly used solution concept for payoff allocation is the core. The core of the TU canonical coalitional game is defined as follows:

(7.16)

The core ensures that the players cannot gain higher payoff by splitting from the grand coalition, since any payoff allocation in the core will be always higher than or equal to the payoff allocation of any subcoalition . However, the core is not guaranteed to exist. Also, if the core exists, it is always an infinite set. Therefore, there are some refined solution concepts for the payoff allocation in canonical coalitional game. One of solution concepts is the Shapley value.

The Shapley value is defined as follows:

(7.17)

where is the marginal contribution of every player in a coalition . is the weight indicating the probability that the player i will join the coalition with a random order. Note that the Shapley value has no relation to the core. In particular, the Shapley value may not be in the core. Also, even though the core is empty, the Shapley value may exist.

Coalition formation game: A coalition formation game focuses on the self-interest behavior of a player in making cooperation with other players. In particular, the players will form coalitions to act as groups strategically to maximize their individual payoffs. Therefore, in the coalition formation game, a grand coalition may not be stable, in which the game may not possess the superadditivity property. The objective of the coalition formation game is to find the stable coalitions formed by players. Let the collection of coalitions be defined as , where is a mutual disjoint coalition and . The collection is basically a partition of the grand coalition .

A distributed coalition formation game is considered, in which the players make decisions to form coalitions based on their individual payoffs. The most commonly used algorithm is the merge-and-split. In the merge-and-split algorithm, the preference relation is defined to compare two collections and . In this case, indicates that is preferred to . Two common preference relations are the utilitarian order and individual-value order.

• In the utilitarian order, the players prefer to form coalitions in the collection if the total social welfare achieved from is strictly higher than that of , that is, .
• The individual-value order is concerned about an individual payoff of each player in a coalition. One example of the individual-value order is the Pareto order, which is defined as follows. Let x and y be the payoff allocations by two collections and , respectively. Then, in the Pareto order if with at least one xi of x such that xi>yi, where xi and yi are the elements of x and y, respectively.

Based on the preference relation, an algorithm can be developed, which is composed of two actions, that is, merge and split, defined as follows:

• Merge: Coalitions can be merged if the resulting coalitions (i.e., collection ) is preferred by the players, that is, .
• Split: Coalitions will be split if the resulting coalitions (i.e., collection ) is preferred by the players, that is, .

The merge-and-split algorithm with an individual-value order (e.g., Pareto order) is the dynamic coalition formation, which can perform in a distributed fashion. It has been shown that if there is a stable collection of coalitions, the algorithm can reach that stable coalition regardless of initial coalitions and the order of the merge or split actions. However, naturally, there could be multiple stable collections in a coalition formation game. In this case, the initial coalitions and order of actions of the algorithm could lead to different stable coalitions.

7.1.5 Game Theory and Radio Resource Management in Multi-Tier Networks

Some considerations of applying game theory to model and analyze the resource management problems in the multi-tier networks such as femtocell networks can be summarized as follows:

• Players and strategies: As the basic components of a game, the players and their strategies have to be defined. Depending on the resource management issues in the femtocell networks, the players can be identified as the entities which influence or relate to the input, process, or output of the resource management. The players could be physical entities (e.g., MUEs and FUEs, macro base stations and femto access points). Alternatively, the players could be logical/business entities (e.g., providers and owners). After the players of the resource management game are identified, their strategies will be determined based on the context of the resource management. For example, in the UL power control problem, the players could be the macro and femto users which interfere with each other. The strategy will be the transmission power.
• Payoff: The payoff of a player is typically defined as utility, which is a function of the strategies and state of players. The utility represents the preference of the players over the performance (e.g., transmission rate) and parameters (e.g., power consumption). The utility function should be defined based on the requirement of the players and objective of the resource management. Specifically, the utility function should be based on the QoS to be provided to the players. For example, in the power control problem, the utility can be defined as the transmission rate minus energy consumption. In many cases, the utility function is defined to simplify the mathematical analysis but can reasonably represent the preference of the actual players in femtocell networks. For example, the utility can be a convex function of a transmission rate, so that the standard technique in the convex optimization can be applied to obtain the equilibrium solution of the game.
• Type of game: The type of a game can be chosen based on the behavior of the players and strategies. The game can be noncooperative if players are concerned about their individual payoffs only. On the other hand, the game can be cooperative if players aim to achieve a group objective. The game can be static or dynamic depending on the assumption and objective of resource management. If the resource management aims to maximize the instantaneous performance, a static game, which is easier to analyze, may be suitable. However, if the players are concerned about their long-term performance, the dynamic game should be used. Sometimes, comparison among different types of games can lead to an interesting result. For example, the price of anarchy, defined as the ratio of efficiency from the noncooperative and cooperative games, can determine the performance degradation if the players have self-interest rather than a cooperative behavior. This phenomenon is known as the tragedy of the commons.
• Solution: For different types of games, different solution concepts exist. For example, in the power control problem, a Nash equilibrium, correlated equilibrium, or dominant-strategy equilibrium can be applied. The solution to be considered in the game depends largely on the objective and nature of the game. For example, the correlated equilibrium can be considered if the players are allowed to coordinate to achieve a more efficient solution than the Nash equilibrium. In addition, the properties of the selected solution of the game should be analyzed (e.g., existence and uniqueness of the correlated and Nash equilibrium). Again, it could be interesting, if different solution concepts are applied and compared in the same game (e.g., how much gain is achieved due to the use of correlated equilibrium over Nash equilibrium).
• Distributed implementation: The self-organizing capability is important for small cell networks. To achieve the self-organizing capability, a distributed implementation of the game-based resource management would be required. The major processes involved in a distributed algorithm are observing, analyzing and learning, reasoning, and adaptation. A set of these processes is commonly known as the cognitive cycle [12]. In the observing process, the distributed algorithm has to determine which information can be collected or exchanged in small cell networks. The analyzing and learning process is applied to the observation to obtain the knowledge and state of the system. Then, the reasoning process is used to determine the best action (e.g., throughput optimization). The adaptation process is to perform the selected action to achieve the objective of the algorithm. Most of the distributed algorithms implemented for game-based resource management are iterative. In particular, the aforementioned processes are repeated until the final equilibrium result is reached. In this case, a convergence analysis will be important. Also, due to lack of complete information of the system, the optimal solution may not be achieved by the distributed algorithm. In this case, the efficiency of an algorithm has to be evaluated. As in the algorithm design, an overhead in terms of communication, computation, and storage space should be also quantified.

7.2 GAME FORMULATIONS FOR POWER CONTROL AND SUB-CHANNEL ALLOCATION

The sub-channels and the transmission power are the radio resources which are shared among the macrocells and small cells in OFDMA-based multi-tier networks (e.g., LTE networks). Therefore, power control and sub-channel allocation are the most important issues to achieve the optimal network performance [13].

Game theory has been applied to model and analyze the power control and sub-channel allocation. One of the seminal works is [2], which analyzes the interference among macro and femto users. A noncooperative game is formulated to obtain the Nash equilibrium in terms of transmission power, which maximizes the individual utility. Alternatively, [3] considers the sub-channel allocation, in which the femto access points can choose to transmit on selected sub-channels. Instead of a Nash equilibrium, a correlated equilibrium is considered as the solution of this game. It is shown that the correlated equilibrium strategies are more efficient than the Nash equilibrium strategies. The spectrum resource (i.e., sub-channel) allocation is also considered in [4]. However, the allocation is performed in a hierarchical manner. Specifically, the spectrum resource is allocated to the macro users and femto access points first. Then, the femto access point allocate the received resource to femto users. The macro and femto users can request the resources based on their demands and a noncooperative game model is formulated to analyze the resource request strategies. The solution is the dominant-strategy equilibrium, which ensures that the macro and femto users can obtain the highest payoffs.

A game model is proposed in [14] in which the players are the femto access points with the strategy to allocate transmission power to femto users. Instead of considering an achievable rate to be the payoff (e.g., as in [15]), the payoff of the femto access point is the logarithmic function of the achievable rate minus the weighted transmission power (i.e., cost due to the energy consumption). A decentralized power control algorithm for femto users in a closed access femtocell network is proposed to achieve the Nash equilibrium at the steady state. The game is shown to be a supermodular game, which has the following attractive properties. Firstly, the pure strategy Nash equilibrium exists. Also, if the Nash equilibrium is unique, it is also globally stable when the decentralized power control algorithm is used. [16] extends the game model in [14] by considering also the sub-channel allocation and the best reply dynamics is adopted for the distributed implementation, which is proved to converge to the Nash equilibrium (i.e., by means of a potential game). [17] extends the existing game model to consider the average utility of the macro and femto users. Due to random location and mobility of these users, the macrocell and femtocells (i.e., players) must optimize the transmission power (i.e., strategy), such that the average aggregated utility is maximized. A Nash equilibrium is considered as the solution of this game. Similarly, with the randomness of a wireless channel, [18] models the interferer’s activity as a two-state Markov chain. Then, a game model is formulated to maximize the payoff defined as the expected transmission rates of the femto access points (i.e., players). To obtain the Nash equilibrium, the game model is transformed into the variational inequality (VI) problem [19], and an iterative gradient projection algorithm (IGPA) [20] is applied. The convergence of this algorithm is then proved.

The power control problem in a multi-tier network can be modeled as a hierarchical game where the macrocell is the leader and the small cells (e.g., femtocells) are the followers [21, 22]. With this hierarchical game model (i.e., Stackelberg game), the macrocell can allocate the transmission power to the macro users before the femtocells allocate the transmission powers to femto users. Based on the transmission power chosen by the macrocell, the femtocells will adjust the transmission powers accordingly. The Stackelberg equilibrium is considered to be the solution of the hierarchical game model.

Dynamic spectrum access based on cognitive radio can be used in small cell networks. In particular, as a secondary user, an SBS can opportunistically use the same channel allocated to the macro users that can be considered as primary users. In this case, the interference from the SBS to the primary users has to be constrained. Reference 23 considers the power control problem in a cognitive radio environment. The aim is to maintain the DL CTI at the target level. Also, to guarantee the performances of macro and small cell users, their outage probabilities must be maintained below the target thresholds. A noncooperative game model is presented, in which the players are macro and femto users. The strategy is the transmission power and the payoff is the throughput, given the constraints on the interference to the primary users and the outage probability. The game is proved to be a supermodular game.

In the following, the detailed formulations of the selected game models for power control and sub-channel allocation are discussed.

7.2.1 Utility-Based Distributed SINR Adaptation

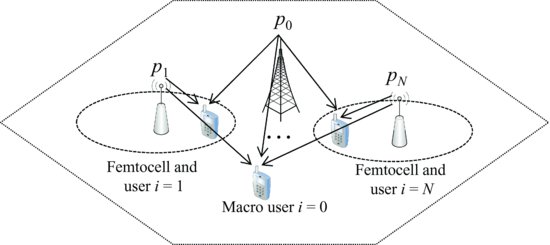
Due to the advantages of limited coordination and control, game theoretic models have been proposed to optimize the power control as an alternative to the centralized optimal power control [2]. The aim is to optimize the transmission powers of macrocell and femto users noncooperatively such that the individual utility (or payoff) is maximized in a distributed fashion (i.e., without control from a centralized controller). A noncooperative game model is formulated with the following players, strategies, and payoff functions. The players are macrocell and femto users, the set of which is denoted by (Figure 7.1), where N is the total number of femto users. User i=0 is the macro user, while users are femto users. The strategy is the transmission power denoted by pi for user i. The payoff is the utility of a user denoted by Ui(pi, p−i), where p−i denotes the strategies (i.e., transmission powers) of all the users except user i. The utility of macrocell and femto users are defined differently. The macro user wants to achieve the minimum SINR requirement. Therefore, the utility of the macro user considered in [2] is expressed as follows:

(7.18)

where is the SINR of user i defined as , hi,i is the channel gain between the transmitter and receiver of user i, and is the target SINR. The interference experienced by user i is defined as follows:

(7.19)

where hi,j is the channel gain between users i and j, and is the noise power. The utility of the macro user can be maximized when the macro user uses the lowest power to meet the SINR requirement. The utility in (7.18) is defined to be a concave function.

FIGURE 7.1 Macrocell and femtocell users in noncooperative game presented in [2].

On the other hand, the utility function of a femto user is based on the reward and penalty , that is,

(7.20)

where wi is the weighting constant of penalty. The reward function is defined such that the user i associated with a femtocell wants to maximize its individual SINR. On the other hand, a penalty function is defined such that the femto user is discouraged to use excessive power to avoid cross-tier interference (CTI) to the macro user.

For mathematical tractability, several assumptions are made for the utility function in (7.20). Firstly, given the fixed transmission power pi, the utility is a monotonically increasing concave function of SINR . Secondly, given the fixed SINR , the utility is a monotonically decreasing concave function of the transmission power pi. The rationale behind the first assumption is that the femto user has declining satisfaction if the SINR already exceeds the requirement. For the second assumption, the femto user has an increased penalty for causing more interference. In [2], the reward function is chosen to be

(7.21)

where ai is a constant, and

(7.22)

is used for the penalty function.

The solution of the above noncooperative game is the Nash equilibrium for the transmission power denoted by . The Nash equilibrium satisfies the condition defined as follows:

(7.23)

for all and . Based on the continuity and strict convexity of the utility function of the transmission power, it is proved that the Nash equilibrium exists for the above game. The Nash equilibrium of the macro user is given by

(7.24)

The Nash equilibrium of the femto user is given by

(7.25)

where [x]+=max(x, 0) and

(7.26)

The proof of existence of the solution in (7.25) is based on the fact that the partial derivative of is monotonically decreasing with increasing pi. Therefore, the necessary condition for the existence of the local optimal solution can be met, in which the derivative of is equal to zero within [0, pmax]. However, if the necessary condition is not met, the transmission power will be chosen to be zero or maximum power if the derivative of the utility function is positive and negative, respectively.

More importantly, given the chosen reward and penalty functions, [2] proves that the SINR equilibrium for the users is unique. The proof is based on using the iterative power control update, that is, p(t+1)=g(p(t)), for iteration t+1, where is the power update function. The function is given by

(7.27)

for a macro user, and

(7.28)

for femto users. Then, it is proved that the iterative power control update has a fixed point [24]. In addition, the iterative power control update can be used for the distributed implementation, where a femto user only needs to know its own SINR requirement and its channel gain.

However, there could be the case that the macro user may not be able to meet the SINR requirement, which is undesirable. Therefore, an algorithm is proposed for the macro user quality protection. In this case, the algorithm will attempt to achieve the solution close to the required SINR (i.e., the achievable SINR of the macro user becomes ) within a certain number of iterations. This can be achieved by choosing a subset of femto users to reduce their SINR. From the example presented in [2], the macro user can achieve 95% of the initial required SINR.

7.2.2 Multi-Tier Cognitive Cellular Radio Networks

Based on a noncooperative game formulation for the resource management problem in two-tier macrocell–femtocell networks, the Nash equilibrium can be obtained, which maximizes the individual payoff of the players [25]. Alternatively, a game formulation can be developed with an aim to maximizing the global utility function of the network. The benefit of using such a game formulation is that it enables a distributed implementation of channel access by femtocells, which does not require global information and full control of their transmission parameters. The optimal global utility is obtained by defining the payoff of each player (i.e., femto access point) based on different components, that is, its own benefit, fairness, and power consumption.

A different solution concept, namely, the correlated equilibrium is considered in [3]. The advantage of correlated equilibrium over Nash equilibrium is that, at the correlated equilibrium, the players are allowed to coordinate, which could result in a more efficient solution. In the system model considered in [3], the femto access points and macro base station are the secondary and primary users sharing the same pool of spectrum, respectively. The non-overlapping channel sharing scenario is considered, that is, femto access points and macro base station use different channels (i.e., called RBs). BFAP and BMBS RBs are for F femto access points and the macro base station, respectively, where BFAP+BMBS=B is the total number of RBs available in the macrocell. Figure 7.2 shows the system model with 3 femto access points and 4 RBs.

FIGURE 7.2 System model of cognitive femtocell networks [3].

A noncooperative game for the femto access point RB allocation is formulated as follows: The players are the femto access points. The strategy is whether to transmit on the RB f or not. The strategy can be represented by the variable pi,f, where pi,f=1 if player i transmits on RB f and pi,f=0 otherwise. Figure 7.2 also shows an example of strategies of players. The payoff is defined as the utility function. Firstly, the global utility function is considered which is defined as follows:

(7.29)

where ri is the achievable capacity and di is the demand of femto access point i. min(ri/di, 1) represents the satisfaction level of femto access point i, which should not be greater than one. The achievable capacity can be expressed as follows:

(7.30)

(7.31)

where is the channel gain and pi,f is the actual transmission power of femto access point i, Ii,f is the total interference, is the noise power, and is the cross channel gain between femto access points i and j on RB f. p is composed of the strategy variable pi,f. In this case, maximizing the global utility function defined in (7.29) is equivalent to maximizing the performance of the worst femto access point. However, maximizing the global utility function can be done only when the global information about the network is available and the strategies of all the femto access points can be controlled. However, a distributed environment may lack of such capability. To solve this problem, the local utility function of the femto access points (i.e., players of a noncooperative game) is defined to mimic the global utility function, such that maximizing the local utility function will tend to maximize the global utility function. The local utility function of a femto access point i is defined as follows:

(7.32)

This local utility function is composed of three components. min(ri/di, 1) is the self-interest component which is basically the satisfaction level of each femto access point, and is the fairness component which is a negative penalty for the transmission rate exceeding the demand di. Here, is the cost component due to the transmission power, wpen and wpow are the weighting factors for the penalty and power cost components, respectively.

The solution considered in [3] is a correlated equilibrium, which is defined based on the policy π (i.e., probability distribution of choosing the strategies). The condition for the correlated equilibrium can be defined as follows:

(7.33)

where policy is the correlated equilibrium, for any alternative policy . At the correlated equilibrium, no player can deviate to gain a higher expected payoff. In general, the Nash equilibrium can be represented as the correlated equilibrium, when the players make their decisions independently.

To obtain the correlated equilibrium, a decentralized algorithm based on the regret matching procedure [26] is proposed. This algorithm allows the femto access points to adapt their RB allocation strategies dynamically. The convergence of the regret matching procedure algorithm is proved. The proof is based on the fact that the Blackwell’s sufficient condition for approachability can be achieved. Specifically, a Markov chain is defined to model the regret update mechanism. The stationary probability of this Markov chain is used to verify the Blackwell’s sufficient condition.

In the performance evaluation, a small number of femto access points (i.e., six) is considered to avoid huge computational complexity. However, for a larger network scenario with more number of femto access points, [3] suggests an approach to combine multiple femto access points together into a composite player so that the strategy space can be reduced. A comparison between the proposed regret matching procedure algorithm and the best response dynamics algorithm (i.e., a player chooses the best strategy to maximize its payoff based on the observation in the last iteration) is provided. The result shows that the regret matching algorithm performs better than the best response dynamics algorithm. The reason is that the best response dynamics algorithm does not take the historical outcome of the game into account to update the strategy selection. However, since the equilibrium is not unique, both the algorithms may not converge to a single solution.

7.2.3 On-Demand Resource Sharing in Multi-Tier Networks

An on-demand resource sharing mechanism can be designed taking the users’ selfishness behavior and private traffic characteristic into account [4]. Specifically, the mechanism provides an incentive for the users to reveal the true information (i.e., traffic characteristics) so that this information can be used for efficient and fair resource allocation in two-tier macrocell–femtocell networks. Three main properties of the on-demand resource sharing mechanism proposed in [4] are as follows:

The system model considered for the on-demand resource sharing mechanism is shown in Figure 7.3. There is one macro base station serving multiple macro users whose set is denoted by . There is one femto access point, which is denoted by f. This femto access point serves femto users whose set is denoted by . The total number of resources (e.g., sub-channels in OFDMA) available for both macro and femto users is denoted by R. The macro and femto users have the following attributes.

• Traffic demand is denoted by di for or .
• Transmission rates are denoted by rmi and rfi for macro and femto users, respectively.
• Resource demands are denoted by and for macro and femto users, respectively. The resource demand can be calculated from and .
• Weights are denoted by wmi and wfi for macro and femto users, respectively. The weight is assigned by the system (e.g., based on the priority of users) for the resource allocation.

FIGURE 7.3 System model for on-demand resource sharing in femtocell networks.

The traffic and resource demands are assumed to be private information of the macro and femto users.

The on-demand resource sharing mechanism works as follows (Figure 7.4). Firstly, the macro users and femto access point send the resource requests denoted by smi where to the macro base station. The macro base station assigns the resource denoted by ami(sm) back to the macro users and the femto access point, where sm is composed of smi. Then, the femto users send the resource requests denoted by sfi (where ) to the femto access point. Given the resource allocated from the macro base station, the femto access point assigns the resource to femto user i denoted by afi(sm, sf), where sf is composed of sfi. Some assumptions are made for the resource requests. Firstly, the transmission rate of the femto access point is normalized to be one, and the weight of the femto access point is the sum of weights of all the femto users, that is, .

FIGURE 7.4 Traffic demand request and resource allocation.

A hierarchical game model is formulated to analyze the behavior of the macro and femto users. This hierarchical game is composed of two sub-games, that is, the macrocell and femtocell games.

• Macrocell game: The macro players are the macro users and the femto access point, whose set is . Their strategies are the resource requests smi. The payoff is the utility defined as Umi(sm)=min(di, rmiami(sm)), where ami(sm) is the allocated resource to macro player .
• Femtocell game: The femto players are the femto users, whose set is . Their strategies are the resource requests sfi. The payoff is the utility defined as Ufi(sm, sf)=min(di, rfiafi(sm, sf)), where afi(sm, sf) is the allocated resource to femto player . Observe that the allocated resource to the femto users depends on the strategies of the macro players (i.e., sm).

To obtain the allocated resource, which is an important factor for the payoff of players, the weighted water-filling resource allocation method is proposed [4]. The allocation is divided into two parts, that is, for macrocell and femtocell. For the macrocell, the allocation works as follows:

1. Sorting: The macro base station sorts the macro players based on their weighted resource request (i.e., smi/wmi for ). In this case, i=1 and indicate the macro players with the smallest and the largest weighted resource requests, respectively.

2. Weighted water filling: The macro base station allocates the resource R to all macro players. The allocation is performed iteratively for R iterations. In the tth iteration, the macro base station allocates the resource which is proportional to the weight to every macro player for . The allocation is performed until the macro player has received all the requested resource or until all the resources have been allocated.

Based on this allocation, the allocated resource to macro player i is

(7.34)

where is the macro player with the largest index that its requested resource is fully allocated. For the femtocell, the allocation works similarly.

Instead of the Nash equilibrium, [4] considers the dominant-strategy equilibrium as the solution of the game. In general, the dominant-strategy equilibrium is stronger but harder to achieve. Nevertheless, it is proved that the equilibrium of the on-demand resource sharing mechanism always exists with the strategy proofness property. Firstly, the dominant strategy is defined as the strategy that maximizes the payoff of player i given all possible strategies of other players, that is,

(7.35)

The dominant-strategy equilibrium is then the strategy profile whose each strategy is a dominant strategy for every player i. An attractive property of the dominant-strategy equilibrium, if exists in the game, is that the player can choose the dominant strategy to achieve the dominant-strategy equilibrium without knowing the information of other players. Therefore, it enables a fully distributed implementation and reduces information exchange.

The equilibrium analysis is performed for the on-demand resource sharing mechanism in [4]. The major results can be summarized as follows:

• The proposed game has the truth-revealing dominant strategy equilibrium. This equilibrium is also strategy proof (i.e., , where is the true resource demand). This property can be proved by showing that the best strategy of each player is to submit the true resource demand to maximize the payoff. There is no chance that the player can gain a higher payoff by submitting a resource demand lower or higher than the true resource demand.
• The resource allocation at the truth-revealing dominant strategy equilibrium of the game achieves the weighted max–min fairness. Let denote the resource allocation at such an equilibrium, which is composed of ai for or for macro or femto players, respectively. The condition of the weighted max–min fairness is for some i, and then

  (7.36)

• The resource allocation at the truth-revealing dominant strategy equilibrium is weighted proportional fair. Again, let denote the resource allocation at such an equilibrium. It is the solution of the following optimization problem,

  (7.37)

  where K is the available resource, which is K=R or K=amf for the macrocell or femtocell, respectively.

• The resource allocation at the truth-revealing dominant strategy equilibrium is Pareto efficient. This Pareto efficiency ensures that none of the players (i.e., either macro or femto players) can increase her payoff without decreasing the payoff of other players, that is, for some , then .

In addition to analyzing the properties of the dominant strategy equilibrium in the game for the on-demand resource sharing mechanism, [4] also discusses about accepting macro users as the open access mode in the femtocell. Specifically, the femtocell grouping scheme is proposed to allow the macro users near to the femto access point (i.e., having the transmission rate to the femto access point higher than that to the macro base station) to join the femtocell. With the grouping scheme, the femto users are divided into the closed access users (i.e., users subscribed to femtocell) and general users. A weighted water-filling resource allocation can be applied to the general femto users and closed access group. Then, the resource is allocated to the femto users in the close access group. In this case, the resource can be reallocated from one femto user group to another group efficiently.

Then, a rate-related weight configuration is proposed. The weight configuration allows the weight of macro or femto users to be adjusted to achieve a better performance. Specifically, less resource is required for the high transmission rate users to meet their traffic demand. In this case, the weight is defined as a function of the transmission rate, that is, wi(ri). The key design issue for the weight function is that the weight should be smaller when the transmission rate is higher (i.e., to reduce requested resource) and the weight should be chosen such that the user will receive the higher payoff. In the numerical results, the weight function is chosen to be wi(ri)=(1/ri)1/2.

Although the on-demand resource sharing mechanism proposed in [4] is for a single femtocell, its extension for the multiple femto access points is also given. The same weighted water-filling resource allocation can be applied. However, the challenge is at the proofs of different properties (e.g., truth-revealing dominant strategy equilibrium), which require further studies. In addition, the hierarchical game model is not shown to achieve the Stackelberg equilibrium. The Stackelberg equilibrium will be more suitable solution if the macro users have higher priority to obtain the resource.

7.3 GAME FORMULATIONS FOR PRICING

A pricing scheme and incentive mechanism can be adopted in the femtocell networks to control interference [27]. This economic approach can be modeled and analyzed using game theory, especially when there are multiple rational and self-interested entities in the networks. In [27], the interference from femtocells to the macro users is controlled through a pricing mechanism. Specifically, the femto users are charged with a certain price according to the interference that they cause to the macro users. A hierarchical game model is proposed, where the leader player is the macro base station optimizing the price charged to femto users. The femto users as the follower players optimize the transmission power according to the price.

Reference [28] also considers the cognitive radio capability, where the MBS can obtain the spectrum resource from the primary users. The first tier players (i.e., primary users) optimize the price to maximize their revenue. The second tier player (i.e., macro base station) determines the spectrum resource demand and allocation to the macro users and femto access points. The third tier players (i.e., femto access points) optimize the transmission power. A similar game structure is considered in [29], where the game model is divided into three stages. In the first stage, a femto service provider determines the optimal ratio of the resource for an open access mode (i.e., for macro users). In the second stage, a macro service provider determines the price for the spectrum resource leasing to a femto access point. Then, in the third stage, the femto access point optimizes the spectrum demand. A three-stage Stackelberg equilibrium is derived as the solution of this game.

Reference [30] considers a pricing issue in the femtocell networks under the randomness of the interference. In particular, the activity of macro users is modeled as a two-state homogeneous discrete-time Markov chain. The femto access points measure the interference and adjust the transmission power given the price charged per unit of transmission power. The Nash equilibrium is considered to be the solution. Reference [31] considers the pricing issue in the open or close access modes of the femtocell networks. Specifically, the provider can charge a certain price to the users and the users determine their traffic demand and choose to join the macrocell or femtocell (i.e., by connecting to the macro base station or a femto access point, respectively). A two-stage game model is proposed. In the first stage, the provider selects the optimal prices to maximize its revenue. In the second stage, the user determines the traffic demand and chooses to join macrocell or femtocell.

In the following, the detailed formulations of the selected game models for pricing and incentive mechanism in the femtocell networks are discussed.

7.3.1 Price-Based Spectrum Sharing

The utility-based distributed SINR adaptation proposed in [2] considers only the power allocation. Also, the macro and femto users have the same priority, which may not be applicable in some cases. References [32, 27] extend the work in [2] by considering the case that the macro user should be protected from the interference caused by the femto users. Also, a macrocell (i.e., macro base station) can obtain revenue by charging the price from the femto users given the interference caused by the femto users. This is referred to as the price-based spectrum sharing scheme, which is modeled as a Stackelberg game in [27].

Figure 7.5 shows the system model of the femtocell network considered for price-based spectrum sharing [27]. There is one macro base station and there are N femto users associated with the femto access points. The macrocell and femtocells use the same sub-channel. The macro base station can tolerate the interference from femto users up to Imax, that is, , where Ii is the interference power from femto user i. The macro base station sets and charges the prices per unit of received interference power from each femto user. Then, based on this price, the femto user adjusts their transmission power to maximize their individual payoffs. The price charged to the different femto users can be different or the same, which are referred to as the non-uniform and uniform pricing schemes, respectively. The price charged to femto user i is denoted by and μ for the former and latter pricing schemes, respectively.

FIGURE 7.5 System model for price-based spectrum sharing [27].

Two femtocell network scenarios are considered, that is, sparsely and densely deployed scenarios (Figure 7.5). In the sparsely deployed scenario, there is no mutual interference among femtocells, since each femtocell could be deployed far away from each other. On the other hand, in the densely deployed scenario, mutual interference among femtocells exists. In this case, the aggregate interference at the femto access point due to the transmission of femto users associated with other femto access points must be maintained below a specified threshold.

A Stackelberg game model is formulated in [27] and its structure is shown in Figure 7.6. In the Stackelberg game, there are the leader and follower players. The leader can make a decision before the follower. Since the follower can observe the decision of the leader, the leader can optimize its payoff given the belief that the follower will apply the best response strategy (i.e., strategy of the follower that maximizes its own payoff). In the price-based spectrum sharing, the leader player is the macro base station, whose strategy is the price charged to the femto users. The follower players are the femto users (i.e., N femto users), whose strategy is the transmission power denoted by pi. The payoff of the leader is defined as the revenue,that is,

(7.38)

where is the price charged to femto user i, and Ii(pi) is the interference quota that the femto user i is permitted to cause to the macro base station, and hence to be charged. This interference quota is given by Ii(pi)=h0,ipi, where h0,i is the channel gain between femto user i and the macro base station. contains all prices charged to all the femto users and p contains transmission powers of all the femto users. In (7.38), transmission power pi could depend on the price (to be discussed later). The payoff of the follower is defined as the utility of the transmission rate and price paid to the macro base station, that is,

(7.39)

Here hi,i and hi,j are the channel gains from femto user i to its corresponding femto access point and from femto user i to the femto access point of femto user j, respectively. wi is the weighting factor. p−i contains the transmission powers of all the femto users except femto user i. Notice that the payoff of the femto users in (7.39) does not account for the interference from macro users.

FIGURE 7.6 Stackelberg game model of price-based spectrum sharing.

Since the macro base station and femto users are rational players, optimization models can be formulated for them to obtain the optimal strategies given the strategies of other players. The optimization model for the macro base station in the Stackelberg game is expressed as follows:

(7.40)

That is, the macro base station optimizes the price charged to the femto users given that the interference must not exceed the threshold Imax. Similarly, the optimization model for the femto user in the Stackelberg game is expressed as follows:

(7.41)

The solution of the Stackelberg game is the Stackelberg equilibrium, which ensures that the leader gains the highest payoff, while the followers cannot deviate to use other strategies which are not the Stackelberg equilibrium. Let , , and are the Stackelberg equilibrium for the strategies , pi, and p−i of the leader and followers, respectively. They satisfy the following conditions:

(7.42)

(7.43)

The Stackelberg equilibrium can be obtained by finding the subgame perfect Nash equilibrium. In this case, there are multiple followers (i.e., femto users). They will play the noncooperative power control subgame (Figure 7.6) given the price set by the leader (i.e., macro base station). In other words, if the price is fixed, and are the Nash equilibrium strategies. From the macro base station’s perspective, and are the best response strategies that the followers will apply given price . Therefore, as a standard method (i.e., backward induction) to solve for the Stackelberg equilibrium, the optimization model of the follower defined in (7.41) will be solved first. Then, the optimization model of the leader defined in (7.40) will be solved.

In the following, non-uniform and uniform pricing will be presented for a sparsely deployed scenario. Since the mutual interference is avoided in the sparsely deployed scenario, solving for the Stackelberg equilibrium is simpler than that in the densely deployed scenario. Also, a closed-form solution can be obtained.

In the non-uniform pricing scheme, the price could be different for the different femto users, which is denoted by . With the sparsely deployed scenario, the optimization model of the follower becomes

(7.44)

This optimization model is a convex problem, which can be solved using the KKT conditions. The solution (i.e., best response) of the follower is expressed as follows:

(7.45)

It can be observed that if the price charged by the macro base station is too high (i.e., ), the femto user will not transmit.

The optimization model of the leader becomes

(7.46)

However, the optimization model of the leader in (7.46) is non-convex, e.g., due to the constraints. To obtain the globally optimal solution, the optimization model can be transformed into multiple convex sub-problems by using an indicator function defined as follows:

(7.47)

The indicator function implies whether the femto user should be allowed to transmit or not. Then, the optimization model of the leader becomes

(7.48)

(7.49)

where contains all for . Given , the above problem is convex, which can be solved to obtain the globally optimal solution (i.e., Stackelberg equilibrium). Now, it is possible to solve for . This can be done by identifying the interference threshold Imax to which should be one or zero. As shown in [27], the Stackelberg equilibrium for the price can be obtained in the closed form [27, Eq. (21)]. For example, if the transmission of all femto users can meet the interference threshold, the optimal price can be expressed as follows:

(7.50)

Also, since the Stackelberg equilibrium can be obtained through the indicator function, it is possible to design an admission control scheme. That is, femto user i is admitted and allowed to transmit data if . In other words, the macro base station sets the price such that the femto users want to be admitted or not.

A centralized algorithm to obtain the Stackelberg equilibrium is also proposed. However, it is found that, in this algorithm, the macro base station needs to compute for each femto user. This will incur a substantial amount of overhead. To avoid this overhead, a uniform pricing scheme is proposed in which the macro base station needs to measure the total received interference power only.

In the uniform pricing scheme, the price charged to all the femto users is the same, that is, . Given the uniform price μ, the best response strategy of the follower can be expressed similar to that in (7.45). Also, the optimization model of the leader becomes

(7.51)

(7.52)

Again, this optimization model of the leader can be solved directly to obtain a unique solution in a closed form. A distributed algorithm is proposed in which only the total received interference power is required to compute the Stackelberg equilibrium for the price of the macro base station. This property is desirable from a practical point of view, since the complexity is much lower than that of the non-uniform pricing scheme. However, only the non-uniform pricing scheme, which takes the individual femto user’s parameters into account, can maximize the payoff of the macro base station (i.e, price for each femto user can be customized based on channel quality and weighting factor). On the other hand, a uniform pricing scheme can maximize the sum-rate of the femto users, but the payoff of the leader may not be maximized.

Then, a densely deployed scenario is considered and a similar analysis to obtain the Stackelberg equilibrium is applied. Although there is the bound on the aggregate interference at the femto access point of femto user i, the best response strategy of the femto user i can be obtained in the close form as follows:

(7.53)

The Stackelberg equilibrium for the case of uniform pricing scheme is obtained in a similar way. Note that the Stackelberg equilibrium in terms of the price of macro base station cannot be obtained in a closed form anymore for the densely deployed scenario.

7.3.2 Energy-Efficient Spectrum Sharing and Power Allocation

While throughput is mostly considered to be a main performance metric for the femtocell networks, EE is another important performance metric. Reference 28 introduces the energy-efficient spectrum sharing and power allocation scheme for cognitive femtocell networks. A resource allocation scheme similar to the on-demand resource sharing mechanism in [4] is considered. However, the available resource is sold by the primary networks in [28] instead of being always available as in [4].

The system model considered for the energy-efficient spectrum sharing and power allocation is shown in Figure 7.7. There are K primary users (i.e., primary BSs) owning the non-overlapping spectrum resources. The primary BS k sells part of its spectrum resource whose size is denoted by bk to a cognitive macro base station. This cognitive macro base station pays the price to the primary BS k. The cognitive macro base station serves M macro users and F femto access points. It is assumed that the spectrum resource is allocated to either macro user j or one of the femto access points i, that is, for all k. The spectrum resource allocation is denoted by xk,j and xk,i for macro user j and femto access point i, respectively. xk,j=1 or xk,i=1 if the spectrum resource from primary BS k is allocated to macro user j or FBS i, respectively. Otherwise, xk,j=0 or xk,i=0.

FIGURE 7.7 Stackelberg game model of energy-efficient spectrum sharing and power allocation.

A hierarchical game theoretic model is developed to analyze the energy-efficient spectrum sharing and power allocation. This game model is composed of three tiers, which can be considered as an extension of the model proposed in [27], considering the pricing issue. The first-tier players are the primary networks (i.e., primary BSs). The second-tier player is the cognitive macro base station for a macrocell. The third-tier players are the femto access points for femtocells. The strategy of the first-tier player is the price charged to the cognitive macro base station. This price is optimized through the “price competition” component as shown in Figure 7.7. The strategy of the second-tier player is composed of the size of spectrum bk to be bought from primary BS k and spectrum allocation xk,j and xk,i. The strategy of the third-tier player is the transmission power denoted by pi for femto access point i. The transmission power is optimized through the “resource allocation” component as shown in Figure 7.7. The size of spectrum to be bought and spectrum allocation of the second-tier player is optimized through the “spectrum demand” and “resource allocation,” respectively.

The payoff of the femto access point i is the utility defined as follows:

(7.54)

where is the revenue for femto access point i (e.g., obtained from a femto user) and is the price charged by the cognitive macro base station for the allocated resource, for . is the EE of femto access point i using spectrum resource from primary BS k. The EE is defined as follows:

(7.55)

where hk,i is the channel gain, is the noise power, and pcir is the energy consumption of the transceiver circuit. Note that the EE denoted by of macro user j can be defined similarly. It is proved that the payoff function of the femto access point defined in (7.54) is quasiconcave.

The payoff of the cognitive macro base station is defined as follows:

(7.56)

where b contains the sizes of spectrum resource bk bought from the primary BS k. is the spectrum substitutability factor. If s=1, the femto access point and macro user can switch among the spectrum resources freely. If s=0, they cannot switch among the spectrum resources. If s<0, the spectrum resources used by them are complementary. is the price paid by the macro user j to the cognitive macro base station. The utility of the cognitive macro base station in (7.56) is chosen to be a quadratic function due to its mathematical tractability (e.g., concavity and linear demand function obtained from its derivative).

The payoff of the primary BS is the revenue defined as follows:

(7.57)

where w is a weighting factor, Bk is the total available spectrum resource of primary BS k, and rk is the transmission efficiency. is composed of the prices of all primary BSs . The first part of the revenue (i.e., w(Bk−bk)rk) is from serving primary users while the second part (i.e., ) is from selling the spectrum resource to the cognitive macro base station.

The solution of the hierarchical game model is the Stackelberg equilibrium. The backward induction method is applied to obtain such an equilibrium.

Power allocation of femto access point: Firstly, the optimal transmission power of a FAP to the femto user is obtained. The optimal transmission power denoted by is obtained under the condition of function Ri(pi) defined as follows:

(7.58)

In particular, if Ri(pi) is strictly concave, there is a unique globally optimal transmission power for the femto access point. The gradient assisted binary search algorithm is used to obtain the optimal solution.

Spectrum demand and resource allocation by cognitive macro base station: Secondly, the spectrum demand of the cognitive macro base station is obtained. By differentiating the payoff of the cognitive macro base station defined in (7.56) and equating it to zero, the linear function for the spectrum demand denoted by can be obtained in a closed form [28, Eq. (13)]. Then, the spectrum allocation is performed to allocate each of to one of the femto access points or one of the macro users. A greedy-based algorithm is adopted. In particular, the allocation is performed iteratively, and in each iteration, the allocation xk,i or xk,j is chosen such that the revenue of the cognitive macro base station is maximized (i.e., ).

Price competition of primary BS: Thirdly, the price of the spectrum resource is determined by the primary BS. The objective is to maximize the revenue defined in (7.57). However, the revenue of one primary BS is affected by the prices offered by the other primary BSs. Therefore, a subgame for the price competition is formulated for the primary BSs. The best response function is defined as , where is composed of the prices of all the primary BSs except the primary BS k. The Nash equilibrium of the primary BSs, given the spectrum demand from the cognitive macro base station, is the solution of . The proof for existence of the Nash equilibrium is based on the nonempty convex and compact subset of Euclidean space for the price . Also, the revenue function defined in (7.57) is concave. Then, the uniqueness of the Nash equilibrium is proved by showing that the best response is a standard function. That is, the standard function has the positivity (i.e., ), monotonicity (i.e., for , then ), and scalability (i.e., for all y>1, then ) properties.

Then, the Stackelberg equilibrium is obtained, which are denoted by , , and , and . is the optimal price for the primary BS. is the optimal spectrum demand, and and are the optimal spectrum allocation of the femto access point i and macro user j, respectively. is the optimal transmission power for the femto access point. A gradient iteration algorithm is proposed to obtain the Stackelberg equilibrium. The gradient update in iteration t+1 can be expressed as follows:

(7.59)

where Δ is a step size. The simulation results show that the proposed algorithm converges to the Stackelberg equilibrium. However, the mathematical proof of such convergence is open for the future study.

7.4 GAME FORMULATIONS FOR ACCESS CONTROL

In open and closed access modes of a multi-tier network, users can connect to a macro base station or a SBS (e.g., femto access point) if they are in their coverage. The selection can be done by the rational and self-interested users. Alternatively, femtocell and macrocell can control the users’ access to maximize their own benefits. These situations can be modeled using game theory. [33] considers the BS (e.g., macro base station and femto access point) selection problem and proposes a game theoretic model to analyze the decision of users. Different preferences of the users in choosing the BS are considered, that is, equal transmission time and equal throughput. If the users are concerned about the equal transmission time, the solution is shown to be the unique Nash equilibrium, which also achieves proportional fairness. If the users are concerned about the equal throughput, there could be multiple Nash equilibria, some of which could be far from the optimal solution. Reference [34] presents an incentive mechanism, namely refund framework, to motivate femto access points to accept and serve macro users. In particular, the mobile BS pays money to allow some of their macro users to connect to the femto access point, off-loading traffic from macrocell. Reference [35] considers the situation where a femto access point can accept macro users who are the non-subscribers of the femtocell based on the utility.

Coalitional game has been applied to model and analyze the access control problem of the femtocell network. In [25], a macro user can choose to transmit data directly to the macro base station or to form a coalition with a femto user and let the femto user relay the macro user’s traffic to the femto access point to improve the performance. A coalition formation game model is proposed to analyze the stable coalition among macro and femto users. In [36], to reduce interference, the coalition formation among femto access points is considered as the solution. In particular, the femto access points forming a coalition can coordinate their spectrum resource usage to avoid co-tier interference. In [6], the cell selection of users between macrocell and femtocell is considered as a coalition formation game. Specifically, the user chooses to connect to the macro base station or femto access point based on their optimized transmission power and utility. The stable coalitions are analyzed by using the Markov chain.

In the following, the detailed formulations of the selected game models for access control in the femtocell networks are discussed.

7.4.1 Refunding Framework for Hybrid Access Small Cell Network

Open and closed access modes of small cells have limitations in terms of limited QoS guarantee and low resource utilization, respectively. Therefore, a hybrid access mode is more suitable for a small cell. For example, a femtocell with the hybrid access mode can reserve the radio resource for femto users (i.e., controlled by the femtocell owner) and at the same time can provide service to other users (e.g., unregistered roaming macro users). Therefore, the QoS guarantee can be supported by reducing CTI, and the radio resource utilization can be improved [31]. However, since the femtocell owner is rational, the service provider of the macrocell has to provide an incentive to motivate the femtocell owner to share the femtocell service. In [34], an access control mechanism is considered to address an incentive issue in hybrid access femtocell networks. Specifically, a utility-aware refunding framework is developed for the femtocell owner and service provider to maximize their utilities. A game model is proposed to analyze the equilibrium strategies in terms of the refund (i.e., money) to be paid by the service provider to the femtocell owner and the radio resource (i.e., transmission period) to be allocated for the roaming macro users by the femtocell owner.

Note that the refunding framework proposed in [34] is opposite to the case of the price-based spectrum sharing in [2]. That is, in the price-based spectrum sharing, the macro base station earns revenue from the interference caused by the femto users (i.e., the same sub-channel is used). On the other hand, in the refunding framework, the femtocell owner earns revenue by allowing macro users to access its femtocell (i.e., the different sub-channels are used, and hence there is no CTI). In contrast, the refunding framework is similar to the macro–femto cooperation proposed in [25] in the sense that the femtocell owner can cooperate to allow the macro users to access the femtocell. However, instead of granting a transmission period for the femto users as an incentive, in the refunding framework, the service provider of the macrocell will pay the refund in terms of money to the femtocell owner in return.

The system model considered in the refunding framework is shown in Figure 7.8. There is one macrocell (i.e., one macro base station) and N underlaid femtocells. The macro users subscribed to the service provider can communicate with the macro base station. The registered femto users can communicate with the femto access point. When the macro users move into the coverage of the femto access point, the macro users can communicate with the femto access point (i.e., off-loading), if the femtocell is in a hybrid access mode. It is assumed that the macrocell and femtocells operate using TDMA for data transmission, and they are allocated with different frequencies. Therefore, the CTI does not occur.

FIGURE 7.8 System model for refunding framework for hybrid access femtocell network [34].

The transmission frame of the femtocell is divided into two parts, that is, one for femto users and another for macro users. is the fraction of the transmission frame (i.e., transmission period) that the owner of femtocell i allocates for the transmission by the macro users. Macro user m is allocated with fraction of the transmission frame for its own transmission, where and Mi is the number of macro users in femtocell i. A simple fair share of the transmission period can be applied, for example, each macro user is allocated with a transmission period equal to . The rest of the frame (i.e., ) is used for the transmission by the femto users registered to femtocell i. Femto user j is assigned with fraction of the transmission frame. Note that corresponds to the case of a closed access mode (i.e., macro users are not allowed to communicate with the femto access point). Figure 7.8 shows the example of the transmission frame. There are femtocells 1 and 2. Femtocell 1 operates in the hybrid access mode, while femtocell 2 operates in the closed access mode. For femtocell 1, there are one macro user and two femto users. Fractions and of the frame are allocated for the transmission of femto users 1 and 2, respectively, where . Since there is only one macro user, the fraction of the frame is allocated for the transmission of this macro user.

In the aforementioned system model, the refund mechanism works as follows (Figure 7.9). Since femtocells belong to the femtocell owners, the service provider intending to off-load macro users to the femtocell has to pay the refund (i.e., money) to the femtocell owner. The total refund paid to all the femtocell owners is denoted by μ. The refund from the service provider is distributed among femtocell owners proportionally to the fractions of a transmission frame allocated to the macro users as follows:

(7.60)

where is the refund given to femtocell owner i. The femtocell owners observe the received amount of refund and adjust the size of the transmission period for the macro users.

FIGURE 7.9 Refund mechanism for a hybrid access femtocell network.

A Stackelberg game model is formulated to analyze the interaction among the service provider operating the macrocell and the femtocell owners operating different femtocells. The leader player is the service provider. The follower players are the femtocell owners. The strategy of the leader is the refund μ. The strategy of the follower is the transmission period allocated to the macro users. The payoff of the leader (i.e., service provider) is the benefit from off-loading the macro users to femtocells, expressed as follows:

(7.61)

where c is the off-loading rate of macro users and wM is the weighting factor of the macrocell. When the macrocell can off-load the macro users, the macrocell can provide a better QoS performance, yielding higher satisfaction to the users. The off-loading rate is estimated as the sigmoid function, defined as follows:

(7.62)

where Rm is the transmission rate of macro user m. a and b are the sensitivity parameters due to the QoS increment and reserved traffic demand of the macro users, respectively. The payoff of the follower (i.e., femtocell owner) is a function of the transmission rate of femto users and the refund obtained from the service provider is defined as follows:

(7.63)

where ri is the transmission rate of femto user i and wF is the weighting factor. The transmission rates of the macro user m and femto user i can be obtained from and , respectively. Cm and ci are the channel rates obtained from and , where and are the SINRs of macro and femto users, respectively.

A standard method of backward induction is applied to solve the Stackelberg game. In the first step, an optimization model of the follower is formulated as and solved for the best response strategy. Then, based on the best response strategies of the followers, the leader formulates and solves another optimization model to obtain the optimal strategy. Since there are multiple femtocell owners as the followers, the optimization model is the noncooperative access control subgame (i.e., to determine the transmission period for the macro users). It is shown that the best response strategy of the femtocell owner i given the strategies of other femtocell owners can be expressed as follows:

(7.64)

if , and otherwise. It is proved that the best response strategy of the femtocell owner is the unique Nash equilibrium of the noncooperative access control subgame. This Nash equilibrium can be expressed as follows:

(7.65)

if , and otherwise.

Then, the service provider solves for the refund which is shown to be

(7.66)

(7.67)

It is observed that the above solution is locally optimal. Clearly, the convexity of the optimization model of the leader cannot be guaranteed, that is, due to the sigmoid function.

Finally, a hybrid access protocol is introduced to implement the above Stackelberg game. The protocol is composed of two steps, that is, optimal refunding for the service provider and access control for the femtocell owners. In the optimal refunding step, the femto access point periodically collects the channel information of the macro and femto users in its coverage. This information is forwarded to the service provider. The service provider checks whether the current condition will be profitable to off-load the macro users or not (i.e., by checking the payoff given the optimal refund ). If it is profitable, the optimal refund is paid to the femtocell owners. In the access control step, the femtocell owner chooses the transmission period for the macro users. However, if the condition is not favorable (e.g., the channel quality to the macro user is too poor or there are too many connected femto users), the femtocell owner will switch to the closed access mode (i.e., ).

7.4.2 Selection of Network Tier

With the open access mode, macro users can connect to a femto access point if they are in its coverage. However, the performance of connecting to the femto access point can be degraded due to congestion. To analyze the cell selection behavior of the rational users in a femtocell with the open access mode, a game model is formulated and the Nash equilibrium is analyzed in [35]. The system model considers one macrocell and one femtocell. A user can be a subscriber or non-subscriber of the femtocell. When the subscriber is in the femtocell, this subscriber will connect to the femto access point. However, when the non-subscriber is in the femtocell, this non-subscriber has a choice to connect to the macro base station or the femto access point. The non-subscriber is a rational agent, and hence will decide on its connection to maximize the individual utility.

A noncooperative game model is formulated for the cell selection of the non-subscribers. The players are non-subscribers in the coverage of the femtocell. The strategy is to connect to either the macro base station or femto access point. The payoff is the utility of non-subscriber i, defined as follows:

(7.68)

where uM(n) and uF(n) are the utilities of connecting to the macro base station and femto access point, respectively, given the number of non-subscribers n connecting to the femto access point. Firstly, for the case of selecting the macrocell, the utility is expressed as follows:

(7.69)

where B is the spectrum size, p is the transmission power, hm is the channel gain to the macro base station, and is the noise power. In [35], the transmission power p is chosen such that all the users connected to the macro base station achieve the same SINR. For the case of selecting the femtocell, the utility is expressed as follows:

(7.70)

Here H is the number of subscribers of the femtocell, L is the total spectrum available for the femto access point, N is the total number of non-subscribers in the coverage of the femtocell, pmax is the maximum transmission power, and hf is the channel gain from the femto user to the femto access point. is a set of non-subscribers which use the same spectrum as that of macro user (i.e., interference exists). pi is the transmission power of non-subscriber i, hf,i is the channel gain to the femto access point, pm is the transmission power of the macro user, and hf,m is the channel gain from the macro user to the femto access point. α is the ratio of the total capacity for the femtocell. If , the femtocell is completely closed and cannot accept the macro users in the femtocell. In contrast, if , the femtocell is completely open and all the macro users in the femtocell will be accepted. The utility of selecting the femtocell defined in (7.70) is composed of two parts. Firstly, is the transmission rate of the non-subscribers accessing the non-interfered spectrum (i.e., only one non-subscriber transmits on one spectrum). Secondly, is the transmission rate of the non-subscribers accessing the interfered spectrum (i.e., non-subscriber and macro user access the same spectrum).

A Nash equilibrium is considered to be the solution of the cell selection game. The existence of the Nash equilibrium is proved by showing that the cell selection game is a potential game. The potential game has the potential function . The potential function satisfies the following condition, , for all strategies si and . The Nash equilibrium is a pure strategy of this potential game if and only if for all i and si. It is shown that the cell selection game has a potential function, which is defined as follows:

(7.71)

Although the cell selection game is proved to have a Nash equilibrium, the algorithm to reach the Nash equilibrium is not discussed. An efficient algorithm would be required, especially in a distributed environment, where the non-subscribers have to select the cell independently.

7.4.3 Coalitional Game for Cooperation among Macrocells and Small Cells

In a two-tier macrocell–femtocell network, a macro user, especially at a cell boundary area, usually suffers from low SINR. On the other hand, femtocells are interference limited. Nevertheless, the cooperation between macro and femto users can alleviate such trade-off. This cooperation under a closed access mode is considered in [25]. In this cooperation scheme, the cooperative femto user (i.e., FUE) can relay the data transmission of the cooperative macro user, consequently improving the SINR. In return, the cooperative macro user grants the fraction of the transmission time to the cooperative femto user. This cross-tier cooperation scheme introduces a mutual benefit for co-channel femtocell networks, by avoiding CTI at the femtocell.

An example of the cross-tier cooperation is shown in Figure 7.10. There are femto users 1 and 2, and there are two macro users 1 and 2. Femto user 1 does not cooperate with macro user 1. Therefore, in this noncooperative case, macro user 1 has to transmit to the macro base station directly, creating strong interference to a femtocell using the same sub-channel. On the other hand, femto user 2 cooperates with macro user 2. Therefore, the transmission of macro user 2 can be relayed by the femto user 2 to the corresponding femto access point. Also, macro user 2 allows femto user 2 to access part of its transmission frame. In this cooperative case, macro user 2 gains the benefit in terms of better transmission quality and low transmission power due to shorter range transmission. Likewise, femto user 2 gains the benefit in terms of larger transmission bandwidth.

FIGURE 7.10 Cooperation between macro user 2 and femto user 2 and the frame structure [25].

An example of the frame structure due to cooperation is also shown in Figure 7.10. In this case, the frame is divided into three parts. The first part is for the transmission by macro user 2. The size of the first part is of the frame. The second part is for the femto user to relay the transmission of macro user 2 (e.g., using a decode-and-forward scheme). The size of the second part is , where is the proportion that femto user i (i.e., i=2 in this example) uses to relay the transmission from the cooperative macro user. The third part is for the femto user 2 to transmit its own data, and the size of the third part is . Note that this cooperative scheme is also known as the spectrum leasing, which is originally proposed for a cognitive radio network [37].

To analyze and obtain the solution for the cross-tier cooperation scheme, [25] proposes a coalition game model. The players are macro users and femto users. The strategy is to cooperate or not. If the macro user cooperates, this user will allow the femto user to transmit in its frame. If the femto user cooperates, this user will relay the transmission from the corresponding cooperative macro user. Let denote a set of macro users. Let denote a set of femto users associated with femto access point f, for , where is the set of femto access points. Each femto access point is allocated with a dedicated sub-channel in OFDMA-based networks. The set of players is . One femto user can cooperate with multiple macro users. Therefore, if the strategies of the macro and femto users are to cooperate, then the coalition of femto user i denoted by can be formed. The payoff is defined as follows:

(7.72)

where is the achievable rate of the macro and femto users from cooperation. This achievable rate depends on the cooperation parameters α and for femto user i, which will be optimized. For example, the achievable rate of the cooperative femto user i can be obtained from , where rRi is the transmission rate of the femto user i. This transmission rate is obtained from

(7.73)

where hi is the channel gain between femto user i and the corresponding femto access point, and hi,j is the channel gain between macro user j and the femto access point of the femto user i. pi and pj are the transmission powers of femto and macro users i and j, respectively. denotes the set of macro users who are not in a coalition using the same sub-channel as that of femto user i, and is the noise power.

However, due to the interference, the achievable rate of one user also depends on the cooperation of other users. The cooperation (i.e., coalitions) of all the users in the game is defined as the partition Π, which is a parameter of the payoff defined in (7.72). DCi is the transmission delay of user i from cooperation. This transmission delay is composed due to transmission delay from the macro user to the cooperative femto user and from the cooperative femto user to the femto access point. In [25], the delay performance is obtained from an M/D/1 queueing model. Finally, δ is the transmission capacity-delay trade-off parameter in the payoff.

For example, in Figure 7.10, let f1 and f2 denote femto users 1 and 2, respectively. Let m1 and m2 denote macro users 1 and 2, respectively. The set of players is . There is one cooperation, whose coalition is defined as . The partition is defined by . Clearly, the achievable rate of macro and femto users m2 and f2 will be affected by the transmission of macro and femto users m1 and f1, if all of them use the same sub-channel.

Based on the payoff defined in (7.72), it is observed that the coalitional game is in a partition form with NTU. The reason is that the payoff depends on transmission rate and delay which could not be arbitrarily allocated to any player. The solution of this game is to find a stable cooperation scheme, which is defined as the stable coalitions (or stable partition for all the users). Also, it is important to derive the optimal solutions for the cooperation parameters (i.e., α and ), and for the transmission parameter (i.e., transmission power pi) of each user. In [25], the recursive core [38] is considered as a solution of this coalitional game. The recursive core is a set of partitions that the players can form coalitions within such that each player gains the highest payoff. The recursive core is a desirable solution due to the following properties.

• Rationality: A player will never choose to cooperate if its payoff will be degraded.
• Well-definition: If it exists, the recursive core will always be unique.
• Efficiency: All partitions in the recursive core are equivalent in terms of individual payoff of each player.

In short, at the recursive core, none of the players has an incentive to deviate from the current coalition, which is the notion of stability.

For the coalitional game for macro–femto cooperation proposed in [25], the existence of the recursive core is also discussed. It is shown that the recursive core exists. The reason is that there is no case that all possible partitions will result in the same payoff.

Reference 25 also presents a distributed algorithm to reach the recursive core and also to obtain the optimal cooperation and transmission parameters. Figure 7.11 shows the major three steps of the distributed algorithm. In the interference discovery step, the macro user periodically transmits the received signal strength indicator (RSSI) to the macro base station. The potential femtocells to cooperate are identified from the RSSI. A similar procedure is performed by the femto users. Then, for the potential macro and femto users, the payoffs are calculated as in (7.72), given the optimal cooperation and transmission parameters of the femto user. The optimal cooperation and transmission parameters are obtained from solving the following optimization, that is,

(7.74)

(7.75)

where pTi and pRi are the transmission powers for the femto user’s own transmission and relay transmission, respectively. pmax is the maximum transmission power. After the payoff is computed, in the coalition formation step, the macro and femto users send a request to initiate cooperation to gain the highest payoff. In the spectrum leasing and cooperative transmission step, if the macro and femto users agree to cooperate, they will establish a relay connection and the cooperative macro user will inform and off-load the transmission from the macro base station.

FIGURE 7.11 Distributed coalition formation algorithm for macro–femto cooperation.

The convergence of the distributed algorithm for the macro–femto cooperation is discussed. It is observed that the payoff will always decrease in each iteration. The algorithm can terminate in the first iteration, if the femto user cannot form any coalition which improves the payoff. Therefore, the stable coalition is reached. The simulation results show that the proposed macro–femto cooperation can achieve significant performance gain. For example, the transmission rate of the macro user increases by two times compared with that for noncooperative case in a network with 200 femtocells.

7.4.4 Cooperative Interference Management

In addition to power control (e.g., [2, 27]), cooperation in sub-channel access is regarded as one of the effective approaches to avoid interference. For a two-tier macrocell–femtocell network, [36] introduces the concept of cooperative interference management by letting femto access points form a coalition to share the spectrum resource (i.e., sub-channels), reducing the co-tier interference. Specifically, if the femto access points form the coalition, they can coordinate their transmissions through using traffic scheduling in a time division duplexing (TDD) mode. The system model considered in [36] is based on an OFDMA-based femtocell network. The set of femto access points is denoted by . The set of macro users is denoted by . When the femto access points do not cooperate, they use sub-channels from a set denoted by for their transmission. These sub-channels are in the macrocell UL spectrum.

A coalition formation game model is formulated in [36], where the femto access points can be self-organizing to form a coalition and share the sub-channels to avoid the co-tier interference. The players are the femto access points. The strategy is to form the coalitions. Let denote a coalition of the femto access points. To derive the payoff of each player, first a value of a coalition is given. The value of any coalition can be expressed as follows:

(7.76)

where is the number of players in the coalition . is a set of all coalitions (i.e., partition), defined as . pi,k and hi,k are the transmission power and channel gain of femto access point i using sub-channel k, respectively. Ifi,k and Imi,k are the interferences from the other femto access points and from the macro users, respectively. The interference from macro users can be obtained from

(7.77)

where pm,k and hm,i,k denote, respectively, the transmission power and channel gain of macro user m to the femto access point i on sub-channel k. The interference from the other femto access points can be obtained from

(7.78)

where and are the transmission power and channel gain of femto access point , respectively, which is not in the same coalition as that of the femto access point i on sub-channel k. Clearly, the value function defined in (7.76) of the players in one coalition is affected by the interferences from other players in the different coalitions. Therefore, the externality exists in the game.

However, not all the femto access points can form the coalition, since they may not be able to exchange the coalition formation information among each other (e.g., femto access points which are faraway from each other) through a common control channel. The transmission power required for femto access point i to reach the farthest femto access point such that the coalition can be formed among them is given as follows:

(7.79)

where and are the minimum required SINR and the channel gain for the communication between femto access points i and , respectively. is the noise power. The transmission power of the femto access point i in a coalition must be bounded by

(7.80)

Therefore, if , then the value of the coalition will be zero (i.e., there is no transmission power left for data transmission).

In the same coalition , the femto access points must also divide the value of the coalition . The value of the coalition is assumed to be transferable (i.e., TU). In this case, the Egalitarian fair method is adopted. The payoff of the player i in a coalition can be expressed as follows:

(7.81)

Figure 7.12 shows the example of the system model for the coalition formation among femto access points. There are two macro users (i.e., ). There are four femto access points (i.e., ). Femto access points f1 and f2 form the coalition , while f3 and f4 form the coalition . Therefore, the set of coalitions of all the femto access points is denoted by . In this example, the femto access point f1 may not be able to form a coalition with f4 since they are far from each other and cannot exchange the coalition formation information.

FIGURE 7.12 Coalition formation among femto access points to reduce co-tier interference.

To obtain stable coalitions, a femto access point cooperation algorithm is proposed. The algorithm has three steps, that is, neighbor discovery, coalition formation, and coalition-level scheduling.

Simulation results show that if the number of femto access points is small, the chance of a coalition to be formed is small due to the limited capability of the femto access points to communicate and exchange the cooperation information with each other. Consequently, the payoff is small. When the number of femto access points increases, the coalitions can be formed to coordinate the sub-channel allocation and access. As a result, the payoff increases. If the number of femto access points is too large, the coalitions with many femto access points will be formed. However, due to the limited available time slots for the scheduling, the sub-channels cannot be efficiently utilized. Therefore, the payoff decreases. In summary, there will be an optimal network size such that the payoff of the femto access point is maximized.

7.4.5 Coalition-Based Access Control

One way to reduce interference in small cell networks is to perform an access control of the macro and femto users (e.g., to connect to a macro base station or a femto access point). The access control method for a small cell should take the individual user’s performance into account, which is especially important in a distributed environment. Therefore, the access control problem for a small cell network can be formulated as a coalitional game [6] to find the equilibrium and stable solution for cell association. The system model under consideration is composed of a macro base station and femto access point. A set of available sub-channels is and a set of transmitters (i.e., in the UL direction) is , choosing to transmit to the macro base station or femto access point.

A coalition formation game model is presented in [6], in which the players are the transmitters. The strategy of a player is to choose to transmit to either the macro base station or the femto access point. In particular, two coalitions will be formed, that is, and for the transmitters transmitting to the macro base station and femto access point, respectively. An example is shown in Figure 7.13. There are three transmitters (i.e., ). Transmitters 1 and 2 choose to form the coalition to connect to the macro base station (i.e., ), while transmitter 3 forms the singleton coalition to connect to the femto access point (i.e., ).

FIGURE 7.13 Coalition formation among transmitters to connect to the macro base station or femto access point.

Similar to the system model in [36], the transmitters in the same coalition will not interfere with each other (e.g., due to the sub-channel allocation and traffic scheduling). To obtain the payoff, the value of a coalition is first derived considering the worst-case performance of the transmitters in each coalition. The worst-case performance is influenced by the jamming effect of the transmitters in the different coalitions. Therefore, the value of a coalition can be obtained as the solution of the following optimization problem:

(7.82)

(7.83)

where ui(p) is the utility of the transmitter i, which is a function of p for the transmission powers of all the transmitters. pi,k is the transmission power of the transmitter i on a sub-channel k and pmax is the maximum transmission power on all the sub-channels. The value function defined in (7.82) considers the worst case jamming from the transmitters in the different coalition (i.e., ). The utility function of the transmitter i in coalition is defined as follows:

(7.84)

where hi,k is the channel gain of the transmitter i to the receiver (i.e., femto access point). pj,k and hj,i,k are the transmission power and channel gain of the transmitter j in the coalition to the receiver of the transmitter i, respectively. The value function of the transmitters in the coalition can be obtained similarly.

It is proved that the value function of the coalitional game is not necessarily super-additive. The super-additivity of the value function is defined as follows: for two disjoint coalitions and . Therefore, the grand coalition (i.e., all transmitters will be in the same coalition) may not be stable. Two issues arise here, that is, how the value is distributed among the transmitters in the same coalition and how to form the stable coalitions. For the distribution of the value of the coalition, the Shapley value is applied [8]. The Shapley value, which determines the payoff of the player, is defined as follows:

(7.85)

A Markov chain model is formulated to analyze the stable coalitions. For the example shown in Figure 7.13, the state transition diagram is shown in Figure 7.14. The state is denoted as the partition . There are 8 possible states (i.e., 8 possible combinations) for the partition. The transition is assumed to happen when one transmitter changes its strategy. For example, the transition happens when the transmitter 2 chooses to transmit to the macro base station, and hence joins the coalition . The stationary probability is obtained for the Markov chain. The stable coalitions (i.e., partitions) are determined based on the states that the stationary probabilities are larger than zero.

FIGURE 7.14 State transition diagram of the Markov chain to model coalition formation of access control.

Consider a set of three transmitters . There are 12 sub-channels and the total transmission power is 10 dBm for all transmitters. The noise power is -90 dBm. We assume that all the transmitters and receivers are located along the x-axis. Let the receiver s be at the origin, and the receiver r be located at 100 m away from the origin. Let the three transmitters be at 30, 90, and 120 m away from the origin, respectively (Figure 7.15). The antenna gain is 17.95 dB. The random fading in each sub-channel is given by an independent and identical Rayleigh random variable with average gain of -10 dB. Finally, the sub-channels are divided evenly among the transmitters within a coalition.

FIGURE 7.15 Locations of transmitters and receivers.

The power allocation is performed and the coalitional value is calculated. The Shapley value of each player under all possible coalition structures ω is given in Table 7.1. We first consider the coalitional values, and , and apparently they are not super-additive. For instance, and , while , which is clearly less than the sum . Secondly, we observe that the coalition structures , , and are not feasible due to the negative payoff obtained by one of the players. That is, at least one of the players will always have an incentive to join a different coalition.

Table 7.1 Payoff matrix for three transmitter coalition game

Based on the Markov chain, the transition among coalition structure can be determined. For example, in , we have (0.24, 1.55, 14.34), while in we have (70.37, 2.16, 14.24). Since transmitter 1 achieves a higher payoff in than that in without downgrading the payoff of transmitter 2, the transmitter 1 in has the incentive to split from and join to form . Thus . In this case, we observe that is the absorbing state of the corresponding Markov chain. Thus this coalition structure is stable, and therefore, is the required solution for our access control problem.

7.5 FUTURE RESEARCH DIRECTIONS

In this chapter, game theoretic approaches to address the RRM in small cell networks have been presented. First, an overview of game theory including the motivation and different types of games has been introduced. A review of the game models developed for solving three major RRM issues (i.e., power control and sub-channel allocation, pricing, and access control) have been provided. There are still a number of significant issues related to the game theoretic RRM in small cell networks which require further investigation. Some possible future research directions are outlined below.

• Incomplete information game: In the existing game models for resource management of small cell networks, the information about the other players is usually assumed to be completely available. However, in reality, some information is not available, for example, the channel gains of other players to the macro base stations. To address this issue, an incomplete information game model should be developed. By using the Bayesian theorem, the belief on the parameters of other players could be built and used to optimize the strategy. A solution in terms of the Bayesian Nash equilibrium can be obtained for such an incomplete information game.
• Delay and loss of backhaul communication: Most of the game models proposed in the literature assume that the information exchange among players is immediate and perfect. In particular, there is no delay in making a decision. However, in small cell networks, the connections between macro base stations and SBSs are based on a broadband backhaul, whose transmission delay could be substantial and transmission loss can occur. Such a delay and loss must be taken into account when the players choose their strategies. Also, the impact of delay and loss on the payoffs of the players and system efficiency needs to be analyzed.
• Integration with multi radio access technology (multi-RAT): In typical small cell networks, macro base stations and SBSs are assumed to operate using the same technology (e.g., LTE). However, the multi-RAT technology will be used to off-load the users’ traffic from the cellular networks to unlicensed networks (e.g., Wi-Fi networks). When the multi-RAT technology is deployed, competition exists and game theory can be applied to model and analyze the operation of multi-RAT small cell networks. Also, different RATs can be operated by different service providers. Competition and cooperation strategies for the service providers can be analyzed using game theoretic models.

REFERENCES

1. Z. Han, D. Niyato, W. Saad, T. Basar, and A. Hjørungnes, Game Theory in Wireless and Communication Networks: Theory, Models, and Applications. Cambridge University Press, 2011.

2. V. Chandrasekhar, J. G. Andrews, T. Muharemovic, Z. Shen, and A. Gatherer, “Power control in two-tier femtocell networks,” IEEE Transactions on Wireless Communications, vol. 8, no. 8, pp. 4316–4328, August 2009.

3. J. W. Huang and V. Krishnamurthy, “Cognitive base stations in LTE/3GPP femtocells: A correlated equilibrium game-theoretic approach,” IEEE Transactions on Communications, vol. 59, no. 12, pp. 3485–3493, December 2011.

4. C.-H. Ko and H.-Y. Wei, “On-demand resource-sharing mechanism design in two-tier OFDMA femtocell networks,” IEEE Transactions on Vehicular Technology, vol. 60, no. 3, pp. 1059–1071, March 2011.

5. W. Saad, Z. Han, M. Debbah, A. Hjørungnes, and T. Basar, “Coalitional game theory for communication networks: A tutorial,” IEEE Signal Processing Magazine – Special Issue on Game Theory, vol. 26, no. 5, pp. 77–97, September 2009.

6. S. Guruacharya, D. Niyato, and D. I. Kim, “Access control via coalitional power game,” in Proceedings of IEEE Wireless Communications and Networking Conference (WCNC), pp. 2824–2828, April 2012.

7. D. Fudenberg and J. Tirole, Game Theory. The MIT Press, August 1991.

8. R. B. Myerson, Game Theory: Analysis of Conflict. Harvard University Press, September 1997.

9. J. Friedman, Game Theory with Applications to Economics. Oxford University Press, 1990.

10. J. Rosen, “Existence and uniqueness of equilibrium points for concave n-person games,” Econometrica: Journal of the Econometric Society, vol. 33, no. 3, pp. 520–534, 1965.

11. D. Monderer and L. Shapley, “Potential Games,” Games and Economic Behavior, vol. 14, no. 1, pp. 124–143, 1996.

12. E. Hossain, D. Niyato, and Z. Han, Dynamic Spectrum Access and Management in Cognitive Radio Networks. Cambridge University Press, 2009.

13. A. Attar, V. Krishnamurthy, and O. N. Gharehshiran, “Interference management using cognitive base-stations for UMTS LTE,” IEEE Communications Magazine, vol. 49, no. 8, pp. 152–159, August 2011.

14. E. J. Hong, S. Y. Yun, and D.-H. Cho, “Decentralized power control scheme in femtocell networks: A game theoretic approach,” in Proceedings of International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), pp. 415–419, September 2009.

15. S. Barbarossa, S. Sardellitti, A. Carfagna, and P. Vecchiarelli, “Decentralized interference management in femtocells: A game-theoretic approach,” in Proceedings of International Conference on Cognitive Radio Oriented Wireless Networks & Communications (CROWNCOM), June 2010.

16. L. Giupponi and C. Ibars, “Distributed interference control in OFDMA-based femtocells,” in Proceedings of IEEE International Symposium on Personal Indoor and Mobile Radio Communications (PIMRC), pp. 1201–1206, September 2010.

17. W.-Chih Hong and Z. Tsai, “On the femtocell-based MVNO model: A game theoretic approach for optimal power setting,” in Proceedings of IEEE Vehicular Technology Conference (VTC-Spring), May 2010.

18. S. Barbarossa, A. Carfagna, S. Sardellitti, M. Omilipo, and L. Pescosolido, “Optimal radio access in femtocell networks based on Markov modeling of interferers’ activity,” in Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp. 3212–3215, May 2011.

19. F. Facchinei and J. S. Pang, Finite-Dimensional Variational Inequalities and Complementarity Problems-Volume I, Springer-Verlag, New York Inc., December 2003.

20. D. P. Bertsekas and J. N. Tsitsiklis, Parallel and Distributed Computation: Numerical Methods. Athena Scientific, 1989.

21. S. Guruacharya, D. Niyato, E. Hossain, and D. I. Kim, “Hierarchical competition in femtocell-based cellular networks,” in Proceedings of Global Telecommunications Conference (GLOBECOM), December 2010.

22. Z. Huang, Z. Zeng, and H. Xia, “Hierarchical power game with dual-utility in two-tier OFDMA femtocell networks,” in Proceedings of International Conference on Wireless Communications, Networking and Mobile Computing (WiCOM), September 2011.

23. Q. Li, Z. Feng, W. Li, Y. Liu, and P. Zhang, “Joint access and power control in cognitive femtocell networks,” in Proceedings of International Conference on Wireless Communications and Signal Processing (WCSP), November 2011.

24. R. D. Yates, “A framework for uplink power control in cellular radio systems,” IEEE Journal on Selected Areas in Communications, vol. 13, no. 7, pp. 1341–1347, September 1995.

25. F. Pantisano, M. Bennis, W. Saad, and M. Debbah, “Spectrum leasing as an incentive towards uplink macrocell and femtocell cooperation,” IEEE Journal on Selected Areas in Communications, vol. 30, no. 3, pp. 617–630, April 2012.

26. S. Hart and A. Mas-Colell, “A simple adaptive procedure leading to correlated equilibrium,” Econometrica, vol. 68, no. 5, pp. 1127–1150, September 2000.

27. X. Kang, R. Zhang, and M. Motani, “Price-based resource allocation for spectrum-sharing femtocell networks: A Stackelberg game approach,” IEEE Journal on Selected Areas in Communications, vol. 30, no. 3, pp. 538–549, April 2012.

28. R. Xie, F. R. Yu, and H. Ji, “Energy-efficient spectrum sharing and power allocation in cognitive radio femtocell networks,” in Proceedings of IEEE INFOCOM, pp. 1665–1673, March 2012.

29. Y. Yi, J. Zhang, Q. Zhang, and T. Jiang, “Spectrum leasing to femto service provider with hybrid access,” in Proceedings of IEEE INFOCOM, pp. 1215–1223, March 2012.

30. S. Barbarossa, S. Sardellitti, and A. Carfagna, “Pricing mechanisms for interference management games in femtocell networks based on Markov modeling,” in Proceedings of Future Network & Mobile Summit (FutureNetw), June 2011.

31. S. Yun, Y. Yi, D.-H. Cho, and J. Mo, “Open or close: On the sharing of femtocells,” in Proceedings of IEEE INFOCOM, pp. 116–120, April 2011.

32. X. Kang, Y.-C. Liang, and H. K. Garg, “Distributed power control for spectrum-sharing femtocell networks using Stackelberg game,” in Proceedings of IEEE International Conference on Communications (ICC), June 2011.

33. L. Jiang, S. Parekh, and J. Walrand, “Base station association game in multi-cell wireless networks,” in Proceedings of Wireless Communications and Networking Conference (WCNC), pp. 1616–1621, March–April 2008.

34. Y. Chen, J. Zhang, and Q. Zhang, “Utility-aware refunding framework for hybrid access femtocell network,” IEEE Transactions on Wireless Communications, vol. 11, no. 5, pp. 1688–1697, May 2012.

35. J.-S. Lin and K.-T. Feng, “Game theoretical model and existence of win-win situation for femtocell networks,” in Proceedings of IEEE International Conference on Communications (ICC), June 2011.

36. F. Pantisano, M. Bennis, R. Verdone, and M. Latva-aho, “Interference management in femtocell networks using distributed opportunistic cooperation,” in Proceedings of IEEE Vehicular Technology Conference (VTC Spring), May 2011.

37. O. Simeone, I. Stanojev, S. Savazzi, Y. Bar-Ness, U. Spagnolini, and R. Pickholtz, “Spectrum leasing to cooperating secondary ad hoc networks,” IEEE Journal on Selected Areas in Communications, vol. 26, no. 1, pp. 203–213, January 2008.

38. L. Kóczy, “A recursive core for partition function form games,” Theory and Decision, vol. 63, no. 1, pp. 41–51, August 2007.

39. C.-Y. Wang and H.-Y. Wei, “Revenue extraction in overlay macrocell-femtocell system under shared spectrum model,” in Proceedings of International Symposium on Applied Sciences in Biomedical and Communication Technologies (ISABEL), November 2010.