| 18 | More about Differentiation |
The previous chapter showed that successive differentiation of sine waves results in the same equation with its starting point shifted. Starting at sin x, successive derivatives are cos x, −sin x, −cos x, sin x, cos x, −sin x,…, cycling through these four over and over. It is particularly easy with x in radians. If the angle is in degrees, it has to be converted into radians for this method to work. Sometimes the quantity is not itself an angle, but is something that trigonometry can represent as an angle.
FREQUENCY AND PERIOD OF A SINE WAVE
Suppose you are analyzing waves and you come across the equation y = sin 2x instead of y = sin x. Now consider this:

If you let y = sin 2x in the last expression above, then you can substitute, subtract y from each side, and finally divide each side by dx, getting
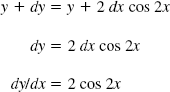
Next, take y = sin 3x. The derivative can be found in the same way. You get
Using a general multiplier a, the derivative is
There are two shortened or alternative forms of writing this:

Using the simple equation y = sin x, the slope of the curve at the zero (starting) point is equal to its magnitude at maximum, which is why the cosine has the same amplitude as the sine wave. When the multiplier a is introduced, then a times as many waves occur in the same amount of time, so the slope of the original wave is a times as steep at every point. The graph of the wave is compressed horizontally (along the time axis) by a factor of a. An engineer or scientist would say that the frequency of the wave (the number of complete cycles per unit time) is multiplied by a. A mathematician might say that the period of the wave (the length of time required for one complete cycle to occur) is divided by a. Both mean the same thing. The amplitude, or top-to-bottom difference, of the derivative is therefore multiplied by a.
SINUSOIDAL MOTION
Now assume the equation y = A sin bt represents the motion of some object with passage of time t. The constant A represents the maximum movement from the reference (or zero) position, and the variable y represents the instantaneous distance from this reference position at time t. The constant b expresses how fast the object moves every time it passes through the reference position, and therefore how many times the object will make one complete excursion back and forth in a given time.
Refer to the diagrams in Fig. 18-1. The graph at A shows the vertical displacement as a function of time for some object moving up and down in a sine wave motion. In illustration B, you see that the instantaneous vertical velocity is the first derivative of the instantaneous displacement, given by dy/dt. It figures to

Figure 18-1
An object oscillating with sine-wave motion. At A, vertical displacement as a function of time. At B, velocity is the first derivative of displacement with respect to time. At C, acceleration is the second derivative of displacement with respect to time.
As shown in drawing C, the instantaneous vertical acceleration is the second derivative of the instantaneous displacement, given by the equation
Notice that the maximum velocity occurs every time the object passes through the reference position, and zero velocity occurs at each extreme. Zero acceleration occurs when velocity is a maximum, and is a maximum at each extreme of the displacement. Notice also that the reference position and points of zero acceleration coincide. Maximum excursion and maximum acceleration also coincide.
The instantaneous acceleration is b2 times the instantaneous displacement (in whatever units are used), and it is of the opposite sign. When the displacement is at its maximum upward, acceleration is at its maximum downward, and vice versa. Here, positive signs mean upward displacement, velocity, or acceleration; negative signs mean downward displacement, velocity, or acceleration.
HARMONIC MOTION
The existence of sine wave motion in mechanical, electrical, acoustical, and other systems is a manifestation of the cyclic interchange of energy. Such a system has a characteristic period and a characteristic frequency, regardless of the amplitude of the movement. When the same consistent units of distance and time are used (feet and seconds, for example), the period is always equal to the reciprocal of the frequency.
Harmonic motion is the name given to the movement an object or variable quantity makes during a cyclic period that is sinusoidal (representable as a sine wave). In the example shown by Fig. 18-2, the displacement and movement are sinusoidal. In an electrical system, the voltage and current would be sinusoidal. In an acoustical system, the airflow and pressure variation would be sinusoidal.

Figure 18-2
Aspects of harmonic motion. At A, graphs of instantaneous displacement and velocity for comparison. At B, the instantaneous acceleration increases with increasing distance from the reference or zero position.
The natural relationship is fixed by the quantity b. Only at one frequency, which makes b = 2π/t, does this natural relationship hold, where energy interchanges with no external force applied. In a spring-loaded system such as the one shown in Fig. 18-2, the value of b2 is determined by the stiffness of the spring, called the spring constant, and by the mass of the moving object. If you change either one of these factors, then b2 changes, and therefore b changes too. The result is a change in the natural frequency, more often called the resonant frequency, of the system.
LINEAR AND NONLINEAR RELATIONSHIPS
In a spring-loaded system, pure harmonic motion, also called simple harmonic motion, at a specific resonant frequency occurs only if the spring is linear. That means the relationship between the amount of compression or tension and the force produced by the spring is a straight-line graph. In a linear spring, if every inch results in a force of 15 poundals (Fig. 18-3A), the force for successive inches will increase in uniform steps: 15, 30, 45, 60, 75, and so on, for both compression and tension (stretching).
In the real world, springs are not always linear. The extra force might increase as the spring becomes more fully compressed (Fig. 18-3B). Instead of increasing to 15, 30, 45, 60, and 75 poundals for successive inches, the figures might run as 16, 34, 54, 76, and 100 poundals. In tension, the effect might be reversed, so successive forces of tension, at inch intervals, would read 14, 26, 36, 44, and 50 poundals. Such a spring is nonlinear, because the force is not proportional to displacement.

Figure 18-3
At A, behavior of a hypothetical linear spring. At B, behavior of a hypothetical nonlinear spring.
Plotting the force/displacement relationship of the nonlinear spring shown in Fig. 18-3B as a graph, you find that it can be resolved in two components, as shown in Fig. 18-4A. The linear part (straight dashed line) is the same as the linear spring: 15 poundals for every inch. Then the nonlinear part, in this case called a square-law component and shown as a dashed parabolic curve, is proportional to the square of displacement. Because displacement is in opposite directions, one is considered positive, the other negative. In one direction, the square-law component will add to the linear force. The other way, it will take away from the linear force. The overall or composite force is shown in Fig. 18-4A as a solid curve.
Now imagine that the movement is somehow made sinusoidal so the force produced is determined by the sinusoidal variation in position. You can show this position by plotting motion and force separately, each against time, as shown in Fig. 18-4B and C. At B, the dashed curve is a true sinusoid, and the solid-line curve represents the force produced by the actual nonlinear spring.

Figure 18-4
At A, components and overall force produced by a nonlinear spring. At B and C, force and motion are plotted separately against time.
MULTIPLES AND POWERS
Finding expressions for multiple angle functions in terms of powers of unit angle functions can be pursued systematically, as shown in Table 18-1. The first step is to extend the multiple angle formulas as far as you need, one multiple at a time. Using sum formulas, first find expressions for sin 2A and cos 2A; regard 2A as A + A. Next, regarding 3A as 2A + A, you can find expressions for sin 3A and cos 3A. Regarding the expression (n + 1)A as A + nA, substitute previously found expressions for sin nA and cos nA. Table 18-1 takes this as far as 6A. The working is not shown. You might wish to put yourself methodically through each step.

Table 18-1
Formulas for multiple angles and powers of the sine and cosine functions.
For the even powers, both sinn A and cosn A use a form of the expression for cos nA, and substitute it for the lower powers. For the odd powers, take the expression for sin nA to get sinn A and the expression for cos nA to get cosn A with similar substitutions. Here again, only the results are listed in Table 18-1. Try a few to see how to do it.
The substitutions used to derive these expressions can become involved in detail working. Nothing is really difficult; it’s just “messy.” The routine becomes familiar with practice, but the sheer number of substitutions means that a mistake can creep in at any point. You need a simple means to check the results.
In Table 18-2, two angles are used for each check: A = 0 and A = π/2 rad, which is 90°. Whatever the multiple, nA is always 0 when A is 0, so sin nA should always be 0 and cos nA always 1 in this column. For the π/2 column, nA should always be equal to n right angles. So for sin nA starting with n = 2, the sequence S will be

Table 18-2
Some numerical examples involving multiple angles and powers of the sine and cosine functions.
For cos nA starting with n = 2, you will have the sequence C as follows:
In the powers table, 0n is always equal to 0, and 1n is always equal to 1. So sinn A will always be 0 for A = 0 and 1 for A = π/2 rad. Similarly, cosn A will always be 1 for A = 0 and 0 for A = π/2 rad. All these check columns should have either 0 or 1 in the appropriate pattern. If one of the coefficients in the detail working has gone wrong, it will almost always cause a different result in one or both of these checks.
FUNCTIONS
An expression that “performs some action” on a variable is a function of that variable. You have already considered several functions without calling them that. Powers, roots, trig ratios, and many other relations are all functions.
To work with functions in a broad sense, because they can take various forms, a general form is y = f (x), which is read “y is a function of x” or “y equals f of x.” This expression can mean any function of x, with the implication that it is a function for which you can figure out successive derivatives.
Of course, you can use letters other than f to denote functions, letters other than x to denote independent variables, and letters other than y to denote dependent variables. You might see expressions like this:
or even symbolic functions and variables like this:
The derivative of a function can be denoted in various ways. Several ways to denote the first derivative where y = f (x) include these:

All these refer to “the derivative of the function f.” The last two do not specify any particular variable, but usually this variable will be evident from context. Second derivatives would be written like this:

DERIVATIVE OF CONSTANT
You’ ve learned some general rules about differentiation. Let’s review these and then look at some more. First, note that the derivative of a constant without any variable attached to it is always equal to 0. Stating this the way a mathematician would do it, we let f be a function of x such that f (x) = c, where c is a real number constant. Then
DERIVATIVE OF SUM OF TWO FUNCTIONS
Now suppose that f and g are two functions of a variable x. Maybe these two functions are identical, but more likely they are different. Consider the sum of these two functions f + g, which is f(x) + g(x) for every possible value of x. We can define this sum another way:
In this sort of situation, as you’ve already learned, the derivative of the sum is equal to the sum of the derivatives:
You can also write it like this:
DERIVATIVE OF DIFFERENCE OF TWO FUNCTIONS
The rule for differentiating the difference of two functions follows directly from the rule for the sum, because subtraction is simply the addition of a negative. Suppose that f and g are functions of a variable x, and let f − g = f (x) − g (x) for all possible values of x. Then
You can also write it like this:
DERIVATIVE OF FUNCTION MULTIPLIED BY A CONSTANT
Here’s another rule that you have already learned. Let f be a function of a variable x. Suppose c is a constant by which f (x) is multiplied to get cf (x), which can be shortened to cf. Then you can move the constant outside the derivative, like this:
You can also write
DERIVATIVE OF PRODUCT OF TWO FUNCTIONS
Suppose f and g are two functions of a variable x. Define the product of f and g as follows:
for any specific value of the variable x. This is just a simplified notation calling f (x) by the shorter name f, and calling g (x) by the shorter name g. Then you can find the derivative of the product function by using this formula:
You might find this expression easier to understand:
DERIVATIVE OF PRODUCT OF THREE FUNCTIONS
The rule for multiplying three functions follows from the rule for multiplying two functions. (In fact, if you are patient, you can derive a general rule for multiplying any number of functions!) Let f, g, and h be three functions of a variable x. Define the product of f, g, and h as follows:
Then you can find the derivative of the product function this way:
You might find this expression simpler:
DERIVATIVE OF QUOTIENT OF TWO FUNCTIONS
Let f and g be two functions of a variable x, and define f/g = [f (x)]/[g (x)]. Then
where g2 = g (x) · g (x), not to be confused with d2g/dg2. You might find it easier to write it like this:
RECIPROCAL DERIVATIVES
Suppose that f is a function, and x and y are variables such that y = f (x). The following formulas are both true as long as the derivatives exist for all values of the variables:
DERIVATIVE OF FUNCTION RAISED TO A POWER
Let f be a function of a variable x. Suppose n is a positive whole number. Then you can find the derivative of f (x) raised to the nth power by using this formula:
where fn denotes f multiplied by itself n times, not to be confused with the nth derivative. You might find it easier to write the formula like this:
CHAIN RULE
Suppose that f and g are both functions of a variable x. The derivative of the composite function (that is, f of g of x), can be found this way:
This is sometimes called by a real tongue-and-brain-twister of a name: the “formula for the derivative of a function of a function.” You must first find the derivative of “f of g of x” and then multiply the result by the derivative of “g of x.”
QUESTIONS AND PROBLEMS
This is an open-book quiz. You may refer to the text in this chapter (and earlier ones, too, if you want) when figuring out the answers. Take your time! Consider all values given as exact, so you don’t have to worry about significant figures. The correct answers are in the back of the book.
1. Refer to Fig. 18-5, which depicts the motion of a heavy weight oscillating with a spring. Assume the maximum positive (upward) and negative (downward) displacements to be precisely six meters (6 m) and −6 m, respectively. Also assume the period of oscillation to be exactly 3 s. At what points in time (values of t) is the velocity of the weight the greatest positively? What is the velocity, in meters per second, at these points? Express your answers to three significant figures.

Figure 18-5
Illustration for problems 1 through 8.
2. At what points in time is the velocity of the weight in the preceding problem greatest negatively? What is the velocity in meters per second at these points? Express your answer to three significant figures.
3. At what points in time is the acceleration of the weight in the preceding problems greatest positively? What is the acceleration in meters per second squared at these points? Express your answer to three significant figures.
4. At what points in time is the acceleration of the weight in the preceding problems greatest negatively? What is the acceleration in meters per second squared at these points? Express your answer to three significant figures.
5. Suppose the tension of the spring in the previous problems is increased so the weight oscillates at the third harmonic of (three times) the original frequency, but the positive and negative peak amplitudes (excursions) remain exactly the same. At what points in time is the velocity of the weight maximum positively? What is the velocity, in meters per second, at these points? Express your answers to three significant figures.
6. In the situation of Prob. 5, at what points in time is the velocity of the weight greatest negatively? What is the velocity in meters per second at these points? Express your answer to three significant figures.
7. In the situation of Prob. 5, at what points in time is the acceleration of the weight greatest positively? What is the acceleration in meters per second squared at these points? Express your answer to three significant figures.
8. In the situation of Prob. 5, at what points in time is the acceleration of the weight greatest negatively? What is the acceleration in meters per second squared at these points? Express your answer to three significant figures.
9. Using the formulas for multiples and powers (Table 18-1), find the following. Assume all angle measures are in radians. You may use a calculator; express your answers to four significant figures.
(a) sin2 (π/2)
(b) cos2 (π/3)
(c) sin3 (π/4)
(d) cos3 (π/4)
(e) sin5 (π/3)
(f) cos6 (2π/5)
10. Suppose you twirl a ball around on a string that is 10 ft long, as shown in Fig. 18-6. The ball makes one complete revolution around your body every 2 s, exactly. What is the tangential speed of the ball in feet per second? Use a calculator and express your answer to four significant figures.

Figure 18-6
Illustration for problems 10 and 11.
11. Assume the ball whose motion is shown in Fig. 18-6 revolves in a horizontal plane. What is the northward-moving component of the ball’s speed at the instant the ball is traveling toward the northwest (exactly 45° west of north)? Express your answer to four significant figures.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
