20
Autoencoders for Conditional Risk Factors and Asset Pricing
This chapter shows how unsupervised learning can leverage deep learning for trading. More specifically, we'll discuss autoencoders that have been around for decades but have recently attracted fresh interest.
Unsupervised learning addresses practical ML challenges such as the limited availability of labeled data and the curse of dimensionality, which requires exponentially more samples for successful learning from complex, real-life data with many features. At a conceptual level, unsupervised learning resembles human learning and the development of common sense much more closely than supervised and reinforcement learning, which we'll cover in the next chapter. It is also called predictive learning because it aims to discover structure and regularities from data so that it can predict missing inputs, that is, fill in the blanks from the observed parts.
An autoencoder is a neural network (NN) trained to reproduce the input while learning a new representation of the data, encoded by the parameters of a hidden layer. Autoencoders have long been used for nonlinear dimensionality reduction and manifold learning (see Chapter 13, Data-Driven Risk Factors and Asset Allocation with Unsupervised Learning). A variety of designs leverage the feedforward, convolutional, and recurrent network architectures we covered in the last three chapters. We will see how autoencoders can underpin a trading strategy: we will build a deep neural network that uses an autoencoder to extract risk factors and predict equity returns, conditioned on a range of equity attributes (Gu, Kelly, and Xiu 2020).
More specifically, in this chapter you will learn about:
- Which types of autoencoders are of practical use and how they work
- Building and training autoencoders using Python
- Using autoencoders to extract data-driven risk factors that take into account asset characteristics to predict returns
You can find the code samples for this chapter and links to additional resources in the corresponding directory of the GitHub repository. The notebooks include color versions of the images.
Autoencoders for nonlinear feature extraction
In Chapter 17, Deep Learning for Trading, we saw how neural networks succeed at supervised learning by extracting a hierarchical feature representation useful for the given task. Convolutional neural networks (CNNs), for example, learn and synthesize increasingly complex patterns from grid-like data, for example, to identify or detect objects in an image or to classify time series.
An autoencoder, in contrast, is a neural network designed exclusively to learn a new representation that encodes the input in a way that helps solve another task. To this end, the training forces the network to reproduce the input. Since autoencoders typically use the same data as input and output, they are also considered an instance of self-supervised learning. In the process, the parameters of a hidden layer h become the code that represents the input, similar to the word2vec model covered in Chapter 16, Word Embeddings for Earnings Calls and SEC Filings.
More specifically, the network can be viewed as consisting of an encoder function h=f(x) that learns the hidden layer's parameters from input x, and a decoder function g that learns to reconstruct the input from the encoding h. Rather than learning the identity function:
which simply copies the input, autoencoders use constraints that force the hidden layer to prioritize which aspects of the data to encode. The goal is to obtain a representation of practical value.
Autoencoders can also be viewed as a special case of a feedforward neural network (see Chapter 17, Deep Learning for Trading) and can be trained using the same techniques. Just as with other models, excess capacity will lead to overfitting, preventing the autoencoder from producing an informative encoding that generalizes beyond the training samples. See Chapters 14 and 15 of Goodfellow, Bengio, and Courville (2016) for additional background.
Generalizing linear dimensionality reduction
A traditional use case includes dimensionality reduction, achieved by limiting the size of the hidden layer and thus creating a "bottleneck" so that it performs lossy compression. Such an autoencoder is called undercomplete, and the purpose is to learn the most salient properties of the data by minimizing a loss function L of the form:
An example loss function that we will explore in the next section is simply the mean squared error evaluated on the pixel values of the input images and their reconstruction. We will also use this loss function to extract risk factors from time series of financial features when we build a conditional autoencoder for trading.
Undercomplete autoencoders differ from linear dimensionality reduction methods like principal component analysis (PCA; see Chapter 13, Data-Driven Risk Factors and Asset Allocation with Unsupervised Learning) when they use nonlinear activation functions; otherwise, they learn the same subspace as PCA. They can thus be viewed as a nonlinear generalization of PCA capable of learning a wider range of encodings.
Figure 20.1 illustrates the encoder-decoder logic of an undercomplete feedforward autoencoder with three hidden layers: the encoder and decoder have one hidden layer each plus a shared encoder output/decoder input layer containing the encoding. The three hidden layers use nonlinear activation functions, like rectified linear units (ReLU), sigmoid, or tanh (see Chapter 17, Deep Learning for Trading) and have fewer units than the input that the network aims to reconstruct.
Figure 20.1: Undercomplete encoder-decoder architecture
Depending on the task, a simple autoencoder with a single encoder and decoder layer may be adequate. However, deeper autoencoders with additional layers can have several advantages, just as for other neural networks. These advantages include the ability to learn more complex encodings, achieve better compression, and do so with less computational effort and fewer training samples, subject to the perennial risk of overfitting.
Convolutional autoencoders for image compression
As discussed in Chapter 18, CNNs for Financial Time Series and Satellite Images, fully connected feedforward architectures are not well suited to capture local correlations typical to data with a grid-like structure. Instead, autoencoders can also use convolutional layers to learn a hierarchical feature representation. Convolutional autoencoders leverage convolutions and parameter sharing to learn hierarchical patterns and features irrespective of their location, translation, or changes in size.
We will illustrate different implementations of convolutional autoencoders for image data below. Alternatively, convolutional autoencoders could be applied to multivariate time series data arranged in a grid-like format as illustrated in Chapter 18, CNNs for Financial Time Series and Satellite Images.
Managing overfitting with regularized autoencoders
The powerful capabilities of neural networks to represent complex functions require tight controls of the capacity of encoders and decoders to extract signals rather than noise so that the encoding is more useful for a downstream task. In other words, when it is too easy for the network to recreate the input, it fails to learn only the most interesting aspects of the data and improve the performance of a machine learning model that uses the encoding as inputs.
Just as for other models with excessive capacity for the given task, regularization can help to address the overfitting challenge by constraining the autoencoder's learning process and forcing it to produce a useful representation (see, for instance, Chapter 7, Linear Models – From Risk Factors to Return Forecasts, on regularization for linear models, and Chapter 17, Deep Learning for Trading, for neural networks). Ideally, we could precisely match the model's capacity to the complexity of the distribution of the data. In practice, the optimal model often combines (limited) excess capacity with appropriate regularization. To this end, we add a sparsity penalty 
that depends on the weights of the encoding layer h to the training objective:
A common approach that we explore later in this chapter is the use of L1 regularization, which adds a penalty to the loss function in the form of the sum of the absolute values of the weights. The L1 norm results in sparse encodings because it forces the values of parameters to zero if they do not capture independent variation in the data (see Chapter 7, Linear Models – From Risk Factors to Return Forecasts). As a result, even overcomplete autoencoders with hidden layers of a higher dimension than the input may be able to learn signal content.
Fixing corrupted data with denoising autoencoders
The autoencoders we have discussed so far are designed to reproduce the input despite capacity constraints. An alternative approach trains autoencoders with corrupted inputs 
to output the desired, original data points. In this case, the autoencoder minimizes a loss L:
Corrupted inputs are a different way of preventing the network from learning the identity function and rather extracting the signal or salient features from the data. Denoising autoencoders have been shown to learn the data generating process of the original data and have become popular in generative modeling where the goal is to learn the probability distribution that gives rise to the input (Vincent et al., 2008).
Seq2seq autoencoders for time series features
Recurrent neural networks (RNNs) have been developed for sequential data characterized by longitudinal dependencies between data points, potentially over long ranges (Chapter 19, RNNs for Multivariate Time Series and Sentiment Analysis). Similarly, sequence-to-sequence (seq2seq) autoencoders aim to learn representations attuned to the nature of data generated in sequence (Srivastava, Mansimov, and Salakhutdinov, 2016).
Seq2seq autoencoders are based on RNN components like long short-term memory (LSTM) or gated recurrent unit. They learn a representation of sequential data and have been successfully applied to video, text, audio, and time series data.
As mentioned in the last chapter, encoder-decoder architectures allow RNNs to process input and output sequences with variable length. These architectures underpin many advances in complex sequence prediction tasks, like speech recognition and text translation, and are being increasingly applied to (financial) time series. At a high level, they work as follows:
- The LSTM encoder processes the input sequence step by step to learn a hidden state.
- This state becomes a learned representation of the sequence in the form of a fixed-length vector.
- The LSTM decoder receives this state as input and uses it to generate the output sequence.
See references linked on GitHub for examples on building sequence-to-sequence autoencoders to compress time series data and detect anomalies in time series to allow, for example, regulators to uncover potentially illegal trading activity.
Generative modeling with variational autoencoders
Variational autoencoders (VAE) were developed more recently (Kingma and Welling, 2014) and focus on generative modeling. In contrast to a discriminative model that learns a predictor given data, a generative model aims to solve the more general problem of learning a joint probability distribution over all variables. If successful, it could simulate how the data is produced in the first place. Learning the data-generating process is very valuable: it reveals underlying causal relationships and supports semi-supervised learning to effectively generalize from a small labeled dataset to a large unlabeled one.
More specifically, VAEs are designed to learn the latent (meaning unobserved) variables of the model responsible for the input data. Note that we encountered latent variables in Chapter 15, Topic Modeling – Summarizing Financial News, and Chapter 16, Word Embeddings for Earnings Calls and SEC Filings.
Just like the autoencoders discussed so far, VAEs do not let the network learn arbitrary functions as long as it faithfully reproduces the input. Instead, they aim to learn the parameters of a probability distribution that generates the input data.
In other words, VAEs are generative models because, if successful, you can generate new data points by sampling from the distribution learned by the VAE.
The operation of a VAE is more complex than the autoencoders discussed so far because it involves stochastic backpropagation, that is, taking derivatives of stochastic variables, and the details are beyond the scope of this book. They are able to learn high-capacity input encodings without regularization that are useful because the models aim to maximize the probability of the training data rather than to reproduce the input. For a detailed introduction, see Kingma and Welling (2019).
The variational_autoencoder.ipynb notebook includes a sample VAE implementation applied to the Fashion MNIST data, adapted from a Keras tutorial by Francois Chollet to work with TensorFlow 2. The resources linked on GitHub contain a VAE tutorial with references to PyTorch and TensorFlow 2 implementations and many additional references. See Wang et al. (2019) for an application that combines a VAE with an RNN using LSTM and outperforms various benchmark models in futures markets.
Implementing autoencoders with TensorFlow 2
In this section, we'll illustrate how to implement several of the autoencoder models introduced in the previous section using the Keras interface of TensorFlow 2. We'll first load and prepare an image dataset that we'll use throughout this section. We will use images instead of financial time series because it makes it easier to visualize the results of the encoding process. The next section shows how to use an autoencoder with financial data as part of a more complex architecture that can serve as the basis for a trading strategy.
After preparing the data, we'll proceed to build autoencoders using deep feedforward nets, sparsity constraints, and convolutions and apply the latter to denoise images.
How to prepare the data
For illustration, we'll use the Fashion MNIST dataset, a modern drop-in replacement for the classic MNIST handwritten digit dataset popularized by Lecun et al. (1998) with LeNet. We also relied on this dataset in Chapter 13, Data-Driven Risk Factors and Asset Allocation with Unsupervised Learning, on unsupervised learning.
Keras makes it easy to access the 60,000 training and 10,000 test grayscale samples with a resolution of 28 × 28 pixels:
from tensorflow.keras.datasets import fashion_mnist
(X_train, y_train), (X_test, y_test) = fashion_mnist.load_data()
X_train.shape, X_test.shape
((60000, 28, 28), (10000, 28, 28))
The data contains clothing items from 10 classes. Figure 20.2 plots a sample image for each class:
Figure 20.2: Fashion MNIST sample images
We reshape the data so that each image is represented by a flat one-dimensional pixel vector with 28 × 28 = 784 elements normalized to the range [0, 1]:
image_size = 28 # pixels per side
input_size = image_size ** 2 # 784
def data_prep(x, size=input_size):
return x.reshape(-1, size).astype('float32')/255
X_train_scaled = data_prep(X_train)
X_test_scaled = data_prep(X_test)
X_train_scaled.shape, X_test_scaled.shape
((60000, 784), (10000, 784))
One-layer feedforward autoencoder
We start with a vanilla feedforward autoencoder with a single hidden layer to illustrate the general design approach using the Functional Keras API and establish a performance baseline.
The first step is a placeholder for the flattened image vectors with 784 elements:
input_ = Input(shape=(input_size,), name='Input')
The encoder part of the model consists of a fully connected layer that learns the new, compressed representation of the input. We use 32 units for a compression ratio of 24.5:
encoding_size = 32 # compression factor: 784 / 32 = 24.5
encoding = Dense(units=encoding_size,
activation='relu',
name='Encoder')(input_)
The decoding part reconstructs the compressed data to its original size in a single step:
decoding = Dense(units=input_size,
activation='sigmoid',
name='Decoder')(encoding)
We instantiate the Model class with the chained input and output elements that implicitly define the computational graph as follows:
autoencoder = Model(inputs=input_,
outputs=decoding,
name='Autoencoder')
The encoder-decoder computation thus defined uses almost 51,000 parameters:
Layer (type) Output Shape Param #
Input (InputLayer) (None, 784) 0
Encoder (Dense) (None, 32) 25120
Decoder (Dense) (None, 784) 25872
Total params: 50,992
Trainable params: 50,992
Non-trainable params: 0
The Functional API allows us to use parts of the model's chain as separate encoder and decoder models that use the autoencoder's parameters learned during training.
Defining the encoder
The encoder just uses the input and hidden layer with about half the total parameters:
encoder = Model(inputs=input_, outputs=encoding, name='Encoder')
encoder.summary()
Layer (type) Output Shape Param #
Input (InputLayer) (None, 784) 0
Encoder (Dense) (None, 32) 25120
Total params: 25,120
Trainable params: 25,120
Non-trainable params: 0
We will see shortly that, once we train the autoencoder, we can use the encoder to compress the data.
Defining the decoder
The decoder consists of the last autoencoder layer, fed by a placeholder for the encoded data:
encoded_input = Input(shape=(encoding_size,), name='Decoder_Input')
decoder_layer = autoencoder.layers[-1](encoded_input)
decoder = Model(inputs=encoded_input, outputs=decoder_layer)
decoder.summary()
Layer (type) Output Shape Param #
Decoder_Input (InputLayer) (None, 32) 0
Decoder (Dense) (None, 784) 25872
Total params: 25,872
Trainable params: 25,872
Non-trainable params: 0
Training the model
We compile the model to use the Adam optimizer (see Chapter 17, Deep Learning for Trading) to minimize the mean squared error between the input data and the reproduction achieved by the autoencoder. To ensure that the autoencoder learns to reproduce the input, we train the model using the same input and output data:
autoencoder.compile(optimizer='adam', loss='mse')
autoencoder.fit(x=X_train_scaled, y=X_train_scaled,
epochs=100, batch_size=32,
shuffle=True, validation_split=.1,
callbacks=[tb_callback, early_stopping, checkpointer])
Evaluating the results
Training stops after some 20 epochs with a test RMSE of 0.1121:
mse = autoencoder.evaluate(x=X_test_scaled, y=X_test_scaled)
f'MSE: {mse:.4f} | RMSE {mse**.5:.4f}'
'MSE: 0.0126 | RMSE 0.1121'
To encode data, we use the encoder we just defined like so:
encoded_test_img = encoder.predict(X_test_scaled)
Encoded_test_img.shape
(10000, 32)
The decoder takes the compressed data and reproduces the output according to the autoencoder training results:
decoded_test_img = decoder.predict(encoded_test_img)
decoded_test_img.shape
(10000, 784)
Figure 20.3 shows 10 original images and their reconstruction by the autoencoder and illustrates the loss after compression:
Figure 20.3: Sample Fashion MNIST images, original and reconstructed
Feedforward autoencoder with sparsity constraints
The addition of regularization is fairly straightforward. We can apply it to the dense encoder layer using Keras' activity_regularizer as follows:
encoding_l1 = Dense(units=encoding_size,
activation='relu',
activity_regularizer=regularizers.l1(10e-5),
name='Encoder_L1')(input_)
The input and decoding layers remain unchanged. In this example with compression of factor 24.5, regularization negatively affects performance with a test RMSE of 0.1229.
Deep feedforward autoencoder
To illustrate the benefit of adding depth to the autoencoder, we will build a three-layer feedforward model that successively compresses the input from 784 to 128, 64, and 32 units, respectively:
input_ = Input(shape=(input_size,))
x = Dense(128, activation='relu', name='Encoding1')(input_)
x = Dense(64, activation='relu', name='Encoding2')(x)
encoding_deep = Dense(32, activation='relu', name='Encoding3')(x)
x = Dense(64, activation='relu', name='Decoding1')(encoding_deep)
x = Dense(128, activation='relu', name='Decoding2')(x)
decoding_deep = Dense(input_size, activation='sigmoid', name='Decoding3')(x)
autoencoder_deep = Model(input_, decoding_deep)
The resulting model has over 222,000 parameters, more than four times the capacity of the previous single-layer model:
Layer (type) Output Shape Param #
=================================================================
input_1 (InputLayer) (None, 784) 0
_________________________________________________________________
Encoding1 (Dense) (None, 128) 100480
_________________________________________________________________
Encoding2 (Dense) (None, 64) 8256
_________________________________________________________________
Encoding3 (Dense) (None, 32) 2080
_________________________________________________________________
Decoding1 (Dense) (None, 64) 2112
_________________________________________________________________
Decoding2 (Dense) (None, 128) 8320
_________________________________________________________________
Decoding3 (Dense) (None, 784) 101136
=================================================================
Total params: 222,384
Trainable params: 222,384
Non-trainable params: 0
Training stops after 45 epochs and results in a 14 percent reduction of the test RMSE to 0.097. Due to the low resolution, it is difficult to visually note the better reconstruction.
Visualizing the encoding
We can use the manifold learning technique t-distributed Stochastic Neighbor Embedding (t-SNE; see Chapter 13, Data-Driven Risk Factors and Asset Allocation with Unsupervised Learning) to visualize and assess the quality of the encoding learned by the autoencoder's hidden layer.
If the encoding is successful in capturing the salient features of the data, then the compressed representation of the data should still reveal a structure aligned with the 10 classes that differentiate the observations. We use the output of the deep encoder we just trained to obtain the 32-dimensional representation of the test set:
tsne = TSNE(perplexity=25, n_iter=5000)
train_embed = tsne.fit_transform(encoder_deep.predict(X_train_scaled))
Figure 20.4 shows that the 10 classes are well separated, suggesting that the encoding is useful as a lower-dimensional representation that preserves the key characteristics of the data (see the variational_autoencoder.ipynb notebook for a color version):
Figure 20.4: t-SNE visualization of the Fashion MNIST autoencoder embedding
Convolutional autoencoders
The insights from Chapter 18, CNNs for Financial Time Series and Satellite Images, on CNNs suggest we incorporate convolutional layers into the autoencoder to extract information characteristic of the grid-like structure of image data.
We define a three-layer encoder that uses 2D convolutions with 32, 16, and 8 filters, respectively, ReLU activations, and 'same' padding to maintain the input size. The resulting encoding size at the third layer is 
, higher than for the previous examples:
x = Conv2D(filters=32,
kernel_size=(3, 3),
activation='relu',
padding='same',
name='Encoding_Conv_1')(input_)
x = MaxPooling2D(pool_size=(2, 2), padding='same', name='Encoding_Max_1')(x)
x = Conv2D(filters=16,
kernel_size=(3, 3),
activation='relu',
padding='same',
name='Encoding_Conv_2')(x)
x = MaxPooling2D(pool_size=(2, 2), padding='same', name='Encoding_Max_2')(x)
x = Conv2D(filters=8,
kernel_size=(3, 3),
activation='relu',
padding='same',
name='Encoding_Conv_3')(x)
encoded_conv = MaxPooling2D(pool_size=(2, 2),
padding='same',
name='Encoding_Max_3')(x)
We also define a matching decoder that reverses the number of filters and uses 2D upsampling instead of max pooling to reverse the reduction of the filter sizes. The three-layer autoencoder has 12,785 parameters, a little more than 5 percent of the capacity of the deep autoencoder.
Training stops after 67 epochs and results in a further 9 percent reduction in the test RMSE, due to a combination of the ability of convolutional filters to learn more efficiently from image data and the larger encoding size.
Denoising autoencoders
The application of an autoencoder to a denoising task only affects the training stage. In this example, we add noise from a standard normal distribution to the Fashion MNIST data while maintaining the pixel values in the range [0, 1] as follows:
def add_noise(x, noise_factor=.3):
return np.clip(x + noise_factor * np.random.normal(size=x.shape), 0, 1)
X_train_noisy = add_noise(X_train_scaled)
X_test_noisy = add_noise(X_test_scaled)
We then proceed to train the convolutional autoencoder on noisy inputs, the objective being to learn how to generate the uncorrupted originals:
autoencoder_denoise.fit(x=X_train_noisy,
y=X_train_scaled,
...)
The test RMSE after 60 epochs is 0.0931, unsurprisingly higher than before. Figure 20.5 shows, from top to bottom, the original images as well as the noisy and denoised versions. It illustrates that the autoencoder is successful in producing compressed encodings from the noisy images that are quite similar to those produced from the original images:
Figure 20.5: Denoising input and output examples
A conditional autoencoder for trading
Recent research by Gu, Kelly, and Xiu (GKX, 2019) developed an asset pricing model based on the exposure of securities to risk factors. It builds on the concept of data-driven risk factors that we discussed in Chapter 13, Data-Driven Risk Factors and Asset Allocation with Unsupervised Learning, when introducing PCA as well as the risk factor models covered in Chapter 4, Financial Feature Engineering – How to Research Alpha Factors. They aim to show that the asset characteristics used by factor models to capture the systematic drivers of "anomalies" are just proxies for the time-varying exposure to risk factors that cannot be directly measured. In this context, anomalies are returns in excess of those explained by the exposure to aggregate market risk (see the discussion of the capital asset pricing model in Chapter 5, Portfolio Optimization and Performance Evaluation).
The Fama-French factor models discussed in Chapter 4 and Chapter 7 explain returns by specifying risk factors like firm size based on empirical observations of differences in average stock returns beyond those due to aggregate market risk. Given such specific risk factors, these models are able to measure the reward an investor receives for taking on factor risk using portfolios designed accordingly: sort stocks by size, buy the smallest quintile, sell the largest quintile, and compute the return. The observed risk factor return then allows linear regression to estimate the sensitivity of assets to these factors (called factor loadings), which in turn helps to predict the returns of (many) assets based on forecasts of (far fewer) factor returns.
In contrast, GKX treat risk factors as latent, or non-observable, drivers of covariance among a number of assets large enough to prevent investors from avoiding exposure through diversification. Therefore, investors require a reward that adjusts like any price to achieve equilibrium, providing in turn an economic rationale for return differences that are no longer anomalous. In this view, risk factors are purely statistical in nature while the underlying economic forces can be of arbitrary and varying origin.
In another recent paper (Kelly, Pruitt, and Su, 2019), Kelly—who teaches finance at Yale, works with AQR, and is one of the pioneers in applying ML to trading—and his coauthors developed a linear model dubbed Instrumented Principal Component Analysis (IPCA) to estimate latent risk factors and the assets' factor loadings from data. IPCA extends PCA to include asset characteristics as covariates and produce time-varying factor loadings. (See Chapter 13, Data-Driven Risk Factors and Asset Allocation with Unsupervised Learning, for coverage of PCA.) By conditioning asset exposure to factors on observable asset characteristics, IPCA aims to answer whether there is a set of common latent risk factors that explain an observed anomaly rather than whether there is a specific observable factor that can do so.
GKX creates a conditional autoencoder architecture to reflect the nonlinear nature of return dynamics ignored by the linear Fama-French models and the IPCA approach. The result is a deep neural network that simultaneously learns the premia on a given number of unobservable factors using an autoencoder, and the factor loadings for a large universe of equities based on a broad range of time-varying asset characteristics using a feedforward network. The model succeeds in explaining and predicting asset returns. It demonstrates a relationship that is both statistically and economically significant, yielding an attractive Sharpe ratio when translated into a long-short decile spread strategy similar to the examples we have used throughout this book.
In this section, we'll create a simplified version of this model to demonstrate how you can leverage autoencoders to generate tradeable signals. To this end, we'll build a new dataset of close to 4,000 US stocks over the 1990-2019 period using yfinance, because it provides some additional information that facilitates the computation of the asset characteristics. We'll take a few shortcuts, such as using fewer assets and only the most important characteristics. We'll also omit some implementation details to simplify the exposition. We'll highlight the most important differences so that you can enhance the model accordingly.
We'll first show how to prepare the data before we explain, build, and train the model and evaluate its predictive performance. Please see the above references for additional background on the theory and implementation.
Sourcing stock prices and metadata information
The GKX reference implementation uses stock price and firm characteristic data for over 30,000 US equities from the Center for Research in Security Prices (CRSP) from 1957-2016 at a monthly frequency. It computes 94 metrics that include a broad range of asset attributes suggested as predictive of returns in previous academic research and listed in Green, Hand, and Zhang (2017), who set out to verify these claims.
Since we do not have access to the high-quality but costly CRSP data, we leverage yfinance (see Chapter 2, Market and Fundamental Data – Sources and Techniques) to download price and metadata from Yahoo Finance. There are downsides to choosing free data, including:
- The lack of quality control regarding adjustments
- Survivorship bias because we cannot get data for stocks that are no longer listed
- A smaller scope in terms of both the number of equities and the length of their history
The build_us_stock_dataset.ipynb notebook contains the relevant code examples for this section.
To obtain the data, we get a list of the 8,882 currently traded symbols from NASDAQ using pandas-datareader (see Chapter 2, Market and Fundamental Data – Sources and Techniques):
from pandas_datareader.nasdaq_trader import get_nasdaq_symbols
traded_symbols = get_nasdaq_symbols()
We remove ETFs and create yfinance Ticker() objects for the remainder:
import yfinance as yf
tickers = yf.Tickers(traded_symbols[~traded_symbols.ETF].index.to_list())
Each ticker's .info attribute contains data points scraped from Yahoo Finance, ranging from the outstanding number of shares and other fundamentals to the latest market capitalization; coverage varies by security:
info = []
for ticker in tickers.tickers:
info.append(pd.Series(ticker.info).to_frame(ticker.ticker))
info = pd.concat(info, axis=1).dropna(how='all').T
info = info.apply(pd.to_numeric, errors='ignore')
For the tickers with metadata, we download both adjusted and unadjusted prices, the latter including corporate actions like stock splits and dividend payments that we could use to create a Zipline bundle for strategy backtesting (see Chapter 8, The ML4T Workflow – From Model to Strategy Backtesting).
We get adjusted OHLCV data on 4,314 stocks as follows:
prices_adj = []
with pd.HDFStore('chunks.h5') as store:
for i, chunk in enumerate(chunks(tickers, 100)):
print(i, end=' ', flush=True)
prices_adj.append(yf.download(chunk,
period='max',
auto_adjust=True).stack(-1))
prices_adj = (pd.concat(prices_adj)
.dropna(how='all', axis=1)
.rename(columns=str.lower)
.swaplevel())
prices_adj.index.names = ['ticker', 'date']
Absent any quality control regarding the underlying price data and the adjustments for stock splits, we remove equities with suspicious values such as daily returns above 100 percent or below -100 percent:
df = prices_adj.close.unstack('ticker')
pmax = df.pct_change().max()
pmin = df.pct_change().min()
to_drop = pmax[pmax > 1].index.union(pmin[pmin<-1].index)
This removes around 10 percent of the tickers, leaving us with close to 3,900 assets for the 1990-2019 period.
Computing predictive asset characteristics
GKX tested 94 asset attributes based on Green et al. (2017) and identified the 20 most influential metrics while asserting that feature importance drops off quickly thereafter. The top 20 stock characteristics fall into three categories, namely:
- Price trend, including (industry) momentum, short- and long-term reversal, or the recent maximum return
- Liquidity, such as turnover, dollar volume, or market capitalization
- Risk measures, for instance, total and idiosyncratic return volatility or market beta
Of these 20, we limit the analysis to 16 for which we have or can approximate the relevant inputs. The conditional_autoencoder_for_trading_data.ipynb notebook demonstrates how to calculate the relevant metrics. We highlight a few examples in this section; see also the Appendix, Alpha Factor Library.
Some metrics require information like sector, market cap, and outstanding shares, so we limit our stock price dataset to the securities with relevant metadata:
tickers_with_metadata = (metadata[metadata.sector.isin(sectors) &
metadata.marketcap.notnull() &
metadata.sharesoutstanding.notnull() &
(metadata.sharesoutstanding > 0)]
.index.drop(tickers_with_errors))
We run our analysis at a weekly instead of monthly return frequency to compensate for the 50 percent shorter time period and around 80 percent lower number of stocks. We obtain weekly returns as follows:
returns = (prices.close
.unstack('ticker')
.resample('W-FRI').last()
.sort_index().pct_change().iloc[1:])
Most metrics are fairly straightforward to compute. Stock momentum, the 11-month cumulative stock returns ending 1 month before the current date, can be derived as follows:
MONTH = 21
mom12m = (close
.pct_change(periods=11 * MONTH)
.shift(MONTH)
.resample('W-FRI')
.last()
.stack()
.to_frame('mom12m'))
The Amihud Illiquidity measure is the ratio of a stock's absolute returns relative to its dollar volume, measured as a rolling 21-day average:
dv = close.mul(volume)
ill = (close.pct_change().abs()
.div(dv)
.rolling(21)
.mean()
.resample('W-FRI').last()
.stack()
.to_frame('ill'))
Idiosyncratic volatility is measured as the standard deviation of a regression of residuals of weekly returns on the returns of equally weighted market index returns for the prior three years. We compute this computationally intensive metric using statsmodels:
index = close.resample('W-FRI').last().pct_change().mean(1).to_frame('x')
def get_ols_residuals(y, x=index):
df = x.join(y.to_frame('y')).dropna()
model = sm.OLS(endog=df.y, exog=sm.add_constant(df[['x']]))
result = model.fit()
return result.resid.std()
idiovol = (returns.apply(lambda x: x.rolling(3 * 52)
.apply(get_ols_residuals)))
For the market beta, we can use statsmodels' RollingOLS class with the weekly asset returns as outcome and the equal-weighted index as input:
def get_market_beta(y, x=index):
df = x.join(y.to_frame('y')).dropna()
model = RollingOLS(endog=df.y,
exog=sm.add_constant(df[['x']]),
window=3*52)
return model.fit(params_only=True).params['x']
beta = (returns.dropna(thresh=3*52, axis=1)
.apply(get_market_beta).stack().to_frame('beta'))
We end up with around 3 million observations on 16 metrics for some 3,800 securities over the 1990-2019 period. Figure 20.6 displays a histogram of the number of stock returns per week (the left panel) and boxplots outlining the distribution of the number of observations for each characteristic:
Figure 20.6: Number of tickers over time and per - stock characteristic
To limit the influence of outliers, we follow GKX and rank-normalize the characteristics to the [-1, 1] interval:
data.loc[:, characteristics] = (data.loc[:, characteristics]
.groupby(level='date')
.apply(lambda x:
pd.DataFrame(quantile_transform(
x,
copy=True,
n_quantiles=x.shape[0]),
columns=characteristics,
index=x.index.get_level_values('ticker'))
)
.mul(2).sub(1))
Since the neural network cannot handle missing data, we set missing values to -2, which lies outside the range for both weekly returns and the characteristics.
The authors apply additional methods to avoid overweighting microcap stocks like market-value-weighted least-squares regression. They also adjust for data-snooping biases by factoring in conservative reporting lags for the characteristics.
Creating the conditional autoencoder architecture
The conditional autoencoder proposed by GKX allows for time-varying return distributions that take into account changing asset characteristics. To this end, the authors extend standard autoencoder architectures that we discussed in the first section of this chapter to allow for features to shape the encoding.
Figure 20.7 illustrates the architecture that models the outcome (asset returns, top) as a function of both asset characteristics (left input) and, again, individual asset returns (right input). The authors allow for asset returns to be individual stock returns or portfolios that are formed from the stocks in the sample based on the asset characteristics, similar to the Fama-French factor portfolios we discussed in Chapter 4, Financial Feature Engineering – How to Research Alpha Factors, and summarized in the introduction to this section (hence the dotted lines from stocks to portfolios in the lower-right box). We will use individual stock returns; see GKX for details on how and why to use portfolios instead.
Figure 20.7: Conditional autoencoder architecture designed by GKX
The feedforward neural network on the left side of the conditional autoencoder models the K factor loadings (beta output) of N individual stocks as a function of their P characteristics (input). In our case, N is around 3,800 and P equals 16. The authors experiment with up to three hidden layers with 32, 16, and 8 units, respectively, and find two layers to perform best. Due to the smaller number of characteristics, we only use a similar layer and find 8 units most effective.
The right side of this architecture is a traditional autoencoder when used with individual asset returns as inputs because it maps N asset returns onto themselves. The authors use it in this way to measure how well the derived factors explain contemporaneous returns. In addition, they use the autoencoder to predict future returns by using input returns from period t-1 with output returns from period t. We will focus on the use of the architecture for prediction, underlining that autoencoders are a special case of a feedforward neural network as mentioned in the first section of this chapter.
The model output is the dot product of the 
factor loadings on the left with the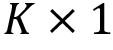 
factor premia on the right. The authors experiment with values of K in the range 2-6, similar to established factor models.
To create this architecture using TensorFlow 2, we use the Functional Keras API and define a make_model() function that automates the model compilation process as follows:
def make_model(hidden_units=8, n_factors=3):
input_beta = Input((n_tickers, n_characteristics), name='input_beta')
input_factor = Input((n_tickers,), name='input_factor')
hidden_layer = Dense(units=hidden_units,
activation='relu',
name='hidden_layer')(input_beta)
batch_norm = BatchNormalization(name='batch_norm')(hidden_layer)
output_beta = Dense(units=n_factors, name='output_beta')(batch_norm)
output_factor = Dense(units=n_factors,
name='output_factor')(input_factor)
output = Dot(axes=(2,1),
name='output_layer')([output_beta, output_factor])
model = Model(inputs=[input_beta, input_factor], outputs=output)
model.compile(loss='mse', optimizer='adam')
return model
We follow the authors in using batch normalization and compile the model to use mean squared error for this regression task and the Adam optimizer. This model has 12,418 parameters (see the notebook).
The authors use additional regularization techniques such as L1 penalties on network weights and combine the results of various networks with the same architecture but using different random seeds. They also use early stopping.
We cross-validate using 20 years for training and predict the following year of weekly returns with five folds corresponding to the years 2015-2019. We evaluate combinations of numbers of factors K from 2 to 6 and 8, 16, or 32 hidden layer units by computing the information coefficient (IC) for the validation set as follows:
factor_opts = [2, 3, 4, 5, 6]
unit_opts = [8, 16, 32]
param_grid = list(product(unit_opts, factor_opts))
for units, n_factors in param_grid:
scores = []
model = make_model(hidden_units=units, n_factors=n_factors)
for fold, (train_idx, val_idx) in enumerate(cv.split(data)):
X1_train, X2_train, y_train, X1_val, X2_val, y_val =
get_train_valid_data(data, train_idx, val_idx)
for epoch in range(250):
model.fit([X1_train, X2_train], y_train,
batch_size=batch_size,
validation_data=([X1_val, X2_val], y_val),
epochs=epoch + 1,
initial_epoch=epoch,
verbose=0, shuffle=True)
result = (pd.DataFrame({'y_pred': model.predict([X1_val,
X2_val])
.reshape(-1),
'y_true': y_val.stack().values},
index=y_val.stack().index)
.replace(-2, np.nan).dropna())
r0 = spearmanr(result.y_true, result.y_pred)[0]
r1 = result.groupby(level='date').apply(lambda x:
spearmanr(x.y_pred,
x.y_true)[0])
scores.append([units, n_factors, fold, epoch, r0, r1.mean(),
r1.std(), r1.median()])
Figure 20.8 plots the validation IC averaged over the five annual folds by epoch for the five-factor count and three hidden-layer size combinations. The upper panel shows the IC across the 52 weeks and the lower panel shows the average weekly IC (see the notebook for the color version):
Figure 20.8: Cross-validation performance for all factor and hidden-layer size combinations
The results suggest that more factors and fewer hidden layer units work better; in particular, four and six factors with eight units perform best with overall IC values in the range of 0.02-0.03.
To evaluate the economic significance of the model's predictive performance, we generate predictions for a four-factor model with eight units trained for 15 epochs. Then we use Alphalens to compute the spreads between equal-weighted portfolios invested by a quintile of the predictions for each point in time, while ignoring transaction costs (see the alphalens_analysis.ipynb notebook).
Figure 20.9 shows the mean spread for holding periods from 5 to 21 days. For the shorter end that also reflects the prediction horizon, the spread between the bottom and the top decile is around 10 basis points:
Figure 20.9: Mean period-wise spread by prediction quintile
To evaluate how the predictive performance might translate into returns over time, we lot the cumulative returns of similarly invested portfolios, as well as the cumulative return for a long-short portfolio invested in the top and bottom half, respectively:
Figure 20.10: Cumulative returns of quintile-based and long-short portfolios
The results show significant spreads between quintile portfolios and positive cumulative returns for the broader-based long-short portfolio over time. This supports the hypothesis that the conditional autoencoder model could contribute to a profitable trading strategy.
Lessons learned and next steps
The conditional autoencoder combines a nonlinear version of the data-driven risk factors we explored using PCA in Chapter 13, Data-Driven Risk Factors and Asset Allocation with Unsupervised Learning, with the risk factor approach to modeling returns discussed in Chapter 4 and Chapter 7. It illustrates how deep neural network architectures can be flexibly adapted to various tasks as well as the fluid boundary between autoencoders and feedforward neural networks.
The numerous simplifications from the data source to the architecture point to several avenues for improvements. Besides sourcing more data of better quality that also allows the computation of additional characteristics, the following modifications are a starting point—there are certainly many more:
- Experiment with data frequencies other than weekly and forecast horizons other than annual, where shorter periods will also increase the amount of training data
- Modify the model architecture, especially if using more data, which might reverse the finding that an even smaller hidden layer would estimate better factor loadings
Summary
In this chapter, we introduced how unsupervised learning leverages deep learning. Autoencoders learn sophisticated, nonlinear feature representations that are capable of significantly compressing complex data while losing little information. As a result, they are very useful to counter the curse of dimensionality associated with rich datasets that have many features, especially common datasets with alternative data. We also saw how to implement various types of autoencoders using TensorFlow 2.
Most importantly, we implemented recent academic research that extracts data-driven risk factors from data to predict returns. Different from our linear approach to this challenge in Chapter 13, Data-Driven Risk Factors and Asset Allocation with Unsupervised Learning, autoencoders capture nonlinear relationships. Moreover, the flexibility of deep learning allowed us to incorporate numerous key asset characteristics to model more sensitive factors that helped predict returns.
In the next chapter, we focus on generative adversarial networks, which have often been called one of the most exciting recent developments in artificial intelligence, and see how they are capable of creating synthetic training data.