2.6 (c) The encoding function is injective on the given domain: suppose there exist x, x ̃ ∈ 00{0, 1}400 with x > x̃ and x2 ≡ x̃2 mod 253. Then, (x − x̃)(x + x̃) ≡ 0 mod 253. Now, there are two cases. Either one of the two factors is 0 or one is a multiple of 11, and the other a multiple of 23.We have x − x ̃ ≠ 0 and x + x ̃ ≢ 0 mod 253 because x + x ̃ cannot exceed 120. Thus, the only remaining case is x − x ̃ being a multiple of 11 or 23. The numbers x and x ̃ are both multiples of 4. From we obtain that x − x ̃ can only be a multiple of 11, and has to hold. With this yields and In particular, x + x ̃ is not divisible by 23. This is a contradiction; and it shows that such x and x ̃ cannot exist.

2.7 (a) The number n is prime, so φ(n) = n − 1 = 46 and the order of g is a divisor of 46 = 2 ⋅ 23. From 52 = 25 ≢ 1 mod 47 and 523 ≡ −1 mod 47, we obtain that the order of g is 46.

2.7 (b) We have A ≡ 5a ≡ 516 ≡ 17 mod 47 and B ≡ 5b ≡ 59 ≡ 40 mod 47. The secret key is k ≡ Ab ≡ Ba ≡ 21 mod 47.

2.7 (c) B = 40 has already been determined. The ciphertext is computed by y ≡ Ab⋅x ≡ k ⋅ x ≡ 21 ⋅ 33 ≡ 35 mod 47.

2.8. Since each element x ∈ X has a unique image y = h(x), each x is counted in exactly one ‖y‖. Thus, Σy∈Y ‖y‖ = |X|. Substituting this equation into m = Σy∈Y ‖y‖/|Y|, directly yields A collision (x, x) with h(x) = h(x) = y accounts for two different elements in ‖y‖. The number of these pairs for a fixed y is This yields The equation is obtained using and Σy∈Y ‖y‖ = |X|. We have

In particular, This yields

2.9. By definition, h1 is collision resistant. Now, let i ≥ 1 and let be a collision of hi+1.We may assume that According to the definition of hi+1, two cases are possible. Either and thus, is a collision of hi. Or, in the other case, is a collision of h1.

2.10. Wehave a80 115 359 ≡ a1 294 755 mod n. Therefore a80 115 359−1 294 755 ≡ 1 mod n. Furthermore, 80 115 359 − 1 294 755 = 78 820 604 = 4 ⋅ 19 705 151. Since φ(n) = 4pq, we try to find a number b such that b19 705 151 ≢ 1 mod n; see Section 3.4.4 for details on this approach. We randomly choose b = 13. Then, 1319 705 151 ≡ 10 067 mod n and 10 0672 ≡ 1 mod n. Thus, (10 067 − 1)(10 067 + 1) ≡ 0 mod n, and we compute gcd(10 066, n) = 719 and gcd(10 068, n) = 839. This yields the factorization n = 719 ⋅ 839.

2.11 (a) First, let uk(x) = (γ, δ) = (αs , (x − mγ)s−1). Then, βγγδ ≡ αmγγδ ≡ αmγαsδ ≡ αmγαs⋅s−1(x−mγ) ≡ αx mod p, and thus υk(x, γ, δ) = true. Conversely, let υk(x, γ, δ) = true and let t be the discrete logarithm of γ to base α. Then, βγγδ ≡ αx mod p, and thus αx−mγ ≡ γδ ≡ αtδ mod p. We further obtain x − mγ ≡ tδ mod (p − 1). This is equivalent to δ ≡ (x − mγ)t−1 mod (p − 1). Thus, (γ, δ) is a valid signature for x.

2.11 (b) Choose u, υ with gcd(υ, p − 1) = 1. Define γ = αuβυ mod p, δ = −γυ−1 mod p − 1 and x = uδ mod p − 1. Then, βγγδ ≡ βγαuδβ−υυ−1γ ≡ αuδ ≡ αx mod p.

2.11 (c) We have to show that βλλμ ≡ αx' mod p holds. Let y = (hγ − jδ)−1 mod p − 1. Since (γ, δ) is a valid signature, we have γδ ≡ β−γαx mod p. This yields βλλμ ≡ βλ(γhαiβj)δλy ≡ βλ(γδ)hλyαiδλyβjδλy ≡ βλβ−γhλyαxhλyαiδλyβjδλy ≡ βλβ−γhλyαxβjδλy ≡ αxβλ−λ(hγ−jδ)(hγ−jδ)−1 ≡ αx' mod p.

2.12. Let the four people be 1, 2, 3, 4.We have and the subsets of {1, 2, 3, 4} with two elements are A1 = {1, 2}, A2 = {1, 3}, A3 = {1, 4}, A4 = {2, 3}, A5 = {2, 4} and A6 = {3, 4}. For the first five of these subsets, we randomly choose the keys k1 = (1, 9), k2 = (2, 4), k3 = (3, 5), k4 = (4, 1) and k5 = (5, 1). Then the key for A6 is k6 = (6, 11) since 11 ≡ 7 − (9 + 4 + 5 + 1 + 1) mod 12. Person 1 gets the keys {k4, k5, k6}, person 2 gets {k2, k3, k6}, person 3 gets {k1, k3, k5} and person 4 gets {k1, k2, k4}. If three of the four participants come together, then they have all the keys kj in their subsets. Thus, they can compute

2.13. We choose the prime number p = 61. We share the secret using the polynomial a(X) = 42+a1X ∈ p[X] with the randomly chosen coefficient a1 = 23. Then, a(1) = 4, a(2) = 27 and a(3) = 50. Thus, the pairs (1, 4), (2, 27) and (3, 50) shall be distributed. Any two of these pairs can be used to reconstruct the secret. For example, let (1, 4) and (2, 27) be given. We obtain the equations a0 + a1 = 4 and a0 + 2a1 = 27. We find a0 = 4 − a1 and substitute 4 − a1 for a0 in the second equation. This results in (4 − a1) + 2a1 = 27, so a1 = 23 and further a0 + 23 = 4, or a0 ≡ −19 ≡ 42 mod 61.

2.14. We use a multi-step algorithm based on Shamir’s secret sharing. First, the secret key is distributed between three keys such that two of them are sufficient to reconstruct the secret key. Two of these keys are given to the directors. The third key is again divided into ten keys with the property that seven of them suffice to decrypt the secret. Seven of these ten keys are passed on to the heads of department. The remaining three keys are again divided as secret (for this, a suitable encoding of the three keys as one secret is required). And finally this secret is divided into a total of 87 keys such that eleven of them are sufficient to reconstruct the secret. Obviously, the keys of eleven of the employees can compensate the lack of three department heads, and seven department heads can compensate the lack of a director.

2.15. Let persons 1, 2 and 3 have salaries g1, g2 and g3, respectively. The protocol works as follows: first, person 1 sends a (large) random number z to person 2, who in turn sends z + g2 to person 3. Since person 3 does not know the number z, it is not possible to infer the salary g2 from this. Then, person 3 sends the sum z + g2 + g3 to person 1. Person 1 is able to compute the sum g1 + g2 + g3 and thus also the average salary. Person 1 communicates it to the other two persons. This protocol can be easily generalized to cases of more employees.

2.16. Let w1 < ⋅ ⋅ ⋅ < wn be the possible salaries. Let cB be Bob’s public encryption function and dB his private decryption function. Alice randomly chooses x and sends d = cB(x) − a to Bob, where a is her salary. Bob now computes y1, . . . , yn with yi = dB(d + wi). For j such that wj = a, we have yj = x. To conceal his salary, Bob applies a one-way function f and computes zi = f(yi ) for all i ∈ {1, . . . , n}. Without loss of generality let zi ≠ zj + 1 for 1 ≤ i, j ≤ n. (Otherwise, Alice has to choose a new x or Alice and Bob agree upon a different hash function.) If b = wk is Bob’s salary, then he sends the sequence z1, . . . , zk , zk + 1, . . . , zn + 1 to Alice. Now, a ≤ b if and only if f(x) occurs in the sequence.

2.17. The dealer commits himself to a number between 0 and 36. Then, all players make their bids in plaintext. Finally, the dealer reveals his number.

2.18. The problem can be solved via dynamic programming. We fill a {0, . . . , c} × n table T. By Ti,j, we denote the entry in row i and column j. The table is initialized with T0,j = 1; and then iteratively filled by the following rule.

The entry Ti,j means that a solution for the weight i already exists using s1, . . . , sj. Thus, a solution of the knapsack instance exists if Tc,n = 1.

2.19. The inverse of u in (ℤ/71ℤ)∗ is w = 5. Alice chose the ai such that si = ai ⋅w mod 47. So she used the superincreasing sequence (2, 5, 9, 17, 37). Alice determined c = 90 ⋅ w = 90 ⋅ 5 ≡ 24 mod 71. The only solution of the knapsack problem is 24 = 1 ⋅ 2 + 1 ⋅ 5 + 0 ⋅ 9 + 1 ⋅ 17 + 0 ⋅ 37. Therefore, the plaintext is (1, 1, 0, 1, 0).

2.20. For i = 0 the statement is trivial. For i ≥ 0, induction yields:

Chapter 3

3.1. Let γ0 > 0 be such that Let further ε > 0 and n0 ∈ ℕ be numbers such that αin0 ≤ n0 − 1 for all i ∈ {1, . . . , k} and for all n ≥ n0. Finally, choose γ large enough to ensure that γ0 < γε and f(n) < γn for all n < n0. By induction on n we show that f(n) < γn. For n < n0 the assertion is satisfied by choice of γ. For n ≥ n0 we have

Remark: A well-known application of the master theorem II is the computation of the median of a sequence of n numbers with only O(n) comparisons. This shows that it is not necessary to sort the whole sequence to determine the median.

3.2. Without loss of generality we assume that a ≠ 0 ≠ b. Divide each of a and b by gcd(a, b). Then, we can independently determine the square roots of the numerator and denominator using binary search.

3.3. The extended binary gcd algorithm is as follows:

3.4. We have 2(n−1)/2 = 2864 ≡ 1 mod 1729 and by Theorem 1.70 (c) we obtain (−1)(n2−1)/8 = 1. Note that 1729 ≡ 1 mod 16 and therefore is an even number, so 1729 is an Eulerian pseudoprime to base 2.

We write 1728 = 2ℓu = 26 ⋅ 27 and let b = 645 ≡ 227 ≢ 1 mod 1729. Thus, (b20 , b21 , b22 , b23 , b24 , b25) = (645, 1065, 1, 1, 1, 1) modulo 1729. Since −1 does not occur in this sequence, 1729 is not a strong pseudoprime to base 2. Further, for c = 1065, we have c2 ≡ 1 mod 1729. Consequently, 1064 ⋅ 1066 = (c − 1)(c + 1) ≡ 0 mod 1729. Therefore, gcd(1064, 1729) = 133 is a nontrivial divisor of 1729 = 133 ⋅ 13 = 7 ⋅ 19 ⋅ 13.

Moreover, let us note that in this particular case out of all a ∈ {1, . . . , n − 1} (or all a ∈ {1, . . . , n − 1} coprime to n, respectively) the Fermat test fails for 75% (or 100%, respectively), the Solovay–Strassen test for 39.5% (or approximately 52.7%, respectively) and the Miller–Rabin test for approximately 9.4% (or 12.5%, respectively). Thus, in particular, 1729 is a Carmichael number.

3.5. Let r be the order of a in (ℤ/nℤ)∗. From (i), we obtain r | n − 1, and with (ii) this yields r = n − 1. Thus, |(ℤ/nℤ)∗| = n − 1, and n is prime.

3.6. Suppose, fn is prime. Then, Euler’s criterion yields mod fn. Together with fn ≡ 1 mod 4 using the law of quadratic reciprocity, we obtain mod 3. The converse direction is a consequence of the Lucas test in Exercise 3.5.

3.7 (a) By the law of quadratic reciprocity we have because 2p − 1 ≡ (−1)p − 1 ≡ 1 mod 3 for odd p. Using the well-known quadratic formula it follows that f is irreducible.

3.7 (b) The polynomial g(Y) = Y2 −4Y +1 in K [Y] has the roots X and 4 −X. These are the only zeros of g because K is a field. The coefficients of g are in n, so 0 = g(X)n = g(Xn) follows. Therefore, Xn ∈ {X, 4 − X}. Since the roots of Yn − Y are exactly the elements of n and X ∉ n, we obtain Xn ≠ X and thus Xn = 4 − X. This yields

Note that a ↦ an is the Frobenius homomorphism and that an = a for all a ∈ n.

3.7 (c) In n and thus also in K by Euler’s criterion we have 2(n−1)/2 = 1 because Moreover, (X − 1)2 = 2X in K. This yields

3.7 (d) We define f(X) = X2 − 4X + 1. For the direction from right to left, let the congruence hold, and let q be the smallest prime divisor of n. In q[X] we have Xn+1 ≡ 1 mod f(X) and X(n+1)/2 ≢ 1 mod f(X). Therefore, in the group of units of R = q[X]/f , the element X has order n + 1. If n is composite, then Since R contains q2 elements, we know n ≥ q2 > |R∗|≥ n + 1, a contradiction. Thus, n is prime.

For the converse direction, let n be prime and let K = n[X]/f. In the field, K we have 2X(n+1)/2 = (X − 1)n+1 = −2 and thus X(n+1)/2 = −1, as desired.

3.8. Let R = ℤ/nℤ, let f(X) = X2 − 4X + 1 and let K = R[X]/f . By induction on j we first show that in K the property ℓj = X2j + (4 − X)2j is satisfied. For j = 0 we have ℓ0 = 4 = X + (4 − X). Nowlet j ≥ 0. Using X(4 − X) = 1, we obtain

We have X(n+1)/2 = −1 if and only if X(n+1)/2−k = −X−k. For k = (n + 1)/4, together with X−1 = 4 − X, we obtain the equivalence

The assertion follows from Exercise 3.7.

3.9. We have the equivalence an+1 ∈ a1ℤ+⋅ ⋅ ⋅+anℤ ⇔ gcd(a1, . . . , an) | an+1. Here, g = gcd(a1, . . . , an) = gcd(gcd(a1, . . . , an−1), an). In particular, using the extended Euclidean algorithm numbers yi ∈ ℤ with a1y1 + ⋅⋅ ⋅ + anyn = g can be computed. Setting xi = yian+1/g, this yields a solution for the equation.

3.10. We let q = 41, u = 5 and ℓ = 3. Then, q − 1 = u2ℓ. Furthermore, from g(q−1)/2 ≡ −1 mod 41, we can see that g is not a square in 41. In the second step we now successively determine bits k0, k1 and k2. Let especially x−1 = a. We determine ki ∈ {0, 1} from k0, . . . , ki−1 and let ki = 0 if and only if mod q is satisfied.

Thus, we obtain k = k0 + 2k1 + 4k2 = 6. Finally b = 2(u+1)/2g−uk/2 = 23145⋅3 ≡ 24 mod 41 is a square root of 2 in 41. The second solution is 17 = 41 − 24.

3.11. First, let a(p−1)/4 = 1 and b = a(p+3)/8. Then, b2 = a(p+3)/4 = a ⋅ a(p−1)/4 = a ⋅ 1 = a. Now let a(p−1)/4 = −1 and b = 2−1(4a)(p+3)/8. From Euler’s criterion and the law of quadratic reciprocity it follows that Thus, we obtain b2 = 2−2(4a)(p+3)/4 = 2−2 ⋅ 2(p+3)/2 ⋅ a(p+3)/4 = 2(p−1)/2 ⋅ a(p−1)/4 ⋅ a = (−1) ⋅ (−1) ⋅ a = a.

3.12 (a) From the law of quadratic reciprocity it follows that so −1 is not a square, that is, X2 = −1 has no solution in p. Since f(X) has degree 2, it is irreducible.

3.12 (b) We have and Therefore, more generally, let 1 ≤ b < c ≤ p −1with and If c = b +1, then we let a = b. Otherwise, we consider d = ⌊(b + c)/2⌋ and compute Depending on this result being either −1 or 1, we recursively continue the algorithm with the numbers b < d or d < c. This binary search returns the requested number a after atmost O(log p) evaluations of the Jacobi symbol.

3.12 (c) Let a be the number computed in the previous part of the exercise. The elements a + 1 and −1 both are no squares, therefore −(a + 1) is a square. Since p ≡ −1 mod 4, one can efficiently compute b, c ∈ p with b2 = a and c2 = −(a + 1). Now b2 + c2 = −1.We let g = b + cX ∈ p2 .

Assume that g is a square. Then there are s, t ∈ p with (s + tX)2 = g. Thus, s2 − t2 = b and 2st = c. Let h = (s − tX)2. Then, h = b − cX and thus gh = b2 + c2 = −1. With r = (s + tX)(s − tX) = s2 + t2 ∈ p, we obtain r2 = gh = −1. This is a contradiction to Consequently, g is not a square. We can now use the deterministic part of Tonelli’s algorithm to extract roots in p2 .

3.13. We let a = 2 and t = 0, and we observe that (t2 − 4a)11 ≡ −1 mod 23; thus, t = 0 is a valid choice for the first step in Cipolla’s algorithm. We now determine X12 by repeatedly replacing X2 by tX − a = −2 and computing coefficients in ℤ/23ℤ:

So, 18 and 5 = 23 − 18 are the two square roots of 2 in 23.

3.14. For B = {2, 3} we find k = 27 ⋅ 35 = 128 ⋅ 243 = 31 104. Using fast modular exponentiation and a = 2 we further obtain ak ≡ 82 mod n. Now, gcd(ak − 1, n) = gcd(81, 253) = 1 and we did not find a factor.

For B = {2, 3, 5} we find k = 27 ⋅ 35 ⋅ 53 = 128 ⋅ 243 ⋅ 125 = 3 888 000. Using fast modular exponentiation and a = 2 we now obtain ak ≡ 133 mod n. Then, gcd(ak − 1, n) = gcd(132, 253) = 11 andwe have found a nontrivial factor of n.

Let us remark that the p − 1 algorithmwith B = {2, 3} finds a nontrivial factor for roughly 24% of all a ∈ {2, . . . , n − 1}. For B = {2, 3, 5} the probability is 84%.

3.15. We let x0 = y0 = 12 and obtain the following values:

Thus, 53 is a divisor of n.

3.16. The order n of (ℤ/19ℤ)∗ is 18.We let g = 2, y = 3 and Performing the baby-steps results in the following table B:

As to the giant-steps, we compute h = 24 = 16 and successively h0 = 1, h1 = 16, h2 ≡ 9. None of these values can be found in the second row of the table. Finally, for s = 3 we obtain hs ≡ 11, which can be found in the table B at r = 1. Thus, x = 3 ⋅ m + r = 13 is the desired value.

3.17. Compute the smallest n ≥ 0 with gn = 1. To this end check the giant-steps s in ascending order and discard the solution r = 0 and s = 0. A small optimization is the following. If two baby-steps (r, a) and (r' , a) with r < r' occur, one only stores the entry (r, a) in the table B.

3.18 (a) The order of G is 22 = 2⋅11.We have g2 = 9 ≢ 1 mod 23 and g11 ≡ 1 mod 23. So, 11 is the order of g.

3.18 (b) We let y = 18, we let f : ℤ/qℤ×ℤ/qℤ→ℤ/qℤ×ℤ/qℤ such that

and we define a sequence (ri , si) with (r1, s1) = (1, 1) and (ri+1, si+1) = f(ri , si) for i ≥ 1. Further, we let hi = gri ysi mod 23. For ℓ ∈ {1, 2, 4} we compute the values of (rℓ , sℓ) as well as hℓ; and for k ∈ {1, . . . , ℓ} the values of (rℓ+k , sℓ+k) and hℓ+k are displayed in the following table:

The algorithm terminates if hℓ = hℓ+k, that is, in the current case at ℓ = 4 and k = 3; the values for ℓ = k = 4 are actually not computed anymore. We have g3y2 = hℓ = hℓ+k = g5y3. If y = gx, then g3+2x = g5+3x and therefore 3 + 2x ≡ 5 + 3x mod 11. One solution of this congruence is 9. Since 39 ≡ 18 mod 23, this is indeed the desired value. Note that the algorithm does not find the accordance with value 6 of h2 and h5, since the values h5, h6, h7, h8 are exclusively compared with h4.

3.19. We let g = 2 and y = 5. The order of (ℤ/19ℤ)∗ is n = 18 = 2 ⋅ 32. We choose parameters as displayed in the following table:

For p ∈ {2, 3} we have np = n/pe(p), gp = gnp mod q and mod q. If we let x = 16, then congruences x ≡ 0 mod 2 and x ≡7 mod 32 are satisfied and by Theorem 3.16 we know that 16 is the desired value.

To determine the value x3 we write x3 = d0+d1⋅3. The value d0 can be determined as a solution of the equation ((g3)3)d0 ≡ (y3)3 mod 19. Now (g3)3 = 43 ≡ 7 mod 19 and (y3)3 = 63 ≡ 7 mod 19 and, moreover, d0 = 1 trivially is a solution. In order to determine d1 we first let z1 = 11. Then, mod 19 and d1 is a solution of the congruence ((g3)3)d1 ≡ z1 mod 19, that is, by insertion 7d1 ≡ 11 mod 19. One solution is d1 = 2 and we obtain x3 = 1 + 2 ⋅ 3 = 7.

3.20. The order of (ℤ/pℤ)∗ is a power of 2. Using the Pohlig–Hellman algorithm, it suffices to compute discrete logarithms in O(log p) two-element groups.

3.21 (a) A simple computation yields ωb/2 ≡ −1 mod 97 and ωb ≡ 1 mod 97.

3.21 (b)

3.21 (c) The degree of f ∗ g is 3, therefore we can choose b = 4 and use ω = −22 as primitive bth root of unity. This yields the following course of the FFT on input f (left) and g (right):

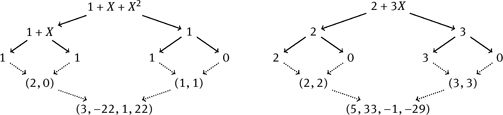
These flowcharts have the following meaning: if f, f0, f1 are polynomials such that f(X) = f0(X2) + Xf1(X2) and w = (1, ω, ω2, . . . , ωb−1), then symbolizes the recursion and the merge of the results, where addition and multiplication are meant componentwise. We compute the componentwise product (3, −22, 1, 22) ⋅ (5, 33, −1, −29) ≡ (15, 50, −1, 41) mod 97. As to the inverse transformation, we use the same scheme, only the primitive bth root of unity used here is ω−1 = 22. Then

To obtain the result, we have to multiply 8 + 20X + 20X2 + 12X3 by b−1 = −24 and we end up with (f ∗ g)(X) = 2 + 5X + 5X2 + 3X3.

3.22. Let u and υ be natural numbers with a binary representation of at most n bits. The time complexity of the method is dominated by the time needed for the FFT and therefore it is (n log n). There are at most m = ⌈n/64⌉ indices i, for which ui as well as υi are nonzero. We consider the product

with the usual convention that uj = υj = 0 for j < 0 and for j ≥ m. In order to have the zj = Σk u kυj−k uniquely determined by wj, the inequality zj < p1p2p3 has to hold. At most m summands in zj are nonzero, and each of these summands is bounded by 264. Therefore, we obtain zj ≤ m ⋅ 264 ⋅ 264. Since pi > 256 it suffices, if the number m of 64-bit blocks of u and υ satisfies m ≤ 23⋅56/22⋅64 = 240. Furthermore, 2m ≤ 256 has to hold in order to have no overflow in the Fourier transform. This already follows from the fact that m ≤ 240. Therefore, using this method numbers with a binary representation of 64 ⋅ 240 bits can be multiplied. This corresponds to a binary representation of more than eight terabytes. With very large primes pi (as close to 64 bits as possible) even larger numbers can be multiplied.

Chapter 5

5.1 (a) If the characteristic is not 2, we complete the square on the left-hand side of Equation (5.2) and obtain where t is a quadratic polynomial in X̃ , which we push to the right-hand side. Now let and and gather the coefficients on the right-hand side.

5.1 (b) Let X ̂ = X − ê/3 and combine the coefficients.

5.2. Our computations are performed in an algebraically closed field k. If the polynomial has a multiple root, then we have X3 + AX + B = (X − a)2(X − b) for some a, b ∈ k. Multiplying out and comparing coefficients yields 2a + b = 0, 2ab + a2 = A and −a2b = B. By substituting b = −2a in the second and third equation, we obtain A = −3a2 and B = 2a3. It follows that 4A3+27B2 = −4⋅27a6+27⋅4a6 = 0 independent of the field’s characteristic. For the converse, let 4A3 + 27B2 = 0. If the characteristic is neither 2 nor 3, then this yields (−A/3)3 = (B/2)2. Let a be a square root of −A/3; then A = −3a2 and B = 2a3. For b = −2a the same computation as in the first part yields (X − a)2(X − b) = X3 + AX + B and thus, a is a multiple root. If the characteristic is 2, then 4A3 + 27B2 = 0 if and only if B = 0. Then, X3 + AX = X(X2 + A) = X(X + a)2 for a ∈ k with a2 = A. If the characteristic is 3, then 4A3 + 27B2 = 0 is equivalent to A = 0.We obtain X3 + B = (X + b)3 for b ∈ k with b3 = B.

5.3. Let s(X) = X3 + AX + B.We show that for every a ∈ p there are points in E (p) with the value a in the X-coordinate. If s(a) = 0, then (a, 0) is the only point. If then there exists a square root b ∈ p of s(a) and the two points (a, b) and (a, −b) are the only ones with this X-coordinate. If then no point on the curve has the value a as an X-coordinate. This yields

5.4 (a) 4 ⋅ 13 + 27 ⋅ 62 = 8 ≠ 0 in 11. By Exercise 5.2, this proves the claim.

5.4 (b) For each x ∈ 11 we distinguish the three possible cases whether x3 + x + 6 equals 0, is a square in 11 or is not a square in 11. Then, we obtain from Exercise 5.3 the set E(11) = {(2, 4), (2, 7), (3, 5), (3, 6), (5, 2), (5, 9), (7, 2), (7, 9), (8, 3), (8, 8), (10, 2), (10, 9)}. Therefore, |Ẽ(11)| = |E(11)∪ | = 12 + 1 = 13 is prime and thus Ẽ(11) is cyclic.

5.5 (a) 4 ⋅ 13 = −1 ≠ 0 in 5. By Exercise 5.2, this proves the claim.

5.5 (b) Similar to the previous exercise, we obtain E(5) = {(0, 0), (2, 0), (3, 0)}. Each of these three elements is of order 2. Hence, Ẽ(5) is isomorphic to the Klein four-group; any two elements of E (5) generate the group.

5.6. It is easy to see that { P ∈ Ẽ(k) | 3P = } is a subgroup of Ẽ(k). Let P = (a, b) ∈ E (k) be a point of order 3. We have b ≠ 0 because otherwise P would be of order 2. Moreover 2P = −P and therefore Together with b2 = a3 + Aa + B, this yields 3a4 + 6Aa2 + 12Ba − A2 = 0.We therefore consider the polynomial t(X) = 3X4 + 6AX2 + 12BX −A2. Every point of order 3 would lead to the same polynomial; in particular, the X-coordinate of every point in { P ∈ E(k) | 3P = } is a root of t. Moreover, every root of t is the X-coordinate of two different points in { P ∈ E(k) | 3P = }. If n is the number of different roots of t, then |{ P ∈ E(k) | 3P = }| = 2n ≤ 8.