4 Polynomial time primality test

In August 2002, a message rapidly spread out, reaching all mathematically interested people throughout the world within hours: “PRIMES is in P.” The scientists Manindra Agrawal, Neeraj Kayal, and Nitin Saxena from India had found a polynomial-time primality test. Composed of the initials of their last names, this method is called the AKS test. It is neither based on unproven hypotheses like, for example, the generalized Riemann hypothesis (Georg Friedrich Bernhard Riemann, 1826–1866), nor does it provide any probabilistic claims like the Miller–Rabin test from Section 3.4.3. The problem called PRIMES, that is, “check whether an integer, given in binary, is prime,” is thus in the complexity class P of problems decidable in deterministic polynomial time.

The simplicity of the method is sensational. We are able to treat all aspects of the proof in full detail here. No specialized number theoretical insight that would go beyond the scope of this book is required. The work of Agrawal, Kayal, and Saxena was awarded the Gödel-Prize (Kurt Gödel, 1906–1978)5in 2006.

By now, a number of textbooks have presented the AKS test; see, for example [19, 32, 41]. Our presentation becomes a little easier due to the use of field extensions instead of cyclotomic polynomials. The necessary prerequisites for understanding the AKS test are modest: only parts of Sections 1.1, 1.4, 1.5, 1.6, and 1.8 are required.

4.1 Basic idea

The following lemma is the main idea behind the AKS primality test. The proof is similar to Fermat’s little theorem.

Lemma 4.1. Let a, n ∈ ℕ with gcd(a, n) = 1. The number n is prime if and only if the following polynomial congruence holds in ℤ[X]:

Proof: First, suppose that n is prime. We have (X + a)n ≡ Xn + an ≡ Xn + a mod n. The first congruence follows from Theorem 1.28 and the second from Fermat’s little Theorem 1.29.

For the converse, consider a prime number p which is a proper divisor of n and let pk be the largest power of p dividing n. Then, pk is also the largest power of p dividing n(n − 1) ⋅⋅ ⋅ (n − p + 1). It follows that pk−1 is the largest power of p dividing Thus, the term does not vanish modulo n.

□

The implication from right to left is not required in the following; as a primality test, it cannot be used in this form, anyway, because if we multiply out (X + a)n, in principle all the n + 1 coefficients have to be computed, and the number of coefficients is exponential in the input size ⌊log2 n⌋ + 1.

The congruence (X + a)n ≡ Xn + a mod n is weakened to (X + a)n ≡ Xn + a mod (Xr−1, n) for a small number r ∈ ℕ. This simplified congruence has to be checked for all a with a ≤ ℓ for some sufficiently large ℓ. The idea is to show that r and ℓ can be chosen to be small, that is, polylogarithmic in n. We first note that the congruence (X + a)n ≡ Xn + a mod (Xr − 1, n) can also be seen as an equality (X + a)n = Xn + a in the quotient ring ℤ[X]/(Xr − 1, n), where (Xr − 1, n) is the ideal generated by the polynomials X r − 1 and n. Put another way: a congruence

means that there are polynomials g(X), h(X) ∈ℤ[X] satisfying

From this description, it is obvious that congruence modulo n implies congruence modulo (Xr − 1, n). The computation of (X + a)n mod (Xr − 1, n) can be done by fast exponentiation and we may replace each power Xr by 1 and compute coefficients modulo n. The polynomials then have at most r coefficients, each of which is smaller than n. Thus, if r is polylogarithmic in n, then (X + a)n ≡ Xn + a mod (Xr − 1, n) can be checked in polynomial time.

4.2 Combinatorial tools

In the next three sections, we provide some tools for the correctness proof of the AKS test. We start with two elementary combinatorial theorems. For a set A let be the set of all k-element subsets of A.

Theorem 4.2. For every finite set A, we have

Proof: Let |A| = n. The theorem is correct for k ≤ 0 or k ≥ n. For 0 < k < n there are n(n − 1) ⋅⋅ ⋅ (n − k + 1) sequences (a1, . . . , ak) of pairwise different elements ai ∈ A. Two such sequences represent the same subset of A if the sequences coincide up to a permutation of the indices. There are k! such permutations.

□

The following theorem often appears in connection with drawing balls from an urn as “unordered selection with repetition.” Note that 0 ∈ ℕ is a natural number.

Theorem 4.3. For all r, s ∈ ℕ, we have

Proof: We imagine r + s points arranged in a horizontal row. From these, we choose s points and replace them by bars. By Theorem 4.2, there are possibilities for choosing the positions of the bars. Each such selection corresponds to one s-tuple (e1, . . . , es) ∈ℕs with

First, e1 points are chopped off by the first bar. After the first bar, e 2 points are chopped off by the second bar, and so on. The sth bar is followed by some remaining points in order to obtain a total of r points. This gives a bijection between the solutions of the inequality and the possible choices of points and bars.

□

For r = t − 1 and s = ℓ + 1, we have Therefore, the previous theorem yields

4.3 Growth of the least common multiple

We denote the least common multiple of the numbers 1, . . . , n by lcm(n). In the following, we derive a lower bound for the growth of lcm(n). The proof we present is based on an article by Nair [79].

Lemma 4.4. For all m, n ∈ ℕ with 1 ≤ m ≤ n, we have

Proof: We investigate the integral The evaluation is done in two different ways. First, we apply the binomial theorem to rewrite (1 − x)n−m as Then, we obtain

Thus, the evaluation of the integral yields

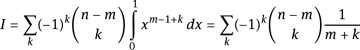
If we multiply I with lcm(n), then I ⋅ lcm(n) becomes an alternating sum of integers since The value of I being positive, we see that I ⋅ lcm(n) is in ℕ. By induction on n − m, we now show that For m = n, we have

Let now 1 ≤ m < n. We use partial integration ∫ uυ dx = uυ − ∫uυ' dx with and u' = xm−1 and with υ = (1 − x)n−m and υ' = −(n − m)(1 − x)n−m−1. Note that u(1) ⋅ υ(1) = u(0) ⋅ υ(0) = 0. Thus, we obtain

This shows and finally

□

Since is the largest binomial coefficient in the binomial expansion of 4n = we see that is greater than the average value 4n/(2n + 1). For n ≥ 3, in particular

By Lemma 4.4, this yields lcm We improve this estimate a little in the following theorem.

Theorem 4.5. For all n ≥ 7, we have lcm(n) > 2n.

Proof: Lemma 4.4 yields two divisors of lcm(2n + 1)

Since n and 2n + 1 are coprime, is a divisor of lcm(2n + 1). With Equation (4.2), we obtain Let n ≥ 4. Then

Therefore, 2n < lcm(n) for all n ≥ 9. The only remaining cases to investigate are n = 7 and n = 8. We directly compute 27 = 128 < 420 = lcm(7) and 28 = 256 < 840 = lcm(8).

□

4.4 Of small numbers and large orders

Let gcd(n, r) = 1. Then ordr(n) denotes the order of n in the multiplicative group (ℤ/rℤ)∗, that is

The following technical lemma states that, under certain assumptions, a small number r is guaranteed to exist such that ordr(n) is large with respect to r. For the rest of this section log, as usual, denotes the logarithm to base 2.

Lemma 4.6. Let m ≥ 2 and let n be a prime number with m2 log n < n. Then there exists a positive number r ≤ m2 log n satisfying ordr(n) > m.

Proof: Let s = ⌊m2 log n⌋. Since n is prime and n > s, the order ordr(n) is defined for all r with 1 ≤ r ≤ s. By contradiction, we assume that ordr(n) ≤ m for all such r. In particular, for each r ∈ {1, . . . , s} there exists i ∈ {1, . . . , m} such that ni ≡ 1 mod r. So r divides ni −1 and therefore also the product This implies that lcm(s) is a divisor of Since m ≥ 2, we have s ≥ 7. Using Theorem 4.5, we obtain

It follows and thus m ≤ 1, a contradiction.

□

Theorem 4.7. Let n ≥ 225 be a prime number. Then there exists r ∈ ℕ such that r ≤ log5 n and ordr(n) > log2 n.

Proof: For n ≥ 225 we have n > log5 n, and with m = ⌊log2 n⌋, by Lemma 4.6 there is a suitable number r satisfying r ≤ log5 n.

□

4.5 Agrawal–Kayal–Saxena primality test

The AKS primality test on input n ∈ ℕworks as follows.

Theorem 4.8. The AKS primality test is correct and it runs in polynomial time (in the input size log n).

The remainder of this section is devoted to the proof of Theorem 4.8. The number 225 is a constant and has no influence on the asymptotic runtime. For each exponent k ≤ log n it can be checked by binary search, whether a number m exists such that n = mk. In particular, the test, whether n = mk can be done in polynomial time. The values a, ℓ, r are bounded by log5 n. The Euclidean algorithm for testing whether gcd(a, n) = 1 has polynomial running time, and for each pair (a, r), the congruence

can be checked in polynomial time as well. For a prime number n, the AKS test outputs that n is prime. This follows from Lemma 4.1 and Theorem 4.7. It remains to show that the test is able to expose composite numbers. We therefore assume, to the contrary, that the AKS algorithm claims n to be prime, even though there exists a prime number p < n which divides n. Overall, we can make the following assumptions:

From these assumptions, we will derive a contradiction. Let be the splitting field of the polynomial f(X) = Xr −1 over p. Then, is a finite field extension of p, in which the polynomial f(X) splits into linear factors

with αi ∈ . Since f (X) = rXr−1 with r ≢ 0 mod p, we have f' (αi) ≠ 0 for all roots αi. Therefore, the roots are pairwise distinct by Proposition 1.49. Thus, the set

is a subgroup of order r which, according to Theorem 1.56, is cyclic. There are φ(r) possibilities for choosing a generator of U. Let

Since neither 0 nor 1 generate U and since ℓ ≤ φ(r), some generator α of U satisfies −α ≠ a for all a ∈ L. We fix α and we note that α + a ≠ 0 in ' for all a ∈ L. We have r < p since gcd(a, n) = 1 for all a ∈ {1, . . . , r}. Because of ℓ < r < p, we can consider L as a subset of p ⊆ .

Definition 4.9. We call a number m ∈ ℕ introspective for a polynomial g(X) ∈ p[X] if

Lemma 4.10. Let m1, m2 be introspective for g(X) ∈ p[X]. Then also m1m2 is introspective for g(X).

Proof: For β ∈ U, we also have βm1 ∈ U. This yields g(β)m1m2 = g(βm1 )m2 = g(βm1m2 ).

□

Lemma 4.11. The numbers and p are introspective for all polynomials (X + a) with a ∈ L.

Proof: The prime p is introspective for every polynomial g(X) ∈ p[X] because in characteristic p, the mapping x ↦ xp is an automorphism of fields. Thus, g(β)p = g(βp) for all β ∈ . It remains to show for all β ∈ U. Again, we take advantage of the fact that x ↦ xp is an automorphism of fields. Therefore, in , we obtain

By assumption, we have (X + a)n ≡ Xn + a mod (Xr − 1, n). This yields (X + a)n ≡ Xn + a mod (Xr − 1, p). Together with βr = 1, we conclude (β + a)n = βn + a in . This shows that is introspective.

□

Lemma 4.12. Let m be introspective for the polynomials g(X), h(X) ∈ p[X]. Then m is introspective for the polynomial (g ⋅ h)(X) = g(X) ⋅ h(X).

Proof: We have (g ⋅ h)(β)m = g(β)m ⋅ h(β)m = g(βm)⋅ h(βm) = (g ⋅ h)(βm).

□

Lemma 4.13. For all i, j ≥ 0, all a ∈ L andall ea ∈ ℕ, the number is introspective for the polynomial g(X) =Πa∈L(X + a)ea .

Proof: By Lemma 4.11 and Lemma 4.12, both and p are introspective for g(X). Lemma 4.10 shows that i and j can be chosen arbitrarily.

□

In the following, let

be the subgroup of (ℤ/rℤ)∗ generated by and p. Define t = |G| and observe that log2 n < ordr(n) ≤ t ≤ φ(r). Let P be the set of polynomials

Equation (4.1) shows Let

Then ⊆ ∗ because α + a ≠ 0 holds for all a ∈ L = {0, . . . , ℓ}. We give two different estimates for ||, and then show that they contradict each other.

Lemma 4.14. The mapping P → ∗ with g(X) ↦ g(α) is injective.

Proof: Let g1(X), g2(X) ∈ P with g1(α) = g2(α). Consider Then, we have

Thus, the polynomial g1(X) − g2(X) has at least the t roots αm with m ∈ G. On the other hand, the degree of g1(X) − g2(X) is less than t, so g1(X) = g2(X) and therefore the mapping g(X) ↦ g(α) is injective.

□

As a consequence of Lemma 4.14, we have We consider a set of introspective numbers Î ⊆ ℕ defined as follows:

At this point, we have to use the assumption that n has at least two prime divisors, thus ensuring that Î contains sufficiently many numbers. Since has a prime divisor different from p, the set Î contains exactly elements, and |Î| > t = |G|. The mapping Î → G: m ↦ (m mod r) thus cannot be injective, which means that there exist m1, m2 with 1 ≤ m1 < m2 and m1, m2 ∈ Î, such that m1 ≡ m2 mod r. We further remark that Now we show that all elements g(α) ∈ G are roots of the nontrivial polynomial Ym1 − Ym2. From αr = 1, we obtain αm1 = αm2. For g(α) ∈ G it follows that g(α)m1 − g(α)m2 = g(αm1) − g(αm2) = 0. As a consequence because the polynomial Ym1 − Ym2 has at most m2 roots. We obtain a contradiction by the following computation:

This proves the correctness of the AKS test and thus Theorem 4.8.

We now summarize the steps of the proof. The assumptions in our proof by contradiction lead us to a field and a choice of α ∈ . A principle used several times is the fact that in fields the zero polynomial is the only polynomial having more roots than indicated by the degree; in combinatorics, this argument is known as the polynomial method. Then, a set G of exponents is considered which applied to α lead to different elements αm from . Depending on |G|, we describe a set P of polynomials. For the set P, by construction, we know its cardinality. The set P is embedded into the multiplicative group of ' by evaluation at α. The subset of ' which corresponds to P is called and we obtain || = |P|. The next step shows that all elements of are roots of a polynomial of small degree. This yields a second estimate of which, however, contradicts the first.

Summary

Notions

Methods and results