Appendix A

Complex Numbers and Euler’s Formula

A.1 Introduction

Complex numbers allow us to solve equations for which no real solution can be found. Consider, for example, the equation

$$\begin{array}{lll}{x}^2+9=0\hfill & \hfill & \left(\text{A}.1\right)\hfill \end{array}$$

which cannot be satisfied for any real number. By introducing an imaginary unit1 $j=\sqrt{-1}$ so that j2 = −1, Eqn. (A.1) can be solved to yield

$$x=\mp j3$$

Similarly, the equation

$$\begin{array}{lll}{\left(x+2\right)}^2+9=0\hfill & \hfill & \left(\text{A}.2\right)\hfill \end{array}$$

has the solutions

$$\begin{array}{lll}x=-2\mp j3\hfill & \hfill & \left(\text{A}.3\right)\hfill \end{array}$$

A general complex number is in the form

$$\begin{array}{lll}x=a+jb\hfill & \hfill & \left(\text{A}.4\right)\hfill \end{array}$$

where a and b are real numbers. The values a and b are referred to as the real part and imaginary part of the complex number x respectively. Following notation is used for real and imaginary parts of a complex number:

$$\begin{array}{ll}a\hfill & =Re\left\{x\right\}\hfill \\ b\hfill & =Im\left\{x\right\}\hfill \end{array}$$

For two complex numbers to be equal, both their real parts and imaginary parts must be equal. Given two complex numbers x1 = a + jb and x2 = c + jd, the equality x1 = x2 implies that a = c and b = d.

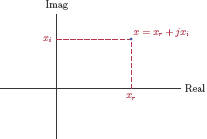
It is often convenient to graphically represent a complex number as a point in the complex plane constructed using a horizontal axis corresponding to the real part and a vertical axis corresponding to the imaginary part as depicted in Fig. A.1.

If the imaginary part of a complex number is equal to zero, the resulting number is said to be purely real. An example is x = 3 + j0. Similarly, a complex number the real part of which is equal to zero is said to be purely imaginary. An example of a purely imaginary number is x = 0 + j5. Purely real and purely imaginary numbers are simply special cases of the more general class of complex numbers.

Another method of graphical representation of a complex number can be found through the use of a vector as shown in Fig. A.2. Vector representation of complex numbers is quite useful since vector operations can be used for manipulating complex numbers.

A complex number written as the sum of its real and imaginary parts such as x = xr + jxi is said to be in Cartesian form. An alternative form referred to as a polar form is derived from the vector representation of a complex number by using the norm |x| and the angle θ of the vector instead of the real and imaginary parts xr and xi. The two forms of the complex number x are:

$$\begin{array}{lll}x\hfill & =x_r+j{x}_{i,}\hfill & \text{Cartesian form}\hfill \\ x\hfill & =\left|x\right|e^{j\theta },\hfill & \text{polar form}\hfill \end{array}$$

The norm |x| is the distance of the point representing the complex number from the origin. The angle θ is the angle measured counterclockwise starting with the positive real axis.

A complex number can easily be converted from Cartesian form to polar form and vice versa. Through simple geometric relationships it can be shown that

$$\begin{array}{lll}\left|x\right|=\sqrt{x_r^2+x_i^2}\hfill & \hfill & \left(\text{A}.5\right)\hfill \end{array}$$

and

$$\begin{array}{lll}\theta ={tan}^{-1}\left(\frac{x_i}{x_r}\right)\hfill & \hfill & \left(\text{A}.6\right)\hfill \end{array}$$

Alternately, real and imaginary parts can be obtained from the norm and the angle through

$$\begin{array}{lll}{x}_r=\left|x\right|cos\left(\theta \right)\hfill & \hfill & \left(\text{A}\text{.7}\right)\hfill \end{array}$$

and

$$\begin{array}{lll}{x}_i=\left|x\right|sin\left(\theta \right)\hfill & \hfill & \left(\text{A}\text{.8}\right)\hfill \end{array}$$

A.2 Arithmetic with Complex Numbers

Definitions of arithmetic operators are easily extended to apply to complex numbers. In Section A.2.1 addition and subtraction operators will be discussed. Multiplication and division of complex numbers will be discussed in Section A.2.2.

A.2.1 Addition and subtraction

Consider two complex numbers x1 = a + jb and x2 = c + jd. Addition of these two complex numbers is carried out as follows:

$$\begin{array}{llll}y\hfill & =x_1+x_2\hfill & \hfill & \hfill \\ \hfill & =\left(a+jb\right)+\left(c+jd\right)\hfill & \hfill & \hfill \\ \hfill & =\left(a+c\right)+j\left(b+d\right)\hfill & \hfill & \left(\text{A}\text{.9}\right)\hfill \end{array}$$

Real and imaginary parts of the result can be written separately as

$$\begin{array}{lll}Re\left\{y\right\}\hfill & =\hfill & Re\left\{x_1\right\}+Re\left\{x_2\right\}\hfill \\ Im\left\{y\right\}\hfill & =\hfill & Im\left\{x_1\right\}+Im\left\{x_2\right\}\hfill \end{array}$$

Subtraction of complex numbers is similar to addition. The difference z = x1 − x2 is computed as follows:

$$\begin{array}{llll}z\hfill & =x_1=x_2\hfill & \hfill & \hfill \\ \hfill & =\left(a+jb\right)-\left(c+jd\right)\hfill & \hfill & \hfill \\ \hfill & =\left(a-c\right)+j\left(b-d\right)\hfill & \hfill & \left(\text{A}.10\right)\hfill \end{array}$$

Real and imaginary parts of the result can be written separately as

$$\begin{array}{lll}Re\left\{z\right\}\hfill & =\hfill & Re\left\{x_1\right\}-Re\left\{x_2\right\}\hfill \\ Im\left\{z\right\}\hfill & =\hfill & Im\left\{x_1\right\}-Im\left\{x_2\right\}\hfill \end{array}$$

Addition and subtraction operators for complex numbers are analogous for addition and subtraction of vectors using the parallelogram rule. This is illustrated in Fig. A.3.

If the complex numbers to be added are expressed in polar form, they must first be converted to Cartesian form before they can be added. Consider two complex numbers in polar form given as

$$\begin{array}{lllll}{x}_1=\left|x_1\right|e^{j\theta 1},\hfill & \text{and}\hfill & x_2=\left|x_2\right|e^{j\theta 2}\hfill & \hfill & \left(\text{A}.11\right)\hfill \end{array}$$

The sum z of these complex numbers is found as

$$\begin{array}{llll}z\hfill & =x_1+x_2\hfill & \hfill & \hfill \\ \hfill & =\left|x_1\right|cos({\theta }_1)+j\left|x_1\right|sin({\theta }_1)+\left|x_2\right|cos({\theta }_2)+j\left|x_2\right|sin({\theta }_2)\hfill & \hfill & \hfill \\ \hfill & =[|x_1|cos({\theta }_1)+|x_2|cos({\theta }_2)]+j[|x_1|sin({\theta }_1)+|x_2|sin({\theta }_2)]\hfill & \hfill & (A.12)\hfill \end{array}$$

which can be put into polar form as

$$\begin{array}{lll}z=\left|z\right|e^{j\theta z}\hfill & \hfill & \left(\text{A}.13\right)\hfill \end{array}$$

where

$$\begin{array}{lll}\left|z\right|=|x_1{|}^2+|x_2{|}^2+2\left|x_1\right|\left|x_2\right|cos({\theta }_1-{\theta }_2)\hfill & \hfill & (A.14)\hfill \end{array}$$

and

$$\begin{array}{lll}{\theta }_z={tan}^{-1}(\frac{\left|x_1\right|sin({\theta }_1)+\left|x_2\right|sin({\theta }_2)}{\left|x_1\right|cos({\theta }_1)+\left|x_2\right|cos({\theta }_2)})\hfill & \hfill & (A.15)\hfill \end{array}$$

A.2.2 Multiplication and division

Again consider two complex numbers x1 = a + jb and x2 = c + jd. The product of these two complex numbers is computed as follows:

$$\begin{array}{llll}y\hfill & =x_1{x}_2\hfill & \hfill & \hfill \\ \hfill & =\left(a+jb\right)\left(c+jd\right)\hfill & \hfill & \hfill \\ \hfill & =ac+jad+jbc+j^{2}bd\hfill & \hfill & \hfill \\ \hfill & =\left(ac-bd\right)+j\left(ad+bc\right)\hfill & \hfill & \left(\text{A}.16\right)\hfill \end{array}$$

Real and imaginary parts of the result can be written separately as

$$\begin{array}{lll}Re\left\{y\right\}\hfill & =\hfill & Re\left\{x_1\right\}-Re\left\{x_2\right\}-Im\left\{x_1\right\}Im\left\{x_2\right\}\hfill \\ Im\left\{y\right\}\hfill & =\hfill & Re\left\{x_1\right\}-Im\left\{x_2\right\}+Im\left\{x_1\right\}Re\left\{x_2\right\}\hfill \end{array}$$

Product of a complex number and its own complex conjugate is equal to the squared norm of the complex number:

$$\begin{array}{ll}{x}_1{x}_1^{*}\hfill & =\left(a+jb\right){\left(a+jb\right)}^{*}\hfill \\ \hfill & =\left(a+jb\right)\left(a-jb\right)\hfill \\ \hfill & =a^2+b^2={\left|x_1\right|}^2\hfill \end{array}$$

Division of complex numbers is slightly more involved. Consider the complex number z defined as

$$\begin{array}{lll}z=\frac{x_1}{x_2}=\frac{\left(a+jb\right)}{\left(c+jd\right)}\hfill & \hfill & \left(\text{A}.17\right)\hfill \end{array}$$

The expression in Eqn. (A.17) can be simplified by multiplying both the numerator and the denominator by the complex conjugate of the denominator:

$$\begin{array}{lll}z=\frac{x_1}{x_2}=\frac{\left(a+jb\right)}{\left(c+jd\right)}\frac{\left(c-jd\right)}{\left(c-jd\right)}\hfill & \hfill & \left(\text{A}.18\right)\hfill \end{array}$$

A.3 Euler’s Formula

A complex exponential function can be expressed in the form

$$\begin{array}{lll}{e}^{jx}=cos(x) + j sin(x)\hfill & \hfill & (A.19)\hfill \end{array}$$

This relationship is known as Euler’s formula, and will be used extensively in working with signals, linear systems and various transforms. If the sign of x changes in Eqn. (A.20), we get

$$\begin{array}{lll}{e}^{-jx}=cos (-x) + j sin (-x)=cos (x)-j sin (x)\hfill & \hfill & (\text{A}.20)\hfill \end{array}$$

Using Eqns. (A.19) and (A.2), trigonometric functions cos (x) and sin (x) may be expressed in terms of complex exponential functions as

$$\begin{array}{lll}cos(x)=\frac{e^{jx}+e^{-jx}}{2}\hfill & \hfill & (\text{A}.21)\hfill \end{array}$$

and

$$\begin{array}{lll}sin(x)=\frac{e^{jx}-e^{-jx}}{2j}\hfill & \hfill & (\text{A}.22)\hfill \end{array}$$

1 The imaginary unit was first introduced by Italian mathematician Gerolamo Cardano as he worked on the solutions of cubic and quartic equations, although its utility was not fully understood and appreciated until the works of Leonhard Euler and Carl Friedrich Gauss almost two centuries later.