CHAPTER
15

Hypothesis Testing with One Population

In This Chapter

• Formulating the null and alternative hypotheses
• Distinguishing between a one-tail and two-tail hypothesis test
• Testing the mean of a population when the population standard deviation is known and when it is unknown
• Examining the role of alpha (α) in hypothesis testing
• Using the p-value to test a hypothesis
• Testing the proportion of a population using a large sample

Now that we know how to make an estimate of a population parameter, such as a mean, using a sample and a confidence interval, let’s move on to the heart and soul of inferential statistics: hypothesis testing.

One thing statisticians like to do is to make a statement about a population parameter, collect a sample from that population, measure the sample, and declare, in a scholarly manner, whether or not the sample supports the original statement. This, in a nutshell, is what hypothesis testing is all about. Of course, I’ve included a few juicy details. Without them, this would be one short chapter!

In this chapter, we will introduce you to the concept of hypothesis testing and apply it to hypothesis testing that involves only one population.

Hypothesis testing involving one population focuses on confirming claims such as the population average is equal to a specific value. We will consider many different cases with this type of hypothesis test in the following sections. This chapter relies on some of the concepts we explored in Chapter 14, so be sure you are comfortable with that material before you dive into this chapter.

Hypothesis Testing: The Traditional Method

In the statistical world, a hypothesis is an assumption about a population parameter, such as the population mean or the population proportion. Examples of hypotheses (that’s plural for hypothesis) include the following:

• The average adult drinks 3.1 cups of coffee per day.
• The average student debt for a college graduate for the class of 2015 was $35,051 (the highest in U.S. history).
• According to the Department of Transportation, the average age of passenger cars on the road in the United States in 2014 was 11.4 years.

In each case, we have made a statement about the population that may or may not be true. The purpose of hypothesis testing is to use sample information and make a statistical conclusion about rejecting or not rejecting such statements. Let’s see how to do that!

Procedures for Hypothesis Testing

A study by Sallie Mae released in April 2009 showed that the average credit card debt for graduating college seniors in 2008 was $4,100. The president of our college believes that our graduating seniors don’t owe $4,100 on their credit cards so he asked me to check this for him. How would I go about doing this? I use a sample of our students and get their average credit card debt. Suppose that the sample average is $3,900. Hypothesis testing will then tell me whether or not $3,900 is significantly different from $4,100, or if the difference is merely due to chance. So how do we do hypothesis testing?

There are five steps that we need to complete for hypothesis testing:

1. State the null and alternative hypotheses.

2. Determine the level of significance.

3. Calculate the test statistic.

4. Determine the critical value(s).

5. State your decision or finding.

So let’s look at each one of these in detail.

1. The Null and Alternative Hypotheses

Every hypothesis test has both a null hypothesis and an alternative hypothesis. The null hypothesis, denoted by H₀, represents the status quo and involves stating the belief that the mean of the population is ≤, =, or ≥ a specific value. The null hypothesis is believed to be true unless there is overwhelming evidence to the contrary. The null hypothesis is the one to be rejected or not rejected. In our example, the null hypothesis would be stated as:

H₀:μ = $4,100

The alternative hypothesis, denoted by H₁, represents the opposite of the null hypothesis and holds true if the null hypothesis is found to be false. The alternative hypothesis always states the mean of the population is <, ≠, or > a specific value. In our example, the alternative hypothesis would be stated as:

H₀ : μ ≠ $4,100

The following table shows the three combinations of the null and alternative hypotheses.

Null Hypothesis	Alternative Hypothesis
H0 : μ = $4,100	H1 : μ ≠ $4,100
H0 : μ ≥ $4,100	H1 : μ < $4,100
H0 : μ ≤ $4,100	H1 : μ > $4,100

When do you use each hypothesis? Good question. This depends on whether you are doing a two-tail or a one-tail test as explained in a following section.

2. The Level of Significance

Remember that the purpose of hypothesis testing is to verify the validity of a claim about a population based on a single sample. Because we are relying on a sample, we expose ourselves to the risk that our conclusions about the population could be wrong because of sampling error.

In our college seniors’ credit card debt example, suppose that we reject H₀. That is, according to the sample, the average credit card debt for our college seniors isn’t $4,100. But what if the true population mean actually is $4,100? In other words, what if our seniors have $4,100 credit card debt but the sample we chose is not fully representative of the population? This can occur primarily because of sampling error, which we discussed in Chapter 12. This type of error, rejecting H₀ when it’s actually true, is known as a Type I error. The probability of making a Type I error is known as α, the level of significance, which we introduced in Chapter 14.

We can also have another type of error with hypothesis testing. Let’s say in our seniors’ credit card debt example, we don’t reject H₀. That is, according to the sample, our college seniors’ credit card debt is $4,100. But what if the true population mean is actually not $4,100? This type of error, when we do not reject H₀ when in reality it’s false, is known as a Type II error. The probability of making a Type II error is known as β.

The following table summarizes the two types of hypothesis errors.

	H0 Is True	H0 Is False
Reject H0	Type I Error P(Type I Error)= α	Correct Decision
Do Not Reject H0	Correct Decision	Type II Error P(Type II Error) = β

Normally, with hypothesis testing, we decide on a value for a that is somewhere between 0.01 and 0.10 before we collect the sample. The value of β can then be calculated, but that topic goes beyond the scope of this book. Be grateful for this because that concept is very complicated!

3. The Test Statistic

Using the information from the sample, we are going to calculate a test statistic that we will use to determine whether to reject or not reject H₀. To calculate the z-test statistic, we use the following formula:

As we will see later in the chapter, we use the z-test statistic formula if σ is known. If σ is not known, we use the t-test statistic.

4. The Critical Value

The critical value divides the area under the normal distribution curve into two regions: the area where we don’t reject H₀ and the area(s) where we reject H₀. We get the critical value from the table, and it differs according to whether we are doing a two-tail or a one-tail test.

I know you might be asking how I get this critical value. It’s very simple! Let me explain.

Two-tail test:

If we choose α = 0.05 and because this is a two-tail test, this area needs to be evenly divided between both tails, with each tail receiving α/2 (0.05/2 = 0.025). According to Figure 15.1, we need to find the critical z-value that corresponds to the area 0.025. Using Table 3 in Appendix B, we look inside the body of the table for the closest value to 0.025. We can find this value by looking across row -1.9 and down column 0.06 to arrive at a critical value of -1.96 for the left tail. How about the right tail? Yes, you don’t need to look it up–it is +1.96 since the normal distribution curve is symmetrical.

Figure 15.1

Critical value for z for a two-tail test for α = 0.05.

One-tail test:

If we have a one-tail test, we will have only one area of rejection, not two. If it is a right tail test, then the area of rejection will be in the right tail, and if we have a left tail test, the area of rejection will be in the left tail. Let’s see how to get the critical value for each one.

If we choose α = 0.01 and use a right tail test, then we will need to determine the critical z-value that corresponds. Because this is a one-tail test, this entire area needs to be in one rejection region in the right side of the distribution. As Figure 15.2 shows, we need to find the z-value that corresponds to the area 0.99 or 1 – α.

Figure 15.2

Critical value for z for a one-tail test for α = 0.01.

Using Table 3 in Appendix B, we look inside the body of the table for the closest value to 0.9900, which results in a critical z-value of 2.33.

For the left tail test, the rejection area will be to the left, and the critical value will be -2.33 instead of +2.33.

5. State Your Decision

Now compare the calculated z-test (or t-test) statistic to the critical value and make your decision as follows:

• If the calculated z-test statistic falls within the white region, we do not reject H₀. That is, we do not have enough evidence to support H₁, the alternative hypothesis, which states that the population mean is not equal to $4,100.
• If the calculated z-test statistic falls in either shaded region, otherwise known as the rejection region, we reject H₀. That is, we have enough evidence to support H₁, which results in our belief that the true population mean is not equal to $4,100.

Because our conclusions are based on a sample, we will never have enough evidence to accept the null hypothesis. It’s a much safer statement to say that we do not have enough evidence to reject H₀. We can use the analogy of the legal system to explain. The jury’s decision is that the defendant is “guilty” or “not guilty.” If a jury finds a defendant “not guilty,” they are not saying the defendant is innocent. Rather, they are saying that there is not enough evidence to prove guilt.

One-Tail vs. Two-Tail Tests

When testing our hypotheses, we can perform either a one-tail test or a two-tail test. Let’s see what each one is and when to use each.

Two-Tail Hypothesis Testing

A two-tail hypothesis test is used whenever the alternative hypothesis is expressed as ≠. As in our seniors’ credit card debt example, the null and alternative hypotheses are stated as:

H₀ : μ = $4,100

H₁ : μ ≠ $4,100

For a two-tail test, we have two areas of rejection: one in the right tail and one in the left tail as in Figure 15.3. Since the z-critical values are used a lot, I’m going to list them for you so they’re handy whenever you need them:

a = 0.01 ⇒ z critical value = ±2.58

a = 0.05 ⇒ z critical value = ±1.96

a = 0.10 ⇒ z critical value = ±1.65

Figure 15.3

Two-tail hypothesis test.

Because there are two rejection regions in this figure, we have a two-tail hypothesis test. If the calculated test statistic falls in either tail (the rejection regions), then we reject the null hypothesis.

One-Tail Hypothesis Testing

A one-tail hypothesis test involves the alternative hypothesis being stated as < or >. Let’s say that our president believes that our seniors have less credit card debt than the national average of $4,100. To test this, we’ll use a left tail test. The null and alternative hypotheses are stated as:

H₀ : μ ≥ $4,100

H₁ : μ < $4,100

For a one-tail test, we have only one area of rejection. In this case, it is in the left tail of the distribution, which is the shaded area in Figure 15.4. The critical z-values in this case are:

a = 0.01 ⇒ z critical value = -2.33

a = 0.05 ⇒ z critical value = -1.65

a = 0.10 ⇒ z critical value = -1.28

Figure 15.4

One-tail hypothesis test.

Since we have just one rejection region in the left tail of the distribution, if the calculated test statistic falls within this rejection region, then we reject the null hypothesis.

Now, let’s say our president believes that our seniors have more credit card debt than the national average of $4,100. To test this, we’ll use a right tail test. The null and alternative hypotheses are stated as:

H₀ : μ ≤ $4,100.

H1 : μ > $4,100.

The rejection area in this case is in the right tail of the distribution, which is the shaded area in Figure 15.5. The critical z-values in this case are:

a = 0.01 ⇒ z critical value = +2.33

a = 0.05 ⇒ z critical value = +1.65

a = 0.10 ⇒ z critical value = +1.28

Figure 15.5

One-tail hypothesis test.

As with the previous cases, if the calculated test statistic falls within this rejection region, then we reject the null hypothesis.

You need to be careful how you state the null and alternative hypotheses. Your choice will depend on the nature of the test and the motivation of the person conducting it.

If the purpose is to test that the population mean is equal to a specific value, such as our seniors’ credit card debt example, assign this statement as the null hypothesis, which results in the following:

H₀ : μ = $4,100

H₁ : μ ≠ $4,100

Often hypothesis testing is performed by researchers who want to prove that their discovery is an improvement over current products or procedures. For example, if Bob invented a golf ball that he claimed would increase your distance off the tee by more than 20 yards, then we would set up the hypotheses as follows:

H₀ : μ ≤ 20 yards

H₁ : μ > 20 yards

Note that we used the alternative hypothesis to represent the claim that we want to prove statistically so that Bob can make a fortune selling these balls to desperate golfers. Because of this, the alternative hypothesis is also known as the research hypothesis because it represents the position that the researcher wants to establish.

Let’s put these concepts to work now and do some hypothesis testing!

Hypothesis Testing for the Population Mean

We’ll start with the case when σ, the population standard deviation, is known and then move on to the case when σ is unknown.

To demonstrate this type of hypothesis testing, let’s apply it to our college seniors’ credit card debt example. We start by setting up our hypotheses as follows:

H₀ : μ = $4,100

H₁ : μ ≠ $4,100

We sample 60 seniors in our college and find that their average credit card debt is $3,900. We’ll say that σ, the population standard deviation, is $1,200, and we’ll test the hypothesis at α = 0.05.

Because the sample size is greater than 30 and we know the value of σ, we calculate the z-test statistic as follows:

For a two-tail test α = 0.05, the critical value = ± 1.96 (shown in Figure 15.6).

Figure 15.6

A two-tail hypothesis test for the college seniors’ credit card debt example.

As you can see in the figure, the calculated z-test statistic of –1.29 falls within the “Don’t Reject H₀” region, which allows us to conclude that the average college senior’s credit card debt in our college is not significantly different from the national average of $4,100.

When Sigma Is Unknown and Using a Large Sample

Many times, we just don’t have enough information to know the value of σ, the population standard deviation. However, as long as our sample size is 30 or more, we can substitute s, the sample standard deviation, for σ. In this case, the only difference will be the calculated z-test statistic in step 3. We will use the following test statistic:

To illustrate this technique, let’s use the following example.

I don’t know about you, but it seems I spend too much time on the phone waiting on hold for a live customer service representative. Let’s say a particular company has claimed that the average time a customer waits on hold is less than five minutes. We’ll assume we do not know the value of σ. The following table represents the wait time in minutes for a random sample of 30 customers.

Using Excel, we can determine that = 4.74 minutes and s = 1.82 minutes. At first glance, it appears the company’s claim is valid. But let’s put it through a hypothesis test with α = 0.01 to be sure.

State the hypothesis as:

H₀ : μ ≥ 5.0 minutes

H₁ : μ < 5.0 minutes

Now, we need to calculate the z-test statistic:

This is a one-tail (left side) hypothesis test with α = 0.01, so the critical value is -2.33. Figure 15.7 shows this test graphically.

According to our figure, we do not reject the null hypothesis. In other words, we do not have enough evidence from this sample to support the company’s claim that the average wait on hold is less than five minutes. Even though the sample average is actually less than five minutes (4.74), it’s too close to five minutes to say there’s a difference between the two values. Another way to state this is to say: “The difference between 4.74 and 5.0 is not statistically significant in this case.”

Figure 15.7

A one-tail hypothesis test for the waiting on hold example.

When Sigma Is Unknown and Using a Small Sample

As we did in Chapter 14, when σ is unknown for a small sample size taken from a normally distributed population, we use the Student’s t-distribution. In this case, both steps 3 and 4 will be slightly altered. In step 3, the calculated t-test statistic will be:

In step 4, we get the critical value(s) using the t-distribution instead of the z-distribution.

Let’s illustrate this with an example. According to the National Association of Colleges and Employers (NACE) September 2014 Salary report, the average starting salary for 2014 college graduates is $48,707. The president of our college believes that our graduates earn more than this, so he asks me to check it for him. I chose a sample of 20 students of our 2014 graduates and found that the average starting salary is $50,230 and the standard deviation of this sample is $5,100. Using this information, I can test the claim with the following hypotheses:

H₀ : μ ≤ $48,707

H₁ : μ > $48,707

We can then determine the calculated t-test statistic using the following equation:

We’ll test this hypothesis using α = 0.05. To find the corresponding critical t-value, we use Table 4 from Appendix B. Here is an excerpt of this table.

If you recall from Chapter 14, we need to determine the degrees of freedom, which is equal to n – 1 = 20 – 1 = 19 for this example. Because this is a one-tail (right side) test, we look under the one tail α row and the α = 0.05 column resulting in a critical t-value equal to +1.729, which is underlined. Figure 15.8 shows this test graphically.

Figure 15.8

Hypothesis test for the average starting salary for college graduates when α = 0.05.

As we can see in the previous figure, the calculated t-test statistic of 1.34 falls within the white “Don’t Reject H₀” region. Therefore, we don’t reject H₀ and we conclude that the starting salary for our college graduates is not higher than the national average. Sorry, Mr. President. I could not support your claim!

Let’s look at another example to demonstrate a two-tail hypothesis test using the t-distribution. I would like to test a claim that the average speed of cars passing a specific spot on the interstate is 65 miles per hour. We can express the hypothesis test as follows:

H₀ : μ = 65 miles per hour

H₁ : μ ≠ 65 miles per hour

We will assume that we do not know σ and that the speeds follow a normal distribution. The following represents a random sample of the speed of seven cars.

Car Speeds:

62        74        65        68        71        64        68

Using Excel, we can determine that mph and s = 4.16 mph for this sample. We can then determine the calculated t-test statistic as follows:

We’ll test this hypothesis using α = 0.05. To find the corresponding critical t-value, we use Table 4 from Appendix B. The degrees of freedom for this example equals n – 1 = 7 – 1 = 6. Looking at the excerpt of the previous t-table, we can get the critical value. Because this is a two-tail test, we look under the two-tail α row and the α = 0.05 column resulting in a critical t-value equal to ±2.447. This test is shown graphically in Figure 15.9.

Figure 15.9

Hypothesis test for the car speed example.

As we can see in the previous figure, the calculated t-test statistic of +1.21 falls within the “Do Not Reject H₀” region, so we don’t reject H₀. Therefore, there’s not enough evidence to conclude that the average speed isn’t 65 miles per hour.

The Role of Alpha in Hypothesis Testing

For all the examples in this chapter, we have just stated a value for α, the level of significance. You’re probably wondering what impact changing the value of α will have on the hypothesis test. Great question!

In our starting salary for college graduates example, we used α = 0.05. Now, if I want to support our college president’s claim, it would be in my best interest if I could reject H₀, which would validate his claim. I can do so by choosing a fairly high value for α, say 0.10. In our example, looking at the previous excerpt of the t-distribution and for degrees of freedom = 19, this corresponds to a critical t-value of +1.328 (we are using the right tail of a one-tail hypothesis test). My calculated t-test statistic of +1.34 falls in the “Reject H₀” region, so we reject H₀. This test is shown graphically in Figure 15.10. This means that we can now support our college president’s claim that our college graduates’ starting salary is higher than the national average.

Figure 15.10

The hypothesis test for the average starting salary for college graduates when α = 0.10.

However, I must admit I chose a pretty “wimpy” value of α = 0.10 in an effort to help prove his claim. In this case, I am willing to accept a 10 percent chance of a Type I error. In general, a hypothesis test that rejects H₀ is most impressive with a low value of α.

The p-Value Method

Just when you thought it was safe to get back in the water, along comes another shark! This is the perfect opportunity to throw another concept at you. You might feel like grumbling a little right now, but in the end you’ll be thanking us.

The p-value is the smallest level of significance at which the null hypothesis will be rejected, assuming the null hypothesis is true. The p-value is sometimes referred to as the observed level of significance. I know this may sound like a lot of mumbo-jumbo right now, but an illustration will help make this clear.

The p-Value for a One-Tail Test

Using the previous example of the average credit card debt for college seniors, let’s say I want to test whether our college seniors owe less than the national average. Our hypotheses are as follows:

H₀ : μ ≥ $4,100

H₁ : μ < $4,100

The calculated z-test statistic is -1.29 as before. To get the p-value, we need to get the P(z<-1.29), so we look in the standardized normal z table for z = -1.29. This gives me 0.0985. This is the p-value! Yes, it’s that easy. This is shown in Figure 15.11.

Figure 15.11

The p-value for the college seniors’ credit card debt example.

Because our p-value of 0.0985 is more than the value of α (set at 0.05), we do not reject H₀. Most statistical software packages (including Excel) provide p-values with the analysis.

Another way to describe this p-value is to say, in a very scholarly voice, “Our results are significant at the 0.0985 level.” This means that as long as the value of α is 0.0985 or larger, we will reject H₀, which is normally good news for researchers trying to validate their findings.

Calculating the p-value for a two-tail hypothesis test is slightly different, and I’ll show you how in the next section.

The p-Value for a Two-Tail Test

Recall that you use a two-tail hypothesis test when the null hypothesis is stated as an equality. For example, let’s test a claim that states the average number of miles driven by a passenger vehicle in a year equals 11,500 miles. Bob had serious reservations about this claim after spending half the day being a taxi driver to his kids. We would state the hypotheses as follows:

H₀ : μ = 11,500 miles

H₁ : μ ≠ 11,500 miles

Let’s assume σ = 3,000 miles, and we want to set α = 0.05. We sample 80 drivers and determine the average number of miles driven is 11,900. What is our p-value, and what do we conclude about the hypothesis?

We can get the calculated z-test statistic as follows:

The shaded area in Figure 15.12 shows the p-value for this test.

According to Table 3 in Appendix B, the P(z ≤ + 1.19) = 0.8830. This means the shaded region in the right tail of Figure 15.12 is P(z > + 1.19) = 1 – 0.8830 = 0.117. Because this is a two-tail test, we need to double this area to arrive at our p-value. According to our figure, the p-value is the total area of both shaded regions, which is 2 × 0.117 = 0.234. Because the p-value > α, we do not reject the null hypothesis. Our data supports the claim that the average number of miles driven per year by a passenger vehicle is 11,500.

Figure 15.12

The p-value for the miles driven per year example.

In general, the smaller the p-value, the more confident we are about rejecting the null hypothesis. In most cases a researcher is attempting to find support for the alternative hypothesis. A low p-value provides support that brings joy to his or her heart.

Using Excel for Hypothesis Testing

We can generate the p-value using Excel functions. For a z-distribution, we use Excel’s NORM.S.DIST function and for a t-distribution, we use Excel’s T.DIST or T.DIST.RT or T.DIST.2T functions. Let’s see examples for each one of them.

Using Excel’s NORM.S.DIST Function

Use Excel’s NORM.S.DIST function to find the p-value when you are using the z-distribution. The function has the following characteristics:

NORM.S.DIST(z, cumulative)

where:

z = the calculated z-test statistic

cumulative = TRUE, to get the area to the left of the z-value

For instance, we would use this function in the previous example of the average credit card debt for college seniors with the following hypotheses:

H₀ : μ ≥ $4,100

H₁ : μ < $4,100

The calculated z-test statistic is -1.29 as before. Figure 15.13 shows the NORM.S.DIST function being used to determine the p-value for this example, which is a one-tail test. As you can see from the figure, the Excel function gives us a p-value of 0.0985. This is the same value we obtained when we used the table.

Figure 15.13

Excel’s NORM.S.DIST function for a one-tail test.

Using Excel’s T.DIST, T.DIST.RT, and T.DIST.2T Functions

Use these functions to find the p-value when you are using the t-distribution. Excel’s T.DIST function gives you the area to the left of the t-value, while Excel’s T.DIST.RT function gives you the area to the right of the t-value. For two-tail testing, use Excel’s T.DIST.2T function.

Excel’s T.DIST functions have the following characteristics:

T.DIST(x,degrees_of_freedom)

where:

x = the calculated t-test statistic

For instance, we would use the T.DIST.RT function in the previous example of our graduates’ average starting salary with the following hypotheses:

H₀ : μ ≤ $48,707

H₁ : μ > $48,707

Figure 15.14 shows the T.DIST.RT function being used to determine the p-value for this example where t = 1.34, which is a right tail test.

For a two-tail test, we would use the T.DIST.2T function, like in the previous example of the average speed of cars with the following hypotheses:

H₀ : μ = 65 miles per hour

H₁ : μ ≠ 65 miles per hour

Figure 15.15 shows the T.DIST.2T function being used to determine the p-value for this example where t = 1.21, which is a two-tail test.

Using Excel’s T.INV and T.INV.2T Functions

We can also use Excel to get the critical t-value using Excel’s T.INV and T.INV.2T functions. Excel’s T.INV functions have the following characteristics:

T.INV(probability,deg_freedom)

Where:

probability = the probability associated with the Student’s t-distribution

For instance, Figure 15.16 shows the T.INV.2T function being used to determine the critical t-value for α = 0.05 and d.f. = 6 from our average speed of cars example, which is a two-tail test. It has the following hypotheses:

H₀ : μ = 65 miles per hour

H₁ : μ ≠ 65 miles per hour

Figure 15.16

Excel’s T.INV.2T function for a two-tail test.

As you can see from the figure, the Excel function =T.INV.2T(0.05, 6) gives us a critical value of 2.447. This is the same value we obtained from the table in our previous average speed of cars example.

Excel’s T.INV function gives the critical t-value for a left-side test. Figure 15.17 shows the T.INV function being used to determine the critical t-value for α = 0.01 and d.f. = 24 for a left tail test.

Figure 15.17

Excel’s T.INV function for a left tail test.

The critical t-value is the same for a right-tail test, except positive instead of negative.

np ≥ 5 and nq ≥ 5

where:

p = the probability of a success in the population

q = the probability of a failure in the population (q = 1 – p)

We will examine both one-tail and two-tail hypothesis testing for the proportion in the following sections.

One-Tail Hypothesis Test for the Proportion

Let’s say we would like to test the hypothesis that more than 30 percent of U.S. households have wireless internet access. We would state the hypotheses as:

H₀ : p ≤ 0.30

H₁ : p > 0.30

Where:

p = the proportion of U.S. households with wireless internet access.

We collect a sample of 150 households and find that 57 of them have wireless internet access. What can we conclude at the α = 0.05 level?

Our first step is to calculate σ_p, the standard error of the proportion, which was described in Chapter 13 using the following equation:

where p = the population proportion, which is the one assumed by the null hypothesis. For our example:

= 0.037

We need to determine the sample proportion , as follows:

Next, we can determine the calculated z-test statistic using:

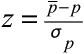
For our example:

The critical z-value for a one-tail test with α = 0.05 is +1.65. This hypothesis test is shown graphically in Figure 15.18.

Figure 15.18

Hypothesis test for the wireless internet access example.

As you can see in Figure 15.18, the calculated z-test statistic of +2.16 is within the “Reject H₀” region. Therefore, we conclude that the proportion of U.S. households with wireless internet access exceeds 30 percent.

We can also get the p-value for this test using our standardized normal z table (Table 3 in Appendix B) as follows:

P(z > + 2.16) = 1 – P(z ≤ + 2.16) = 1 – 0.9846 = 0.0154

Therefore, our results are significant at the 0.0154 level. As long as α = 0.0154, we will be able to reject H₀.

Two-Tail Hypothesis Test for the Proportion

We’ll wrap this chapter up with one final two-tail example. Here, we want to test a hypothesis for a company that claims 50 percent of their customers are male. We state our hypotheses as:

H₀ : p = 0.50

H₁ : p ≠ 0.50

We randomly select 256 customers and find that 47 percent are male. What can we conclude at the α = 0.05 level?

We need to determine σ_p, the standard error of the proportion:

= 0.0312

Next, we can determine the calculated z-test statistic:

= -0.96

The critical z-value for a two-tail test with α = 0.05 is ±1.96. This hypothesis test is shown graphically in Figure 15.19.

As you can see in Figure 15.19, the calculated z-test statistic of -0.96 is within the “Do Not Reject H₀” region. Therefore, we conclude that the proportion of male customers is not significantly different from 50 percent for this company.

We can also calculate the p-value for this test using our standardized normal z table (Table 3 in Appendix B) as follows:

P(z ≤ -0.96) = 0.1685

Because this is a two-tail test, the p-value would be 2 × 0.1685 = 0.337. Since the p-value is greater than α, we don’t reject H₀.

Figure 15.19

Hypothesis test for the percentage of males example.

Practice Problems

1. Formulate a hypothesis statement for the following claim: “The average age of our customers is less than 40 years old.” A sample of 50 customers had an average age of 38.7 years. Assume the population standard deviation is 12.5 years. Using α = 0.05, test your hypothesis. What is your conclusion?

2. Formulate a hypothesis statement for the following claim: “The average life of our light bulbs is more than 1,000 hours.” A sample of 32 light bulbs had an average life of 1,190 hours. Assume the population standard deviation is 325 hours. Using α = 0.02, test your hypothesis. What is your conclusion?

3. Formulate a hypothesis statement for the following claim: “The average delivery time is less than 30 minutes.” A sample of 42 deliveries had an average time of 26.9 minutes. Assume the population standard deviation is 8 minutes. Using α = 0.01, test your hypothesis. What is your conclusion?

4. Formulate a hypothesis statement for the following claim: “Students graduating from college have an average student loan debt of $32,700.” A sample of 40 college graduates averaged $32,450 in student loan debt. Assume the population standard deviation is $950. Using α = 0.05, test your hypothesis. What is your conclusion?

5. Test the claim that the average SAT score for graduating high school students is equal to 1500. A random sample of 70 students was selected, and the average SAT score was 1435. Assume σ = 310 and use α = 0.10. What is the p-value for this sample?

6. A student organization at a small business college claims that the average class size is greater than 35 students. Test this claim at α = 0.02, using the following sample of class size:

42        28        36        47        35        41        33        30        39        48

 Assume the population is normally distributed and that σ is unknown.

7. Test the claim that the average gasoline consumption per car in the United States is more than 7 liters per day. (We’re going metric here!) Use the random sample below, which represents daily gasoline usage for one car:

9        6        4        12        4        3        18        10        4        5

3        8        4        11        3        5        8        4        12        10

9        5        15        17        6        13        7        8        14        9

 Assume the population is normally distributed, and that σ is unknown. Use α = 0.05 and determine the p-value for this sample.

8. Test the claim that the proportion of Republican voters in a particular city is less than 40 percent. A random sample of 175 voters was selected and found to consist of 30 percent Republicans. Use α = 0.01 and determine the p-value for this sample.

9. Test the claim that the proportion of teenage cell phone users exceeding their allotted monthly minutes equals 65 percent. A random sample of 225 teenagers was selected and found to consist of 69 percent exceeding their minutes. Use α = 0.05 and determine the p-value for this sample.

10. Test the claim that the mean number of hours that undergraduate students work at a particular college is less than 15 hours per week. A random sample of 60 students was selected, and the average number of working hours was 13.5 hours per week. Assume σ = 5 hours, and use α = 0.10. What is the p-value for this sample?

The Least You Need to Know

• The null hypothesis, denoted by H₀, represents the status quo and involves stating the belief that the mean of the population is ≤, =, or ≥ a specific value.
• The alternative hypothesis, denoted by H₁, represents the opposite of the null hypothesis and holds true if the null hypothesis is found to be false.
• Use a two-tail hypothesis test whenever the alternative hypothesis is expressed as ≠; whereas a one-tail hypothesis test involves the alternative hypothesis being stated as < or >.
• A Type I error occurs when the null hypothesis is rejected when, in reality, it is true. The probability of this error occurring is known as α, the level of significance.
• A Type II error occurs when the null hypothesis is not rejected when, in reality, it is not true. The probability of this error occurring is known as β.
• The smaller the value of α, the level of significance, the more difficult it is to reject the null hypothesis.
• The p-value is the smallest level of significance at which the null hypothesis will be rejected, assuming the null hypothesis is true.
• If the p-value ≤ α, we reject the null hypothesis. If p-value > α, we do not reject the null hypothesis.
• Use the Student’s t-distribution for the hypothesis test when n < 30, σ is unknown, and the population is normally distributed.