2.3.1 Sine and Cosine as Circular Functions

Sinusoidal waveforms are strongly related to circular motion; indeed, the sine and cosine functions are often referred to as circular functions. The unit circle in Figure 2.2 can be used to define the sine and cosine functions of an arbitrary angle ϕ. If we use the positive x axis as the angular origin, then sin(ϕ) is defined as the projection of the radius on the vertical axis while cos(ϕ) is its projection onto the horizontal axis.

If we allow the radius to rotate at a constant angular frequency ω, in an anticlockwise direction, commencing at t = 0 from a position on the positive x axis, then its projections onto the x and y axes describe the time varying functions cos(ωt) and sin(ωt) respectively, as illustrated in Figure 2.3.

The cosine function can be seen to lead the sine, since it passes through its maximum value 90° before the sine function does. Alternatively, we can say that the sine function lags the cosine, by 90°. The shape of these functions is representative of the voltages and currents that exist in a power system.

If we consider the expressions presented above for our set of phase voltages, we see that only two quantities are required to define each one. The first is its magnitude, expressed in volts RMS, and the second is the phase angle ϕ that it takes when t = 0. For example, the ‘b’ phase voltage in the example above has an RMS magnitude of and a phase angle of radians, while the ‘c’ phase voltage has the same magnitude and a phase angle of radians.

Let us now consider our circle to be drawn on the complex plane. Euler’s formula states that:

This expression represents a unit vector, rotating anticlockwise at ω radians per second, whose real coordinate is cos(ωt) and whose imaginary coordinate is sin(ωt). A rotating vector with an RMS amplitude of |V| can therefore be written as:

The left‐hand side of this equation is the polar form of the vector’s coordinates, while that on the right is their Cartesian form. Alternatively, we can represent an arbitrary cosine function by the Real part of , where:

and a sine function by the Imaginary part:

2.3.2 Phasor Representation

The phasor representation of an AC quantity is obtained by taking a snapshot of its rotating vector, thereby freezing its motion in time. The frozen vector is called a phasor. Its length represents the phasor’s magnitude in volts or amps RMS, and the exact point in time when its rotation is frozen can be chosen arbitrarily. This is usually determined with regard to a reference phasor, generally either a system voltage or current, which is assigned a phase angle of zero degrees.

The phasor in Figure 2.4 represents a voltage whose magnitude is 230V_RMS and whose angle lags the reference position by 30°.

If we describe a rotating voltage vector by and freeze its rotation in time, by putting , we obtain the polar form of the phasor V, representing it. Thus:

(2.1)

Since in the steady state, the frequency of all voltages and currents in a network is the same, the only parameters required to uniquely define any phasor are its magnitude and its phase, both of which are included in the phasor expression in Equation (2.1).

As an example, consider Figure 2.5, which shows a single‐phase induction motor. Because motors are partially inductive, as we shall see later in this chapter, the current they consume lags the applied voltage. In the associated phasor diagram, the applied voltage has been chosen as the reference phasor, and therefore its phase has been assigned a value of zero degrees. The motor current lags this voltage, in this case by an angle of 40°, and therefore it can be described in polar form by the phasor amps.

2.3.3 Three‐Phase Systems and Phasor Diagrams

Figure 2.6a shows the phasor representation of a three‐phase system of voltages. Here the ‘a’ phase has been chosen as the reference phasor, with an angle of zero degrees. Therefore its phase to neutral voltage lies along the positive real axis. If we assume a conventional phase sequence of abc, then ‘b’ phase voltage lags the ‘a’ phase by 120°, and the ‘c’ phase lags the ‘a’ by 240°. The neutral (or star) point lies at the origin. The phase sequence is abc because, with an anticlockwise rotation, this is the sequence in which the phasors pass through the reference position. It is also useful to note that abc, bca and cab all represent this phase sequence.

There are only two possible phase sequences, the other being acb. Thus, if the sequence abc corresponds to an anticlockwise rotation of a machine, then the sequence acb will correspond to a clockwise shaft rotation.

Line voltages can also be represented as phasors, as shown in Figure 2.6b. Note that, in this case, there is no connection to the origin, and the angle between adjacent line voltages on the diagram is 60°, not 120°. The line voltages in Figure 2.6b together with the two associated phase voltages form an isosceles triangle. Since the included angle is 120°, the magnitude of each line voltage is √3 times that of a phase voltage.

Any voltage phasor represents a difference in potential between two points in a network. These points are often included as subscripts in the name of the phasor. For example, Figure 2.6b shows the line voltages derived from Figure 2.6a; these are labelled V_ab, V_ca and V_bc. In each case, the subscripts represent the phases between which each potential is measured. Thus V_ab is the voltage of phase ‘a’ with respect to phase ‘b’ and therefore the arrowhead corresponds to phase ‘a’. Similarly phasor V_ca represents the voltage of phase ‘c’ with respect to phase ‘a’. Therefore . Where the reference potential is the neutral terminal (0 volts), the second subscript is often omitted, thus .

The addition (or subtraction) of phasors is similar to that of vectors, since each has a particular magnitude and phase. Therefore a phasor can be moved about on the complex plane, so long as its magnitude and phase are preserved. Two phasors can thus be added by simply placing them end to end, while preserving the magnitude and phase of each one. For example, in Figure 2.6c we see that . The voltage V_ac results from the vector addition of V_ab and V_bc. Note also that the common subscript ‘b’ vanishes in the summation.

We can see from Figure 2.6b that when laid end to end the line voltages sum to zero, i.e. . We can also demonstrate this as follows:

Therefore

We shall see that the ability to add or subtract phasors is particularly useful when applying Kirchhoff’s voltage and current laws.

Figure 2.7 shows phase currents included on a phasor diagram as well as phase voltages. In this example, each phase current lags its respective phase voltage by a small angle, typical of an industrial load. Three‐phase loads whose currents have the same magnitude and the same relative phase are said to be balanced. Sometimes, as in this case, the neutral reference is dropped from the voltage phasor nomenclature, especially in the case of phase voltages, since it is understood that these are always measured with respect to the neutral terminal.

2.4.1 Resistors

The simplest passive component is the resistive element, R. The voltage developed across a resistance is in direct proportion to the current flowing through it, as defined by Ohm’s law, i.e. , or in terms of RMS quantities we can write: .

The current flowing in a resistor lies exactly in phase with the voltage developed across it, therefore the resistance R is a real number. Thus the voltage and current phasors V_R and I_R lie in the same direction when represented on a phasor diagram. The resistance of a conductor of constant cross‐section is proportional to its length and inversely proportional to its cross‐sectional area; the proportionality constant is called the resistivity and is given the symbol ρ, measured in ohm‐meters. Therefore we may write:

where R is the resistance in ohms, l is the length of the conductor in metres and A is its cross‐sectional area in m².

The resistivity is equal to the resistance between opposite faces of a 1 metre cube of the material in question, and therefore for metals it takes on very small values. For example, the resistivity of copper is 1.68 × 10⁻⁸ ohm‐m at 20 °C, increasing approximately linearly with temperature to 2.04 × 10⁻⁸ ohm‐m at 75 °C.

The resistivity is the reciprocal of the conductivity (σ) of the material, which is related to the electric field strength E within the conductor and the resulting current density, J (A/m²) according to:

Sometimes it is more convenient to use conductances rather than resistances, where the conductance G, is the reciprocal of resistance. Conductances are measured in siemens, and are particularly convenient when resistances are connected in parallel, where they can be added, just as resistances connected in series are additive.

Current flows through a metallic conductor under the influence of a small internal electric field. For example, a copper conductor with a cross‐sectional area of 1 mm², carrying a current of 1 amp has a current density . According to the equation above, the electric field strength E within this conductor is:

Thus an electric field of less than 20 mV/m is sufficient to establish a current density as high as of one million amps per square metre! This is because copper is a particularly good conductor and it is for this reason that it is widely used in the construction of transformers, busbars and electrical cables.

Transmission and distribution losses should be kept as low as practical, and despite having resistivity values slightly higher than that of copper, steel reinforced aluminium conductors are increasingly used in transmission and distribution networks. This is due to the low density of aluminium, coupled with the relatively low coefficient of thermal expansion of the steel reinforcing, enabling greater span distances to be achieved between transmission towers. The minimum clearance below a transmission line is a critical parameter, and it varies with temperature. At high ambient temperatures, or high line loadings, thermal expansion causes an increase in the conductor length, increasing the sag, and reducing the clearance beneath the line.

2.4.2 Capacitors

A capacitor typically consists of two metallic plates, separated by an insulating medium known as a dielectric, as shown in Figure 2.8. If a DC voltage V is applied to a discharged capacitor, a transient current briefly flows, establishing a positive charge on one plate and a negative charge on the other, retarding further charge accumulation. Once the potential between the plates equals the applied voltage, no further current will flow. As a result of the accumulation of this charge, an electric field E is established between the plates, equal to V/d volts per metre, where V is the voltage applied and d is the distance between the plates, illustrated in Figure 2.9.

For a given plate area A and separation d, the accumulated charge is proportional to the voltage applied, according to the equation:

Where ε is the permittivity of the dielectric material between the capacitor’s plates. We define the term as the capacitance C, measured in farads (and named in honour of Michael Faraday). Therefore we can rewrite this equation in the form:

(2.2)

The permittivity ε is a measure of the degree to which a dielectric material is polarised by the presence of an electric field. If we consider a capacitor holding a constant charge, we can show that the inclusion of a dielectric material between its plates acts to reduce the magnitude of the electric field between them. This is because the dielectric materials become polarised by the external electric field. They contain polar molecules that form tiny electric dipoles when the positive and negative charges they contain are slightly separated by the action of the external field. This effect is shown in Figure 2.10.

These electric dipoles create an electric field of their own, which as shown opposes the external field that created them. This can be demonstrated numerically by rewriting Equation (2.2) in terms of the electric field strength E, between the plates:

(2.3)

Since q is assumed to be constant, then increasing the relative permittivity ε_r will result in a corresponding decrease in the electric field strength. This in turn leads to an increase in capacitance value, compared to one with an air dielectric (for which ), since .

When the plates are separated by an air space, or by a vacuum, the permittivity takes on a value given the symbol ε_o = 8.85 × 10⁻¹² farads per metre (F/m). When dielectric materials such as polypropylene or polycarbonate are used, the permittivity increases. The permittivity of dielectric materials is usually expressed relative to the permittivity of free space, to which we give the symbol ε_o. We define the relative permittivity ε_r as:

where ε is the absolute permittivity of the dielectric material.

The relative permittivity ε_r is always greater than or equal to unity, and therefore the absolute permittivity is always greater than or equal to ε_o. For example, the relative permittivity of polycarbonate is 2.9 while that of polypropylene is 11.9. Both of these are used as dielectric materials in capacitor construction.

Capacitive Reactance and Impedance

Equation (2.2) can be rewritten in terms of the capacitance C, the accumulated charge q(t) and the applied voltage v(t), both of which may be considered as functions of time:

(2.4)

Unlike the case of DC excitation, which only results in the establishment of a static electric field between the plates, an alternating potential will result in a continuously changing electric field. This is accompanied by an alternating current required to deliver the charge necessary to establish the field. This current can be obtained by differentiating Equation (2.4):

(2.5)

Equation (2.5) shows that the current flowing in a capacitor is proportional to the rate of change of the voltage applied to it. Therefore we might reasonably expect larger currents to flow at higher frequencies. If we let then Equation (2.5) provides an expression for i(t):

(2.6)

Alternatively, the RMS current can be expressed in terms of the RMS voltage according to . The capacitive reactance, to which we give the symbol X_c, is therefore given by:

Thus the capacitive reactance does indeed fall as the frequency rises, consistent with our previous expectation. Examination of Equation (2.6) also shows that the current is phase shifted with respect to the capacitor voltage, leading it by 90°. If we define the capacitor’s complex impedance Z_c as the ratio of its voltage and current phasors V_c and I_c, we find that:

The complex impedance Z_c includes the phase information necessary to generate the observed phase shift in the capacitor current:

(2.7)

It is worth pointing out that although the impedance is generally a complex number, it is not a phasor, rather it is the ratio of two phasors and does not represent a sinusoidally varying quantity. Equation (2.7) suggests that if we choose the voltage as the reference phasor, then the current flowing in our capacitor lies along the positive j axis, as shown in Figure 2.11. Alternatively, we can say that the current leads the capacitor voltage by 90°.

Capacitive Susceptance and Admittance

When capacitors are parallel connected it is often more convenient to work in terms of capacitive susceptance rather than the capacitive reactance, since susceptances in parallel may be added. The susceptance B_c, is equal to the reciprocal of the reactance, and is measured in siemens, thus . The complex capacitive admittance to which we give the symbol Y_c, contains phase information in the same way as the capacitive impedance does, since:

2.4.3 Inductors (Reactors)

An inductor essentially consists of a coil, within which a magnetic field is created by the action of a current flowing within it. Whereas the current flowing in a capacitor is related to the rate of change of the electric field that exists between its plates, the voltage dropped across an inductor is related to the rate of change of the magnetic field linking its windings. Inductors may be wound on an easily magnetised iron core, or they may be air‐cored. We will discuss the theory of magnetic circuits in a later chapter; for now we will simply consider the electrical properties of inductors, also known as reactors.

Faraday’s law of induction states that a time varying magnetic flux will induce an electric potential within a winding linking that flux. Numerically, this is expressed in Equation (2.8).

(2.8)

where v(t) is the induced potential, N is the number of turns on the winding and Φ(t) is the time varying magnetic flux linking the winding. In a linear inductor where the flux is proportional to the current flowing within its winding, we may write:

(2.9)

where i(t) is the current flowing within the winding and is the reluctance of the magnetic circuit. Reluctance in magnetic circuits is an analogous quantity to resistance in electric circuits. It relates to the physical construction of the magnetic circuit and the material from which it is made. We will discuss reluctance in more detail in Chapter 4.

By substituting Equation (2.9) into Equation (2.8) we find:

(2.10)

where L is the inductance of the winding, and is equal to henries.

Inductive Reactance and Impedance

If we represent the inductive voltage by and substitute this into Equation (2.10), we find that in the steady state the current is given by:

(2.11)

By analogy with the capacitive case, the inductive reactance X_L is given by the ratio of its RMS voltage to its RMS current, thus:

(2.12)

Equation (2.12) suggests that the inductive reactance increases with frequency and therefore, for a given excitation voltage, the current will decrease as the frequency increases. Examination of Equation (2.11) also shows that the inductor current is phase shifted with respect to its voltage, in this case lagging it by 90°. As before, we define the inductor’s complex impedance Z_L as the ratio of its voltage and current phasors, V_L and I_L, thus we find that:

The phasor diagram for an inductor appears in Figure 2.12.

2.4.4 General Impedance and Admittance Expressions

When resistive, inductive and capacitive elements all appear in series, their collective impedance Z can be expressed in rectangular form (Cartesian) as:

Similarly, when these elements appear in parallel, their collective admittance Y, is given by:

Since , in general we may write:

Therefore it is only when that and similarly only when does .

Impedances and admittances may also be expressed in polar form:

Where

2.5.1 Sign Convention

The application of the network theorems that follow requires that the voltage dropped across circuit elements be defined with the correct polarity in relation to the current flowing through them. Although these polarities reverse every half cycle in an AC circuit, the following sign convention defines the instantaneous polarities throughout the circuit at one point in time, in much the same way as they would be defined in a DC circuit.

The instantaneous potentials dropped across elements in an AC circuit arise as a consequence of the current flowing through them. We indicate this polarity by arrows, pointing in the opposite direction to the flow of conventional current which created them. Conventional current is defined as the flow of positive charge (as opposed to actual current which relates to the movement of negatively charged electrons within a conductor).

Generally, we can define the direction of currents within a circuit however we choose, so long as we are consistent in our application of the voltage sign convention. Should the value of a particular current be found to be negative, then in reality it flows in the opposite direction to that in which it was defined.

The polarity of voltage (or current) sources is also shown by use of arrows. The magnitude of a source is the RMS potential between or the RMS current flowing through its terminals. The arrowhead indicates the instantaneous positive terminal and therefore the direction in which conventional current will flow from the source.

This sign convention, when applied correctly, defines the polarity of currents and voltages as they are used in loop and mesh analyses. It is depicted in the simple circuit of Figure 2.13, where phasor E₁ establishes current I₁ and phasor E₂ establishes current I₂. Both these currents return to their respective sources through R₃.

We review the major network theorems that find application in AC circuit analysis. Each of these applies to the instantaneous voltages and currents existing throughout a network, and therefore they also apply to the phasors representing them as well. In the analyses that follow we will use the phasor representation of currents and voltages.

2.5.2 Kirchhoff’s Voltage Law

Kirchhoff’s voltage law (KVL) states that the sum of all voltages dropped around any closed loop is equal to the sum of voltage sources contained within that loop. From the circuit in Figure 2.13a, using KVL we may write:

Although in this simple example we appear to add voltage drops algebraically, in general AC analysis KVL requires that voltage drops be added vectorially, as complex numbers, thereby taking both their magnitude and phase into account.

2.5.3 Kirchhoff’s Current Law

Kirchhoff’s current law (KCL) states that the sum of the currents entering a junction is equal to the sum of those leaving it. Therefore from Figure 2.13a we may write:

Kirchhoff’s current law generally requires that currents be added vectorially, as complex numbers. In this simple example, however, since the voltage sources are in phase with each other and the impedances are resistive, then the currents will also lie in phase.

Suppose, for example, we wish to solve for I₁ and I₂ in Figure 2.13 using KVL and KCL then we might proceed as follows:

We can combine the equations obtained above using KVL and KCL to yield:

and

Using the values given in Figure 2.13, these simultaneous equations are satisfied if and .

2.5.4 Principle of Superposition

The principle of superposition applies to circuits containing linear components only. It states that any voltage or current in a linear circuit, containing multiple energy sources, can be evaluated from the sum of the contributions from each source when acting on its own (with all other sources set to zero).

The contribution from each source acting alone deserves further comment. Consider the circuit of Figure 2.13a where there are two voltage sources. When we consider the source E₁ acting alone, we must remove the effects of the source E₂, without limiting the current that may flow through this branch. Accordingly we must force E₂ to zero, and replace this source by its equivalent internal impedance, which for a voltage source is zero ohms. Thus a voltage source is replaced by a short circuit. Similarly, if the network contains a current source, then when removed, no current must be permitted to flow in the branch, regardless of the potential developed across it. It must therefore be replaced with infinite impedance, i.e. an open circuit.

If we wish to solve for I₁ and I₂ in Figure 2.13a using the superposition theorem, we must add the contributions to I₁ and I₂ from both E₁ and E₂, thus:

where R₂‖R₃  represents the parallel combination of R₂ and R₃, i.e. .

2.5.5 Thévenin’s Theorem

The equivalent circuit of a linear network as seen from any pair of terminals, can be represented by a Thévenin equivalent voltage source V_th in series with the Thévenin equivalent impedance Z_Th shown in Figure 2.14. The Thévenin equivalent voltage V_th is the open circuit potential between the terminals in question, i.e. that which appears with no external impedance connected.

The Thévenin equivalent impedance Z_th is the impedance seen looking into the network terminals, with all voltage sources in the network replaced by short circuits, and all current sources replaced by open circuits.

If we wish to solve for I₁ and I₂ in Figure 2.13a using Thévenin’s theorem, we can consider the Thévenin equivalent of the circuit between nodes ‘A’ and ‘O’, with R₃ removed. The Thévenin equivalent voltage source can be found using the superposition theorem, and is equal to the open circuit voltage, V_AO:

and the Thévenin equivalent resistance R_th is equal to .

If we now connect R₃ to the Thévenin equivalent circuit, we find that the current flowing through it is given by:

And therefore the voltage across R₃ is equal to the voltage at point ‘A’ in Figure 2.13a with respect to that at point ‘O’, i.e. V_AO.

So

and

2.5.6 Norton’s Theorem

Norton’s theorem is an alternative approach to Thévenin’s theorem. It states that the equivalent circuit of a linear network referenced to any pair of terminals in that network can be represented by a current source I_N in parallel with an admittance Y_N, as shown in Figure 2.15.

The Norton equivalent current source is the short circuit current that would flow from the network terminals T1 and T2. The Norton equivalent impedance (1/Y_n) is the same as the Thévenin equivalent impedance and it is found in the same way. From these definitions, we can see that the Thévenin equivalent voltage is equal to the Norton equivalent current divided by the Norton admittance Y_n:

N.B. It should be stressed that both Thévenin and Norton’s theorems do not imply anything about the internal operation of the network to which they refer. They merely provide information relating to the combinations of voltages and currents that can be obtained from the terminals T1 and T2, under various loading conditions.

We can also use Norton’s theorem to find I₁ and I₂ in Figure 2.13a. As before, we proceed by determining the Norton equivalent circuit across R₃, with R₃ removed. The short circuit currents flowing from E₁ and E₂ are amps and amps respectively. Thus the total short circuit current available from node ‘A’, is amps. As in the previous example, the Norton impedance is 0.666 ohms. From the Norton equivalent circuit the potential across R₃ is given by:

And therefore we again find that:

and:

2.5.7 Millman’s Theorem

Millman’s theorem is an extension of Kirchhoff’s current law, and in many applications it is so useful that we shall include it here with the other major network theorems. It can be derived from the circuit shown in Figure 2.16.

Millman’s theorem provides a method of calculating the unknown potential V_x, assuming all the other potentials and their associated admittances are known. All the potentials in Figure 2.16 are measured with respect to ground, and therefore this terminal is omitted in the phasor nomenclature. Since we know that the sum of all the currents flowing towards node x must add to zero then, by applying KCL to this node, we find:

(2.13)

On solving Equation (2.13) for V_x we find:

(2.14)

Equation (2.14) represents Millman’s theorem, and although it looks cumbersome it is surprisingly useful in determining an unknown potential, particularly in the presence of three or more voltage sources. If we wish to solve for I₁ and I₂ using Millman’s theorem, we must first find the potential V_AO, shown in Figure 2.13a.

Thus:

Therefore:

and

2.6.1 Example 1: Series and Parallel Circuits.

In this example, we analyse simple series and parallel connected AC circuits, including their phasor representations. In the series case, Figure 2.17a, we find that an impedance representation is convenient since impedances connected in series can be added, whereas in the parallel case (Figure 2.17b) an admittance approach is preferred, since connected parallel admittances can be added.

Beginning with the series connected circuit, the collective impedance can be evaluated as:

Since the current is common to each component, we assign it as the reference phasor (Figure 2.18). Accordingly, the voltage will be allocated the same phase angle as the circuit impedance. The current I is therefore given by:

The voltage drop across each component can now be plotted on the phasor diagram. The resistive drop (IR), lies in phase with the current, the inductive drop (IX_L), leads the current by 90° and the capacitive drop (IX_C), lags the current by 90°. These voltage drops can now be added vectorially according to KVL, to yield the phasor corresponding to the applied voltage.

Note that since the capacitive drop is larger than the inductive one, the overall impedance is capacitive, and therefore the current leads the applied voltage, in this case by 47°.

In order to analyse the parallel connected circuit of Figure 2.17b, we compute the total admittance according to:

Since the voltage across the combination is common to all elements, we assign it as the reference phasor. Therefore the current must then take on the same phase as the circuit admittance. The voltage is thus given by:

Knowing the circuit voltage enables the current in each element to be found, which can be plotted on a phasor diagram and summed to yield the applied current, as shown in Figure 2.19.

Since the current flowing in the inductance exceeds that in the capacitance, the overall impedance is inductive, and the current lags the circuit voltage by 42°.

2.6.2 Example 2: Three‐Phase Loads

Where three‐phase balanced or near balanced loads are involved, it is unnecessary to represent all phases on a phasor diagram. Instead one phase is usually drawn, since it is representative of the other two. The circuit shown in Figure 2.20a represents one phase of a near balanced industrial load. In practice such a load might comprise motor driven machinery, water heating, air conditioning or refrigeration equipment, together with an assortment of single phase plug loads. Electrically all these can usually be represented by an inductive‐resistive combination, since industrial loads are generally partially inductive.

Since it is common to both components, the current will be chosen as the reference in the phasor diagram shown in Figure 2.20b.

The voltage developed across the resistive element lies in phase with the current, while that associated with the inductive element leads the current by 90°. Kirchhoff’s voltage law requires that the sum of the voltage drops around a circuit equals the applied voltage, so we may write:

In the phasor diagram of Figure 2.20b these voltages are added vectorially. The resultant voltage V, can be seen to lead the current by an angle ϕ, or alternatively the current lags the voltage by the same angle. As we shall see in the next chapter, the cosine of this angle is called the power factor of the load, and for reasons that will be explained, supply authorities prefer customers to ensure that their load operates at a high rather than a low power factor – that the load current lags the voltage by only a small angle.

2.6.3 Example 3: Power Factor Correction

The circuit of Figure 2.21 also shows an inductive load to which has been added a parallel connected capacitor, C, provided for the purpose of power factor correction. By adding a device that consumes a leading current, some of the lagging effects of an inductive industrial load can be offset, and an increase in the power factor of the combination results.

In this circuit the total current splits into two components, one flowing in the load I_L, and the other in the power factor correction capacitance, I_C. Since the applied voltage is common to both branches of this circuit, it will now be used as the reference phasor.

By analogy with Example 2, the inductive current lags the applied voltage by an angle ϕ_L. In contrast, the capacitive current leads the applied voltage by 90°, as shown in Figure 2.22a. The total current, can be found by vector addition of these two phasors. The resultant current I_tot can now be seen to lag the voltage by a smaller angle ϕ. Because the new phase angle is less than the old, the power factor has been increased and thus improved, but the circuit remains under‐compensated. Figure 2.22b depicts the same load with sufficient capacitance applied to make the total current appear resistive, (i.e. ), so with the circuit is now ideally compensated. Finally, Figure 2.22c shows the case where an excessively large capacitive compensation has been applied, and the total current now leads the applied voltage. The circuit is therefore over‐compensated.

2.6.4 Example 4: Capacitive Voltage Rise

Whenever a capacitance is connected to an AC bus, there will usually be an accompanying rise in the bus voltage. This is generally only a few per cent, and is due to the fact that the supply impedance is at least partially inductive. We can demonstrate this effect by considering the single phase Thévenin representation of a three‐phase AC bus, as shown in Figure 2.23a. The bus impedance is represented by an inductive component X, and a resistance R, both of which are quite small, in addition to which R is generally considerably smaller than X.

When the system is unloaded, the bus voltage V_b is equal to the source voltage E. However, when loaded, V_b and E are no longer equal, due to the potential dropped across the source impedance, . The connection of a capacitor, as shown in Figure 2.23b, results in a leading current, causing voltage drops across both R and X, depicted in the phasor diagram in Figure 2.24. Here we have assumed that X > R, which is frequently the case.

The voltage dropped across the source resistance R, lies in phase with the capacitive current, while that across the inductive impedance leads this current by 90°. Kirchhoff’s voltage law requires that , and an inspection of Figure 2.24 shows that as a consequence of this summation V_b has increased in magnitude when compared to E. (Remember that the Thévenin equivalent voltage E, is fixed.) In effect, the capacitive current I_C creates a voltage drop across X that adds to V_b. It can also be seen that because V_X and V_R are in quadrature (i.e. they are 90° apart), V_X has a much larger effect on the magnitude of V_b than does V_R, so we may write:

If we represent the increase in V_b by δV, we can write:

where X_C is the reactance of the connected capacitance. We can express the fractional rise in voltage (also known as the per‐unit voltage rise) as:

(2.15)

By way of example, suppose that the source impedance of a 6.6 kV three‐phase bus is 0.07 + j0.6 ohms per phase, and that a capacitor of 30 ohms reactance is connected between each phase and the neutral terminal. The resulting fractional increase in the bus voltage will be about 2% or 130 V.

For this reason, capacitors are often connected to MV and HV networks to provide voltage support during times of heavy demand. Equation (2.15) can also be used to show that the bus voltage will fall when loaded with an inductive impedance, X_L. This can be achieved by replacing X_C with to yield:

So a 30 ohm inductive impedance connected to the same bus, will result in a fall of about 2% in the bus voltage.

2.6.5 Example 5: Phase Sequence Indicator Analysis

We now consider the design of a phase sequence indicator, which is a simple device capable of indicating the phase sequence of a three‐phase supply. There are many versions of this circuit in existence, all of which operate on the same principle. The basic circuit is shown in Figure 2.25, and consists of two resistive lamps and one capacitor, connected in a star (or wye) configuration.

The phase sequence indicator is connected between the line voltages of the supply in question, so no neutral connection is required. The circuit generates its own star‐point voltage Vs, one that is quite different from that of the unused neutral terminal, which represents zero volts. We will initially analyse the circuit using Millman’s theorem, and once we have a clear understanding of its operation, we will re‐analyse it using phasor analysis.

For the circuit to operate correctly we require that the magnitude of the capacitive admittance connected to the ‘a’ phase, be equal to the effective lamp resistances on the other two:

(2.16)

Recall that Millman’s theorem, as applied to this circuit, states that:

(2.17)

where Y_i is the admittance associated with phase i and V_a, V_b and V_c are the phase voltages. Let us assume that the phase voltages each have a magnitude of 1 volt, and therefore they can be expressed as:

Similarly, let us assign a magnitude of 1 siemen to each admittance, therefore we can write:

Substituting these values into Equation (2.14a) we find that  V, as depicted in the phasor diagram of Figure 2.26. Here we see that there is a much larger potential dropped across the ‘b’ phase lamp than across the ‘c’ phase one. Therefore we expect that the ‘b’ phase lamp will burn more brightly than that on the ‘c’ phase.

So how does this circuit indicate the phase sequence of the connected supply? From the foregoing, the brightest lamp is supplied from the phase following that connected to the capacitor, which in this case is the ‘a’ phase. Therefore in the example above, with an abc phase sequence, the ‘b’ phase lamp will burn the brightest. However, if we reverse the phase sequence, by swapping the incoming ‘b’ and ‘c’ phases, then the ‘c’ phase lamp will be the brightest, since it now follows the ‘a’ phase, thus indicating an acb phase sequence.

This circuit finds application in the connection of three‐phase motors, where the correct phase sequence must be provided in order to ensure the desired direction of rotation. It is also used in metering applications to ensure that the energy meter sees the correct voltage phase sequence, although this requirement is more important with induction‐disc meters than with electronic instruments.

Now that we have an understanding of how the phase sequence indicator works, let us analyse its operation using a phasor diagram. Essentially all we have to do is to locate the star‐point s to complete the diagram for the sequence indicator.

We do need a little information about the circuit, so we begin by applying KCL to the currents flowing towards the star point, s. Thus we find:

Therefore

We can rewrite this equation in the form of two equal currents, I′ and I″, where:

And

The current I′ consists of a component from each phase that can be drawn on a phasor diagram as shown in Figure 2.27. Here each of the three‐phase currents have been added vectorially to generate I′. Since all the admittance values have a magnitude of unity, then the magnitude of each current component will also be unity. Finally, since we have chosen unity voltages as well, both the current and voltage scales on the phasor diagram will be the same.

As shown in Figure 2.27, the current I′ leads the ‘a’ phase voltage by 135° and has a magnitude of amps.

We can similarly construct a phasor diagram for I″, but since at this time we do not yet know the scale of this diagram or how to orient it, we will draw V_sn in the reference direction for convenience. I″ will also have three components and, as shown in Figure 2.28, it will lead V_sn, by 26.6°.

Since we know the currents I′ and I″ are equal, we must rescale Figure 2.28 so that I″ also has a magnitude of amps and superimpose the two phasor diagrams, so that I″ lies on top of I′. However, this must be done in such a way that the current I″ leads V_sn, since this circuit is capacitive. The location of the star point voltage V_sn on the phasor diagram will then be revealed. This has been done in the diagram of Figure 2.29, where we again find that volts.

Our phasor analysis of the phase sequence indicator is probably no simpler than using an analytical approach, but it does illustrate what can be achieved using phasor diagrams. In more complex circuits the phasor approach can save considerable calculation while providing the benefit of a visual appreciation of the circuit’s operation. The next example illustrates such a case.

2.6.6 Example 6: Induction Furnace Operation

This example concerns a low frequency induction furnace of the type used to melt and cast aluminium or zinc. It operates on the principle that molten metal within the furnace forms a shorted secondary winding on the furnace transformer (known colloquially as an inductor). Our interest in this furnace relates to the way in which a single‐phase furnace is supplied from a three‐phase transformer, in such a way that all phases are loaded equally and at unity power factor. This is achieved through the clever use of a line‐connected balancing reactor and capacitor, as shown in the furnace schematic of Figure 2.31. An arrangement of this kind is necessary because an induction furnace is too large a load to be supplied from one phase only.

Figure 2.30 shows a cutaway view of a small induction furnace. In particular, it depicts the location of the furnace transformer, the core of which is mounted horizontally beneath the crucible.

The transformer core and its associated primary winding are enclosed within a refractory material capable of withstanding the temperature of the molten metal. Cast into this are channels through which the metal forms two shorted turns around the core. These channels form the throats of the furnace in which the current flowing rapidly heats and expands the metal. A strong thermosyphon action draws metal into the centre throat and expels it from those on either side, thereby ensuring an even temperature distribution throughout the melt, as depicted in Figure 2.30.

The power delivered to the melt depends on the dimensions of the throats and also of the resistance of the molten metal within them, as well as the leakage inductance that exists between the primary windings and the metallic secondary winding. The cooling of the transformer’s primary winding is critical, and in this case this is achieved by a fan forcing cool air around the winding. Alternatively de‐ionised water pumped through the winding may be employed instead.

Figure 2.31 is a simplified schematic diagram of the furnace. Power is supplied from an 11 kV:460 V three‐phase transformer, where the high voltage winding is delta connected, and the low voltage is star (or wye) connected. The LV windings supply the furnace’s own three‐phase star connected autotransformer, which provides a tapping range from 90 to 600 volts. The power delivered to the furnace can thus be adjusted using the on‐line tap‐changer, enabling precise temperature control of the melt.

The capacitors shown are of two types, each specified according to the quantity of reactive power (V_C²/X_C, expressed in volt‐amps‐reactive, VAr), that it consumes from a 600 volt AC source. Type ‘A’ supplies 200 kVAr @ 600 volts, and comprises 2 × 100 kVAr capacitors, while Type ‘B’, (used only for trimming purposes), supplies 87.5KVAr @ 600 volts, and comprises 1× 12.5KVAr, 1 × 25 kVAr and 1× 50 kVAr capacitor.

The furnace transformer, together with its seven type ‘A’ power factor correction (PFC) capacitors is connected between phases ‘a’ and ‘c’. Power factor correction is required due to the leakage impedance of the furnace transformer, which adds a substantial inductive element in series with the melt resistance, when seen reflected into the primary winding. The power factor correction capacitors are dimensioned so as to restore the furnace transformer’s phase angle to zero, and therefore its power factor to unity. (The type B capacitor is provided for trimming the value of the type A capacitors.) Thus the transformer, its PFC capacitance and the melt resistance, can all be replaced with a single equivalent resistive element connected between phases ‘a’ and ‘c’.

The air‐cored phase balancing reactor is cooled by de‐ionised water, pumped through hollow windings. It is rated at 355 kVAr @ 600 volts and is connected between the ‘b’ and ‘c’ phases. Finally the phase balancing capacitors are connected between phases ‘a’ and ‘b’ and consist of one type A capacitor and two type B, which are adjusted to provide a capacitive reactance exactly equal to that of the balancing reactor.

With the exception of the 355 kVAr rating of the balancing reactor, the technical data presented above is not essential to understanding the phasor analysis of this furnace. In the simplified schematic shown in Figure 2.32, the tap‐changers have been omitted and the furnace transformer and its associated PFC capacitors have been replaced with an equivalent resistor representing the melt, while the balancing reactor and capacitors are unchanged.

We will show that, as a result of these balancing components and the PFC applied to the furnace transformer, the incoming phase currents are balanced, and that each lies exactly in phase with its associated phase voltage. Therefore the power demanded by the furnace is shared equally across all three phases of the supply transformer. We will also use our phasor diagram to determine the maximum power rating of the furnace.

To do this we must plot the phase currents (I_a, I_b and I_c) on a phasor diagram and compare them with the associated phase voltages, making any adjustments necessary to the magnitude of the furnace current, to ensure that a unity power factor is achieved. We begin by plotting the furnace, the reactor and the capacitor currents alongside their associated line voltages, as shown in Figure 2.33. The furnace current therefore lies in phase with V_ac, the reactor current lags V_cb by 90° and the capacitor current leads V_ab by 90°.

Next, from Figure 2.33 we write an equation for each of the three phase currents:

These phase currents are plotted on the phasor diagram in Figure 2.34, where we see that in order to achieve a unity power factor on each phase, the resistive furnace current must be √3 times as large as either the reactor or the capacitor current. Therefore the power rating of the furnace will be √3 times the VAr rating of the balancing reactor, thus: .

The resultant current flowing in each phase is equivalent to supplying a balanced resistive load, in which the power delivered by each phase is one third of that required by the furnace. From our phasor diagram, we see that the current flowing in each phase has the same magnitude as that in either the reactor or the capacitor, and on the maximum tap this is equal to 355 kVar/600 V = 592 A. Therefore the total power delivered by the supply transformer will be given by: as derived above.

Thus, through a clever connection of balancing components, the ‘single phase’ furnace load has been distributed equally across all three phases of the supply transformer. Without such a connection it would not be possible to operate this furnace, since 615 kW is too large a load to apply to one phase alone and would severely unbalance a local LV network.

As well as providing an equation for the rating of the furnace, the phasor diagram can also provide us with a good idea of just how this circuit works; this can be shown as follows. Since the furnace current I_f, is in phase with the line voltage V_ac it lags the ‘a’ phase voltage by 30° while its inverse − I_f, leads the ‘c’ phase voltage by the same amount. In order to bring these line currents into phase with their respective voltages, the ‘a’ phase requires an additional capacitive current component, while the ‘c’ phase requires an inductive one.

The capacitive current is provided to the ‘a’ phase by the balancing capacitor, connected across V_ab. If the magnitude of this current is equal to 1/√3 times that of the furnace current, then the resultant ‘a’ phase line current will lie in phase with the ‘a’ phase voltage, as required. Similarly, the ‘c’ phase furnace current − I_f, leads the ‘c’ phase voltage by 30° (Figure 2.34) and therefore an inductive current component is required to bring the ‘c’ phase current back in phase with the ‘c’ phase voltage. The reactor, connected across V_cb, will inject such a component, and if the magnitude of this current is equal to 1/√3 times that of the furnace current, then the resultant ‘c’ phase current will lie in phase with the ‘c’ phase voltage.

Finally, the ‘b’ phase line current is equal to minus the sum of the balancing capacitor and reactor currents, −(I_L + I_C), and this current conveniently falls in line with the ‘b’ phase voltage, as shown in Figure 2.34. Therefore through the use of a phasor diagram, we have not only been able to determine the furnace rating, but have also obtained an insight into the operation of the phase balancing circuitry.

2.7.1 Quality Factor ‘Q’

The quality factor is a parameter that describes how well a tuned circuit performs close to resonance. High Q circuits exhibit rapid changes in response around the resonant frequency, while in low Q circuits the response changes much more gradually. The Q of a circuit is defined as:

(2.18)

Therefore a high Q circuit will exhibit very low loss per cycle and, as we shall see, it will have a sharp peak in its amplitude response at resonance. The peak energy stored in the circuit can be expressed in terms of the peak current flowing î, as 1/2Lî² and the energy lost per cycle is found by integrating the power loss i(t)²R, over a complete cycle. Thus we may write:

(2.19)

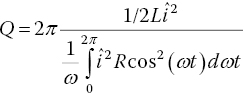
Therefore the Q of a series resonant circuit is simply the reactance of the inductor ωL, divided by its associated series resistance R, and thus a small resistive loss will give rise to a large Q value. It is interesting to note that the Q also rises with the applied frequency ω. This is because at higher frequencies a shorter cycle time is available for energy to be consumed within the resistive element. The Q of a tuned circuit is often expressed in terms of the resonant frequency of a circuit ω_o, and since we have seen that for a series circuit at resonance we may write: .

2.7.2 Parallel Resonance

A parallel resonant circuit can be constructed by connecting the inductor and capacitor in parallel, as shown in Figure 2.36a. Here the small resistance R still appears in series with the inductance. In this form, the parallel circuit lacks the symmetry of the series circuit, and Figure 2.36b shows a simplification of this circuit, through the introduction of a new resistive component R′, in parallel with L, in place of the resistance R in series with it. In this form, the parallel circuit is easier to analyse, although it should be stressed that this change represents an approximation to the circuit of Figure 2.36a, albeit a quite good one, especially for larger Q values.

The value of the new component R′ must be chosen so that the same power loss occurs in each circuit, thus:

This means that:

And for we find:

(2.20)

Thus for larger Q values we can replace the series connected resistance R with an equivalent parallel resistance R ′, where .

2.7.3 Parallel Tuned Circuit Quality Factor

The Q value for a parallel circuit may also be expressed in terms of C and R′ from the definition in Equation (2.18):

Where ϕ is the angle between the circuit voltage and the current in the inductor:

(2.21)

2.7.4 Series Resonant Circuit Normalised Frequency Response

It is often useful to express the magnitude of the current flowing in a series tuned circuit I, at a frequency ω, by normalising it with respect to the current flowing at resonance I_o, assuming a constant excitation potential. Therefore:

(2.22)

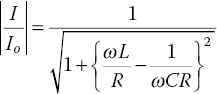
where

Equation (2.22) shows that the response at an arbitrary frequency ω, is always less than that at the resonant frequency, ω_o. Figure 2.37 shows the normalised frequency response for a series resonant circuit, for various values of Q₀.

For circuits with low Q₀ values, the response around the resonant frequency is not particularly sharp, but as Q₀ increases so does the sharpness of the response around the resonant frequency. The maximum normalised response is unity, occurring when ω = ω_o. The series resonant circuit is thus capable of passing signals near its resonant frequency, i.e. it is acting as a band‐pass filter.

2.7.5 Parallel Resonant Circuit Normalised Response

We can analyse the parallel resonant circuit’s normalised response in a similar way to the series circuit. We shall begin with the symmetrical arrangement of the three elements, L, C and R′, connected in parallel, which suggests that we approach the task from an admittance perspective, since admittances in parallel can be summed. Again we shall consider the total current flowing into the circuit from the source, and as before we shall calculate the magnitude ratio .

Thus:

(2.23)

Equation (2.23) is similar in form to Equation (2.22), but at frequencies away from resonance the value of is now considerably greater than one, since the LC combination no longer appears as an open circuit. For example, at low frequencies the inductive admittance is large, generating a high current flow. Similarly, at high frequencies the capacitive admittance is large, allowing high currents to flow. Figure 2.38 shows the normalised response plotted for several Q₀ values and, as expected, as the frequency moves further from resonance, the response of the circuit increases, and as the circuit Q₀ increases, so does the sharpness of the response around resonance.

The parallel tuned circuit is capable of attenuating the signals near its resonant frequency, i.e. it is acting as a band‐stop filter.

2.7.6 Resonant Circuit Bandwidth and Cut‐Off Frequencies

The characteristic shown in Figure 2.37 is typical of a band‐pass filter, while that of Figure 2.38 is characteristic of a band‐stop filter. It is instructive to evaluate the upper and lower cut‐off frequencies for both the series and parallel resonant circuits – those frequencies at which the magnitude of the normalised response falls by 1/√2. This corresponds to a change in the power dissipated in the circuit of a factor of 2, and as a result the cut‐off frequencies are also known as the half‐power frequencies, (or alternatively as the 3 dB frequencies).

From Figure 2.35, the current in a series circuit at resonance is V/R, occurring when the reactance term X equals zero. As the frequency changes the reactance will vary as depicted in Figure 2.39. The magnitude of the normalised response will fall by a factor of 1/√2 when , occurring at the upper cut‐off frequency, or when at the lower cut‐off frequency. The upper frequency can therefore be found from the condition , and the lower one from . Each of these quadratic equations will yield two roots, only one of which will be positive and will represent the respective cut‐off frequency.

The quadratic equation for the upper cut‐off frequency may be written in the form:

Which leads to the result:

(2.24)

Similarly, the lower cut‐off frequency is obtained from the equation:

which yields:

(2.25)

So for large Q values the upper and lower cut‐off frequencies lie close to the resonant frequency ω_o, which is consistent with the sharp band‐pass response we have observed in such circuits. The bandwidth of the circuit (radians/sec) is defined as the range of frequencies between ω_lower and ω_upper which, from Equations (2.24) and (2.25), may be expressed in the form:

(2.26)

Equation (2.26) is often used as an alternate definition for the quality factor Q. The same analysis when applied to a parallel resonant circuit generates identical results.

2.7.7 Parallel Tuned Circuit Resonant Frequency

The analysis thus far has suggested that the effects of the inductor’s winding resistance R can be accounted for by placing a large resistance R′ in parallel with L and C (Figure 2.36). While this approximation is generally quite good, especially for high Q circuits, it fails to predict a slight downward shift in the resonant frequency of the parallel circuit when compared with that of the series circuit.

The approximate circuit suggests that the resonant frequency will be the same for both series and parallel circuits, but this is not quite correct. This assertion can be demonstrated using a phasor diagram, as shown in Figure 2.40.

This phasor diagram can be constructed by first choosing the inductive current as the reference phasor, i.e. lying along the positive horizontal axis. Once this current has been drawn, both the resistive and inductive voltage drops can be included (V_R and V_L respectively). (Remember: V_L leads this current by 90°, while V_r is in phase with it.) From these phasors, the total voltage V can be found, since .

The capacitive current can be included next, since it leads the total voltage by 90°. Finally, the total current phasor can be constructed, since . This phasor diagram has been constructed when the circuit is operating at resonance, which occurs when the applied voltage and the resulting current are in phase. From our knowledge of AC circuit theory, we can write down equations for some of the important quantities in the circuit.

Specifically:

From the geometry of the phasor diagram at resonance we can see that:

therefore:

where ω_p is the parallel resonant frequency.

Thus:

Here ω_s is the series resonant frequency and .

Therefore the parallel resonant frequency, ω_p is often just a little less that the series resonant frequency, particularly when the circuit Q₀ is low, say

By way of example, a 3 mH inductor with a winding resistance of 7 ohms is series resonant with a 1 μF capacitance at 2.91 kHz. When these components are connected in parallel then according to the above equation, the resonant frequency becomes 2.87 kHz. For a high Q circuits like this one the difference is not particularly great and the approximation is quite reasonable. However, for low Q circuits, the parallel resonant frequency can be significantly different. If, for example, the same inductor is resonated with 10 μF, the series resonant frequency would become 919 Hz while the parallel resonant frequency would only be 840 Hz – quite different!