Chapter 5
Longitudinal Data Methods
5.1 Overview
In contrast to the cross-sectional studies discussed in Chapter 4, longitudinal studies have the defining feature of repeated measures collected on individuals over time, enabling a direct study of temporal patterns or trajectories. Although both cross-sectional and longitudinal studies can look at differences among individuals in their baseline values (called cohort effects in population studies), only a longitudinal study can look at changes over time within an individual (called aging effects in population studies). Longitudinal data can be collected prospectively, following individuals forward in time, or retrospectively, looking back at historical records. The methods described in this chapter can be used for either data collection method.
We begin this chapter by introducing two data examples in Section 5.2 and carry out some basic descriptive analysis. Section 5.3 reviews the modeling approaches and statistical inferences for longitudinal data without missing values. We then introduce the settings of missing longitudinal data as well as simple methods to deal with missingness in Section 5.4. When only the response variable is subject to monotone missingness (e.g., dropout), Section 5.5 presents the likelihood-based method and Section 5.6 describes the inverse probability weighted generalized estimating equation approaches. Section 5.7 extends the WEE to the situation of intermittent missingness of the outcome. The multiple imputation (MI) procedures are introduced in Section 5.8. Section 5.9 presents the Bayesian inference framework in the setting where both outcomes and covariates are subject to missingness. Finally, other existing methods in analyzing longitudinal missing data are introduced in Section 5.10. Technical details of some methods and the code we used in this chapter are presented in Appendix 5.A.
5.2 Examples
5.2.1 IMPACT Study
The Improving Mood and Promoting Access to Collaborative Treatment (IMPACT) study has been introduced in Chapters 1 and 4. Briefly, to determine the effectiveness of the IMPACT collaborative care management program for late life depression, a total of 1801 patients aged 60 years or older with major depression (17%), dysthymic disorder (30%), or both (53%) were enrolled and randomized to IMPACT care or usual care. Intervention patients had access for up to 12 months to a depression care manager who was supervised by a psychiatrist and a primary care expert and who offered education, care management, and support of antidepressant management by the patient's primary care physician or a brief psychotherapy for depression. Depression symptoms were assessed by the mean score of the 20 depression items from the Symptom Checklist-90 (SCL-20) at baseline, 3, 6, 12, 18, and 24 months. For details about the study design and primary analysis, see Unützer et al. (2002).
In the following, we conduct longitudinal data analysis using the outcome, the SCL-20 depression score, and contrast various missing data methods. Figure 5.1 shows trajectories of 40 randomly selected individuals and the group mean trajectories over time. It is pretty obvious that individuals from the intervention arm tend to have lower SCL-20 scores.

Figure 5.1 Forty individuals and mean trajectories.
We consider an analysis that addresses the question whether or not the IMPACT treatment reduces the depression symptoms as measured by the SCL-20 scores. To address this question, we compare the subject-specific changes, from baseline to follow-up, in the SCL-20 scores for the patients in the two study arms. We consider the following linear mixed effects regression model for the subject-specific mean SCL-20 scores:
where Yij is the SCL-20 score for the ith patient at the jth time point of assessment (j = 0, 3, 6, 12, 18, 24). The variable group is an indicator variable for the treatment group, with group = 0 if an individual was randomized to the usual care group and group = 1 if randomized to the IMPACT treatment group. The binary variable period denotes the baseline and follow-up periods, with period = 0 for the baseline and period = 1 for the follow-up periods (3–24 months). This allows us to assess the time-averaged intervention effect. We can also replace period with the actual month variable, which then allows us to assess treatment effect at specific months. Although the SCL-20 score is bounded between 0 and 4, because it is an average of 20 items, we assume that it follows a normal distribution in our analysis. Finally, we assume that the random intercepts and slopes, bi, follow a bivariate normal distribution, with zero mean and an unstructured 2 × 2 covariance matrix G.
We decided to illustrate our analysis using the Stata software version 13.0. The point is that many missing data methods have been implemented in various software packages, and the readers can choose the ones that they are already familiar with or more comfortable using.
The misstable command in Stata allows us to examine the missing data pattern in SCL-20 scores, which is shown in Table 5.1. It can be seen that 162 (9%) subjects had intermittent missingness, 370 (20%) subjects dropped out during the 24-month period, and 1269 (71%) patients had complete data.
Table 5.1 The Missing Data Pattern in the SCL-20 Scores at Baseline, 3, 6, 12, 18, and 24 Months
| Frequency | SCL0 | SCL3 | SCL6 | SCL12 | SCL18 | SCL24 |
| 1269 | 1 | 1 | 1 | 1 | 1 | 1 |
| 117 | 1 | 0 | 0 | 0 | 0 | 0 |
| 69 | 1 | 1 | 0 | 0 | 0 | 0 |
| 64 | 1 | 1 | 1 | 0 | 0 | 0 |
| 60 | 1 | 1 | 1 | 1 | 0 | 0 |
| 60 | 1 | 1 | 1 | 1 | 1 | 0 |
| 45 | 1 | 0 | 1 | 1 | 1 | 1 |
| 22 | 1 | 1 | 1 | 1 | 0 | 1 |
| 14 | 1 | 1 | 1 | 0 | 1 | 1 |
| 12 | 1 | 0 | 1 | 0 | 0 | 0 |
| 11 | 1 | 1 | 0 | 1 | 1 | 1 |
| 5 | 1 | 0 | 0 | 1 | 1 | 1 |
| 5 | 1 | 1 | 0 | 1 | 0 | 0 |
| 4 | 1 | 0 | 0 | 1 | 0 | 0 |
| 4 | 1 | 0 | 1 | 1 | 1 | 0 |
| 4 | 1 | 1 | 0 | 1 | 0 | 1 |
| 4 | 1 | 1 | 1 | 0 | 0 | 1 |
| 4 | 1 | 1 | 1 | 0 | 1 | 0 |
| 3 | 1 | 0 | 0 | 0 | 1 | 0 |
| 3 | 1 | 0 | 1 | 0 | 0 | 1 |
| 3 | 1 | 0 | 1 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 0 | 0 | 0 | 1 | 1 |
| 2 | 1 | 0 | 0 | 1 | 0 | 1 |
| 2 | 1 | 0 | 1 | 0 | 1 | 1 |
| 2 | 1 | 1 | 0 | 0 | 1 | 1 |
| 2 | 1 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 | 0 | 1 | 0 |
| The total number of patients in the study is 1801. | ||||||
5.2.2 NACC UDS Data
The National Alzheimer's Coordinating Center (NACC) Uniform Data Set has already been introduced in Chapter 1. The data set was also analyzed by Monsell et al. 2012). Our aim is to model the decline of the outcome, mini-mental state examination (MMSE), since the first diagnosis of amnestic mild cognitive impairment (aMCI).
Missing data occur in the outcome MMSE as well as in the covariates education, Hachinski ischemic score (HIS), and apolipoprotein E (APOE) e4 alleles. The missing pattern is nonmonotone, as shown in Table 5.2.
Table 5.2 Missing Data Pattern for the UDS Data
| Frequency (by Visits) | MMSE | Education | HIS | APOE e4 |
| 5809 | 1 | 1 | 1 | 1 |
| 98 | 0 | 1 | 1 | 1 |
| 13 | 1 | 0 | 1 | 1 |
| 23 | 1 | 1 | 0 | 1 |
| 2482 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 156 | 0 | 1 | 0 | 1 |
| 49 | 0 | 1 | 1 | 0 |
| 21 | 1 | 1 | 0 | 0 |
| 100 | 0 | 1 | 0 | 0 |
The data set is in a “long format,” meaning that each row corresponds to one person-visit, and each subject contributes multiple rows. We observe that HIS was missing for 300 clinical visits and MMSE for 404 visits. Education and APOE e4 are on the subject level; it turns out that 4 subjects had missing education and 949 subjects had missing APOE e4.
5.3 Longitudinal Regression Models for Complete Data
The analysis of longitudinal data requires us to account for the correlation structure among observations of the same individual measured repeatedly over time. There are three major categories of methods for analyzing longitudinal data: marginal models, random effects models, and transition models. In this chapter, we briefly review the first two methods because they are relatively easy to implement in many software packages, and most missing data methodologies are based on the first two methods. More detailed description of the longitudinal data analysis can be found in Diggle et al. (2002).
Suppose that N individuals are independently observed in the sample. Let Yij be the response for ith subject measured at time tij, where i = 1, ..., N and j = 1, ..., ni. Note that the number of observations is allowed to be different across the individuals, which is also known as an unbalanced design. We write ![]() to denote the ni × 1 response vector for subject i that may be missing at some time points. Let
to denote the ni × 1 response vector for subject i that may be missing at some time points. Let ![]() be an ni × q matrix of covariates for subject i at each time point. The jth row of Xi,
be an ni × q matrix of covariates for subject i at each time point. The jth row of Xi, ![]() , corresponds to the q covariates observed at time tij. For now, we do not distinguish the covariates that change over time (e.g., age, longitudinal MMSE score measured at each tij) from those that do not (e.g., gender, baseline MMSE score measured at ti0).
, corresponds to the q covariates observed at time tij. For now, we do not distinguish the covariates that change over time (e.g., age, longitudinal MMSE score measured at each tij) from those that do not (e.g., gender, baseline MMSE score measured at ti0).
5.3.1 Linear Mixed Models for Continuous Longitudinal Data
5.3.1.1 Model Setting
Suppose the outcome vector Yi takes continuous values, so that we could consider a linear regression model. A linear mixed model (LMM) could be illustrated from a two-stage model formulation. We first fit a regression line for each subject separately:
where βi is a q-dimensional vector of subject-specific regression coefficients, Zi is the design matrix of covariates, and εi ~ N(0, Σi) is the Gaussian residual. Note that εi describes the within-subject variability, and usually we assume that the elements of εi are independent, that is, ![]() . The second-stage model imposes a structure on βi:
. The second-stage model imposes a structure on βi:
where Ki is the design matrix, β is the vector of regression parameters of interest, and bi ~ N(0, D) is the residual. Note that bi represents the variability between subjects, whose elements are usually correlated. We could regard β as the “average” covariates effect, and then bi is the effect deviation from the population average for subject i.
The two-stage model, defined by (5.2) and (5.3), could be combined into the following one-stage model:
We call β the fixed effects and bi the random effects due to the fact that β is the unknown parameter vector, whereas bi is a random vector. More generally, the following four assumptions constitute an LMM:

where ![]() and
and ![]() are called the variance components and α is a vector of nuisance parameters specifying these variance components. The LMM can be equivalently viewed as a hierarchical model; that is, a conditional model for Yi given bi and a marginal model for bi:
are called the variance components and α is a vector of nuisance parameters specifying these variance components. The LMM can be equivalently viewed as a hierarchical model; that is, a conditional model for Yi given bi and a marginal model for bi:
Marginally, Yi also follows a multivariate normal (MVN) distribution:
The LMM implies the marginal model, but the converse is not true. So, the parameter vector β may have two interpretations: the population-average covariate effects, or the covariate effects conditional on a given subject. The compatibility of the marginal and conditional model interpretation holds only for the LMM, not the generalized linear mixed models (GLMM), as we will see in the later sections.
5.3.1.2 Model Estimation and Inference
We first assume that the vector of nuisance parameters in the variance components, α, is known, and write ![]() . Now β could be solved from weighted least squares:
. Now β could be solved from weighted least squares:
It is easy to verify that (5.7) is the maximum likelihood estimator (MLE) since the likelihood function is
We should note that the likelihood inference utilizes only the marginal model (5.6), but not the hierarchical models (5.4) and (5.5).
In most cases, however, α is unknown and needs to be estimated. Two common methods for estimating α are maximum likelihood (ML) and restricted maximum likelihood (REML). The ML method estimates α and β simultaneously by maximizing the likelihood function (5.8). The score equations can be derived as follows:

where αj is the jth element of α and tr(A) is the trace of matrix A.
The ML estimation may result in a substantial amount of bias for α in small samples, due to the estimation of β. A simple analogy is that the ML estimator ![]() is a biased estimation of the population variance. Bias correction involves replacing N−1 by (N − 1)−1. The REML approach uses a similar technique, and gives a better estimation of the variance components. The idea is to construct a likelihood function that is no longer a function of β. Note that
is a biased estimation of the population variance. Bias correction involves replacing N−1 by (N − 1)−1. The REML approach uses a similar technique, and gives a better estimation of the variance components. The idea is to construct a likelihood function that is no longer a function of β. Note that ![]() in (5.7) is the sufficient statistic for β, and REML is indeed a conditional likelihood function
in (5.7) is the sufficient statistic for β, and REML is indeed a conditional likelihood function ![]() . We give the form of the restricted likelihood as follows, and more details and derivations can be found in Patterson and Thompson 1971):
. We give the form of the restricted likelihood as follows, and more details and derivations can be found in Patterson and Thompson 1971):

With α estimated using the ML or REML method, β is estimated by plugging ![]() into (5.7). Conditional on α,
into (5.7). Conditional on α, ![]() follows a multivariate normal distribution with mean β and variance
follows a multivariate normal distribution with mean β and variance

In practice, we again replace α by its ML or REML estimate to evaluate this variance.
5.3.1.3 Empirical Bayes Estimates for Random Effects
In some situations, we may wish to know the value of the random effects bi, so that the individual trajectories could be portrayed. Since bi is random, the Bayesian idea is a natural choice in order to “guess” the most plausible value of a random variable. If we can find the posterior distribution ![]() , the random effects would be easily estimated by the posterior mean
, the random effects would be easily estimated by the posterior mean ![]() , with the parameters replaced by the ML or REML estimates. The estimation of bi relies on the hierarchical model, and we have
, with the parameters replaced by the ML or REML estimates. The estimation of bi relies on the hierarchical model, and we have
This leads to the conditional distribution,
where
So the empirical Bayes estimator for bi is
This is also referred to as the best linear unbiased predictor for bi (Robinson, 1991).
5.3.2 Generalized Estimating Equations
5.3.2.1 Model and Inference
In cross-sectional studies, if we suppose that the scalar response Yi comes from the exponential family, then the score equation has the following form:
where ![]() . With longitudinal data, the idea of generalized estimating equations (GEE) comes from analogy of the score equation (5.9):
. With longitudinal data, the idea of generalized estimating equations (GEE) comes from analogy of the score equation (5.9):
where
and Vi is a working covariance matrix for Yi. We usually decompose the working covariance as ![]() , where
, where ![]() is a diagonal matrix and Ri(α) is a working correlation matrix with a vector of unknown parameters α. For the exponential family, Si follows from the mean–variance relationship, and we only need to specify a plausible guess of Ri(α). Common choices of Ri are listed in Table 5.3.
is a diagonal matrix and Ri(α) is a working correlation matrix with a vector of unknown parameters α. For the exponential family, Si follows from the mean–variance relationship, and we only need to specify a plausible guess of Ri(α). Common choices of Ri are listed in Table 5.3.
Table 5.3 Common Choices of Working Correlation Ri with the Cluster Size ni = 4
| Independence | AR-1 |
 |
 |
| Exchangeable | Unstructured |
 |
 |
When the sample size N is large,![]() , defined as the solution to (5.10), approximately follows the normal distribution with mean β and variance
, defined as the solution to (5.10), approximately follows the normal distribution with mean β and variance ![]() , where
, where
and
In practice, we could replace ![]() by
by ![]() . Although this is a rather crude estimator for every single
. Although this is a rather crude estimator for every single ![]() , it leads to a good estimate of I1 with many replications. The variance
, it leads to a good estimate of I1 with many replications. The variance ![]() is also referred to as the sandwich variance estimator. One advantage of GEE is that the inference is always valid even if the working correlation matrix is incorrect. In other words, the only assumption of GEE is the mean structure:
is also referred to as the sandwich variance estimator. One advantage of GEE is that the inference is always valid even if the working correlation matrix is incorrect. In other words, the only assumption of GEE is the mean structure:
with the link function g, and the working correlation is not so important. With the correct working correlation, GEE is similar to the likelihood inference, and the sandwich variance simplifies to ![]() , which can be seen as the inverse of the information matrix. The vector of parameters, β, is interpreted as the population-average effect of the covariates.
, which can be seen as the inverse of the information matrix. The vector of parameters, β, is interpreted as the population-average effect of the covariates.
5.3.2.2 Estimation of Working Correlation
The working correlation may be specified up to the unknown vector of nuisance parameters, α, which needs to be estimated from the data. Liang and Zeger 1986) proposed to use a moment estimator for α. Their estimator is based on the Pearson residual:
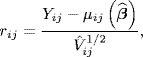
where ![]() is the estimated variance for Yij. For example, under the exchangeable working correlation, the nuisance parameter vector α becomes a scalar of within-cluster correlation coefficient α. The moment estimator for α is given by
is the estimated variance for Yij. For example, under the exchangeable working correlation, the nuisance parameter vector α becomes a scalar of within-cluster correlation coefficient α. The moment estimator for α is given by

The standard GEE procedure implemented in most software packages is as follows:
- Compute the initial estimate of
 using generalized linear models.
using generalized linear models. - Compute the Pearson residual rij and estimate for
 (and thus Ri and Vi).
(and thus Ri and Vi). - Update the estimate for
 using the estimated correlation from step 2.
using the estimated correlation from step 2. - Iterate steps 2 and 3 until convergence.
More advanced estimators for α are also proposed in the literature. Interested readers should refer to Prentice 1988), Lipsitz et al. 1991), Carey et al. 1993), and Prentice and Zhao 1991). These approaches generally need to specify another set of estimating equations for the second moments, in order to estimate α.
5.3.3 Generalized Linear Mixed Models
5.3.1 Model Setting
In Section 5.3.1, we introduced the mixed model for linear regression. The same idea could be applied to generalized linear models, when multiple observations on each subject are taken over time. Suppose that given the random effects bi, all the responses Yij are independent and follow a distribution in the exponential family. The generalized linear mixed model assumes that

where “⊥” denotes independence. Note that the vector of parameters, β, is interpreted as the subject-specific effect of the covariates (conditional on the random effects). In contrast, the parameters in GEE have a completely different marginal interpretation—the population-average effect of the covariates. Generally, GEE and GLMM are not compatible models: if one integrates out bi in ![]() according to the GLMM specification, then the marginal mean
according to the GLMM specification, then the marginal mean ![]() usually does not possess the generalized linear form.
usually does not possess the generalized linear form.
Let ![]() be the conditional density of Yij given bi, and
be the conditional density of Yij given bi, and ![]() be the marginal density of bi. Then, the likelihood function of β and D is
be the marginal density of bi. Then, the likelihood function of β and D is
If fij is the normal density, the integral could be calculated analytically, which is the LMM in Section 5.3.1. Otherwise, approximations are needed to evaluate the likelihood function.
5.3.3.2 Approximation Methods
We introduce four methods to approximate the integral in (5.11), namely, penalized quasi-likelihood (PQL), marginal quasi-likelihood (MQL), Laplace approximation, and Gaussian quadrature. The technical details of the four approximation methods are shown in Appendix 5.A.
Both the PQL and MQL use the idea of linearization in the generalized linear models (McCullagh and Nelder, 1989). Their computation is relatively simple. However, the approximation is rather crude with a small cluster size, that is, a small number of observations per subject. The performance of both methods is particularly poor for the binary outcome, usually yielding serious underestimation of the fixed effects and variance components. The MQL approximation adopts a Taylor series expansion around bi = 0, so it is recommended only when the variance of the random effects is very small. Higher order PQL and MQL approaches could potentially reduce the bias (Rodriguez and Goldman, 1995); Goldstein and Rasbash, 1996), but they are currently not implemented in R, STATA, or SAS.
The Laplace approximation uses a multivariate normal density to approximate the integrand for each subject. The Laplace approximation is also quite fast for computation, but has similar limitations to the PQL method. Since the approximation is performed on each subject, it would be more accurate with more observations per subject. With binary data, the approximation often behaves poorly. Raudenbush et al. 2000) developed higher order Laplace approximations, which have a good improvement on the accuracy and are computationally fast.
The Gaussian quadrature method is the slowest among all the approximation methods, but it leads to the best approximation of the likelihood and hence more reliable estimates of the GLMM. As long as the computation facility allows, the Gaussian quadrature is always recommended for practical use.
The first-order PQL and MQL, the first-order Laplace approximation, and Gaussian quadrature methods have all been implemented in standard software packages, for example, R, STATA, and SAS. Other statistical packages such as MLwiN (Rasbash et al., 2012) and HLM (Raudenbush et al., 2000) are also available for some higher order approaches. Breslow 2003) gave a comprehensive review of the existing methods for estimating GLMM.
5.3.4 Time-Dependent Covariates
In the discussion of the methods for longitudinal data analysis, so far we are interested in the mean of Yij given Xij, which is also called the cross-sectional mean. In practice, however, it is often the case that the mean of Yij can be affected by previous observations of covariates, Xi1, ..., Xi,j−1. For example, when studying the association between lung function and air pollution, there is usually a lag between the peak of the pollutant and the change of lung function, so the quantity of interest might be E(Yij|Xi,j−1). When studying the effect of a new drug in clinical trials, it is more reasonable to assume a cumulative treatment effect, so the interest is in E(Yij|Xi1, ..., Xij), where we condition on the whole treatment history.
We introduce an important concept for the time-dependent covariates—exogeneity. A covariate process is exogenous to the outcome process if the distribution of current covariate value is completely determined by its previous values, that is,
where ![]() and
and ![]() are the past observations of Y and X until time j and Wi is the vector of baseline or time-invariant covariates. If the conditional independence is not satisfied, then the covariate process is said to be endogenous. For example, in a clinical trial with a crossover design, if the treatment is prescribed at the start of the trial, then the treatment variable is exogenous. On the contrary, if the treatment assignment changes according to the patients' response to the drug, then the treatment variable is endogenous. In general, one can check for endogeneity by regressing Xij on both
are the past observations of Y and X until time j and Wi is the vector of baseline or time-invariant covariates. If the conditional independence is not satisfied, then the covariate process is said to be endogenous. For example, in a clinical trial with a crossover design, if the treatment is prescribed at the start of the trial, then the treatment variable is exogenous. On the contrary, if the treatment assignment changes according to the patients' response to the drug, then the treatment variable is endogenous. In general, one can check for endogeneity by regressing Xij on both ![]() and
and ![]() .
.
The advantage of exogeneity is that the joint likelihood of Y and X can be factored out:

where ni is the number of observations for subject i, ![]() , and
, and ![]() . Therefore, if one is interested only in fY|X, no assumptions on the covariate process are needed. Exogeneity also suggests that
. Therefore, if one is interested only in fY|X, no assumptions on the covariate process are needed. Exogeneity also suggests that
When a covariate is endogenous, we need to be careful in choosing the meaningful model of interest.
Pepe and Anderson 1994) have shown that when including endogenous variables into the regression model, GEE could be biased unless either of the following assumptions holds:
- Full covariate conditional mean assumption:

- A working-independent correlation assumption.
5.4 Missing Data Settings and Simple Methods
5.4.1 Setup
In Section 5.3, we summarized commonly used methods for analyzing longitudinal data without missingness. In this section, we will introduce statistical methods to handle longitudinal missing data. Sections 5.5–5.7 will focus on missing outcome only. The scenario of missing both outcome and covariates is discussed in Sections 5.8–5.10.
The pattern of the missing data can be classified as monotone and nonmonotone missingness. As a special case of monotone missingness, dropout means that if Yij is missing, all the observations after time j are missing. Otherwise, the missingness is said to be intermittent.
In Chapter 1, we distinguished the missingness mechanisms as missing completely at random (MCAR), missing at random (MAR), and missing not at random (MNAR). For longitudinal missing data, we further define covariate-dependent missingness (CDM): an MAR missingness process is CDM if the probability of nonresponse depends only on covariate X and not on Y. Chapter 5 is entirely based on the MAR assumption, and MNAR models will be introduced in Chapter 7.
5.4.2 Simple Methods
approach for handling missing longitudinal data is simply to remove all the subjects with any missing observations, known as the complete-case analysis. Although easily implemented, this method is usually biased when the missingness mechanism is MAR or MNAR. Even under the MCAR situation, deleting subjects with incomplete observations could lead to substantial loss of information, and hence result in inefficient estimators.
Another way to handle the missing data is single imputation, that is, to replace the missing value with some kind of “guess.” One of the most widely used single imputation methods is last observation carried forward (LOCF). This method replaces every missing value by the last observed value of the same subject. The LOCF method makes a very strong assumption that the value of the outcome remains unchanged after missing. When the missing data are due to cure, this assumption might be appropriate. But in many other settings, LOCF is likely to yield biased results. Saha and Jones (2009) derived an explicit expression for the bias of LOCF under a linear mixed effects model. They found that the bias for the two-group mean comparison is more severe if the time to drop out is shorter, or the dropout probability is more strongly associated with the individual random effects. They also noticed that the variance is always underestimated. Other single imputation methods, such as mean imputation or hot deck imputation, could be used as well. The disadvantage of all these single imputation methods is that the imputed observations are treated as known, so the inference does not reflect the sample variability without special adjustments.
5.5 Likelihood Approach
Let Rij be the missingness indicator of Yij, which takes the value of 1 if Yij is observed and 0 otherwise. We write ![]() . The outcome vector Yi could be partitioned into
. The outcome vector Yi could be partitioned into ![]() . For the ith subject, its contribution to the likelihood is
. For the ith subject, its contribution to the likelihood is

The second equality above holds because of the MAR assumption. Here, θ is the vector of parameters of interest and η is the vector of nuisance parameters involved in modeling the missingness mechanism. The last equality suggests that η and θ are separated in the likelihood, so the inference for θ can be simply based on ![]() . In other words, the available case analysis with the full likelihood approach would produce consistent and efficient estimators. The LMM and GLMM are both likelihood methods; therefore, when the missing data are present, we could fit the same model on
. In other words, the available case analysis with the full likelihood approach would produce consistent and efficient estimators. The LMM and GLMM are both likelihood methods; therefore, when the missing data are present, we could fit the same model on ![]() without any special treatment.
without any special treatment.
However, the available case analysis does not always work if the analysis method is not likelihood based. Typically, a GEE model on ![]() is unbiased only when the missingness mechanism is CDM. A heuristic proof is provided as follows. The estimating equation for the available case analysis is
is unbiased only when the missingness mechanism is CDM. A heuristic proof is provided as follows. The estimating equation for the available case analysis is
where
We have

where Πi(·) is the expectation of Δi given Yi and Xi. Only under CDM, Πi(·) does not depend on ![]() , and thus the expectation of the estimation equation is 0. Under MAR, the expectation would depend on the second moment of
, and thus the expectation of the estimation equation is 0. Under MAR, the expectation would depend on the second moment of ![]() and is not necessarily 0. In the situations where Ri depends on both
and is not necessarily 0. In the situations where Ri depends on both ![]() and Xi, a weighted GEE approach could be used, as shown in Section 5.6.
and Xi, a weighted GEE approach could be used, as shown in Section 5.6.
5.5.1 Example: IMPACT Study
Table 5.4 lists percentages of missingness by treatment and month. It appears that the intervention arm had a slightly lower percentage of missing data in SCL-20 scores, but the differences did not appear to be significant between the two arms.
Table 5.4 Percentages of Missingness by Treatment and Month
| Usual Care | Intervention | Both Arms | |
| Month 3 | 12.4 | 10.26 | 11.33 |
| Month 6 | 14.08 | 11.59 | 12.83 |
| Month 12 | 18.44 | 15.01 | 16.71 |
| Month 18 | 22.12 | 19.43 | 20.77 |
| Month 24 | 23.46 | 22.08 | 22.77 |
Note that we model the IMPACT data by (5.1). We carry out some inferences in the following sections. There are more efficient imputation techniques available for monotone missingness. To illustrate the method, we first drop the subjects with intermittent missing outcome values and then return to the full sample toward the end.
5.5.1.1 Complete-Case Analysis
We first consider the subjects with complete data (N = 1269). The intervention arm is estimated to have 0.3115 more reduction in change from baseline for the SCL-20 score than the usual care group.
For the complete-case analysis, the estimated fixed effects and variance components from the linear mixed effects model are displayed in Table 5.5. A test of the null hypothesis, H0 : β4 = 0, indicates that there is a significant group × period interaction at the 0.05 level. These results suggest that there are differences between the two treatment arms in terms of subject-specific changes in the expected SCL-20 scores. In particular, there is a greater reduction in the expected SCL-20 score from baseline for patients treated with IMPACT care (compared with patients who received the usual care).
Table 5.5 Estimates Based on the Complete-Case Analysis
| Parameter | Estimate | Robust SE | 95% CI |
| β1 | 1.689 | 0.025 | (1.639, 1.738) |
| β2 | −0.347 | 0.024 | (−0.395, −0.299) |
| β3 | −0.006 | 0.034 | (−0.073, 0.060) |
| β4 | −0.312 | 0.034 | (−0.378, −0.245) |
| 0.452 | 0.016 | (0.422, 0.484) | |
| 0.412 | 0.019 | (0.377, 0.450) | |
| Corr(b1i, b2i) | −0.235 | 0.051 | (−0.332, −0.134) |
The estimated variance components for the random intercept and slope indicate that there is substantial variability in the baseline SCL-20 score in the study population and also substantial variability in the patient-to-patient changes in the SCL-20 score in response to the treatment. For example, the estimated standard deviation of the random intercepts, ![]() , implies that there is substantial patient-to-patient variability in terms of their baseline SCL-20 score, since ~95% of the patients have a baseline SCL-20 score that varies from 1.689 − 1.96 × 0.452 to 1.689 + 1.96 × 0.452, or from 0.803 to 2.575. Similarly, there is moderate heterogeneity in the patient-to-patient changes in the SCL-20 score. Finally, the negative correlation among the random intercepts and slopes is significant, indicating that the expected change in the SCL-20 score is directly related to the baseline SCL-20 score, and patients with higher baseline SCL-20 scores tend to have smaller changes in SCL-20 scores, compared with those with lower baseline SCL-20 scores.
, implies that there is substantial patient-to-patient variability in terms of their baseline SCL-20 score, since ~95% of the patients have a baseline SCL-20 score that varies from 1.689 − 1.96 × 0.452 to 1.689 + 1.96 × 0.452, or from 0.803 to 2.575. Similarly, there is moderate heterogeneity in the patient-to-patient changes in the SCL-20 score. Finally, the negative correlation among the random intercepts and slopes is significant, indicating that the expected change in the SCL-20 score is directly related to the baseline SCL-20 score, and patients with higher baseline SCL-20 scores tend to have smaller changes in SCL-20 scores, compared with those with lower baseline SCL-20 scores.
5.5.1.2 Available Data Analysis
One advantage with the mixed effects model is that it allows all available data to be included in the analysis. In the following example, we again consider the sample with monotone missingness (N = 1639), and the results based on the available data analysis are reported in Table 5.6. Compared to the complete-case analysis, the estimated intervention effect (group × period) is smaller with smaller standard error too.
Table 5.6 Estimates Based on the Available Data Analysis
| Parameter | Estimate | Robust SE | 95% CI |
| β1 | 1.686 | 0.022 | (1.644, 1.729) |
| β2 | −0.335 | 0.022 | (−0.378, −0.291) |
| β3 | −0.003 | 0.030 | (−0.056, 0.062) |
| β4 | −0.295 | 0.031 | (−0.356, −0.235) |
| 0.455 | 0.014 | (0.428, 0.484) | |
| 0.414 | 0.018 | (0.380, 0.451) | |
| Corr(b1i, b2i) | −0.200 | 0.048 | (−0.292, −0.105) |
5.5.1.3 Last Observation Carried Forward Analysis with Monotone Missingness
A popular and less sophisticated approach is the last observation carried forward approach. By its name, the last observed value is used to replace all missing values if a subject drops out. The results of the LOCF analysis are listed in Table 5.7. Note that the estimated intervention effect is much smaller than both complete-case analysis and available data analysis, suggesting that such an approach is very prone to bias.
Table 5.7 Estimates Based on the LOCF Analysis
| Parameter | Estimate | Robust SE | 95% CI |
| β1 | 1.686 | 0.022 | (1.644, 1.729) |
| β2 | −0.313 | 0.021 | (−0.354, −0.271) |
| β3 | −0.003 | 0.030 | (−0.056, 0.062) |
| β4 | −0.264 | 0.030 | (−0.323, −0.206) |
| 0.481 | 0.013 | (0.458, 0.508) | |
| 0.449 | 0.016 | (0.419, 0.482) | |
| Corr(b1i, b2i) | −0.193 | 0.040 | (−0.270, −0.113) |
5.6 Inverse Probability Weighted GEE with MAR Dropout
The standard GEE model is valid only under the CDM assumption. Under a weaker assumption of MAR, two different formulations of the inverse probability weighted GEE were proposed by Robins et al. (1995) and Fitzmaurice et al. 1995), which we refer to as the IPWGEE1 and IPWGEE2 methods, respectively. The difference is that IPWGEE1 (Robins et al., (1995) uses observation-level weights and IPWGEE2 (Fitzmaurice et al., 1995) uses cluster-level weights.
5.6.1 Modeling the Selection Probability
The dropout pattern implies that if Rij = 0, then Ri,j+1 = 0. Assume that Ri1 = 1 for the first time point. Let ![]() , which indicates the time of dropout and takes the value between 2 and ni + 1. The maximum value Mi = ni + 1 corresponds to a subject with complete longitudinal observations.
, which indicates the time of dropout and takes the value between 2 and ni + 1. The maximum value Mi = ni + 1 corresponds to a subject with complete longitudinal observations.
The continuation ratio model (CRM) can be used to estimate the selection model. Define
Assume that
where Wij is the design matrix expanded by Xi, Yi1, ... , Yi,j−1. The CRM can be regarded as a discrete-time survival model, which estimates the dropout probability at the current time point, given the dropout not occurring at previous time points. Note that

which is the likelihood contribution for the ith subject in estimating the selection model. The MLE for the continuation ratio model are readily available from many standard statistical packages.
5.6.2 IPWGEE1 and IPWGEE2
Robins et al. (1995) proposed to weight the observation Yij using
in which the denominator is denoted as πij. Note that

The second equation is due to factoring out the joint distribution of Ri1, ..., Rij. This leads to the following estimating equation for IPWGEE1:
where
Here, ![]() is the estimated selection probability from the continuation ratio model. Because λik is always smaller than 1, πij decreases as j increases. In other words, more weights are assigned to the later observations.
is the estimated selection probability from the continuation ratio model. Because λik is always smaller than 1, πij decreases as j increases. In other words, more weights are assigned to the later observations.
An alternative approach is to weight each subject by the inverse of the probability of dropping out at the observed time (Fitzmaurice et al., 1995). In this formulation, the estimating equation for IPWGEE2 becomes
where
Here, ![]() is the estimated dropout probability from the continuation ratio model, with mi being the observed dropout time for subject i.
is the estimated dropout probability from the continuation ratio model, with mi being the observed dropout time for subject i.
If the true value of λik is used instead of being estimated from the continuation ratio model, the standard theory of estimating equations leads to the sandwich variance estimator for ![]() :
:
Here, Ui is the summand in (5.13) or (5.14) and IN is the derivative of ∑iUi:

However, estimating the selection model contributes an additional term to the sandwich variance formula (5.15), and a rigorous proof is given in Robins et al. (1995). For simplicity, we just ignore the additional term, and the sandwich variance formula seems to work well in our simulation study.
5.6.3 A Simulation Study
We conduct a simulation study to compare the two IPWGEE methods with the naive GEE estimator that ignore the missing data. Consider N = 400 subjects, each with ni = 5 observations. The true model is generated by a mixed effects model:
The Age variable follows the uniform distribution between 0 and 1, indicating the baseline age of the subject; the Time variable takes values from 1 up to 5, being the time of observation; the Treatment variable is equal to 0 for half of the subjects and 1 for the other half; bi is the random intercept and εij is the random error, both of which independently follow a normal distribution with variance 1.22 and 1, respectively. The marginal mean model is a probit model:
where Φ is the cumulative distribution function of a standard normal distribution. The dropout process is generated from a continuation ratio model:

The averaged parameter estimation and the 95% CI coverage are shown in Table 5.8. Both IPWGEE1 and IPWGEE2 are consistent and the CI coverage rates are close to the nominal level. The ordinary GEE is biased as we expected.
Table 5.8 The Average of Estimated Regression Parameters (Coverage Rate in Percentage of a CI with Nominal Level 95%) for the Full Data Estimator, Available Case Analysis (GEE), IPWGEE1, and IPWGEE2
| True | Full Data | GEE | IPWGEE1 | IPWGEE2 | |
| Intercept | −3.841 | −3.867 (94.6) | −3.697 (84.6) | −3.871 (92.6) | −3.892 (93.8) |
| Age | 1.280 | 1.282 (95.0) | 1.157 (89.0) | 1.277 (93.2) | 1.261 (95.0) |
| Time | 0.768 | 0.774 (94.4) | 0.716 (71.6) | 0.775 (94.0) | 0.781 (91.8) |
| Treatment | 0.960 | 0.969 (96.2) | 0.949 (94.0) | 0.973 (95.4) | 0.991 (94.0) |
More extensive simulations that compare IPWGEE1 and IPWGEE2 can be found in Preisser et al. 2002). They found that IPWGEE2 is considerably less efficient than IPWGEE1, while both are consistent. When the dropout probability is low, IPWGEE2 could be quite inefficient and anticonservative (larger type 1 error rate than expected) for small samples.
5.6.4 Example: IMPACT Study
We next illustrate how to implement the two IPWGEE methods to analyze longitudinal data with dropouts (therefore, the missing data pattern is monotone).
With the Stata code presented in Appendix 5.A, we first estimate the probability that an outcome is observed at a specific time point, given the prior observed outcome variables and some selected baseline characteristics using the continuation ratio model. We then generate both observation-level weights and cluster (subject)-level weights based on the estimated probabilities. It is worth noting that the uncertainty in the estimated weights will not be accounted for in the IPWGEE analysis. One way to get around this is to apply a bootstrap method.
The results obtained from the two IPWGEE methods are listed in Tables 5.9 and 5.10. It can be seen that the estimated treatment effect (β4 = − 0.3140) of the IPWGEE1 is close to what we had before. The estimated intervention effect (β4 = − 0.2044) of the IPWGEE2 is much smaller with a much wider confidence interval, suggesting that the estimator using cluster-level weights may not be stable in this case.
Table 5.9 Estimates Based on the IPWGEE1 Analysis
| Parameter | Estimate | Robust SE | 95% CI |
| β1 | 1.686 | 0.022 | (1.644, 1.729) |
| β2 | −0.327 | 0.023 | (−0.372, −0.282) |
| β3 | −0.003 | 0.030 | (−0.056, 0.062) |
| β4 | −0.314 | 0.032 | (−0.377, −0.251) |
Table 5.10 Estimates Based on the IPWGEE2 Analysis
| Parameter | Estimate | Robust SE | 95% CI |
| β1 | 1.679 | 0.041 | (1.599, 1.759) |
| β2 | −0.374 | 0.050 | (−0.472, −0.276) |
| β3 | −0.013 | 0.060 | (−0.105, 0.131) |
| β4 | −0.204 | 0.070 | (−0.343, −0.066) |
5.7 Extension to Nonmonotone Missingness
It is common in longitudinal studies that subjects may miss intermittent visits, or some measurements in a particular visit are missing, for example, item nonresponse. In this case, likelihood-based inferences remain valid, but IPWGEE methods need to be modified. The modified IPWGEE is referred to as IPWGEE3.
We continue to use Rij as the missing indicator, but Rij = 0 no longer implies Ri,j+1 = 0. The extension is based on IPWGEE2, where the weight is the inverse of the probability of observing the current missing pattern, that is,
A simpler case is when one is willing to assume conditional independence for Rij within the same subject i. We can use logistic regression to estimate ![]() , and multiplying over all j yields the joint probability (5.16). An example might be in the clustered survey sampling, where i represents a class and j represents a student in the class. Then after conditioning on some student characteristics, the nonresponse of one student is independent of other students.
, and multiplying over all j yields the joint probability (5.16). An example might be in the clustered survey sampling, where i represents a class and j represents a student in the class. Then after conditioning on some student characteristics, the nonresponse of one student is independent of other students.
However, conditional independence is less likely in longitudinal studies. A subject may be more prone to missingness due to some of his/her unobserved characteristics. So, the missing indicators on different occasions are often positively correlated. For example, in the NACC UDS data, a patient with more serious cognitive impairment tends to miss more test results. Of course, we could adjust for the disease severity (e.g., clinical dementia rating sum of boxes) and assume conditional independence anyway. But a more realistic modeling framework would be a random effects model. The joint distribution (5.16) is indeed the ith subject's contribution to the likelihood after the integration over the random effects distribution, which is the by-product of estimating the random effects model using the Gaussian quadrature.
λi estimated, we can weight the available case GEE with 1/λi for subject i, which we call IPWGEE3a if independent missingness is assumed and IPWGEE3b if the random effects model is used to estimate the selection probability. The same variance formula (5.15) for IPWGEE1 and IPWGEE2 can be directly applied to IPWGEE3.
5.8 Multiple Imputation
The likelihood approach and the weighted estimating equation approach provide valid inference with the monotone missingness pattern (dropout), and their extensions to the intermittent missingness are straightforward. However, if some of the covariates are subject to missingness too, neither approach has simple extensions. Multiple imputation, as we have seen in Chapter 4, is now a flexible choice to deal with the complicated missing patterns. As long as the imputation model is carefully specified to approximate the true data generation mechanism (although usually hard in practice), the inference immediately simplifies to the analysis model of the full data, and is usually valid using Rubin's combination rule. As commented by van Buuren and Groothuis-Oudshoorn 2011), a good imputation model should reflect the true data generation process, preserve the correlations of the variables, and include uncertainty about the correlations. In the context of longitudinal studies, the difficulty is that the imputation model should take into account the multivariate relationship of the missing variables at one time point, as well as their longitudinal patterns. In this section, we introduce two major ways to set up the imputation model: joint modeling and conditional modeling.
5.8.1 Joint Imputation Model
Schafer (1997a 1997) proposed a Bayesian framework for MI using a multivariate linear mixed model. An important assumption he made was that all the variables subject to missingness follow a multivariate normal distribution. We will outline this method below.
We introduce the following notations that are different from previous sections. Let yi be an ni × r matrix, where each row of yi corresponds to an observation time point for subject i, and each column corresponds to a variable subject to missingness. So this “outcome” matrix includes all the variables to be imputed: not only the outcome variables for the main analysis, but also the covariates with missing values. Assume that yi follows a multivariate linear mixed model:
where Xi is an ni × p matrix of covariates that are not subject to missingness, Zi is an ni × q design matrix for the random components, β is a p × r matrix of the fixed effects, and bi is a q × r matrix of the random effects. We further assume that each row of the residual matrix, εi, independently follows N(0, Σ), while the random effects are distributed as
independently for i = 1, ..., N. The superscript V indicates vectorization of a matrix by stacking its columns. By integration over bi, the marginal model becomes
where Ir is the identity matrix of r dimensions and ⊗ is the Kronecker product. We partition yi into yi(obs) and yi(mis), denoting the observed and missing parts of yi, respectively. Let ![]() and
and ![]() . Let
. Let ![]() and θ = (β, Σ, Ψ). The Gibbs sampler updates bi, θ, and yi(mis) iteratively, in the following three steps:
and θ = (β, Σ, Ψ). The Gibbs sampler updates bi, θ, and yi(mis) iteratively, in the following three steps:

These three steps give the sequences {θ(t)} and ![]() , which converge in distribution to P(θ|Yobs) and P(Ymis|Yobs), respectively. The first step is to draw a sample from a multivariate normal distribution. The second step is a full Bayesian analysis pretending we have the complete data. With conjugate priors on θ, it can be shown that the posterior of β is from a multivariate normal distribution, whereas the variance components Σ−1 and Ψ−1 are from Wishart distributions. The last step is to draw a sample from the multivariate normal distribution, because of the normality assumption of the multivariate linear mixed model. The whole algorithm is implemented in the R library PAN.
, which converge in distribution to P(θ|Yobs) and P(Ymis|Yobs), respectively. The first step is to draw a sample from a multivariate normal distribution. The second step is a full Bayesian analysis pretending we have the complete data. With conjugate priors on θ, it can be shown that the posterior of β is from a multivariate normal distribution, whereas the variance components Σ−1 and Ψ−1 are from Wishart distributions. The last step is to draw a sample from the multivariate normal distribution, because of the normality assumption of the multivariate linear mixed model. The whole algorithm is implemented in the R library PAN.
The Gibbs sampler resembles the idea of data augmentation (Tanner and Wong, 1987) in drawing random sample from the posterior predictive distribution. The major difference is that the estimation of θ is not of high priority, as the multiple imputation model (5.17) itself is a nuisance. The interest here is only in drawing samples from the posterior predictive distribution P(Ymis|Yobs). In practice, after a suitable number of burn-in cycles, samples from every kth iteration are stored as the imputed data, in order to remove the autocorrelation within the samples. The advantage of the joint imputation model is that proper imputation (in the sense that the imputation comes from the posterior predictive distribution) is guaranteed, as long as the multivariate linear mixed model (5.17) holds. However, it cannot handle the missingness of categorical variables.
5.8.2 Imputation by Chained Equations
For a longitudinal study with a fixed-time design, the imputation could be performed on a “wide format” of the data set, meaning that each subject takes up one row. The outcome and time-varying covariates, which are observed at different but fixed time points, are treated as different variables (columns). In this case, the multiple imputation procedure is the same as that in cross-sectional studies. The outcome variable at one time point could predict the outcome at another time point in the imputation model, which reflects the within-subject dependence. If a longitudinal study does not have the fixed-time design, the data set can only be recorded in a “long format”; that is, each row corresponds to one observation of a subject and each subject contributes multiple rows. The NACC UDS data set is such an example, since the participants visited the clinics at different times. Then the imputation model should distinguish the subject-level and observation-level variables. The general framework of chained equations described in Section 2.3.2 still works. But for observational-level variables, the conditional distribution ![]() should specify the clustering structure, often by including random effects. For subject-level variables, the imputation should be performed only once for each subject. We will demonstrate these in detail with the analysis of NACC UDS data.
should specify the clustering structure, often by including random effects. For subject-level variables, the imputation should be performed only once for each subject. We will demonstrate these in detail with the analysis of NACC UDS data.
Beunckens et al. 2008) compared the MI and IPWGEE approaches in analyzing binary longitudinal data with dropout. They found that in finite sample settings, MI is less biased and more precise. In addition, MI is not very sensitive to the misspecification of the imputation model. The efficiency issue of IPWGEE could potentially be addressed by augmented IPW estimators, as we will introduce in the next section. However, the implementation of the augmented IPW estimators may be quite difficult, especially when the missingness involves both the outcome and the covariates. In these cases, the MI approach is generally recommended.
5.8.3 Example: NACC UDS Data
The NACC UDS example was introduced in Section 5.2, and we now demonstrate the use of R library mice to impute and analyze this example. Recall that our aim is to explore the risk factors that affect the decline of the MMSE score. Let Yij be the MMSE score for subject i at the jth time tij; let Xij be the vector of covariates, including baseline age, gender, education, HIS, and APOE e4. Using generalized estimating equations, we can fit the following regression model:
The interaction term is of primary interest, which is interpreted as the increase in the average rate of MMSE decline per unit increase in Xij.
Four variables are subject to missingness: the outcome, MMSE score, is a continuous-scale observation-level variable; HIS is an ordinal observation-level variable; APOE e4 is a binary subject-level variable; and education is an ordinal subject-level variable. Since the interaction terms are included in the analysis model (5.18), it is recommended that they should also be included in the imputation model.
We conduct the multiple imputation in several steps:
- Prepare the data set for imputation by appending the transformation of variables, dummy variables, and interaction terms. Initialize the imputation parameters by “dry run” with the maximum number of iteration set to 0.
- Specify the imputation methods. A two-level linear mixed effects model (2l.norm in the R package mice) is used to impute MMSE. MMSE is bounded between 0 and 30, whereas the 2l.norm method draws posterior samples from an unbounded normal distribution. Therefore, we transform the MMSE score as
 to force it unbounded and impute the transformed score. The back-transformed original score is generated by a “passive imputation.” The passive imputation means that the imputed values are computed from other imputed variables, as opposed to be generated from an imputation model. For the ordinal HIS, mice cannot handle the two-level clustering, so we can choose either the predictive mean matching (pmm) or the ordinal logit model (polr) method, both of which ignore the longitudinal structure. In our example, we use the pmm method. For imputing education and APOE e4, we choose the predictive mean matching at the subject level only (2lonly.pmm in the R package mice). The observation-level variables are aggregated within each cluster to serve as covariates in the imputation model. All the dummy variables and interaction terms that involve missing data were passively imputed.
to force it unbounded and impute the transformed score. The back-transformed original score is generated by a “passive imputation.” The passive imputation means that the imputed values are computed from other imputed variables, as opposed to be generated from an imputation model. For the ordinal HIS, mice cannot handle the two-level clustering, so we can choose either the predictive mean matching (pmm) or the ordinal logit model (polr) method, both of which ignore the longitudinal structure. In our example, we use the pmm method. For imputing education and APOE e4, we choose the predictive mean matching at the subject level only (2lonly.pmm in the R package mice). The observation-level variables are aggregated within each cluster to serve as covariates in the imputation model. All the dummy variables and interaction terms that involve missing data were passively imputed. - Specify the prediction matrix of the imputation model. Each row of the prediction matrix corresponds to an imputation model for a variable, where “1” indicates the column variable is used as a predictor, whereas 0 means it is not used. In the two-level imputation methods, “−2” indicates the clustering variable and “2” indicates the random effects. Passive imputation overrules the predictor matrix elements, so the rows of passively imputed variables can be set as any value.
- Specify the visit scheme, that is, the order of imputation. We need to keep the passive imputations synchronized with the imputed variables. In our case, the imputation of mmse2, education, apoee4, and hachin should be updated first, and then the transformations, dummy variables, and interactions are generated.
- Call the mice function to impute the data set.
We also try to impute MMSE using the predictive mean matching method and see whether the result changes as we ignore the within-cluster correlation. Two imputation models are implemented for m = 20 times. We set m = 20 mainly for diagnostic purposes. The imputed values are plotted in Figure 5.2, which shows that the 20 imputations are well mixed indicating healthy convergence.

Figure 5.2 Diagnostic plot for the imputed hachin, education, mmse2, and apoee4.
We can now conduct the analysis for the 20 imputed data sets. The combination is performed using Rubin's rule. The analysis results are shown in Table 5.11. CC refers to the complete-case analysis, imputation 1 uses 2l.norm for MMSE, and imputation 2 uses pmm for MMSE. We can see that both imputation methods give similar results, and the results of CC might be a bit biased with larger standard errors. Since baseline age is centered at 75 years, the coefficient for “year since aMCI” is interpreted as the average rate of decline per year (about 0.3 point decrease every year) for a female aged 75 at the baseline, with 0–12 years of education, 0 point HIS, and no APOE e4 allele. Imputation model 2 identifies all five risk factors to affect the level of MMSE; three of the risk factors significantly affect the rate of MMSE decline, namely, age, APOE e4, and education. For example, a subject with APOE e4 allele has about 0.44 point more decrease in MMSE every year compared with a subject without APOE e4 allele.
Table 5.11 Analysis Results of NACC UDS Data
| Imputation 1 | Imputation 2 | CC | ||
| (Intercept) | 26.51 (0.15) | 26.51 (0.15) | 26.55 (0.18) | |
| Age | Per 10 years | −0.39 (0.08) | −0.37 (0.07) | −0.33 (0.09) |
| Gender | Male | −0.40 (0.10) | −0.36 (0.10) | −0.44 (0.13) |
| APOE e4 | −0.48 (0.13) | −0.49 (0.12) | −0.45 (0.13) | |
| Education | 13–16 years | 1.31 (0.14) | 1.35 (0.14) | 1.25 (0.17) |
| 17+ years | 1.71 (0.15) | 1.74 (0.14) | 1.81 (0.18) | |
| HIS | 1 point | −0.12 (0.11) | −0.11 (0.11) | −0.09 (0.13) |
| 2+ points | −0.33 (0.16) | −0.32 (0.16) | −0.10 (0.19) | |
| Year since aMCI | −0.26 (0.10) | −0.29 (0.11) | −0.24 (0.12) | |
| Age:year | Per 10 years | −0.06 (0.05) | −0.14 (0.06) | −0.14 (0.06) |
| Gender:year | Male | −0.02 (0.07) | −0.04 (0.07) | −0.05 (0.08) |
| APOE e4:year | −0.42 (0.08) | −0.44 (0.09) | −0.53 (0.09) | |
| Education:year | 13–16 years | −0.21 (0.09) | −0.22 (0.09) | −0.18 (0.10) |
| 17+ years | −0.14 (0.09) | −0.13 (0.10) | −0.12 (0.11) | |
| HIS:year | 1 point | 0.09 (0.08) | 0.09 (0.09) | 0.10 (0.10) |
| 2+ points | 0.02 (0.11) | −0.03 (0.12) | −0.10 (0.14) |
Although in this example ignoring the clustering in the imputation model does not seem to affect the final results, this is not warranted in other settings. Future research is needed to explore the effect of misspecifying the imputation model. The linear mixed effects model is the only available build-in function for the two-level imputation in mice, but the multivariate normality assumption is quite strong in practice. If more complicated imputation models are to be used in mice, the readers should refer to van Buuren and Groothuis-Oudshoorn 2011) for the user-defined imputation functions.
5.8.4 Example: IMPACT Study
5.8.4.1 Multiple Imputation with Monotone Missingness
With monotone missingness, the joint imputation method greatly simplifies in terms of the computation load. The basic idea is that missing data are imputed sequentially, from the variable with the least proportion of missingness to the one with the most missingness. While imputing for longitudinal data, the within-subject correlation needs to be taken into account as well. In general, we recommend multivariate imputation methods such as multivariate normal or chained equations for this type of imputation task. In the Stata code, given in Appendix 5.A, baseline covariates such as age, gender, study site, and so on are first used to impute the SCL-20 score at baseline using the linear regression model, and then baseline covariates plus the SCL-20 score at baseline are used to impute the SCL-20 score at month 3, and so on until missing SCL-20 scores at month 24 are imputed. In the following code, 10 imputed data sets are generated. Estimation is performed on each imputed data set, and the results are then pooled together to produce the final result. Because the analysis model examines the interaction between time and treatment, we conduct the imputation for the subjects in the intervention and control arms separately.
The results are listed in Table 5.12. The estimated intervention effect (group × period) is slightly smaller than that estimated based on available data analysis.
Table 5.12 Estimates Based on the Multiple Imputation with Monotone Missingness
| Parameter | Estimate | Robust SE | 95% CI |
| β1 | 1.686 | 0.022 | (1.644, 1.729) |
| β2 | −0.335 | 0.022 | (−0.379, −0.291) |
| β3 | −0.003 | 0.030 | (−0.056, 0.062) |
| β4 | −0.288 | 0.031 | (−0.350, −0.227) |
| 0.453 | 0.014 | (0.426, 0.482) | |
| 0.415 | 0.018 | (0.382, 0.451) | |
| Corr(b1i, b2i) | −0.202 | 0.048 | (−0.293, −0.108) |
5.8.4.2 Multiple Imputation Based on Multivariate Normal Distribution
For a continuous longitudinal outcome with missing values, another approach for missing data imputation is to first assume a multivariate normal distribution on the outcome vector and then to proceed with the imputation using the likelihood approach. The details have been provided in Schafer (1997b 1997). Also note that this imputation approach works for arbitrary missing data patterns. For categorical outcome with missing values, latent variable models could be employed with this imputation approach.
Table 5.13 shows the results of the multiple imputation method based on MVN. It can be seen that the results are close to those based on the multiple imputation with monotone missingness (Table 5.12).
Table 5.13 Estimates Based on the Multiple Imputation with Multivariate Normal Distribution
| Parameter | Estimate | Robust SE | 95% CI |
| β1 | 1.686 | 0.022 | (1.644, 1.729) |
| β2 | −0.338 | 0.023 | (−0.383, −0.293) |
| β3 | −0.003 | 0.030 | (−0.056, 0.062) |
| β4 | −0.286 | 0.032 | (−0.348, −0.224) |
| 0.454 | 0.014 | (0.427, 0.482) | |
| 0.422 | 0.019 | (0.386, 0.462) | |
| Corr(b1i, b2i) | −0.207 | 0.049 | (−0.301, −0.109) |
5.8.4.3 Multiple Imputation Based on Chained Equations
We next apply the multiple imputation with chained equations (MICE) approach to the IMPACT data set with monotone missingness. The results are shown in Table 5.14, from which it can be seen that the results are similar to the results based on the above two multiple imputation methods. It is worth noting that MICE applies to general missing data patterns. The results are very similar to those from both monotone MI and MVN MI.
Table 5.14 Estimates Based on Multiple Imputation with Chained Equations
| Parameter | Estimate | Robust SE | 95% CI |
| β1 | 1.686 | 0.022 | (1.644, 1.729) |
| β2 | −0.335 | 0.022 | (−0.379, −0.291) |
| β3 | −0.003 | 0.030 | (−0.056, 0.062) |
| β4 | −0.288 | 0.031 | (−0.350, −0.227) |
| 0.453 | 0.014 | (0.426, 0.482) | |
| 0.415 | 0.018 | (0.382, 0.451) | |
| Corr(b1i, b2i) | −0.202 | 0.048 | (−0.293, −0.108) |
5.8.4.4 Multiple Imputation with Chained Equations for a General Missing Data Pattern
We now illustrate MICE when there are both the missing outcome and missing covariates with a general missing data pattern. In The IMPACT data, not only there are missing values in the SCL-20 score, there are also missing values in baseline number of chronic diseases (numdis1), preference on depression treatment (pref00), race (white), baseline general health status (ghlth00), and income (inc400). It is conceivable that we could do a better imputation of the missing outcome if we can gather more information on these important covariates. Specifically, we used logistic regression to impute race, ordinal logistic regression for treatment preference and general health status given they are multilevel categorical variables, Poisson regression model for a number of chronic conditions, predictive mean matching for income, and finally linear regression for SCL-20 scores. The results are shown in Table 5.15. It can be seen that for the IMPACT study, the results using all four multiple imputation methods generally agree.
Table 5.15 Estimates Based on Multiple Imputation with Chained Equations for a General Missing Data Pattern
| Parameter | Estimate | Robust SE | 95% CI |
| β1 | 1.672 | 0.020 | (1.632, 1.712) |
| β2 | −0.315 | 0.022 | (−0.358, −0.273) |
| β3 | −0.010 | 0.029 | (−0.046, 0.066) |
| β4 | −0.289 | 0.031 | (−0.349, −0.227) |
| 0.448 | 0.014 | (0.422, 0.476) | |
| 0.419 | 0.019 | (0.384, 0.457) | |
| Corr(b1i, b2i) | −0.206 | 0.047 | (−0.295, −0.112) |
From Tables 5.5–5.7, 5.9, 5.10, and 5.12 –5.15, it is seen that for the IMPACT study, all the missing data methods show similar results, except the IPWGEE1. In general, we recommend the mixed effects model and multiple imputation methods for longitudinal data analysis with missing data. This is also the recommendation given by Schafer and Graham 2002).
5.9 Bayesian Inference
The Bayesian approach for a cross-sectional regression model has been discussed in Chapter 4. Under the assumption of MAR, the missing mechanism model can be ignored. So, the data augmentation procedures can be used to estimate the posterior distribution of the regression parameters. The same model framework applies to longitudinal studies, except that in the missing data model, the within-cluster correlation needs to be characterized by mixed effects models.
The outcome vector Yi is partitioned into ![]() . The covariate matrix Xi can also be partitioned as
. The covariate matrix Xi can also be partitioned as ![]() , where
, where ![]() includes the covariates subject to missingness and
includes the covariates subject to missingness and ![]() includes the completely observed covariates. For simplicity, assume that only one covariate is subject to missingness, so
includes the completely observed covariates. For simplicity, assume that only one covariate is subject to missingness, so ![]() has one column. If
has one column. If ![]() is a time-varying covariate, we can further partition
is a time-varying covariate, we can further partition ![]() to be
to be ![]() . And we use
. And we use ![]() to denote
to denote ![]() , and
, and ![]() to denote
to denote ![]() . Let θ be the vector of unknown parameters in the regression model of Yi versus Xi, as well as the nuisance parameters used to specify the missing covariate model,
. Let θ be the vector of unknown parameters in the regression model of Yi versus Xi, as well as the nuisance parameters used to specify the missing covariate model, ![]() .
.
Estimation of the posterior distribution ![]() is of our primary interest. The data augmentation procedures can be used to draw the target posterior distribution in two iteration steps: imputation step and posterior step. In the
is of our primary interest. The data augmentation procedures can be used to draw the target posterior distribution in two iteration steps: imputation step and posterior step. In the ![]() th iteration, the imputation step draws the missing data from the conditional distribution:
th iteration, the imputation step draws the missing data from the conditional distribution:
The imputation step results in a complete data set with no missing values. Then, the posterior step takes a random draw from the posterior conditional distribution:
where ![]() is the complete-data likelihood for subject i and p(θ) is the prior distribution for the parameters.
is the complete-data likelihood for subject i and p(θ) is the prior distribution for the parameters.
The posterior step is simply a standard Bayesian analysis without missing data, and the posterior sample can be drawn using Gibbs sampling. The difficulty mainly lies in the imputation step. Note that

Here, the density of ![]() can be ignored as it does not include any missing values. It suffices to specify the full data models Yi|Xi and
can be ignored as it does not include any missing values. It suffices to specify the full data models Yi|Xi and ![]() . The conditional distribution of Yi|Xi is given by the regression model of interest, which is often a generalized linear mixed effects model; the conditional distribution
. The conditional distribution of Yi|Xi is given by the regression model of interest, which is often a generalized linear mixed effects model; the conditional distribution ![]() can be specified by another regression model.
can be specified by another regression model.
Although the Bayesian inference can be outlined simply in two iterative procedures, the computation load could be quite intensive for several reasons. First, if the outcome Yi is categorical, the marginal likelihood involves intractable integrals. So additional steps are taken to “augment” the random effects as if they were the missing data. Second, in practice, multiple covariates could be subject to missingness, so the imputation step could involve calculation of the quite complicated multivariate distribution of the missing data. It could be time-consuming to draw imputation samples.
5.10 Other Approaches
Many other missing data methods have been proposed in the literature. However, they are not implemented in standard statistical packages and are less commonly used in practice. We briefly review some estimating equation approaches in this section and provide references for the interested readers. Particularly, we first discuss a mean score imputation approach, and then review several doubly robust methods.
5.10.1 Imputing Estimating Equations
Paik (1997) proposed an imputation approach that could handle the dropout of the outcome variable. The approach is based on generalized estimating equations, and the equations with missing observations are replaced by their conditional expectations. This idea is the same as the “mean score imputation” in the cross-sectional setting (Chapter 4). Two important assumptions are as follows: (a) The longitudinal observations are all scheduled at fixed time points, j = 1, ..., M. (b) The dropout process depends only on observed variables, that is, the MAR dropout process.
Let ![]() be the full vector of outcome variables for subject i and
be the full vector of outcome variables for subject i and ![]() be the full matrix of corresponding covariates. The primary interest is the regression model of
be the full matrix of corresponding covariates. The primary interest is the regression model of ![]() . The observed data for subject i are from the first ni visits:
. The observed data for subject i are from the first ni visits: ![]() and
and ![]() . Let Hij = (Xi, Yi1, ..., Yij) be the history of ith subject up to time j. Let Rij be the missing indicator of Yij, similar as in the previous sections.
. Let Hij = (Xi, Yi1, ..., Yij) be the history of ith subject up to time j. Let Rij be the missing indicator of Yij, similar as in the previous sections.
The full data estimating equation can be written as
where ![]() and
and ![]() is a working covariance matrix for
is a working covariance matrix for ![]() . Paik's approach uses
. Paik's approach uses ![]() to replace those missing Yij (j > ni). Then, the imputed estimating equation becomes
to replace those missing Yij (j > ni). Then, the imputed estimating equation becomes
where ![]() . The expectation of equation (5.20) is 0, which leads to a consistent estimator of β. Now the crucial step is to estimate the conditional expectation
. The expectation of equation (5.20) is 0, which leads to a consistent estimator of β. Now the crucial step is to estimate the conditional expectation ![]() .
.
Note that under MAR dropout,
So, a regression model can be fitted to the observed data, in order to estimate the first missing observation after dropout. For the second missing observation after dropout, we have
Hence, another regression model can be fitted to estimate the conditional expectation E(Yij|Hi,j−2, Ri,j−1 = 1). Now the regression model includes not only the observed data (those with Ri,j−1 = 1 and Ri,j = 1) but also the previously imputed observations (those with Ri,j−1 = 1 and Ri,j = 0). In other words, in fitting the regression models to impute the second missing observation, the imputed value of the first missing observation is also used as the outcome. If the previous imputation is consistent, the current regression model is also consistent. The same techniques can be repeated for the third potential observation, and so on, until all the missing data are replaced by the fitted conditional expectations. Eventually, the consistency of estimating ![]() is guaranteed in this procedure, if all the imputation models are correctly specified.
is guaranteed in this procedure, if all the imputation models are correctly specified.
The whole procedure can be illustrated in Figure 5.3. The rows represent the missing patterns and the columns represent the observation times. The shaded cells are the missing observations that are to be imputed. We put each one of the subjects into a row according to their dropout times. The ni observations for subject i enter the ni cells in its row. The first diagonal of missing values is imputed in the first place, then the second diagonal, and so on. For the imputation of a cell c, the regression model uses all the cells in the same column but below cell c. For example, when imputing cell (3, 4) in the first diagonal, a regression model is fitted to observations in cells (4, 4) and (5, 4)—both are observed cells. When imputing cell (2, 4) in the second diagonal, not only cells (4, 4) and (5, 4) but also the imputed cell (3, 4) will enter the regression model as outcomes. The design matrix, however, is the history up to the second time point (Hi,j−2 in (5.44) is now Hi2), which does not involve any imputed cell or missing cell. The sequential imputation of the diagonals will eventually generate the complete data, and the estimation of the regression coefficients is followed by solving equation (5.20).

Figure 5.3 Illustration of the imputation procedures.
The explicit variance formula is given in Theorem 1 and Appendix B of Paik 1997). The variance indeed comes from two sources: one is from the estimating equation (5.20) while pretending all the imputed data were observed; the other one is from estimating the additional regression models for imputation.
In Paik's mean score imputation, the missing variables are replaced with the fitted values because the full data estimating equations are linear in the missing Yij. In the multiple imputation, as a comparison, the missing Yij are replaced with a random draw from the posterior predictive distribution. Under the correct imputation model, the multiply imputed values ![]() would be close on average to the fitted value
would be close on average to the fitted value ![]() in the regression model, that is, Paik's mean score:
in the regression model, that is, Paik's mean score:
when M gets larger. In a sense, Paik's mean score imputation is the limit situation of the multiple imputation. As shown in the simulation results of Paik 1997), the results of Paik's imputation and multiple imputation are similar in many settings.
5.10.2 Doubly Robust Estimation
Seaman and Copas 2009) proposed a doubly robust estimating equation approach to handle the monotone dropout of the outcome variable. Their approach is closely related to Paik's mean score imputation. The idea is to augment the complete-case IPW (IPWCC) estimating equations. The augmentation term is the expected complete-data estimating equation, which can be computed in the same way as in Paik 1997).
We continue to use all the notations in the previous section. Note that the IPWCC estimating equations are given by
The IPWCC equations ignore the available data on individuals who drop out before the end of study (time M), and hence are often quite inefficient. One way to improve the efficiency is to add an additional term A, which is a function of both the available data and the parameter vector β and satisfies E(A|HiM) = 0. The augmented IPWCC (AIPWCC) equations are given by
Let Cij be the indicator function, which is equal to 1 if Rij = 1 and Ri,j+1 = 0, and 0 otherwise. One choice of the augmentation function Ai is
where λi,j+1 = Pr (Ri,j+1 = 1|Rij = 1, Hij) is defined in Section 5.6.1. Note that the expectation is taken with respect to future outcome variables, given the history up to time j and the patient not having dropped out at time j.
As ![]() is linear in all the outcome variables Yij, it suffices to compute the expectation
is linear in all the outcome variables Yij, it suffices to compute the expectation ![]() . If m ≤ j, the expectation is just the observed value Yim. Otherwise, the Paik's imputation procedures are used to compute the fitted mean.
. If m ≤ j, the expectation is just the observed value Yim. Otherwise, the Paik's imputation procedures are used to compute the fitted mean.
The AIPWCC estimator is doubly robust, meaning that it is consistent when either the dropout model or the imputation model is misspecified (but not both). If both models are correct, the choice of Ai in (5.23) is optimal in terms of the best efficiency for β.
The variance estimator for β has the sandwich form, and the formula is given in Section 4 of Seaman and Copas 2009). When the dropout model and the imputation model are both correct, it is valid to ignore the uncertainty of the nuisance parameters. In other words, using the true dropout and imputation models is approximately the same as using the estimated models.
5.10.3 Missing Outcome and Covariates
The literature on missing data methodologies mainly focuses on either missing response or missing covariates. In practice, it is often inevitable that data are incomplete for both the longitudinal outcome and some important time-varying covariates. We will now discuss some methods that address this issue (Chen et al., 2010; Chen and Zhou, 2011). One of these methods was based on a weighted GEE approach that extended the results of Robins et al. (1995), whereas the other one further developed a doubly robust estimator when the outcome was binary.
We need to redefine some of the notations. Consider a data set with N subjects indexed by i, and subject i is to be examined at time points j = 1, ..., ni. Let ![]() be the outcome vector,
be the outcome vector, ![]() be the covariate vector that is subject to missingness, and
be the covariate vector that is subject to missingness, and ![]() be the matrix of covariates that are fully observed. For simplicity, we assume that only one covariate is missing. The model of interest is the conditional mean of Yi, that is,
be the matrix of covariates that are fully observed. For simplicity, we assume that only one covariate is missing. The model of interest is the conditional mean of Yi, that is, ![]() . Suppose that the marginal regression model is given by
. Suppose that the marginal regression model is given by
for i = 1, ..., N, j = 1, ..., ni, where g is a known link function. Let Rij be the indicator of the missingness patterns for the pair (Yij, Xij):

Let ![]() be the full missingness record for subject i and
be the full missingness record for subject i and ![]() be the missingness record before time j. Suppose that the baseline outcome and covariates are always observed, that is, Ri1 ≡ 3.
be the missingness record before time j. Suppose that the baseline outcome and covariates are always observed, that is, Ri1 ≡ 3.
Chen and Zhou 2011) proposed to model each Rij conditional on the past missingness profile, ![]() , to obtain the joint probability of Ri. The joint probability of Ri is then expressed as
, to obtain the joint probability of Ri. The joint probability of Ri is then expressed as
Under the MAR assumption, it is natural to assume that
where ![]() and
and ![]() , respectively, denote the history of observed component of Yi and Xi before time j. Let
, respectively, denote the history of observed component of Yi and Xi before time j. Let ![]() . A multinomial logit model can then be assumed for Rij:
. A multinomial logit model can then be assumed for Rij:
where Wijk is a subset of ![]() Let πij = P(Rij = 3|Yi, Xi, Zi) be the marginal probability of observing both Yij and Xij, which can be written as a function of λijk by summing over all possible combinations of Ri1, ..., Ri,j−1. The marginal probability πij is crucial to construct a weight function in the next step.
Let πij = P(Rij = 3|Yi, Xi, Zi) be the marginal probability of observing both Yij and Xij, which can be written as a function of λijk by summing over all possible combinations of Ri1, ..., Ri,j−1. The marginal probability πij is crucial to construct a weight function in the next step.
Similar to the spirit of Robins et al. (1995), a weight matrix is defined as
Then, the estimating equation for β is obtained as
where Di = ∂ μi/∂ β and Vi is the working covariance matrix of Yi. We could also express Vi as ![]() , where Ci is the working correlation matrix and
, where Ci is the working correlation matrix and ![]() describes the variance–mean relationship. Equation (5.24) is computable only when Ci is the identity matrix, that is, under working-independent correlation structure. Otherwise, as Di may involve some unobserved covariates Xij, equation (5.24) cannot be evaluated. A modification is to define a new weight matrix Δi:
describes the variance–mean relationship. Equation (5.24) is computable only when Ci is the identity matrix, that is, under working-independent correlation structure. Otherwise, as Di may involve some unobserved covariates Xij, equation (5.24) cannot be evaluated. A modification is to define a new weight matrix Δi:

Let ![]() , where
, where ![]() denotes the Hadamard product of ni × ni matrices
denotes the Hadamard product of ni × ni matrices ![]() and
and ![]() . Now the following modified estimating equation can be solved for β:
. Now the following modified estimating equation can be solved for β:
Equation (5.25) is the key result in Chen et al. (2010), which no longer contains the missing Xij. It is also worth noting that Chen et al. (2010) adopted a slightly different approach to model the missingness mechanism. Instead of constructing a conditional model, they used the Bahadur model framework and specified the marginal missingness mechanisms for Xij and Yij, as well as the pairwise correlations. Interested readers should refer to their work and Bahadur 1961) for more details.
It is well known in the literature that the inverse probability weighted estimator is usually not efficient, especially if the selection probability is low. In general, one can augment the weighted estimating equations to gain efficiency (Chen and Zhou, 2011), that is,
An optimal choice of ϕi is
with ![]() , where 1i is an ni × ni square matrix of 1's.
, where 1i is an ni × ni square matrix of 1's.
In order to evaluate the conditional expectation (5.27), one needs to specify two missing data models of ![]() and
and ![]() . The missing data model for Yi is specified from the Bahadur model, when the outcome is binary. Let
. The missing data model for Yi is specified from the Bahadur model, when the outcome is binary. Let ![]() and
and

Then, the Bahadur model specifies the joint probability density function for Yi as

Assuming that the third-and higher order associations are zero, we can write the Bahadur model as follows:
With this joint probability, we can use the law of total probability to derive the conditional distribution of ![]() . Note that both μij and ρi,jk are functions of parameter vector β. We also write the joint probability as P(Yi|Xi, Zi; β).
. Note that both μij and ρi,jk are functions of parameter vector β. We also write the joint probability as P(Yi|Xi, Zi; β).
For the missing covariate model, ![]() , we consider a conditional model given the past observations. The joint density of Xi can be written as
, we consider a conditional model given the past observations. The joint density of Xi can be written as
Again, ![]() and
and ![]() represent the history of the covariate and outcome observed before time point j. To emphasize the nuisance parameter vector γ that specifies the missing covariate model, we also write the joint probability as
represent the history of the covariate and outcome observed before time point j. To emphasize the nuisance parameter vector γ that specifies the missing covariate model, we also write the joint probability as ![]() . This model can be estimated by maximizing the observed likelihood function:
. This model can be estimated by maximizing the observed likelihood function:
Now we turn to the augmented estimating equation and try to evaluate ϕi,opt in (5.27). When ![]() is discrete, the augmented term becomes
is discrete, the augmented term becomes
where

If ![]() is continuous, the summation
is continuous, the summation ![]() is replaced by an integral
is replaced by an integral ![]() . A reject sampling procedure can be used to evaluate the integral. An EM type algorithm is proposed to solve equation (5.26) for β, and the iteration procedures are described as follows:
. A reject sampling procedure can be used to evaluate the integral. An EM type algorithm is proposed to solve equation (5.26) for β, and the iteration procedures are described as follows:
- Initialize the parameters β(0).
- In the kth iteration, β(k) is obtained and used to update
 ,
,  , and
, and  .
. - Treat
 ,
,  , and
, and  as fixed, and then solve the following equation:
as fixed, and then solve the following equation:

for β(k+1).
- Iterate steps 2 and 3 until convergence.
It was shown in Chen and Zhou 2011) that the estimator ![]() is asymptotic normal and a sandwich variance formula is derived.
is asymptotic normal and a sandwich variance formula is derived.
Appendix 5.A: Technical Details of the Approximation Methods for GLMM and Computer Code for the Examples
5.A.1 PQL and MQL
The PQL method borrows the idea of linearization used in the generalized linear models. Rewrite the mean structure model as
where h is the inverse link function g−1 and εij is the error term with mean 0. Define ϕ to be the overdispersion parameter. With the canonical link function, the derivative of inverse link function, h′, characterizes the mean–variance relationship:
By Taylor series expansion around the current ![]() and
and ![]() , we have
, we have
where ![]() and
and ![]() are the current fit of conditional mean and variance, respectively. Define the working response variable
are the current fit of conditional mean and variance, respectively. Define the working response variable
Reorganizing (5A.1) yields an LMM:
The new residual ![]() is rescaled as
is rescaled as ![]() . Therefore, one can iterate between fitting the LMM and updating
. Therefore, one can iterate between fitting the LMM and updating ![]() until convergence.
until convergence.
The MQL method is very similar to the PQL method, except that h(·) is expanded around ![]() and bi = 0:
and bi = 0:
Here, ![]() and
and ![]() are the current fit of marginal mean and variance:
are the current fit of marginal mean and variance:
Hence, we have
where the residual is rescaled as ![]() . The GLMM can be estimated by iterating between updating
. The GLMM can be estimated by iterating between updating ![]() and fitting the above LMM.
and fitting the above LMM.
5.A.2 Laplace Approximation
The integrals in ![]() can be written in the form of
can be written in the form of ![]() . The idea of Laplace approximation is to approximate the integrand using a multivariate normal density, or equivalently, to replace
. The idea of Laplace approximation is to approximate the integrand using a multivariate normal density, or equivalently, to replace ![]() by a quadratic form of b. By the second-order Taylor series expansion of
by a quadratic form of b. By the second-order Taylor series expansion of ![]() around its mode
around its mode ![]() , we have
, we have
and hence
The mode ![]() is solved from
is solved from ![]() as a function of β and D. Now the likelihood can be evaluated approximately in the closed form and could be maximized for estimating β and the variance components.
as a function of β and D. Now the likelihood can be evaluated approximately in the closed form and could be maximized for estimating β and the variance components.
5.A.3 Gaussian Quadrature
The idea of the Gaussian quadrature is to use the bins to approximate the integral. The integral has the form ∫f(z)ϕ(z)dz, where ϕ(z) is the density of multivariate normal distribution. It can be replaced by a weighted sum:

where zq is the prespecified qth quadrature point or node (the position to use a bin to evaluate the integral) and ![]() is the well-chosen weight. An algorithm is available to calculate all zq and
is the well-chosen weight. An algorithm is available to calculate all zq and ![]() for any number of quadrature points Q. The adaptive Gaussian quadrature is proposed by Pinheiro and Bates 1995) to reduce the approximation error. The idea is to rescale the nodes into the support of f(z)ϕ(z) and change the weights correspondingly. It is worth noting that the Laplace approximation is equivalent to the adaptive Gaussian quadrature with only one quadrature point.
for any number of quadrature points Q. The adaptive Gaussian quadrature is proposed by Pinheiro and Bates 1995) to reduce the approximation error. The idea is to rescale the nodes into the support of f(z)ϕ(z) and change the weights correspondingly. It is worth noting that the Laplace approximation is equivalent to the adaptive Gaussian quadrature with only one quadrature point.
5.A.4 Code for This Chapter
5.A.4.1 Stata Code Used in Section 5.5.1.1
The following code conducts the complete-case analysis for the IMPACT data:
5.A.4.2 Stata Code Used in Section 5.5.1.2
The following code is to conduct the available data analysis for the IMPACT study:
5.A.4.3 Stata Code Used in Section 5.5.1.3
The following Stata code illustrates the LOCF analysis for the IMPACT study:
5.A.4.4 Stata Code Used in Section 5.6.4
Here we present the Stata code for the IMPACT study using IPWGEE1 and IPWGEE2. In the following code, we estimate the probability that an outcome is observed at a specific time point, given the prior observed outcome variables and some selected baseline characteristics using logistic regression, and then generate both observation-level weights and cluster (subject)-level weights based on the estimated probabilities.
The following code implements IPWGEE1 using observation-level weights. Because this approach is not currently implemented in Stata, a workaround using glm command is implemented.
The following code then performs IPWGEE2 using cluster-level weights:
5.A.4.5 R Code Used in Section 5.8.3
Here, we present the R code for implementing multiple imputation analysis for the NACC UDS data. The package mice is used. The following code appends the transformation of variables, dummy variables, and interaction terms.
> attach(NACCUDS)> NACCUDS2=cbind(NACCUDS,cons=1,logcdr=log(cdr+1),+ mmse2=logit((mmse+0.5)/31),edu2=(education==2)+0,+ edu3=(education==3)+0,hachin2=(hachin==2)+0,+ hachin3=(hachin==3)+0,age.year=age0*year,+ gender.year=gender*year,edu.year2=(education==2)*year,+ edu.year3=(education==3)*year,his.year2=(hachin==2)*year,+ his.year3=(hachin==3)*year,ap.year=apoee4*year,+ mmse.year=mmse*year)> detach()
A “dry run” with the maximum number of iteration set to 0 is the first step to initialize the imputation parameters.
> ini=mice(NACCUDS2,maxit=0)
Then the imputation methods are specified.
> meth=ini $dollar $ meth> meth[”mmse2”]=”2l.norm”> meth[”mmse”]=”~I(round(1/(1+exp(-mmse2))*31-0.5))”> meth[”hachin”]=”pmm”> meth[”education”]=”2lonly.pmm”> meth[”apoee4”]=”2lonly.pmm”> meth[”edu2”]=”~I(education==2)”> meth[”edu3”]=”~I(education==3)”> meth[”hachin2”]=”~I(hachin==2)”> meth[”hachin3”]=”~I(hachin==3)”> meth[”edu.year2”]=”~I((education==2)*year)”> meth[”edu.year3”]=”~I((education==3)*year)”> meth[”his.year2”]=”~I((hachin==2)*year)”> meth[”his.year3”]=”~I((hachin==3)*year)”> meth[”ap.year”]=”~I(apoee4*year)”> meth[”mmse.year”]=”~I(mmse*year)”
The next step is to specify the prediction matrix of the imputation model. The following is a print of our specified prediction matrix:
> pred[c(”mmse2”,”education”,”apoee4”,”hachin”),]mmse age0 gender education apoee4 year cdr hachin IDmmse2 0 1 1 0 1 1 0 0 -2education 1 1 1 0 1 0 0 0 -2apoee4 1 1 1 0 0 0 0 0 -2hachin 1 1 1 0 1 1 0 0 0cons logcdr mmse2 edu2 edu3 hachin2 hachin3 age.yearmmse2 2 1 0 1 1 1 1 1education 0 1 0 0 0 1 1 0apoee4 0 1 0 1 1 1 1 0hachin 0 1 0 1 1 0 0 1gender.year edu.year2 edu.year3 his.year2 his.year3mmse2 1 1 1 1 1education 0 0 0 0 0apoee4 0 0 0 0 0hachin 0 1 1 0 0ap.year mmse.yearmmse2 1 0education 0 0apoee4 0 0hachin 1 1
The visit scheme specifies the order of imputation. We need to keep the passive imputations synchronized with the imputed variables.
> vis=ini $dollar $ vis> vis[”mmse2”]=1> vis[”mmse”]=12> vismmse education apoee4 hachin mmse2 edu212 4 5 8 1 13edu3 hachin2 hachin3 edu.year2 edu.year3 his.year214 15 16 19 20 21his.year3 ap.year mmse.year22 23 24
We also try imputing MMSE using the predictive mean matching method. The pmm does not make any distributional assumption, but only requires a mean model with identity link.
> meth2=meth> meth2[”mmse2”]=”pmm”> pred2=pred> pred2[”mmse2”,”ID”]=0> pred2[”mmse2”,”cons”]=0
The following code generates 20 complete data sets with missing values imputed by the two methods:
> imp2=mice(NACCUDS2,m=20,me=meth2,pred=pred2,vis=vis,maxit=20,+ seed=10065)> imp1=mice(NACCUDS2,m=20,me=meth,pred=pred,vis=vis,maxit=20,+ seed=7523)> plot(imp1,c(”hachin”,”education”,”apoee4”,”mmse”),+ layout=c(2,4))
The analysis for the 20 imputed data sets is conducted by the following code.
> library(gee)> fitC=gee(mmse~(I((age0-75)/10)+gender+apoee4++ as.factor(education)+as.factor(hachin))*year,+ corstr=”independence”,id=ID,data=NACCUDS)> fit1=with(imp1,gee(mmse~(I((age0-75)/10)+gender+apoee4++ as.factor(education)+as.factor(hachin))*year,+ corstr=”independence”,id=ID))> fit2=with(imp2,gee(mmse~(I((age0-75)/10)+gender+apoee4++ as.factor(education)+as.factor(hachin))*year,+ corstr=”independence”,id=ID))
The code for combining fit1 using Rubin's rule is given below.
> PE1=VAR1=matrix(0,20,16)> for(i in 1:20)+ PE1[i,]=(fit1 $dollar $ analyses[[i]]) $dollar $ coef+ VAR1[i,]=summary(fit1 $dollar $ analyses[[i]]) $dollar $ coef[,4]supstri 2+> COEF1=apply(PE1,2,mean)> U1=apply(VAR1,2,mean)> B1=apply(PE1,2,var)> SE1=(U1+(1+1/20)*B1)supstri .5> RES1=cbind(COEF1,SE1)
5.A.4.6 Stata Code Used in Section 5.8.4.1
The following Stata code is for the analysis of multiple imputation with monotone missingness:
5.A.4.7 Stata Code Used in Section 5.8.4.2
The following is the Stata code for multiple imputation based on the multivariate normal distribution for the IMPACT data:
5.A.4.8 Stata Code Used in Section 5.8.4.3
The multiple imputation with chained equations is applied to the IMPACT data and achieved by the following chunk of code:
5.A.4.9 Stata Code Used in Section 5.8.4.4
The following is the Stata code to conduct analysis of IMPACT data based on the multiple imputation with chained equations for a general missing data pattern. We recommend readers to start by following the steps listed in the following code chunk. One tip is to use “mi describe” often so that we can keep a close eye on our imputation.





