Chapter 12 Plastic Behavior of Materials

12.1 Introduction

The subject of plasticity is perhaps best introduced by recalling the principal characteristics of elastic behavior. First, a material subjected to stressing within the elastic regime will return to its original state upon removal of those external influences causing application of load or displacement. Second, the deformation corresponding to a given stress depends solely on that stress and not on the history of strain or load. In plastic behavior, opposite characteristics are observed. The permanent distortion that takes place in the plastic range of a material can assume considerable proportions. This distortion depends not only on the final state of stress, but on the stress states existing from the start of the loading process as well.

The equations of equilibrium (1.11), the conditions of compatibility (2.9), and the strain–displacement relationships (2.3) are all valid in plastic theory. New relationships must, however, be derived to connect stress and strain. The various yield criteria, which strictly speaking are not required in solving a problem in elasticity, play a direct and important role in plasticity.

This chapter can provide only an introduction to what is an active area of contemporary design and research in the mechanics of solids.^* The basics presented can, however, indicate the potential of the field, as well as its complexities.

*For a detailed discussion of problems in plasticity, see Refs. 12.1 through 12.3.

12.2 Plastic Deformation

We shall here deal with the permanent alteration in the shape of a polycrystalline solid subject to external loading. The crystals are assumed to be randomly oriented. As has been demonstrated in Sec. 2.13, the stresses acting on an elemental cube can be resolved into those associated with change of volume (dilatation) and those causing distortion or change of shape. The distortional stresses are usually referred to as the deviator stresses.

The dilatational stresses, such as hydrostatic pressures, can clearly decrease the volume while they are applied. The volume change is recoverable, however, upon removal of external load. This is because the material cannot be compelled to assume, in the absence of external loading, interatomic distances different from the initial values. When the dilatational stresses are removed, therefore, the atoms revert to their original position. Under the conditions described, no plastic behavior is noted, and the volume is essentially unchanged upon removal of load.

In contrast with the situation described, during change of shape, the atoms within a crystal of a polycrystalline solid slide over one another. This slip action, referred to as dislocation, is a complex phenomenon. Dislocation can occur only by the shearing of atomic layers, and consequently it is primarily the shear component of the deviator stresses that controls plastic deformation. Experimental evidence supports the assumption that associated with plastic deformation essentially no volume change occurs; that is, the material is incompressible (Sec. 2.9):

(12.1)

Therefore, from Eq. (2.33), Poisson’s ratio ν = for a plastic material.

Slip begins at an imperfection in the lattice, for example, along a plane separating two regions, one having one more atom per row than the other. Because slip does not occur simultaneously along every atomic plane, the deformation appears discontinuous on the microscopic level of the crystal grains. The overall effect, however, is plastic shear along certain slip planes, and the behavior described is approximately that of the ideal plastic solid. As the deformation continues, a locking of the dislocations takes place, resulting in strain hardening.

In performing engineering analyses of stresses in the plastic range, we do not usually need to consider dislocation theory, and the explanation offered previously, while overly simple, will suffice. What is of great importance to the analyst, however, is the experimentally determined curves of stress and strain.

12.3 True Stress-True Strain Curve in Simple Tension

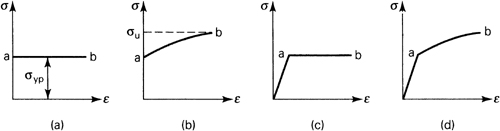
The bulk of present day analysis in plasticity is predicated on materials displaying idealized stress-strain curves as in Fig. 12.1a. Such materials are referred to as rigid, perfectly plastic. Examples include mild steel and nylon, which exhibit negligible elastic strains in comparison with large plastic deformations at practically constant stress. A more realistic portrayal including strain hardening is given in Fig. 12.1b for what is called a rigid plastic solid. In the curves, a and b designate the tensile yield and ultimate stresses, σ_yp and σ_u, respectively. The curves of Fig. 12.1c and d do not ignore the elastic strain, which must be included in a more general stress-strain depiction. The latter figures thus represent idealized elastic-plastic diagrams for the perfectly plastic and plastic materials, respectively. The material in Figs. 12.c, d is also called a strain-hardening or work-hardening material. For a linearly strain-hardening material, the regions ab of the diagrams become a sloped straight line.

Figure 12.1. Idealized stress-strain diagrams: (a) rigid, perfectly plastic material; (b) rigid plastic material; (c) elastic, perfectly plastic material; and (d) elastic plastic material.

True Stress-True Strain Relationships

Various theoretical analyses have been advanced to predict plastic behavior. Equations relating stress and strain beyond the proportional limit range from the rather empirical [Ref. 12.4] to those leading to complex mathematical approaches applicable to materials of specific type and structure. We shall confine our discussion to that of a perfectly plastic material displaying a horizontal straight-line relationship and to the parabolic relationship described next.

For many materials, the true stress-true strain curve may be represented by the parabolic form

(12.2)

where n and K are the strain-hardening index and the strength coefficient, respectively. The definitions of true stress and true strain are given in Sec. 2.6. The curves of Eq. (12.2) are shown in Fig. 12.2a. We observe from the figure that the slope dσ/dε grows without limit as ε approaches zero for n ≠ 1. Thus, Eq. (12.2) should not be used for small strains when n ≠ 1. The stress-strain diagram of a perfectly plastic material is represented by this equation when n = 0 (and hence K = σ_yp). Clearly, for elastic materials (n = 1 and hence K = E), Eq. (12.2) represents Hooke’s law, wherein E is the modulus of elasticity.

Figure 12.2. (a) Graphical representation of σ = Kεⁿ; (b) true stress versus true strain on log-log coordinates.

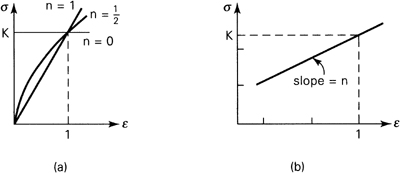
For a particular material, with true stress-true strain data available, K and n are readily evaluated inasmuch as Eq. (12.2) plots as a straight line on logarithmic coordinates. We can thus rewrite Eq. (12.2) in the form

(a)

Here n is the slope of the line and K the true stress associated with the true strain at 1.0 on the log-log plot (Fig. 12.2b). The strain-hardening coefficient n for commercially used materials falls between 0.2 and 0.5.

12.4. Instability in Simple Tension

We now describe an instability phenomenon in uniaxial tension of practical importance in predicting the maximum allowable plastic stress in a rigid-plastic material. At the ultimate stress in a tensile test (Fig. 2.8), an unstable flow results from the effects of strain hardening and the decreasing cross-sectional area of the specimen. These tend to weaken the material. When the rate of the former effect is less than the latter, an instability occurs. This point corresponds to the maximum tensile load and is defined by

(a)

Since axial load P is a function of both the true stress and the area (P = σA), Eq. (a) is rewritten

(b)

The condition of incompressibility, A₀ L₀ = AL, also yields

(c)

as the original volume A₀ L₀ is constant. Expressions (b) and (c) result in

(d)

From Eqs. (2.20) and (d), we thus obtain the relationships

(12.3)

for the instability of a tensile member. Here the subscript o denotes the engineering strain and stress (Sec. 2.6).

Introduction of Eq. (12.2) into Eq. (12.3) results in

or

(12.4)

That is, at the instant of instability of flow in tension, the true strain ε has the same numerical value as the strain-hardening index. The state of true stress and the true strain under uniaxial tension are therefore

(e)

The problem of instability under simple compression or plastic buckling is discussed in Sec. 11.5. The instability condition for cases involving biaxial tension is derived in Secs. 12.10 and 12.11.

Example 12.1

Determine the maximum allowable plastic stress and strain in the pin-jointed structure sustaining a vertical load P, shown in Fig. P10.28. Assume that α = 45° and that each element is constructed of an aluminum alloy with the following properties:

σ_yp = 350 MPa, K = 840 MPa, n = 0.2

A_AD = A_CD = 10 × 10⁻⁵m², A_BD = 15 × 10⁻⁵m², L₀ = 3 m

Solution The structure is elastically statically indeterminate, and the solution may readily be obtained on applying Castigliano’s theorem (Sec. 10.7). Plastic yielding begins upon loading:

P = σ_ypA_BD + 2σ_ypA_AD cosα

= 350 × 10⁶[15 + 2 × 10 cos 45°]10⁻⁵ = 101,990 N

On applying Eqs. (e), the maximum allowable stress

σ = Knⁿ = 840 × 10⁶(0.2)^0.2 = 608.9 MPa

occurs at the following axial and transverse strains:

ε₁ = n = 0.2, ε₂ = ε₃ = −0.1

For example, the total elongation for instability of the central bar is thus 3(0.2) = 0.6 m.

Example 12.2

A tube of original mean diameter d₀ and thickness t₀ is subjected to axial tensile loading. Assume a true stress-engineering strain relation of the form and derive expressions for the thickness and diameter at the instant of instability. Let n = 0.3.

Solution Differentiating the given expression for stress,

This result and Eq. (12.3) yield the engineering axial strain at instability:

(f)

The transverse strains are −ε₀/2, and hence the decrease of wall thickness equals nt₀/2 (1 − n). The thickness at instability is thus

(g)

Similarly, the diameter at instability is

(h)

From Eqs. (g) and (h), with n = 0.3, we have t = 0.79t₀ and d = 0.79d₀. Thus, for the tube under axial tension, the diameter and thickness decrease approximately 21% at the instant of instability.

12.5. Plastic Deflection of Beams

In this section we treat the inelastic deflection of a beam, employing the mechanics of materials approach. Consider a beam of rectangular section, as in Fig. 12.3a, wherein the bending moment M produces a radius of curvature r. The longitudinal strain of any fiber located a distance y from the neutral surface, from Eq. (5.9), is given by

(12.5)

Figure 12.3. Inelastic pure bending of a beam of rectangular cross section.

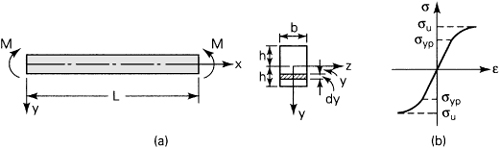
Assume the beam material to possess equal properties in tension and compression. Then, the longitudinal tensile and compressive forces cancel, and the equilibrium of axial forces is satisfied. The following describes the equilibrium of moments about the z axis (Fig. 12.3a):

(a)

For any specific distribution of stress, as, for example, that shown in Fig. 12.3b, Eq. (a) provides M and then the deflection, as is demonstrated next.

Consider the true stress-true strain relationship of the form σ = Kεⁿ. Introducing this together with Eq. (12.5) into Eq. (a), we obtain

(b)

where

(12.6)

From Eqs. (12.5), σ = Kεⁿ, and (b) the following is derived:

(c)

In addition, on the basis of the elementary beam theory, we have, from Eq. (5.7),

(d)

Upon substituting Eq. (c) into Eq. (d), we obtain the following equation for a rigid plastic beam:

(12.7)

It is noted that when n = 1 (and hence K = E) this expression, as expected, reduces to that of an elastic beam [Eq. (5.10)].

Example 12.3

Determine the deflection of a rigid plastic simply supported beam subjected to a downward concentrated force P at its midlength. The beam has a rectangular cross section of depth 2h and width b (Fig. 12.4).

Figure 12.4. Examples 12.3 and 12.6

Solution The bending moment for segment AC is given by

(e)

where the minus sign is due to the sign convention of Sec. 5.2.

Substituting Eq. (e) into Eq. (12.7) and integrating, we have

(f)

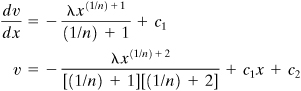
where

(g)

The constants of integration c₁ and c₂ depend on the boundary conditions υ(0) = dυ/dx(L/2) = 0:

Upon introduction of c₁ and c₂ into Eq. (f), the beam deflection is found to be

(12.8)

Interestingly, in the case of an elastic beam, this becomes

For x = L/2, the familiar result is

The foregoing procedure is applicable to the determination of the deflection of beams subject to a variety of end conditions and load configurations. It is clear, however, that owing to the nonlinearity of the stress law, σ = Kεⁿ, the principle of superposition cannot validly be applied.

12.6. Analysis of Perfectly Plastic Beams

By neglecting strain hardening, that is, by assuming a perfectly plastic material, considerable simplification can be realized. We shall, in this section, focus our attention on the analysis of a perfectly plastic straight beam of rectangular section subject to pure bending (Fig. 12.3a).

The bending moment at which plastic deformation impends, M_yp, may be found directly from the flexure relationship:

(12.9)

Here σ_yp represents the stress at which yielding begins (and at which deformation continues in a perfectly plastic material). The stress distribution corresponding to M_yp, assuming identical material properties in tension and compression, is shown in Fig. 12.5a. As the bending moment is increased, the region of the beam that has yielded progresses in toward the neutral surface (Fig. 12.5b). The distance from the neutral surface to the point at which yielding begins is denoted by the symbol e, as shown.

Figure 12.5. Stress distribution in a rectangular beam with increase in bending moment: (a) elastic; (b) partially plastic)

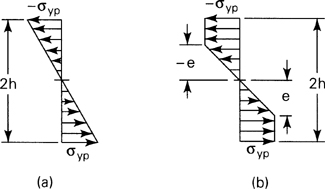
It is clear, upon examining Fig. 12.5b, that the normal stress varies in accordance with the relations

(a)

and

(b)

It will be useful to determine the manner in which the bending moment M relates to the distance e. To do this, we begin with a statement of the x equilibrium of forces:

Cancelling the first and third integrals and combining the remaining integral with Eq. (a), we have

This expression indicates that the neutral and centroidal axes of the cross section coincide, as in the case of an entirely elastic distribution of stress. Note that in the case of a nonsymmetrical cross section the neutral axis is generally in a location different from that of the centroidal axis [Ref. 12.5]. Next, the equilibrium of moments about the neutral axis provides the following relation:

Substituting σ_x from Eq. (a) into this equation gives, after integration,

(12.10)

The general stress distribution is thus defined in terms of the applied moment, inasmuch as e is connected to σ_x by Eq. (a). For the case in which e = h, Eq. (12.10) reduces to Eq. (12.9) and M = M_yp. For e = 0, which applies to a totally plastic beam, Eq. (12.10) becomes

(12.11)

where M_u is the ultimate moment.

Through application of the foregoing analysis, similar relationships can be derived for other cross-sectional shapes. In general, for any cross section the plastic or ultimate resisting moment for a beam is

(12.12)

where Z is the plastic section modulus. Clearly, for the rectangular beam analyzed here, Z = bh². The Steel Construction Manual (Sec. 11.6) lists plastic section moduli for many common geometries.

Plastic Hinge

To express the beam curvature in terms of the yield stress, we begin by noting that the longitudinal strain given by Eq. (12.5), combined with Hooke’s law, leads to

The curvature and yield stress are thus related by

(12.13)

A plot of Eq. (12.10) combined with Eq. (12.13) (Fig. 12.6) reveals that, after the yielding moment M_yp is achieved, M and 1/r are connected by a nonlinear relationship. As M approaches M_u, the curvature grows without limit. The ultimate moment is also referred to as the plastic hinge moment. The rationale for the term hinge becomes apparent upon describing the behavior of a beam under a concentrated loading, discussed next.

Figure 12.6. Moment versus curvature for an elastic-plastic rectangular beam

Consider a simply supported beam of rectangular cross section, subjected to a load P at its midspan (Fig. 12.7a). The corresponding bending moment diagram is shown in Fig. 12.7b. Clearly, when M_yp < |PL/4| < M_u, a region of plastic deformation occurs, as indicated in the figure by the shaded areas. The depth of penetration of these zones can be found from h – e, where e is determined using Eq. (12.10), because M at midspan is known. The length of the middle portion of the beam where plastic deformation occurs can be readily determined with reference to the figure. The magnitude of bending moment at the edge of the plastic zone is M_yp = (P/2) (L – L_p)/2, from which

(c)

Figure 12.7. Bending of a rectangular beam: (a) plastic region; (b) moment diagram; (c) plastic hinge

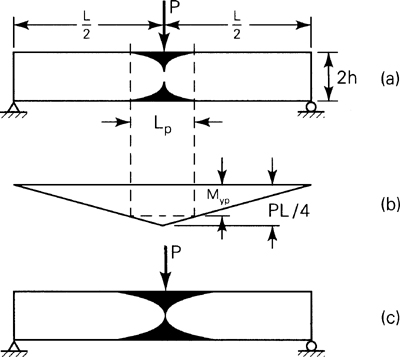
With the increase of P, M_max → M_u, and the plastic region extends farther inward. When the magnitude of the maximum moment PL/4 is equal to M_u, the cross section at the midspan becomes fully plastic (Fig. 12.7c). Then, as in case of pure bending, the curvature at the center of the beam grows without limit, and the beam fails. The beam halves on either side of the midspan experience rotation in the manner of a rigid body about the neutral axis, as about a plastic hinge, under the influence of the constant ultimate moment M_u, For a plastic hinge, P = 4M_u/L is substituted into Eq. (c), leading to L_p = L(1 – M_yp/M_u).

The capacity of a beam to resist collapse is revealed by comparing Eqs. (12.9) and (12.11). Note that the M_u is 1.5 times as large as M_yp. Elastic design is thus conservative. Considerations such as this lead to concepts of limit design in structures, discussed in the next section.

Example 12.4

A link of rectangular cross section is subjected to a load N (Fig. 12.8a). Derive general relationships involving N and M that govern, first, the case of initial yielding and, then, fully plastic deformation for the straight part of the link of length L.

Figure 12.8. Example 12.4

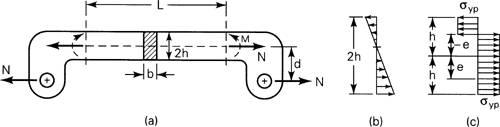
Solution Suppose N and M are such that the state of stress is as shown in Fig. 12.8b at any straight beam section. The maximum stress in the beam is then, by superposition of the axial and bending stresses,

(d)

The upper limits on N (M = 0) and M (N = 0), corresponding to the condition of yielding, are

(e)

Substituting 2hb and I/h from Eq. (e) into Eq. (d) and rearranging terms, we have

(12.14)

If N₁ is zero, then M₁ must achieve its maximum value M_yp for yielding to impend. Similarly, for M₁ = 0, it is necessary for N₁ to equal N_yp to initiate yielding. Between these extremes, Eq. (12.14) provides the infinity of combinations of N₁ and M₁ that will result in σ_yp.

For the fully plastic case (Fig. 12.8c), we shall denote the state of loading by N₂ and M₂. It is apparent that the stresses acting within the range –e < y < e contribute pure axial load only. The stresses within the range e < y < h and –e > y > –h form a couple, however. For the total load system described, we may write

(f)

(g)

Introducing Eqs. (12.11) and (f) into Eq. (g), we have

Finally, dividing by M_u and noting that and N_yp = 2bhσ_yp, we obtain

(12.15)

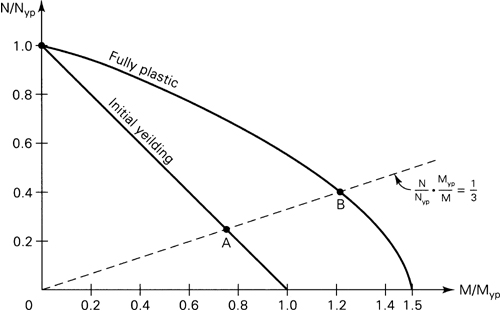
Figure 12.9 is a plot of Eqs. (12.14) and (12.15). By employing these interaction curves, any combination of limiting values of bending moment and axial force is easily arrived at.

Let, for instance, d = h, h = 2b = 24 mm (Fig. 12.8a), and σ_yp = 280 MPa. Then the value of and, from Eq. (e), M_yp/N_yp = h/3 = 8. The radial line representing is indicated by the dashed line in the figure. This line intersects the interaction curves at A(0.75, 0.25) and B(1.24, 0.41). Thus, yielding impends for N₁ = 0.25N_yp = 0.25(2bh·σ_yp) = 40.32 kN, and for fully plastic deformation, N₂ = 0.41N_yp = 66.125 kN.

Note that the distance d is assumed constant and the values of N found are conservative. If the link deflection were taken into account, d would be smaller and the calculations would yield larger N.

Figure 12.9. Example 12.4. Interaction curves for N and M for a rectangular cross-sectional member

Example 12.5

An I-beam (Fig. 12.10a) is subjected to pure bending resulting from end couples. Determine the moment causing initial yielding and that resulting in complete plastic deformation.

Figure 12.10. Example 12.5

Solution The moment corresponding to σ_yp is, from Eq. (12.9),

(h)

Refer now to the completely plastic stress distribution of Fig. 12.10b. The moments of force owing to σ_yp, taken about the neutral axis, provide

(i)

Combining Eqs. (h) and (i), we have

From this expression, it is seen that while it is for a beam of rectangular section (h₁ = 0). We conclude therefore that, if a rectangular beam and an I-beam are designed plastically, the former will be more resistant to complete plastic failure.

Example 12.6

Determine the maximum deflection due to an applied force P acting on the perfectly plastic simply supported rectangular beam (Fig. 12.4).

Solution The center deflection in the elastic range is given by

(j)

At the start of yielding,

(k)

Expression (j), together with Eqs. (k) and (12.9), leads to

(l)

In a like manner, we obtain

(m)

for the center deflection at the instant of plastic collapse.

12.7. Collapse Load of Structures

On the basis of the simple examples in the previous section, it may be deduced that structures may withstand loads in excess of those that lead to initial yielding. We recognize that, while such loads need not cause structural collapse, they will result in some amount of permanent deformation. If no permanent deformation is to be permitted, the load configuration must be such that the stress does not attain the yield point anywhere in the structure. This is, of course, the basis of elastic design.

When a limited amount of permanent deformation may be tolerated in a structure, the design can be predicated on higher loads than correspond to initiation of yielding. On the basis of the ultimate or plastic load determination, safe dimensions can be determined in what is termed limit design. Clearly, such design requires higher than usual factors of safety. Examples of ultimate load determination are presented next.

Consider first a built-in beam subjected to a concentrated load at midspan (Fig. 12.11a). The general bending moment variation is sketched in Fig. 12.11b. As the load is progressively increased, we may anticipate plastic hinges at points 1, 2, and 3, because these are the points at which maximum bending moments are found. The configuration indicating the assumed location of the plastic hinges (Fig. 12.11c) is the mechanism of collapse. At every hinge, the hinge moment must clearly be the same.

Figure 12.11. (a) Beam with built-in ends; (b) elastic bending moment diagram; (c) mechanism of collapse with plastic hinges at 1 through 3

The equilibrium and the energy approaches are available for determination of the ultimate loading. Electing the latter, we refer to Fig. 12.11c and note that the change in energy associated with rotation at points 1 and 2 is M_u · δθ, while at point 3, it is M_u(2δθ). The work done by the concentrated force is P · δν. According to the principle of virtual work, we may write

P_u(δν) = M_u(δθ) + M_u(δθ) + M_u(2δθ) = 4M_u(δθ)

where P_u represents the ultimate load. Because the deformations are limited to small values, it may be stated that and Substituting in the preceding expression for δν, it is found that

(a)

where M_u is calculated for a given beam using Eq. (12.12). It is interesting that, by introduction of the plastic hinges, the originally statically indeterminate beam is rendered determinate. The determination of P_u is thus simpler than that of P_yp, on which elastic analysis is based. An advantage of limit design may also be found in noting that a small rotation at either end of the beam or a slight lowering of a support will not influence the value of P_u. Moderate departures from the ideal case, such as these, will, however, have a pronounced effect on the value of P_yp in a statically indeterminate system.

While the positioning of the plastic hinges in the preceding problem is limited to the single possibility shown in Fig. 12.11c, more than one possibility will exist for situations in which several forces act. Correspondingly, a number of collapse mechanisms may exist, and it is incumbent on the designer to select from among them the one associated with the lowest load.

Example 12.7

Determine the collapse load of the continuous beam shown in Fig. 12.12a.

Figure 12.12. Example 12.7

Solution The four possibilities of collapse are indicated in Figs. 12.12b through d. We first consider the mechanism of Fig. 12.12b. In this system, motion occurs because of rotations at hinges 1, 2, and 3. The remainder of the beam remains rigid. Applying the principle of virtual work, noting that the moment at point 1 is zero, we have

P(δν) = M_u(2δθ) + M_u(δθ) = 3M_u(δθ)

Because

this equation yields P_u = 6M_u/L.

For the collapse mode of Fig. 12.12c,

and thus P_u = 2M_u/L.

The collapse mechanisms indicated by the solid and dashed lines of Fig. 12.12d are unacceptable because they imply a zero bending moment at section 3. We conclude that collapse will occur as in Fig. 12.11c, when P → 2M_u/L.

Example 12.8

Determine the collapse load of the beam shown in Fig. 12.13a.

Figure 12.13. Example 12.8

Solution There are a number of collapse possibilities, of which one is indicated in Fig. 12.13b. Let us suppose that there exists a hinge at point 2, a distance e from the left support. Then examination of the geometry leads to θ₁ = θ₂(L − e)/e or θ₁ + θ₂ = Lθ₂/e. Applying the principle of virtual work,

or

from which

(b)

The minimization condition for p in Eq. (b), dp/de = 0, results in

(c)

Thus, Eqs. (b) and (c) provide a possible collapse configuration. The remaining possibilities are similar to those discussed in the previous example and should be checked to ascertain the minimum collapse load.

Determination of the collapse load of frames involves much the same analysis. For complex frames, however, the approaches used in the foregoing examples would lead to extremely cumbersome calculations. For these, special-purpose methods are available to provide approximate solutions [Ref. 12.6].

Example 12.9

Apply the method of virtual work to determine the collapse load of the structure shown in Fig. 12.14a. Assume that the rigidity of member BC is 1.2 times greater than that of the vertical members AB and CD.

Figure 12.14. Example 12.9

Solution Of the several collapse modes, we consider only the two given in Figs. 12.14b and c. On the basis of Fig. 12.14b, plastic hinges will be formed at the ends of the vertical members. Thus, from the principle of virtual work,

Substituting u = Lθ, this expression leads to P_u = 8M_u/L.

Referring to Fig. 12.14c, we have M_uE = 1.2M_u, where M_u is the collapse moment of the vertical elements. Applying the principle of virtual work,

Noting that u = Lθ and this equation provides the following expression for the collapse load: P_u = 2.56M_u/L.

12.8. Elastic-Plastic Torsion

Recall from Chapter 6 that the maximum shearing stress in a slender bar of arbitrary section subject to pure torsion is always found on the boundary. As the applied torque is increased, we expect yielding to occur on the boundary and to move progressively toward the interior, as sketched in Fig. 12.15a for a bar of rectangular section. We now determine the ultimate torque T_u that can be carried. This torque corresponds to the totally plastic state of the bar, as was the case of the beams previously discussed. Our analysis treats only perfectly plastic materials.

Figure 12.15. (a) Partially yielded rectangular section; (b) membrane-roof analogy applied to elastic-plastic torsion of a rectangular bar; (c) sand hill analogy applied to plastic torsion of a circular bar

The stress distribution within the elastic region of the bar is governed by Eq. (6.9),

(a)

where Φ represents the stress function (Φ = 0 at the boundary) and θ is the angle of twist. The shearing stresses, in terms of Φ, are

(b)

Inasmuch as the bar is in a state of pure shear, the stress field in the plastic region is, according to the Mises yield criterion, expressed by

(c)

where τ_yp is the yield stress in shear. This expression indicates that the slope of the Φ surface remains constant throughout the plastic region and is equal to τ_yp.

Bearing in mind the condition imposed on Φ by Eq. (c), the membrane analogy (Sec. 6.5) may be extended from the purely elastic to the elastic-plastic case. As shown in Fig. 12.15b, a roof abc of constant slope is erected with the membrane as its base. Figure 12.15c shows such a roof for a circular section. As the pressure acting beneath the membrane increases, more and more contact is made between the membrane and the roof. In the fully plastic state, the membrane is in total contact with the roof, membrane and roof being of identical slope. Whether the membrane makes partial or complete contact with the roof clearly depends on the pressure. The membrane-roof analogy thus permits solution of elastic-plastic torsion problems.

For the case of a totally yielded bar, the membrane-roof analogy leads quite naturally to the sand hill analogy. We need not construct a roof at all, using this method. Instead, sand is heaped on a plate whose outline is cut into the shape of the cross section of the torsion member. The torque is, according to the membrane analogy, proportional to twice the volume of the sand figure so formed. The ultimate torque corresponding to the fully plastic state is thus found.

Referring to Fig. 12.15c, let us apply the sand hill analogy to determine the ultimate torque for a circular bar of radius r. The volume of the corresponding cone is , where h is the height of the sand hill. The slope h/r represents the yield point stress τ_yp. The ultimate torque is therefore

(12.16)

Note that the maximum elastic torque is T_yp = (πr³/2)τ_yp. We may thus form the ratio

(12.17)

Other solid sections may be treated similarly [Ref. 12.7]. Table 12.1 lists the ultimate torques for bars of various cross-sectional geometry.

Table 12.1.

The procedure may also be applied to members having a symmetrically located hole. In this situation, the plate representing the cross section must contain the same hole as the actual cross section.

12.9 Elastic-Plastic Stresses in Rotating Disks

This section treats the stresses in a flat disk fabricated of a perfectly plastic material, rotating at constant angular velocity. The maximum elastic stresses for this geometry are, from Eqs. (8.29) and (8.28) as follows:

For the solid disk at r = 0,

(a)

For the annular disk at r = a,

(b)

Here a and b represent the inner and outer radii, respectively, ρ the mass density, and ω the angular speed. The following discussion relates to initial, partial, and complete yielding of an annular disk. Analysis of the solid disk is treated in a very similar manner.

Initial Yielding

According to the Tresca yield condition, yielding impends when the maximum stress is equal to the yield stress. Denoting the critical speed as ω₀ and using , we have, from Eq. (b),

(12.18)

Partial Yielding

For angular speeds in excess of ω₀, but lower than speeds resulting in total plasticity, the disk contains both an elastic and a plastic region, as shown in Fig. 12.16a. In the plastic range, the equation of radial equilibrium, Eq. (8.26), with σ_yp replacing the maximum stress σ_θ, becomes

(12.19)

or

Figure 12.16. (a) Partially yielded rotating annular disk; (b) stress distribution in complete yielding

The solution is given by

(c)

By satisfying the boundary condition σ_r = 0 at r = a, Eq. (c) provides an expression for the constant c₁, which when introduced here results in

(d)

The stress within the plastic region is now determined by letting r = c in Eq. (d):

(12.20)

Referring to the elastic region, the distribution of stress is determined from Eq. (8.27) with σ_r = σ_c at r = c, and σ_r = 0 at r = b. Applying these conditions, we obtain

(e)

The stresses in the outer region are then obtained by substituting Eqs. (e) into Eq. (8.27):

(12.21)

To determine the value of ω that causes yielding up to radius c, we need only substitute σ_θ for σ_yp in Eq. (12.21) and introduce σ_c as given by Eq. (12.20).

Complete Yielding

We turn finally to a determination of the speed ω₁ at which the disk becomes fully plastic. First, Eq. (c) is rewritten

(f)

Applying the boundary conditions, σ_r = 0 at r = a and r = b in Eq. (f), we have

(g)

and the critical speed (ω = ω₁) is given by

(12.22)

Substitution of Eqs. (g) and (12.22) into Eq. (f) provides the radial stress in a fully plastic disk:

(12.23)

The distributions of radial and tangential stress are plotted in Fig. 12.16b.

12.10 Plastic Stress–Strain Relations

Consider an element subject to true stresses σ₁, σ₂, and σ₃ with corresponding true straining. The true strain, which is plastic, is denoted ε₁, ε₂, and ε₃. A simple way to derive expressions relating true stress and strain is to replace the elastic constants E and ν by E_s and , respectively, in Eqs. (2.28). In so doing, we obtain equations of the total strain theory or the deformational theory, also known as Hencky’s plastic stress–strain relations:

(12.24a)

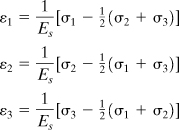
The foregoing may be restated as

(12.24b)

Here E_s, a function of the state of plastic stress, is termed the modulus of plasticity or secant modulus. It is defined by Fig. 12.17

(12.25)

in which the quantities σ_e and ε_e are the effective stress and the effective strain, respectively.

Although other yield theories may be employed to determine σ_e, the maximum energy of distortion or Mises theory (Sec. 4.7) is most suitable. According to the Mises theory, the following relationship connects the uniaxial yield stress to the general state of stress at a point:

(12.26)

Here the effective stress σ_e is also referred to as the von Mises stress. It is assumed that expression (12.26) applies not only to yielding or the beginning of inelastic action (σ_e = σ_yp), but to any stage of plastic behavior. That is, σ_e has the value σ_yp at yielding, and as inelastic deformation progresses, σ_e increases in accordance with the right side of Eq. (12.26). Equation (12.26) then represents the logical extension of the yield condition to describe plastic deformation after the yield stress is exceeded.

Collecting terms of Eqs. (12.24), we have

(a)

Figure 12.17. True stress–true strain diagram for a rigid-plastic material

The foregoing, together with Eqs. (12.25) and (12.26), leads to the definition

(12.27a)

or (on the basis of ε₁ + ε₂ + ε₃ = 0), in different form,

(12.27b)

relating the effective plastic strain and the true strain components. Note that, for simple tension, σ₂ = σ₃ = 0, ε₂ = ε₃ = −ε₁/2, and Eqs. (12.26) and (12.27) result in

(b)

Therefore, if we know σ_e, ε_e can be read directly from true stress-strain diagram for uniaxial tension (Fig. 12.17).

Hencky’s equations as they appear in Eqs. (12.24) have little utility. To give these expressions generality and convert them to a more convenient form, it is useful to employ the empirical relationship (12.2)

σ_e = K(ε_e)ⁿ

from which

(c)

The true stress–strain relations, upon substitution of Eqs. (12.26) and (c) into (12.24), then assume the following more useful form:

(12.28a)

(12.28b)

(12.28c)

where α = σ₂/σ₁ and β = σ₃/σ₁.

In the case of an elastic material (K = E and n = 1), it is observed that Eqs. (12.28) reduce to the familiar generalized Hooke’s law.

Example 12.10

A thin-walled cylindrical tube of initial radius r_o is subjected to internal pressure p. Assume that the values of r_o, p, and the material properties (K and n) are given. Apply Hencky’s relations to determine (a) the maximum allowable stress and (b) the initial thickness t_o for the cylinder to become unstable at internal pressure p.

Solution The current radius, thickness, and the length are denoted by r, t, and L, respectively. In the plastic range, the hoop, axial, and radial stresses are

(d)

We thus have α = σ₂/σ₁ and β = 0 in Eqs. (12.28).

Corresponding to these stresses, the components of true strain are, from Eq. (2.19),

(e)

Based on the constancy of volume, Eq. (12.1), we then have

or

(f)

The first of Eqs. (e) gives

(g)

The tangential stress, the first of Eqs. (d), is therefore

from which

(h)

Simultaneous solution of Eqs. (12.28) leads readily to

(i)

Equation (h) then appears as

(j)

For material instability,

which, upon substitution of ∂ p/∂ σ₁ and ∂ p/∂ ε₁ derived from Eq. (j), becomes

or

(k)

In Eqs. (12.28) it is observed that σ₁ depends on α and εⁿ₁. That is,

(l)

Differentiating, we have

(m

Expressions (k), (l), and (m) lead to the instability condition:

(12.29)

a. Equating expressions (12.29) and (12.28a), we obtain

and the true tangential stress is thus

(12.30)

b. On the other hand, Eqs. (d), (f), (g), and (12.28) yield

From this expression, the required original thickness is found to be

(12.31)

wherein σ₁ is given by Eq. (12.30).

In the case under consideration, α = 1/2 and Eqs. (12.29), (12.30), and (12.31) thus become

(12.32)

For a thin-walled spherical shell under internal pressure, the two principal stresses are equal and hence α = 1. Equations (12.29), (12.30), and (12.31) then reduce to

(12.33)

Based on the relations derived in this example, the effective stress and the effective strain are determined readily. Table 12.2 furnishes the maximum true and effective stresses and strains in a thin-walled cylinder and a thin-walled sphere. For purposes of comparison, the table also lists the results (12.4) pertaining to simple tension. We observe that at instability the maximum true strains in a sphere and cylinder are much lower than the corresponding longitudinal strain in uniaxial tension.

Table 12.2.

It is significant that, for loading situations in which the components of stress do not increase continuously, Hencky’s equations provide results that are somewhat in error, and the incremental theory (Sec. 12.11) must be used. Under these circumstances, Eqs. (12.24) or (12.28) cannot describe the complete plastic behavior of the material. The latter is made clearer by considering the following. Suppose that subsequent to a given plastic deformation the material is unloaded, either partially or completely, and then reloaded to a new state of stress that does not result in yielding. We expect no change to occur in the plastic strains; but Hencky’s equations indicate different values of the plastic strain, because the stress components have changed. The latter cannot be valid because during the unloading-loading process the plastic strains have, in reality, not been affected.

12.11. Plastic Stress-Strain Increment Relations

We have already discussed the limitations of the deformational theory in connection with a situation in which the loading does not continuously increase. The incremental theory offers another approach, treating not the total strain associated with a state of stress, but rather the increment of strain.

Suppose now that the true stresses at a point experience very small changes in magnitude dσ₁, dσ₂, and dσ₃. As a consequence of these increments, the effective stress σ_e will be altered by dσ_e and the effective strain ε_e by dε_e. The plastic strains thus suffer increments dε₁, dε₂, and dε₃.

The following modification of Hencky’s equations, due to Lévy and Mises, describe the foregoing and give good results in metals:

(12.34a)

An alternative form is

(12.34b)

The plastic strain is, as before, to occur at constant volume; that is,

dε₁ + dε₂ + dε₃ = 0

The effective strain increment, referring to Eq. (12.27b), may be written

(12.35)

The effective stress σ_e is given by Eq. (12.26). Alternatively, to ascertain dε_e from a uniaxial true stress-strain curve such as Fig. 12.17, it is necessary to know the increase of equivalent stress dσ_e. Given σ_e and dε_e, it then follows that at any point in the loading process application of Eqs. (12.34) provides the increment of strain as a unique function of the state of stress and the increment of the stress. According to the Lévy-Mises theory, therefore, the deformation suffered by an element varies in accordance with the specific loading path taken.

In a particular case of straining of sheet metal under biaxial tension, the Lévy-Mises equations (12.34) become

(12.36)

where α = σ₂/σ₁ and σ₃ taken as zero. The effective stress and strain increment, Eqs. (12.26) and (12.35), is now written

(12.37)

(12.38)

Combining Eqs. (12.36) and (12.38) and integrating yields

(12.39)

To generalize this result, it is useful to employ Eq. (12.2), σ_e = K(ε_e)ⁿ, to include strain-hardening characteristics. Differentiating this expression, we have

(12.40)

Note that, for simple tension, n = ε_e = ε and Eq. (12.40) reduces to Eq. (12.3).

The utility of the foregoing development is illustrated in Examples 12.11 and 12.12.

In closing, we note that the total (elastic-plastic) strains are determined by adding the elastic strains to the plastic strains. The elastic-plastic strain relations, together with the equations of equilibrium and compatibility and appropriate boundary conditions, completely describe a given situation. The general form of the Lévy-Mises relationships, including the elastic incremental components of strain, are referred to as the Prandtl and Reuss equations.

Example 12.11

Redo Example 12.10 employing the Lévy-Mises stress-strain increment relations.

Solution For the thin-walled cylinder under internal pressure, the plastic stresses are

(a)

where r and t are the current radius and the thickness. At instability,

(b)

Because , introduction of Eqs. (a) into Eq. (b) provides

(12.41)

Clearly, dr/r is the hoop strain increment dε₂, and dt/t is the incremental thickness strain or radial strain increment dε₃. Equation (12.41) is the condition of instability for the cylinder material.

Upon application of Eqs. (12.37) and (12.38), the effective stress and the effective strains are found to be

(c)

It is observed that axial strain does not occur and the situation is one of plane strain. The first of Eqs. (c) leads to , and condition (12.41) gives

from which

A comparison of this result with Eq. (12.40) shows that

(12.42)

The true stresses and true strains are then obtained from Eqs. (c) and σ_e = K(ε_e)ⁿ and the results found to be identical with that obtained using Hencky’s relations (Table 12.2).

For a spherical shell subjected to internal pressure σ₁ = σ₂ = pr/2t, α = 1 and dε₁ = dε₂ = −dε₃/2. At stability dp = 0, and we now have

(d)

Equations (12.37) and (12.38) result in

(e)

Equations (d) and (e) are combined to yield

(f)

From Eqs. (f) and (12.40), it is concluded that

(12.43)

True stress and true strain are easily obtained, and are the same as the values determined by a different method (Table 12.2).

12.12 Stresses in Perfectly Plastic Thick-Walled Cylinders

The case of a thick-walled cylinder under internal pressure alone was considered in Sec. 8.2. Equation (8.11) was derived for the onset of yielding at the inner surface of the cylinder owing to maximum shear. This was followed by a discussion of the strengthening of a cylinder by shrinking a jacket on it (Sec. 8.5). The same goal can be achieved by applying sufficient pressure to cause some or all of the material to deform plastically and then releasing the pressure. This is briefly described next [Ref. 12.8].

A continuing increase in internal pressure will result in yielding at the inner surface. As the pressure increases, the plastic zone will spread toward the outer surface, and an elastic-plastic state will prevail in the cylinder with a limiting radius c beyond which the cross section remains elastic. As the pressure increases further, the radius c also increases until, eventually, the entire cross section becomes fully plastic at the ultimate pressure. When the pressure is reduced, the material unloads elastically. Thus, elastic and plastic stresses are superimposed to produce a residual stress pattern (see Example 12.12). The generation of such stresses by plastic action is called autofrettage. Upon reloading, the pressure needed to produce renewed yielding is greater than the pressure that produced initial yielding; the cylinder is thus strengthened by autofrettage.

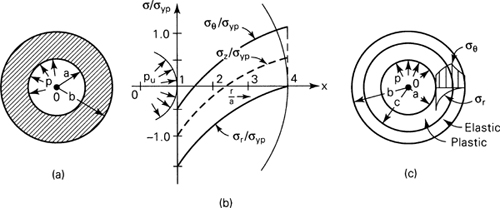
This section concerns the fully plastic and elastic-plastic actions in a thick-walled cylinder fabricated of a perfectly plastic material of yield strength σ_yp under internal pressure p as shown in Fig. 12.18(a).

Figure 12.18. (a) Thick-walled cylinder of perfectly plastic material under internal pressure; (b) fully plastic stress distribution in the cylinder at the ultimate pressure for b = 4a; (c) partially yielded cylinder.

Complete Yielding

The fully plastic or ultimate pressure as well as the stress distribution corresponding to this pressure is determined by application of the Lévy-Mises relations with σ_e = σ_yp. In polar coordinates, the axial strain increment is

(12.44)

If the ends of the cylinder are restrained so that the axial displacement w = 0, the problem may be regarded as a case of plane strain, for which ε_z = 0. It follows that dε_z = 0 and Eq. (12.44) gives

(a)

The equation of equilibrium is, from Eq. (8.2),

(b)

subject to the following boundary conditions:

(c)

Based on the maximum energy of distortion theory of failure, Eqs. (4.4b) or (12.26), setting σ₁ = σ_θ, σ₃ = σ_r, and results in . From this, we obtain the yield condition:

(12.45)

Alternatively, according to the maximum shearing stress theory of failure (Sec. 4.6), the yield condition is

(12.46)

Introducing Eq. (12.45) or (12.46) into Eq. (b), we obtain dσ_r/dr = kσ_yp/r, which has the solution

(d)

The constant of integration is determined by applying the second of Eqs. (c):

c₁ = −kσ_yp ln b

Equation (d) is thus

(e)

The first of conditions (c) now leads to the ultimate pressure:

(12.47)

An expression for σ_θ can now be obtained by substituting Eq. (e) into Eqs. (12.45) or (12.46). Consequently, Eq. (a) provides σ_z. The complete plastic stress distribution for a specified σ_yp is thus found to be

(12.48)

The stresses given by Eqs. (12.48) are plotted in Fig. 12.18, whereas the distribution of elastic tangential and radial stresses is shown in Fig. 8.3a.

Example 12.12

A perfectly plastic closed-ended cylinder (σ_yp = 400 MPa) with 50- and 100-mm internal and external diameters is subjected to an internal pressure p (Fig. 12.18a). On the basis of the maximum distortion energy theory of failure, determine (a) the complete plastic stresses at the inner surface and (b) the residual tangential and axial stresses at the inner surface when the cylinder is unloaded from the ultimate pressure p_u.

Solution The magnitude of the ultimate pressure is, using Eq. (12.47),

a. From Eqs. (12.48), with r = a,

Note, as a check, that σ_Z = (σ_r + σ_θ)/2 yields the same result.

b. Unloading is assumed to be linearly elastic. Thus, we have the following elastic stresses at r = a, using Eqs. (8.13) and (8.20):

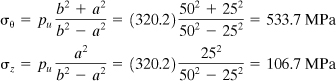
The residual stresses at the inner surface are therefore

(σ_θ)_res = 141.7 − 533.7 = −392 MPa

(σ_z)_res = −89.2 − 106.7 = −195.9 MPa

The stresses at any other location may be obtained in a like manner.

Partial Yielding

For the elastic segment for which c ≤ r ≤ b (Fig. 12.18c), the tangential and radial stresses are determined using Eqs. (8.12) and (8.13) with a = c. In so doing, we obtain

(12.49a)

(12.49b)

Here p_c is the magnitude of the (compressive) radial stress at the elastic-plastic boundary r = c where yielding impends. Accordingly, by substituting these expressions into the yield condition σ_θ − σ_r = kσ_yp, we have

(12.50)

This pressure represents the boundary condition for a fully plastic segment with inner radius a and outer radius c. That is, constant c₁ in Eq. (d) is obtained by applying (σ_r)_r=c = −p_c:

Substituting this value of c₁ into Eq. (d), the radial stress in the plastic zone becomes

(12.51a)

Then, using the yield condition, the tangential stress in the plastic zone is obtained in the following form:

(12.51b)

Equations (12.49) and (12.51), for a given elastic-plastic boundary radius c, provide the relationships necessary for calculation of the elastic-plastic stress distribution in the cylinder wall (Fig. 12.18c).

Problems

Secs. 12.1 through 12.5

12.1. A solid circular cylinder of 100-mm diameter is subjected to a bending moment M = 3.375 kN · m, an axial tensile force P = 90 kN, and a twisting end couple T = 4.5 kN · m. Determine the stress deviator tensor. [Hint: Refer to Sec. 2.13.]

12.2. In the pin-connected structure shown in Fig. P10.28., the true stress-engineering strain curves of the members are expressed by and . Verify that, for all three bars to reach tensile instability simultaneously, they should be set initially at an angle described by

(P12.02)

Calculate the value of this initial angle for n₁ = 0.2 and n₂ = 0.3.

12.3. Determine the deflection of a uniformly loaded rigid plastic cantilever beam of length L. Locate the origin of coordinates at the fixed end, and denote the loading by p.

12.4. Redo Prob. 12.3 for p = 0 and a concentrated load P applied at the free end.

12.5. Consider a beam of rectangular section, subjected to end moments as shown in Fig. 12.3a. Assuming that the relationship for tensile and compressive stress for the material is approximated by σ = Kε^¼, determine the maximum stress.

12.6. A simply supported rigid plastic beam is described in Fig. P12.6. Compute the maximum deflection. Reduce the result to the case of a linearly elastic material. . Let P = 8 kN, E = 200 GPa, L = 1.2 m, and a = 0.45 m. Cross-sectional dimensions shown are in millimeters.

Figure P12.6

Secs. 12.6 and 12.7

12.7. A ductile bar (σ_yp = 350 MPa) of square cross section with sides a = 12 mm is subjected to bending moments M about the z axis at its ends (Fig. P12.7). Determine the magnitude of M at which (a) yielding impends; (b) the plastic zones at top and bottom of the bar are 2 mm thick.

Figure P12.7

12.8. A beam of rectangular cross section (width a, depth h) is subjected to bending moments M at its ends. The beam is constructed of a material displaying the stress–strain relationship shown in Fig. P12.8. What value of M can be carried by the beam?

Figure P12.08

12.9. A perfectly plastic beam is supported as shown in Fig. P12.9. Determine the maximum deflection at the start of yielding.

Figure P12.9

12.10. Consider a uniform bar of solid circular cross section with radius r, subjected to axial tension and bending moments at both ends. Derive general relationships involving N and M that govern, first, the case of initial yielding and, then, fully plastic deformation. Sketch the interaction curves.

12.11. Figure P5.32 shows a hook made of steel with σ_yp = 280 MPa, equal in tension and compression. What load P results in complete plastic deformation in section A-B? Neglect the effect of curvature on the stress distribution.

12.12. A propped cantilever beam made of ductile material, is loaded as shown in Fig. P12.12. What are the values of the collapse load p_u and the distance x?

Figure P12.12

12.13. Obtain the interaction curves for the beam cross section shown in Fig. 12.10a. The beam is subjected to a bending moment M and an axial load N at both ends. Take b = 2h, b₁ = 1.8h, and h₁ = 0.7h.

12.14. Obtain the collapse load of the structure shown in Fig. P12.14. Assume that plastic hinges form at 1, 3, and 4.

Figure P12.14

12.15. What is the collapse load of the beam shown in Fig. P12.15.? Assume two possible modes of collapse such that plastic hinges form at 2, 3, and 4.

Figure P12.15

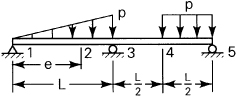
12.16. A propped cantilever beam AB, made of ductile material, supports a uniform load of intensity p (Fig. P12.16). What is the ultimate limit load p_u?

Figure P12.16

12.17. Figure P12.17 shows two beam cross sections. Determine M_u/M_yp for each case.

Figure P12.17

Secs. 12.8 through 12.12

12.18. Determine the elastic-plastic stresses in a rotating solid disk.

12.19. For a rectangular bar of sides a and b, determine the ultimate torque corresponding to the fully plastic state (Table 12.1). Use the sand hill analogy.

12.20. For an equilateral triangular bar of sides 2a, determine (a) the ultimate torque corresponding to the fully plastic state (Table 12.1) (use the sand hill analogy) and (b) the maximum elastic torque by referring to Table 6.2. (c) Compare the results found in (a) and (b).

12.21. An annular disk of equilateral hyperbolic profile with outer and inner radii b and a (Fig. 8.12) is shrunk onto a solid shaft so that the interfacial pressure is p_i. Demonstrate that, according to the Tresca yield criterion, when the disk becomes fully plastic,

(P12.21)

Here σ_yp is the yield point stress and r represents any arbitrary radius.

12.22. Consider a thin-walled cylinder of original radius r_o, subjected to internal pressure p. Determine the value of the required original thickness at instability employing Hencky’s relations. Use the following:

K = 900 MPa, n = 0.2

ro = 0.5 m, p = 14 MPa

12.23. Redo Example 12.10 for the cylinder under uniform axial tensile load P and p = 0.

12.24. A thin-walled tube of original thickness t_o and outer radius R_o just fits over a rigid rod of radius r_o. Employ the Lévy-Mises relations to verify that the axial load the tube can sustain before instability occurs is represented by

(P12.24)

Assume the tube rod interface to be frictionless. Use σ = Kεⁿ as the true stress-true strain relationship of the tube material in simple tension.

12.25. A thick-walled cylinder (σ_yp = 250 MPa) of inner radius a = 50 mm is subjected to an internal pressure of p_i = 60 MPa. Determine the outer radius b such as to provide (a) a factor of safety n = 2.5 against yielding; (b) a factor of safety n = 3 against ultimate collapse based on maximum shearing stress theory of failure.

12.26. A thick-walled cylinder has an inner radius a and outer radius b = 2a. What is the internal pressure at which the elastic-plastic boundary is at r = 1.4a, based on maximum energy of distortion criterion? Let σ_yp = 260 MPa.

12.27. Consider a perfectly plastic pipe (σ_yp = 420 MPa) having an outer radius of 60 mm and inner radius of 50 mm. Determine the maximum internal pressures at the onset of yielding and for complete yielding on the basis of a factor of safety n = 3 and the following theories of failure: (a) maximum shearing stress and (b) maximum energy of distortion.

12.28. A perfectly plastic, closed-ended cylinder is under internal pressure p (Fig. 12.18a). Applying the maximum shearing stress criterion of failure, calculate the residual stress components at r = 0.25 m when the cylinder is unloaded from pu. Use a = 0.2 m, b = 0.3 m, and σ_yp = 400 MPa.

12.29. A thick-walled compound cylinder having a = 20 mm, b = 30 mm, and c = 50 mm is subjected to internal pressure. Material yield strengths are 280 MPa and 400 MPa for inner and outer cylinders, respectively. Determine the fully plastic pressure on the basis of the maximum shearing stress criterion of failure.

12.30. A perfectly plastic cylinder for which b/a = 3 is subjected to internal pressure causing yielding of the material to the mid-depth c = (a + b)/2. In terms of k and σ_yp, determine (a) the pressure between the elastic and plastic zones, (b) the radial stress at r = a, and (c) the tangential stresses at r = b, r = c, and r = a. Note: Relationships derived (Sec. 12.12) depend on the ratios of the radii, rather than on their magnitudes. Accordingly, convenient numbers such as a = 1, c = 2, and b = 3 may be employed.