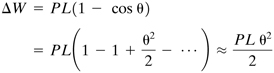Chapter 11 Elastic Stability
11.1 Introduction
We have up to now dealt primarily with the prediction of stress and deformation in structural elements subject to various load configurations. Failure criteria have been based on a number of theories relying on the attainment of a particular stress, strain, or energy level within the body. This chapter demonstrates that the beginnings of structural failure may occur prior to the onset of any seriously high levels of stress. We thus explore failure owing to elastic instability and seek to determine those conditions of load and geometry that lead to a compromise of structural integrity.
We shall deal only with beam and slender members subject to axial compression. The problem is essentially one of ascertaining those configurations of the system that lead to sustainable patterns of deformation. The principal difference between the theories of linear elasticity and linear stability is that, in the former, equilibrium is based on the undeformed geometry, whereas in the latter the deformed geometry must be considered.
11.2 Critical Load
To demonstrate the concepts of stability and critical load, consider a rigid, weightless bar AB, shown in Fig. 11.1a. This member is pinned at B and acted on by a force P. In the absence of restoring influences such as the spring shown, any small lateral disturbance (causing a displacement δ) will result in rotation of the bar, indicated by the dashed lines, with no possibility of return to the original configuration. Without the spring, therefore, the situation depicted in the figure is one of unstable equilibrium. With a spring present, different possibilities arise.
Figure 11.1. Buckling of a rigid bar pinned at the base and supported by a spring at the top.
Equilibrium Method
A small momentary disturbance δ can now be sustained by the system (provided that P is also small) because the disturbing moment Pδ is smaller than the restoring moment kδL (where k represents the linear spring constant, force per unit of deformation). For a small enough value of P, the moment kδL will thus be sufficient to return the bar to δ = 0. Since the system reacts to a small disturbance by creating a counterbalancing effect acting to diminish the disturbance, the configuration is in stable equilibrium.
If now the load is increased to the point where
(a)
![]()
it is clear that any small disturbance δ will be neither diminished nor amplified. The system is now in neutral equilibrium at any small value of δ. Expression (a) defines the critical load:
(b)
![]()
If P > Pcr, the net moment acting will be such as to increase δ, tending to further increase the disturbing moment Pδ, and so on. For P > Pcr, the system is in unstable equilibrium because any lateral disturbance will be amplified, as in the springless case discussed earlier.
The equilibrium regimes are shown in Fig. 11.1b. Note that C, termed the bifurcation point, marks the two branches of the equilibrium solution. One is the vertical branch (P ≤ Pcr, δ = 0), and the other is the horizontal (P = Pcr, δ > 0).
Energy Method
Stability may also be interpreted in terms of energy concepts, however. Referring again to Fig. 11.1a, the work done by P as it acts through a distance L(1 − cos θ) is
The elastic energy acquired as a result of the corresponding spring elongation Lθ is
![]()
If ΔU > ΔW, the configuration is stable; the work done is insufficient to result in a displacement that grows subsequent to a lateral disturbance. However, if ΔW > ΔU, the system is unstable because now the work is large enough to cause the displacement to grow following a disturbance. The boundary between stable and unstable configurations corresponds to ΔW = ΔU,
Pcr = kL
as before.
The buckling analysis of compression members usually follows in essentially the same manner. Either the static equilibrium or the energy approach may be used for determination of the critical load. The choice depends on the particulars of the situation under analysis. Although the static equilibrium method leads to exact solutions, the results offered by the energy approach (sometimes approximate) are often preferable because of the physical insights that may be more readily gained.
11.3 Buckling of a Column
Consideration is now given to a relatively slender straight bar subject to axial compression. This member, a column, is similar to the element shown in Fig. 11.1a, in that it too can experience unstable behavior. In the case of a column, the restoring force or moment is provided by elastic forces established within the member, rather than by springs external to it.
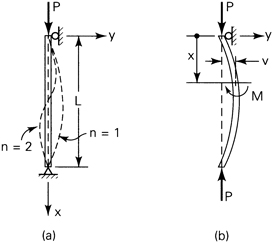
Refer to Fig. 11.2a, in which is shown a straight, homogeneous, pin-ended column. For such a column, the end moments are zero. This is regarded as the fundamental or most basic case. It is reasonable to suppose that the column can be held in a deformed configuration by a load P while remaining in the elastic range. Note that the requisite axial motion is permitted by the movable end support. In Fig. 11.2b, the postulated deflection is shown, having been caused by collinear forces P acting at the centroid of the cross section. The bending moment at any section, M = −Pυ, when inserted into the equation for the elastic behavior of a beam, EIυ″ = M, yields
(11.1)
![]()
Figure 11.2. Column with pinned ends.
The solution of this differential equation is
(a)
![]()
where the constants of integration, c1 and c2, are determined from the end conditions: υ(0) = υ(L) = 0. From υ(0) = 0, we find that c2 = 0. Substituting the second condition into Eq. (a), we obtain
(b)
![]()
It must be concluded that either c1 = 0, in which case υ = 0 for all x and the column remains straight regardless of load, or sin![]() . The case of c1 = 0 corresponds to a condition of no buckling and yields a trivial solution [the energy approach (Sec. 11.9) sheds further light on this case]. The latter is the acceptable alternative because it is consistent with column deflection. It is satisfied if
. The case of c1 = 0 corresponds to a condition of no buckling and yields a trivial solution [the energy approach (Sec. 11.9) sheds further light on this case]. The latter is the acceptable alternative because it is consistent with column deflection. It is satisfied if
(c)
![]()
The value of P ascertained from Eq. (c), that is, the load for which the column may be maintained in a deflected shape, is the critical load,
(11.2)
![]()
where L represents the original length of the column. Assuming that column deflection is in no way restricted to a particular plane, the deflection may be expected to occur about an axis through the centroid for which the second moment of area is a minimum. The lowest critical load or Euler buckling load of the pin-ended column is of greatest interest; for n = 1,
(11.3)
![]()
The deflection is found by combining Eqs. (a) and (c) and inserting the values of c1 and c2:
(11.4)
![]()
Inasmuch as c1, the amplitude of the elastic curve, is undetermined (and independent of Pcr), we are led to conclude that the critical load and deflection are independent and that Pcr will sustain any small lateral deflection.
The foregoing conclusions are predicated on the linearized beam theory with which the analysis began. Recall that in Eq. (11.1) the term d2υ/dx2 is actually an approximation to the curvature, Eq. (5.7). Were the exact curvature used, the differential equation derived would apply to large deformations within the elastic range, and the results would be less restricted. For this case it is found that P depends on the magnitude of the deflection or c1. The exact or large-amplitude analysis also reveals values of P exceeding Pcr. Because of practical considerations, large deflections are generally not permitted to occur in structures. The bending stresses accompanying large deflection could carry the material into the inelastic regime, thus leading to diminished buckling loads [Ref. 11.1]. In most applications, Pcr is usually regarded as the maximum load sustainable by a column.
Returning to Eq. (11.4), we note that while, theoretically, any buckling mode is possible the column will ordinarily deflect into the first mode (n = 1). The first two modes of buckling are indicated by the dashed lines in Fig. 11.2a. To initiate second-mode buckling (n = 2) requires one lateral support at the nodal point, at midlength. As n increases, the number of nodal points also increases. We are therefore interested primarily in the lowest buckling mode.
We conclude this section by recalling that the boundary conditions employed in the solution of the differential equation led to an infinite set of discrete values of load, (Pcr)n. These solutions, typical of many engineering problems, are termed eigenvalues, and the corresponding deflections ν are the eigenfunctions.
11.4 End Conditions
It is evident from the foregoing derivation that Pcr depends on the end conditions of the column. For other than the pin-ended, fundamental case discussed, we need only substitute the appropriate conditions into Eq. (a) of Sec. 11.3 and proceed as before.
Consider an alternative approach, beginning with the following revised form of the Euler buckling formula for a pin-ended column and applicable to a variety of end conditions:
(11.5)
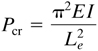
Here Le denotes the effective column length, which for the pin-ended column is the column length L. The effective length, shown in Fig. 11.3 for several end conditions, is determined by noting the length of a segment corresponding to a pin-ended column. In so doing we seek the distance between points of inflection on the elastic curve or the distance between hinges, if any exist.
Figure 11.3. Effective lengths of columns with different restraints.
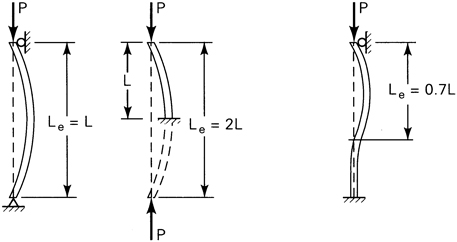
Regardless of end condition, it is observed that the critical load depends not on material strength but rather on the flexural rigidity, EI. Buckling resistance can thus be enhanced by deploying material so as to maximize the moment of inertia, but not to the point where the section thickness is so small as to result in local buckling or wrinkling.
11.5. Critical Stress in a Column
Assuming that at buckling the column material is stressed within the elastic regime, the stress corresponding to Pcr is simply
(11.6)

where A is the cross-sectional area and r is the radius of gyration defined by I = Ar2. We seek the minimum value of σcr, and consequently the minimum radius of gyration should be used in Eq. (11.6). The quotient Le/r, known as the slenderness ratio, is an important parameter in the classification of compression members.
For a member of sufficiently large slenderness ratio, a long column, buckling occurs at a stress lower than the proportional limit. The Euler formula (11.6)is appropriate to this case. For very short members, on the other hand, failure occurs by compression, without appreciable buckling, at stresses exceeding the proportional limit. Between these extremes lies a column classified as intermediate,* characterized by slenderness ratios that are neither large nor small, which does not fail by direct compression. The failure of intermediate columns occurs subsequent to the onset of inelastic behavior. Presented next is one approach to the determination of the inelastic buckling load, referred to as the tangent modulus theory.
*The range of Le/r depends on the material under consideration. In the case of structural steel, for example, long columns are those for which Le/r > 100; for intermediate columns, 30 < Le/r, < 100, and for short struts, Le/r, < 30.
Consider the concentric compression of an intermediate column, and imagine the loading to occur in small increments until such time as the buckling load Pt is achieved. As we would expect, the column does not remain perfectly straight, but displays slight curvature as the increments in load are imposed. It is fundamental to the tangent modulus theory to assume that accompanying the increasing loads and curvature is a continuous increase, or no decrease, in the longitudinal stress and strain in every fiber of the column. That this should happen is not at all obvious, for it is reasonable to suppose that fibers on the convex side of the member might elongate, thereby reducing the stress. Accepting the former assumption, the stress distribution is as shown in Fig 11.4a. The increment of stress, Δ σ is attributable to bending effects; σcr is the value of stress associated with the attainment of the critical load Pt. The distribution of strain will display a pattern similar to that shown in Fig. 11.4b.
Figure 11.4. (a) Stress distribution for tangent-modulus load; (b) stress-strain diagram.

For small deformations Δ υ, the increments of stress and strain will likewise be small, and as in the case of elastic bending, sections originally plane are assumed to remain plane subsequent to bending. The change of stress Δ σ is thus assumed proportional to the increment of strain, Δε; that is, Δσ = Et Δ ε. The constant of proportionality Et is the slope of the stress-strain diagram beyond the proportional limit, termed the tangent modulus (Fig. 11.4b). Note that within the linearly elastic range, Et = E. The stress–strain relationship beyond the proportional limit during the change in strain fromε to ε + Δε is thus assumed linear, as in the case of elastic buckling. The critical or Engesser stress may, on the basis of the foregoing rationale, be expressed by means of a modification of Eq. (11.6) in which Et replaces E:
(11.7)

The buckling load Pt predicted by Eq. (11.7) is in good agreement with test results. This expression is therefore recommended for design purposes [Ref. 11.2].
Figure 11.5 is a plot of critical stress as a function of slenderness ratio. Portions cd and ce are represented by Eqs. (11.6) and (11.7), respectively. Point c, the yield stress (approximately equal to the proportional stress), is denoted by σyp. The segment denoted ef represents the range of failure by axial compression.
Figure 11.5. Critical stress versus slenderness ratio.
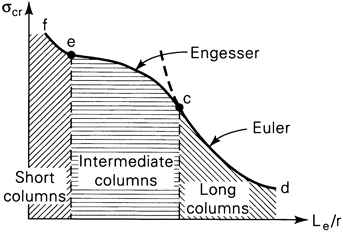
When the critical stress is known and the slenderness ratio required, the application of Eq. (11.7) is straightforward. The value of Et corresponding to σcr is read from the stress-strain curve obtained from a simple compression test, following which Le/r is calculated using Eq. (11.7). If, however, Le/r, is known and σcr is to be ascertained, a trial-and-error approach is necessary (see Prob. 11.10).
11.6. Allowable Stress
The foregoing discussion and analysis have related to ideal, homogeneous, concentrically loaded columns. Inasmuch as such columns are not likely candidates for application in structures, actual design requires the use of empirical formulas based on a strong background of test and experience. Care must be exercised in applying such special-purpose formulas. The designer should be prepared to respond to the following questions:
To what material does the formula apply?
Does the formula already contain a factor of safety, or is the factor of safety separately applied?
For what range of slenderness ratios is the formula valid?
Included among the many special-purpose relationships developed are the following, recommended by the American Institute of Steel Construction (AISC) and valid for a structural steel column:*
* The specifications of the AISC are given in Ref. 11.3. Similar formulas are available for aluminum and timber columns; see, for example, Ref. 11.4.
(11.8)

Here σall, σyp, Cc, and n denote, respectively, the allowable and yield stresses, a material constant, and the factor of safety. The values of Cc and n are given by
(11.9)

This relationship provides a smaller n for a short strut than for a column of higher Le/r, recognizing the fact that the former fails by yielding and the latter by buckling. The use of a variable factor of safety provides a consistent buckling formula for various ranges of Le/r. The second equation of (11.8) includes a constant factor of safety and gives the value of allowable stress in pascals. Both formulas apply to principal load-carrying (main) members.
Example 11.1
The boom of a crane, shown in Fig. 11.6, is constructed of steel, E = 210 GPa; the yield point stress is 210 MPa. The cross section is rectangular with a depth of 100 mm and a thickness of 50 mm. Determine the buckling load of the column.
Figure 11.6. Example 11.1.

Solution The moments of inertia of the section are Iz = 0.05(0.1)3/12 = 4.17 × 10−6 m4 and Iy = 0.1(0.05)3/12 = 1.04 × 10−6 m4. The least radius of gyration is thus ![]() , and the slenderness ratio is L/r = 194. The Euler formula is applicable in this range. From statics, the axial force in terms of W is P = W/tan 15° = 3.732W. Applying the formula for a hinged-end column, Eq. (11.5), for buckling in the yx plane, we have
, and the slenderness ratio is L/r = 194. The Euler formula is applicable in this range. From statics, the axial force in terms of W is P = W/tan 15° = 3.732W. Applying the formula for a hinged-end column, Eq. (11.5), for buckling in the yx plane, we have
![]()
or
W = 305.9 KN
To calculate the load required for buckling in the xz plane, we must take note of the fact that the line of action of the compressive force passes through the joint and thus causes no moment about the y axis at the fixed end. Therefore, Eq. (11.5) may again be applied:
or
W = 76.3 kN
The member will thus fail by lateral buckling when the load W exceeds 76.3 kN. Note that the critical stress Pcr/A = 76.3/0.005 = 15.26 MPa. This, compared with the yield strength of 210 MPa, indicates the importance of buckling analysis in predicting the safe working load.
11.7 Initially Curved Members
As might be expected, the load-carrying capacity and deformation under load of a column are significantly affected by even a small initial curvature. To ascertain the extent of this influence, consider a pin-ended column for which the unloaded shape is described by
(a)
![]()
as shown by the dashed lines in Fig. 11.7. Here ao is the maximum initial deflection. An additional deflection υ1 will accompany a subsequently applied load P, so the total deflection is
(b)
![]()
Figure 11.7. Initially curved column with pinned ends.
The differential equation of the column is thus
(c)
![]()
which together with Eq. (a) becomes
![]()
When the trial particular solution
![]()
is substituted into Eq. (c), it is found that
(d)
![]()
The general solution of Eq. (c) is therefore
(e)
![]()
The constants c1 and c2 are evaluated upon consideration of the end conditions υ1(0) = υ1(L) = 0. The result of substituting these conditions is c1 = c2 = 0; the column deflection is thus
(11.10)
![]()
As for the critical stress, we begin with the expression applicable to combined axial loading and bending: σx = (P/A) ± (My/I), where A and I are the cross-sectional area and the moment of inertia. On substitution of Eqs. (c) and (11.10) into this expression, the maximum compressive stress at midspan is found to be
(11.11)
![]()
Here S is the section modulus I/c, where c represents the distance measured in the y direction from the centroid of the cross section to the extreme fibers. In Eq. (11.11), σmax is limited to the proportional or yield stress of the column material. Thus, setting σmax = σyp and P = PL, we rewrite Eq. (11.11) as follows:
(11.12)
![]()
where PL is the limit load that results in impending yielding and subsequent failure. Given σyp, a0, E, and the column dimensions, Eq. (11.12) may be solved exactly by solving a quadratic or by trial and error for PL. The allowable load Pall can then be found by dividing PL by an appropriate factor of safety, n.
11.8 Eccentrically Loaded Columns: Secant Formula
In contrast with the cases considered up to this point, we now analyze columns that are loaded eccentrically, that is, those in which the load is not applied at the centroid of the cross section. This situation is clearly of great practical importance, since we ordinarily have no assurance that loads are truly concentric. As seen in Fig. 11.8a, the bending moment at any section is −P(υ + e), where e is the eccentricity, defined in the figure. It follows that the beam equation is given by
(a)
![]()
Figure 11.8. (a) Eccentrically loaded column; (b) graph of secant formula.
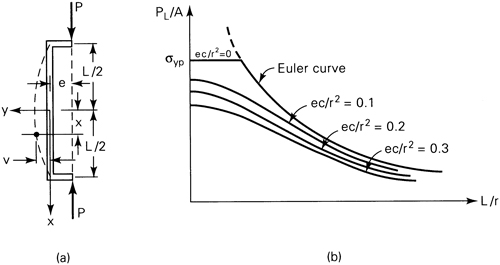
or
![]()
The general solution is
(b)
![]()
To determine the constants c1 and c2, the end conditions υ(L/2) = υ(−L/2) = 0 are applied, with the result
![]()
Substituting these values into Eq. (b) provides an expression for the column deflection:
(c)
![]()
In terms of the critical load Pcr = π2EI/L2, the midspan deflection is
(11.13)
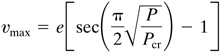
As P approaches Pcr, the maximum deflection is thus observed to approach infinity.
The maximum compressive stress, (P/A) + (Mc/I), occurs at x = 0 on the concave side of the column; it is given by
(11.14)

where r represents the radius of gyration and c is the distance from the centroid of the cross section to the extreme fibers, both in the direction of eccentricity. Expression (11.14) is referred to as the secant formula, giving σmax in the column as a function of the average stress (P/A), the eccentricity ratio (ec/r2), and the slenderness ratio (L/r). As in case of initially curved columns, if we let σmax = σyp and the limit load P = PL, Eq. (11.14) becomes
(11.15)

For any prescribed yield stress and eccentricity ratio, Eq. (11.15) can be solved by trial and error and PL/A plotted as a function of L/r with E held constant (Fig. 11.8b). The allowable value of the average compressive load is found from Pall = PL/n. The development on which Eq. (11.14) is based assumes buckling to occur in the xy plane. It is also necessary to investigate buckling in the xz plane, for which Eq. (11.14) does not apply. This possibility relates especially to narrow columns.
The behavior of a beam subjected to simultaneous axial and lateral loading, the beam column, is analogous to that of the bar shown in Fig. 11.1a, with an additional force acting transverse to the bar. For problems of this type, energy methods are usually more efficient than the equilibrium approach previously employed.
11.9 Energy Methods Applied to Buckling
Energy techniques usually offer considerable ease of solution compared with equilibrium approaches to the analysis of elastic stability and the determination of critical loads. Recall from Chapter 10 that energy methods are especially useful in treating members of variable cross section, where the variation can be expressed as a function of the beam axial coordinate.
To illustrate the method, let us apply the principle of virtual work in analyzing the stability of a straight, pin-ended column. Locate the origin of coordinates at the stationary end. Recall from Sec. 10.8 that the principle of virtual work may be stated as
(a)
![]()
where W and U are the virtual work and strain energy, respectively. Consider the configuration of the column in the first buckling mode, denoting the arc length of a column segment by ds. The displacement, δu = ds — dx, experienced by the column in the direction of applied load P is given by Eq. (10.29). Since the load remains constant, the work done is therefore
(11.16)
![]()
Next, the strain energy must be evaluated. There are components of strain energy associated with column bending, compression, and shear. We shall neglect the last. From Eq. (5.62), the bending component is
![]()
The energy due to a uniform compressive loading P is, according to Eq. (2.49),
(11.18)
![]()
Inasmuch as U2 is constant, it plays no role in the analysis. The change in the strain energy as the column proceeds from its original to its buckled configuration is therefore
(b)
![]()
since the initial strain energy is zero. Substituting Eqs. (11.16) and (b) into Eq. (a), we have
(11.19a)
![]()
from which
(11.19b)

This result applies to a column with any end condition. The end conditions specific to this problem will be satisfied by a solution
![]()
where a1 is a constant. After substituting this assumed deflection into Eq. (11.19b) and integrating, we obtain
![]()
The minimum critical load and the deflection to which this corresponds are
(c)
![]()
It is apparent from Eq. (11.19a) that for P > Pcr the work done by P exceeds the strain energy stored in the column. The assertion can therefore be made that a straight column is unstable when P > Pcr. This point, with regard to stability, corresponds to c1 = 0 in Eq. (b) of Sec. 11.3; it could not be obtained as readily from the equilibrium approach. In the event that P = Pcr, the column exists in neutral equilibrium. For P < Pcr, a straight column is in stable equilibrium.
Example 11.2
A simply supported beam is subjected to a moment M0 at point A and axial loading P, as shown in Fig. 11.9. Determine the equation of the elastic curve.
Figure 11.9. Example 11.2.

Solution The displacement of the right end, which occurs during the deformation of the beam from its initially straight configuration to the equilibrium curve, is given by Eq. (b). The total work done is evaluated by adding to Eq. (11.16) the work due to the moment. In Sec. 10.9, we have already solved this problem for P = 0 by using the following Fourier series for displacement:
(d)
![]()
Proceeding in the same manner, Eq. (b) of Sec. 10.9, representing δU = δW, now takes the form
![]()
From this expression,
(e)
![]()
For purposes of simplification, let b denote the ratio of the axial force to its critical value:
(11.20)
![]()
Then, by substituting Eqs. (11.20) and (e) into Eq. (d), the following expression for deflection results:
(11.21)
![]()
Note that, when P approaches its critical value in Eq. (11.20), b→1. The first term in Eq. (11.21) is then
(11.22)
![]()
indicating that the deflection becomes infinite, as expected.
Comparison of Eq. (11.22) with the solution found in Sec. 10.9 (corresponding to P = 0 and n = 1) indicates that the axial force P serves to increase the deflection produced by the lateral load (moment Mo) by a factor of 1/(1 – b).
In general, if we have a beam subjected to several moments or lateral loads in addition to an axial load P, the deflections owing to the lateral moments or forces are found for the P = 0 case. This usually involves superposition. The resulting deflection is then multiplied by the factor 1/(1 – b) to account for the deflection effect due to P. This procedure is valid for any lateral load configuration composed of moments, concentrated forces, and distributed forces.
Example 11.3
Apply the Rayleigh-Ritz method to determine the buckling load of a straight, uniform cantilever column carrying a vertical load (Fig. 11.10).
Figure 11.10. Example 11.3.

Solution The analysis begins with an assumed parabolic deflection curve,
(f)
![]()
where a represents the deflection of the free end and L the column length. (The parabola is actually a very poor approximation to the true curve, since it describes a beam of constant curvature, whereas the curvature of the actual beam is zero at the top and a maximum at the bottom.) The assumed deflection satisfies the geometric boundary conditions pertaining to deflection and slope: υ(0) = 0, υ′(0) = 0. In accordance with the Rayleigh-Ritz procedure (see Sec. 10.10), it may therefore be used as a trial solution. The static boundary conditions, such as υ"(0) ≠ 0 or M ≠ 0, need not be satisfied.
The work done by the load P and the strain energy gained are given by Eqs. (11.16) and (11.17). The potential energy function Π is thus given by
(g)
![]()
Substituting Eq. (f) into this expression and integrating, we have
(h)
![]()
Applying Eq. (10.34), ∂Π/∂a = 0, we find that
(i)
![]()
Let us rework this problem by replacing the strain–energy expression due to bending,
(j)
![]()
with one containing the moment deduced from Fig. 11.10, M = P(a − υ):
(k)
![]()
Equation (h) becomes
![]()
Substituting Eq. (f) into this expression and integrating, we obtain
![]()
Now ∂∏/∂a = 0 yields
(l)
![]()
Comparison with the exact solution, 2.4674EI/L2, reveals errors for the solutions (i) and (l) of about 22% and 1.3%, respectively. The latter result is satisfactory, although it is predicated on an assumed deflection curve differing considerably in shape from the true curve.
It is apparent from the foregoing example and a knowledge of the exact solution that one solution is quite a bit more accurate than the other. It can be shown that the expressions (j) and (k) will be identical only when the true deflection is initially assumed. Otherwise, Eq. (k) will give better accuracy. This is because when we choose Eq. (k) the accuracy of the solution depends on the closeness of the assumed deflection to the actual deflection; with Eq. (j), the accuracy depends instead on the rate of change of slope, d2υ/dx2.
An additional point of interest relates to the consequences, in terms of the critical load, of selecting a deflection that departs from the actual curve. When other than the true deflection is used, not every beam element is in equilibrium. The approximate beam curve can be maintained only through the introduction of additional constraints that tend to render the beam more rigid. The critical loads thus obtained will be higher than those derived from exact analysis. It may be concluded that energy methods always yield buckling loads higher than the exact values if the assumed beam deflection differs from the true curve.
More efficient application of energy techniques may be realized by selecting a series approximation for the deflection, as in Example 11.2. Inasmuch as a series involves a number of parameters, as for instance in Eq. (d), the approximation can be varied by appropriate manipulation of these parameters, that is, by changing the number of terms in the series.
Example 11.4
A pin-ended, tapered bar of constant thickness is subjected to axial compression (Fig. 11.11). Determine the critical load. The variation of the moment of inertia is given by
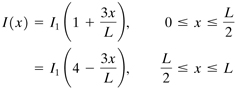
where I1 is the constant moment of inertia at x = 0 and x = L.
Figure 11.11. Example 11.4. Tapered column with pinned ends.

Solution As before, we begin by representing the deflection by
![]()
Taking symmetry into account, the variation of strain energy and the work done [Eqs. (11.16) and (11.17)] are expressed by

From the principle of virtual work, δW = δU, we have
![]()
or
![]()
In Example 11.7, this problem is solved by numerical analysis, revealing that the preceding solution overestimates the buckling load.
Example 11.5
Consider the beam of Fig. 11.12, representing a rail on a track experiencing compression owing to a rise in temperature. Determine the critical load.
Figure 11.12. Example 11.5. Beam with hinged ends, embedded in an elastic foundation of modulus k, subjected to compressive end forces.
Solution We choose the deflection shape in the form of a series given by Eq. (10.23). The solution proceeds as in Example 10.12. Now the total energy consists of three sources: beam bending and compression and foundation displacement. The strain energy in bending, from Eq. (10.25), is
The strain energy due to the deformation of the elastic foundation is given by Eq. (10.30):
![]()
The work done by the forces P in shortening the span, using Eq. (10.31), is
![]()
Applying the principle of virtual work, δW = δ(U1 + U2), we obtain
![]()
The foregoing results in the critical load:
(11.23)

Note that this expression yields exact results. The lowest critical load may occur with n = 1, 2, 3, ..., depending on the properties of the beam and the foundation [Ref. 11.5].
Interestingly, taking n = 1, Eq. (11.23) becomes
(m)
![]()
which is substantially greater than the Euler load. The Euler buckling load is the first term; it is augmented by kL2/π2 due to the foundation.
11.10 Solution by Finite Differences
The equilibrium analysis of buckling often leads to differential equations that resist solution. Even energy methods are limited in that they require that the moment of inertia be expressible as a function of the column length coordinate. Therefore, to enable the analyst to cope with the numerous and varied columns of practical interest, numerical techniques must be relied on. The examples that follow apply the method of finite differences to the differential equation of a column.
Example 11.6
Determine the buckling load of a pin-ended column of length L and constant cross section. Use four subdivisions of equal length. Denote the nodal points by 0, 1, 2, 3, and 4, with 0 and 4 located at the ends. Locate the origin of coordinates at the stationary end.
Solution The governing differential equation (11.1) may be put into the form
![]()
by substituting λ2 = P/EI. The boundary conditions are υ(0) = υ(L) = 0. The corresponding finite difference equation is, according to Eq. (7.9),
(11.24)
![]()
valid at every node along the length. Here the integer m denotes the nodal points, and h the segment length. Applying Eq. (11.24) at points 1, 2, and 3, we have
(a)

or, in convenient matrix form,
(b)

This set of simultaneous equations has a nontrivial solution for υ1, υ2, and υ3 only if the determinant of the coefficients vanishes:
(c)
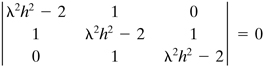
The solution of the buckling problem is thus reduced to determination of the roots (the λ’s of the characteristic equation) resulting from the expansion of the determinant.
To expedite the solution, we take into account the symmetry of deflection. For the lowest critical load, the buckling configuration is given by the first mode, shown by the dashed lines in Fig. 11.2a. Thus, υ1 = υ3, and the Eqs. (a) become
(λ2h2−2)υ1+υ2 = 0
2υ1+(λ2h2−2)υ2 = 0
Setting equal to zero the characteristic determinant of this set, we find that (λ2h2 − 2)2 − 2 = 0, which has the solution ![]() Selecting
Selecting ![]() to obtain a minimum critical value and letting h = L/4, we obtain
to obtain a minimum critical value and letting h = L/4, we obtain ![]() . Thus,
. Thus,
![]()
This result differs from the exact solution by approximately 5%. By increasing the number of segments, the accuracy may be improved.
If required, the critical load corresponding to second-mode buckling, indicated by the dashed line in Fig. 11.2a, may be determined by recognizing that for this case υ0 = υ2 = υ4 = 0 and υ1 = −υ3. We then proceed from Eqs. (a) as before. For buckling of higher than second mode, a similar procedure is followed, in which the number of segments is increased and the appropriate conditions of symmetry satisfied.
Example 11.7
What load will cause buckling of the tapered pin-ended column shown in Fig. 11.11?
Solution The finite difference equation is given by Eq. (11.24):
(d)
![]()
The foregoing becomes, after substitution of I(x),
(e)
![]()
where λ2 = P/EI1. Note that the coefficient of υm is a variable, dependent on x. This introduces no additional difficulties, however.
Dividing the beam into two segments, we have h = L/2 (Fig. 11.13a). Applying Eq. (e) at x = L/2,
![]()
Figure 11.13. Example 11.8. Division of the column of Fig. 11.11 into a number of segments.

The nontrivial solution corresponds to υ1 ≠ 0; then (λ2L2/10) − 2 = 0 or, by letting λ2 = P/EI,
(f)
![]()
Similarly, for three segments h = L/3 (Fig. 11.13b). From symmetry, we have υ1 = υ2, and υ0 = υ3 = 0. Thus, Eq. (e) applied at x = L/3 yields
![]()
The nontrivial solution is
(g)
![]()
For h = L/4, referring to Fig. 11.13c, Eq. (e) leads to
![]()
For a nontrivial solution, the characteristic determinant is zero:
![]()
Expansion yields
λ4L4−136λ2L2 + 2240 = 0
for which
(h)
![]()
Similar procedures considering the symmetry shown in Figs. 11.13d and e lead to the following results:
For h = L/5,
(i)
![]()
For h = L/6,
(j)
![]()
Results (f) through (j) indicate that, for columns of variable moment of inertia, increasing the number of segments does not necessarily lead to improved Pcr. An energy approach to this problem (Example 11.4) gives the result Pcr = 20.25EI1/L2. Because this value is higher than those obtained here, we conclude that the column does not deflect into the half sine curve assumed in Example 11.4.
Example 11.8
Figure 11.14 shows a column of constant moment of inertia I and of length L, fixed at the left end and simply supported at the right end, subjected to an axial compressive load P. Determine the critical value of P using m = 3.
Figure 11.14. Example 11.8.

Solution The characteristic value problem is defined by
(k)
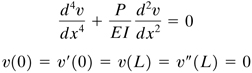
where the first equation is found from Eq. (P11.20) by setting p = 0; the second expression represents the end conditions related to deflection, slope, and moment. Equations (k), referring to Sec. 7.2 and letting λ2 = P/EI, may be written in the finite difference form as follows:
(l)
![]()
and
(m)
![]()
The quantities υ−1 and υm+1 represent the deflections at the nodal points of the column prolonged by h beyond the supports. By dividing the column into three subintervals, the pattern of the deflection curve and the conditions (m) are represented in the figure by dashed lines. Now, Eq. (1) is applied at nodes 1 and 2 to yield, respectively,
υ1+(6−2λ2h2)υ1+(λ2h2−4)υ2 = 0
(λ2h2−4)υ1 + (6 − 2λ2h2)υ2−υ2 = 0
We have a nonzero solution if the determinant of the coefficients of these equations vanishes:

From this and setting h = L/3, we obtain λ2 = 16.063/L. Thus,
(n)
![]()
The exact solution is 20.187EI/L2. By increasing the number of segments and by employing an extrapolation technique, the results may be improved.
11.11 Finite Difference Solution for Unevenly Spaced Nodes
It is often advantageous, primarily because of geometrical considerations, to divide a structural element so as to produce uneven spacing between nodal points. In some problems, uneven spacing provides more than a saving in time and effort. As seen in Sec. 7.4, some situations cannot be solved without resort to this approach.
Consider the problem of the buckling of a straight pin-ended column governed by
![]()
Upon substitution from Eq. (7.21), the following corresponding finite difference equation is obtained:
(11.25)
![]()
where
(11.26)
![]()
Equation (11.25), valid throughout the length of the column, is illustrated in the example to follow.
Example 11.9
Determine the buckling load of a stepped pin-ended column (Fig. 11.15a). The variation of the moment of inertia is indicated in the figure.
Figure 11.15. Example 11.9. Stepped column with pinned ends.

Solution The nodal points are shown in Fig. 11.15b and are numbered in a manner consistent with the symmetry of the beam. Note that the nodes are unevenly spaced. From Eq. (11.26), we have α1 = 2 and α2 = 1. Application of Eq. (11.25) at points 1 and 2 leads to

or
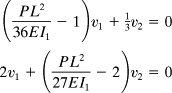
For a nontrivial solution, it is required that
![]()
Solving, we find that the root corresponding to minimum P is
![]()
Employing additional nodal points may result in greater accuracy. This procedure lends itself to columns of arbitrarily varying section and various end conditions.
We conclude our discussion by noting that column buckling represents but one case of structural instability. Other examples include the lateral buckling of a narrow beam; the buckling of a flat plate compressed in its plane; the buckling of a circular ring subject to radial compression; the buckling of a cylinder loaded by torsion, compression, bending, or internal pressure; and the snap buckling of arches. Buckling analyses for these cases are often not performed as readily as in the examples presented in this chapter. The solutions more often involve considerable difficulty and subtlety.*
* For a complete discussion of this subject, see Refs. 11.6 and 11.7.
Problems
Secs. 11.1 through 11.6
11.1. A column of length 3L is approximated by three bars of equal length connected by a torsional spring of appropriate stiffness k at each joint. The column is supported by a torsional spring of stiffness k at one end and is free at the other end. Derive an expression for determining the critical load of the system. Generalize the problem to the case of n connected bars.
11.2. A 3-m-long fixed ended column (Le = 1.5 m) is made of a solid bronze rod (E = 110 GPa) of diameter D = 30 mm. To reduce the weight of the column by 25%, the solid rod is replaced by the hollow rod of cross section shown in Fig. P11.2. Compute (a) the percent reduction in the critical load and (b) the critical load for the hollow rod.
Figure P11.2.

11.3. A 2-m-long pin-ended column of square cross section is to be constructed of timber for which E = 11 GPa and σall = 15 MPa for compression parallel to the grain. Using a factor of safety of 2 in computing Euler’s buckling load, determine the size of the cross section if the column is to safely support (a) a 100-kN load and (b) a 200-kN load.
11.4. A horizontal rigid bar AB is supported by a pin-ended column CD and carries a load F (Fig. P11.4). The column is made of steel bar having 50 by 50 mm square cross section, 3 m length, and E = 200 GPa. What is the allowable value of F based a factor of safety of n = 2.2 with respect to buckling of the column?
Figure P11.4.

11.5. A uniform steel column, with fixed- and hinge-connected ends, is subjected to a vertical load P = 450 kN. The cross section of the column is 0.05 by 0.075 m and the length is 3.6 m. Taking σyp = 280 MPa and E = 210 GPa, calculate (a) the critical load and critical Euler stress, assuming a factor of safety of 2, and (b) the allowable stress according to the AISC formula, Eq. (11.8).
11.6. Figure P11.6 shows a square frame. Determine the critical value of the compressive forces P. All members are of equal length L and of equal
Figure P11.6.

modulus of rigidity EI. Assume that symmetrical buckling, indicated by the dashed lines in the figure, occurs.
11.7. A rigid block of weight W is to be supported by three identical steel bars. The bars are fixed at each end (Fig. P11.7). Assume that sidesway is not prevented and that, when an additional downward force of 2W is applied at the middle of the block, buckling will take place as indicated by the dashed lines in the figure. Find the effective lengths of the columns by solving the differential equation for deflection of the column axis.
Figure P11.7.

11.8. A simply supported beam of flexural rigidity EIb is propped up at its center by a column of flexural rigidity EIc (Fig. P11.8). Determine the midspan deflection of the beam if it is subjected to a uniform load p per unit length.
Figure P11.8.

11.9. Two in-line identical cantilevers of cross-sectional area A, rigidity EI, and coefficient of thermal expansion α are separated by a small gap δ. What temperature rise will cause the beams to (a) just touch and (b) buckle elastically?
11.10. A W203 × 25 column fixed at both ends has a minimum radius of gyration r = 29.4 mm, cross-sectional area A = 3230 mm2, and length 1.94 m. It is made of a material whose compression stress-strain diagram is given in Fig. P11.10 by dashed lines. Find the critical load. The stress-strain diagram
Figure P11.10.
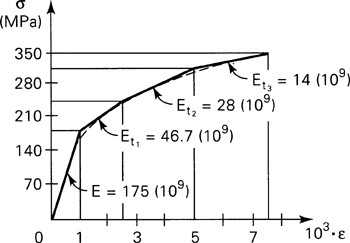
may be approximated by a series of tangentlike segments, the accuracy improving as the number of segments increases. For simplicity, use four segments as indicated in the figure. The modulus of elasticity and various tangent moduli (the slopes) are labeled.
11.11. The pin-jointed structure shown in Fig. P11.11 is constructed of two 0.025-m-diameter tubes having the following properties: A = 5.4 × 10−5 m2, I = 3.91 × 10−9 m4, E = 210 GPa. The stress-strain curve for the tube material can be accurately approximated by three straight lines as shown. If the load P is increased until the structure fails, which tube fails first? Describe the nature of the failure and determine the critical load.
Figure P11.11.

11.12. Two 0.075- by 0.075-m equal leg angles, positioned with the legs 0.025 m apart back to back, as shown in Fig. P11.12, are used as a column. The angles are made of structural steel with σyp = 203 MPa and E = 210 GPa. The area properties of an angle are thickness t = 0.0125 m, A = 1.719 × 10−3 m2, Ic = 8.6 × 10−7 m4, I/c = S = 1.719 × 10−5 m3, rc = 0.0225 m, and ![]() . Assume that the columns are connected by lacing bars that cause them to act as a unit. Determine the critical stress of the column by using the AISC formula, Eq. (11.8), for effective column lengths (a) 2.1 m and (b) 4.2 m.
. Assume that the columns are connected by lacing bars that cause them to act as a unit. Determine the critical stress of the column by using the AISC formula, Eq. (11.8), for effective column lengths (a) 2.1 m and (b) 4.2 m.
Figure P11.12.

11.13. Redo Prob. 11.12(b) using the Euler formula.
11.14. A 1.2-m-long, 0.025- by 0.05-m rectangular column with rounded ends fits perfectly between a rigid ceiling and a rigid floor. Compute the change in temperature that will cause the column to buckle. Let α = 10 × 10−6/°C, E = 140 GPa, and σyp = 280 MPa.
11.15. A pin-ended W150 × 24 rolled-steel column of cross section shown in Fig. P11.15 (A = 3.06 × 103 mm2, rx = 66 mm, and ry = 24.6 mm) carries an axial load of 125 kN. What is the longest allowable column length according to the AISC formula? Use E = 200 GPa and σyp = 250 Pa.
Figure P11.15.

Secs. 11.7 and 11.8
11.16. A steel bar (E = 210 GPa) of b = 50 mm by h = 25 mm rectangular cross section (Fig. P11.16) and length L = 1.5 m is eccentrically compressed by axial loads P = 10 kN. The forces are applied at the middle of long edge of the cross section. What are the maximum deflection υmax and maximum bending moment Mmax?
Figure P11.16.
11.17. A 0.05-m square, horizontal steel bar, 9 m long, is simply supported at each end. The only force acting is the weight of the bar. (a) Find the maximum stress and deflection. (b) Assume that an axial compressive load of 4.5 kN is also applied at each end through the centroid of cross-sectional area. Determine the stress and deflection under this combined loading. For steel, the specific weight is 77 kN/m3, E = 210 GPa, and v = 0.3.
11.18. The properties of a W203 × 46 steel link are A = 5880 mm2, Iz ≈ 45.66 × 106mm4, Iy ≈ 15.4 × 106mm4, depth = 203.2 mm, width of flange = 203.2 mm, and E = 210 GPa. What maximum end load P can be applied at both ends, given an eccentricity of 0.05 m along axis yy? A stress of 210 MPa is not to be exceeded. Assume that the effective column length of the link is 4.5 m.
11.19. A hinge-ended bar of length L and stiffness EI has an initial curvature expressed by υ0 = a1sin(πx/L) + 5a1sin(2πx/L). If this bar is subjected to an increasing axial load P, what value of the load P, expressed in terms of L, E, and I, will result in zero deflection at x = 3L/4?
11.20. Employing the equilibrium approach, derive the following differential equation for a simply supported beam-column subjected to an arbitrary distributed transverse loading p(x) and axial force P:
(P11.20)
![]()
Demonstrate that the homogeneous solution for this equation is
![]()
where the four constants of integration will require, for evaluation, four boundary conditions.
Sec. 11.9
11.21. Assuming υ = a0[l – (2x/L)2], determine the buckling load of a pin-ended column. Employ the Rayleigh-Ritz method, placing the origin at midspan.
11.22. The cross section of a pin-ended column varies as in Fig. P11.22. Determine the critical load using an energy approach.
Figure P11.22.

11.23. A cantilever column has a moment of inertia varying as I = I1(1 – x/2L), where I1 is the constant moment of inertia at the fixed end (x = 0). Find the buckling load by choosing υ = υ1(x/L)2. Here υ1 is the deflection of the free end.
11.24. Derive an expression for the deflection of the uniform pin-ended beam-column of length L, subjected to a uniform transverse load p and axial compressive force P. Use an energy approach.
11.25. A simply supported beam-column of length L is subjected to compression forces P at both ends and lateral loads F and 2F at quarter-length and midlength, respectively. Employ the Rayleigh-Ritz method to determine the beam deflection.
11.26. Determine the critical compressive load P that can be carried by a cantilever at its free end (x = L). Use the Rayleigh-Ritz method and let υ = x2(L – x)(a + bx), where a and b are constants.
Secs. 11.10 and 11.11
11.27. A stepped cantilever beam with a hinged end, subjected to the axial compressive load P, is shown in Fig. P11.27. Determine the critical value of P, applying the method of finite differences. Let m = 3 and L1 = L2 = L/2.
Figure P11.27.

11.28. A uniform cantilever column is subjected to axial compression at the free end (x = L). Determine the critical load. Employ the finite differences, using m = 2. [Hint:The boundary conditions are υ(0) = υ′(0) = υ″(L) = υ″′(L) = 0.]
11.29. The cross section of a pin-ended column varies as in Fig. P11.22. Determine the critical load using the method of finite differences. Let m = 4.
11.30. Find the critical value of the load P in Fig. P11.27 if both ends of the beam are simply supported. Let L1 = L/4 and L2 = 3L/4. Employ the method of finite differences by taking the nodes at x = 0, x = L/4, x = L/2, and x = L.