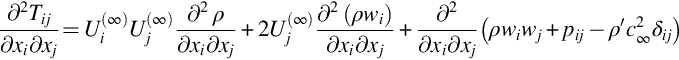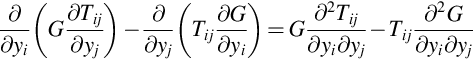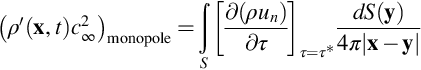4.1 Lighthill's analogy

In the previous chapters we discussed sound radiation from sources in a uniform stationary medium. We showed that in ideal conditions the propagation of sound could be described by the linear acoustic wave equation with a pressure perturbation as the dependent variable. Sound was only generated by disturbances that caused a prescribed motion of a boundary, and boundary conditions were matched using the linearized momentum equation. With the invention of the jet engine it was soon realized that the theory of linear acoustics could not be used to specify the radiation of sound from this very loud source. When a jet exhausts into a stationary fluid a large region of turbulent flow is generated but there are no surfaces with prescribed motions, so some other mechanism of creating sound waves must be present. In general, turbulence occurs in high Reynolds number flows where viscous effects are small, and the motion of the fluid is dominated by nonlinear interactions. To describe the noise generated by turbulence we must be very careful about making assumptions that allow the equations of motion to be linearized, and this is the reason why the concepts of linear acoustics cannot provide the basis for sound generation by an unconfined fluid flow.

Lighthill's analogy specifically addresses the problem of sound generation by a region of high speed turbulent flow in an otherwise stationary fluid as illustrated in Fig. 4.1. The objective is to determine the equations that describe the generation of sound waves that propagate to the acoustic far field, as distinct from defining the fluid motion in the turbulent flow. The magnitude of turbulent velocity fluctuations is typically 10% of the mean flow speed, and for subsonic flows of interest in air, will probably exceed 2–3 m/s. In contrast an acoustic wave has a particle velocity u=pʹ/ρ_oc_o=ρʹc_o/ρ_o and, for a high intensity acoustic wave in air, we showed in Chapter 3 that ρʹ/ρ_o is of order 1/1000. Since c_o=343 m/s it follows that the acoustic wave will only be a small part of the unsteady motion and so we must be very cautious about the coupling of the turbulent flow to the acoustic waves. If, for example, we blindly assume the turbulence to be incompressible then no sound is generated because this assumption eliminates all acoustic effects. Alternatively, if we assume a weakly incompressible flow we can permit acoustic motion in a fluid flow, which is dominated by incompressible turbulence, but do we get the right result? For this reason, Lighthill's analogy is based on the exact equations of fluid flow, without making any assumptions about the compressibility effects in the region of turbulence, and is valuable because it provides the correct equations for coupling the acoustic wave motion outside the turbulent region to the large velocity fluctuations, which occur inside the flow.

To derive Lighthill's equation we take the time derivative of the continuity equation (2.2.6)

$\frac{\partial }{\partial t}\left(\frac{\partial \rho }{\partial t}+\frac{\partial \left(\rho v_i\right)}{\partial x_i}\right)=0$

and subtract the divergence of the momentum equation (2.3.9)

$\frac{\partial }{\partial x_i}\left(\frac{\partial \left(\rho v_i\right)}{\partial t}+\frac{\partial \left(\rho v_i{v}_j+p_{ij}\right)}{\partial x_j}\right)=0$

to give

$\frac{{\partial }^2\rho }{\partial t^2}=\frac{{\partial }^2\left(\rho v_i{v}_j+p_{ij}\right)}{\partial x_i\partial x_j}$

In this equation the diagonal elements of the stress tensor are defined as gauge pressure, so they are relative to the surrounding ambient pressure, giving p_ij=(p−p_∞)δ_ij−σ_ij. We then define the density perturbation relative to the surrounding medium as ρʹ=ρ−ρ_∞ and subtract ${\partial }^2\left({\rho }^{\prime }{c}_{\infty }^2\right)/\partial x_i^2$ from each side of Eq. (4.1.3), where c_∞ is the ambient speed of sound outside the flow, which is constant, and note that ∂ρ/∂t=∂ρʹ/∂t, to obtain a wave equation in the form

$\frac{{\partial }^2{\rho }^{\prime }}{\partial t^2}-c_{\infty }^2\frac{{\partial }^2{\rho }^{\prime }}{\partial x_i^2}=\frac{{\partial }^2{T}_{ij}}{\partial x_i\partial x_j}{T}_{ij}=\rho v_i{v}_j+\left(p-p_{\infty }\right)-\left(\rho -{\rho }_{\infty }\right)c_{\infty }^2{\delta }_{ij}-{\sigma }_{ij}$

This is known as Lighthill's wave equation [1]. The left side specifies the propagation of an acoustic wave in a uniform medium with sound speed c_∞ using density as the dependent variable. The right side is frequently referred to as a source term, which contains all the effects that generate acoustic waves. However, it would appear that the choice of the sound speed c_∞ is arbitrary but that is not the case. Lighthill's equation represents an analogy for the waves that radiated from a finite volume of turbulent flow into a surrounding stationary medium. The speed of sound c_∞ must be chosen as the speed of sound in the stationary medium, not the region of turbulence where it could have a very different value due to compressible flow effects, combustion, or entrained air in underwater applications. This choice is appropriate because the objective is to evaluate the acoustic waves that propagate away from the region of turbulent flow in the stationary medium, and the source term defines how the turbulence, or fluid perturbations in the turbulent region, will couple with the sound waves in the far field.

It is important to appreciate that in deriving Lighthill's equation no approximations have been made, and so Eq. (4.1.4) is an exact rearrangement of the equations of fluid flow. In linear acoustics ρʹ=ρ−ρ_∞ is replaced by $\left(p-p_{\infty }\right)/c_{\infty }^2$, it is assumed that nonlinear interactions are not important so ρv_iv_j=0 and viscous effects can be ignored. Consequently T_ij is approximated as being equal to zero and so is the right side of Eq. (4.1.4).

Lighthill's equation is also referred to as Lighthill's acoustic analogy because it treats the turbulent flow as if it contained sound waves propagating in the same manner as in the surrounding fluid. All the issues about the modeling of the turbulence, which cannot be addressed by linear acoustics, are addressed in Lighthill's equation by the inclusion of the term on the right side. However, since this equation is all inclusive, it also hides some important details of what is happening in the flow region. It should be remembered here that Lighthill's equation, although exact, is designed to provide insight into the sound waves outside the flow, not in the region of turbulent motion where the speed of sound propagation may be distinctly different from c_∞.

4.3 Curle's theorem

A solution to Lighthill's wave equation can be obtained by using the method of Green's functions described in Chapter 3. Specifically, we will determine the acoustic field in a stationary uniform medium, which includes a bounded region of unsteady flow (in which the assumptions of linear acoustics need not apply). In line with Lighthill's analogy, the solution will not necessarily be correct in the turbulent flow, but should apply everywhere outside the flow where the medium is uniform and at rest. We will start by writing Lighthill's wave equation (4.1.4), in terms of y and τ, as

$\frac{1}{c_{\infty }^2}\frac{{\partial }^2\left({\rho }^{\prime }{c}_{\infty }^2\right)}{\partial {\tau }^2}-\frac{{\partial }^2\left({\rho }^{\prime }{c}_{\infty }^2\right)}{\partial y_i^2}=\frac{{\partial }^2{T}_{ij}}{\partial y_i\partial y_j}$

which has the same structure as Eq. (3.9.1) with p′ replaced by $\rho \prime c_{\infty }^2$ and a source term on the right side. As before we obtain a solution by multiplying this equation by a Green's function G and subtracting it from $\rho \prime c_{\infty }^2$ times Eq. (3.9.2). Then, as in Eq. (3.9.7), we obtain

$\frac{1}{c_{\infty }^2}\left({\rho }^{\prime }{c}_{\infty }^2\frac{{\partial }^{2}G}{\partial {\tau }^2}-G\frac{{\partial }^2\left({\rho }^{\prime }{c}_{\infty }^2\right)}{\partial {\tau }^2}\right)-\left({\rho }^{\prime }{c}_{\infty }^2\frac{{\partial }^{2}G}{\partial y_i^2}-G\frac{{\partial }^2\left({\rho }^{\prime }{c}_{\infty }^2\right)}{\partial y_i^2}\right)=\delta \left(\mathbf{x}-\mathbf{y}\right)\delta \left(t-\tau \right){\rho }^{\prime }\left(\mathbf{y},\tau \right)c_{\infty }^2-G\frac{{\partial }^2{T}_{ij}}{\partial y_i\partial y_j}$

When this equation is integrated over time and space the left side reduces in exactly the same way as it did in the previous chapter giving a surface integral as in Eq. (3.9.12). However, in this case we must also include the additional term on the right of Eq. (4.3.2) giving

${\rho }^{\prime }\left(\mathbf{x},t\right)c_{\infty }^2={\displaystyle \underset{-T}{\overset{T}{\int }}{\displaystyle \underset{S}{\int }\left({\rho }^{\prime }\left(\mathbf{y},\tau \right)c_{\infty }^2\frac{\partial G}{\partial y_i}-G\frac{\partial \left({\rho }^{\prime }\left(\mathbf{y},\tau \right)c_{\infty }^2\right)}{\partial y_i}\right)n_{i}dS\left(\mathbf{y}\right)d\tau +{\displaystyle \underset{-T}{\overset{T}{\int }}{\displaystyle \underset{V}{\int }G\left(\frac{{\partial }^2{T}_{ij}\left(\mathbf{y},\tau \right)}{\partial y_i\partial y_j}\right)dV\left(\mathbf{y}\right)d\tau }}}}$

This equation, while correct, is a dangerous result. The issue is that if we assume that the source region, where T_ij is nonzero, is very small, then we can neglect the propagation times between different points y inside the volume and the observer at x, then the Green's function can be taken outside the volume integral and it becomes the integral of a divergence. This can be evaluated as a surface integral, and if there are no objects in the flow, the only contributions to the integrand comes from surfaces that can be placed where T_ij=0. Consequently, for sound radiation from turbulence, in the absence of any nearby surfaces, Eq. (4.3.3) gives a result that is identically zero if the turbulent region is so small that the retarded times can be neglected in the volume integral. To use Eq. (4.3.3) we must know the value of integrand precisely at the correct source times τ and carry out an integration with no rounding error in order to get the correct result, but the danger is that numerical errors in the integration will be larger than the contribution from the source terms. Lighthill recognized this issue and proposed an important simplification of this equation that identified the leading order source terms in the volume integral, so that it could be evaluated without requiring exact retarded time calculations. This concept was later extended by both Curle [2] and Doak [3] to apply to turbulent flow in the presence of surfaces. Using Doak's approach, which describes the acoustic propagation using a Green's function, we can derive Curle's equation by using the expansion

$\frac{\partial }{\partial y_i}\left(G\frac{\partial T_{ij}}{\partial y_j}\right)-\frac{\partial }{\partial y_j}\left(T_{ij}\frac{\partial G}{\partial y_i}\right)=G\frac{{\partial }^2{T}_{ij}}{\partial y_i\partial y_j}-T_{ij}\frac{{\partial }^{2}G}{\partial y_i\partial y_j}$

The volume integral in Eq. (4.3.3) then becomes

${\displaystyle \underset{-T}{\overset{T}{\int }}{\displaystyle \underset{V}{\int }G\left(\frac{{\partial }^2{T}_{ij}\left(\mathbf{y},\tau \right)}{\partial y_i\partial y_j}\right)dV\left(\mathbf{y}\right)d\tau ={\displaystyle \underset{-T}{\overset{T}{\int }}{\displaystyle \underset{V}{\int }\left(\frac{{\partial }^{2}G}{\partial y_i\partial y_j}\right)T_{ij}\left(\mathbf{y},\tau \right)dV\left(\mathbf{y}\right)d\tau }}}}+{\displaystyle \underset{-T}{\overset{T}{\int }}{\displaystyle \underset{V}{\int }\frac{\partial }{\partial y_i}\left(G\frac{\partial T_{ij}\left(\mathbf{y},\tau \right)}{\partial y_j}\right)dV\left(\mathbf{y}\right)d\tau -{\displaystyle \underset{-T}{\overset{T}{\int }}{\displaystyle \underset{V}{\int }\frac{\partial }{\partial y_j}\left(T_{ij}\left(\mathbf{y},\tau \right)\frac{\partial G}{\partial y_i}\right)dV\left(\mathbf{y}\right)d\tau }}}}$

The volume integrals in the last two terms can be evaluated using the divergence theorem, using a unit normal n_i that points into the fluid, and if we also note that T_ij=T_ji, we obtain

${\displaystyle \underset{-T}{\overset{T}{\int }}{\displaystyle \underset{V}{\int }G\left(\frac{{\partial }^2{T}_{ij}\left(\mathbf{y},\tau \right)}{\partial y_i\partial y_j}\right)dV\left(\mathbf{y}\right)d\tau ={\displaystyle \underset{-T}{\overset{T}{\int }}{\displaystyle \underset{V}{\int }\left(\frac{{\partial }^{2}G}{\partial y_i\partial y_j}\right)T_{ij}\left(\mathbf{y},\tau \right)dV\left(\mathbf{y}\right)d\tau }}}}+{\displaystyle \underset{-T}{\overset{T}{\int }}{\displaystyle \underset{S}{\int }\left(T_{ij}\left(\mathbf{y},\tau \right)\frac{\partial G}{\partial y_i}-G\frac{\partial T_{ij}\left(\mathbf{y},\tau \right)}{\partial y_i}\right)n_{j}dS\left(\mathbf{y}\right)d\tau }}$

We are now able to replace the volume integral in Eq. (4.3.3) using Eq. (4.3.6), but we note that the integrand of the surface integral is modified giving

${\rho }^{\prime }\left(\mathbf{x},t\right)c_{\infty }^2={\displaystyle \underset{-T}{\overset{T}{\int }}{\displaystyle \underset{S}{\int }\left(\left({\rho }^{\prime }{c}_{\infty }^2{\delta }_{ij}+T_{ij}\right)\frac{\partial G}{\partial y_i}-G\frac{\partial \left({\rho }^{\prime }{c}_{\infty }^2{\delta }_{ij}+T_{ij}\right)}{\partial y_i}\right)n_{j}dS\left(\mathbf{y}\right)d\tau }}+{\displaystyle \underset{-T}{\overset{T}{\int }}{\displaystyle \underset{V}{\int }\left(\frac{{\partial }^{2}G}{\partial y_i\partial y_j}\right)T_{ij}\left(\mathbf{y},\tau \right)dV\left(\mathbf{y}\right)d\tau }}$

Finally, we make use of the definition of Lighthill's stress tensor to replace

${\rho }^{\prime }{c}_{\infty }^2{\delta }_{ij}+T_{ij}=p_{ij}+\rho v_i{v}_j$

and then use the momentum equation to give

${\rho }^{\prime }\left(\mathbf{x},t\right)c_{\infty }^2={\displaystyle \underset{-T}{\overset{T}{\int }}{\displaystyle \underset{S}{\int }\left(\left(p_{ij}+\rho v_i{v}_j\right)\frac{\partial G}{\partial y_i}+G\frac{\partial \left(\rho v_j\right)}{\partial \tau }\right)n_{j}dS\left(\mathbf{y}\right)d\tau }}+{\displaystyle \underset{-T}{\overset{T}{\int }}{\displaystyle \underset{V}{\int }\left(\frac{{\partial }^{2}G}{\partial y_i\partial y_j}\right)T_{ij}\left(\mathbf{y},\tau \right)dV\left(\mathbf{y}\right)d\tau }}$

This is a very general result and we will discuss it term by term in the next section. However, before proceeding, it is valuable to compare Eq. (4.3.9) and the results for linear acoustics. In the previous chapter we derived a solution to the homogeneous wave equation (with no source terms on the right side), and showed that the acoustic field can be determined by the boundary conditions on the surfaces in the region of interest. The two important quantities that contributed to the sound generation were shown to be the surface acceleration and the force per unit area applied to the fluid by the surface (see Eq. 3.9.14). In this section a more general analysis has been carried out, which is not limited by the assumptions of linear acoustics used in Chapter 3. The only restrictions are that the surfaces bounding the fluid are stationary and that the medium is at rest outside the region of turbulent flow. The solution to Lighthill's wave equation is then given by Eq. (4.3.9), with source terms that depend on (i) the rate of change of mass flux on the surface, (ii) the force per unit area p_ijn_j applied to the fluid by the surface, (iii) the momentum flux across the surface, and (iv) a volume integral contribution from the distribution of Lighthill's stress tensor T_ij throughout the fluid. The additional contributions that appear in Eq. (4.3.9) and not in Eq. (3.9.13) are the momentum flux and the contribution from the volume sources, both of which are nonlinear and so not part of the linear acoustic wave equation. These are important because they identify the sources of sound in a turbulent flow.

It is also of interest to note that the result given by Eq. (4.3.9) depends on a Green's function that only needs to be a solution to Eq. (3.9.2) and satisfy a causality condition. We can therefore choose G in a fairly arbitrary manner. In the previous chapter we gave the solution for G in a free field, but if there are rigid surfaces present then we can also find solutions for G that satisfy the boundary conditions. This technique is useful for certain problems and will be discussed in more detail later in this chapter.

One final note on Eq. (4.3.9), we can easily show that since the free field Green's function

$G_o\left(\mathbf{x},t|\mathbf{y},\tau \right)=\frac{\delta \left(t-\tau +|\mathbf{x}-\mathbf{y}|/c_{\infty }\right)}{4\pi |\mathbf{x}-\mathbf{y}|}$

is only a function of |x−y|, and so has the properties

$\frac{\partial G_o}{\partial y_i}=-\frac{\partial G_o}{\partial x_i}\frac{{\partial }^2{G}_o}{\partial y_i\partial y_j}=\frac{{\partial }^2{G}_o}{\partial x_i\partial x_j}$

and so we can rewrite Eq. (4.3.9) as

${\rho }^{\prime }\left(\mathbf{x},t\right)c_{\infty }^2={\displaystyle \underset{-T}{\overset{T}{\int }}{\displaystyle \underset{S}{\int }\frac{\partial \left(\rho v_j\right)}{\partial \tau }{G}_o{n}_{j}dS\left(\mathbf{y}\right)d\tau -\frac{\partial }{\partial x_i}{\displaystyle \underset{-T}{\overset{T}{\int }}{\displaystyle \underset{S}{\int }\left(p_{ij}+\rho v_i{v}_j\right)G_o{n}_{j}dS\left(\mathbf{y}\right)d\tau }}}}+\frac{{\partial }^2}{\partial x_i\partial x_j}{\displaystyle \underset{-T}{\overset{T}{\int }}{\displaystyle \underset{V}{\int }{T}_{ij}\left(\mathbf{y},\tau \right)G_{o}dV\left(\mathbf{y}\right)d\tau }}$

Then if we use the definition of G_o in Eq. (4.3.10) and carry out the time integrals we find

${\rho }^{\prime }\left(\mathbf{x},t\right)c_{\infty }^2={\displaystyle \underset{S}{\int }{\left[\frac{\partial \left(\rho v_j\right)}{\partial \tau }\right]}_{\tau =\tau ⁎}\frac{n_{j}dS\left(\mathbf{y}\right)}{4\pi |\mathbf{x}-\mathbf{y}|}-\frac{\partial }{\partial x_i}{\displaystyle \underset{S}{\int }{\left[p_{ij}+\rho v_i{v}_j\right]}_{\tau =\tau ⁎}\frac{n_{j}dS\left(\mathbf{y}\right)}{4\pi |\mathbf{x}-\mathbf{y}|}}}+\frac{{\partial }^2}{\partial x_i\partial x_j}{\displaystyle \underset{V}{\int }{\left[T_{ij}\left(\mathbf{y},\tau \right)\right]}_{\tau =\tau ⁎}\frac{dV\left(\mathbf{y}\right)}{4\pi |\mathbf{x}-\mathbf{y}|}}$

In this solution we have written the results so the source terms are evaluated at the correct retarded times τ=τ⁎=t−|x−y|/c_∞. The surfaces are stationary so y is independent of τ, and fluctuations that occur in different parts of the flow at the same source time τ will contribute to the received signal at x at different reception times t. The effect of retarded time is therefore a key component of accurately predicting far field sound from flow noise sources. If the source region is sufficiently small that retarded times can be ignored, then the integrals can be evaluated approximately at a fixed source time. In contrast to Eq. (4.3.3) we now see that the volume source term is given by the integral of T_ij and does not integrate to zero. It therefore represents the acoustic source term in a flow to leading order.

4.4 Monopole, dipole, and quadrupole sources

The results given in the previous section are sufficiently important that we need to spend some time fully evaluating the importance of each term. To facilitate this, we will split Eq. (4.3.12) into three parts so

${\rho }^{\prime }{c}_{\infty }^2={\left({\rho }^{\prime }{c}_{\infty }^2\right)}_{\mathrm{monopole}}+{\left({\rho }^{\prime }{c}_{\infty }^2\right)}_{\mathrm{dipole}}+{\left({\rho }^{\prime }{c}_{\infty }^2\right)}_{\mathrm{quadrupole}}$

The first term of interest is given by the monopole term, which we obtain from the mass flux term of Eq. (4.3.12). For a surface on which the fluid moves with a normal velocity v_in_i=u_n the monopole term is

$\begin{array}{l}{\left({\rho }^{\prime }\left(\mathbf{x},t\right)c_{\infty }^2\right)}_{\mathrm{monopole}}={\displaystyle \underset{S}{\int }{\left[\frac{\partial \left(\rho u_n\right)}{\partial \tau }\right]}_{\tau =\tau ⁎}\frac{dS\left(\mathbf{y}\right)}{4\pi |\mathbf{x}-\mathbf{y}|}}\\ \end{array}$

This equation shows that sound can be generated by the flux of mass across the surface, which is determined by the local density and the motion across the surface. If the surface is rigid or impenetrable (and of course stationary) then this term is zero. If the surface is sufficiently small that retarded time effects can be ignored, it is said to be acoustically compact, and in the acoustic far field, we can write Eq. (4.4.2) in terms of the position x (relative to a point inside or on the surface) as

$\begin{array}{l}{\left({\rho }^{\prime }\left(\mathbf{x},t\right)c_{\infty }^2\right)}_{\mathrm{monopole}}=\frac{1}{4\pi \left|\mathbf{x}\right|}{\left[{\displaystyle \underset{S}{\int }\frac{\partial \left(\rho u_n\right)}{\partial \tau }dS\left(\mathbf{y}\right)}\right]}_{\tau =\tau ⁎}\\ \end{array}$

This term is omnidirectional in the acoustic far field, and so is labeled the monopole term, as discussed in Chapter 3. It shows that the source term depends on the net rate of mass flux at the surface ρu_n, and does not depend on the shape of the surface. Consequently the acoustic field does not distinguish between an acoustically compact spherical surface or an acoustically compact surface of any other shape. The discussion of the acoustic field from a spherical source is therefore far more general than it would appear from first sight, and the sound radiation from a vibrating surface of arbitrary shape is the same as the sound radiation from a spherical surface with the same net rate of mass flux injection.

Next consider the dipole term of Eq. (4.3.12), which is the surface integral with terms related to the surface loading

${\left({\rho }^{\prime }\left(\mathbf{x},t\right)c_{\infty }^2\right)}_{\mathrm{dipole}}=-\frac{\partial }{\partial x_i}{\displaystyle \underset{S}{\int }{\left[p_{ij}+\rho v_i{v}_j\right]}_{\tau =\tau ⁎}\frac{n_{j}dS\left(\mathbf{y}\right)}{4\pi |\mathbf{x}-\mathbf{y}|}}$

To evaluate the space derivative we can use the chain rule to define

$\frac{\partial f\left(\tau ⁎\right)}{\partial x_i}=\frac{\partial \tau ⁎}{\partial x_i}{\left[\frac{\partial f\left(\tau \right)}{\partial \tau }\right]}_{\tau =\tau ⁎}$

but since τ⁎=t−|x−y|/c_∞ we find that

$\frac{\partial f\left(\tau ⁎\right)}{\partial x_i}=\frac{-\left(x_i-y_i\right)}{|\mathbf{x}-\mathbf{y}|c_{\infty }}{\left[\frac{\partial f\left(\tau \right)}{\partial \tau }\right]}_{\tau =\tau ⁎}$

An alternate form of Eq. (4.4.3) is then

${\left({\rho }^{\prime }\left(\mathbf{x},t\right)c_{\infty }^2\right)}_{\mathrm{dipole}}={\displaystyle \underset{S}{\int }{\left[\frac{\partial \left(p_{ij}+\rho v_i{v}_j\right)}{\partial \tau }+\frac{\left(p_{ij}+\rho v_i{v}_j\right)c_{\infty }}{\left|\mathbf{x}-\mathbf{y}\right|}\right]}_{\tau =\tau ⁎}\frac{\left(x_i-y_i\right)n_{j}dS\left(\mathbf{y}\right)}{4\pi |\mathbf{x}-\mathbf{y}|{}^2{c}_{\infty }}}$

Note that if the surface is impermeable then ρv_iv_jn_j=0 and the only significant term is the compressive stress tensor. We also see that there is a near field and far field term in this result. The second term in square brackets will be important when the observer is close to the source, but becomes less and less important when the observer moves away from the source region, as is often the case. In most applications, we need only consider the far field approximation of Eq. (4.4.5) for a rigid stationary surface, which is

${\left({\rho }^{\prime }\left(\mathbf{x},t\right)c_{\infty }^2\right)}_{\mathrm{dipole}}\approx \frac{x_i}{4\pi \left|\mathbf{x}\right|{}^2{c}_{\infty }}{\displaystyle \underset{S}{\int }{\left[\frac{\partial \left(p_{ij}{n}_j\right)}{\partial \tau }\right]}_{\tau =\tau ⁎}dS\left(\mathbf{y}\right)}$

We now see that for a rigid surface it is only the surface loading which causes the sound, and this depends on both the pressure and the viscous stresses, although in general the latter is assumed to be negligibly small and cannot be included without also evaluating the volume sources in the boundary layer close to the wall. Furthermore if the surface is acoustically compact then we can neglect the effects of retarded time over the surface and write Eq. (4.4.6) in the form

${\left({\rho }^{\prime }\left(\mathbf{x},t\right)c_{\infty }^2\right)}_{\mathrm{dipole}}\approx \frac{x_i}{4\pi \left|\mathbf{x}\right|{}^2{c}_{\infty }}{\left[\frac{\partial F_i}{\partial \tau }\right]}_{\tau =\tau ⁎}{F}_i\left(\tau \right)={\displaystyle \underset{S}{\int }{p}_{ij}{n}_{j}dS\left(\mathbf{y}\right)}$

where F_i is the net force applied to the fluid by the surface, including viscous drag. It follows therefore that for an acoustically compact surface that applies a force to the fluid the sound radiation has the characteristics of a compact dipole (as discussed in Chapter 3) orientated in the direction of the force. Consequently this term is defined as the dipole term because it has an inherent cosine directionality if retarded time effects are ignored.

We can also derive a scaling law for the dipole source term because in general the force on the surface scales with the square of the mean flow velocity around the body, so $F_i\propto {\rho }_{\infty }{U}^{2}S$, where S is the surface area of the body. In addition the time scale of the fluctuations is given by a typical dimension of the turbulence, say L divided by the mean flow speed U. Hence the time derivative of F_i will scale as $\partial F_i/\partial \tau \propto {\rho }_{\infty }{U}^{3}S/L$. It follows that the acoustic intensity in the far field, $I_r=p_{rms}^2/{\rho }_{\infty }{c}_{\infty }$, is proportional to the square of the acoustic wave amplitude in the far field (Note in Chapter 3 we considered a harmonic wave and showed that the acoustic intensity was $I_r=\left|\hat{p}\right|{}^2/2{\rho }_{\infty }{c}_{\infty }$. For the more general case, we can define the acoustic intensity using the root mean square pressure $p_{rms}=\left|\hat{p}\right|/\sqrt{2}$ and the speed of sound in the stationary fluid). The far field intensity of a dipole source will then scale as

$I_r\propto \frac{{\rho }_{\infty }{U}^6{S}^2{cos}^2\theta }{{\left(4\pi \left|\mathbf{x}\right|\right)}^2{c}_{\infty }^3{L}^2}$

where θ is the observer angle relative to the dipole axis.

The important conclusion from Eq. (4.4.8) is that the far field sound scales on the sixth power of the mean flow velocity. This simple scaling law has proven to be invaluable in many applications where dipole sources are expected to dominate. For example in applications where we have an acoustically compact rigid surface in a turbulent flow, the flow noise is expected to scale as the sixth power of the velocity. We can conclude that noise will be significantly reduced if we lower the flow speed and in many practical applications this is the most effective way to obtain a noise level reduction.

Finally we will consider the volume integral in Eq. (4.3.12) which is referred to as the quadrupole term. Using Eq. (4.4.4) to change the space derivatives to derivatives over source time gives the quadrupole term as

$\frac{{\partial }^2{\left[T_{ij}/r\right]}_{\tau =\tau ⁎}}{\partial x_i\partial x_j}={\left[\frac{{\partial }^2{T}_{ij}}{\partial {\tau }^2}\right]}_{\tau =\tau ⁎}\frac{\partial \tau ⁎}{\partial x_i}\frac{\partial \tau ⁎}{\partial x_j}\frac{1}{r}+2{\left[\frac{\partial T_{ij}}{\partial \tau }\right]}_{\tau =\tau ⁎}\frac{\partial \tau ⁎}{\partial x_i}\frac{\partial }{\partial x_i}\left(\frac{1}{r}\right)+{\left[T_{ij}\right]}_{\tau =\tau ⁎}\frac{{\partial }^2}{\partial x_i\partial x_j}\left(\frac{1}{r}\right)$

where r=|x−y| and ∂τ⁎/∂x_i=−(x_i−y_i)/rc_∞. In the acoustic far field where Lighthill's analogy applies, this term can be simplified by dropping all the terms that are of order 1/r² and 1/r³ so

${\left({\rho }^{\prime }\left(\mathbf{x},t\right)c_{\infty }^2\right)}_{\mathrm{quadrupole}}\approx \frac{x_i{x}_j}{4\pi c_{\infty }^2{r}^3}{\displaystyle \underset{V}{\int }{\left[\frac{{\partial }^2{T}_{ij}}{\partial {\tau }^2}\right]}_{\tau =\tau ⁎}dV\left(\mathbf{y}\right)}$

Furthermore, if the turbulence is limited to a volume that is small compared to the acoustic wavelength, then the effects of retarded time across the volume can be ignored, leading to

${\left({\rho }^{\prime }\left(\mathbf{x},t\right)c_{\infty }^2\right)}_{\mathrm{quadrupole}}\approx \frac{x_i{x}_j}{4\pi c_{\infty }^2\left|\mathbf{x}\right|{}^3}{\left[{\displaystyle \underset{V}{\int }\frac{{\partial }^2{T}_{ij}}{\partial {\tau }^2}dV\left(\mathbf{y}\right)}\right]}_{\tau =\tau ⁎}$

The inherent directionality of this source, if retarded time effects are ignored, is the same as the quadrupole sources we considered in Chapter 3. For example the T₁₁ term has a (x_i/|x|)²=(cos θ)² directionality which is the same as a longitudinal quadrupole, Eq. (3.7.5), and T₁₂ has the same directionality as Eq. (3.7.7), as illustrated in Fig. 3.6.

In principle, this result gives the far field noise from a region of unbounded turbulent flow and shows that it is the second time derivative of Lighthill's stress tensor that generates the sound. We can also obtain a scaling law for the noise from turbulence using this result. The volume integral of the stress tensor T_ij is expected to scale as ρ_∞U²V where V is the volume of the fluid, and, as for the dipole source, we expect the time scale to be L/U where L is the lengthscale of the turbulence in the flow. The far field pressure is therefore proportional to U⁴, and the far field acoustic intensity scales as

$I_r\propto \frac{{\rho }_{\infty }{U}^8{V}^2}{{\left(4\pi \left|\mathbf{x}\right|\right)}^2{c}_{\infty }^5{L}^4}\left(\frac{x_i{x}_j}{\left|\mathbf{x}\right|{}^2}\right)$

and shows that the noise from turbulence in the flow scales with the eighth power of the flow speed, U⁸. This is one of the most important results of Lighthill's theory because it shows how the noise from free turbulence is very sensitive to mean flow speed. For example if the exit velocity of a jet is reduced by 30% the acoustic intensity in the far field is reduced by 80log₁₀(0.7)=−12.4 dB, which is a significant reduction. However, a decrease in jet exit velocity is also accompanied by a reduction in thrust, which often limits the noise reduction that can be achieved. The thrust is proportional to ρ_∞U²A where A is the exit area of the jet, hence if we increase the jet diameter or exit area we can reduce the exit velocity for a given thrust. Since the noise is determined by the eighth power of the velocity, an increase in jet diameter for the same thrust is accompanied by a reduction in noise, and this is one of the reasons why many modern commercial aircraft have large diameter engines.

Another important conclusion from these scaling laws is to estimate the sound from a finite volume of turbulence compared to the sound from a surface dipole source. Taking the ratio of Eq. (4.4.12) to Eq. (4.4.8) gives

$\frac{{\left(I_r\right)}_{\mathrm{quadrupole}}}{{\left(I_r\right)}_{\mathrm{dipole}}}<\frac{U^2{V}^2}{c_{\infty }^2{L}^2{S}^2}$

It follows that the quadrupole source strength is of order (U/c_∞)²=M² times the dipole source strength where M is the flow Mach number, providing the ratio V/LS is of order one. For low Mach number flows M≪1 and this implies that the volume source terms of quadrupole order are negligible compared to the surface source terms that are of dipole order.

4.5 Tailored Green's functions

As pointed above the solution to Lighthill's wave equation given by Eq. (4.3.9) depends on a Green's function that only needs to be a solution to the inhomogeneous wave equation (3.9.2). We therefore have some latitude in choosing this function and we can also require that the Green's function satisfies boundary conditions on the surfaces within the flow. This can be important when we consider high Reynolds number flows over rigid surfaces. Eq. (4.3.9) shows that the acoustic field is given by

${\rho }^{\prime }\left(\mathbf{x},t\right)c_{\infty }^2={\displaystyle \underset{-T}{\overset{T}{\int }}{\displaystyle \underset{S}{\int }\left(\left(p_{ij}+\rho v_i{v}_j\right)\frac{\partial G}{\partial y_i}+G\frac{\partial \left(\rho v_j\right)}{\partial \tau }\right)n_{j}dS\left(\mathbf{y}\right)d\tau }}+{\displaystyle \underset{-T}{\overset{T}{\int }}{\displaystyle \underset{V}{\int }\left(\frac{{\partial }^{2}G}{\partial y_i\partial y_j}\right)T_{ij}\left(\mathbf{y},\tau \right)dV\left(\mathbf{y}\right)d\tau }}$

If the surface is stationary and impenetrable then v_jn_j=0 and the only remaining term in the surface integral depends on p_ij. In high Reynolds number flow the viscous shear stress terms can be considered to be negligible and so the compressive stress tensor is determined by the pressure term alone, giving

${\rho }^{\prime }\left(\mathbf{x},t\right)c_{\infty }^2={\displaystyle \underset{-T}{\overset{T}{\int }}{\displaystyle \underset{S}{\int }\left(p^{\prime }\frac{\partial G}{\partial y_i}{n}_i\right)dS\left(\mathbf{y}\right)d\tau +{\displaystyle \underset{-T}{\overset{T}{\int }}{\displaystyle \underset{V}{\int }\left(\frac{{\partial }^{2}G}{\partial y_i\partial y_j}\right)T_{ij}\left(\mathbf{y},\tau \right)dV\left(\mathbf{y}\right)d\tau }}}}$

where pʹ=p−p_∞. The surface integral is then only dependent on the distribution of surface pressure. However, if the Green's function is chosen to satisfy the rigid wall boundary condition so that n_i∂G/∂y_i=0 on the surface then the only remaining term in Eq. (4.5.1) is the volume integral. A Green's function that satisfies additional boundary conditions is specified as a tailored Green's function, and will be given the notation G_T. The acoustic field is then

${\rho }^{\prime }\left(\mathbf{x},t\right)c_{\infty }^2={\displaystyle \underset{-T}{\overset{T}{\int }}{\displaystyle \underset{V}{\int }\left(\frac{{\partial }^2{G}_T\left(\mathbf{x},t|\mathbf{y},\tau \right)}{\partial y_i\partial y_j}\right)T_{ij}\left(\mathbf{y},\tau \right)dV\left(\mathbf{y}\right)d\tau }}$

This of course is an important simplification because it eliminates the need to calculate the surface pressure and allows the acoustic far field to be calculated directly from the volume source terms. The main difficulties with this approach are finding the tailored Green's function for bodies of arbitrary shape, and modeling the Lighthill source term with sufficient accuracy. Analytical models of the surface pressure below a turbulent boundary layer are often more readily available than models of the nonlinear terms in Lighthill's stress tensor. Furthermore, in low Mach number flows the volume source terms in Eq. (4.3.9) are of quadrupole order, as discussed in Section 4.4, and so can be neglected in comparison to the surface integral terms. For these reasons many problems can be most easily addressed by using the surface integral term in Eq. (4.3.9) with an appropriate analytical model for the surface pressure. However, when numerical calculations of the unsteady flow are available Eq. (4.5.2) gives an attractive alternative to Eq. (4.3.9) because the volume integral need only be evaluated over the volume where the flow is turbulent, and the form of the tailored Green's function may also help to window or limit that volume to the region close to discontinuities. However, for flow over streamlined bodies the wake can be an extremely important contributor to T_ij and integrating this correctly needs to be done carefully with the correct downstream boundary conditions.

The simplest example of a tailored Green's function is a hard flat surface of infinite extent, as shown in Fig. 4.2.

The acoustic waves from the source at y reach the observer at x by two different paths, the direct path and the reflected path, and the length of the reflected path is the same as the distance from an image source below the surface at the location y^#. Since the surface is rigid the boundary condition on the surface is ∂p/∂y₂=0 so the tailored Green's function also needs to satisfy this condition. If we define

$G_T\left(\mathbf{x},t|\mathbf{y},\tau \right)=G_o\left(\mathbf{x},t|\mathbf{y},\tau \right)+G_o\left(\mathbf{x},t|{\mathbf{y}}^{\#},\tau \right)$

then it is relatively simple to verify that ∂G_T/∂y₂=0 for all points on the surface and G_T is a solution to Eq. (3.9.2) for y₂>0. This particular Green's function is important to problems involving sources close to a large rigid surface. If the source is within a fraction of an acoustic wavelength of the surface, then we can approximate y and y^# by their values on the surface, so G_T=2G_o where G_o is evaluated on the surface at y₂=0.

Tailored Green's functions are available for simple shapes in the frequency domain, and can be computed using boundary element methods for more complex shapes. The frequency domain approach is based on taking the Fourier transform, defined by Eq. (3.10.1), of Eq. (4.5.1), using Eq. (3.10.7) and the convolution theorem, to give

$\tilde{\rho }\left(\mathbf{x},\omega \right)c_{\infty }^2={\displaystyle \underset{S}{\int }\left(\tilde{p}\left(\mathbf{y},\omega \right)\frac{\partial \tilde{G}\left(\mathbf{x}|\mathbf{y}\right)}{\partial y_i}{n}_i\right)dS\left(\mathbf{y}\right)+{\displaystyle \underset{V}{\int }\left(\frac{{\partial }^2\tilde{G}\left(\mathbf{x}|\mathbf{y}\right)}{\partial y_i\partial y_j}\right){\tilde{T}}_{ij}\left(\mathbf{y},\omega \right)dV\left(\mathbf{y}\right)}}$

where $\tilde{G}\left(\mathbf{x}|\mathbf{y}\right)$ is the Green's function in the frequency domain defined by Eq. (3.10.7). We can reduce this to a volume integral by introducing a tailored Green's function that satisfies the inhomogeneous Helmholtz equation (3.10.4),

$\frac{{\partial }^2{\tilde{G}}_T\left(\mathbf{x}|\mathbf{y}\right)}{\partial y_i^2}+k^2{\tilde{G}}_T\left(\mathbf{x}|\mathbf{y}\right)=-\delta \left(\mathbf{x}-\mathbf{y}\right)$

and matches the boundary condition on the surface. For an impenetrable surface we find a solution for which $n_i\partial {\tilde{G}}_T/\partial y_i=0$ on S and so the integrand of the first integral in Eq. (4.5.4) is zero, and

$\tilde{\rho }\left(\mathbf{x},\omega \right)c_{\infty }^2={\displaystyle \underset{V}{\int }\left(\frac{{\partial }^2{\tilde{G}}_T\left(\mathbf{x}|\mathbf{y}\right)}{\partial y_i\partial y_j}\right){\tilde{T}}_{ij}\left(\mathbf{y},\omega \right)dV\left(\mathbf{y}\right)}$

The two results given by Eqs. (4.5.4), (4.5.6), or Eqs. (4.5.1), (4.5.2), give some insight into the sources of sound as they appear in the acoustic far field. From Eq. (4.5.6) it would appear that the only sound source is the turbulence in the volume of the fluid. However, that is a misconception hidden in the nature of the tailored Green's function. If we consider Eq. (4.5.4), it is seen that there are two apparent noise sources, one being the turbulence in the volume and the other being the radiation from the surface, which directly relates the outgoing waves to their “source as observed from the acoustic far field.” The tailored Green's function includes not only these outgoing waves but also the waves that are reflected by the surface, and indicates that the sound radiation in the far field is “driven” by the turbulence, and so is best described as the “origin” of the sound. One must therefore be careful in choosing the terms that describe the mechanisms of sound generation and distinguish between the “origin” of the sound and the “source of sound as observed from the acoustic field.”

4.6 Integral formulas for tailored Green's functions

To calculate the tailored Green's function for an arbitrary shape we can combine Eqs. (4.5.5), (3.10.4) which defines the free field Green's function and is rewritten as

$\frac{{\partial }^2{\tilde{G}}_o\left(\mathbf{z}|\mathbf{y}\right)}{\partial y_i^2}+k^2{\tilde{G}}_o\left(\mathbf{z}|\mathbf{y}\right)=-\delta \left(\mathbf{z}-\mathbf{y}\right)$

Multiplying Eq. (4.6.1) by ${\tilde{G}}_T\left(\mathbf{x}|\mathbf{y}\right)$ and Eq. (4.5.5) by ${\tilde{G}}_o\left(\mathbf{z}|\mathbf{y}\right)$, subtracting the two equations, integrating over the volume V(y), and using the divergence theorem, gives

${\displaystyle \underset{S}{\int }\left({\tilde{G}}_o\left(\mathbf{z}|\mathbf{y}\right)\frac{\partial {\tilde{G}}_T\left(\mathbf{x}|\mathbf{y}\right)}{\partial y_i}-{\tilde{G}}_T\left(\mathbf{x}|\mathbf{y}\right)\frac{\partial {\tilde{G}}_o\left(\mathbf{z}|\mathbf{y}\right)}{\partial y_i}\right)n_{i}dS\left(\mathbf{y}\right)={\tilde{G}}_T\left(\mathbf{x}|\mathbf{z}\right)-{\tilde{G}}_o\left(\mathbf{z}|\mathbf{x}\right)}$

Since $n_i\partial {\tilde{G}}_T\left(\mathbf{x}|\mathbf{y}\right)/\partial y_i=0$ the first term in the surface integral is eliminated and the tailored Green's function is given by

${\tilde{G}}_T\left(\mathbf{x}|\mathbf{z}\right)={\tilde{G}}_o\left(\mathbf{z}|\mathbf{x}\right)-\underset{S}{\int }\left({\tilde{G}}_T\left(\mathbf{x}|\mathbf{y}\right)\frac{\partial {\tilde{G}}_o\left(\mathbf{z}|\mathbf{y}\right)}{\partial y_i}\right)n_{i}dS\left(\mathbf{y}\right)$

In principle, for a source at z, the acoustic field at x can be calculated using the free field Green's function and the surface integral in Eq. (4.6.2). However, to use this result we need to know the tailored Green's function for a source on the surface and an observer at x. This can be obtained using a boundary element method and solving Eq. (4.6.2) for a point z that lies on the surface. Some care is required because the surface integral becomes singular when y=z, and so the limiting form of the integral must be used. The approach is to indent the surface about the point z with a hemisphere of radius ɛ and then let ɛ tend to zero. On the hemisphere |z−y|=r=ɛ where r is in the radial direction pointing away from the point z. The surface integral can be defined as

$-{\tilde{G}}_T\left(\mathbf{x}|\mathbf{z}\right){\displaystyle \underset{S_{{}_{\varepsilon }}}{\int }{\left[\frac{\partial }{\partial r}\left(\frac{e^{ikr}}{4\pi r}\right)\right]}_{r=\varepsilon }dS}$

where the negative sign is the result of the normal being chosen to point into the fluid in the opposite direction to the radial coordinate r. Evaluating the radial derivative in the limit that ɛ tends to zero gives 1/4πɛ² and, since the integrand is constant on the surface the integral is simply the area of a hemisphere times the integrand, or 2πɛ²/4πɛ²=1/2. It follows that

$\frac{1}{2}{\tilde{G}}_T\left(\mathbf{x}|\mathbf{z}\right)={\tilde{G}}_o\left(\mathbf{z}|\mathbf{x}\right)-{\displaystyle \underset{S,\mathbf{z}\ne \mathbf{y}}{\int }\left({\tilde{G}}_T\left(\mathbf{x}|\mathbf{y}\right)\frac{\partial {\tilde{G}}_o\left(\mathbf{z}|\mathbf{y}\right)}{\partial y_i}\right)n_{i}dS\left(\mathbf{y}\right)\mathrm{f}\mathrm{o}\mathrm{r}\mathbf{z}\mathrm{on}S\left(\mathbf{y}\right)}$

is a suitable form for the evaluation of the tailored Green's function on the surface that can be evaluated numerically using a boundary element method. The tailored Green's function for different source and receiver positions can then be obtained from Eq. (4.6.2).

4.7 Wavenumber and Fourier transforms

Wavenumber methods are very important in aeroacoustics because they directly relate the source fluctuations to the propagating waves in the acoustic far field. To illustrate this we will first consider the general definition of a Fourier transform and then extend it to both time and space.

As described in Section 3.10 the Fourier transform with respect to time is defined as

$\tilde{f}\left(\omega \right)=\frac{1}{2\pi }{\displaystyle \underset{-T}{\overset{T}{\int }}f\left(t\right)e^{i\omega t}dt}$

The integral converges for all functions f(t) provided that they are piecewise continuously differentiable and the integral of |f(t)| exists over the limits −T to T. This usually requires that T is less than infinity. In the limit that T becomes very large we can define the inverse transform as

$f\left(t\right)={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\tilde{f}\left(\omega \right)e^{-i\omega t}d\omega }$

The frequency content of the acoustic field generated by a turbulent flow can be determined using Eq. (4.7.1). For example the far field sound generated by turbulence in the absence of scattering surfaces, is given by Eq. (4.4.7) as

${\left({\rho }^{\prime }\left(\mathbf{x},t\right)c_{\infty }^2\right)}_{\mathrm{quadrupole}}\approx \frac{x_i{x}_j}{4\pi c_{\infty }^2\left|\mathbf{x}\right|{}^3}{\displaystyle \underset{V}{\int }{\left[\frac{{\partial }^2{T}_{ij}\left(\mathbf{y},\tau \right)}{\partial {\tau }^2}\right]}_{\tau =\tau ⁎}dV\left(\mathbf{y}\right)}$

By introducing the inverse Fourier transform of the Lighthill stress tensor,

$T_{ij}\left(\mathbf{y},\tau \right)={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{\tilde{T}}_{ij}\left(\mathbf{y},\omega \right)e^{-i\omega \tau }d\omega }$

and evaluating τ at the correct retarded time we find that, after rearranging the order of integration,

${\left({\rho }^{\prime }\left(\mathbf{x},t\right)c_{\infty }^2\right)}_{\mathrm{quadrupole}}\approx {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\left\{\frac{-{\omega }^2{x}_i{x}_j}{4\pi c_{\infty }^2\left|\mathbf{x}\right|{}^3}{\displaystyle \underset{V}{\int }{\tilde{T}}_{ij}\left(\mathbf{y},\omega \right)e^{ikr}dV\left(\mathbf{y}\right)}\right\}{e}^{-i\omega t}d\omega }$

Taking the Fourier transform of this with respect to time we obtain

${\left(\tilde{\rho }\left(\mathbf{x},\omega \right)c_{\infty }^2\right)}_{\mathrm{quadrupole}}\approx \frac{-{\omega }^2{x}_i{x}_j}{4\pi c_{\infty }^2\left|\mathbf{x}\right|{}^3}{\displaystyle \underset{V}{\int }{\tilde{T}}_{ij}\left(\mathbf{y},\omega \right)e^{ikr}dV\left(\mathbf{y}\right)}$

This result shows that all the retarded time effects are now accounted for by the exponential factor under the integral, and we no longer require the rather complicated evaluation of emission time at the source. This can have some advantages in the evaluation of some simple problems, especially when the distribution of the sources are well defined and we can use the far field approximation that r=|x|−x·y/|x|, so

${\left(\tilde{\rho }\left(\mathbf{x},\omega \right)c_{\infty }^2\right)}_{\mathrm{quadrupole}}\approx \frac{-{\omega }^2{x}_i{x}_j{e}^{ik\left|\mathbf{x}\right|}}{4\pi c_{\infty }^2\left|\mathbf{x}\right|{}^3}{\displaystyle \underset{V}{\int }{\tilde{T}}_{ij}\left(\mathbf{y},\omega \right)e^{-ik\mathbf{x}\cdot \mathbf{y}/\left|\mathbf{x}\right|}dV\left(\mathbf{y}\right)}$

The concept of a Fourier transform in time can be extended to a four dimensional transform in both time and space and is defined as wavenumber transform

$\tilde{\tilde{q}}\left(\mathbf{k},\omega \right)=\frac{1}{{\left(2\pi \right)}^4}{\displaystyle \underset{-T}{\overset{T}{\int }}{\displaystyle \underset{-R_{\infty }}{\overset{R_{\infty }}{\int }}{\displaystyle \underset{-R_{\infty }}{\overset{R_{\infty }}{\int }}{\displaystyle \underset{-R_{\infty }}{\overset{R_{\infty }}{\int }}q\left(\mathbf{x},t\right)e^{i\omega t-i\mathbf{k}\cdot \mathbf{y}}d{y}_{1}d{y}_{2}d{y}_{3}dt}}}}$

and its inverse

$q\left(\mathbf{y},t\right)={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\tilde{\tilde{q}}\left(\mathbf{k},\omega \right)e^{-i\omega t+i\mathbf{k}\cdot \mathbf{y}}d{k}_{1}d{k}_{2}d{k}_{3}d\omega }}}}$

An important point to note here is that the Fourier transform definition given by Eq. (4.7.6) uses an exponent +iωt−ik·x.

Using these results the frequency dependence of the acoustic field given by Eq. (4.7.5) is defined in terms of a wavenumber transform by

${\left(\tilde{\rho }\left(\mathbf{x},\omega \right)c_{\infty }^2\right)}_{\mathrm{quadrupole}}\approx \frac{-2{\pi }^2{x}_i{x}_j{\omega }^2{e}^{ik|\mathbf{x}|}{\stackrel{\approx }{T}}_{ij}\left({\mathbf{k}}^{\left(o\right)},\omega \right)}{c_{\infty }^2\left|\mathbf{x}\right|{}^3}{\mathbf{k}}^{\left(o\right)}=\omega \mathbf{x}/c_{\infty }|\mathbf{x}|$

This is an important result because it shows that the far field sound from a turbulent flow can be directly related to the wavenumber transform of the source distribution. Furthermore, it is only the wavenumbers which have a magnitude |k^(o)|=ω/c_∞ that couple with the far field, and fluctuations at any other wavenumber are not important. In deriving this result we made use of the far field solution given by Eq. (4.7.4), and it is an interesting exercise (which will be left to the reader) to show that the same result can be obtained from Eq. (4.3.3) (in the absence of a scattering surface), in which the derivatives are applied to the Green's function.

The fact that Eq. (4.7.8) only depends on the acoustic wavenumber k=ω/c_∞ has some important implications. For example, if we consider the turbulence to be purely convected at the mean velocity U, then T_ij will be a function of y−Ut and the frequency associated with any wavenumber will be ω=k·U. There will be no sound radiation to the acoustic far field unless |k|=ω/c_∞=|k·U|/c_∞, which requires that |U| is greater than or equal to the speed of sound. Eq. (4.7.8) also shows that we need only evaluate the source term for wavenumbers where |k|<ω/c_∞, which, in principle, simplifies the modeling process. Unfortunately the measurement or numerical simulation of turbulence at these wavenumbers is very difficult, and this inhibits the application of this method.

The same approach can be used for dipole surface sources. Starting with Eq. (4.4.6) we take its Fourier transform with respect to time and apply the far field approximation $r\approx \left|\mathbf{x}\right|-\mathbf{x}\cdot \mathbf{y}/\left|\mathbf{x}\right|$ to give

${\left(\tilde{\rho }\left(\mathbf{x},\omega \right)c_{\infty }^2\right)}_{\mathrm{dipole}}\approx \frac{-i\omega x_i{e}^{ik\left|\mathbf{x}\right|}}{4\pi c_{\infty }\left|\mathbf{x}\right|{}^2}{\displaystyle \underset{S}{\int }{\tilde{p}}_{ij}\left(\mathbf{y},\omega \right)n_j{e}^{-ik\mathbf{x}\cdot \mathbf{y}/\left|\mathbf{x}\right|}dS\left(\mathbf{y}\right)}$

For thin airfoils in an inviscid flow, which will be discussed in later chapters, the surface integral can be expressed in terms of the pressure jump Δp across the airfoil planform where

${\left[\mathrm{\Delta }\tilde{p}{n}_{i}d\Sigma \right]}_{\mathrm{planform}}={\left[\tilde{p}{n}_{i}dS\right]}_{\mathrm{upper}}-{\left[\tilde{p}{n}_{i}dS\right]}_{\mathrm{lower}}$

and the subscripts refer to the upper and lower surfaces of the airfoil. Choosing the planform to lie in the y₂=0 plane then gives

${\left(\tilde{\rho }\left(\mathbf{x},\omega \right)c_{\infty }^2\right)}_{\mathrm{dipole}}\approx \frac{-i\omega x_2{e}^{ik\left|\mathbf{x}\right|}}{4\pi c_{\infty }\left|\mathbf{x}\right|{}^2}{\displaystyle \underset{0}{\overset{c}{\int }}{\displaystyle \underset{-b/2}{\overset{b/2}{\int }}\mathrm{\Delta }\tilde{p}\left(\mathbf{y},\omega \right)e^{-ik{x}_1{y}_1/\left|\mathbf{x}\right|-ik{x}_3{y}_3/|\mathbf{x}}d{y}_{1}d{y}_3}}$

where the span of the blade is b and the blade chord is c. Since the pressure jump is zero on all parts of the plane y₂=0 not on the airfoil, the limits of the integrals in Eq. (4.7.10) can be extended to ±R_∞. The integral then represents a wavenumber transform giving

${\left(\tilde{\rho }\left(\mathbf{x},\omega \right)c_{\infty }^2\right)}_{\mathrm{dipole}}\approx \frac{-i\pi \omega x_2\mathrm{\Delta }\tilde{\tilde{p}}\left(k_1^{\left(o\right)},k_3^{\left(o\right)},\omega \right)e^{ik\left|\mathbf{x}\right|}}{c_{\infty }\left|\mathbf{x}\right|{}^2}$

where

$\mathrm{\Delta }\tilde{\tilde{p}}\left(k_1,k_3,\omega \right)=\frac{1}{{\left(2\pi \right)}^2}{\displaystyle \underset{-R_{\infty }}{\overset{R_{\infty }}{\int }}{\displaystyle \underset{-R_{\infty }}{\overset{R_{\infty }}{\int }}\mathrm{\Delta }\tilde{p}\left(\mathbf{y},\omega \right)e^{-i{k}_1{y}_1-i{k}_3{y}_3}d{y}_{1}d{y}_3}}$

is the wavenumber transform of the surface pressure and $k_i^{\left(o\right)}=\omega x_i/\left|\mathbf{x}\right|c_{\infty }$ is the acoustic wavenumber in the direction of the observer.

This is an important result because it shows that the acoustic field only depends on the wavenumber transform of the surface pressure fluctuations at the acoustic wavenumbers. As with the turbulence sources discussed above, any disturbance that convects over the surface at a subsonic speed will not couple with the acoustic far field. Any attempts to measure the surface pressure fluctuations on an airfoil and relate them to the acoustic far field are therefore very difficult because the measurement needs to distinguish between hydrodynamic pressure fluctuations, convected subsonically over the surface, and acoustic fluctuations (which also may be contaminated by facility noise). A much easier approach is to infer the surface pressure fluctuations at the acoustic wavenumbers from a far field sound measurement. If the left side of Eq. (4.7.11) is measured for values of k₁^(o) and k₃^(o) in the range $-\omega /c_{\infty }<k_i^{\left(o\right)}<\omega /c_{\infty }$ (or for all angles at all frequencies), then we can obtain the wavenumber spectrum of the pressure jump at all the wavenumbers that are important for acoustic calculations in other environments.

Finally, we note that at low frequencies the acoustic wavenumbers tend to zero and so the wavenumber spectrum defined by Eq. (4.7.12) reduces to the net unsteady loading on the airfoil, divided by (2π)². In contrast at very high frequencies the wavenumber transform (4.7.12) will be dominated by edge effects because the oscillatory nature of the integrand tends to suppress the contributions from parts of the surface where the pressure varies smoothly. Because of the importance of edges on sound radiation we will consider their effect on blade noise in great detail in Part 3 of the text.