11
Multi-period binomial tree model
The one-period and two-period binomial trees presented in Chapters 9 and 10 had the advantage of introducing important concepts and procedures, such as replication, portfolio dynamics and risk-neutral formulas, in fairly simple setups. Now, we seek to generalize these ideas to a model with more than two time steps.
The main objective of this chapter is to introduce the general multi-period binomial tree model and its own challenges. The algorithmic approach we will use throughout the chapter will allow a straightforward computer implementation of the model and it will lay the foundations for the limiting case known as the Black-Scholes-Merton model. The specific objectives are to:
- build a general binomial tree and relate the asset price observed at a given time step to the binomial distribution;
- understand the difference between simple options and path-dependent options;
- establish the dynamic replicating strategy to price an option;
- apply risk-neutral pricing in a multi-period model.
11.1 Model
Fix n ≥ 1, the number of time steps or periods. In an n-period model there are n + 1 time points: 0, 1, 2, …, n. One should think of time 0 as today while time 1, time 2, etc. are in the future. Often, time 0 will represent the issuance date of a derivative whose maturity occurs at time n.
When time is expressed without units, the timeline is as follows:

As is the case for most discrete-time financial models, it is often more convenient to express time points 0, 1, 2, …, n in units of true time such as a year. Suppose we have a time horizon [0, T] in mind, with 0 being the initial time and T the end of the investment period (in years). We divide the time interval [0, T] in n periods given by (0, T/n), (T/n, 2T/n), …, ((n − 1)T/n, T). The whole timeline is represented graphically by

Alternatively, defining h = T/n as the length of a time step, then each time interval (0, h), (h, 2h), …, ((n − 1)h, nh) can be represented graphically by

In this chapter, we will express time both ways.
Finally, an n-period binomial model is a frictionless financial market with only two basic assets:
- a risk-free asset (a bank account or a bond) which evolves according to the risk-free interest rate r;
- a risky asset (a stock or an index) with a known initial value and unknown future values.
Investors in this market act and make transactions only at those n + 1 time points and not in between.
11.1.1 Risk-free asset
The risk-free asset is modeled by a (deterministic) process B = {Bk, k = 0, 1, 2, n − 1, n} with B0 = 1 and where Bk ≥ Bk − 1, for each k = 1, 2, ..., n. If r is the constant continuously compounded (annual) interest rate, then
and, if r is the periodically compounded (annual) interest rate, i.e. compounded n times per year, then
In other words,
is independent of k: it is the constant one-period discount factor. Of course, units of h and r must coincide for everything to make sense.
11.1.2 Risky asset
The risky asset is modeled by a stochastic process S = {Sk, k = 0, 1, 2, …, n − 1, n}, where S0 is a known (deterministic) quantity and
For simplicity, we assume that {Uk, k = 1, 2, …, n − 1, n} are independent and identically distributed random variables taking values in {u, d} with (real-world or actuarial) probabilities {p, 1 − p}. Once again, we assume that d < u and 0 < p < 1.
As before, in order to verify the no-arbitrage assumption, we must make sure that
when interest is compounded continuously, or
when interest is compounded at each period. In plain words, one dollar accumulated at the risk-free rate over each period does not earn systematically more (or less) than an equivalent investment in the risky asset.
It should be clear that in this multi-period setup, we restrict ourselves to the simplified version of the binomial tree model as discussed in Chapter 10. Consequently, the n-period binomial tree model is based upon five parameters (r, S0, u, d, p) and it is recombining. Because the tree is recombining, the 2n possible trajectories lead to only n + 1 possible prices at time n.
The following illustration shows all possible trajectories of the risky asset price (time series) in a three-step binomial tree:

The sample space and the price of the risky asset
It is sometimes useful to describe the full probability model on which the binomial tree is constructed. For an n-period binomial model, one can choose its sample space Ωn as follows:
It is then clear that each state of nature ω ∈ Ωn, that is each scenario, corresponds to a full trajectory of the risky asset S (a path in the tree). For example, if n = 3 as in the previous illustration, then the possible paths and prices at maturity are

Example 11.1.1 Construction of a three-step binomial tree
Assume that, each week, a stock price can increase by 3% or decrease by 2%. If the initial stock price is 50, build the corresponding three-step binomial tree.
For each time point k = 1, 2, 3, the corresponding random variable Sk, modeling the stock price in k weeks from now, can take one of the following values:
where i = 0, 1, …, k. The corresponding tree is

where the highlighted path {50, 51.50, 50.47, 49.46} is a possible realization (time series) for the weekly stock price process S.
As illustrated by the previous trees (with n = 3), after k periods/steps there are k + 1 (different) nodes or, in other words, k + 1 different time-k prices. But overall, after k periods/steps, there are 2k different price trajectories for the process S = {Sk, k = 0, 1, 2, …, n − 1, n}. One of these particular paths was illustrated in the preceding and the next trees: one upward movement followed by two downward movements.
At maturity (after n periods), the rationale is similar: there are n + 1 different prices for the risky asset but a total of 2n paths leading to those values. Such a distinction is fundamental when pricing path-dependent derivatives as opposed to simple vanilla derivatives (see Section 11.1.3).

Two popular choices for u and d
There are two popular specifications for u and d in the finance literature:
-
Cox-Ross-Rubinstein (CRR) model:

-
Jarrow-Rudd (JR) model:

where σ stands for the (annualized) volatility of the risky asset return. In practice, σ is in the range of [0.1, 0.4]. These formulas for u and d are practical because:
- they automatically adjust with the length of the time step h;
- they will become useful later to relate the binomial tree to the lognormal distribution (and hence the Black-Scholes formula).
Therefore, once n (or h) is fixed, the CRR or JR trees have four parameters: S0, r, σ and p.
11.1.2.1 Probability distribution
We now look at the probability distribution of the risky asset time-k price, where k = 1, 2, …, n. We can write
where the random variable Ik counts the number of upward movements in the trajectory after k periods. Mathematically, it is defined as
If there are i upward movements after k time steps, then
where i can be as little as 0 but at most equal to k (k up-moves in k trials).
It is clear that Ik follows a binomial distribution (with respect to ![]() ) with parameters (k, p):
) with parameters (k, p):
which means that
and consequently
Example 11.1.2 Probability distribution in a three-step binomial tree
We follow example 11.1.1 and we add that the probability of an up-move is 58%. We want to determine the probability distribution of the random variables S1, S2 and S3.
The probability distribution of S1 is simply
Also, we find that
because there are two possible paths leading to a price of 50.47 (up & down, down & up). Moreover, ![]() . Finally,
. Finally,

where again the constant 3 comes from the three possible paths leading to the price 51.9841 (same reasoning applies to 49.4606).
11.1.3 Derivatives
We now introduce a derivative (a third asset) in our model which is an asset whose value V is derived from the risky asset S. Therefore, the derivative’s price is modeled by a stochastic process V = {Vk, k = 0, 1, …, n}, where once again V0 is today’s value and V1, V2, …, Vn are (random) future values. It is assumed that the derivative matures at time n which means that Vn is a random variable representing the payoff.
We will consider two types of derivatives:
- simple (vanilla) options, whose final payoff Vn is some function g of the final asset price, i.e. Vn = g(Sn). Examples include standard call and put options, binary and gap options, etc.;
- exotic or path-dependent options, whose final payoff Vn is some function g of the entire trajectory, i.e. Vn = g(S1, S2, …Sn). Examples include Asian, lookback and barrier options.
Again, when dealing with call (resp. put) options, we will use C (resp. P) instead of V to represent the option’s price.
11.1.4 Labelling the nodes
The notation of the form vuu, xd or sud (with superscripts) was appropriate for a one-period or a two-period binomial tree to emphasize on the path taken by the price of the risky asset. Unfortunately, for n large, this notation is not convenient.
Therefore, we will use a more efficient notation relying on the fact that the underlying tree is recombining. The idea is that a node in the tree is uniquely identified by:
- time;
- number of upward movements needed to reach this node.
Therefore, for k = 1, 2, …, n and j = 0, 1, …, k, the pair (k, j) uniquely identifies the node at time k reached by a total of j upward movements (and therefore k − j downward movements) after k steps. This notation will be useful to simplify and formalize some, but not all, computations and eventually for coding the binomial tree model with a programming language.
The following tree illustrates how each node is identified in a three-step binomial tree. We see that, for each time point k, nodes are numbered j = 0, 1, …, k, from bottom to top.

To code the tree in a spreadsheet, or in an array-oriented programming language, we can also organize the tree as a table/matrix as illustrated next, where j corresponds to rows and k to columns. Note that nodes are numbered j = 0, 1, …, k from top to bottom which is much more convenient for referencing array cells.
| j/k | 0 | 1 | 2 | 3 |
| 0 | (0, 0) | (1, 0) | (2, 0) | (3, 0) |
| 1 | – | (1, 1) | (2, 1) | (3, 1) |
| 2 | – | – | (2, 2) | (3, 2) |
| 3 | – | – | – | (3, 3) |
As a first application of this notation, we can define Sk( j) as the realization/value of the random variable Sk corresponding to the j-th node. For a given path, in which we observe j upward movements from time 0 to time k, we define: for each j = 0, 1, …, k,
Simple vanilla options are easier to handle than path-dependent options as there is no need to analyze all possible paths: only the final asset price matters. Therefore, we define Vk( j) as the realization/value of the random variable Vk corresponding to the j-th node.
We have the following relationship at maturity: for each j = 0, 1, …, n,
Our goal, in the next sections, is to determine the derivative’s price for all times and nodes prior to maturity. In other words, we will compute Vk( j), for all k = 0, 1, …, n − 1 and j = 0, 1, …, k.
Moreover, when dealing with call (resp. put) options, we will use C (resp. P) instead of V to represent the option price. In particular, for a call option with exercise price K and maturing after n time steps, we have
whereas for a similar put option, we have
The evolution of the risky asset price and the corresponding derivative price is depicted in the following tree over three periods:

Example 11.1.3 Call option payoff in a general tree
The initial stock price is 32 and it may go up by 6% or down by 4% every period. Let us represent the evolution of the stock price by a three-step binomial tree along with the payoff of an at-the-money call option.
We have S0 = 32 and Sk = 32 × 1.06 j × 0.96k − j, for j = 0, 1, …, k and k = 1, 2, 3. Moreover, the payoff of the call option is
Those values are illustrated in the following tree:

11.1.5 Path-dependent payoffs
Exotic or path-dependent options such as Asian or lookback options cannot be treated as easily in the n-step binomial tree. One has to be very careful with the current notation (labeling of the nodes) because it focuses on the risky asset price at any given node, not taking into account the different paths reaching that node. Unless we rely on advanced techniques,1 the only choice we have when computing the final payoff of an exotic option is to consider each possible path separately. This is illustrated in the following example.
Example 11.1.4 Payoff of a fixed-strike Asian call option
Using the context of example 11.1.3, we now introduce a fixed-strike Asian call option with strike price K = 31.50. Determine the behavior of the random variable V3.
Asian options are path-dependent derivatives so we have to be careful and consider all eight possible payoffs (eight possible trajectories) in the three-step binomial tree of example 11.1.3. For this option, we cannot use the algorithmic notation Vk( j). This Asian option has a payoff given by ![]() whose realizations/values are computed in the next table. Note that the random variable
whose realizations/values are computed in the next table. Note that the random variable ![]() is based on an arithmetic average.
is based on an arithmetic average.
| Path | S0 | S1 | S2 | S3 | Average | Payoff |
| uuu | 32 | 33.92 | 35.9552 | 38.112512 | 35.995904 | 4.495904 |
| uud | 32 | 33.92 | 35.9552 | 34.516992 | 34.7973973 | 3.29739733 |
| udu | 32 | 33.92 | 32.5632 | 34.516992 | 33.6667307 | 2.16673067 |
| udd | 32 | 33.92 | 32.5632 | 31.260672 | 32.5812907 | 1.08129067 |
| duu | 32 | 30.72 | 32.5632 | 34.516992 | 32.600064 | 1.100064 |
| dud | 32 | 30.72 | 32.5632 | 31.260672 | 31.514624 | 0.014624 |
| ddu | 32 | 30.72 | 29.4912 | 31.260672 | 30.490624 | 0 |
| ddd | 32 | 30.72 | 29.4912 | 28.311552 | 29.507584 | 0 |
For example, the path corresponding to udu is highlighted in the following tree:

For this path, the computation of the average goes as follows:

So, the payoff in this scenario is given by
Computations are done the same way for other trajectories.
As we saw in the previous example, pricing exotic options in an n-period binomial tree can be tedious, especially when n is large. Therefore, unless stated otherwise, the rest of this chapter will focus on simple vanilla options, even if most of the upcoming material could apply to path-dependent options with some adaptation to the notation.
11.2 Pricing by replication
Replicating a derivative in a multi-step binomial tree is similar to what we did in a two-step binomial tree. We will decompose the tree into 1 + 2 + 3 + … + n = n(n + 1)/2 one-period sub-trees and, for each, we will solve a system of two equations with two unknowns.
However, before looking at the replication procedure, we need to define and analyze trading/investment strategies, the portfolio value process, etc.
11.2.1 Trading strategies/portfolios
We now look at the concept of trading or investment strategies, also called portfolios, of which replicating strategies are a sub-group. Let us first define by Δk (resp. Θk), the number of units of the risky asset (resp. risk-free asset) that we hold during the k-th period, that is from time k − 1 to time k or during the time interval [k − 1, k). It is important to note that both Δk and Θk are determined at time k − 1, therefore using the information about the tree available up to that time point. This is illustrated on the following timeline:

The evolution of the number of units held in the risk-free asset and in the risky asset is represented by the corresponding (stochastic) processes Θ = {Θk, k = 1, 2, …, n} and Δ = {Δk, k = 1, 2, …, n}. Note that the time-index starts at k = 1, since Θ1 and Δ1 are the quantities held in the portfolio during the first period (from time 0 to time 1). A trading strategy is given by (Θ, Δ).
An investment strategy (Θ, Δ) is said to be static if Θk and Δk are constant over time, that is
This is also known as a buy-and-hold strategy. Otherwise, when the strategy (Θ, Δ) is updated periodically as asset prices evolve, the strategy is said to be dynamic.
Example 11.2.1 Static and dynamic investment strategies
We know from Chapter 3 that to replicate a forward contract we need to hold one unit of stock and borrow the present value of K. Therefore, using the previously defined notation, this trading strategy is given by
and
This is a static strategy.
An example of a dynamic investment strategy is when we update our portfolio to maintain a fixed proportion of, say, 60%–40% (of the portfolio value) in stocks and bonds. Suppose a stock and a bond trade at $100 each and we want/need to invest $10,000. Therefore, at time 0, we choose Δ1 = 60 and Θ1 = 40, for a total investment of
After one period, if for example the stock price is worth 150 and the bond 110, then the portfolio will be worth 60 × 150 + 40 × 110 = 13400. However, the position in the stock is worth 9000, which corresponds to 9000/13400 = 67.16% of the portfolio value at time 1. To maintain, our 60–40 strategy, we need to sell some shares of stock and buy more bonds, so that we ultimately set
and
In other words, we sell 60 − 53.6 shares of stock and buy 48.73 − 40 units of the bond. Those are the quantities set up at time 1 and prevailing during the second period. Because the portfolio has been rebalanced following the information observed at time 1, we say the investment strategy is dynamic.
Similar trades would need to be performed in the future, depending on the values of the basic assets at those times.
11.2.2 Portfolio value process
Let us now define by Πk the value of a trading strategy at time k (before rebalancing). Thus, for each k = 1, 2, …, n, set
This portfolio value is computed before rebalancing takes place. In particular, Πn = ΘnBn + ΔnSn is the value of the portfolio at maturity, a time where no rebalancing is needed.
At time k, based upon asset prices Bk and Sk, we will choose (Θk + 1, Δk + 1) for the upcoming period, i.e. the (k + 1)-th period (from time k to time k + 1). This is the rebalancing procedure.
To complete the definition of the portfolio value process, started in equation (11.2.1), we define the portfolio initial value as follows:
It is the value of the portfolio at time 0 (inception).
The notation for trading strategies and its corresponding portfolio value is complicated by the fact that the portfolio quantities Θk and Δk are set up at time k − 1 and remain unchanged during the whole k-th period. They affect the portfolio value at both time k − 1 (after rebalancing) and time k (before rebalancing).
Moreover, we can see that the portfolio value at time k, that is Πk, depends on the risky asset price, so it is also a random variable. Therefore,
is a stochastic process and it is often called the portfolio value process.
Example 11.2.2 Portfolio value process of the 60–40 portfolio
We continue example 11.2.1 where we had S0 = B0 = 100. Recall that to hold 60% in stocks and 40% in bonds, we need to set Δ1 = 60 and Θ1 = 40 initially, so that
One period later, i.e. at time 1, in the scenario that S1 = 150 and B1 = 110, the portfolio would be worth
before any rebalancing takes place.
To maintain the 60–40 proportion (of the new portfolio value of 13, 400), we need to update our portfolio quantities. Based upon the information available at time 1 (in the given scenario), we set Δ2 = 53.6 and Θ2 = 48.73 for the second period (from time 1 to time 2).
Finally, at time 2, the portfolio value will be given by
which depends on the realization of the random variable S2.
11.2.3 Self-financing strategies
A trading strategy (Θ, Δ) is said to be self-financing if, when it is rebalanced, no money is injected or withdrawn: the portfolio value, before and after rebalancing, is equal. Mathematically, this means that, at each time step k = 1, 2, …, n − 1,
where the left-hand side is in fact Πk as given in equation (11.2.1). Thus, a self-financing strategy does not generate any cash flows (in or out) between inception and maturity. Only at maturity or inception does it require/allow money to be injected or withdrawn from it, making it comparable to the cash flows of most derivatives (premium at inception, payoff at maturity, no other cash flow). Note that equation (11.2.2) is an equality of random variables.
The profit or loss during the k-th period, for any investment portfolio, is given by
For a self-financing strategy, using the self-financing condition of equation (11.2.2), we get
This provides another interpretation of the self-financing condition: the variation in the portfolio value comes from changes in values from both assets within the portfolio. This interpretation is the one to have in mind when we consider continuous-time models.
Example 11.2.3 Self-financing condition in the 60–40 portfolio
We continue example 11.2.2 and want to verify that the investment strategy satisfies the self-financing condition at time 1, at least in the given scenario.
Indeed, at time 1, in the given scenario, we have
and
So, the self-financing condition is satisfied because the gain/loss of the portfolio corresponds to the sum of the gains/losses made on each asset. Alternatively, still in the given scenario, we have
In other words, before and after rebalancing, the portfolio is worth the same.
11.2.4 Replicating strategy
The main objective now is to determine the initial value V0 of a derivative having final payoff Vn. The key idea is that we need to set up a (self-financing) trading strategy such that
in each possible scenario. Moreover, if the strategy is self-financing, which means it has no cash flows except at time 0 and time n (just like the derivative we want to replicate), the strategy is called a replicating strategy for this derivative.
By the no-arbitrage assumption, we can conclude that the portfolio process Π mimics the price of the derivative at each time point and in each possible scenario. Consequently, we have
for all k = 0, 1, …, n. In particular, the initial values are equal: V0 = Π0. The price of the derivative is equal to the cost of the replicating portfolio.
11.2.5 Backward recursive procedure
Recall that in what follows, we consider only simple options. Using the labeling of nodes presented in section 11.1.4, let
be the realized number of units of each asset an investor holds during the k-th period and in the scenario corresponding to the one-period sub-tree with root (k − 1, j). In other words, if at time k − 1 we have observed so far j upward movements, then during the next period (the k-th), we will hold Θk( j) units of the risk-free asset and Δk( j) units of the risky asset. Then, the time-(k − 1) value of the corresponding portfolio in this scenario is
Graphically, we have

In this case, we emphasize that, for each fixed k = 1, 2, …, n, the possible values for j are 0, 1, …, k − 1.
For k = 0, the only possible value for j is of course 0, which is in agreement with the fact that Θ1 and Δ1 are deterministic values, i.e. are fixed at time 0.
Example 11.2.4 Relating the notation from Chapters 9 and 10
In the one-step binomial tree, the investment strategy set up at inception to replicate the realizations vu and vd of a payoff V1 was the pair (x, y). Using this chapter’s notation, we thus have
In the two-step binomial tree, the quantities (xd, yd) were chosen at time 1, in the scenario S1 = sd, to replicate the values vdu and vdd, while the quantities (xu, yu) were chosen, in the scenario S1 = su, to replicate vuu and vud. With the new notation, in the scenario S1 = sd (i.e. no up-move so far), we have
and, in the scenario S1 = su (i.e. one up-move so far), we have
The one-period sub-tree with root at node (k − 1, j) is given by:

In this tree, to replicate the value of the derivative, it should be clear that we need to solve the following system of equations:
where the only two unknowns at this point/stage are Θk( j) and Δk( j). As in Chapter 10, the solution is

which can be further simplified to obtain

Again, to avoid arbitrage opportunities, we must have
where Πk − 1( j) is given in equation (11.2.4).
The full n-period binomial tree and replicating strategy for payoff Vn is obtained by pasting together all the one-period sub-trees, i.e. for each k = 1, …, n and j = 0, 1, …, k − 1.
11.2.6 Algorithm
Replication and valuation in the general n-step binomial tree are summarized by the following algorithm:
-
At maturity (time n), in each possible scenario, we must:
-
compute the payoff for each j = 0, 1, …, n

-
compute the corresponding (replicating) portfolio quantities

as given in (11.2.5) for j = 0, 1, …, n − 1.
-
compute the value of the replicating portfolio (at time n − 1):

-
compute the value of the derivative:

-
-
Then, we work backward and recursively: for each time k = n − 1, n − 2, …, 1, and in each possible scenario, i.e. for each j = 0, 1, ..., k, we must:
- from the previous step, retrieve the derivative’s value Vk( j);
-
compute the corresponding (replicating) portfolio quantities: for each j = 0, 1, …, k − 1, compute

as given in (11.2.5).
-
compute the value of the replicating portfolio (at time k − 1):

-
compute the value of the derivative:

Note that in the very last step, i.e. for k = 1, we compute (Θ1(0), Δ1(0)) and then set V0(0) = Π0(0) or, written as before, V0 = Π0.
Example 11.2.5 Pricing a put option
Consider a European put option on a stock with spot price 50, maturity 2 years and exercise price 52. Assume the stock price evolves according to a two-period binomial tree, where each time step corresponds to 1 year and during which the price increases or decreases by 20%. In this model, the continuously compounded annual interest rate is 5%. Let us find the replicating portfolio of this option.
We have T = 2, K = 52, S0 = 50, u = 1.2, d = 0.8, n = 2, h = 1 and r = 0.05. We have graphically:

Using the expressions in (11.2.5), we find the replicating strategies for the second period: in the sub-tree with root (1, 0), i.e. for S1 = 40,
whereas, in the sub-tree with root (1, 1), i.e. for S1 = 60,
So, the option price after 1 period (at time k = 1) is given by

During the first period, the portfolio quantities are given by

In conclusion, the initial price of the option is
and more generally we have obtained

Example 11.2.6 Replicating a GMMB in a binomial tree
A GMMB was issued by your insurance company several years ago. It has an annual premium of 2% with a guaranteed minimum payout of 102. As of today, the sub-account balance is $98.74 and the guarantee will apply 3 years from now. Given that the reference stock actually trades for 50 and increases by 7% or decreases by 5% every year, let us describe the replicating strategy covering the loss on the guarantee. Assume the risk-free rate is 3% (annually compounded) and use a binomial tree with annual time steps.
As we did in Chapter 10, replicating the loss on a variable annuity is similar to replicating options. Recall that the payoff is computed on the sub-account (after premiums and withdrawals), whereas replication is performed with the reference asset. Therefore, we will first build the binomial tree for the reference stock index and for the sub-account value. The tree for the reference stock is constructed using
for each j = 0, 1, 2, 3, with S0 = 50, u = 1.07 and d = 0.95. The evolution of the reference asset is shown in the next table:
| j/k | 0 | 1 | 2 | 3 |
| 0 | 50 | 47.5 | 45.125 | 42.86875 |
| 1 | 53.5 | 50.825 | 48.28375 | |
| 2 | 57.245 | 54.38275 | ||
| 3 | 61.25215 |
Then, the sub-account balance of the policyholder gets credited with the returns of the reference asset whereas premiums are withdrawn. Recursively, as we saw in Chapter 8, we have
which is equivalent to
knowing that A0 = 98.74. Therefore, the values Ak( j) of the sub-account balance are:
| j/k | 0 | 1 | 2 | 3 | Loss |
| 0 | 98.74 | 91.92694 | 85.5839811 | 79.6786864 | 22.3213136 |
| 1 | 103.538764 | 96.3945893 | 89.7433626 | 12.2566374 | |
| 2 | 108.570748 | 101.079366 | 0.92063368 | ||
| 3 | 113.847286 | 0 |
The minimum guaranteed amount is G = 102 and hence the loss for the insurer is computed in the last column as max (102 − A3, 0). Therefore, the insurance company must implement an investment strategy to replicate the payoff values {22.3213136, 12.2566374, 0.92063368, 0} in the final nodes of the tree. Indeed, when the sub-account balance is $79.68 upon maturity, the company needs to provide for an extra $22.32 in order for the policyholder to receive at least 102.
We will illustrate how to replicate in a single sub-tree. The whole replicating strategy and its cost are provided in the tables below.
For example, the one-period sub-tree with root (2, 0), i.e. at time 2 with no up-move so far, is given by

Using the formulas in (11.2.5), we get
and

Hence,

In order to cover a random loss of either $22.32 or $12.26, the insurance company must have $15.16 to short-sell 1.86 shares of stock and invest 93.34 at the risk-free rate.
Repeating the same procedure for each sub-tree, we can determine the replicating strategy. This is given in the next table.
| Δk( j) | Θk( j) | |||||
| j/k | 1 | 2 | 3 | 1 | 2 | 3 |
| 0 | −1.0314657 | −1.85866596 | −1.85866596 | 55.1968642 | 93.3444493 | 93.3444493 |
| 1 | −0.66425063 | −1.85866596 | 36.1230717 | 93.3444493 | ||
| 2 | −0.13401952 | 7.51238289 | ||||
Finally, the realizations Πk( j) of the replicating portfolio value process are given in the last table. Note that this also corresponds to the no-arbitrage values of the insurer's loss.
| j/k | 0 | 1 | 2 | 3 |
| 0 | 3.62357939 | 7.85814956 | 15.1568247 | 22.3213136 |
| 1 | 1.66935538 | 4.56242872 | 12.2566374 | |
| 2 | 0.2979397 | 0.92063368 | ||
| 3 | 0 |
11.3 Pricing with risk-neutral probabilities
As in the one- and two-period models, we can reorganize equation (11.2.6) (combined with the positions of equation (11.2.5)) in order to write the option price in node (k − 1, j) as a linear combination of its values one step ahead: for all k = 0, 1, …, n − 1 and j = 0, 1, …, k,
where

is the one-period discount factor (applying from time k to time k − 1) and

Since the model is arbitrage-free (cf. (11.1.1)), then 0 < q < 1 and we can interpret q as a (conditional) risk-neutral probability. Again, the expression in (11.3.1) can be interpreted as a risk-neutral expectation, i.e. using risk-neutral weights. Specifically, for each k = 0, 1, …, n − 1, we can write

and, using iterated expectations, we further get
As in Chapters 9 and 10, it is important to recall that the (conditional) risk-neutral probability q has nothing to do with the (conditional) real-world probability p: it is only a convenient way to rewrite the value of the replicating portfolio as an expectation.
In conclusion, valuation in the general n-step binomial tree using risk-neutral formulas is summarized by the following algorithm:
- At time n, calculate the payoff of the derivative Vn( j) = g(Sn( j)) for each j = 0, 1, ..., n.
- Then, proceed recursively, from time k = n − 1 back to time k = 0: compute Vk( j) using equation (11.3.1) for each j = 0, 1, 2, …, k.
Example 11.3.1 Pricing a put option with risk-neutral formulas
Let us have a second look at example 11.2.5, now using risk-neutral formulas. We start by computing the risk-neutral probability of an up-move:
The values of the payoff are
Then, for (k, j) = (1, 0) and (k, j) = (1, 1), and then for (k, j) = (0, 0), using the relationship
we obtain
and finally
We already know that the random variable Ik follows a binomial distribution with parameters (k, p) for each k = 1, 2, …, n. This is denoted as ![]() where we use
where we use ![]() to emphasize that each up-move has a (conditional) probability p. The probability measure
to emphasize that each up-move has a (conditional) probability p. The probability measure ![]() is thus known as the real-world or actuarial probability measure.
is thus known as the real-world or actuarial probability measure.
But if instead each up-move had a (conditional) probability q, then we would have ![]() where
where ![]() emphasizes the use of q instead of p. The probability measure
emphasizes the use of q instead of p. The probability measure ![]() is known as the risk-neutral probability measure. It results that, for j = 0, 1, 2, …, k,
is known as the risk-neutral probability measure. It results that, for j = 0, 1, 2, …, k,
Combining equation (11.3.2) with equation (11.3.3), we deduce that the initial price of a simple option with payoff Vn = g(Sn) can be written as a risk-neutral binomial sum:

Example 11.3.2 Pricing a put option with risk-neutral formulas (continued)
Let us use equation (11.3.4) to simplify the computations of example 11.3.1. We know that q = 0.628177741 and hence
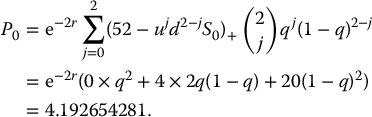
Example 11.3.3 Replicating a GMMB in a binomial tree (continued)
We illustrate how to use risk-neutral formulas in example 11.2.6. Given the equivalence between replicating portfolios and risk-neutral formulas, we can easily combine the two approaches to determine the replicating strategy the actuary should implement during the first time period.
First, we compute the risk-neutral probability of an up-move for the reference stock. We find
Second, the replicating strategy that applies in the first period requires to find the no-arbitrage price of the GMMB at time 1, i.e. corresponding to nodes (1, 0) and (1, 1). Using risk-neutral formulas, we get

and

Hence, initially the actuary must hold
and
as already obtained in example 11.2.6.
Applying equation (11.3.4) to a call option with payoff (Sn − K)+, we find that the initial price can be written as

However, in many scenarios, the payoff is equal to zero. Indeed, when the realization of Sn is less than K, the corresponding term in the summation is equal to zero. Therefore, if we define
as the smallest i such that the payoff is strictly positive, then we can get rid of the positive part and write2

We can do similar computations for a put option. The next example shows a numerical application to a 12-step binomial tree.
Example 11.3.4 Pricing a 1-year call option
Assume the 1-year rate is 5% (continually compounded) and the evolution of a stock price is represented by a 12-period binomial tree: every month, the stock price can increase by 1% or decrease by 0.7%. If the current stock price is 52, let us compute the no-arbitrage price of a 1-year call option with strike 54.
Although the problem seems daunting, the call option is a vanilla option whose price will be easy to compute with equation (11.3.5). We start by computing the risk-neutral (conditional) probability of an up-move:
We compute the payoff in the extremal upper nodes when the price of the underlying is big enough, in which case the option will mature in the money. The possible outcomes for the payoff and the corresponding risk-neutral probabilities are given in the following table:
| j | C12( j) | |
| 12 | 4.59490157 | 0.00651255 |
| 11 | 3.60865075 | 0.04073238 |
| 10 | 2.63900019 | 0.11676431 |
| 9 | 1.68567049 | 0.20286004 |
| 8 | 0.74838692 | 0.23789574 |
| ≤ 7 | 0 | irrelevant |
Consequently,

A risk-neutral probability measure
The probability measure ![]() is an example of what is called a risk-neutral probability measure. It is such that:
is an example of what is called a risk-neutral probability measure. It is such that:
-
 is equivalent to
is equivalent to  , which means here that 0 < q < 1;
, which means here that 0 < q < 1; -
the stochastic process {Sk/Bk, k = 0, 1, 2, …, n} is such that:

for all k = 0, 1, …, n − 1.
The second condition says that the process given by Sk/Bk is a ![]() -martingale.
-martingale.
11.4 Summary
Multi-period binomial tree model- Risk-free interest rate: r.
-
Risk-free asset price: B = {Bk, k = 0, 1, 2, …, n}, where B0 = 1 and, for k = 1, 2, …, n,

-
Risky asset price: S = {Sk, k = 0, 1, 2, …, n − 1, n}, where S0 is a constant and, for k = 1, 2, …, n,

where the Ujs are iid random variables taking values in {u, d} with (real-world) probabilities {p, 1 − p}. Consequently, for each k = 1, 2, …, n,

-
No-arbitrage condition:

- Derivative (written on S): V = {Vk, k = 0, 1, 2, …, n − 1, n}, where V0 is a constant (to be determined) and where Vn = g(Sn) (simple payoff) or Vn = g(S1, S2, …Sn) (exotic path-dependent payoff).
- Important characteristics of the multi-period model:
- – at time k: there are k + 1 possible stock prices but there are 2k different paths leading to those prices;
- – it contains
 one-period binomial sub-trees.
one-period binomial sub-trees.
- Labelling the nodes:
- – the pair (k, j) corresponds to the node at time k reached by a total of j upward movements (after k steps), where k = 0, 1, 2, …, n and j = 0, 1, …, k;
- – Sk( j) = ujdk − jS0: realization of Sk in node (k, j);
- – for a simple payoff Vn = g(Sn) with realization Vn( j) = g(Sn( j)) = g(ujdn − jS0) in node (n, j), the realizations of the time-k derivative prices Vk are given by Vk( j) in node (k, j);
- – for exotic path-dependent payoffs: we cannot use this notation.
- Trading strategy/portfolio
Portfolio: a pair (Θ, Δ), where Θ = {Θk, k = 1, 2, …, n} and Δ = {Δk, k = 1, 2, …, n} are such that:
- – number of units of B held from time k − 1 to time k (k-th period): Θk;
- – number of units of S held from time k − 1 to time k (k-th period): Δk.
- Number of units of the risk-free asset set up in node (k − 1, j): Θk( j).
- Number of units of the risky asset set up in node (k − 1, j): Δk( j).
Portfolio value process: Π = {Πk, k = 0, 1, …n}, where

and where, for k = 1, 2, …, n,

Self-financing condition: (Θ, Δ) is self-financing if, at each time step k = 1, 2, …, n − 1,

or equivalently

A self-financing trading strategy (Θ, Δ) is a replicating strategy for V if

Consequently, Vk = Πk, for all k = 0, 1, …, n.
Replicating portfolio for Vn: for each sub-tree with root (k, j), we solve

and find

Pricing with risk-neutral probabilities
Risk-neutral probability:
 , where
, where

Risk-neutral pricing formula for a derivative with payoff Vn: for each k = 0, 1, …, n − 1,

or, written differently,

for all j = 0, 1, …, k.
- Initial price:
 .
. - Risk-neutral probabilities are only a mathematical convenience used for no-arbitrage pricing.
11.5 Exercises
In a four-period binomial tree, the stock price can increase by 3% or decrease by 1%. If the initial stock price is $100 and analysts have determined that the probability that the stock price increases is 72%, compute:
- probability that the stock price is 108.18 after four periods (three ups, one down);
- probability of observing the path 100, 103, 101.97, 105.0291 and 108.18.
You model the evolution of stock prices using a three-period binomial tree. You are given:
- u = 1.07 and d = 0.98;
- S0 = 37
Detail all possible scenarios/paths taken by the stock price over the next three periods. Then, compute the payoff in each possible scenario for the following derivatives:
- at-the-money call option;
- floating-strike lookback put option;
- fixed-strike Asian call option with strike $35;
- up-and-out put option with H = 41 and strike $38;
- asset-or-nothing call option with strike $43.
In a 3-month CRR binomial tree, you are given:
- volatility of the stock price is 25%;
- S0 = 40;
- risk-free rate is 3% (compounded continuously).
- Build the tree for the stock price where one time step corresponds to one month.
- What is the no-arbitrage price of an at-the-money 3-month put option?
- How many shares of stock do you need to buy/sell at time 0 to replicate the option price at time 1 (for the option in (b))?
- What is the no-arbitrage price of the option in (b) at time 2 given that the stock price went down twice?
A share of stock trades for $45 and a 3-year zero-coupon bond can be bought for $87 (face value of 100). The stock price evolves according to a three-period binomial tree with u = 1.07 and d = 0.96 (h = 1) and the interest rate is constant. You have $1000 to invest.
- You buy 60% of your initial investment in stocks and 40% in bonds. You make no more adjustments to your portfolio over the course of time. Describe your strategy (Δk, Θk) mathematically and compute the portfolio value after 3 years.
- Suppose now you want to make sure that as the stock price evolves, you always hold 60% of the investment in stocks. Describe your strategy (Δk, Θk) mathematically and compute the portfolio value after 3 years.
In a 20-period binomial tree, you are given that:
- the risk-free asset is such that B0 = B1 = B2 = … = B20 = 1;
- the risky asset price can increase by 0.4% or decrease by 0.2% on each period;
- the initial stock price is 1000;
- one period corresponds to 1 day;
- according to analysts, the probability that the asset price goes up on any given day is 62%.
A 20-day at-the-money put option is issued. What is the no-arbitrage price of this option?
In a three-period binomial tree, you are given:
- S0 = 100;
- u = 1.04 and d = 0.98;
- the risk-free asset is such that Bk = 1.01k, k = 0, 1, 2, 3;
- one period is 4 months.
A 1-year floating-strike lookback call option is issued.
- There are eight possible paths for the stock price. Describe them all.
- Compute the payoff of this option on each of the possible paths. Note that the maximum/minimum is computed over S1, S2, S3.
- You believe that over any given period, the probability that the stock price goes up is 65%. What is the expected payoff of the option?
- What is the risk-neutral probability of observing each path?
- What should be the no-arbitrage price of this option at time 0?
- What is the replicating strategy applying during the first period to ultimately replicate the option’s payoff at maturity?
In the binomial tree of exercise 11.6, a down-and-out call option with strike $102 and barrier $95 is issued.
- Compute the payoff of the option on each of the possible paths.
- Using risk-neutral probabilities, compute the option’s initial price.
- At each node, determine the replicating portfolio. What do you observe whenever the stock price is close to the barrier (over or below)?
The price of a stock can increase by 5% or decrease by 2%. A dividend of $2.50 will be paid two periods from now and the initial stock price is $30. You build a four-period binomial tree.
- Build the binomial tree for the ex-dividend stock price.
- Compute the payoff of a four-period 28-strike put option.
- Given that the stock price went down twice after two periods, compute the put option price at time 2 if the periodic interest rate is 1%.
In a three-period binomial tree, you are given:
- each period is 3 months;
- the initial stock price is $57;
- the stock price can increase by a factor of u = 1.03 or decrease by a factor of d = 0.99;
- the 3-month interest rate observed at time 0 is 2% (annualized, compounded quarterly)
 ;
; - future 3-month interest rate, i.e.
 , is such that
, is such that  ;
; - when the interest rate goes up, the stock price goes down.
- Build the binomial tree for the stock, for the interest rate and for a simple bank account with B0 = 1.
- Verify that the no-arbitrage condition holds in each sub-tree.
- Using replicating portfolios, compute the initial no-arbitrage price of an at-the-money call option.
- Using risk-neutral probabilities, verify the option price with the replicating portfolio value in each node of your work in (c).
Equity-indexed annuities (EIAs)
You are using the binomial tree of exercise 11.6.
- Compute the payoff a three-period compound annual ratchet EIA whose participation rate is 80%.
- Find the participation rate β such that the no-arbitrage value of the benefit is equal to the initial investment.
Guaranteed minimum maturity benefit (GMMB)
A 5-year GMMB is issued to a policyholder on a reference portfolio whose value can increase by 7% annually or decrease by 3% over the same period. The annual premium is 1.75% whereas the initial investment is 100,000. Calculate the loss in each possible scenario if the guaranteed amount is 85% of the capital. Assume one period corresponds to a year.
Guaranteed minimum withdrawal benefit (GMWB)
There are 3 years remaining on a GMWB whose sub-account balance is currently $26,000. The policyholder is allowed to withdraw 10,000 at the end of each year. If the reference index has a volatility of 30% and you are using a CRR binomial tree, calculate the loss in each possible scenario when the annual premium is 2.25%. Assume one period corresponds to a year.
