4
Swaps
A swap is an agreement between two parties to exchange cash flows at predetermined dates with contractual terms set at inception. A swap usually involves exchanging periodically variable (random) payments, whose value is based on a financial benchmark or an underlying asset (a stock, a bond, an index or some economic or financial quantity), for fixed payments. No premium is exchanged at inception. Figure 4.1 illustrates cash flows of a swap, where the words variable, floating and risky are used interchangeably.

Figure 4.1 Periodic cash flows of a general swap
Based upon this definition of a swap, common insurance policies can also be viewed as swaps for ordinary people. For example, a 2-year car insurance policy is similar to a swap since the policyholder makes a fixed monthly payment in exchange for variable/random amounts, i.e. the compensation for losses due to car accidents, theft or vandalism. In Figure 4.1, the policyholder is the investor in the left box whereas the insurance company is the investor in the right box.
Just like other financial derivatives, swaps are mostly used for risk management, i.e. to offset a risk exposure, or for speculation, i.e. to bet on/against the underlying asset. Risks that investors may want to swap are interest rate risk, currency risk, credit risk, etc. Examples of applications include:
- When interest rates go down, the present value of actuarial liabilities can increase significantly. Insurance companies and pension plan sponsors can use interest rate swaps to mitigate the impact of a decrease in interest rates.
- Your company uses gold to make jewelry and needs to regularly buy ounces of gold. To help fix those periodic cash outflows, your company can enter into a gold swap to fix the price it will pay for regular deliveries of gold over the next few months.
- A company based in the U.S. receives a regular stream of Euros from its subsidiaries. Those cash flows need to be converted into U.S. dollars, but this is of course subject to fluctuations of the USD/EUR exchange rate. The company may enter into a currency swap to fix the value, in U.S. dollars, of cash inflows in Euros.
- A bank has a large portfolio of fixed-rate loans, which is an asset for the bank. The investment manager believes interest rates will increase, so they enter into an interest rate swap to convert these fixed-rate loans into variable-rate loans. In this case, the swaps are used for speculative reasons.
As in the first three applications, insurance companies typically use swaps for risk management purposes. Table 4.1 shows the types of swaps used by insurers and their main purpose as of December 31st, 2014 according to the NAIC.
Table 4.1 Insurance industry swaps exposure by type and purpose/strategy in millions of US$ as of December 31st, 2014
| Contract type | Hedging | Replication | Other | Total | % |
| Interest rate | 807 108 | 9 123 | 2 132 | 818 363 | 83.45 |
| Currency and FX | 65 256 | − | 4 230 | 69 486 | 7.09 |
| Credit default | 11 323 | 22 641 | 966 | 34 930 | 3.56 |
| Total return | 38 758 | 275 | 863 | 39 897 | 4.07 |
| Other | 17 907 | − | 71 | 17 978 | 1.83 |
| Total | 940 353 | 32 040 | 8 263 | 980 655 | 100.00 |
| Percentage | 95.89 | 3.27 | 0.84 | 100.00 | − |
Source: Table 11, Capital Markets Special Reports, NAIC.
Even though swaps are traded over-the-counter, the legal aspects of swaps have been formalized by the International Swaps and Derivatives Association (ISDA).
The role of this chapter is to provide an introduction to swaps with an emphasis on those used in the insurance industry, namely interest rate swaps, currency swaps and credit default swaps. For completeness, we will also discuss commodity swaps. The specific objectives are to:
- define the characteristics of interest rate, currency, credit default swaps and commodity swaps;
- calculate the cash flows of a swap;
- compute the value of a swap.
4.1 Framework
A swap is usually specified by:
- an underlying asset or financial variable;
- the dates of the payments;
- the maturity date, which is known as the swap term or tenor;
- how the payments are calculated.
The stream of predetermined fixed payments is known as the fixed leg, whereas the stream of variable payments is called the variable leg or floating leg.
Most swaps fall into the fixed-for-floating category, meaning that a variable (risky, random, floating) payment is exchanged periodically for a fixed amount.
In what follows, we will focus on the following swaps:
- Interest rate swap: exchange payments based on a variable/random interest rate for payments based on a fixed interest rate.
- Currency swap: exchange payments based on a given currency for payments based on another currency.
- Credit default swap: compensation, if the underlying bond defaults, in exchange for a fixed periodic payment/premium.
- Commodity swap: delivery of a commodity (whose price varies) at different dates, in exchange for a fixed periodic payment.
Interest rate swaps are by far the most popular swaps used by insurance companies to manage interest rate risk: 83% of all swaps are used to manage this risk only (see Table 4.1). In the entire OTC swap market, the amount of notional outstanding in interest swaps is about 400 trillion dollars (see Table 2.2).
The most popular types of swaps include the above-mentioned, as well as equity swaps, which is an exchange of payments based on the returns of a stock (or stock index) for payments based on an interest rate, and total return swaps, which is an exchange of an interest rate (fixed or floating) for the total return of a bond (including default).
Minor variations on standard swaps are prepaid swaps and deferred swaps. A prepaid swap is a regular swap whose fixed leg is paid as an up-front premium at inception, while a deferred swap is issued today but payments are exchanged later at a predetermined date.
4.2 Interest rate swaps
In an interest rate swap, parties exchange a variable interest rate, applied to a given amount, in exchange for a fixed interest rate, applied on the same amount. This amount on which the payments are calculated is known as the notional (principal, par value, face value). The swaps of payments occur at predetermined dates for a given period of time. Typically, payments are exchanged quarterly or semi-annually and interest rate swaps usually last from 2 to 15 years. Because their cash flows are similar, we will use the words loans and bonds interchangeably.
4.2.1 Fixed-rate and floating-rate loans
A fixed-rate loan is simple: the borrower receives the principal F at inception in exchange for future periodic interest payments of size c. The principal is repaid at maturity. No matter how the term structure of interest rates evolves over time, i.e. if it increases or decreases, all interest payments will be of size c. Therefore, for this type of loan, the interest rate risk is assumed by the lender. This is similar to a bond with fixed coupons.
In a floating-rate loan, the interest payments are variable because they are based on a variable interest rate. The borrower does not know in advance the payments she will have to make: when interest rates increase (resp. decrease), the borrower pays more (resp. less). Therefore, for this type of loan, the interest rate risk is assumed by the borrower. This is similar to a bond with variable coupons.
Example 4.2.1 5-year floating-rate loan, renewable annually
Suppose you borrow $100 from your bank by entering into a 5-year floating-rate loan, renewable annually. Therefore, you are committed to make interest payments every year according to the 1-year rate observed upon each renewal. Principal must be repaid at maturity. Let us compute the cash flows for this loan.
At inception, your bank gives you $100 and you observe that the current 1-year rate is 4%. Therefore, you will have to make a payment of $4 at the end of the year.
At the end of this first year, you make your payment of $4. Now, suppose that the 1-year rate is at 4.5%. Therefore, you will have to make a payment of $4.50 at the end of the second year.
At the end of the second year, you make the payment of $4.50. Now, suppose that the 1-year rate is at 3.7%. Therefore, you will have to make a payment of $3.70 at the end of the third year.
The same reasoning applies for the remaining payments.
◼
Recall from Section 2.1.3 that we use the notation rTt for the (annual and annually compounded) spot interest rate we will observe at time t, i.e. in t years from now, to invest/borrow from time t up to time t + T.
In the previous example, we considered a scenario where r10 = 0.04, r11 = 0.045 and r12 = 0.037.
4.2.2 Cash flows
Now that we understand fixed-rate and floating-rate loans, let us look at the cash flows of a very simple interest rate swap.
Example 4.2.2 Cash flows of a simplified interest rate swap
Investors A and B enter into a 5-year interest rate swap agreement with a notional amount of $100. Investor A agrees to pay investor B a fixed interest rate of 4% in exchange for the 1-year rate (from investor B). Interest rates are compounded annually and payments also occur annually. Let us compute the cash flows of this interest rate swap in a scenario where the 1-year rate evolves as follows:
Date 1-year rate Today 3.8% In 1 year 3.95% In 2 years 4.12% In 3 years 4.29% In 4 years 3.73% In 5 years 3.87% Meanwhile, for the fixed-rate loan, we have:
Time Amount 0 0 1 4 2 4 3 4 4 4 5 100+4
The floating leg of the swap behaves like a 5-year floating-rate loan, renewable annually. Each and every year, the interest payment made at the end of the year depends on the 1-year rate observed at the beginning of that same year, not before. At inception, the 1-year rates that will be observed are unknown. In the scenario considered above, the evolution of the 1-year rate gives us the following interpretation:
- a loan contracted at time 0 and maturing at time 1 is subject to an interest rate of r10 = 3.8%;
- a loan contracted at time 1 and maturing at time 2 will be subject to an interest rate of r11 = 3.95%;
- a loan contracted at time 2 and maturing at time 3 will is subject to an interest rate of r12 = 4.12%;
- etc.
Therefore, the cash flows are:
Time Amount 0 0 1 3.80 2 3.95 3 4.12 4 4.29 5 100+3.73 Overall, the cash flows of the swap are:
Time Fixed Floating Net 1 4 3.80 0.2 2 4 3.95 0.05 3 4 4.12 −0.12 4 4 4.29 −0.29 5 104 103.73 0.27 The column “Net” corresponds to the net amount received by the investor paying the floating rate.
◼
Example 4.2.3 Cash flows of a standard interest rate swap
Let us now consider the case of a standard fixed-for-floating interest rate swap, on a principal of $100, where interest rates are compounded semi-annually and payments occur every 6 months for 3 years. Investor A agrees to pay, to investor B, a fixed interest rate of 3.8% in exchange for a floating interest rate. We will illustrate how cash flows on both sides of the swap are computed.
For this swap, the floating interest rate is the 6-month rate. Mathematically, the rates used to compute the floating-rate interest payments are r0.5t for t = 0, 0.5, 1, 1.5, …, 2.5. All those rates, except for r0.50, are unknown at inception.
Let us consider the following scenario and the resulting cash flows:
time t r0.5t Fixed Floating Net 0 0.04 0.5 0.035 1.9 2 −0.1 1 0.037 1.9 1.75 0.15 1.5 0.042 1.9 1.85 0.05 2 0.045 1.9 2.1 −0.2 2.5 0.041 1.9 2.25 −0.35 3 0.038 1.9 2.05 −0.15 The fixed leg is easy to determine: every 6 months, a payment of $1.90 should be made. This is due to the fixed 6-month rate of 1.9% = 3.8%/2 applied to $100.
The first variable payment, to be made 6 months after inception, is already known: it corresponds to
, since the interest rate between time 0 and time 0.5 is r0.50 = 0.04. As for the rest of the variable leg, we need to look at the realizations (time series) of the floating rate in the chosen scenario. The second variable payment, due after 1 year, depends on the realization of r0.50.5, which in this scenario is r0.50.5 = 0.035. Consequently, this second interest payment is
. The other cash flows are calculated in a similar fashion for the rest of the payment schedule.
◼
Of course, payments are made only by the investor who is the net payer. In the above example and scenario, investor B would pay 0.1 to investor A at time 0.5 (6 months after inception), while investor A would pay 0.15 to investor B at time 1 (1 year after inception).
In most swaps, the principal upon which payments are calculated is not exchanged at maturity.
In most fixed-for-floating (or floating-for-floating) interest rate swaps, the floating payment is determined by the interest rate observed at the beginning of the corresponding period. For example, the floating payment to be made in 6 months from now is based on the current 6-month rate. This is similar to a loan contracted today and maturing in 6 months. Moreover, the principal/notional is not exchanged at maturity (it is the same on both sides anyway).
When entering a swap (no matter what is the underlying risk), both sides assume the default/credit risk of the counterparty. In an interest rate swap, where the notional is not exchanged at maturity, credit risk is much smaller than on conventional loans.
4.2.3 Valuation
Our approach to valuation of interest rate swaps is based on the fact that a long fixed-for-floating interest rate swap is equivalent to holding simultaneously:
- a long position in a fixed-rate bond;
- a short position in a variable-rate bond.
The short position in the swap is equivalent to holding the reversed positions in the bonds.
Therefore, under the absence-of-arbitrage assumption, the value of the swap is equal to the difference between these two positions.1
4.2.3.1 Fixed-rate bonds
Assume the principal of the bond is F and its holder receives periodic payments/coupons of size c at dates t1, t2, …, tn = T. Those payments are fixed and known in advance.
The principle underlying bond valuation is simple: future cash flows are discounted using the observed term structure of interest rates. Let ![]() be the time-t value of a fixed-rate bond.2
be the time-t value of a fixed-rate bond.2
We already know that the initial value is given by

This is the same formula as in equation (2.1.1) but using the notation ![]() rather than B0. It corresponds to the present value of cash flows occurring after time 0.
rather than B0. It corresponds to the present value of cash flows occurring after time 0.
If t = tk (right after the k-th payment/coupon), for any k = 1, 2, …, n − 1, then
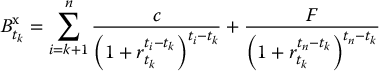
which corresponds to the present value of cash flows paid after tk.
In general, for any time t ∈ [0, tn), we have

where the sum is taken over all is such that ti > t. The formula in equation (4.2.2) is simply the present value of both coupons and principal to be paid immediately after time t.
This is also illustrated in Figure 4.2.

Figure 4.2 Valuation of a fixed-rate bond
Example 4.2.4 Valuation of a fixed-rate bond
A fixed-rate 5-year bond with a principal of $100 pays fixed annual coupons of $3. It was issued 2 years ago. Let us compute the value of this bond (at time t = 2) if the term structure of interest rates is such that r12 = 0.03, r22 = 0.04, r32 = 0.045, r42 = 0.05, r52 = 0.055.
There are three payments remaining (3, 3 and 103) that should be discounted with the current 1-year, 2-year and 3-year rates respectively. We get
◼
4.2.3.2 Floating-rate bond
The fundamental bond valuation principle states that future cash flows should be discounted using the current interest rate term structure. In what follows, for simplicity, we will consider bonds paying coupons only on an annual basis, i.e. at times 1, 2, …, n = T. Again, we will start by finding the price at coupon dates and then deduce the value at any other dates.
The cash flows of a floating-rate bond are random since future 1-year rates are unknown. In fact, they are equal to F × r1k, for each k = 1, 2, …, n. To handle this difficulty, we will work backward from maturity to inception. Let us illustrate the idea with an n-year floating-rate loan with interest compounded annually.
After n − 1 years, immediately after the coupon payment, the remaining value of the bond is a cash flow of F + Fr1n − 1 (principal + final interest payment) to be paid at time n, i.e. 1 year later. To compute the corresponding value of the bond at that time, we need to discount F(1 + r1n − 1) back from time n to time n − 1 using the 1-year rate observed at time n − 1. Letting Bℓt be the time-t value of a floating-rate bond then, we have
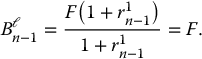
In other words, the value of this floating-rate bond at time n − 1 is equal to the principal value.
The bond value at time n − 2 comes from the present value of both:
- the bond value at time n − 1, which is given by Bℓn − 1 = F;
- the interest payment due at time n − 1, which is given by F × r1n − 2.
Discounting these two components back from time n − 1 to n − 2 using the 1-year rate observed at time n − 2, we have

Again, the value of this floating-rate bond at time n − 2 is equal to the principal value.
In fact, it is easy to deduce that right after any coupon payment, we have

for each k = 1, 2, …, n.
Now, let us determine the bond value between two coupon payments. Let t ∈ [k − 1, k), for k = 1, 2, …, n. Since Bℓk = F and an additional cash flow of F × r1k − 1 is due at time k, then

It corresponds to the present value of F × (1 + r1k − 1), which is paid at time k, discounted back from time k to time t using the (k − t)-rate observed at time t. This is also shown in Figure 4.3.

Figure 4.3 Valuation of a floating-rate bond
Example 4.2.5 Valuation of a floating-rate bond with annual coupons
A 10-year floating-rate bond of $10,000 was issued 3.5 years ago. Coupons are annual and calculated using the 1-year rate observed at the beginning of each year. Suppose that we observe the following term structure of interest rates: r0.53.5 = 0.01 and r13.5 = 0.015. Six months ago, the 1-year rate was r13 = 0.0125. All rates are compounded annually. Find the value, at time t = 3.5, of this floating-rate bond.
In 6 months, after the coupon payment, the value of the bond will be equal to its principal, i.e. $10,000. The coupon payment due in 6 months is based upon the 1-year rate observed six months ago, i.e. 1.25%, so it is equal to $125. We discount this total value of $10,125, due in 6 months from now, using r0.53.5 = 0.01 and then we obtain
◼
If coupons/payments are paid on a semi-annual or a quarterly basis (and compounded accordingly), then the valuation methodology presented above is still valid, up to some minor modifications. Suppose interest is paid and compounded m times per year. At time t = k/m, for any k = 1, 2, …, mn, that is right after a coupon payment, we still have
To obtain the value of the bond between two coupon payments, we need to discount the next coupon and the principal value.
Let us illustrate this with an example.
Example 4.2.6 Valuation of a floating-rate bond with semi-annual coupons
A 3-year floating-rate bond with principal F = 10, 000 was issued 3 months ago. Coupons are paid semi-annually and determined by using the 6-month rates. We observe r0.50 = 2%. Let us consider the following scenario: r0.250.25 = 1.78%.
In this scenario, the current value of this bond is given by
◼
4.2.3.3 Valuation of a swap: the difference of two bonds
Using the above, we have that the time-t value of an interest swap for an investor:
- paying fixed and receiving floating is
 ;
; - paying floating and receiving fixed is
 .
.
Example 4.2.7 Valuation of an interest rate swap
A 2-year interest rate swap was initiated 3 months ago. At that time, the 6-month rate was 1.14%. Coupons are semi-annual and the face value is $10,000. An investor has agreed to pay 2% per year whereas the counterparty has agreed to pay coupons based upon the observed 6-month rate. All rates are semi-annually compounded.
Assuming the current term structure of interest rates is given by rT0.25 = 0.01 + 0.004T, let us find the current value of this swap, i.e. at time t = 0.25.
There are four cash flow dates remaining:
- At time 0.5, which is 6 months after inception or 3 months from now.
- At time 1, which is 1 year after inception or 9 months from now.
- At time 1.5, which is 18 months after inception or 15 months from now.
- At time 2, which is 2 years after inception or 21 months from now.
We need to identify the rates at which payments will be discounted:
- Cash flow at time 0.5: 3-month rate observed at time 0.25.
- Cash flow at time 1: 9-month rate observed at time 0.25.
- Cash flow at time 1.5: 15-month (1.25-year) rate observed at time 0.25.
- Cash flow at time 2: 21-month (1.75-year) rate observed at time 0.25.
The following table shows the corresponding rates and the present value of each fixed payment.
Maturity Rate Amount PV 0.25 0.011 100 99.72613 0.75 0.013 100 99.03286 1.25 0.015 100 98.14934 1.75 0.017 10100 9805.183 For example, for the second fixed payment occurring at time 1 which is 9 months from now, we have r0.750.25 = 0.01 + (0.004 × 0.75) = 0.013. The coupon value is 10000 × (0.5 × 0.02) = 100 whereas the present value is
Therefore, summing up the elements in the last column, we get
On the other hand, the floating-rate payment due in 3 months is equal to
and hence the value of the floating-rate bond at the next coupon date will be $10,057. We discount this value at the current 3-month rate r0.250.25 = 0.011 (which is semi-annually compounded) and we get
Therefore, the current value of this swap, for the fixed-rate receiver, is given by
. Of course, we have a value of Bℓ0.25 = −72.63 for the floating-rate receiver.
◼
4.2.4 Market specifics
At inception, it costs nothing to enter a swap. Therefore, the floating-rate bond should be worth the same as the fixed-rate bond, i.e. we should observe ![]() . Recall from equation (4.2.3) that a floating-rate bond is always worth F at inception and immediately after any coupon payment. Consequently, the fixed-rate bond should also be worth F at inception of the swap. Consequently, to avoid arbitrage opportunities, there is only one possible coupon rate for this fixed-rate bond. This coupon rate is known as the swap rate. Mathematically, the swap rate is the coupon rate such that
. Recall from equation (4.2.3) that a floating-rate bond is always worth F at inception and immediately after any coupon payment. Consequently, the fixed-rate bond should also be worth F at inception of the swap. Consequently, to avoid arbitrage opportunities, there is only one possible coupon rate for this fixed-rate bond. This coupon rate is known as the swap rate. Mathematically, the swap rate is the coupon rate such that ![]() , where an expression for
, where an expression for ![]() can be found in equation (4.2.1). This is how swaps are usually quoted.
can be found in equation (4.2.1). This is how swaps are usually quoted.
Example 4.2.8 Swap rate
The current term structure of interest rates is such that r10 = 0.03, r20 = 0.04, r30 = 0.045, r40 = 0.05, r50 = 0.055. Let us find the swap rate on a 5-year interest rate swap with a principal of $100.
Recall that the swap rate is the coupon rate on the fixed-rate bond such that it trades at par. Using equation (4.2.1), we must solve for c in the following equality:
We find c = 5.387366193. Therefore, the swap rate is 5.39%.
◼
Until now, we have not been specific about which floating interest rate to use. In the financial market, the floating rate most commonly used is the LIBOR rate, which is the London Interbank Offered Rate. For example, the 6-month LIBOR rate is a common benchmark used to compute floating interest payments.
We have not specified either what interest rates should be used to discount cash flows from the swap. We know, however, they should be consistent with the benchmark used to compute floating interest payments. In this chapter, we will say it is obtained from a LIBOR zero curve which should not be confused with LIBOR rates (see below).
London Interbank Offered Rate (LIBOR)
The LIBOR is fixed by a council of banks doing business in London. It represents the interest rate an average bank from that council would need to pay for a short-term loan contracted from any of the other banks. The US LIBOR is the rate a U.S. bank would pay if it were to borrow from these leading banks.
The LIBOR rate is available for seven different maturities: 1 day (overnight), 1 week, 1 month, 2, 3, 6 and 12 months. Since most swaps have semi-annual payments, the 6-month LIBOR rate is thus often used to determine the periodic payment of the floating-rate leg of an interest rate swap.
The LIBOR zero curve is an interest rate term structure obtained from LIBOR rates (for maturities below 1 year) and Eurodollar futures for maturities between 1 year and 5 years.
Example 4.2.9 Another swap rate
Let us find the swap rate on a 2-year interest rate swap with semi-annual payments based upon the 6-month LIBOR. It should be noted the LIBOR zero curve is such that:
- 6-month rate: 3%
- 12-month rate: 3.66%
- 18-month rate: 4.04%
- 24-month rate: 4.26%.
All rates are compounded semi-annually.
We need to find c such that
and thus the semi-annual coupon is c = 2.1217414 or, said differently, the (semi-annual) swap rate is 4.2434828%.
◼
Finally, swaps are commonly and formally initiated by an intermediary whose role is to either match two investors in a swap or play the role of the counterparty in the swap. The intermediary will incur costs and usually charge a fixed spread over the LIBOR rate, as shown in Figure 4.4.

Figure 4.4 Swap between two parties initiated with an intermediary such as a financial institution
4.3 Currency swaps
Generally speaking, a swap on currencies is an agreement between two parties to exchange future cash flows in different currencies. There are two commonly traded types of swaps on currencies: cross-currency basis swaps and foreign exchange (FX) swaps. In what follows, we will focus on the former type.
In a cross-currency basis swap, simply called a currency swap in what follows, both parties agree to exchange a principal and its interests in one currency for the same principal and its interests in another currency. There are three types of currency swaps:
- Fixed-for-fixed: the interest rates are fixed on both sides of the swap.
- Floating-for-floating: the interest rates are variable on both sides of the swap.
- Fixed-for-floating: the interest rate is fixed on one side and is floating on the other side.
Interests in each currency, either fixed or floating, are exchanged on both sides. Currency swaps are used by institutional investors and multinational companies to swap foreign-denominated loans or to lower borrowing costs abroad.
Example 4.3.1 Constant flow of foreign revenues
A U.S.-based insurance company also operates in Europe. Once every quarter, it will receive €1 million to be converted immediately into U.S. dollars. Let us explain how this American insurer can manage this foreign exchange rate risk over the next 12 months.
The company has three options:
- If the investment manager believes the USD/EUR exchange rate will move favorably in the next couple of months, then she could simply wait, receive €1 million every quarter and then convert it using the spot exchange rate. In this case, the company is fully exposed to foreign exchange rate risk.
- They could simply enter into four separate forward contracts, each to sell €1 million with maturities 3, 6, 9 and 12 months, respectively. This way, the company would fix the exchange rate for the next year.
- They could also enter into a currency swap to pay €1 million every quarter and receive in exchange a certain amount in U.S. dollars. This amount would need to be determined. Depending on the agreement, this might also require an exchange of principal at inception and at maturity.
◼
An FX swap is an agreement to buy (sell) one unit of a currency in exchange for selling (buying) it back at a predetermined date in the future. The price at which it is traded in the future is the forward exchange rate (as seen in Chapter 3). Therefore, a FX swap is a long (short) spot transaction combined with a short (long) forward transaction.
According to the Triennial Central Bank Survey conducted by the BIS in 2013, $2.2 trillion of FX swaps were traded daily compared with only $54 billion of currency swaps.3
4.3.1 Cash flows
The cash flows of a currency swap are similar to exchanging interest payments from two loans each denominated in a different currency. This is illustrated in the next example.
Example 4.3.2 Currency swap to lower borrowing costs
A U.S.-based insurance company wants to start doing business in Europe, whereas a European reinsurance company wants to expand in the United States. The companies have access to the following rates.
On one hand, the American company may borrow:
- at 2% in USD from an American bank;
- at 4% in EUR from a European bank, which is a foreign bank for the company.
On the other hand, the European company may borrow:
- at 1% in EUR from a European bank;
- at 5% in USD from an American bank, which is a foreign bank for the company.
Today, both companies need 100 million U.S. dollars, or its equivalent in Euros according to the current exchange rate, i.e. 90 million Euros. We see it is much cheaper for each company to borrow from a domestic bank than from a foreign bank. Let us illustrate how the two companies can enter into a currency swap to lower their borrowing costs.
Indeed, if the companies enter into a fixed-for-fixed currency swap with a notional of 100 million USD, which is currently equal to 90 million EUR, and if each company borrows from its domestic bank, then they will both lower their costs.
At inception, the notional is exchanged in their respective currencies, i.e. the American company receives 90 million EUR, a loan worth 100 million USD, while the European company receives 100 million USD, a loan worth 90 million EUR. The net cash flow is zero.
Periodically, the European company will pay 1% on its loan, i.e. 0.9 million EUR. It receives the same amount through the swap from the U.S.-based company. Similarly, the American company will pay 2% on its loan, i.e. 2 million USD, but will receive the same amount through the swap from the Europe-based company.
At maturity, when the loans expire, the swap requires an exchange of notional and then each company can repay its respective loans.
The next two tables illustrate the cash flows for the U.S.-based company and for the European-based company, respectively (unit is 1 million):
Time Local loan Swap Inception +100 USD −100 USD, +90 EUR Periodic −2 USD +2 USD, −0.9 EUR Maturity −100 USD +100 USD, −90 EUR and
Time Local loan Swap Inception +90 EUR −90 EUR, +100 USD Periodic −0.9 EUR +0.9 EUR, −2 USD Maturity −90 EUR +90 EUR, −100 USD
If the American company borrows from its local bank and enters into a currency swap, then this will be equivalent to a loan at 1% in EUR. If the European company borrows from its local bank and enters into a currency swap, then this will be equivalent to a loan at 2% in USD.
◼
It is worth mentioning that credit risk on a currency swap is larger than on an interest rate swap (which is on a single currency) as the notional is exchanged at maturity.
4.3.2 Valuation
Similar to interest rate swaps, it is possible to view a currency swap as a long (short) position in a locally-denominated bond (either fixed-rate or floating-rate) and a short (long) position in a foreign-denominated bond (either fixed-rate or floating-rate). Therefore, under the no-arbitrage assumption, pricing a currency swap is equivalent to pricing the difference of two bonds (or loans), each denominated in its own currency.4 As a result, it suffices to value each bond in its local currency and convert the foreign-denominated bond using the current exchange rate.
Again, let Bdt (d for domestic) be the time-t value of the locally-denominated bond (either fixed-rate or floating-rate), B ft ( f for foreign) be the time-t value of the foreign-denominated bond (either fixed-rate or floating-rate), and St be the time-t exchange rate expressed as the number of local currency needed to buy one unit of the foreign currency.
For example, if the domestic currency is USD and the foreign currency is EUR, then ![]() is the time-t price in EUR of the European bond. Consequently,
is the time-t price in EUR of the European bond. Consequently, ![]() is the time-t value in USD of this European bond. Of course,
is the time-t value in USD of this European bond. Of course, ![]() is the time-t price in USD of the American bond. It is important to note that
is the time-t price in USD of the American bond. It is important to note that ![]() and
and ![]() are computed using equation (4.2.2), or equation (4.2.3) (depending on whether interest is fixed or floating), in their respective currency.
are computed using equation (4.2.2), or equation (4.2.3) (depending on whether interest is fixed or floating), in their respective currency.
Therefore, at time t, a currency swap where we receive the domestic interest and pay the foreign interest is worth
while a currency swap where we pay the domestic interest and receive the foreign interest is worth
Note that both values Vdt and V ft are expressed in the domestic currency.
Example 4.3.3 Valuation of a fixed-for-fixed currency swap
The following fixed-for-fixed currency swap has been issued for some time:
- At inception, the USD and EUR were trading at par.
- Notional is 100.
- 5% in USD is exchanged for 4% in EUR.
- Maturity is in 3 years.
- Payments are annual.
The current market conditions are described as follows:
- U.S. LIBOR curve is flat at 4.5%.
- Euro LIBOR curve is flat at 4.7%.
- Current exchange rate is 0.90 USD/EUR.
All rates are compounded annually. Let us find the current value of this swap.
First note that as the exchange rate between the U.S. dollar and the Euro was at par at inception, hence the notional is 100 (USD and EUR) on both bonds.
We need to find the value of the 3-year bonds using the appropriate discount rates: the U.S.-(Euro-) denominated bond is discounted with the U.S.(Euro) LIBOR curve. We have
Therefore, this swap is worth
from the point of view of a company paying U.S. dollars and receiving Euros.
◼
4.4 Credit default swaps
A bond issuer defaults (on its obligation) whenever it is unable to make one or several coupon payments on that bond. The risk of occurrence of such an event, and the loss associated with it, are known as credit risk (see Chapter 2). Therefore, investing in a bond, or equivalently lending to a borrower, entails credit risk.
A credit default swap is a credit derivative similar to an insurance against default, compensating an investor losing because of a default event. Using the terminology for swaps, a CDS is an agreement between two parties to receive a (random) compensation in case of default in exchange for a fixed stream of payments. The protection buyer is the investor paying the fixed stream of cash flows, known as CDS premiums. The protection seller assumes the credit risk of the reference bond and agrees to compensate the protection buyer in case a pre-specified credit event occurs. The cash flows are illustrated in Figure 4.5.

Figure 4.5 Cash flows of a typical credit default swap
CDS are offered with maturities (tenors) varying between 1 and 10 years, 5 years being the most popular. As with many other swaps, the ISDA formalizes the agreements. Credit default swaps are among the most popular credit derivatives traded in the market but lost much popularity after the financial crisis of 2007–2009. As of December 2014, the market size of CDS was about $16 trillion (BIS) but was almost four times larger in the months prior to the burst of the financial crisis (ISDA).
As life insurance companies use corporate bonds to manage their long-term liabilities, they are exposed to credit risk. The financial crisis of 2007–2009 has shown that even investment-grade securities could default and, therefore, asset managers use CDS to protect against such insolvency. According to the NAIC, 93% of insurers who hedge credit risk on their assets use credit default swaps. However, only 4% of their total use of swaps involves CDS.5
4.4.1 Cash flows
Cash flows and valuation of CDS are based upon an underlying reference bond. There are two scenarios:
- If the borrowing company does not default on the reference bond, which is the most likely scenario, the protection buyer will pay a semi-annual premium for the CDS and receive nothing in return. This is just like a conventional insurance policy where the insured event does not occur.
- If the reference company does default prior to the maturity of the CDS, then the protection buyer receives a compensation and stops paying premiums. Compensation is tied to the market value of the reference bond upon default.
Whenever there is default, the buyer chooses between a physical or a cash settlement. In a physical settlement, the protection buyer sells the underlying reference bond to the protection seller at some given price, thus compensating the loss in value following default. Whenever the CDS is settled in cash, the difference between the market value of the defaulted bond and that given price is provided in cash to the protection buyer. This is illustrated in the next example.
Example 4.4.1 Cash flows of a credit default swap
A life insurance company holds 100M in a 20-year corporate bond issued by a highly-reputable company named ABC inc. However, the insurer fears that if default occurs on that bond, it will suffer important losses. It thus seeks default protection and enters into a CDS.
The CDS issuer sells a 5-year protection for a premium of 1% per year. The premium is paid at the end of each year and compensation in case of default is paid at year end. If default occurs, the protection buyer sells the defaulted bond to the protection seller at a price equivalent to a similar Treasury bond.
Let us illustrate the cash flows of the CDS if the bond issuer:
- does not default; or,
- defaults towards the end of the second year.
In the latter case, each defaulted bond is worth 50 whereas an equivalent 3-year Treasury bond trades at 94 (for a face value of 100).
In the most likely scenario, ABC inc. does not default over the next 5 years and the insurer pays 0.01 × 100 = 1 million per year for 5 years. In this scenario, it will receive nothing in return.
In the second scenario, the cash flows are as follows:
- Time 0: nothing;
- Time 1: payment of a premium of 1 million;
- Time 2: payment of a premium of 1 million, settlement of the CDS.
There are two options for the settlement of the CDS:
- If it is settled physically, the investor (life insurer) delivers the defaulted bond to the protection seller who provides for 94 million in exchange.
- If it is settled in cash, the protection buyer receives 94 − 50 = 44 per 100 of face value, i.e. 44 million. The life insurer should also sell the underlying bond for 50 per 100 of face value and earn an extra 50 million, for a total of 94 million as well.
◼
CDS are usually quoted in basis points (bps) where 100 bps corresponds to 1% of face value. The CDS premium is also known as the CDS spread and it is usually paid quarterly until maturity or default, whichever comes first.
CDS and the financial crisis
The CDS depicted above are written on typical bonds whose issuer could go bankrupt. However, CDS became famous during the financial crisis of 2007–2009 for CDS written on other securities that could potentially fail.
For example, American International Group (AIG), a major U.S. insurance company operating mostly in property and casualty insurance, expanded in the early 2000s in the CDS market. AIG sold CDS written on collateralized debt obligations themselves secured by residential mortgages (see “Securitization” in Chapter 2). When the residential market collapsed in 2008, billions of dollars worth of CDO also collapsed triggering payments on the CDS issued by AIG. Unfortunately, the reserves set aside by AIG to cover these events were insufficient. AIG was on the verge of declaring bankruptcy in 2008 when it was salvaged by the U.S. federal government.
The book and movie called ”The Big Short” depict the story of several investors who bet on the collapse of the U.S. housing market. One of them asked several investment banks to issue CDS on mortgage bonds (written on residential mortgages) that would trigger a payment upon the failure of these bonds. In exchange for a low periodic premium, the CDS would provide a very high reward whenever the mortgage bonds would fail. Therefore, these CDS were used for speculation purposes.
4.4.2 Valuation
Valuation of a CDS is based upon a very important principle: holding the reference bond and a CDS on that reference bond should be a risk-free investment, or there would be arbitrage opportunities. Thus, we have:
The following example illustrates this.
Example 4.4.2 Valuation of a single-premium CDS
Suppose there are two assets traded in the market:
- a risk-free zero-coupon bond, with B0 = 0.95 and BT = 1;
- a defaultable zero-coupon bond with DB0 = 0.93 and random payoff DBT.
Moreover:
- If the issuer of the defaultable bond does not default, then DBT = 1;
- If it defaults, the creditor recovers DBT = 0.6.
Let us find the (single) CDS premium to compensate the protection buyer in case the bond defaults.
Obviously, when the firm does not default, the return on the bond should be higher than a risk-free bond to compensate a risk-averse buyer for investing in that bond. That explains why DB0 < B0.
We want to issue a CDS that will compensate a bondholder in case of default. Therefore, the payoff of the CDS should be 0.4 when the firm defaults and 0 otherwise.
We know that the defaultable zero-coupon bond DBT combined with the CDS should yield a risk-free position. Therefore, the up-front premium of the CDS should be 0.02, i.e. 0.95 − 0.93. Indeed, buying the defaultable bond and the CDS cost 0.95 in total and the portfolio provides a final payoff of 1, no matter whether the firm survives or not (1 + 0 vs. 0.6 + 0.4). Since the defaultable bond combined with the CDS yields the same payoffs as a risk-free bond in any scenario, they must trade at the same price to avoid arbitrage opportunities.
◼
Computing the periodic CDS spread usually involves assessing default risk over time using a credit risk model setup under no arbitrage. This is beyond the scope of this book.
4.4.3 Comparing a CDS with an insurance policy
From its definition, it is easy to view a CDS as being similar to a term life insurance, but instead of paying a fixed or random benefit at death of an individual, the benefit is paid upon default of a reference company. This is possibly the only similarity between CDS and term insurance because there are many differences. Most of these differences stem from where CDS and insurance are sold as the financial market is much less regulated than the insurance market, as discussed in Chapter 1.
First, it is not required to have an insurable interest in the reference bond or company as is the case for insurance policies. Whereas an insurance policy can be viewed solely as a risk management instrument for an individual or a family, a CDS can be used for both speculation and risk management. As investors, life insurance companies use CDS for hedging purposes in a large proportion. In some sense, the life insurer has an insurable interest because, when investing in bonds, they lend money and are exposed to credit risk.
Second, insurance companies are also required to hold reserves to protect from future random claims whereas no such regulation is necessary for CDS protection sellers.
Another important difference between CDS and insurance policies comes from the nature of the insured risks. Typical risks covered in insurance policies are diversifiable whereas defaults (and in turn bankruptcies) are often tied to economic conditions which are much harder to diversify over a portfolio (see Chapter 1).
4.5 Commodity swaps
At inception, a commodity swap fixes the price paid for several deliveries of the underlying commodity, on a specified set of dates and forming the fixed leg. The floating leg of a commodity swap agreement consists of the unknown (at inception) values of this commodity at the predetermined dates. On each exchange date, the fixed-amount payer has the choice between receiving the commodity (physical settlement) or its cash equivalent (cash settlement).
A commodity swap can be viewed as a portfolio of commodity forwards. Indeed, to fix today the price we pay for delivery of a good at times t1, t2, …, tn = T, we can simply enter into n commodity forwards with maturities at times t1, t2, …, tn, each at an initial cost of zero (as a forward contract costs nothing to enter). Because we can easily replicate the cash flows of a commodity swap with a portfolio of forward contracts, the initial no-arbitrage price of a commodity swap should also be equal to zero.
Valuation of a commodity swap is therefore based upon forward commodity prices. Recall that FTt is the delivery price determined at time t and to be paid at time T (for delivery at time T). Let us define by ηi the number of units of the commodity the swap promises to deliver (or its cash equivalent) at time ti in exchange for a fixed payment of c. The value of the fixed-leg side of the swap is

i.e. the present value of future fixed payments whereas the value of the floating-leg is

i.e. the value of the remaining forwards in the swap. Because the delivery price is paid at future dates ti (with respect to time t), we need to discount these prices back to time t. Finally, at inception, the fixed premium c is the unique one such that
Example 4.5.1 Crude oil swap
An airline company would like to manage the risk tied to the price of jet fuel. To do so, it enters a commodity swap on the crude oil barrel. Although the company does not have the expertise to transform crude oil into jet fuel, it enters a swap on crude oil as its price is highly correlated with the price of jet fuel. Of course, the swap will be cash settled. Such a crude oil swap allows the airline to receive the cash value of 1000 barrels of crude oil every month, for the next 3 months, in exchange for a fixed periodic payment. Let us find the fixed periodic premium given the following scenario for the term structure of crude oil forward prices and the term structure of Treasury rates:
Maturity Forward price Treasury rate 1 month 30 1% 2 months 31 1.2% 3 months 32 1.5% At inception, we must have Bℓ0 = Bx0. In this scenario, on one side, we have
and, on the other side, we have
Combining the two equations, we get 2.993469795c = 92.79467725 and thus the periodic premium is c = 30.999.
◼
4.6 Summary
Swaps
- Periodic exchange of (fixed or variable) cash flows related to the value of a given asset, at predetermined dates. Usually, a fixed payment is exchanged for a variable (random) payment.
- Interest rate swap: exchange a variable interest rate, applied to a notional, for a fixed interest rate, applied on the same notional.
- No cash flows (no premium) exchanged at inception (at time 0).
- Currency swap: exchange a principal and its interests in one currency for the same principal and its interests in another currency.
- Credit default swap: compensation in case a bond defaults in exchange for a fixed periodic premium.
- Commodity swap: periodic delivery of a commodity (or its cash equivalent) for a fixed periodic payment.
Terminology
- Maturity, swap term or swap tenor, is the date of the last cash flow.
- Fixed leg: stream of the fixed payments.
- Floating/variable leg: stream of the floating/variable/random payments.
Interest rate swaps
- Equivalent to exchanging a fixed-rate loan/bond for a floating-rate loan/bond.
- Fixed cash flows: periodic coupon and principal paid back at maturity.
- Variable cash flows: interests paid at the end of each period, and computed with a variable rate, and principal paid back at maturiy.
Valuation of a fixed-rate loan/bond
- Principal: F.
- Payment dates: t1, t2, …, tn = T.
- Fixed payment (coupon): c.
- Fixed-rate bond’s time-t value for t ∈ [0, tn):

Valuation of a floating-rate loan/bond
- Value at inception: Bℓ0 = F.
- Value immediately after a coupon payment: Bℓk = F, for all k = 1, 2, …, mT.
- Value between two coupon payments: for t ∈ [k − 1, k),

Valuation of interest rate swaps
- Pays fixed, receives floating:
 .
. - Pays variable, receives fixed:
 .
. - Swap rate: fixed (coupon) rate such that
 (bond is priced at par).
(bond is priced at par).
Currency swaps
- Fixed-for-fixed: fixed interest in one currency against fixed interest in another currency.
- Fixed-for-floating: fixed interest in one currency against floating interest in another currency.
- Floating-for-floating: floating interest in one currency against floating interest in another currency.
- Time-t value of the domestic bond (in the domestic currency): Bdt.
- Domestic currency: U.S. dollar.
- Time-t value of the foreign bond (in the foreign currency): B ft.
- Time-t price (in USD) to purchase one unit of the foreign currency: St (exchange rate at time t).
- Swap value for the party receiving the domestic currency: Vdt = Bdt − StB ft.
- Swap value for the party receiving the foreign currency: V ft = StB ft − Bdt.
Credit default swaps
- Issuer of a bond may be unable to meet its obligations: default.
- Credit default swap (CDS): offers protection to the bondholder in case of default.
- Fixed periodic premium paid in exchange for a unknown/random compensation in case of default.
- Protection buyer: pays fixed premium until maturity or until default.
- Protection seller: pays compensation in case of default.
- Valuation principle: defaultable bond + CDS = risk-free (Treasury) bond.
Commodity swaps
- Equivalent to a portfolio of commodity forwards but with a constant periodic premium.
- Fixed leg:

- Number of units of the commodity delivered at time ti: ηi.
- T-forward commodity price at time t: FTt.
- Floating leg:

- Periodic cash flow c determined such that
 .
.
4.7 Exercises
-
You are given the following zero-coupon bond prices.
Maturity (term) Price 1 year 99.01 2 years 97.07 3 years 93.54 4 years 88.85 5 years 82.19 A 5-year interest rate swap exchanging fixed for floating is initiated today. Cash flows are exchanged annually.
- Find the swap rate.
- Suppose the swap is prepaid. As a fixed-rate payer, how much do you need to pay at inception to enter such a swap?
- Now suppose instead the swap is deferred by 1 year, meaning the first payment occurs at time 2. If a 6-year zero-coupon bond currently trades at $78.13, find the swap rate of this 1-year deferred swap.
-
Over the years 2011 to 2015, you have recorded the following interest rates (spot):
Date/Maturity Jan 1st, 2011 Jan 1st, 2012 Jan 1st, 2013 Jan 1st, 2014 Jan 1st, 2015 1 year 1% 1.10% 1.54% 1.39% 1.94% 2 years 1.46% 1.61% 2.25% 2.02% 2.83% 3 years 2.12% 2.33% 3.26% 2.94% 4.11% 4 years 2.79% 3.07% 4.30% 3.87% 5.41% 5 years 3.47% 3.82% 5.34% 4.81% 6.73% A 5-year interest rate swap (with annual payments) has been issued on January 1st, 2011.
- What is the swap rate?
- Calculate the cash flows of the fixed and floating legs over the entire duration of the swap.
- What is the value of the swap on January 1st 2012 for the side receiving floating and paying fixed?
-
Two loans of $10,000 have been issued 3 months ago. Interest is paid annually and principal is paid at maturity. You have the following data regarding interest rates:
- The one-year rate at inception of the loans was 4.2%.
- The current term structure of interest rates is given by the function rT0.25 = 0.04 + 0.004T.
- Calculate the value as of today of a 5-year floating-rate loan for the issuing bank.
- Calculate the value as of today of a 5-year fixed-rate loan with an annual coupon of 4.5% for the issuing bank.
-
A 4-year fixed-for-floating interest rate swap with semi-annual payments has been issued today. The 6-month LIBOR rate is exchanged for some fixed rate. All rates are compounded semi-annually.
- The current LIBOR curve is rT0 = 0.04 + 0.004T. Calculate the (semi-annual) swap rate.
- Thirteen months later, the LIBOR curve evolves to rT13/12 = 0.038 + 0.0041T. Calculate the value of the swap for the fixed payer. Note that r0.51 = 0.041.
-
A fixed-for-floating interest rate swap is initiated between two parties by an intermediary. The fixed-rate payer agrees to pay 4% in exchange for the 6-month LIBOR. The intermediary charges a spread of 0.1% to both sides of the swap. The current 6-month LIBOR rate is 3.5%. Assume all interest rates are semi-annually compounded and that the 6-month LIBOR rate 6 months from now is 3%. Describe the cash flows to the three parties in 6 months and in 1 year for a notional of 10,000.
-
A 3-year fixed-for-floating currency swap is initiated today. The fixed side agrees to pay 100c% annually in USD in exchange for the 1-year EUR LIBOR rate.
- The current exchange rate is 1.10 USD/EUR.
- The USD LIBOR curve is: rT0 = 0.01T.
- The EUR LIBOR curve is: rT0 = 0.009T.
Find c such that the swap costs nothing at inception.
-
A fixed-for-fixed currency swap was initiated some time ago. Fixed interest of 3.5% in USD is exchanged for 3.0% in CAD. You also know that:
- the exchange rate at inception was 1.33 CAD/USD;
- the current exchange rate is 0.85 USD/CAD;
- notional at inception was 100 USD;
- there are 4 years remaining in the swap;
- the USD LIBOR curve is: rT0 = 0.01T;
- the CAD LIBOR curve is: rT0 = 0.012T.
Find the current value of the swap in USD for the party that pays in USD.
-
ABC inc. some time ago issued a 10-year corporate bond with semi-annual coupons of 4% which is currently traded at $91.25. If ABC inc. defaults on such bond, creditors will recover 40% of par upon default. Describe the cash flows of a 5-year credit default swap with semi-annual payments of 0.25% of par in two situations:
- ABC inc. does not default on the bond.
- ABC inc. defaults on the bond 4 years from now and the compensation upon default is 60% of a Treasury bond whose price is $95.25.
-
You require delivery of 500 pounds of copper in 1 month, 600 pounds in 2 months and 650 pounds in 3 months. The term structure of interest rates and forward copper price (per pound) are shown in the next table.
Maturity (term) Spot rate Copper price 1 month 1.0% 2.10 2 months 1.1% 2.25 3 months 1.3% 2.45 - Describe the strategy necessary to fix today the price of future copper delivery using forwards. Calculate the related cash flows at each month (including inception).
- Compute the swap rate of a 3-month copper swap initiated today to receive 500, 600 and 650 pounds in 1, 2 and 3 months respectively.
- Compare the cash flows of the swap in (b) with the cash flows in (a). Why are they different?




