BONUS
CHAPTER
2

Chi-Square Tests

In This Chapter

• Performing a goodness-of-fit test with the chi-square distribution
• Using the goodness-of-fit test to check if a distribution follows a binomial probability distribution
• Using the goodness-of-fit test to check if a distribution follows a Poisson probability distribution
• Performing a test of independence with the chi-square distribution

In the previous chapters, we explored the wonderful world of hypothesis testing as we compared means and proportions of one, two, three, and more populations, making an educated conclusion about our initial claims. With that technique under our belt, we are now ready for bigger and better things.

In this chapter, we will use a new probability distribution, the chi-square, to confirm whether a set of data follows a specific probability distribution, such as the binomial or Poisson. (Remember those? They’re back!) We can also use this distribution to determine whether two variables are statistically independent. It’s actually a lot of fun–really it is!

Let me introduce you to the chi-square distribution before we start hypothesis testing. There is a family of chi-square distributions based on the number of degrees of freedom, shown in Figure 2.1.

Figure 2.1

Family of chi-square distributions.

The chi-square distribution has the following characteristics:

• It is not symmetrical, but rather it is positively skewed (to the right).
• The shape of the chi-square distribution will change with the number of degrees of freedom.
• As the number of degrees of freedom increases, the shape of the chi-square distribution becomes more symmetrical.
• The total area under the curve is equal to 1.
• It can’t be negative.

Why do we care about the chi-square distribution? Because it can be used in many tests, such as comparing three or more population proportions, performing hypothesis testing for a variance or a standard deviation, performing goodness-of-fit tests, testing for independence between two categorical variables, and many more. In addition, as mentioned previously, it can be used with nominal and ordinal data.

Review of Data Measurement Scales

In Chapter 2, we discussed the different type of data measurement scales, which were nominal, ordinal, interval, and ratio. Here is a brief refresher of each:

• Nominal level of measurement deals strictly with qualitative variables. Observations are simply assigned to predetermined categories. One example is gender of the respondent with the categories being male and female.
• Ordinal measurement is the next level up. It has all the properties of nominal data with the added feature that we can rank-order the values from highest to lowest. An example would be ranking a movie as great, good, fair, or poor.
• Interval level of measurement involves strictly quantitative variables. Here we can use the mathematical operations of addition and subtraction when comparing values. For this data, the difference between the different categories can be measured with actual numbers and also provides meaningful information. Temperature measurement in degrees Fahrenheit is a common example here.
• Ratio level is the highest measurement scale. Now we can perform all four mathematical operations to compare values. Examples of this type of data are age, weight, height, and salary. Ratio data has all the features of interval data with the added benefit of a “true zero point,” meaning that a zero data value indicates the absence of the object being measured.

The two major techniques that we will learn about in this chapter are using the chi-square distribution to perform a goodness-of-fit test and to test for the independence of two variables. So let’s get started!

The Chi-Square Goodness-of-Fit Test

One of the many uses of the chi-square distribution is to perform a goodness-of-fit test, which uses a sample to test whether a frequency distribution fits the predicted distribution. As an example, let’s say that a new movie in the making has an expected distribution of ratings summarized in the following table.

After its debut, a sample of 400 moviegoers was asked to rate the movie, with the results shown in the following table.

Observed Movie-Rating Distribution

Number of Stars	Number of Observations
5	145
4	128
3	73
2	32
1	22
	Total = 400

Can we conclude that the expected movie ratings are true based on the observed ratings of 400 people?

Stating the Null and Alternative Hypotheses

The null hypothesis in a chi-square goodness-of-fit test states that the sample of observed frequencies supports the claim about the expected frequencies. The alternative hypothesis states that there is no support for the claim pertaining to the expected frequencies. For our movie example, the hypotheses statement would be:

H₀: The actual rating distribution can be described by the expected distribution.

H₁: The actual rating distribution differs from the expected distribution.

We will test this hypothesis at the α = 0.10 level.

Observed vs. Expected Frequencies

The chi-square test basically compares the observed (O) and expected (E) frequencies to determine whether there is a statistically significant difference. For our movie example, the observed frequencies are simply the number of observations collected for each category of our sample. The expected frequencies are the expected number of observations for each category and are calculated in the following table.

Expected Frequency Table

The chi-square test requires that the expected frequency be 5 or more in each category. Looking at the previous table, we satisfy this requirement, so we are now ready to calculate the chi-square test statistic.

Calculating the Chi-Square Test Statistic

The chi-square test statistic is found using the following equation:

where:

O = the number of observed frequencies for each category

E = the number of expected frequencies for each category

The calculation using this equation is shown in the following table.

The calculated chi-square test statistic is = 9.95

Determining the Critical Chi-Square Value

The critical chi-square value, , depends on the number of degrees of freedom, which for this test would be:

d.f. = k – 1

where k equals the number of categories in the frequency distribution. For the movie example, there are five categories, so d.f. = k – 1 = 5 – 1 = 4.

The critical chi-square value is read from the chi-square table found on Table 5 in Appendix B of this book. Here is an excerpt of this table.

For α = 0.10 and d.f. = 4, the critical chi-square value, = 7.779, is indicated in the underlined part of the table. Figure 2.2 shows the results of our hypothesis test.

According to Figure 2.2, the calculated chi-square test statistic of 9.95 is within the “Reject H₀” region, which leads us to the conclusion that the actual movie-rating frequency distribution differs from the expected distribution.

Figure 2.2

Chi-square test for the movie rating example.

Also, because the calculated chi-square test statistic for the goodness-of-fit test can only be positive, the hypothesis test will always be a one-tail with the rejection region on the right side.

As an example, suppose that a certain major league baseball player claims the probability that he will get a hit at any given time is 30 percent. The following table is a frequency distribution of the number of hits per game over the last 100 games. Assume he has come to bat four times in each of the games.

Data for the Baseball Player

Number of Hits	Number of Games
0	26
1	34
2	30
3	7
4	3
	Total = 100

In other words, in 26 games he had 0 hits, in 34 games he had 1 hit, etc. Test the claim that this distribution follows a binomial distribution with p = 0.30 using α = 0.05.

The hypotheses statement would be:

H₀: The distribution of hits by the baseball player can be described with the binomial probability distribution using p = 0.30.

H₁: The distribution differs from the binomial probability distribution using p = 0.30.

Our first step is to calculate the frequency distribution for the expected number of hits per game. To do this, we need to look up the binomial probabilities in Table 1 from Appendix B for n = 4 (the number of trials per game) and p = 0.30 (the probability of a success). These probabilities, along with the calculations for the expected frequencies, are shown in the following table.

Before continuing, we need to make one adjustment to the expected frequencies. When using the chi-square test, we need at least five observations in each of the expected frequency categories. If there are less than five, we need to combine categories. In the previous table, we will combine 3 and 4 hits per game into one category to meet this requirement.

Now we are ready to determine the calculated chi-square test statistic using the following table:

The Calculated Chi-Square Test Statistic for the Baseball Example

* 7 + 3 = 10

** 7.56 + 0.81 = 8.37

The calculated chi-square test statistic is = 2.20.

According to Table 5 in Appendix B, the critical chi-square value for α = 0.05 and d.f. = k – 1 = 4 – 1 = 3 is 7.815. This test is shown in Figure 2.3.

Figure 2.3

Chi-square test for the baseball example.

According to Figure 2.3, the calculated chi-square test statistic of 2.20 is within the “Do Not Reject H₀” region, which leads us to the conclusion that the baseball player’s hitting distribution can be described with the binomial distribution using p = 0.30.

I know you must be thinking at this point, “I don’t need to draw the graph each time to determine my conclusion.” Well then, go for it! Make your conclusion by comparing the calculated test statistic to the critical chi-square value, , as follows:

• If ≤ 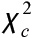⇒ Don’t reject H₀
• If > 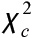⇒ Reject H₀

A Goodness-of-Fit Test with the Poisson Distribution

Now let’s do an example to test whether a distribution follows a Poisson probability distribution. The following table gives the number of spam emails I received per day over the last 100 days.

Data for the Number of Spam Emails

Number of Spam Emails	Frequency
0	2
1	21
2	30
3	20
4	17
5	7
6	3
	Total = 100

In other words, in 2 out of the 100 days I received no spam emails, in 21 out of the 100 days I received 1 spam email, etc. Test the claim that this distribution follows a Poisson distribution with λ (the mean number of occurrences over the interval) = 2.5 using α = 0.01.

The hypotheses statement would be:

H₀: The number of spam emails can be described with the Poisson probability distribution using λ = 2.5.

H₁: The number of spam emails differs from the Poisson probability distribution using λ = 2.5.

Our first step is to calculate the frequency distribution for the expected number of spam emails per day. To do this, we need to look up the Poisson probability distribution in Table 2 from Appendix B for λ = 2.5. These probabilities, along with the calculations for the expected frequencies, are shown in the following table.

Expected Frequency Calculations for Spam Emails

Since there is no upper limit for the Poisson distribution and because I didn’t receive more than 6 spam emails per day over the last 100 days (lucky me, right?), we need to combine the probabilities of 6, 7, 8, 9, 10, and 11 spam emails per day to get:

P(x ≥ 6) = 0.0278 + 0.0099 + 0.0031 + 0.0009 + 0.0002 + 0.0000 = 0.0419

Before continuing, we need to make the same adjustment we made for the binomial distribution example. Since the expected frequency in the last category is <5, we are going to combine the 5 and 6 or more spam emails per day categories into one category (5 or more) to meet the chi-square test requirement.

Now we are ready to determine the calculated chi-square test statistic using the following table:

The Calculated Chi-Square Test Statistic for the Spam Emails Example

* 7 + 3 = 10

** 6.68 + 4.19 = 10.87

The calculated chi-square test statistic is = 6.60.

According to Table 5 in Appendix B, the critical chi-square value for α = 0.01 and d.f. = k – 1 = 6 – 1 = 5 is 15.086. Applying our decision rule, since the calculated chi-square test statistic of 6.60 is less than the critical chi-square value, = 15.086, then we don’t reject H₀. This leads us to the conclusion that the number of spam emails distribution can be described with the Poisson distribution using λ = 2.5.

Chi-Square Test for Independence

In addition to the goodness-of-fit test, the chi-square distribution can also test for independence between variables. To demonstrate this technique, I’m going to use the following example.

Let’s say I want to test whether the grades students receive in a course are related to the type of course they are taking. So I collected data for 200 students in three different classes at the MBA level, which is presented in the following table:

Observed Frequencies for the Grade Example

Do you remember the name of this table back in Chapter 3? Yes, it is a contingency table, which shows the observed frequencies of two variables. In this case, the variables are grades and courses. The table is organized into r rows and c columns. For our table, r = 3 and c = 3. An intersection of a row and column is known as a cell. A contingency table has r · c cells, which in our case, would be 9.

The chi-square test of independence will determine whether the type of course students take and their grades are independent of each other or not.

First we state the null and alternative hypotheses as:

H₀: The course type and grade are independent of each other

H₁: The course type and grade are not independent of each other

We will test this hypothesis at α = 0.05 level.

Our next step is to determine the expected frequency of each cell in the contingency table under the assumption that the two variables are independent. We do this using the following equation:

where E_r,c = the expected frequency of the cell that corresponds to the intersection of Row r and Column c.

The following table summarizes the calculations for the expected frequencies:

We now need to make sure the expected frequency in each cell is 5 or more before we continue. Since this condition is satisfied, then we can determine the calculated chi-square test statistic using:

This calculation is summarized in the following table:

The calculated chi-square test statistic is = 12.745.

To determine the critical chi-square value, we need to know the number of degrees of freedom, which for the independence test would be:

d.f. = (r – 1)(c – 1)

For this example, we have (r – 1)(c – 1) = (3 – 1)(3 – 1) = 4 degrees of freedom.

According to Table 5 in Appendix B, the critical chi-square value for α = 0.05 and d.f. = 4 is 9.488. Applying our decision rule, since the calculated chi-square test statistic of 12.745 is greater than the critical chi-square value, = 9.488, then we reject H₀. This leads us to the conclusion that the grades students receive and the types of courses they are taking aren’t independent of each other. Having taught two of these courses (Can you guess which ones? Yes, Economics and Finance), I’m not surprised by this conclusion.

Note, however, that the chi-square test of independence only investigates whether a relationship exists between two variables. It does not conclude anything about the direction of the relationship. In other words, from a statistical perspective, we cannot claim that one variable causes the other. All we can claim is that the two variables are not independent of each other. We statisticians always leave ourselves a way out!

Using Excel’s CHISQ Functions

You don’t have a chi-square distribution table handy? No need to panic. We can generate the critical chi-square value using Excel’s CHISQ.INV.RT function, which has the following characteristics:

CHISQ.INV.RT(probability, deg-freedom)

where:

probability = the level of significance, α

deg-freedom = the number of degrees of freedom

For instance, Figure 2.4 shows the CHISQ.INV.RT function being used to determine the critical chi-square value for α = 0.10 and d.f. = 4 from our movie rating example.

Figure 2.4

Selecting Excel’s CHISQ.INV.RT function.

Click OK and fill in the data as in Figure 2.5.

Figure 2.5

Output for Excel’s CHISQ.INV.RT function.

Cell A1 contains the Excel formula =CHISQ.INV.RT(0.10, 4) with the result being 7.779. This is the exact value we obtained from the table.

We can also use Excel’s CHISQ.DIST.RT function to get the p-value for our calculated chi-square test statistic, which has the following characteristics:

CHISQ.DIST,RT(x, deg-freedom)

where:

x = the calculated chi-square test statistic

deg-freedom = the number of degrees of freedom

For instance, Figure 2.6 shows the CHISQ.DIST.RT function being used to determine the p-value for x = 9.95 and d.f. = 4 from our movie rating example.

Figure 2.6

Excel’s CHISQ.DIST.RT function.

Cell A1 contains the Excel formula =CHISQ.DIST.RT(9.95, 4) with the result being p = 0.04. Since the p-value is less than α, we reject H₀, which is the same conclusion we reached in our previous movie rating example.

Can Excel help, you ask, with the independence test? Of course. We can use Excel’s CHISQ.TEST function to get the p-value for the chi-square independence test, which has the following characteristics:

CHISQ.TEST(actual_range, expected_range)

where:

actual_range = the observed values

expected_range = the expected values

Let’s apply this to our independence test for grades and courses. We will place the observed values in Columns A, B, C, D, and E, and place the expected values in columns G, H, I, J, and K. Then select CHISQ.TEST, as in Figure 2.7.

Figure 2.7

Setting up Excel’s CHISQ.TEST function.

Click OK and fill in the data as in Figure 2.8.

Figure 2.8

Output for Excel’s CHISQ.TEST function.

Cell F1 contains the Excel formula =CHISQ.TEST result as p = 0.013. Since the p-value is less than α, we reject H₀, which is the same conclusion we reached in our grades and courses example. I know you are saying that Excel makes statistics fun and easy, and I agree!

Practice Problems

1. A company believes that the distribution of customer arrivals during the week are as follows:

Day	Expected Percentage of Customers
Monday	10
Tuesday	10
Wednesday	15
Thursday	15
Friday	20
Saturday	30
	Total = 100

  A week was randomly chosen and the number of customers each day was counted. The results were: Monday–31, Tuesday–18, Wednesday–36, Thursday–23, Friday–47, and Saturday–60. Use this sample to test the expected distribution using α = 0.05.

2. An e-commerce site would like to test the hypothesis that the number of hits per minute on their site follows the Poisson distribution with λ = 3. The following data was collected:

Number of Hits Per Minute or More	0	1	2	3	4	5	6	7
Frequency	22	51	72	92	60	44	25	14

  Test the hypothesis using α = 0.01.

3. An English professor would like to test the relationship between an English grade and the number of hours per week a student reads. A survey of 500 students resulted in the following frequency distribution.

  Test the hypothesis using α = 0.05.

4. John Armstrong, salesman for the Dillard Paper Company, has five accounts to visit each day. It is suggested that the random variable, successful sales visits by Mr. Armstrong, may be described by the binomial distribution, with the probability of a successful visit being 0.4. Given the following frequency distribution of Mr. Armstrong’s number of successful sales visits per day, can we conclude that the data actually follows the binomial distribution? Use α = 0.05.

Number of Successful Visits per Day	0	1	2	3	4	5
Observed Frequency	10	41	60	20	6	3

The Least You Need to Know

• The chi-square distribution is not symmetrical but rather has a positive skew. As the number of degrees of freedom increases, the shape of the chi-square distribution becomes more symmetrical.
• The chi-square distribution allows us to perform hypothesis testing on nominal and ordinal data.
• We can use the chi-square distribution to perform a goodness-of-fit test, which uses a sample to test whether a frequency distribution fits a predicted distribution.
• The chi-square test for independence investigates whether a relationship exists between two variables. It does not, however, test the direction of that relationship.