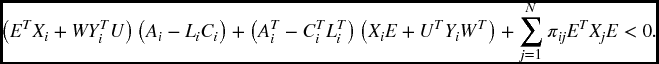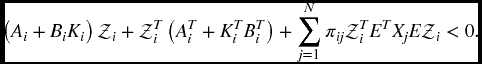2
State Estimation and SMC of Markovian Jump Singular Systems
In this chapter, we are aiming at the investigation of state estimation and SMC problems for Markovian jump singular systems. Although there has been some existing work on the stability analysis of such systems based on the LMI technique, the results are not all of strict LMI form since there are usually some matrix equality constraints. This may cause a lot of trouble in checking the analysis results numerically. Therefore, a natural question is immediately raised: are there any techniques that can release the matrix equality constraints? In this chapter, we extend the approach proposed in [195] to the stability analysis of Markovian jump singular systems, and a new necessary and sufficient stability condition is established in terms of strict LMI. Also, the analysis and synthesis of singular systems have been extensively investigated in the past decades, but little progress has been made toward solving the SMC problem of singular systems. This problem may become difficult and complicated due to the singular matrix E in the systems. Since the rank of E may not be equal to that of B in a simple singular LTI system of In this chapter, a new integral-type sliding surface is designed by taking the singular matrix E into account. Then, by using the integral SMC technique, the sliding mode dynamics described by a Markovian jump singular differential equation can be derived. A necessary and sufficient condition for the stochastic stability of the sliding mode dynamics is presented in terms of strict LMI, by which the sliding surface can be designed. In practice, the system states are not always available owing to the limit of physical conditions or the expense of measuring it. Thus, the estimation problem has become more important in this case. In this chapter, we investigate the state estimation and SMC problems for Markovian jump singular systems with unmeasured states. An observer is first designed to estimate the system states, and then a discontinuous SMC law is synthesized based on feedback of the estimated states, which forces the system state trajectories onto the sliding surface in a finite time. Consider the continuous-time Markovian jump singular system described by
where x(t) ∈ Rn is the state vector; u(t) ∈ Rm is the control input; y(t) ∈ Rp is the measured output. Matrix E ∈ Rn × n may be singular, and we assume that rank(E) = r ≤ n. A( · ), B( · ), and C( · ) are known real matrices with appropriate dimensions. These matrices are functions of rt. Here, let {rt, t ≥ 0} be a continuous-time Markov process which takes values in a finite state space
where Δ > 0 and limΔ → 0o(Δ)/Δ = 0; πij > 0, i ≠ j, and πii = −∑j ≠ iπij for each For each possible value
The following preliminary assumption is made for system (2.3a)–(2.3b). Assumption 2.1 For each Before proceeding, we first consider the unforced system of (2.3a), that is,
Definition 2.2.1 The following lemma provides a necessary and sufficient condition for the stochastic admissibility of the Markovian jump singular system in (2.4). Lemma 2.2.2 [244] The Markovian jump singular system in (2.4) is stochastically admissible if and only if there exist nonsingular matrices Pi such that for
Remark 2.1 Notice that the conditions in Lemma 2.2.2 are not all of strict LMI form due to the matrix equality constraint of (2.5a). This may cause major problems in checking the conditions numerically, since the matrix equality constraint is fragile and is not usually perfectly satisfied. Therefore, the strict LMI conditions are more desirable than non-strict ones from the numerical point of view. ♦ In the section, we propose a strict LMI condition (easy to check by using standard software) of the stochastic admissibility for the Markovian jump singular system in (2.4), and present the following result. Theorem 2.3.1 The Markovian jump singular system in (2.4) is stochastically admissible if and only if there exist matrices Xi > 0, Yi, U, and W such that for
where U ∈ R(n − r) × n and W ∈ Rn × (n − r) are matrices satisfying UE = 0 and EW = 0. Proof. (Sufficiency) Letting Pi≜XiE + UTYiWT, (Necessity) Suppose that the system in (2.4) is stochastically admissible, then there exist nonsingular matrices M and N such that, for each Since the system in (2.4) is regular and impulse free we have that matrices A4i are nonsingular for Then, it follows that
where It follows that there exist matrices Now, let
By Schur complement, (2.10) is equivalent to
where
Furthermore, (2.11) can be rewritten as
Considering (2.7), it follows from (2.12) that
Let
Since which is equivalent to (2.6). This completes the proof. ▀ Remark 2.2 Note that Theorem 2.3.1 presents a new necessary and sufficient condition of stochastic admissibility in terms of strict LMI for the Markovian jump singular system in (2.4), which is less conservative and more useful than Lemma 2.2.2. ♦ In this section, we consider the state estimation and SMC problems for the Markovian jump singular systems with unmeasured states in (2.1a)–(2.1b). First, we design an observer to estimate unmeasured states, and then we design a sliding surface and an SMC law based on the state estimates. The designed observer-based SMC law can drive the system state trajectories onto the predefined sliding surface in a finite time. The following observer is employed to provide the estimates of the unmeasured states for the system in (2.3a)–(2.3b):
where Let Design the following integral switching function:
where Ki ∈ Rm × n are real matrices to be designed such that
is stochastically admissible. The matrices Gi ∈ Rm × n are to be chosen so that GiBi are nonsingular. Design the following state estimate-based SMC law:
where ϵ > 0 is a real constant and
The following theorem shows that the sliding motion in the specified sliding surface s(t) = 0 is attained in a finite time. Theorem 2.4.1 Under the SMC law (2.18), the state trajectories of the observer dynamics (2.14a)–(2.14b) can be driven onto the sliding surface s(t) = 0 in a finite time and remain there in subsequent time. Proof. Choose the following Lyapunov function:
where Zi > 0 are matrices to be specified such that BTiZiBi > 0. Thus, we choose Gi = BTiZi in (2.16), and then GiBi = BTiZiBi > 0 are nonsingular. According to (2.14a)–(2.14b) and (2.16), we have
Substituting (2.18) into (2.19) yields
Thus taking the derivation of V(t) and considering |s(t)| ≥ ‖s(t)‖, we have
where When the system operates in the sliding mode, it follows that s(t) = 0 and Substituting (2.21) into (2.14a), the sliding mode dynamics can be obtained as
In the following, we will analyze the stochastic admissibility of the estimation error dynamics in (2.15). By Theorem 2.3.1, we give the following result. Theorem 2.4.2 The estimation error dynamics in (2.15) is stochastically admissible if and only if there exist symmetric positive definite matrices Xi ∈ Rn × n, nonsingular matrices Yi ∈ R(n − r) × (n − r), and matrices
where U and W are matrices satisfying UE = 0 and EW = 0. Moreover, the parametric matrices Li can be computed by
Proof. According to Theorem 2.3.1, we know that the estimation error dynamics in (2.15) is stochastically admissible if and only if there exist matrices Xi > 0,Yi, U and W such that for Letting Next, we shall analyze the stochastic admissibility of the dynamics in (2.17), and give a solution to parameter Ki. Before proceeding, we give the following lemma. Lemma 2.4.3 Let Xi be symmetric such that ETLXiEL > 0 and matrices Yi are nonsingular, then XiE + UTYiWT are nonsingular and their inverse are expressed as
where Proof. Decompose E as E = ELETR, where EL ∈ Rn × r and ER ∈ Rn × r are of full column rank. Since UE = 0 and EW = 0, thus we have that UEL = 0, ETRW = 0 and According to (2.27), we have
which implies that XiE + UTYiWT are nonsingular and
where
Define Now, according to Theorem 2.3.1, we present the following result without proof. Theorem 2.4.4 The dynamics in (2.17) is stochastically admissible if and only if there exist matrices Xi > 0, Yi, U and W such that for where U ∈ R(n − r) × n and W ∈ Rn × (n − r) are matrices satisfying UE = 0 and EW = 0. The following sufficient condition is proposed for the stochastic admissibility of the dynamics in (2.17), by which the parametric matrices Ki can be solved. Theorem 2.4.5 The dynamics in (2.17) is stochastically admissible if there exist symmetric positive definite matrices where where U and W are matrices satisfying UE = 0 and EW = 0. Moreover, the parametric matrices Ki are given by
Proof. By Theorem 2.4.4 we know that the dynamics in (2.17) is stochastically admissible if there exist matrices Xi > 0 and nonsingular matrices Yi such that (2.29) holds for Letting
Also, the following fact is true:
Considering πii < 0 in (2.2), we have
Therefore, (2.33) holds if the following inequality holds:
where Ψ11i is defined in (2.30). By Schur complement, LMI (2.30) implies inequality (2.34). This completes the proof. ▀ Remark 2.3 Notice from Definition 2.2.1 that the stochastic admissability implies the stochastic stability of a Markovian jump singular system. Thus, we know that the estimation error dynamics in (2.15) is stochastically stable if LMI (2.23) in Theorem 2.4.2 holds. Also, the dynamics in (2.17) is stochastically stable if LMI (2.30) in Theorem 2.4.5 holds. It is not difficult to show from stochastic stability of dynamics (2.15) and (2.17) that the sliding mode dynamics (2.22) is stochastically stable. ♦ Example 2.5.1 Consider the Markovian jump singular system in (2.1a)–(2.1b) with two operating modes, that is, N = 2, and the following parameters:
Our aim is to design an observer in the form of (2.14a)–(2.14b) to estimate the states of system (2.1a)–(2.1b), and then synthesize an SMC law u(t) as (2.18) (based on the state estimate) such that the closed-loop system is stochastically admissible. Solving the LMI condition (2.23) in Theorem 2.4.2 by using LMI Toolbox in the Matlab environment and then by (2.24), we have
However, solving the LMI condition (2.30) in Theorem 2.4.5, and then by (2.31) we have
Here, parameters G1 and G2 in (2.16) are chosen as
Thus, the switching function in (2.16) can be computed as
Let the adjustable parameter ϵ be ϵ = 0.5, then the observer-based SMC law designed in (2.18) can be obtained as
where To prevent the control signals from chattering, we replace sign(si(t)) with
For given initial condition of Figure 2.1 States of the closed-loop system Figure 2.2 Switching function In this chapter, the state estimation and SMC problems have been investigated for continuous-time Markovian jump singular systems with unmeasured states. First, we have proposed a strict LMI necessary and sufficient condition of the stochastic admissibility for the unforced Markovian jump singular systems. Then, an observer has been designed and an observer-based sliding mode controller has been synthesized to guarantee the reachability of the system state trajectories to the predefined integral sliding surface. Finally, a numerical example has been provided to illustrate the effectiveness of the proposed design scheme.2.1 Introduction
![]() , it is difficult to obtain the so-called ‘regular form’ through conventional model transformation approach. As a result, the linear sliding surface is not suitable for singular systems. Therefore, a key issue in the study of this problem is how to design a suitable sliding surface such that the resulting sliding mode dynamics exists.
, it is difficult to obtain the so-called ‘regular form’ through conventional model transformation approach. As a result, the linear sliding surface is not suitable for singular systems. Therefore, a key issue in the study of this problem is how to design a suitable sliding surface such that the resulting sliding mode dynamics exists.2.2 System Description and Preliminaries
![]() , and the generator matrix Π = πij,
, and the generator matrix Π = πij, ![]() with transition probability from mode i at time t to mode j at time t + Δ is given by
with transition probability from mode i at time t to mode j at time t + Δ is given by![]() .
.![]() , A(rt) = Ai, B(rt) = Bi, and C(rt) = Ci. Then, the system (2.1a)–(2.1b) can be described by
, A(rt) = Ai, B(rt) = Bi, and C(rt) = Ci. Then, the system (2.1a)–(2.1b) can be described by
![]() , the pair (Ai, Bi) in (2.3a)–(2.3b) is controllable, the pair (Ai, Ci) is observable, and matrix Bi is full column rank.
, the pair (Ai, Bi) in (2.3a)–(2.3b) is controllable, the pair (Ai, Ci) is observable, and matrix Bi is full column rank.
![]() is not identically zero for each
is not identically zero for each ![]() .
.![]() for each
for each ![]() .
.![]() , there exists a positive scalar T(x0, r0) such that
, there exists a positive scalar T(x0, r0) such that

![]() ,
, 2.3 Stochastic Stability Analysis
![]() ,
,
![]() in (2.6), we can satisfy (2.5a) and (2.5b). Thus, according to Lemma 2.2.2 we know that the continuous Markovian jump singular system in (2.4) is stochastically admissible.
in (2.6), we can satisfy (2.5a) and (2.5b). Thus, according to Lemma 2.2.2 we know that the continuous Markovian jump singular system in (2.4) is stochastically admissible.![]() ,
,
![]() . Thus, we can set
. Thus, we can set

![]()
![]()
![]() . Therefore, it is easy to see that the stochastic stability of system (2.4) implies that the following continuous Markovian jump system is stochastically stable:
. Therefore, it is easy to see that the stochastic stability of system (2.4) implies that the following continuous Markovian jump system is stochastically stable:
![]()
![]() such that, for
such that, for ![]() ,
,

![]() and
and ![]() , thus by (2.9) we have
, thus by (2.9) we have ![]() , where the partitions of N and
, where the partitions of N and ![]() are compatible for algebraic operations. Therefore, for a sufficient small α > 0, we have
are compatible for algebraic operations. Therefore, for a sufficient small α > 0, we have


![]()
![]()
![]()
![]()
![]()
 in (2.13) (obviously, Xi > 0), we have
in (2.13) (obviously, Xi > 0), we have

![]() is of full row rank, it can be written as
is of full row rank, it can be written as ![]() , where
, where ![]() is nonsingular (thus, by (2.8)
is nonsingular (thus, by (2.8) ![]() implies UE = 0). Then, defining
implies UE = 0). Then, defining ![]() and W≜N2 (it is easily seen from (2.7) that EW = EN2 = 0), we have
and W≜N2 (it is easily seen from (2.7) that EW = EN2 = 0), we have

2.4 Main Results
2.4.1 Observer and SMC Law Design
![]() represents the estimate of x(t), and Li ∈ Rn × p are the observer gains to be designed.
represents the estimate of x(t), and Li ∈ Rn × p are the observer gains to be designed.![]() denote the estimation error. Considering (2.3a)–(2.3b) and (2.14a)–(2.14b), the estimation error dynamics is obtained as
denote the estimation error. Considering (2.3a)–(2.3b) and (2.14a)–(2.14b), the estimation error dynamics is obtained as
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() . It can be seen from (2.20) that there exists a time
. It can be seen from (2.20) that there exists a time ![]() such that V(t) = 0, and consequently s(t) = 0, for t ≥ t*, which means that the system state trajectories can reach onto the predefined sliding surface in a finite time. This completes the proof. ▀
such that V(t) = 0, and consequently s(t) = 0, for t ≥ t*, which means that the system state trajectories can reach onto the predefined sliding surface in a finite time. This completes the proof. ▀2.4.2 Sliding Mode Dynamics Analysis
![]() . Thus, by
. Thus, by ![]() in (2.19), we can obtain the equivalent control ueq(t) as
in (2.19), we can obtain the equivalent control ueq(t) as
![]() ,
, ![]() , U ∈ R(n − r) × n, W ∈ Rn × (n − r) such that for
, U ∈ R(n − r) × n, W ∈ Rn × (n − r) such that for ![]() ,
,
![]()
![]() ,
,
![]() and
and ![]() in (2.25) yields (2.23), thus the proof is completed. ▀
in (2.25) yields (2.23), thus the proof is completed. ▀![]() are symmetric matrices and
are symmetric matrices and ![]() are nonsingular matrices with
are nonsingular matrices with
![]()
![]() is nonsingular. Then,
is nonsingular. Then,

![]()
![]()
![]()

![]() and
and ![]() in (2.28), and we have (2.26)–(2.27). This completes the proof. ▀
in (2.28), and we have (2.26)–(2.27). This completes the proof. ▀![]() ,
,
![]() , nonsingular matrices
, nonsingular matrices ![]() , and matrices
, and matrices ![]() ,
, ![]() , U ∈ R(n − r) × n, and W ∈ Rn × (n − r) such that for
, U ∈ R(n − r) × n, and W ∈ Rn × (n − r) such that for ![]() ,
,
![]() and
and

![]() . However, by Lemma 2.4.3, XiE + UTYiWT are nonsingular and their inverse matrices are
. However, by Lemma 2.4.3, XiE + UTYiWT are nonsingular and their inverse matrices are ![]() . Now, performing a congruence transformation to (2.29) by
. Now, performing a congruence transformation to (2.29) by ![]() , we have
, we have
![]() and
and ![]() in (2.32), we have
in (2.32), we have
![]()

![]()
![]()
2.5 Illustrative Example






![]() .
.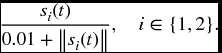
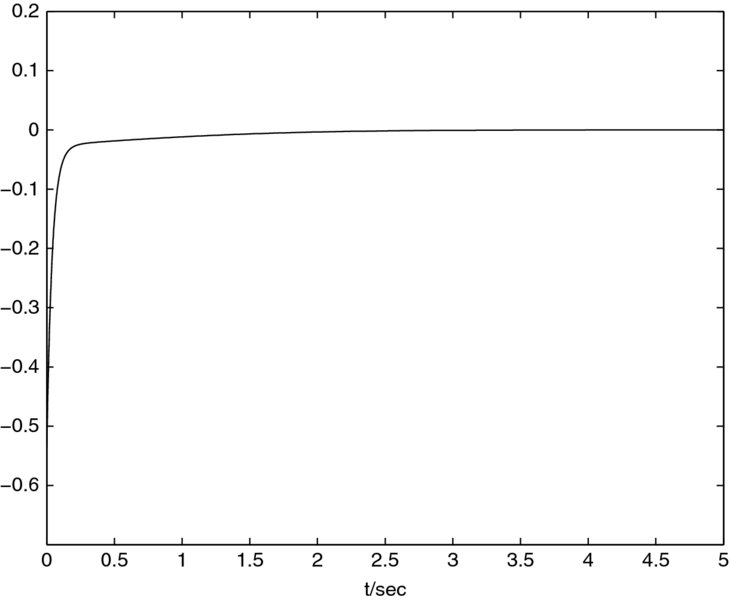
![]() , the simulation results are given in Figures 2.1–2.2. Specifically, in Figure 2.1 shows the states of the closed-loop system, while Figure 2.2 depicts the switching function s(t).
, the simulation results are given in Figures 2.1–2.2. Specifically, in Figure 2.1 shows the states of the closed-loop system, while Figure 2.2 depicts the switching function s(t).
2.6 Conclusion