1
Introduction
1.1 Sliding Mode Control
Sliding mode control (SMC) has proven to be an effective robust control strategy for incompletely modeled or nonlinear systems since its first appearance in the 1950s [70, 103, 197]. One of the most distinguished properties of SMC is that it utilizes a discontinuous control action which switches between two distinctively different system structures such that a new type of system motion, called sliding mode, exists in a specified manifold. The peculiar characteristic of the motion in the manifold is its insensitivity to parameter variations, and its complete rejection of external disturbances [260]. SMC has been developed as a new control design method for a wide spectrum of systems including nonlinear, time-varying, discrete, large-scale, infinite-dimensional, stochastic, and distributed systems [101]. Also, in the past two decades, SMC has successfully been applied to a wide variety of practical systems such as robot manipulators, aircraft, underwater vehicles, spacecraft, flexible space structures, electrical motors, power systems, and automotive engines [60, 77, 199, 259].
In this section, we will first present some preliminary background and fundamental theory of SMC, which will be helpful to some readers who have little or no knowledge on SMC, and then we will give an overview of recent development of SMC methodologies.
1.1.1 Fundamental Theory of SMC
We first formulate the SMC problem as follows. For a general nonlinear system of the form
where x(t) ∈ Rn is the system state vector, u(t) ∈ Rm is the control input. We need to design a sliding surface
where s(x) is called the switching function, and the order of s(x) is usually the same as that of the control input, i.e. s(x) ∈ Rm, and
Then a sliding mode controller ![]() is designed in the form of
is designed in the form of

where u+i(t) ≠ ui+(t), such that the following two conditions hold:
- Condition 1. The sliding mode is reached in a finite time and subsequently maintained, that is, the system state trajectories can be driven onto the specified sliding surface s(x) = 0 by the sliding mode controller in a finite time and maintained there for all subsequent time;
- Condition 2. The dynamics in sliding surface s(x) = 0, that is, the sliding mode dynamics, is stable with some specified performances.
Further consider (1.1) with single input, that is, u(t) ∈ R and s(x) ∈ R, and suppose that the sliding mode can be reached in a finite time, then the solutions of the equation
will approach s(x) = 0 and reach there in a finite time. During the approaching phase, ![]() . Similarly, the solutions of the equation
. Similarly, the solutions of the equation
will also approach s(x) = 0 and reach there in a finite time, thus we have ![]() . To summarize the above analysis, we have
. To summarize the above analysis, we have

or, equivalently,
which is the so-called ‘reaching condition’. This is the condition under which the state will move toward and reach a sliding surface. The system state trajectories under the reaching condition is called the reaching phase [77, 101].
In summary, Condition 1 requires the reachability of a sliding mode, which is guaranteed through designing a sliding mode controller, while Condition 2 requires the sliding mode dynamics to be stable with some specified performances, which is assured by designing an appropriate sliding mode surface. Therefore, a conventional SMC design consists of two steps:
-
Step 1. Design a sliding surface s(x) = 0 such that the dynamics restricted to the sliding surface has the desired properties such as stability, disturbance rejection capability, and tracking;
- Step 2. Design a discontinuous feedback control u(t) such that the system state trajectories can be attracted to the designed sliding surface in a finite time and maintained on the surface for all subsequent time.
In the following, we will briefly introduce some commonly used methods in the design of sliding surfaces and sliding mode controllers, and in the elimination/reduction of chattering. Readers can refer to various books on SMC theory for more details, for example, [60, 77, 197, 199].
Sliding Surface Design
In this section, three kinds of sliding surfaces, namely, linear sliding surface, integral sliding surface, and terminal sliding surface, are introduced.
Linear Sliding Surface
The linear sliding surface, due to its simplicity of implementation, is commonly used in SMC design. There are two approaches to designing linear sliding surface. First, we introduce the ‘regular form’ model transformation approach. Consider the following nonlinear system:
where x(t) ∈ Rn and u(t) ∈ Rm are the system states and control inputs, respectively. f(x, t) ∈ Rn and B(x, t) ∈ Rn × m are assumed to be continuous with bounded continuous derivatives with respect to x. B(x, t) is bounded away from zero at any time.
By applying an appropriate diffeomorphic transformation  , system (1.2) can be written in the following regular form [120]:
, system (1.2) can be written in the following regular form [120]:

where z1(t) ∈ Rn − m and z2(t) ∈ Rm are the transformed system states. ![]() is nonsingular (to ensure this, the matrix B(x, t) should be of full column rank for all t for the existence of such a transformation).
is nonsingular (to ensure this, the matrix B(x, t) should be of full column rank for all t for the existence of such a transformation).
Design a switching function as
where ℏ( · ) is a function to be defined. When the system state trajectories reach onto the sliding surface, we have s(z) = 0, thus z2(t) = −ℏ(z1(t)). Substituting this into the first equation of the regular form yields
which is a reduced-order system representing the sliding mode dynamics. The remaining work of the sliding surface design is to choose a function ℏ( · ) such that the above nonlinear sliding mode dynamics is stable and/or satisfies a specified performance.
For a linear time-invariant (LTI) system of the form
where x(t) ∈ Rn is the system state vector, u(t) ∈ Rm is the control input, and the matrices A ∈ Rn × n and B ∈ Rn × m. The matrix B is assumed to have full column rank and the pair (A, B) is assumed to be controllable.
It is well known that for the controllable system (1.3) there exists a nonsingular transformation, defined by

such that
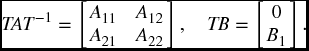
Thus, by z(t) = Tx(t) system (1.3) can be transformed into the following regular form:
where z1(t) ∈ Rn − m and z2(t) ∈ Rm are the transformed system states. A11 ∈ R(n − m) × (n − m), A12 ∈ R(n − m) × m, A21 ∈ Rm × (n − m), A22 ∈ Rm × m, B1 ∈ Rm × m, and B1 is nonsingular.
Now, a sliding surface can be designed under the model of (1.4). For example, we can choose the following linear one:
where C is the design parameter to be designed. Similarly, when the system state trajectories reach onto the sliding surface, that is, s(z) = 0, it follows that
Substituting (1.6) into the first equation of (1.4) yields
The above reduced-order system is the so-called sliding mode dynamics (that is, the motion equation in the sliding surface), which is an autonomous system. Therefore, the design of sliding surfaces becomes choosing the matrix parameter C such that the sliding mode dynamics is stable. Furthermore, since it can be shown that, if the pair (A, B) is controllable, then the pair (A11, A12) is controllable as well, the problem of finding the design matrix C is in fact a classical state feedback problem with matrix C as a feedback gain and A12 as an input matrix. Therefore, all existing linear state feedback control design methods can be used to solve this problem, for example, the conventional eigenvalue allocation method and linear-quadratic regulator (LQR) design method.
There is another approach to linear surface design, named the Lyapunov approach [186]. Let V(x) be a Lyapunov function for system (1.2), that is, V(x) > 0 and ![]() . The sliding surface can be chosen as
. The sliding surface can be chosen as
where

Lemma 1.1.1 [186] System (1.2) with sliding mode on the sliding surface (1.8) is asymptotically stable.
For linear system (1.3), since (A, B) is controllable we know that there exists a feedback matrix K such that ![]() is stabilizable. Thus, there exist matrices P > 0 and Q > 0 such that the following Lyapunov equation holds:
is stabilizable. Thus, there exist matrices P > 0 and Q > 0 such that the following Lyapunov equation holds:
Now, design the sliding surface as
and rewrite system (1.3) as
where ![]() , and Kx is a fictitious feedback to system (1.3).
, and Kx is a fictitious feedback to system (1.3).
Let V(x) = xT(t)Px(t) > 0, and we have
When the system state trajectories are driven onto the sliding surface, that is, s(x) = BTPx(t) = 0, it follows that
for x(t) ≠ 0. Therefore, the system states are asymptotically stable on the sliding surface. Therefore, we have the following lemma.
Lemma 1.1.2 [186] System (1.10) with sliding mode on the sliding surface (1.9) is asymptotically stable.
We can see from Lemmas 1.1.1–1.1.2 that for the Lyapunov approach, the design of sliding surface is given by the positive definite matrix P.
Integral Sliding Surface
In the above-mentioned linear sliding surface design, the order of the resulting sliding mode dynamics is (n − m), with n being the dimension of the state space and m being the dimension of the control input. Unlike in linear sliding surface design, in the integral sliding surface, the order of the sliding motion equation is the same as that of the original system, rather than being reduced by the number of the dimension of the control input. As the result, the robustness of the system can be guaranteed throughout an entire response of the system starting from the initial time instance [198].
Consider system (1.3) with a nonlinear perturbation included in the input channel (called matched perturbation), that is,
where d(x, t) is a nonlinear perturbation with known upper bound d0(x, t), that is, |d(x, t)| < d0(x, t). Design control u(t) = u0(t) + u1(t) for the above system, and suppose that there exists a feedback control law u(t) = u0(t) such that the perturbation-free system, that is, ![]() can be stabilized in a desired way. That is, the state trajectories of the closed-loop system
can be stabilized in a desired way. That is, the state trajectories of the closed-loop system ![]() follow pre-specified reference trajectories with a desired accuracy. Here, u0(t) may be designed through linear static feedback control, such as u0(t) = Kx(t) in which the feedback gain K can be determined by eigenvalue allocation or LQR methods.
follow pre-specified reference trajectories with a desired accuracy. Here, u0(t) may be designed through linear static feedback control, such as u0(t) = Kx(t) in which the feedback gain K can be determined by eigenvalue allocation or LQR methods.
Design the integral switching function as
and C is the parameter matrix to be designed such that CB is nonsingular. Notice that, at t = t0, the switching function ![]() , and hence the reaching phase is eliminated. By (1.11), the resulting sliding mode dynamics coincides with that of the ideal system
, and hence the reaching phase is eliminated. By (1.11), the resulting sliding mode dynamics coincides with that of the ideal system ![]() , which means that the integral sliding surface is robust to the perturbation throughout the entire response of the system starting from the initial time instance.
, which means that the integral sliding surface is robust to the perturbation throughout the entire response of the system starting from the initial time instance.
The approaches to integral sliding surface design were then developed for uncertain systems with mismatched uncertainties/perturbations [27, 30, 32, 43, 170], higher order SMC systems [114, 118], stochastic systems [12, 155, 156, 157, 158], singular systems [219, 221, 223, 225], and switched hybrid systems [125]. For discrete-time SMC systems, the integral sliding surface design approaches were developed in [1, 107, 233].
Terminal Sliding Surface
The terminal SMC technique was first proposed in [201]. Compared to the conventional SMC, the terminal SMC has some superior properties such as fast and finite-time convergence and high steady-state tracking precision.
Consider the second-order linear system

where x1(t) and x2(t) are the system states and u(t) is the control input.
The following terminal switching function is designed:
where p and q are positive odd integers that satisfy p > q.
Similar to the conventional SMC technique, if the system state trajectories are driven onto the sliding surface, that is, s(x1, x2) = 0, then
Let the initial condition of x1(t) at t = 0 be x1(0)( ≠ 0), then the relaxation time t1 for a solution of above equation is
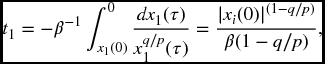
which means that on the terminal sliding surface, the system state trajectories converge to zero in a finite time.
For a high-order single-input single-output (SISO) linear system

the following terminal switching functions are designed:
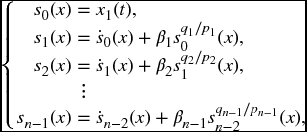
where βi > 0 are constants and pi and qi are positive odd integers satisfying pi > qi, i = 1, 2, …, n − 1.
The terminal SMC technique for multiple-input multiple-output (MIMO) systems was proposed in [141], and then developed in [39, 72, 142].
Sliding Mode Controller Design
Having designed the sliding mode via the design of switching functions, the next step is to design a sliding mode controller such that the system state trajectories can be driven onto the specified sliding surface in a finite time and maintained there for all subsequent time. The main requirement in this step is that the control should be designed to satisfy the reaching condition, thus guaranteeing the existence of a sliding mode on the sliding surface. Additional requirements in this reaching phase include some desired properties such as fast reaching and low chattering. In the following, we will introduce some commonly used methods to the sliding mode controller design.
Equivalent Control Design
Equivalent control is designed in the reaching phase, which can satisfy the reachability of the system state trajectories to the sliding surfaces if the system is free of parameter uncertainties and external disturbances. Consider system (1.2) with switching function being s(x). Suppose that the system state trajectories reach onto the sliding surface at time instant t1 and remain there in the subsequent time. We then have s(x) = 0 for all t > t1. Along sliding mode trajectories, s(x) is constant, and so sliding mode trajectories are described by the differential equation ![]() . Differentiating s(x) yields
. Differentiating s(x) yields

where

is called the gradient of s(x). Here, we suppose that ![]() is nonsingular for all x and t, thus the equivalent control can be solved as follows:
is nonsingular for all x and t, thus the equivalent control can be solved as follows:
Substituting the above equivalent control into the original system, it follows that on the sliding surface s(x) = 0 the system dynamics satisfy
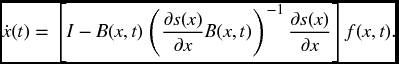
The above differential equation represents the sliding mode dynamics, which is actually is a reduced-order model of order n − m. (Considering s(x) = 0, thus m of the system states can be eliminated from the equation.)
Reaching Condition Approach
A straightforward method of sliding mode controller design is based on the reaching condition, that is, for i = 1, 2, …, m,

or, equivalently,
With the designed controller satisfying the above reachability condition, the tangent vectors of the state trajectories are guaranteed to point toward the sliding surface, hence, the reachability of the system state trajectories to the sliding surface can be guaranteed. Some more discussions of this approach can be found in [101].
Lyapunov Function Approach
The Lyapunov function approach is commonly used in sliding mode controller design. Choosing a Lyapunov function of the form
a sufficient condition for the sliding surface to be globally attractive is that the control u(t) is designed such that
Finite reaching time can be guaranteed by [103]
where ε > 0 is a constant.
For system (1.2), design the sliding mode controller as
where ueq(t) is the equivalent control which is designed in (1.12), and the discontinuous control uN(t) is to be chosen such that

Clearly, this approach leads to the global attraction of the system state trajectories to the sliding surface.
Reaching Law Approach
The reaching law is a differential equation which specifies the dynamics of a switching function, and by the choice of the parameters in the reaching law, the dynamic quality of SMC system in the reaching mode can be controlled [78]. A general form of the reaching law can be described by the differential equation
where
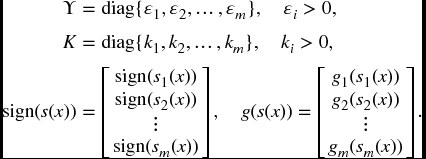
The functions gi(si(x)) satisfy gi(0) = 0 and
Therefore, using reaching law (1.13) directly to system (1.2) with

the sliding mode controller can be obtained as

Equation (1.13) is a general form of the reaching law, and some special cases are
- The constant rate reaching law:

- The constant plus proportional rate reaching law:

- The power rate reaching law:

The reaching law approach not only guarantees the reaching condition but also specifies the dynamic characteristics of the motion during the reaching phase [101, 78].
Chattering Problem
The chattering problem is one of the most common handicaps for applying SMC to real applications. Chattering in SMC systems is usually caused by 1) the unmodeled dynamics with small time constants, which are often neglected in the ideal model; and 2) utilization of digital controllers with finite sampling rate, which causes so called ‘discretization chattering’. Theoretically, the ideal sliding mode implies infinite switching frequency. Since the control is constant within a sampling interval, switching frequency can not exceed that of sampling, which also leads to chattering. From the control engineer’s point of view, chattering is undesirable because it often causes control inaccuracy, high heat loss in electric circuitry, and high wear of moving mechanical parts. In addition, the chattering action may excite the unmodeled high-order dynamics, which probably leads to unforeseen instability. Therefore, a good deal of research work has been reported in literature on the chattering elimination/reduction problem; see for example, [2, 11, 9, 10, 19, 36, 44, 83, 116, 117, 183, 200, 209, 258] and references therein. In the following, we will review some chattering elimination/reduction approaches.
Boundary Layer Approach
Roughly speaking, an SMC law consists of two parts, that is, u(t) = ueq(t) + uN(t). The continuous control ueq(t), known as the equivalent control, controls the system when its states are on the sliding surface, and the discontinuous control uN(t) handles the system uncertainties. Since the discontinuous control uN(t) will switch between two structures during operation, the SMC system will undergo oscillation near the sliding surface. A commonly used method to alleviate chattering is to insert a boundary layer near the sliding surface so that a continuous control replaces the discontinuous one when the system is inside the boundary layer [52, 183, 196]. For this purpose, the discontinuous controller of
is often replaced by the saturation control of

or
for some, preferably small, δ > 0.
The boundary layer approach has been utilized extensively in practical applications. However, this method has some disadvantages such as: 1) it may give a chattering-free system but a finite steady-state error must exist; 2) the boundary layer thickness has a trade-off relation between control performance of SMC and chattering migration; and 3) within the boundary layer, the characteristics of robustness and accuracy of the system are no longer assured.
Dynamic SMC Approach
The second way to eliminate chatter is the dynamic SMC approach [9, 10, 36]. The main idea of this method is to insert an integrator (or any other strictly proper low-pass filter) between the SMC and the controlled plant, see Figure 1.1. The time derivative of the control input, ![]() , is treated as the new control input for the augmented system (including the original system and the integrator). Since the low-pass integrator in Figure 1.1 filters out the high frequency chattering in w, the control input to the real plant u = ∫wdt becomes chattering free [36].
, is treated as the new control input for the augmented system (including the original system and the integrator). Since the low-pass integrator in Figure 1.1 filters out the high frequency chattering in w, the control input to the real plant u = ∫wdt becomes chattering free [36].

Figure 1.1 Dynamic sliding mode control
Chattering reduction using the dynamic SMC approach is achieved by using an integrator, and the property of perfect disturbance rejection is guaranteed (no boundary layer is used in the controller). Such a method can eliminate chattering and ensure zero steady-state error; however, the system order is increased by one and the transient responses will be degraded [209].
Reaching Law Approach
Another way of reducing chattering is to decrease the amplitude of the discontinuous control. However, the robustness property of the controller is affected, and the transient performance of the system will also be degraded. There is a trade-off between the chattering reduction and the robustness property. A compromise approach is to decrease the amplitude of the discontinuous control when the system state trajectories are near to the sliding surface (to reduce the chattering), and to increase the amplitude when the system states are not near to the sliding surface (to guarantee the robustness to system uncertainties and unmodeled dynamics). This can be implemented by tuning the parameters of the reaching law
where ϵi and ki, i = 1, 2, …, m, are positive parameters to be tuned. When the system state trajectories are closed to the sliding surface, we have si(x, t) ≈ 0 and ![]() . Here, the parameter ϵi represents the reaching velocity. By choosing ϵi small, the momentum of the motion will be reduced as the system state trajectories approach the sliding surface. As a result, the amplitude of the chattering will be reduced. However, in this case, the transient performance of the system is also degraded. To guarantee the transient performance, a large value for the parameter ki should be chosen to increase the reaching rate when the state is not near the sliding surface.
. Here, the parameter ϵi represents the reaching velocity. By choosing ϵi small, the momentum of the motion will be reduced as the system state trajectories approach the sliding surface. As a result, the amplitude of the chattering will be reduced. However, in this case, the transient performance of the system is also degraded. To guarantee the transient performance, a large value for the parameter ki should be chosen to increase the reaching rate when the state is not near the sliding surface.
Apart from the above-mentioned chattering elimination/reduction approaches, there have been some others, which can be found in [2, 11, 19, 44, 83, 116, 117, 200, 258].
1.1.2 Overview of SMC Methodologies
Due to its simplicity and robustness against parameter variations and disturbances, SMC has been studied extensively for many kinds of systems such as uncertain systems, time-delay systems, stochastic systems, parameter-switching systems, and singular systems. Many important SMC methodologies have been reported in literature. Here, we review some recently developed results in this area.
SMC of Uncertain Systems
Uncertainties exist in all practical physical systems, and the robust control, as a branch of control theory, is invented to explicitly deal with system uncertainties and to achieve robust performance and/or stability for controlled systems. SMC, as one of the robust control strategies, is well known for its strong robustness to system uncertainties in sliding motion. However, the uncertainties should satisfy the so-called ‘matching’ condition, that is, the uncertainties act within channels implicit in the control input. If a system has mismatched uncertainties in the state matrix or/and the input matrix, the conventional SMC approaches are not directly applicable. Therefore, in the past two decades, many researchers have investigated the SMC of uncertain systems with mismatched uncertainties/disturbances – see for example [31, 40, 41, 43, 112, 193] and references therein. To mention a few, in [112], the SMC of uncertain second-order single-input systems with mismatched uncertainties, was considered; in [40, 193], the authors investigated the SMC design for uncertain systems, in which the uncertainties are mismatched and exist only in state matrix. The related approaches were then developed in [41, 43] to deal with a more complicated case that the mismatched uncertainties are involved in not only the state matrix but also the input matrix. In addition, the integral SMC techniques were extensively used to deal with uncertain systems with mismatched uncertainties – see for example, [27, 30, 43, 170, 233] – and some other SMC approaches to deal with uncertain systems can be found in [65, 108, 172, 194, 229].
SMC of Time-Delay Systems
It is well known that time delays appear commonly in various practical systems, such as communication, electronic, hydraulic, and chemical processes. Their existence can introduce instability, oscillation, and poor performance [168]. Time-delay systems have continuously been receiving considerable attention over the past decades. The main reason is that many processes include after-effect phenomena in their inner dynamics, and engineers need their models to approximate the real processes more accurately due to the ever-increasing expectations of dynamic performance. Stability analysis is a fundamental and vital issue in studying time-delay systems, and the conservativeness of a stability condition is an important index to evaluate a stability result. Several methods have been proposed to develop delay-dependent stability conditions (which have less conservativeness compared to delay-independent ones), such as the model transformation approach (based on Newton–Leibniz formula) [121, 110], the descriptor system approach [74], the slack matrix approach [228, 243], the delay partitioning approach [86], and the input-output method (based on the small gain theorem) [88]. There have been a number of excellent survey papers on the stability analysis of time-delay systems – see for example, [168, 246]. SMC of time-delay systems have also been receiving considerable attention over the past decades – see for example, [69, 75, 85, 91, 120, 123, 160, 162, 212, 234, 250] and the references therein. To mention a few, El-Khazali in [69] proposed an output feedback robust SMC for uncertain time-delay systems, and the delay variables were considered as external perturbation when designing the sliding surface; Fridman et al. in [75] presented a descriptor approach to SMC of systems with time-varying delays; Xia and Jia in [234] considered the SMC of time-delay systems with mismatched parametric uncertainties by using a delay-independent approach and the LMI technique; Yan in [250] studied the SMC of uncertain time-delay systems with a class of nonlinear inputs by using a delay-dependent approach; Wu et al. in [212] investigated a sliding mode observer design and an observer-based SMC for a class of uncertain nonlinear neutral delay systems; Han et al. in [91] addressed the SMC design for time-varying input-delayed systems by using a singular perturbation approach.
SMC of Stochastic Systems
Stochastic systems and processes have come to play an important role in many fields of science, engineering, and economics. Thus, stochastic systems have received considerable attention, in which the stochastic differential equations are the most useful stochastic models with extensive applications in aeronautics, astronautics, chemical or process control system, and economic systems. A great number of methods and techniques have been developed for stochastic systems governed by Itô stochastic differential equations – see for example, [144, 145, 240, 241]. SMC design scheme for stochastic systems has also been developed – see for example, [8, 12, 13, 33, 98, 99, 155, 156, 158] and references therein. In [33], based on the concept of SMC, the steady-state covariance assignment problem was investigated for perturbed stochastic multivariable systems. The robust integral SMC and the robust sliding mode observer were designed for uncertain stochastic systems with time-varying delay in [155, 156], respectively. In [98], SMC of nonlinear stochastic systems was addressed by using a fuzzy approach. In [158], by utilizing the ![]() disturbance attenuation technique, a novel SMC method was proposed for nonlinear stochastic systems. In [8], a covariance control scheme was proposed for stochastic uncertain multivariable systems via SMC strategy. In [99], a robust SMC design scheme was developed for discrete-time stochastic systems with mixed time delays, randomly occurring uncertainties, and randomly occurring nonlinearities.
disturbance attenuation technique, a novel SMC method was proposed for nonlinear stochastic systems. In [8], a covariance control scheme was proposed for stochastic uncertain multivariable systems via SMC strategy. In [99], a robust SMC design scheme was developed for discrete-time stochastic systems with mixed time delays, randomly occurring uncertainties, and randomly occurring nonlinearities.
SMC of Parameter-Switching Hybrid Systems
The parameter-switching hybrid system, which is the main plant considered in this book, consists of two types: Markovian jump systems and switched hybrid systems. Parameter-switching systems have received considerable research attention in the past two decades – see for example, [53, 131, 136] – since such systems are capable of modeling a wide range of practical systems that are subject to abrupt variations in their structures, owing to random failures or repairs of components, sudden environmental disturbances, changing subsystem interconnections, abrupt variations, and so on. An overview of the development of uncertain parameter-switching hybrid systems is presented in Section 1.12, from which we can see that the study on such systems, including the problems of stability analysis, stabilization, optimal control, filtering and model reduction, have been fully developed. However, SMC of parameter-switching hybrid systems, as a relatively new problem, has had only limited attention, and further research in this area is needed. There have been some results reported in the literature – see for example, [34, 35, 125, 135, 157, 178, 210, 224, 227] and references therein. More recently, for Markovian jump systems, Shi et al. in [178] presented an SMC design scheme by designing a linear mode-dependent sliding surface; Niu et al. in [157] investigated the SMC of Markovian stochastic systems by designing an integral mode-dependent sliding surface; Ma and Boukas in [135] proposed a singular system approach to robust sliding mode control for uncertain Markovian jump systems; Chen et al. in [35] developed an adaptive SMC for stochastic Markovian jump systems with actuator degradation. For switched hybrid systems, Wu and Lam in [210] proposed a linear mode-independent sliding surface in designing SMC for switched hybrid systems with time delay, and then the results were developed to deal with the SMC design problem for switched stochastic systems in [224]. Wu et al. in [227] investigated the dissipativity-based SMC design for switched stochastic systems, in which an integral mode-dependent sliding surface was designed such that the sliding motion is strictly dissipative.
Output Feedback SMC
The conventional implementation of SMC schemes is usually based on state feedback, which requires the assumption that all the state variables of the controlled systems are completely accessible for feedback. Such an assumption, however, is not always valid in practice since some state components cannot be measured. Roughly, there are two commonly used methods to deal with the controller design in the case that the system state components are not fully accessible. One approach is first to design an observer or a filter to estimate the immeasurable state components, and then synthesize an observer-based sliding mode controller – see for example, [154, 184, 212, 252]. However, the observer-based SMC scheme will require more hardware and will increase system dimension. The other approach is to design a feedback controller by using the measurable output information, which is called the output feedback SMC approach.
During the past two decades, output feedback SMC approaches have been intensively studied, and many important results have been reported in the literature – see for example, [32, 42, 48, 61, 62, 63, 64, 68, 90, 113, 163, 253, 263] and references therein. To mention a few, output feedback SMC design for uncertain dynamic systems was investigated in [263], and an algorithm for output-dependent hyperplane design was proposed based upon eigenvector methods. The eigenvalue assignment approach was proposed in [68] to design the sliding surface of the output feedback SMC scheme. The LMI technique was applied to output feedback SMC design in [62, 63]. Output feedback SMC design for state-delayed systems was investigated in [90, 253]. The above-mentioned results are all for static output feedback (SOF) SMC problems. In fact, output feedback control has two different forms: the SOF control and dynamic output feedback (DOF) control. Generally speaking, DOF control is more flexible than SOF control since the additional dynamics of the controller is introduced. Although DOF control involves more design parameters, for linear systems the closed-loop system can usually be written in a more compact form where certain parameters can be embedded into augmented matrix variables. Compared to the SOF SMC design, the DOF SMC design problem has received less attention, and only a few results have been reported, for example, in [32, 163] the DOF SMC was studied for MIMO linear systems with mismatched norm-bounded uncertainties and matched nonlinear disturbances.
1.2 Uncertain Parameter-Switching Hybrid Systems
1.2.1 Analysis and Synthesis of Switched Hybrid Systems
Switched systems form a class of hybrid systems consisting of a family of subsystems described by continuous- or discrete-time dynamics, and a rule specifying the switching among them [129, 191]. The switching rule in such systems is usually considered to be arbitrary. Switched systems have received increasing attention in the past few years, since many real-world systems such as, chemical processes, transportation systems, computer-controlled systems, and communication industries can be modeled as switched systems [131]. More importantly, many intelligent control strategies are designed based on the idea of controllers switching to overcome the shortcomings of the traditionally used single controller and to improve their performance, thus making the corresponding closed-loop systems into switched systems.
Switched hybrid systems with all subsystems described by linear differential or difference equations are called switched linear hybrid systems. A continuous-time switched linear system can be modeled as
where x(t) ∈ Rn is the state vector; u(t) ∈ Rm is the control input; {(A(α(t)), B(α(t))): . ![]() is a family of matrices parameterized by an index set
is a family of matrices parameterized by an index set ![]() and
and ![]() is a piecewise constant function of time t called a switching signal. At a given time t, the value of α(t), denoted by α for simplicity, might depend on t or x(t), or both, or may be generated by any other hybrid scheme. Therefore, the switched hybrid system effectively switches among N subsystems with the switching sequence controlled by α(t). It is assumed that the value of α(t) is unknown a priori, but its instantaneous value is available in real time.
is a piecewise constant function of time t called a switching signal. At a given time t, the value of α(t), denoted by α for simplicity, might depend on t or x(t), or both, or may be generated by any other hybrid scheme. Therefore, the switched hybrid system effectively switches among N subsystems with the switching sequence controlled by α(t). It is assumed that the value of α(t) is unknown a priori, but its instantaneous value is available in real time.
Similarly, a discrete-time switched linear hybrid system can be described by
where x(k) ∈ Rn is the state vector; u(k) ∈ Rm is the control input; {(A(α(k)), B(α(k))): . ![]() is a family of matrices parameterized by an index set
is a family of matrices parameterized by an index set ![]() , and
, and ![]() is a piecewise constant function of time, called a switching signal, which takes its values in the finite set
is a piecewise constant function of time, called a switching signal, which takes its values in the finite set ![]() . At an arbitrary discrete time k, the value of α(k), denoted by α for simplicity, might depend on k or x(k), or both, or may be generated by any other hybrid scheme.
. At an arbitrary discrete time k, the value of α(k), denoted by α for simplicity, might depend on k or x(k), or both, or may be generated by any other hybrid scheme.
Stability of Switched Hybrid Systems
The stability analysis of switched hybrid systems is a fundamental issue for the synthesis of such systems. Note that there are two facts related with the stability of switched hybrid systems: 1) a switched hybrid system may have divergent trajectories even when all the subsystems are stable; and 2) a switched hybrid system may have convergent trajectories even when some of the subsystems are unstable. These two facts show that the stability of a switched hybrid system depends not only on the dynamics of each subsystem but also on the properties of the switching signals.
When focusing on stability analysis of switched hybrid systems, there are many valuable results that have appeared in the past two decades, and interested readers may refer to survey papers, such as [53, 128, 131, 148], and books, such as [129, 191]. In the following, we will briefly overview some recently developed results.
Arbitrary Switching
We first consider the stability analysis of the switched hybrid systems without any restrictions on switching signal, that is, the switching is arbitrary. Several approaches have been reported on the stability analysis of switched hybrid systems with arbitrary switching, for example:
- Common Quadratic Lyapunov Functions. For the stability analysis problem of switched hybrid systems under arbitrary switching, it is necessary to require that all the subsystems are asymptotically stable. However, even when all the subsystems of a switched system are exponentially stable, the stability of the switched hybrid system still can not be guaranteed [129]. Therefore, in general, all subsystems’ stability assumptions are not sufficient to ensure stability for the switched systems under arbitrary switching. On the other hand, if there exists a common quadratic Lyapunov function (CQLF) for all the subsystems, then the stability of the switched system is guaranteed under arbitrary switching. Generally speaking, the existence of a CQLF is only sufficient for the asymptotic stability of linear switched hybrid systems under arbitrary switching, and could be rather conservative. For the switched linear system
 with the parameter matrices A(α(t)) replaced by A(i) denoting that the ith subsystem is activated, by constructing a CQLF as V(x) = xT(t)Px(t) where P > 0, it can be shown that the switched linear system is asymptotically stable if there exists a positive definite symmetric matrix P such that
with the parameter matrices A(α(t)) replaced by A(i) denoting that the ith subsystem is activated, by constructing a CQLF as V(x) = xT(t)Px(t) where P > 0, it can be shown that the switched linear system is asymptotically stable if there exists a positive definite symmetric matrix P such that

For discrete-time switched linear system x(k + 1) = A(α(k))x(k), it is asymptotically stable if there exists a positive definite symmetric matrix P such that
The above stability results are both expressed in the form of LMIs, which can be tested easily by using standard software such as the LMI Toolbox in Matlab [25]. In [127], a sufficient condition was presented for asymptotic stability of a switched linear system in terms of Lie algebra generated by the individual matrices. Namely, if this Lie algebra is solvable, then the switched system is exponentially stable for arbitrary switching. In [146], a stability criterion was proposed for switched nonlinear systems which involves Lie brackets of the individual vector fields but does not require that these vector fields commute. However, the stability conditions are both only sufficient conditions, not necessary and sufficient ones. In [180], some necessary and sufficient conditions were proposed for the existence of a CQLF for two stable second-order LTI systems, and then the related results were extended for a set of stable LTI systems in [181, 182]. In [109], the authors studied a singularity test for the existence of CQLF for pairs of stable LTI systems, and some necessary and sufficient algebraic conditions were given. A necessary and sufficient condition for the existence of a common Lyapunov function for all subsystems was proposed in [128] for a switched hybrid system under arbitrary switching. A considerable number of approaches to construct such a CQLF were presented in [159]. - Switched Quadratic Lyapunov Functions. Since the existence conditions of a CQLF are conservative for all subsystems of a switched hybrid system with arbitrary switching, some attention has been paid to a less conservative class of Lyapunov functions, namely switched quadratic Lyapunov functions (SQLF). By using the SQLF, the values of such a Lyapunov function still decrease at the switching instants – see Figure 1.2. Compared with the CQLF, the SQLF contains the switching information (mode-dependent), and a typical form of such Lyapunov function can be constructed as V(x) = xT(t)P(α(t))x(t) for continuous-time switched systems or V(x) = xT(k)P(α(k))x(k) for discrete-time switched systems, where
 are mode-dependent. Using an SQLF approach, the stability analysis condition for the discrete-time switched linear system x(k + 1) = A(α(k))x(k) can be formulated as: it is asymptotically stable if there exist positive definite symmetric matrices
are mode-dependent. Using an SQLF approach, the stability analysis condition for the discrete-time switched linear system x(k + 1) = A(α(k))x(k) can be formulated as: it is asymptotically stable if there exist positive definite symmetric matrices  such that
such that
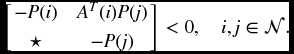
The above stability analysis result based on the SQLF approach will turn out to be the above-mentioned one with the CQLF approach if
 . Obviously, the SQLF approach is less conservative than the CQLF approach. Some results on the SQLF approach to stability analysis and control synthesis for switched hybrid systems can be found in [46, 71].
. Obviously, the SQLF approach is less conservative than the CQLF approach. Some results on the SQLF approach to stability analysis and control synthesis for switched hybrid systems can be found in [46, 71].
Restricted Switching
Stability analysis approaches for arbitrary switching have been developed, but a natural question may still be raised, that is, can switched hybrid systems be stable under some restricted switchings in spite of the fact that they fail to preserve stability under arbitrary switching? If so, what kinds of restrictions should be put on the switching signals to guarantee the stability of switched hybrid systems? To answer such questions, there have been some stability analysis approaches for switched hybrid systems under restricted switching, for example,
- Dwell Time Approach. Recently, there has been enormous growth of interest in using the dwell time approach to deal with stability analysis of switched hybrid systems – see for example, [92, 93, 102, 149, 151, 165, 188, 215, 216, 217, 219, 220, 264, 265]. A positive constant Td ∈ R is called the dwell time of a switching signal if the time interval between any two consecutive switchings is no smaller than Td. The basic idea of the dwell time approach can be formulated as follows: given a dwell time, and let
 denote the set of all switching signals with interval between consecutive discontinuities not smaller than Td, it has been shown that one can pick Td sufficiently large such that the switched system considered is exponentially stable for any switching signal belonging to
denote the set of all switching signals with interval between consecutive discontinuities not smaller than Td, it has been shown that one can pick Td sufficiently large such that the switched system considered is exponentially stable for any switching signal belonging to  . The dwell time approach was used to analyze the local asymptotic stability of nonlinear switched systems. Subsequently, this concept was extended and the average dwell time approach was developed [92], which means that the average time interval between consecutive switchings is no less than a specified constant Ta. Specifically, a positive constant Ta is called an average dwell time for a switching signal α(t) if
. The dwell time approach was used to analyze the local asymptotic stability of nonlinear switched systems. Subsequently, this concept was extended and the average dwell time approach was developed [92], which means that the average time interval between consecutive switchings is no less than a specified constant Ta. Specifically, a positive constant Ta is called an average dwell time for a switching signal α(t) if

For any T2 > T1 ≥ 0, let Nα(T1, T2) denote the number of switching of α(t) over (T1, T2). Here, Ta is called an average dwell time and N0 is the chatter bound. It has been proved in [92] that if all the subsystems are exponentially stable then the switched hybrid system remains exponentially stable provided that the average dwell time Td is sufficiently large. By using the average dwell time approach, Zhai et al. in [264] investigated the disturbance attenuation properties of continuous-time switched hybrid systems, and then the exponential stability and ℓ2 gain properties for discrete-time switched hybrid systems was investigated in [265]; Sun et al. in [188] studied the exponential stability and weighted
 -gain for switched delay systems; Wu and Lam in [215] considered the filtering problem of switched hybrid systems with time-varying delay. As well as the above-mentioned results, the model reduction problem for switched hybrid systems with time-varying delay was addressed in [219] by using the average dwell time approach incorporated with a piecewise Lyapunov function; and the DOF controller design problem was considered in [216, 217].
-gain for switched delay systems; Wu and Lam in [215] considered the filtering problem of switched hybrid systems with time-varying delay. As well as the above-mentioned results, the model reduction problem for switched hybrid systems with time-varying delay was addressed in [219] by using the average dwell time approach incorporated with a piecewise Lyapunov function; and the DOF controller design problem was considered in [216, 217]. - Multiple Lyapunov Functions Approach. By using the Lyapunov function approach to the stability analysis of switched hybrid systems, the above-mentioned CQLF and SQLF approaches require that the Lyapunov functions are globally monotonically decreasing as with the state trajectories. This is, however, conservative since such Lyapunov functions may not exist for all subsystems of switched hybrid systems. For such cases, one can construct a set of Lyapunov-like functions, which only require non-positive Lie-derivatives for certain subsystems in certain regions of the state space, instead of being negative globally. Multiple Lyapunov functions (MLF), is a non-traditional Lyapunov stability approach, and the key point of the method is the non-increasing requirement on any Lyapunov function over the exiting (switch from) or starting (switch to) time sequences of the corresponding subsystem [94, 128, 148, 164]. Specifically, the Lyapunov-like function is selected for each subsystem, and the values of the Lyapunov-like function at the exiting (the starting) instant of the next running interval are smaller than that of the current running interval, then the energy of the Lyapunov-like functions are decreasing globally. There are several versions of MLF results in the literature, for example, Case 1: the Lyapunov-like function is decreasing when the corresponding mode is active and does not increase its value at each switching instant [53] – see Figure 1.3 – and in this case, the switched hybrid system is asymptotically stable; Case 2: the value of the Lyapunov-like function at every exiting instant is smaller than its value at the previous exiting time, then the switched system is asymptotically stable [26] – see Figure 1.4. Case 3: the Lyapunov-like function may increase its value during a time interval, only if the increment is bounded by certain kind of continuous functions [257] – see Figure 1.5 – and in this case, the switched system can remain stable.
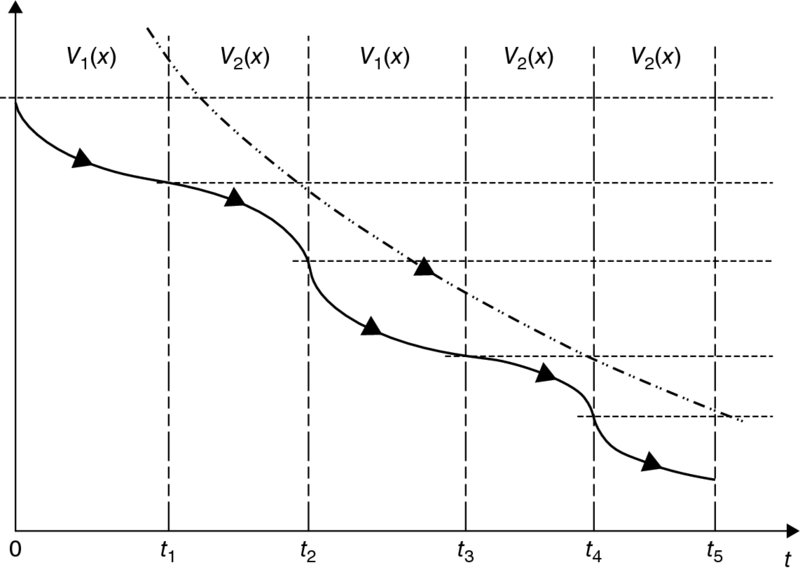
Figure 1.2 Switched quadratic Lyapunov functions

Figure 1.3 Multiple Lyapunov stability (Case 1: the values of Lyapunov-like functions at the switching instants form a monotonically decreasing sequence)

Figure 1.4 Multiple Lyapunov stability (Case 2: the values of Lyapunov-like function for each subsystem at every exiting instant form a monotonically decreasing sequence)

Figure 1.5 Multiple Lyapunov stability (Case 3: the Lyapunov-like function for each subsystem increases its value during a certain period)
Synthesis of Switched Hybrid Systems
Over the past several decades, considerable interest has been devoted to synthesis problems of switched hybrid systems, including stabilization, robust/optimal control, state estimation/ filering, fault detection, model approximation, and so on. Here, we will review some relevant literature on the synthesis of switched hybrid systems. First, we introduce two important properties of switched hybrid systems, namely, the controllability and the observability. Roughly speaking, the concept of controllability denotes the ability to move a system around in its entire configuration space using only certain admissible manipulations. Observability is a measure for how well internal states of a system can be inferred by knowledge of its external outputs. Observability and controllability are dual aspects of the same problem. Some results on the controllability and the observability analysis for switched hybrid systems were reported in [16, 37, 105, 132, 166, 185, 189, 206, 235, 236, 270] and references therein.
In the previous section, we discussed the stability properties of switched hybrid systems. As mentioned earlier, the stability of a switched hybrid system depends not only on the dynamics of each subsystem but also on the properties of the switching signals, thus the synthesis problems include two strategies for implementation. The first is based on the subsystems’ dynamics with given switching signals, and the second is based on the switching signals. The stabilization problem for switched hybrid systems was investigated in [4, 6, 14, 38, 45, 46, 79, 84, 95, 100, 102, 124, 130, 140, 143, 190, 192, 222, 237, 247, 249, 267] and references therein.
Over the past decade, considerable attention has been paid to robust and optimal control problems for switched hybrid systems, and many important results have been reported – see for example, [17, 47, 51, 67, 80, 81, 106, 126, 138, 153, 161, 171, 217, 216, 232, 248, 264, 268] and references therein. To mention a few, Geromel et al. in [81] considered the passivity analysis and controller design problems; Kamgarpour and Tomlin in [106] studied the optimal control problem for non-autonomous switched systems with a fixed mode sequence; Lian and Ge in [126] addressed robust ![]() output tracking control for switched systems under asynchronous switching; Mahmoud in [138] proposed a generalized
output tracking control for switched systems under asynchronous switching; Mahmoud in [138] proposed a generalized ![]() control design approach for discrete-time switched systems with unknown delays; Niu and Zhao in [153] used the average dwell time approach to the robust
control design approach for discrete-time switched systems with unknown delays; Niu and Zhao in [153] used the average dwell time approach to the robust ![]() control problem for a class of uncertain nonlinear switched systems; Orlov in [161] presented finite time stability analysis and robust control synthesis methods for uncertain switched systems; Seatzu et al. in [171] studied the optimal control problem for continuous-time switched affine systems. The above-mentioned results are all based on state feedback control, and the output feedback control problem was also investigated – see for example, [51, 67, 80, 216, 217]. In addition, SMC design methodologies for switched hybrid systems were proposed in [210, 224, 227, 262].
control problem for a class of uncertain nonlinear switched systems; Orlov in [161] presented finite time stability analysis and robust control synthesis methods for uncertain switched systems; Seatzu et al. in [171] studied the optimal control problem for continuous-time switched affine systems. The above-mentioned results are all based on state feedback control, and the output feedback control problem was also investigated – see for example, [51, 67, 80, 216, 217]. In addition, SMC design methodologies for switched hybrid systems were proposed in [210, 224, 227, 262].
It is well known that one of the fundamental problems in control systems and signal processing is the estimation of the state variables of a dynamical system through available noisy measurements, which is referred to as the filtering problem. The celebrated Kalman filter has been considered as the best possible (optimal) estimator for a large class of systems; it is an algorithm that uses a series of measurements observed over time, containing noise (random variations) and other inaccuracies, and produces estimates of unknown variables that tend to be more precise than those based on a single measurement alone. The Kalman filter for switched discrete-time linear systems was designed in [3]. However, the application of the Kalman filter is subject to two initial assumptions: the underlying system is linear with complete knowledge of the dynamical model, and the noise concerned is white/colored with known spectral density. Thus the Kalman filtering scheme is no longer applicable when a priori information on the external noises is not precisely known. Therefore, the past two decades have witnessed significant progress on robust filtering involving various approaches such as ![]() filtering,
filtering, ![]() filtering,
filtering, ![]() -
-![]() filtering, and mixed
filtering, and mixed ![]() /
/![]() filtering. The robust filtering problem for switched hybrid systems has also been developed over the past decade – see for example, [50, 137, 139, 167, 202, 215, 216, 272] and references therein. To mention a few important robust filtering results for switched hybrid systems, Deaecto et al. in [50] developed a trajectory-dependent filter design approach for discrete-time switched linear systems; Mahmoud in [137] presented a delay-dependent
filtering. The robust filtering problem for switched hybrid systems has also been developed over the past decade – see for example, [50, 137, 139, 167, 202, 215, 216, 272] and references therein. To mention a few important robust filtering results for switched hybrid systems, Deaecto et al. in [50] developed a trajectory-dependent filter design approach for discrete-time switched linear systems; Mahmoud in [137] presented a delay-dependent ![]() filter design approach for a class of discrete-time switched systems with state delay; Qiu et al. in [167] investigated the robust mixed
filter design approach for a class of discrete-time switched systems with state delay; Qiu et al. in [167] investigated the robust mixed ![]() /
/![]() filtering design for discrete-time switched polytopic linear systems; Wang et al. in [202] addressed the
filtering design for discrete-time switched polytopic linear systems; Wang et al. in [202] addressed the ![]() filtering problem for discrete-time switched systems with state delays via switched the Lyapunov function approach; Wu and Lam in [215] proposed an average dwell time approach to the weighted
filtering problem for discrete-time switched systems with state delays via switched the Lyapunov function approach; Wu and Lam in [215] proposed an average dwell time approach to the weighted ![]() filter design for switched systems with time-varying delay; Wu and Ho in [216] developed a reduced-order
filter design for switched systems with time-varying delay; Wu and Ho in [216] developed a reduced-order ![]() -
-![]() filter design scheme for a class of nonlinear switched stochastic systems.
filter design scheme for a class of nonlinear switched stochastic systems.
The issues of fault detection and isolation are increasingly required in various kinds of practical complex systems for guaranteeing reliability and pursuing performance. Hence, how to develop effective methods for timely and accurate diagnosis of faults becomes a crucial problem. To combat this, many significant schemes have been introduced, such as model-based approaches and knowledge-based methods. Among them, the model-based approach is the most favored. The basic idea of model-based fault detection is to construct a residual signal and, based on this, determine a residual evaluation function to compare with a predefined threshold. When the residual evaluation function has a value larger than the threshold, an fault alarm is generated. Since accurate mathematical models are not always available, the unavoidable modeling errors and external disturbances may seriously affect the performance of model-based fault detection systems. Thus, the designed fault detection systems should be both sensitive to faults and suppressive to external disturbances. Fortunately, the ![]() fault detection filter or observer is known to be able to do a good job of achieving the above-mentioned requirements. The
fault detection filter or observer is known to be able to do a good job of achieving the above-mentioned requirements. The ![]() fault detection problem for switched hybrid systems was studied in [203, 261], and some other approaches can be found in [15, 49, 119]. Fault-tolerant control is a related issue that makes it possible to develop a control feedback that allows the required system performance to be maintained in the case of faults. The fault-tolerant control problem for switched hybrid systems has also been investigated: for example, Du et al. in [59] proposed an active fault-tolerant controller design scheme for switched systems with time delay; Li and Yang in [119] developed a simultaneous fault detection and control technique for switched systems under asynchronous switching; Wang et al. in [205] designed a robust fault-tolerant controller for a class of switched nonlinear systems in lower triangular form.
fault detection problem for switched hybrid systems was studied in [203, 261], and some other approaches can be found in [15, 49, 119]. Fault-tolerant control is a related issue that makes it possible to develop a control feedback that allows the required system performance to be maintained in the case of faults. The fault-tolerant control problem for switched hybrid systems has also been investigated: for example, Du et al. in [59] proposed an active fault-tolerant controller design scheme for switched systems with time delay; Li and Yang in [119] developed a simultaneous fault detection and control technique for switched systems under asynchronous switching; Wang et al. in [205] designed a robust fault-tolerant controller for a class of switched nonlinear systems in lower triangular form.
Mathematical modeling of physical systems often results in complex high-order models, which bring serious difficulties to analysis and synthesis of the systems concerned. Therefore, in practical applications it is desirable to replace high-order models by reduced ones with respect to some given criterion, which is the model reduction problem. Over the past decades, the model reduction problem has been the concern of many researchers. Many important results have been reported, which involve various efficient model reduction approaches, such as the balanced truncation approach [89], the Hankel-norm approach [82], Krylov projection approach [87], the Padé reduction approach [7], the ![]() approach [251], and the
approach [251], and the ![]() approach [217, 219]. Readers can refer to [5] for a detailed survey of model reduction. The model reduction problem for switched hybrid systems has also received considerable attention – see for example, [18, 133, 150, 173, 179, 204, 217, 219] and references therein. To mention a few important results, Birouche et al. in [18] investigated the model order-reduction for discrete-time switched linear systems by the balanced truncation approach; Monshizadeh et al. in [150] developed a simultaneous balanced truncation approach to model reduction of switched linear systems; Shi et al. in [179] studied the model reduction problem for discrete-time switched linear systems over finite frequency ranges; Wang et al. in [204] developed a delay-dependent model reduction approach for continuous-time switched state-delayed systems; and Wu and Zheng in [219] proposed a weighted
approach [217, 219]. Readers can refer to [5] for a detailed survey of model reduction. The model reduction problem for switched hybrid systems has also received considerable attention – see for example, [18, 133, 150, 173, 179, 204, 217, 219] and references therein. To mention a few important results, Birouche et al. in [18] investigated the model order-reduction for discrete-time switched linear systems by the balanced truncation approach; Monshizadeh et al. in [150] developed a simultaneous balanced truncation approach to model reduction of switched linear systems; Shi et al. in [179] studied the model reduction problem for discrete-time switched linear systems over finite frequency ranges; Wang et al. in [204] developed a delay-dependent model reduction approach for continuous-time switched state-delayed systems; and Wu and Zheng in [219] proposed a weighted ![]() model reduction approach for linear switched systems with time-varying delay.
model reduction approach for linear switched systems with time-varying delay.
1.2.2 Analysis and Synthesis of Markovian Jump Linear Systems
Markovian jump linear systems (MJLSs) are another typical class of parameter-switching systems, and they are modeled by a set of linear systems with the transitions between the models determined by a Markov chain, taking values in a finite set [136]. MJLSs can also be considered as a special case of switched hybrid systems with the switching signals governed by a Markov chain. Applications of MJLSs may be found in many processes, such as target tracking problems, manufactory processes, solar thermal receivers, fault-tolerant systems, and economic problems. From a mathematical point of view, MJLSs can be regarded as a special class of stochastic system with system matrices changed randomly at discrete time points governed by a Markov process and remaining LTI between random jumps. Over the past decades, owing to a large number of applications in control engineering, MJLSs have received increasing interest. Many results in this field can be found in the literature, and in the following, we will review some recently published results on MJLSs.
The stability analysis and stabilization problems for MJLSs were addressed in [20, 22, 28, 56, 76, 104, 144, 174, 176, 187, 207, 238, 239]. Specifically, Cao and Lam in [28] investigated the stochastic stabilizability and ![]() control for discrete-time jump linear systems with time delay; de Souza in [56] studied the robust stability and stabilization problems for uncertain discrete-time MJLSs; Gao et al. in [76] considered the stabilization and
control for discrete-time jump linear systems with time delay; de Souza in [56] studied the robust stability and stabilization problems for uncertain discrete-time MJLSs; Gao et al. in [76] considered the stabilization and ![]() control problems for two-dimensional MJLSs; Sun et al. in [187] dealt with the robust exponential stabilization of MJLSs with mode-dependent input delay; Xiong et al. in [238] studied the robust stabilization problem for MJLSs with uncertain switching probabilities. In addition, there have been some results on the stability and stabilization for Markovian jump stochastic systems. For example, Boukas and Yang in [20] proposed an exponential stabilizability condition for stochastic systems with Markovian jump parameters; Wang et al. in [207] solved the stabilization problem for bilinear uncertain time-delay stochastic systems with Markovian jump parameters; and some other results on Markovian jump stochastic systems can be found in [144].
control problems for two-dimensional MJLSs; Sun et al. in [187] dealt with the robust exponential stabilization of MJLSs with mode-dependent input delay; Xiong et al. in [238] studied the robust stabilization problem for MJLSs with uncertain switching probabilities. In addition, there have been some results on the stability and stabilization for Markovian jump stochastic systems. For example, Boukas and Yang in [20] proposed an exponential stabilizability condition for stochastic systems with Markovian jump parameters; Wang et al. in [207] solved the stabilization problem for bilinear uncertain time-delay stochastic systems with Markovian jump parameters; and some other results on Markovian jump stochastic systems can be found in [144].
The ![]() control for MJLSs was investigated in [21, 24, 28, 29, 76, 115, 230, 245]; robust
control for MJLSs was investigated in [21, 24, 28, 29, 76, 115, 230, 245]; robust ![]() control of MJLSs with unknown nonlinearities was studied in [21].
control of MJLSs with unknown nonlinearities was studied in [21]. ![]() control was addressed in [24] for discrete-time MJLSs with bounded transition probabilities; the robust
control was addressed in [24] for discrete-time MJLSs with bounded transition probabilities; the robust ![]() control problem was considered in [29] for uncertain MJLSs with time delay; the robust
control problem was considered in [29] for uncertain MJLSs with time delay; the robust ![]() control of descriptor discrete-time Markovian jump systems is covered in [115]; delay-dependent
control of descriptor discrete-time Markovian jump systems is covered in [115]; delay-dependent ![]() control for singular Markovian jump systems with time delay appears in [230]; delay-dependent
control for singular Markovian jump systems with time delay appears in [230]; delay-dependent ![]() control and filtering for uncertain Markovian jump systems with time-varying delays are found in [245].
control and filtering for uncertain Markovian jump systems with time-varying delays are found in [245].
The filtering problem for MJLSs was considered in [54, 55, 57, 134, 175, 177, 208, 211, 231, 242, 254, 256]. To mention a few, de Souza and Fragoso studied the ![]() filter design problem for continuous- and discrete-time MJLSs in [54, 55], respectively; Ma and Boukas in [134] investigated robust
filter design problem for continuous- and discrete-time MJLSs in [54, 55], respectively; Ma and Boukas in [134] investigated robust ![]() filtering for uncertain discrete Markovian jump singular systems with mode-dependent time delay; Shi et al. in [175] considered Kalman filtering for continuous-time uncertain MJLSs; Wu et al. in [211] addressed the
filtering for uncertain discrete Markovian jump singular systems with mode-dependent time delay; Shi et al. in [175] considered Kalman filtering for continuous-time uncertain MJLSs; Wu et al. in [211] addressed the ![]() filtering problem for Markovian jump two-dimensional systems; Yao et al. in [254] dealt with robust
filtering problem for Markovian jump two-dimensional systems; Yao et al. in [254] dealt with robust ![]() filtering of Markovian jump stochastic systems with uncertain transition probabilities; and then they studied quantized
filtering of Markovian jump stochastic systems with uncertain transition probabilities; and then they studied quantized ![]() filtering for Markovian jump LPV systems with intermittent measurements in [256].
filtering for Markovian jump LPV systems with intermittent measurements in [256].
The fault detection problem for MJLSs was investigated in [147, 152, 226, 255, 273, 274]. Specifically, Meskin and Khorasani in [147] investigated fault detection and isolation problems for discrete-time MJLSs with application to a network of multi-agent systems having imperfect communication channels; Nader and Khashayar proposed a geometric approach to fault detection and isolation of continuous-time MJLSs in [152]; Wu et al. in [226] studied generalized ![]() fault detection for Markovian jump two-dimensional systems; Yao et al. in [255] considered fault detection filter design for Markovian jump singular systems with intermittent measurements; and Zhong et al. in [273, 274] addressed robust fault detection problem for continuous- and discrete-time MJLSs, respectively.
fault detection for Markovian jump two-dimensional systems; Yao et al. in [255] considered fault detection filter design for Markovian jump singular systems with intermittent measurements; and Zhong et al. in [273, 274] addressed robust fault detection problem for continuous- and discrete-time MJLSs, respectively.
The SMC design problem was also addressed for MJLSs in [34, 35, 135, 157, 178, 221, 223, 225]. Chen et al. studied SMC of MJLSs with actuator nonlinearities in [34], and adaptive SMC design for Markovian jump stochastic systems with actuator degradation in [35]; Ma and Boukas in [135] proposed a singular system approach to robust SMC for uncertain MJLSs; Shi et al. in [178] considered the SMC design problem for MJLSs; Wu and Ho in [221] solved the SMC problem for Markovian jump singular stochastic hybrid systems; Wu et al. in [223] investigated state estimation and SMC of Markovian jump singular systems; and then they considered SMC design with bounded ![]() gain performance for Markovian jump singular time-delay systems in [225].
gain performance for Markovian jump singular time-delay systems in [225].
Apart from the above-mentioned synthesis problems for MJLSs, the model reduction problem for such systems was also investigated – see for example, [111, 266]. Kotsalis et al. in [111] studied the model reduction problem for discrete-time MJLSs; and Zhang et al. in [266] considered ![]() model reduction for both continuous- and discrete-time MJLSs.
model reduction for both continuous- and discrete-time MJLSs.
1.3 Contribution of the Book
This book represents the first of a number of attempts to reflect the state-of-the-art of the research area for handling the SMC problem for uncertain parameter-switching hybrid systems (including Markovian jump systems, switched hybrid systems, singular systems, stochastic systems, and time-delay systems). The content of this book can be divided into three parts. The first part is focused on SMC of Markovian jump singular systems. Some necessary and sufficient conditions are derived for the stochastic stability, stochastic admissibility, and optimal performances by developing new techniques for the considered Markovian jump singular systems. Then, a set of new SMC methodologies are proposed, based on the analysis results. In the second part, the problem of SMC of switched delayed hybrid systems is investigated. A unified framework under ‘average dwell time’ is established for analyzing the considered switched delayed hybrid systems. Then some sufficient conditions are derived for the stability, stabilizability, existence of the desired DOF controllers, and existence of the sliding mode dynamics in the SMC issue. More importantly, a set of SMC methodologies under a unique framework are proposed for the considered hybrid systems. In the third part, the parallel theories and techniques developed in the previous part are extended to deal with switched stochastic hybrid systems. Specifically, in this third part, the main attention will be focused on stochastic stability analysis, stabilization, ![]() control, and SMC of switched stochastic hybrid systems. Sufficient conditions are established first for the stochastic exponential stability and optimal performances (such as
control, and SMC of switched stochastic hybrid systems. Sufficient conditions are established first for the stochastic exponential stability and optimal performances (such as ![]() and dissipativity) of the continuous- and discrete-time switched stochastic systems. Based on the obtained analysis results, the synthesis issues, including
and dissipativity) of the continuous- and discrete-time switched stochastic systems. Based on the obtained analysis results, the synthesis issues, including ![]() control and SMC design, are solved.
control and SMC design, are solved.
The features of this book can be highlighted as follows. 1) A unified framework is established for SMC of Markovian jump singular systems, where the parameters are jumping from one mode to another stochastically, and at the same time there are time delays in existing system states. 2) A series of problems are solved with new approaches for analysis and synthesis of continuous- and discrete-time switched hybrid systems, including stability analysis and stabilization, DOF control, and SMC. 3) Three correlated problems, ![]() control (state feedback control and DOF control), SMC, and state estimation problems, are dealt with for switched stochastic systems. 4) A set of newly developed techniques (e.g. average dwell time method, piecewise Lyapunov function approach, parameter-dependent Lyapunov function approach, cone complementary linearization (CCL) approach, slack matrix approach, and sums of squares technique) are exploited to handle the emerging mathematical/computational challenges.
control (state feedback control and DOF control), SMC, and state estimation problems, are dealt with for switched stochastic systems. 4) A set of newly developed techniques (e.g. average dwell time method, piecewise Lyapunov function approach, parameter-dependent Lyapunov function approach, cone complementary linearization (CCL) approach, slack matrix approach, and sums of squares technique) are exploited to handle the emerging mathematical/computational challenges.
This book is a timely reflection on the developing area of system analysis and SMC theories for systems with uncertain switching parameters, typically resulting from varying operation environments. It is a collection of a series of latest research results and therefore serves as a useful textbook for senior and/or graduate students who are interested in knowing: 1) the state of the art of the SMC area; 2) recent advances in Markovian jump systems; 3) recent advances in switched hybrid systems; and 4) recent advances in singular systems, stochastic systems and time-delay systems. Readers will also benefit from new concepts, models and methodologies with theoretical significance in system analysis and control synthesis. The book can also be used as a practical research reference for engineers dealing with SMC, optimal control, and state estimation problems for uncertain parameter-switching hybrid systems. The aim of this book is to close the gap in literature by providing a unified, neat framework for SMC of uncertain parameter-switching hybrid systems.
In general, this book aims at third- or fourth-year undergraduates, postgraduates and academic researchers. Prerequisite knowledge includes linear algebra, matrix analysis, linear control system theory, and stochastic systems. It should be described as an advanced book.
More specifically, the readers should include: 1) control engineers working on nonlinear control, switching control, and optimal control; 2) system engineers working on switched hybrid systems and stochastic systems; 3) mathematicians and physicists working on hybrid systems and singular systems; and 4) postgraduate students majoring on control engineering, system sciences, and applied mathematics. This book could also serve as a useful reference to: 1) mathematicians and physicists working on complex dynamic systems; 2) computer scientists working on algorithms and computational complexity; and 3) third- or fourth-year students who are interested in knowing about advances in control theory and applications.
1.4 Outline of the Book
The organization structure of this book is shown in Figure 1.6. The general layout of this book is divided into three parts: Part One: SMC of Markovian jump singular systems; Part Two: SMC of switched hybrid systems with time-varying delay; and Part Three: SMC of switched stochastic hybrid systems. The main contents of this book are shown in Figure 1.7.

Figure 1.6 The organization structure of the book

Figure 1.7 The main contents of the book
- Chapter 1 first presents the research background, motivations and research problems of this book which mainly involve SMC methodologies and the uncertain parameter-switching hybrid systems. A survey is provided on the fundamental theory of the SMC methodologies, which include some basic concepts (SMC problem, reaching condition, and two SMC design steps), sliding surface design (linear sliding surface, integral sliding surface, and terminal sliding surface), sliding mode controller design (equivalent control design, reaching condition approach, Lyapunov function approach, and reaching law approach), chattering problem (boundary layer approach, dynamic SMC approach, and reaching law approach). Then, an overview of recent developments of SMC Methodologies is also presented, which includes SMC of uncertain systems, SMC of time-delay systems, SMC of stochastic systems, SMC of parameter-switching hybrid systems, and the output feedback SMC technique. Another focus in this chapter is to provide a timely review on the recent advances of the analysis and synthesis issues for uncertain parameter-switching hybrid systems (including switched hybrid systems and Markovian jump linear systems). Most commonly used methods for the stability analysis of the switched hybrid systems are summarized. Subsequently, recently developed results on synthesis issues (such as control, filtering, fault detection, and model reduction) for the uncertain parameter-switching hybrid systems are reviewed with a lot of references involved. Finally, we summarize the main contributions of this book and give the outline of this book.
Part One presents the analysis and SMC design procedure for Markovian jump singular systems. It begins with Chapter 2, and consists of three chapters as follows.
- Chapter 2 investigates SMC of Markovian jump singular systems. The main difficulties of such a problem come from switching function design and stochastic admissibility analysis for the resulted sliding mode dynamics (termed Markovian jump singular systems). Thus, the chapter solves the two key problems of how to design an appropriate switching function and how to establish a necessary and sufficient condition of the stochastic admissibility for the resulted sliding mode dynamics. But it should be pointed out that the existing results on the stochastic admissibility (and stochastic stability) of Markovian jump singular systems are not all of strict LMI form owing to some matrix equality constraints involved. This may cause considerable trouble in checking the conditions numerically. How to get a condition in strict LMI form is also a key problem to be discussed. Motivated by the above-mentioned three key issues, we will consider the stability analysis and SMC design problems for Markovian jump singular systems in this chapter. First, a new integral-type switching function is designed by taking the singular matrix E into account, by which the sliding mode dynamics can be derived. Then, a necessary and sufficient condition for the existence of such a sliding mode (the stochastic stability of the sliding mode dynamics) is established in terms of strict LMIs, by which the sliding surface can be designed. Considering that the system states are not always available in practice owing to the limits of the physical situation or the expense of measuring them, the state estimation problem has become more important. In this case, an observer is designed to estimate the system’s states, and an observer-based SMC law is then synthesized to guarantee the reachability of the state trajectories of the closed-loop system to the predefined sliding surface.
- Chapter 3 studies the problems of the bounded
 gain performance analysis and SMC of Markovian jump singular time-delay systems. The purpose is to contribute to the development of SMC and the bounded
gain performance analysis and SMC of Markovian jump singular time-delay systems. The purpose is to contribute to the development of SMC and the bounded  gain performance analysis for the considered system. We will pay particular attention to the singular matrix E in the design of an integral-type switching function, which leads to a full-order Markovian jump singular time-delay system for describing the sliding mode dynamics. We will then apply the slack matrix approach to derive a delay-dependent sufficient condition in the form of LMIs, which guarantees that the sliding mode dynamics is stochastically stable with a bounded
gain performance analysis for the considered system. We will pay particular attention to the singular matrix E in the design of an integral-type switching function, which leads to a full-order Markovian jump singular time-delay system for describing the sliding mode dynamics. We will then apply the slack matrix approach to derive a delay-dependent sufficient condition in the form of LMIs, which guarantees that the sliding mode dynamics is stochastically stable with a bounded  gain performance. In addition, the analysis conditions of the sliding mode dynamics and the solvability condition for the desired switching function are both established. Finally, we will synthesize an SMC law for driving the system state trajectories onto the predefined sliding surface.
gain performance. In addition, the analysis conditions of the sliding mode dynamics and the solvability condition for the desired switching function are both established. Finally, we will synthesize an SMC law for driving the system state trajectories onto the predefined sliding surface. - Chapter 4 addresses the SMC of a nonlinear singular stochastic system with Markovian switching. An integral switching function is designed, and the resulting sliding mode dynamics is expressed by a full-order Markovian jump singular stochastic system. By introducing some specified matrices, a sufficient condition is proposed in terms of strict LMIs, which guarantees the stochastic stability of the sliding mode dynamics (thus the existence of such a sliding mode can be guaranteed). A sliding mode controller is then synthesized for reaching motion. Moreover, when there is an external disturbance in the considered control system, the
 disturbance attenuation performance (
disturbance attenuation performance ( performance) is analyzed. Some corresponding sufficient conditions are also established for the existence of the sliding mode dynamics, and some algorithms (including the CCL algorithm) are presented to cast the SMC design problem into a nonlinear minimization problem involving LMI conditions instead of the original nonconvex feasibility problem.
performance) is analyzed. Some corresponding sufficient conditions are also established for the existence of the sliding mode dynamics, and some algorithms (including the CCL algorithm) are presented to cast the SMC design problem into a nonlinear minimization problem involving LMI conditions instead of the original nonconvex feasibility problem.
Part Two presents the analysis and SMC design procedure for switched state-delayed hybrid systems. It begins with Chapter 5, and consists of four chapters as follows.
- Chapter 5 deals with the stability analysis and stabilization problems for continuous- and discrete-time switched hybrid systems with time-varying delays. For a continuous-time system, the time-varying delay d(t) is assumed to satisfy either (A1) 0 ≤ d(t) ≤ d and
 or (A2) 0 ≤ d(t) ≤ d. By using the average dwell time approach and the piecewise Lyapunov function technique, two delay-dependent sufficient conditions are established for the exponential stability of the considered hybrid system with (A1) and (A2), respectively. Here, the slack matrix approach is applied to further reduce the conservativeness of the stability conditions caused by the time delay. For the discrete-time system, the stability conditions are also derived by the average dwell time approach, and the results are all delay-dependent, and thus less conservative. The stabilization problem is then solved by designing a memoryless state feedback controller, and then an explicit expression for the desired controller is given. The research in this chapter is an important foundation for the development of the SMC methodologies for switched hybrid systems in subsequent chapters.
or (A2) 0 ≤ d(t) ≤ d. By using the average dwell time approach and the piecewise Lyapunov function technique, two delay-dependent sufficient conditions are established for the exponential stability of the considered hybrid system with (A1) and (A2), respectively. Here, the slack matrix approach is applied to further reduce the conservativeness of the stability conditions caused by the time delay. For the discrete-time system, the stability conditions are also derived by the average dwell time approach, and the results are all delay-dependent, and thus less conservative. The stabilization problem is then solved by designing a memoryless state feedback controller, and then an explicit expression for the desired controller is given. The research in this chapter is an important foundation for the development of the SMC methodologies for switched hybrid systems in subsequent chapters. - Chapter 6 is concerned with the DOF control problem for continuous-time switched hybrid systems with time-varying delays. Specifically, two issues are investigated: 1) the
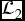 -
- control problem for continuous-time switched hybrid systems with time-varying delay. A DOF controller is designed, which is assumed to be switching with the same switching signal as in the original system. A delay-dependent sufficient condition is proposed, to guarantee the exponential stability and a weighted
control problem for continuous-time switched hybrid systems with time-varying delay. A DOF controller is designed, which is assumed to be switching with the same switching signal as in the original system. A delay-dependent sufficient condition is proposed, to guarantee the exponential stability and a weighted  -
- performance for the closed-loop system with the decay estimate is explicitly given. The corresponding solvability condition for a desired DOF controller is established, and an explicit parametrization of all desired DOF controllers is also given; 2) the guaranteed cost DOF controller design for continuous-time linear switched hybrid system with both discrete and neutral delays. A sufficient condition is first proposed, in terms of a set of LMIs, to guarantee the exponential stability and a certain bound for the cost function of the closed-loop system, where the decay estimate is explicitly given to quantify the convergence rate. Then, the corresponding solvability conditions for a desired DOF controller under guaranteed cost are established by using the approach of linearizing variable transforms. Since these obtained conditions are not all expressed by strict LMIs, the CCL algorithm is exploited to cast them into sequential minimization problems subject to LMI constraints, which can be easily solved numerically.
performance for the closed-loop system with the decay estimate is explicitly given. The corresponding solvability condition for a desired DOF controller is established, and an explicit parametrization of all desired DOF controllers is also given; 2) the guaranteed cost DOF controller design for continuous-time linear switched hybrid system with both discrete and neutral delays. A sufficient condition is first proposed, in terms of a set of LMIs, to guarantee the exponential stability and a certain bound for the cost function of the closed-loop system, where the decay estimate is explicitly given to quantify the convergence rate. Then, the corresponding solvability conditions for a desired DOF controller under guaranteed cost are established by using the approach of linearizing variable transforms. Since these obtained conditions are not all expressed by strict LMIs, the CCL algorithm is exploited to cast them into sequential minimization problems subject to LMI constraints, which can be easily solved numerically. - Chapter 7 studies the SMC design problem for continuous-time switched hybrid systems with time-varying delay. First, the original system is transformed into a regular form through model transformation, and then, by designing a linear sliding surface, the dynamical equation for the sliding mode dynamics is derived. A delay-dependent sufficient condition for the existence of a desired sliding mode is proposed, and an explicit parametrization of the desired sliding surface is also given. Since the obtained conditions are not all expressed in terms of strict LMIs (some matrix equality constraints are involved), the CCL method is exploited to cast them into a sequential minimization problem subject to LMI constraints, which can be easily solved numerically. Then, a discontinuous SMC law is synthesized, by which the system state trajectories can be driven onto the prescribed sliding surface in a finite time and maintained there for all subsequent time. Since the designed SMC law contains state-delay terms, it requires the time-varying delay to be explicitly known a priori in the practical implementation of the controller. However, in some practical situations, the information for time delay is usually unavailable, or difficult to measure. In such a case, the designed SMC law is not applicable. To overcome this, we suppose that the state-delay terms in the controller are norm-bounded with an unknown upper bound. We will design an adaptive law to estimate the unknown upper bound, and thus an adaptive SMC law is synthesized, which can also guarantee the system state trajectories reach the prescribed sliding surface.
- Chapter 8 is concerned with the problem of SMC of discrete-time switched delayed hybrid systems with time-varying delay. First, we transform the original system into a new one with regular form, and then by designing a linear switching function, a reduced-order sliding mode dynamics, described by a switched state-delayed hybrid system, is developed. By utilizing the average dwell time approach and the piecewise Lyapunov function technique, a delay-dependent sufficient condition for the existence of the desired sliding mode is proposed in terms of LMIs, and an explicit parametrization of the desired switching surface is also given. Here, to reduce the conservativeness induced by the time delay in the system, both the slack matrix technique and also the delay partitioning method are employed, which make the proposed existence condition less conservative. In this chapter, the time delay considered is a time-varying one with a known lower bound. In this case, combined with construction of an appropriate Lyapunov–Krasovskii function, the delay partitioning method is employed by partitioning the lower bound evenly into several components. We then show that the conservativeness of the obtained existence condition becomes less and less with the partitioning getting thinner. Finally, a discontinuous SMC law is designed to drive the state trajectories of the closed-loop system onto a prescribed sliding surface in a finite time and maintained there for all subsequent time.
Part Three presents the analysis and SMC design procedure for switched stochastic hybrid systems. It begins with Chapter 9, and consists of four chapters as follows.
- Chapter 9 investigates the problems of stability and performance analysis, stabilization and
 control (including state feedback control and DOF control) for continuous-time switched stochastic hybrid systems. The average dwell time approach combined with the piecewise Lyapunov function technique is applied to derive the main results. There are two main advantages to using this approach to the switched system. First, this approach uses a mode-dependent Lyapunov function, which avoids some conservativeness caused by using a common Lyapunov function for all the subsystems. Then the other advantage is that the obtained result is not just an asymptotic stability condition, but an exponential one. Therefore, by this approach, a sufficient condition is first proposed, which guarantees the mean-square exponential stability of the unforced switched stochastic hybrid system. When system states are available, a state feedback controller is designed such that the closed-loop system is mean-square exponentially stable with an
control (including state feedback control and DOF control) for continuous-time switched stochastic hybrid systems. The average dwell time approach combined with the piecewise Lyapunov function technique is applied to derive the main results. There are two main advantages to using this approach to the switched system. First, this approach uses a mode-dependent Lyapunov function, which avoids some conservativeness caused by using a common Lyapunov function for all the subsystems. Then the other advantage is that the obtained result is not just an asymptotic stability condition, but an exponential one. Therefore, by this approach, a sufficient condition is first proposed, which guarantees the mean-square exponential stability of the unforced switched stochastic hybrid system. When system states are available, a state feedback controller is designed such that the closed-loop system is mean-square exponentially stable with an  performance. However, when system states are not all available, a DOF controller is designed and the mean-square exponential stability with an
performance. However, when system states are not all available, a DOF controller is designed and the mean-square exponential stability with an  performance is also guaranteed.
performance is also guaranteed.
Sufficient solvability conditions for the desired controllers are proposed in terms of LMIs. - Chapter 10 considers the stability and performance analysis, stabilization and
 control problems for discrete-time switched stochastic systems with time-variant delays. By applying the average dwell time method and the piecewise Lyapunov function technique, a sufficient condition is first proposed to guarantee the mean-square exponential stability for the considered system. A condition on a weighted
control problems for discrete-time switched stochastic systems with time-variant delays. By applying the average dwell time method and the piecewise Lyapunov function technique, a sufficient condition is first proposed to guarantee the mean-square exponential stability for the considered system. A condition on a weighted  performance is also proposed. Then, the stabilization and
performance is also proposed. Then, the stabilization and  state feedback control problems are solved with some sufficient conditions presented in terms of LMI.
state feedback control problems are solved with some sufficient conditions presented in terms of LMI. - Chapter 11 is concerned with the SMC of a continuous-time switched stochastic hybrid system, and some results developed in Chapter 9 are used in the research. Firstly, by designing an integral switching function, we obtain the sliding mode dynamics, which is expressed by a switched stochastic hybrid system with the same order as the original systems. Based on the stability analysis result in Chapter 9, a sufficient condition for the existence of the sliding mode is proposed in terms of LMIs, and an explicit parametrization of the desired switching function is also given. Then, a discontinuous SMC law for reaching motion is synthesized such that the state trajectories of the SMC system can be driven onto a prescribed sliding surface and maintained there for all subsequent time. Moreover, considering that some system state components may not be available in practical applications, we further study the state estimation problem by designing an observer. Sufficient conditions are also established for the existence of the sliding mode and the solvability of the desired observer, and then the observer-based SMC law is synthesized.
- Chapter 12 shows the dissipativity analysis and the SMC design for switched stochastic hybrid systems. A more general supply rate is proposed, and a strict
 -dissipativity is defined, which includes
-dissipativity is defined, which includes  , positive realness, and passivity as its special cases. The main idea is to introduce the strict
, positive realness, and passivity as its special cases. The main idea is to introduce the strict  -dissipativity concept into the analysis of the sliding mode dynamics so as to improve the transient performance of the SMC system. The objective is to conduct dissipativity analysis and investigate the dissipativity-based SMC design scheme, with a view to contributing to the development of SMC design and the dissipativity analysis methods for the switched stochastic hybrid system. Specifically, an integral sliding surface is designed such that the sliding mode dynamics exists with the same order as the original system. Then, a sufficient condition, which guarantees the sliding mode dynamics mean-square exponentially stable with a strict dissipativity, is then established in terms of LMIs by using the average dwell time approach and the piecewise Lyapunov function technique. In addition, a solution to the dissipativity synthesis is provided by designing a discontinuous SMC law such that the system state trajectories can be driven onto the predefined sliding surface in a finite time.
-dissipativity concept into the analysis of the sliding mode dynamics so as to improve the transient performance of the SMC system. The objective is to conduct dissipativity analysis and investigate the dissipativity-based SMC design scheme, with a view to contributing to the development of SMC design and the dissipativity analysis methods for the switched stochastic hybrid system. Specifically, an integral sliding surface is designed such that the sliding mode dynamics exists with the same order as the original system. Then, a sufficient condition, which guarantees the sliding mode dynamics mean-square exponentially stable with a strict dissipativity, is then established in terms of LMIs by using the average dwell time approach and the piecewise Lyapunov function technique. In addition, a solution to the dissipativity synthesis is provided by designing a discontinuous SMC law such that the system state trajectories can be driven onto the predefined sliding surface in a finite time.




