The conditional probability in a linear regression model is a linear function of its weights [6:13]. The logistic regression model addresses the nonlinear regression problem by defining the logarithm of the conditional probability as a linear function of its parameters.

First, let's introduce the logistic function and its derivative, which are defined as follows (M12):

The logistic function and its derivative are illustrated in the following graph:

The graph of the logistic function and its derivative

The remainder of this section is dedicated to the application of the multivariate logistic regression to the binomial classification.

The logistic regression is popular for several reasons; some are as follows:

Let's consider the classification problem using two classes. As discussed in the Validation section in Chapter 2, Hello World!, even the best classifier produces false positives and false negatives. The training procedure for a binomial classification is illustrated in the following diagram:

An illustration of the binomial classification for a two-dimension dataset

The purpose of the training is to compute the hyperplane that separates the observations into two categories or classes. Mathematically speaking, a hyperplane in an n-dimensional space (number of features) is a subspace of n - 1 dimensions, as described in the Manifolds section in Chapter 4, Unsupervised Learning. The separating hyperplane of a three-dimension space is a curved surface. The separating hyperplane of a two-dimension problem (plane) is a line. In our preceding example, the hyperplane segregates/separates a training set into two very distinct classes (or groups), Class 1 and Class 2, in an attempt to reduce the overlap (false positive and false negative).

The equation of the hyperplane is defined as the logistic function of the dot product of the regression parameters (or weights) and features.

The logistic function accentuates the difference between the two groups of training observations, separated by the hyperplane. It pushes the observations away from the separating hyperplane toward either classes.

In the case of two classes, c1 and c2 with their respective probabilities, p(C=c1| X=x_i|w) = p(x_i|w) and p(C=c2 |X= x_i|w) = 1- p(x_i|w), where w is the model parameters set or weights in the case of the logistic regression.

Note

The logistic regression

M13: The log likelihood for N observations x_i given regression weights w is defined as:

M14: Conditional probabilities p(x|w) with regression weights w, using the logistic function for N observations with d features {x_ij} _j=0;d-1 is defined as:

M15: The sum of square errors, sse, for the binomial logistic regression with weights w, input values x _i, and expected binary outcome y is as follows:

M16: The computation of the weights w of the logistic regression by maximizing the log likelihood, given the input data x_i and expected outcome (labels) y_i is defined as:

Let's implement the logistic regression without regularization using the Apache Commons Math library. The library contains several least squares optimizers that allow you to specify the optimizer minimizing algorithm for the loss function in the logistic regression class, LogisticRegression.

The constructor for the LogisticRegression class follows a very familiar pattern: it defines an ITransform data transformation, whose model is implicitly derived from the input data (training set), as described in the Monadic data transformation section in Chapter 2, Hello World! (line 2). The output of the |> predictor is a class ID, and therefore, the V type of the output is an Int (line 3):

class LogisticRegression[T <: AnyVal](
    xt: XVSeries[T], 
    expected: Vector[Int], 
    optimizer: LogisticRegressionOptimizer)  //1
    (implicit f: T => Double)
   extends ITransform[Array[T]](xt) with Regression 
       with Monitor[Double] { //2

  type V = Int //3
    override def train: RegressionModel  //4
  def |> : PartialFunction[Array[T], Try[V]]
}

The parameters of the logistic regression class are the multivariate xt time series (features), the target or expected classes, expected, and the optimizer used to minimize the loss function or residual sum of squares (line 1). In the case of the binomial logistic regression, expected are assigned the value of 1 for one class and 0 for the other.

The Monitor trait is used to collect the profiling information during training (refer to the Monitor section under Utility classes in the Appendix A, Basic Concepts).

The purpose of the training is to determine the regression weights that minimize the loss function, as defined in the M14 formula as well as the residual sum of squares (line 4).

For convenience, the definition and configuration of the optimizer are encapsulated in the LogisticRegressionOptimizer class.

The implementation of the logistic regression uses the following components:

The key software components of the logistic regression are described in the following UML class diagram:

The UML class diagram for the logistic regression

The UML diagram omits the helper traits or classes such as Monitor or the Apache Commons Math components.

Our implementation of the training of the logistic regression model leverages either the Gauss-Newton or the Levenberg-Marquardt nonlinear least squares optimizers, (refer to the Nonlinear least squares minimization section in the Appendix A, Basic Concepts) packaged with the Apache Commons Math library.

The training of the logistic regression is performed by the train method.

The implementation of the training method, train, relies on the following five steps:

The workflow and the Apache Commons Math classes used in the training of the logistic regression are visualized by the following flow diagram:

The workflow for training the logistic regression using the Apache Commons Math library

The first four steps are required by the Apache Commons Math library to initialize the configuration of the logistic regression prior to the minimization of the loss function. Let's start with the configuration of the least squares optimizer:

def train: RegressionModel = {
  val weights0 = Array.fill(data.head.length +1)(INITIAL_WEIGHT)
  val lrJacobian = new RegressionJacobian(data, weights0) //5
  val exitCheck = new RegressionConvergence(optimizer) //6

  def createBuilder: LeastSquaresProblem  //7
  val optimum = optimizer.optimize(createBuilder) //8
  RegressionModel(optimum.getPoint.toArray, optimum.getRMS)
}

The train method implements the last four steps of the computation of the regression model:

class LogisticRegressionOptimizer(
     maxIters: Int, 
     maxEvals: Int,
     eps: Double, 
     lsOptimizer: LeastSquaresOptimizer) {  //9
  def optimize(lsProblem: LeastSquaresProblem): Optimum = 
       lsOptimizer.optimize(lsProblem)
}

class RegressionJacobian[T <: AnyVal](  //10
    xv: XVSeries[T], 
    weights0: DblArray)(implicit f: T => Double) 
  extends MultivariateJacobianFunction {

  type GradientJacobian = Pair[RealVector, RealMatrix]
  override def value(w: RealVector): GradientJacobian = { //11
    val gradient = xv.map( g => { //12
      val f = logistic(dot(g, w))//13
     (f, f*(1.0-f))  //14
   })
   xv.zipWithIndex   //15
    ./:(Array.ofDim[Double](xv.size, weights0.size)) {
     case (j, (x,i)) => {   
       val df = gradient(i)._2
       Range(0, x.size).foreach(n => j(i)(n+1) = x(n)*df)
       j(i)(0) = 1.0; j //16
     }
   }
   (new ArrayRealVector(gradient.map(_._1).toArray), 
      new Array2DRowRealMatrix(jacobian))  //17
  }
}

val exitCheck = new ConvergenceChecker[PointVectorValuePair] {
  override def converged(
      iters: Int, 
      prev: PointVectorValuePair, 
      current:PointVectorValuePair): Boolean =  
   sse(prev.getValue, current.geValue) < optimizer.eps 
           && iters >= optimizer.maxIters //18
}

def createBuilder: LeastSquaresProblem = 
   (new LeastSquaresBuilder).model(lrJacobian)    //19
   .weight(MatrixUtils.createRealDiagonalMatrix(
             Array.fill(xt.size)(1.0)))  //20
   .target(expected.toArray) //21
   .checkerPair(exitCheck)  //22
   .maxEvaluations(optimizer.maxEvals)  //23
   .start(weights0)  //24
   .maxIterations(optimizer.maxIters) //25
   .build

val optimum = optimizer.optimize(lsp)
(optimum.getPoint.toArray, optimum.getRMS)

import YahooFinancials._ 
val maxIters = 250
val maxEvals = 4500
val eps = 1e-7

val src = DataSource(path, true, true, 1)  //26
val optimizer = new LevenbergMarquardtOptimizer  //27

for {
  price <- src.get(adjClose) //28
  volatility <- src.get(volatility)  //29
  volume <- src.get(volume)  //30
  (features, expected) <- differentialData(volatility, 
volume, price, diffInt) //31
  lsOpt <- LogisticRegressionOptimizer(maxIters, maxEvals, 
                        eps, optimizer) //32
  regr <- LogisticRegression[Double](features, expected, lsOpt)      
  pfnRegr <- Try(regr |>) //33
} 
yield {
   show(s"${LogisticRegressionEval.toString(regr)}")
   val predicted = features.map(pfnRegr(_))
   val delta = predicted.view.zip(expected.view)
            .map{case(p, e) => if(p.get == e) 1 else 0}.sum
   show(s"Accuracy: ${delta.toDouble/expected.size}")
}

As mentioned earlier and despite its name, the binomial logistic regression is actually a binary classifier. The classification method is implemented as an implicit data transformation |>:

val HYPERPLANE = - Math.log(1.0/INITIAL_WEIGHT -1)
def |> : PartialFunction[Array[T], Try[V]] = {
  case x: Array[T] if(isModel && 
      model.size-1 == x.length && isModel)  => 
       Try (if(dot(x, model) > HYPERPLANE) 1 else 0 ) //34
}

The dot (or inner) product of the observation x with the weights model is evaluated against the hyperplane. The predicted class is 1 if the produce exceeds HYPERPLANE, and 0 otherwise (line 34).

The direction of the price variation of the Copper ETF, CU price(t+1) – price(t), is compared to the direction predicted by the logistic regression. The result is plotted with the success value if the positive or negative direction is correctly predicted; otherwise, it is plotted with the failure value:

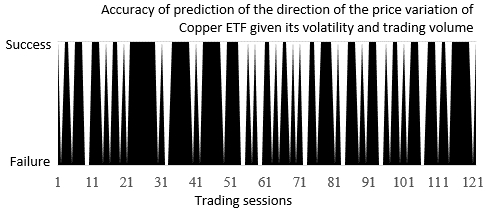
The prediction of the direction of the variation of price of the Copper ETF using the logistic regression

The logistic regression was able to classify 78 out of 121 trading sessions (65 percent accuracy).

Now, let's use the logistic regression to predict the positive price variation for the Copper ETF, given its volatility and trading volume. This trading or investment strategy is known as being long on the market. This particular use case ignores the trading sessions for which the price was either flat or declined:

The prediction of the direction of the variation of price of the Copper ETF using the logistic regression

The logistic regression was able to correctly predict the positive price variation for 58 out of 64 trading sessions (90.6 percent accuracy). What is the difference between the first and second test cases?

In the first case, the w₀ + w₁.volatility + w₂.volume separating hyperplane equation is used to segregate the features generating either the positive or negative price variation. Therefore, the overall accuracy of the classification is negatively impacted by the overlap of the features from the two classes.

In the second case, the classifier has to consider only the observations located on the positive side of the hyperplane equation, without taking into account the false negatives.

The accuracy of the binary classifier can be further improved by considering the positive variation of the price using a margin error EPS as price(t+1) – price(t) > EPS.