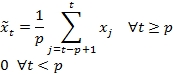The simple moving average is the simplest form of the moving averages algorithms [3:1]. The simple moving average of period p estimates the value at time t by computing the average value of the previous p observations using the following formula.

Note

The simple moving average

M1: The simple moving average of a time series {x_t} with a period p is computed as the average of the last p observations:

M2: The computation is implemented iteratively using the following formula:

Here, is the estimate or simple moving average value at time t.

Let's build a class hierarchy of moving average algorithms, with the parameterized MovingAverage trait as its root:

trait MovingAverage[T]

We use the generic XSeries[T] type and the data transform with the ETransform explicit configuration, introduced in the Explicit models section under Monadic data transformation in Chapter 2, Hello World!, to implement the simple moving average, SimpleMovingAverage:

class SimpleMovingAverage[T <: AnyVal](period: Int)
     (implicit num: Numeric[T], f: T => Double) //1
  extends Etransform[Int](period) with MovingAverage[T] {

  type U = XSeries[T]  //2
  type V = DblVector   //3
  
  val zeros = Vector.fill(0.0)(period-1) 
  override def |> : PartialFunction[U, Try[V]] = {
    case xt: U if( xt.size >= period ) => {
      val splits = xt.splitAt(period)
      val slider = xt.take(xt.size - period).zip(splits._2)  //4

      val zero = splits._1.sum/period //5
      Try( zeros ++ slider.scanLeft(zero) {
         case (s, (x,y)) => s + (x - y)/period }) //7
  }
}

The class is parameterized for the T type of elements of the input time series; we cannot make any assumption regarding the type of input data. The type of the elements of the output time series is Double. The implicit instantiation of the Numeric[T] class is required by the sum and / arithmetic operators (line 1). The simple moving average implements ETransform by defining the abstract U types for the input (line 2) and V for the output ( line 3) as a time series, DblVector.

The implementation has a few interesting elements. First, the set of observations is duplicated and the index in the resulting clone instance is shifted by p observations before being zipped with the original to the array of a pair of slider values (line 4):

The sliding algorithm to compute moving averages

The average value is initialized with the mean value of the first period data points (line 5). The first period values of the trends are initialized to zero (line 6). The method concatenates the initial null values and the computed average values to implement the M2 formula (line 7).

The weighted moving average method is an extension of the simple moving average by computing the weighted average of the last p observations [3:2]. The weights α_j are assigned to each of the last p data points x_j and are normalized by the sum of the weights.

Note

The weighted moving average

M3: The weighted moving average of a series {x_t} with a period p and a normalized weights distribution {α_j} is given by the following formula:

Here, x_t is the estimate or simple moving average value at time t.

The implementation of the WeightedMovingAverage class requires the computation of the last p (weights.size) data points. There is no simple iterative formula to compute the weighted moving average at time t + 1 using the moving average at time t:

class WeightedMovingAverage[@specialized(Double) T <: AnyVal]( 
    weights: DblArray)
    (implicit num: Numeric[T], f: T => Double) 
  extends SimpleMovingAverage[T](weights.length) {  //8

  override def |> : PartialFunction[U, Try[V]] = {
    case xt: U if(xt.size >= weights.length ) => {
      val smoothed =  (config to xt.size).map( i => 
       xt.slice(i- config, i).zip(weights) //9
             .map { case(x, w) => x*w).sum  //10
      )
      Try(zeros ++ smoothed) //11
    }
  }
}

The computation of the weighted moving average is a bit more involved than the simple moving average. Therefore, we specify the generation of the byte code that is dedicated to the Double type using the specialized annotation. The weighted moving average inherits the SimpleMovingAverage class, and therefore, implements the ETransform explicit transformation for a configuration of weights, with input observations of the XSeries[T] type and output observations of the DblVector type. The implementation of M3 formula generates a smoothed time series by slicing (line 9) the input time series and then computing the inner product of weights and the slice of the time series (line 10).

As with the simple moving average, the output is the concatenation of the initial weights.size null values, zeros, and the smoothed data (line 11).

The exponential moving average is widely used in financial analysis and marketing surveys because it favors the latest values. The older the value, the less impact it has on the moving average value at time t [3:3].

Note

The exponential moving average

M4: The exponential moving average of a series {x_t} and smoothing factor α is computed by the following iterative formula:

Here, is the value of the exponential average at t.

The implementation of the ExpMovingAverage class is rather simple. The constructor has a single α argument (the decay rate) (line 12):

class ExpMovingAverage[@specialized(Double) T <: AnyVal](  
    alpha: Double)    //12
    (implicit f: T => Double) 
  extends ETransform[Double](alpha) with MovingAverage[T]{ //13
  
  type U = XSeries[T]    //14
  type V = DblVector    //15

  override def |> : PartialFunction[U, Try[V]] = {
    case xt: U if( xt.size > 0) => {
      val alpha_1 = 1-alpha
      var y: Double = data(0)
      Try( xt.view.map(x => {
        val z = x*alpha + y*alpha_1; y = z; z})) //16
    }
}
}

The exponential moving average implements the ETransform (line 13) by defining the abstract U types for the input (line 14) as a time series named XSeries[T] and V for the output (line 15) as a time series named DblVector. The |> method applies the M4 formula to all the observations of the time series within a map (line 16).

The version of the constructor that uses the p period to compute alpha = 1/(p+1) as an argument is implemented using the Scala apply method:

def apply[T <: AnyVal](p: Int)
     (implicit f: T => Double): ExpMovingAverage[T] = 
  new ExpMovingAverage[T](2/(p + 1))

Let's compare the results generated from these three moving averages methods with the original price. We use a data source, DataSource, to load and extract values from the historical daily closing stock price of Bank of America (BAC), which is available at the Yahoo Financials pages. The DataSink class is responsible for formatting and saving the results into a CSV file for further analysis. The DataSource and DataSink classes are described in detail in the Data extraction section in the Appendix A, Basic Concepts:

import YahooFinancials._
val hp = p >>1
val w = Array.tabulate(p)(n => 
       if(n == hp) 1.0 else 1.0/(Math.abs(n - hp)+1)) //17
val sum = w.sum
val weights = w.map { _ / sum }                          //18

val dataSrc = DataSource(s"$RESOURCE_PATH$symbol.csv", false)//19
val pfnSMvAve = SimpleMovingAverage[Double](p) |>         //20   
val pfnWMvAve = WeightedMovingAverage[Double](weights) |>  
val pfnEMvAve = ExpMovingAverage[Double](p) |>

for {
   price <- dataSrc.get(adjClose)   //21
   if(pfnSMvSve.isDefinedAt(price) )
   sMvOut <- pfnSMvAve(price)         //22
   if(pfnWMvSve.isDefinedAt(price)
   eMvOut <- pfnWMvAve(price)
  if(pfnEMvSve.isDefinedAt(price)
   wMvOut <- pfnEMvAve(price)
} yield {
  val dataSink = DataSink[Double](s"$OUTPUT_PATH$p.csv")
  val results = List[DblSeries](price, sMvOut, eMvOut, wMvOut)
  dataSink |> results  //23
}

The coefficients for the weighted moving average are generated (line 17) and normalized (line 18). The trading data regarding the ticker symbol, BAC, is extracted from the Yahoo Finances CSV file (line 19), YahooFinancials, using the adjClose extractor (line 20). The next step is to initialize the pfnSMvAve, pfnWMvAve, and pfnEMvAve partial functions related to each of the moving average (line 21). The invocation of the partial functions with price as an argument generates the three smoothed time series (line 22).

Finally, a DataSink instance formats and dumps the results into a file (line 23).

The weighted moving average method relies on a symmetric distribution of normalized weights computed by a function passed as an argument of the generic tabulate method. Note that the original price time series is displayed if one of the specific moving averages cannot be computed. The following graph is an example of a symmetric filter for weighted moving averages:

An example of a symmetric filter for weighted moving averages

The three moving average techniques are applied to the price of the stock of Bank of America stock (BAC) over 200 trading days. Both the simple and weighted moving averages use a period of 11 trading days. The exponential moving average method uses a scaling factor of 2/(11+1) = 0.1667:

11-day moving averages of the historical stock price of Bank of America

The three techniques filter the noise out of the original historical price time series. The exponential moving average reacts to a sudden price fluctuation despite the fact that the smoothing factor is low. If you increase the period to 51 trading days (which is equivalent to two calendar months), the simple and weighted moving averages produce a time series smoother than the exponential moving average with alpha = 2/(p+1) = 0.038:

51-day moving averages of the historical stock price of Bank of America

You are invited to experiment further with different smooth factors and weight distributions. You will be able to confirm the following basic rule: as the period of the moving average increases, noise with decreasing frequencies is eliminated. In other words, the window of allowed frequencies is shrinking. The moving average acts as a low-pass filter that preserves only lower frequencies.

Fine-tuning the period of a smoothing factor is time consuming. Spectral analysis, or more specifically, Fourier analysis transforms a time series into a sequence of frequencies, which provide the statistician with a more powerful frequency analysis tool.

   val pfnMv = SimpleMovingAverage[Double](period) |>
   val smoothed = transform(xt, pfnMv)