Measures of center are how we define the middle, or center, of a dataset. We do this because sometimes we wish to make generalizations about data values. For example, perhaps we're curious about what the average rainfall in Seattle is or what the median height for European males is. It's a way to generalize a large set of data so that it's easier to convey to someone.

A measure of center is a value in the "middle" of a dataset.

However, this can mean different things to different people. Who's to say where the middle of a dataset is? There are so many different ways of defining the center of data. Let's take a look at a few.

The arithmetic mean of a dataset is found by adding up all of the values and then dividing it by the number of data values.

This is likely the most common way to define the center of data, but can be flawed! Suppose we wish to find the mean of the following numbers:

import numpy as np

np.mean([11, 15, 17, 14]) == 14.25

Simple enough, our average is 14.25 and all of our values are fairly close to it. But what if we introduce a new value: 31?

np.mean([11, 15, 17, 14, 31]) == 17.6

This greatly affects the mean because the arithmetic mean is sensitive to outliers. The new value, 31, is almost twice as large as the rest of the numbers and, therefore, skews the mean.

Another, and sometimes better, measure of center is the median.

The median is the number found in the middle of the dataset when it is sorted in order, as shown:

np.median([11, 15, 17, 14]) == 14.5
np.median([11, 15, 17, 14, 31]) == 15

Note how the introduction of 31 using the median did not affect the median of the dataset greatly. This is because the median is less sensitive to outliers.

When working with datasets with many outliers, it is sometimes more useful to use the median of the dataset, while if your data does not have many outliers and the data points are mostly close to one another, then the mean is likely a better option.

But how can we tell if the data is spread out? Well, we will have to introduce a new type of statistic.

Measures of center are used to quantify the middle of the data, but now we will explore ways of measuring how "spread out" the data we collect is. This is a useful way to identify if our data has many outliers lurking inside. Let's start with an example.

Consider that we take a random sample of 24 of our friends on Facebook and wrote down how many friends that they had on Facebook. Here's the list:

friends = [109, 1017, 1127, 418, 625, 957, 89, 950, 946, 797, 981, 125, 455, 731, 1640, 485, 1309, 472, 1132, 1773, 906, 531, 742, 621]

np.mean(friends) == 789.1

The average of this list is just over 789. So, we could say that according to this sample, the average Facebook friend has 789 friends. But what about the person who only has 89 friends or the person who has over 1,600 friends? In fact, not a lot of these numbers are really that close to 789.

Well, how about we use the median, as shown, because the median generally is not as affected by outliers:

np.median(friends) == 769.5

The median is 769.5, which is fairly close to the mean. Hmm, good thought, but still, it doesn't really account for how drastically different a lot of these data points are to one another. This is what statisticians call measuring the variation of data. Let's start by introducing the most basic measure of variation: the range. The range is simply the maximum value minus the minimum value, as illustrated:

np.max(friends) – np.min(friends) == 1684

The range tells us how far away the two most extreme values are. Now, typically, the range isn't widely used but it does have its use in application. Sometimes we wish to just know how spread apart the outliers are. This is most useful in scientific measurements or safety measurements.

Suppose a car company wants to measure how long it takes for an air bag to deploy. Knowing the average of that time is nice, but they also really want to know how spread apart the slowest time is versus the fastest time. This literally could be the difference between life and death.

Shifting back to the Facebook example, 1,684 is our range, but I'm not quite sure it's saying too much about our data. Now, let's take a look at the most commonly used measure of variation, the standard deviation.

I'm sure many of you have heard this term thrown around a lot and it might even incite a degree of fear, but what does it really mean? In essence, standard deviation, denoted by s when we are working with a sample of a population, measures how much data values deviate from the arithmetic mean.

It's basically a way to see how spread out the data is. There is a general formula to calculate the standard deviation, which is as follows:

Here:

Before you freak out, let's break it down. For each value in the sample, we will take that value, subtract the arithmetic mean from it, square the difference, and, once we've added up every single point this way, we will divide the entire thing by n, the number of points in the sample. Finally, we take a square root of everything.

Without going into an in-depth analysis of the formula, think about it this way: it's basically derived from the distance formula. Essentially, what the standard deviation is calculating is a sort of average distance of how far the data values are from the arithmetic mean.

If you take a closer look at the formula, you will see that it actually makes sense:

Let's go back to our Facebook example for a visualization and further explanation of this. Let's begin to calculate the standard deviation. So, we'll start calculating a few of them. Recall that the arithmetic mean of the data was just about 789, so, we'll use 789 as the mean.

We start by taking the difference between each data value and the mean, squaring it, adding them all up, dividing it by one less than the number of values, and then taking its square root. This would look as follows:

On the other hand, we can take the Python approach and do all this programmatically (which is usually preferred).

np.std(friends) # == 425.2

What the number 425 represents is the spread of data. You could say that 425 is a kind of average distance the data values are from the mean. What this means, in simple words, is that this data is pretty spread out.

So, our standard deviation is about 425. This means that the number of friends that these people have on Facebook doesn't seem to be close to a single number and that's quite evident when we plot the data in a bar graph and also graph the mean as well as the visualizations of the standard deviation. In the following plot, every person will be represented by a single bar in the bar chart, and the height of the bars represent the number of friends that the individuals have:

import matplotlib.pyplot as plt
%matplotlib inline
y_pos = range(len(friends))

plt.bar(y_pos, friends)
plt.plot((0, 25), (789, 789), 'b-')
plt.plot((0, 25), (789+425, 789+425), 'g-')
plt.plot((0, 25), (789-425, 789-425), 'r-')

The blue line in the center is drawn at the mean (789), the red line on the bottom is drawn at the mean minus the standard deviation (789-425 = 364), and, finally, the green line towards the top is drawn at the mean plus the standard deviation (789+425 = 1,214).

Note how most of the data lives between the green and the red lines while the outliers live outside the lines. Namely, there are three people who have friend counts below the red line and three people who have a friend count above the green line.

It's important to mention that the units for standard deviation are, in fact, the same units as the data's units. So, in this example, we would say that the standard deviation is 425 friends on Facebook.

So, now we know that the standard deviation and variance is good for checking how spread out our data is, and that we can use it along with the mean to create a kind of range that a lot of our data lies in. But what if we want to compare the spread of two different datasets, maybe even with completely different units? That's where the coefficient of variation comes into play.

Example – employee salaries

If we look at the mean and standard deviation of employees' salaries in the same company but among different departments, we see that, at first glance, it may be tough to compare variations.

This is especially true when the mean salary of one department is $25,000, while another department has a mean salary in the six-figure area.

However, if we look at the last column, which is our coefficient of variation, it becomes clearer that the people in the executive department may be getting paid more but employees in the executive department are getting wildly different salaries. This is probably because the CEO is earning way more than an office manager, who is still in the executive department, which makes the data very spread out.

On the other hand, everyone in the mailroom, while not making as much money, are making just about the same as everyone else in the mailroom, which is why their coefficient of variation is only 8%.

With measures of variation, we can begin to answer big questions, such as how spread out this data is or how we can come up with a good range that most of the data falls in.

We can combine both the measures of centers and variations to create measures of relative standings.

Measures of variation measure where particular data values are positioned, relative to the entire dataset.

Let's begin by learning a very important value in statistics, the z-score.

The z-score is a way of telling us how far away a single data value is from the mean.

The z-score of a x data value is as follows:

Where:

Remember that the standard deviation was (sort of) an average distance that the data is from the mean, and, now, the z-score is an individualized value for each particular data point. We can find the z-score of a data value by subtracting it from the mean and dividing it by the standard deviation. The output will be the standardized distance a value is from a mean. We use the z-score all over statistics. It is a very effective way of normalizing data that exists on very different scales, and also to put data in context of their mean.

Let's take our previous data on the number of friends on Facebook and standardize the data to the z-score. For each data point, we will find its z-score by applying the preceding formula. We will take each individual, subtract the average friends from the value, and divide that by the standard deviation, as shown:

z_scores = []

m = np.mean(friends)  # average friends on Facebook
s = np.std(friends)   # standard deviation friends on Facebook

for friend in friends:
    z = (friend - m)/s  # z-score
    z_scores.append(z)  # make a list of the scores for plotting

Now, let's plot these z-scores on a bar chart. The following chart shows the same individuals from our previous example using friends on Facebook, but, instead of the bar height revealing the raw number of friends, now each bar is the z-score of the number of friends they have on Facebook. If we graph the z-scores, we'll notice a few things:

plt.bar(y_pos, z_scores)

This chart makes it very easy to pick out the individuals with much lower and higher friends on an average. For example, the individual at index 0 has fewer friends on an average (they had 109 friends where the average was 789).

What if we want to graph the standard deviations? Recall that we earlier graphed three horizontal lines: one at the mean, one at the mean plus the standard deviation (), and one at the mean minus the standard deviation ().

If we plug in these values into the formula for the z-score, we will get:

Z-score of () =

Z-score of () =

Z-score of ()

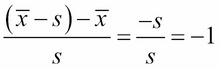
This is no coincidence! When we standardize the data using the z-score, our standard deviations become the metric of choice. Let's see our new graph with the standard deviations plotted:

plt.bar(y_pos, z_scores)
plt.plot((0, 25), (1, 1), 'g-')
plt.plot((0, 25), (0, 0), 'b-')
plt.plot((0, 25), (-1, -1), 'r-')

The preceding code is adding in the following three lines:

The colors of the lines match up with the lines drawn in the earlier graph of the raw friend count. If you look carefully, the same people still fall outside of the green and the red lines. Namely, the same three people still fall below the red (lower) line, and the same three people fall above the green (upper) line.

Under this scaling, we can also use statements as follows:

Z-scores are an effective way to standardize data. This means that we can put the entire set on the same scale. For example, if we also measure each person's general happiness scale (which is between 0 and 1), we might have a dataset similar to the following dataset:

friends = [109, 1017, 1127, 418, 625, 957, 89, 950, 946, 797, 981, 125, 455, 731, 1640, 485, 1309, 472, 1132, 1773, 906, 531, 742, 621]

happiness = [.8, .6, .3, .6, .6, .4, .8, .5, .4, .3, .3, .6, .2, .8, 1, .6, .2, .7, .5, .3, .1, 0, .3, 1]

import pandas as pd

df = pd.DataFrame({'friends':friends, 'happiness':happiness})
df.head()

These data points are on two different dimensions, each with a very different scale. The friend count can be in the thousands while our happiness score is stuck between 0 and 1.

To remedy this (and for some statistical/machine learning modeling, this concept will become essential), we can simply standardize the dataset using a prebuilt standardization package in scikit-learn, as follows:

from sklearn import preprocessing

df_scaled = pd.DataFrame(preprocessing.scale(df), columns = ['friends_scaled', 'happiness_scaled'])

df_scaled.head()

This code will scale both the friends and happiness columns simultaneously, thus revealing the z-score for each column. It is important to note that by doing this, the preprocessing module in sklearn is doing the following things separately for each column:

The result is two columns, as shown, that exist on the same scale as each other even if they were not previously:

Now, we can plot friends and happiness on the same scale and the graph will at least be readable.

df_scaled.plot(kind='scatter', x = 'friends_scaled', y = 'happiness_scaled')

Now our data is standardized to the z-score and this scatter plot is fairly easily interpretable! In later chapters, this idea of standardization will not only make our data more interpretable, but it will also be essential in our model optimization. Many machine learning algorithms will require us to have standardized columns as they are reliant on the notion of scale.

The insightful part – correlations in data

Throughout this book, we will discuss the difference between having data and having actionable insights about your data. Having data is only one step to a successful data science operation. Being able to obtain, clean, and plot data helps to tell the story that the data has to offer but cannot reveal the moral. In order to take this entire example one step further, we will look at the relationship between having friends on Facebook and happiness.

In subsequent chapters, we will look at a specific machine learning algorithm that attempts to find relationships between quantitative features, called linear regression, but we do not have to wait until then to begin to form hypotheses. We have a sample of people, a measure of their online social presence and their reported happiness. The question of the day here is—can we find a relationship between the number of friends on Facebook and overall happiness?

Now, obviously, this is a big question and should be treated respectfully. Experiments to answer this question should be conducted in a laboratory setting, but we can begin to form a hypothesis about this question. Given the nature of our data, we really only have the following three options for a hypothesis:

• There is a positive association between the number of online friends and happiness (as one goes up, so does the other)
• There is a negative association between them (as the number of friends goes up, your happiness goes down)
• There is no association between the variables (as one changes, the other doesn't really change that much)

Can we use basic statistics to form a hypothesis about this question? I say we can! But first, we must introduce a concept called correlation.

Correlation coefficients are a quantitative measure that describe the strength of association/relationship between two variables.

The correlation between two sets of data tells us about how they move together. Would changing one help us predict the other? This concept is not only interesting in this case, but it is one of the core assumptions that many machine learning models make on data. For many prediction algorithms to work, they rely on the fact that there is some sort of relationship between the variables that we are looking at. The learning algorithms then exploit this relationship in order to make accurate predictions.

A few things to note about a correlation coefficient are as follows:

• It will lie between -1 and 1
• The greater the absolute value (closer to -1 or 1), the stronger the relationship between the variables:
  • The strongest correlation is a -1 or a 1
  • The weakest correlation is a 0
• A positive correlation means that as one variable increases, the other one tends to increase as well
• A negative correlation means that as one variable increases, the other one tends to decrease

We can use Pandas to quickly show us correlation coefficients between every feature and every other feature in the Dataframe, as illustrated:

# correlation between variables
df.corr()

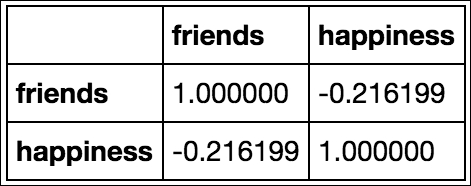
This table shows the correlation between friends and happiness. Note the first two things, shown as follows:

• The diagonal of the matrix is filled with positive is. This is because they represent the correlation between the variable and itself, which, of course, forms a perfect line, making the correlation perfectly positive!
• The matrix is symmetrical across the diagonal. This is true for any correlation matrix made in Pandas.

There are a few caveats to trusting the correlation coefficient. One is that, in general, a correlation will attempt to measure a linear relationship between variables. This means that if there is no visible correlation revealed by this measure, it does not mean that there is no relationship between the variables, only that there is no line of best fit that goes through the lines easily. There might be a non-linear relationship that defines the two variables.

It is important to realize that causation is not implied by correlation. Just because there is a weak negative correlation between these two variables does not necessarily mean that your overall happiness decreases as the number of friends you keep on Facebook goes up. This causation must be tested further and, in later chapters, we will attempt to do just that.

To sum up, we can use correlation to make hypotheses about the relationship between variables, but we will need to use more sophisticated statistical methods and machine learning algorithms to solidify these assumptions and hypotheses.