Chapter 2
Two-point methods
This chapter is devoted to two-point root-finding methods. Traub’s study (Traub, 1964) of two-point methods of third order is the first systematic investigation of multipoint methods. Although these methods are not optimal, in Section 2.1 we give a short review of Traub’s methods for their great influence to the later development of multipoint methods. To demonstrate developing techniques, several different derivations of the Ostrowski method originally proposed in 1960 (the first two-point method of order four) are presented in Section 2.2. Derivation and convergence analysis of two families of optimal two-point methods, proposed by the authors of this book, are presented in Sections 2.3 and 2.4. These families give a variety of fourth-order methods. Aside from the well-known Jarratt methods, in Section 2.6 we present a generalized family of Jarratt’s type that produces many two-point methods of optimal order four. Section 2.7 concerns with optimal two-point methods for finding multiple roots. It is interesting to note that the first two-point methods for multiple roots of optimal order were not constructed until 2009, almost half a century after the first optimal two-point method (Ostrowski, 1960) for finding simple roots.
2.1 Cubically convergent two-point methods
According to Theorem 1.6, any one-point iteration function which depends explicitly on f and its first 
derivatives cannot attain higher order than r, that is, the informational efficiency 
of any one-point method 
cannot exceed 1 even by employing additional derivatives of higher order, where 
is the number of F.E. per iteration. This was the reason and motivation for developing multipoint or multistep methods (both terms are used in the literature). The full benefit of multipoint methods occurs in their increased efficiency, namely, higher order of convergence is attained with fewer F.E. This is possible only by the reuse of information in every iteration step.
2.1.1 Composite multipoint methods
Composite multipoint methods were extensively described in Traub’s book (Traub, 1964). The first two-point methods, based on Theorem 1.3, are illustrated by the following example.
Example 2.1
Let
According to Theorem 1.3, the iterative method defined by the composition
has the order 
. If 
is an initial approximation to the root 
, Newton-Halley’s composite method can be written as
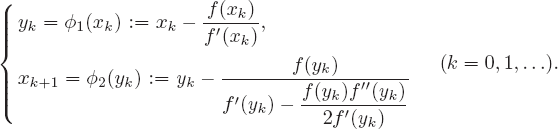(2.1)
We note that this method uses the calculation at two points 
and 
so that it can be referred to as two-point method or two-step method.
The computational efficiencies of Newton’s method 
, Halley’s method 
, and the composite two-step method 
are (in view of (1.13))
Notice that Halley’s method possesses the highest efficiency so that the construction of the composite method in this case is not justified. Any construction of composite I.F. should be performed with a tendency to decrease the number of F.E., inducing the increase of computational efficiency.
Newton’s method has distinction of being most frequently used for the construction of composite multipoint methods. Namely, Newton’s method serves as the first step while the next steps can be constructed in various manners. We will see later that the Steffensen-like method (2.18) or Jarratt’s step
can also be used as the first step. We now present some composite two-point methods with cubic convergence based on Newton’s method.
Let f be a real sufficiently smooth analytic function, defined on an interval 
that contains a simple zero 
of f. Throughout this book we will often use the following quantities and abbreviations:
(2.2)
where 
denotes a divided difference of the first order. Divided differences of higher order are defined recursively. A divided difference of order m, denoted by 
, is defined as
(2.3)
For simplicity, we will sometimes omit iteration indices in iterative formulae and write 
instead of 
, where 
denotes the subsequent approximation. Theorem 1.2 gives a simple way for constructing multipoint methods.
Example 2.2
Let 
be given by Newton’s method 
. Then, according to Theorem 1.2, the I.F.
(2.4)
defines a method of third order.
Example 2.3
Consider an I.F. constructed as a combination of the Newton method and the secant method in the following manner:
Here the derivative 
is replaced by the corresponding divided difference 
. Hence we obtain the Newton-secant two-point method of third order
(2.5)
The two-point method (2.5) can be visualized as the intersection of the x-axis and the secant line set through the points 
and 
, represented by the dashed line in Figure 2.1, where 
.
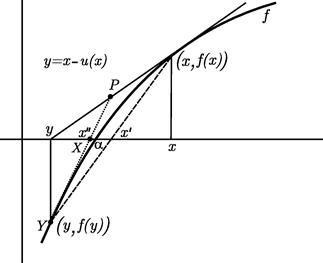
Figure 2.1 Geometric interpretation of some two-point methods
Both two-point methods (2.4) and (2.5) have cubic convergence and require three F.E. Therefore, their computational efficiency is 
. We also note that these methods are not optimal in the sense of the Kung-Traub conjecture (see Section 1.3) assuming that three F.E. should provide the optimal order four. The first optimal two-point method was constructed by Ostrowski (1960), several years before Traub’s extensive investigation in this area described in Traub (1964). Ostrowski’s method and its variants will be presented later, together with some other optimal methods.
2.1.2 Traub’s two-point methods
In his 1964’s book (Traub, 1964), Traub derived a number of cubically convergent two-point methods. One of the presented approaches relies on interpolation, which will be illustrated by several examples.
Let x be fixed and let f be a real function whose zero is sought. We construct an interpolation function 
such that
(2.6)
which makes use of 
values of functions 
. The aim is to substitute the higher order derivatives by lower derivatives of f evaluated at a certain number of points. We do not require that 
is necessarily an algebraic polynomial. A general approach to the construction of multipoint methods of interpolatory type is presented in Traub (1964, Sec. 8.2). To construct two-point methods of third order avoiding the second derivative, we restrict ourselves to the special case when
(2.7)
The condition 
is automatically fulfilled and we only impose that (2.6) holds at the point 
for 
. In this way we obtain the following system of equations
This system has a solution for any 
. For 
, it follows that 
, so that (2.7) becomes
(2.8)
For 
there follows 
, and from (2.7) we get
(2.9)
Let 
be a zero of 
, that is, 
. Putting 
in (2.8), we get
(2.10)
This is an implicit relation in 
. Substituting 
by Newton’s approximation 
on the right-hand side of (2.10), we get the iteration function
(2.11)
On the basis of (2.11) Traub constructed the following iterative method
(2.12)
Note that the iterative method (2.12) was rediscovered much later by Frontini and Sormani (2003) who used the quadrature rule of midpoints
Hence
Assuming that 
is a zero of f, from the last relation there follows
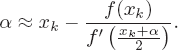
Replacing 
on the right-hand side by Newton’s approximation 
, one obtains Traub’s method (2.12). Note that Homeier (2003) and Özban (2004) also rediscovered this method 40 years after Traub.
Theorem 2.1
The iterative process (2.12) has cubic convergence for sufficiently good initial approximation 
.
Proof 1
Using Taylor’s series we get
Substituting into (2.12) yields
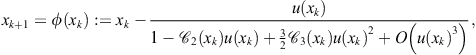
or, after developing into Taylor’s series,
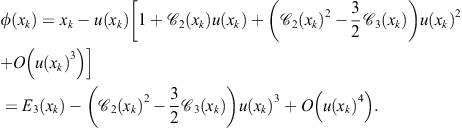
In this manner the I.F. (2.12) reduces to the Schröder basic sequence (more precisely, to the Chebyshev third-order method 
, see Example 1.4). Hence, according to Theorem 1.7, the iterative method (2.12) has cubic convergence. The asymptotic error constant is determined using Theorem 1.8,
Another two-point method can be obtained from (2.9) by taking 
, with 
. Then from (2.9) we get the relation
(2.13)
Replacing 
by 
(Newton’s approximation) on the right-hand side of (2.13), we obtain the two-point method of third order
(2.14)
The proof of cubic convergence of the method (2.14) is similar to that of Theorem 2.1.
Traub’s method (2.14) was rediscovered many years later by Weerakoon and Fernando (2000), who derived this method by the use of numerical integration. Starting from the Newton-Leibniz formula
and applying the trapezoidal rule to estimate the definite integral
one obtains
Assuming that 
is a zero of f, we evaluate 
from this relation and replace the argument of 
by some approximation 
to 
to obtain the iterative formula
This is an implicit relation for 
. Taking 
to be the argument of 
, we get Traub’s two-point method (2.14).
Applying different formulae for numerical integration, some other iterative methods can be obtained. However, they usually appear to be special cases of the already existing methods.
Let us now employ the function 
which is inverse to f, into the interpolation formula (2.9). Then it takes the form
For 
we define 
. Then, due to the relations
we obtain
(2.15)
Replacing 
by the approximation 
, from (2.15) there follows the iterative method of third order
(2.16)
(see Traub, 1964, p. 165). This method was later rediscovered by Homeier (2005) and Özban (2004).
A one-parameter third-order family of two-point methods
was derived by Traub, see Traub (1964, pp. 198–200). In particular, for 
and 
the last iterative formula generates the already presented methods (2.12) and (2.16), respectively.
2.1.3 Two-point methods generated by derivative estimation
The efficiency of multipoint methods is improved by the reuse of information in every iteration. For example, it is possible to substitute higher derivatives by some suitable approximations. Here we describe Traub’s general method from which many particular methods can be derived.
Let 
be an I.F. function of the second order. Assume that 
is of the form
(2.17)
where g is some function to be determined. Then 
, that is, 
.
Let us take g in the form
where 
is a constant. The I.F. (2.17) becomes
(2.18)
Expanding 
into Taylor series, we get
In particular, choosing 
where 
is a zero of f, it follows that 
. Consequently, 
, which means that (2.18) defines a second-order iteration (according to Theorem 1.1). Note that 
produces the well-known quadratically convergent method of Steffensen (1933)
Expanding the denominator in (2.18) into geometric series we arrive at the relation
Taking 
and having in mind that 
, from the last relation we conclude that
(2.19)
For this particular choice of 
, from (2.18) we get the I.F.
(2.20)
which is, according to (2.19), of third order. This I.F. has already been derived as a composition of Newton’s method and the secant method, see (2.5).
We will now consider approximations to the second derivative, which always appears in one-point methods of third order. Using Taylor’s series we find
(2.21)
We recall that the third-order well-known Chebyshev method is the second member of the Schröder basic sequence
(2.22)
Approximating 
by the left-hand side of (2.21), Traub derived a one-parameter family of two-step methods of third order
(2.23)
see Traub (1964, p. 181). The choice 
in (2.23) gives the method
(2.24)
considered later by Kou et al. (2006). The choice 
in (2.23) produces the method
(2.25)
rediscovered by Potra and Pták (1984). There is no essential difference between the methods (2.24) and (2.25).
Substituting 
in (2.21) yields the estimation to the second derivative
(2.26)
Replacing the obtained approximation into Halley’s iterative method
(2.27)
we obtain once more the two-point I.F. of third order
Another approximation to the second derivative is by
Replacing this into the Chebyshev iterative formula (2.22) produces a one-parameter two-point family of iterative methods with cubic convergence
Its asymptotic error constant is (see Traub, 1964, p. 181)
Remark 2.1
Some of the presented two-point third-order methods can be obtained from Chun’s two-parameter family of methods derived in Chun (2007e),
where 
and 
.
The estimation (2.26) can be suitably applied to the well-known Laguerre’s method
We first transform this into the more suitable form
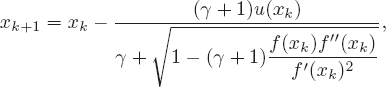(2.28)
where we have introduced a new constant 
and take the sign + in front of the square root. Note that the use of the parameter 
transforms Laguerre’s method into Hansen-Patrick’s family, considered in Hansen and Patrick (1977). Replacing (2.26) into (2.28), we obtain a one-parameter family of two-point iterative methods
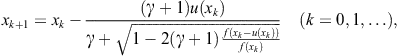(2.29)
which was studied by Petković and Petković (2007c) and Petković et al. (1998).
Theorem 2.2
The iterative method (2.29) is of order three for all values of 
, and of order four for 
.
Proof 2
The proof is based on Theorem 1.1. The Taylor expansion of 
about the point x is
(2.30)
where
Then the I.F. (2.29) reads
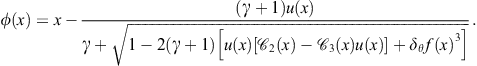(2.31)
Using symbolic evaluation (say, in the computational software package Mathematica or Maple), we establish that 
and
(2.32)
Accordingly, the order of convergence of the family of two-point methods is three for all 
. From (2.32) we find the asymptotic error constant
It is obvious from (2.32) that for the particular value 
we get 
, which means that this value of 
gives the two-point method of fourth order of Euler-Cauchy’s type (see (1.23)). This method reads
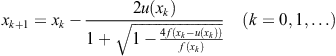(2.33)
and its asymptotic error constant is
Remark 2.2
The iterative method identical to (2.29) was recently rediscovered by Sharma and Guha (2011) starting from Hansen-Patrick’s method (1.25).
All methods from the two-point family (2.29) for 
require three F.E. per iteration and have the computational efficiency
the same one as the previously considered two-point methods and one-point cubically convergent methods presented in Section 1.5. The iterative method (2.33), obtained for 
, possesses the highest computational efficiency since it is of fourth order. For this method we have 
. We also observe that, substituting back the approximation (2.26) in (2.33), we get the third-order method
(2.34)
known in the literature as Euler-Cauchy’s method.
Rewrite (2.29) in the equivalent form
then it is easy to check that the limit 
gives the Newton-secant two-point method
(2.35)
of third order, stated by Traub (1964), see (2.5).
Taking 
in (2.29) we obtain the method
(2.36)
Using the approximation (2.26), from (2.36) we find
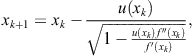
which is the well-known square-root method or Ostrowski’s method stated by Ostrowski (1960), see also Petković and Petković (1993). Therefore, the iterative method (2.36) could be regarded as the Ostrowski-like method.
If we let 
in (2.29), then we obtain Newton’s method of second order. Therefore, choosing large values of 
will slow down the convergence speed of the family (2.29).
Example 2.4
We have compared the methods from the family (2.29) for 
(the fourth-order method (2.33)), 
(method (2.36)), 
(method (2.34)) and Newton’s method (
) with the two-point methods (2.12), (2.14), (2.16), and (2.24) of third order. Beside these methods, we have also tested the fourth-order method of Ostrowski (1960)
(2.37)
developed in 1960. All tested methods require three F.E. per iteration.
We have applied the mentioned methods for finding zeros of the following six functions:
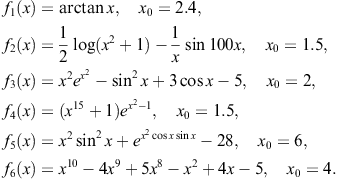
The listed functions have been tested by Mathematica in multi-precision arithmetic. The stopping criterion has been given by 
.
Let 
be the zero of the function 
. Most methods converge to the zeros
However, there are five exceptions stressed in Table 2.1 by the comments (1)–(5) and listed below the table. The term div points to the divergence and 
means that 
in the kth iteration.
Table 2.1 Results of numerical experiments
(2)
(1)
.
(4)
(5)
.
(3)
Observe that the family (2.29) possesses the square root structure which enables finding a complex zero of real functions having conjugate complex zeros, especially in solving algebraic equations. In that case, a mathematical computation system of Mathematica automatically continues to work in complex arithmetic. The same happens when an initial approximation produces negative value under the square root. In most cases the square root methods, such as the family (2.29), overcome this difficulty producing in complex arithmetic an approximation 
to a real zero 
, where 
(to the wanted accuracy) and b is a very small number in magnitude (“parasite” part) that should be neglected.
We conclude this section with the comment that most of the discussed two-point methods of third order were constructed by Traub (1964) but later rediscovered by other authors. This fact was the subject of several papers, see, e.g., Chun (2007b), Chun and Neta (2009b), and Petković and Petković (2007a).
2.2 Ostrowski’s fourth-order method and its generalizations
The consideration in the previous section shows that most of the presented two-point methods possess the computational efficiency 
, which is equivalent to the one-point iterative methods of third order, such as Halley’s, Laguerre’s, Euler’s, or Chebyshev’s. However, since these methods require the evaluation of the first and the second derivative of a function, two-point methods are advantageous always when the evaluation of derivatives is not simple. On the other hand, if an initial approximation 
is not sufficiently close to the sought zero, then the predictor employed in the first step (usually Newton’s approximation) cannot provide a qualitative improvement to the approximation in the second step. Figure 2.2 displays an extreme case when the sought zero is overshot due to the poor choice of the initial approximation outside of the range of convergence.
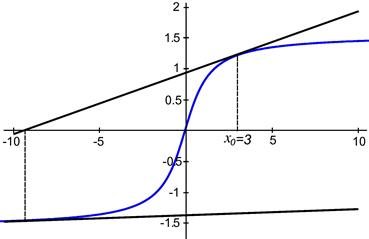
Figure 2.2 The overshooting problem of Newton’s method; 
A significant advance in the construction of efficient two-point methods was achieved by two-point methods that require only three F.E. yet attain order four. This means that such methods support the Kung-Traub hypothesis (see Section 1.3) and reach optimal order of convergence. Their computational efficiency is 
.
Let 
be a real analytic function defined on some interval 
that contains a simple zero 
of f, and let us assume that 
does not vanish on 
. As in Section 1.3, we will use the notation 
to denote the class of iteration functions 
which generate n-step iterative methods with the optimal order of convergence 
with fixed 
. In this section we present some two-step methods of fourth order from the class 
.
The first optimal two-point method was constructed by Ostrowski (1960), several years before Traub’s extensive investigation in this area. For its historical importance, but also for its good convergence properties, we devote a special attention to this method in this chapter. Ostrowski (1960, Ch. 11, App. G) derived his two-point method (2.37) using the interpolation of a given function f by a linear fraction
(2.38)
at three interpolation points 
, and 
, where 
and d are constants. Let 
and assume that 
. It is well-known from projective geometry that if w is related to x by (2.38), then the following relation is valid,
(2.39)
that is, the points 
have the same cross ratio as the points 
. By introducing
(2.40)
from (2.39) we find
(2.41)
The function w given by (2.38) should be determined by three points 
so that the conditions 
are satisfied. However, since we want to construct a two-point method using only two points, we will consider the case where two of 
coincide, for example, 
. We assume that 
, and 
are known and 
. The corresponding interpolating function w is determined as the limit of 
and (2.41) as 
. From (2.40) and (2.41) one obtains
(2.42)
(2.43)
It is easy to verify that 
satisfies the conditions
Let 
. Solving (2.43) with respect to x, we get a function 
, implicitly expressed by
(2.44)
Hence
(2.45)
Let 
be a zero of f, that is, 
. Then we can take 
(for 
) as the new approximation to 
. Putting 
in (2.45), we obtain
(2.46)
Now let us choose 
to be Newton’s approximation, that is,
Then from (2.42) it follows that 
and we get from (2.46)
Substituting 
by 
by 
, and 
by 
, we obtain Ostrowski’s two-point method
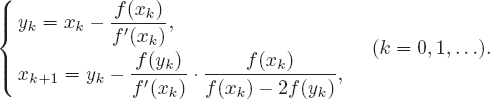(2.47)
This iterative formula is equivalent to (2.37).
Ostrowski’s method can also be derived starting from double Newton’s method
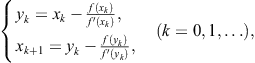(2.48)
and replacing 
by a suitable approximation which does not require new information. Let us emphasize that (2.48) is not a proper two-point method but Newton’s method successively applied two times. In fact, we use (2.48) as an auxiliary scheme in constructing optimal two-point methods. We shall encounter similar schemes again in Chapter 4.
First we apply Hermite’s interpolating polynomial of second degree
(2.49)
where the coefficients 
, and 
are determined from the conditions
(2.50)
According to (2.50) we find
Now we obtain
and substituting 
yields after short arrangement
(2.51)
Replacing the derivative 
in the second step of (2.48) by 
given by (2.51), one obtains Ostrowski’s two-point method (2.47).
Another derivation of Ostrowski’s method can be obtained using suitable approximations arising from Taylor’s series. Let 
. Since
we have
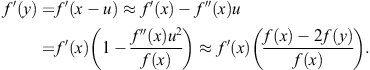
Replacing this approximation of 
in the second step of (2.48), we obtain (2.47).
The approximation of 
can be obtained by combining the Newton-Leibniz formula
and the quadrature rule
Taking 
in the last quadrature formula, we obtain the system of linear equations
, so that
(see (2.51)). The substitution of this approximation of 
in (2.48) leads to the Ostrowski method (2.47).
Finally, we derive Ostrowski’s method by a geometric approach using Figure 2.1. Let the point 
bisect the line segment determined by the points 
and 
, where
is Newton’s approximation. In fact, this segment is a part of the tangent line at 
. A new approximation 
is the intersection of the x-axis and the secant line drawn through the points P and 
(dotted line in Figure 2.1). From the similarity of the right-angle triangles (with hypotenuses 
and 
), from Figure 2.1 we observe that the equality
holds. Solving the last equation for 
, we obtain Ostrowski’s two-point method upon setting 
.
We have demonstrated geometric construction of Ostrowski’s method (2.47). Many new and old iterative methods can also be derived by geometric techniques. As well-known, Newton’s method may be geometrically constructed by the point of intersection of the tangent line to the graph of 
at the point 
with x-axis. Halley’s method (1.20) is geometrically interpreted by tangent hyperbolas, see Salehov (1952), while Euler-Cauchy’s method (1.23) may be derived finding the point of intersection of a quadratic parabola with x-axis, etc. Chun and Kim (2010) have used the circle of curvature, a fundamental concept in differential geometry, to derive the following third-order method of simple form,
where 
.
Chun (2007b) has developed a new I.F. geometrically, as follows. Let 
be a fixed parameter and let 
be an I.F. of second order. Let 
denote the intersection of the x-axis and the line passing through two points 
and 
. Then
(2.52)
The next theorem was proved in Chun (2007b).
Theorem 2.3
Let 
be a simple zero of f and let 
be an I.F. of second order such that 
is continuous in a neighborhood of 
. Then the order of the I.F. 
given by (2.52) is at least three when 
and at least four if
Chun gives two examples of I.F. of fourth order. Taking Newton’s I.F. 
, it follows from (2.52) with 
which is the Ostrowski method of fourth order (2.47). Note that the condition 
of Theorem 2.3 is satisfied in the case of Newton’s method so that the order four could have been predicted.
The second example uses quadratically convergent method
considered by Mamta et al. (2005). This method also gives 
and the corresponding method
is of fourth order (according to Theorem 2.3), where
Note that a two-step method of order three can be generated from (2.52) using the Newton-like I.F.
(with 
).
Observe that Ostrowski’s method (2.47) can be obtained as a special case of many families of two-point methods developed later. This fact points that Ostrowski’s method could be regarded as an “essential method” which makes the “core” of many families of two-point methods. Since this method often gives the best results in practice in the class of methods with similar characteristics, this assertion is justified to a large extent.
Theorem 2.4
The iterative process (2.47) is of fourth order for a sufficiently close initial approximation 
.
Proof 3
From Taylor’s expansion of f, we get (omitting the argument x)
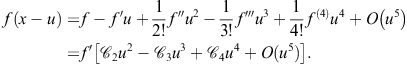(2.53)
According to this, we have
(2.54)
Using (2.53) and (2.54), we obtain
(2.55)
Taylor’s series gives
and substituting this expression back into (2.55), we obtain
According to this, the I.F. 
in (2.37) can be written in the form
To prove the fourth order of convergence of Ostrowski’s method (2.47), we use Theorem 1.8. We note that the member 
in Schröder’s basic sequence generated by (1.27) is given by
(2.56)
Since 
when 
and
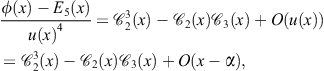
it follows that the limit
exists and it is not 0. In view of Theorem 1.8 it follows that Ostrowski’s two-point method (2.47) has order of convergence equal to four and the asymptotic error constant is given by
Remark 2.3
Note that Traub (1964, p. 184) gave the error relation (without proof)
pointing to the fourth order of the method (2.47). The expression on the right-hand side gives the asymptotic error constant.
Remark 2.4
According to the above consideration, we see that Ostrowski’s two-point method (2.47) belongs to the class 
of optimal methods of order 
with 3 function evaluations. Note that good convergence behavior of Ostrowski’s method has been demonstrated by Yun and Petković (2009), where initial approximations were provided by Yun’s efficient method based on numerical integration of sigmoid-like functions; see Yun (2008) and Section 1.4.
A generalization of Ostrowski’s method (2.47) was proposed by King (1973a) in the form
(2.57)
where 
is a parameter. King’s family (2.57) of two-point methods is optimal and has the order four. It is easy to see that Ostrowski’s method (2.47) is a special case of (2.57) for 
.
One of several derivations of King’s family (2.57) goes as follows. We start from the expression
(2.58)
and, using (2.53) and Taylor’s series, in a similar manner as in the proof of Theorem 2.4 we find
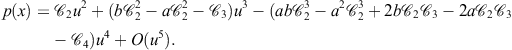
Then we have
(2.59)
Since the member 
of the Schröder basic sequences 
is given by
(2.60)
(see Section 1.5), by comparing the expressions (2.59) and (2.60) we conclude that the method 
will reach fourth order if 
. Setting 
and 
in (2.58) we obtain King’s family 
given by (2.57). Using these values of the parameters we find the asymptotic error constant
We have mentioned that Ostrowski’s method (2.47) follows from King’s family (2.57) for 
. The following two rediscovered optimal methods are also special cases of King’s family:
:
:
Remark 2.5
Some other rediscovered iterative formulae, in a less obvious form, can also be obtained from King’s family (2.57). For example, the family of two-point methods of the form
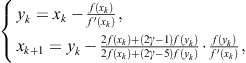
was presented by Chun and Ham (2008b). Introducing 
and 
, it is easy to see that this method is equivalent to King’s method (2.57).
Regarding the second step of (2.48) and the iterative formula (2.57), we observe that the derivative 
is approximated in the following way:
(2.63)
Some variants of King’s family (2.57), based on different approximations to 
, were presented by Chun (2007c). Assuming that the quotient 
is a reasonably small quantity, the right-hand side of (2.63) can be expanded into series
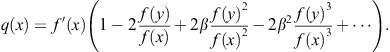(2.64)
Taking the first three terms in (2.64) to approximate q in (2.63), Chun (2007c) obtained the family of two-point methods of fourth order,
(2.65)
It is obvious that the family (2.65) reduces to (2.47) for 
.
Another Chun’s family (Chun, 2007a) belonging to 
is given by the iterative formula
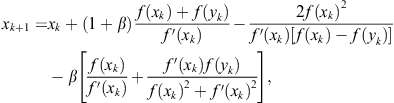
where 
. Substituting 
yields the method (2.61).
Note that Kou et al. (2007c) derived the following two-parameter method,
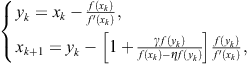
and showed that this family is of third order for any 
. In particular, for 
, this method attains the order four. However, in this special case the above family reduces to King’s family (2.57).
One more comment. Ostrowski’s method (2.47) can be obtained as a special case from many two-point methods belonging to the class 
, for instance, in the case of King’s method (2.57). Another example is the Chun-Ham family (Chun and Ham, 2007a)
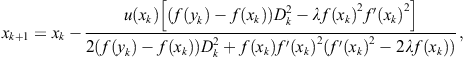
where
and 
. Ostrowski’s method (2.47) is obtained for 
.
We end this section with two methods of King-Ostrowski’s type. First we present a two-point method developed by Chun and Neta (2009b) by using the method of undetermined coefficients. Let 
stand for any second-order method. The iterative scheme
(2.66)
has order four, see Traub (1964), possessing the same computational efficiency as standard Newton’s method. To derive a new method of higher efficiency, Chun and Neta (2009b) have considered the expression
(2.67)
Let 
. By Taylor’s series we obtain
Substituting the expressions on the right-hand sides of the above expansions in (2.67) and upon comparing the coefficients of f and its derivatives at 
, the following system of equations is obtained:
The solution of this system is
Putting these values into (2.67), the following method follows from (2.66)
(2.68)
where 
is calculated by any second-order method.
It was proved in Chun and Neta (2009b) that the order of convergence of the two-point method (2.68) is four. The iterative method (2.68) can be regarded as a generalization of Ostrowski’s method (2.47). In particular, if we take the Newton iteration as first step, that is,
then the method (2.68) reduces to the Ostrowski method (2.47).
The second method of King-Ostrowski’s type is due to Kou et al. (2007a). Combining Potra-Pták’s third-order method (Potra and Pták, 1984)
(2.69)
and Sharma’s third-order method (Sharma, 2005)
(2.70)
Kou et al. (2007a) stated the following one-parameter two-point method
(2.71)
where
is Newton’s approximation and 
. Obviously, for 
formula (2.71) becomes (2.69), while the choice 
gives (2.70).
Other values of 
produce methods of third order, which are not of practical interest since they require three F.E. and attain the efficiency index 
. However, the choice 
in (2.71) delivers the two-point method
(2.72)
of order four. The method (2.72) is a special case of King’s method setting 
in (2.57), see (2.61).
2.3 Family of optimal two-point methods
In this section we present a family of two-point methods, proposed in the paper Petković and Petković (2010). Consider again the composite two-step scheme (2.48) with a reasonably good initial approximation 
. The presented double Newton’s scheme is simple and its rate of convergence is equal to four, which is a consequence of the fact that Newton’s method is of second order and Theorem 1.3.
It is obvious that the computational efficiency of the iterative scheme (2.48) is the same as that of Newton’s method. This “naive” two-step method requires four F.E. per iteration. To reduce the number of evaluations and thus increase the computational efficiency, Chun (2008) introduced a useful technique for approximating the first derivative using a suitably chosen weight function h,
where 
. Here h is a real-valued function to be chosen so that the two-point method
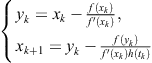(2.73)
is of order four. Chun showed that any function h, satisfying 
, and 
, provides the fourth order of the two-point iterative scheme (2.73).
The presented idea is both simple and fruitful. Sometimes it is necessary to develop the function h into Taylor’s or geometric series to generate suitable (both new and existing) iteration functions. Chun (2008) listed the following examples:
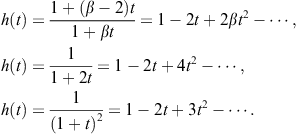
A slightly more direct approach without altering the weight function, considered in Petković and Petković (2010), is based on Chun’s idea to approximate 
by
assuming that a real-weight function g and its derivatives 
and 
are continuous in the neighborhood of 0. Now the two-step scheme (2.48) becomes
(2.74)
The weight function g in (2.74) has to be determined so that the two-point method (2.74) attains the optimal order four using only three function evaluations: 
, and 
. This is the subject of the following theorem (see Petković and Petković, 2010).
Theorem 2.5
Let 
be a simple zero of a real single-valued function 
possessing a certain number of continuous derivatives in the neighborhood of 
, where 
is an open interval. Let g be a function satisfying 
and 
. If 
is sufficiently close to 
, then the order of convergence of the family of two-step methods (2.74) is four and the error relation
(2.75)
holds.
Proof 4
Let 
as before and let us introduce the errors
Expanding f into Taylor’s series about 
, we find
(2.76)
Hence, applying again Taylor’s series to 
, we get
(2.77)
Furthermore, we have
(2.78)
Let us approximate the function g by its Taylor’s polynomial of second degree at the point 
,
(2.79)
Now, using (2.76)–(2.79), we find for 
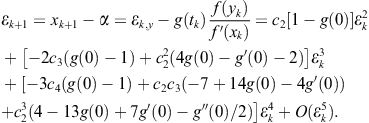
Substituting the conditions 
and 
of the theorem in the expression for 
, we obtain
which is exactly the error relation (2.75). Hence we conclude that the order of the family (2.74) is four. 
Remark 2.6
From (2.75) we notice that the asymptotic error constant of the method (2.74) is
To determine the corresponding expression of the asymptotic error constant in the case of a particular method obtained by choosing a specific function g, it is necessary to find 
and substitute this value in the above expression. For example, for King’s method (2.57) we have
and hence 
.
We give some special cases of the two-point family (2.74) of methods. This family produces a variety of new methods as well as some existing optimal two-point methods which appear as special cases. The chosen function g in the subsequent examples satisfies the conditions 
and 
, given in Theorem 2.5. We write 
for short.
Method 2.1. For g given by
we obtain King’s fourth-order family of two-point methods given by (2.57). Recall that King’s family produces as special cases Ostrowski’s method (2.47)
, Kou-Li-Wang’s method (2.61)
and Chun’s method (2.62)
.
Method 2.2. Choosing g in the form
one obtains a family of fourth-order methods
(2.80)
Taking 
in (2.80) we get Chun’s method (2.62), while the choice 
gives Ostrowski’s method (2.47). The choice 
gives the iterative method
(2.81)
Method 2.3. For g defined by
we obtain a one-parameter family of two-point methods
(2.82)
Substituting 
in (2.82) yields Ostrowski’s method (2.47).
Method 2.4. The choice
gives a family of optimal two-point methods defined by the I.F.
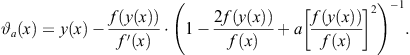(2.83)
Ostrowski’s method (2.47) is obtained as a special case putting 
in (2.83). In fact, the method (2.83) is Chun’s method (2.65) with 
.
Method 2.5. Choosing
we construct the I.F.
(2.84)
which defines a one-parameter family of two-point methods 
of order four. Taking 
in (2.84), we obtain Maheshwari’s method (Maheshwari, 2009) as a special case,
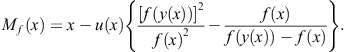(2.85)
Method 2.6. The weight function
satisfies the conditions of Theorem 2.5 in a limit case when 
and produces the fourth-order method of Euler-Cauchy’s type
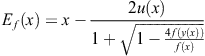(2.86)
proposed in Petković and Petković (2007c) and already discussed in Section 2.1, see (2.33).
Remark 2.7
Cordero et al. (2010) presented the optimal two-point fourth-order method in the form
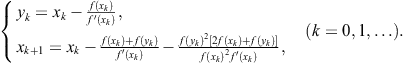
This method is referred to as modified Potra-Pták method after Potra-Pták method (2.25). However, the above two-point method is a special case of the family (2.74) for 
. Moreover, the addend 
, which follows after 
in the second step, can be omitted (that is, taking 
) preserving order four. Then the second step takes a simple form
which can be obtained from Ostrowski’s method (2.47) by approximating 
.
Example 2.5
The convergence behavior of some optimal two-point methods, considered in this section, has been tested using the function
for finding its zero 
which lies in the interval [2,5]. We have chosen the initial approximation 
. The computational software package Mathematica with multi-precision arithmetic has been employed.
Table 2.2 contains absolute values of the errors of approximations in the first three iterations, where 
means 
. This table also contains the entries of the computational order of convergence, evaluated by (1.10).
Table 2.2 Example 2.5 – 
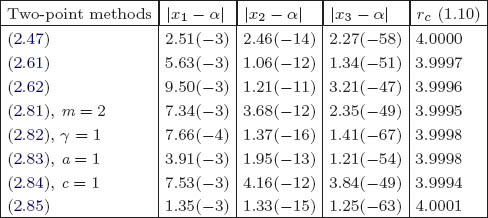
2.4 Optimal derivative free two-point methods
In many real-life problems it is preferable to avoid calculations of derivatives of f. The classical Steffensen’s method (Steffensen, 1933)
(2.87)
derived from Newton’s method
by substituting the derivative 
with the ratio
is an example of a derivative free root-finding method. The efficiency index of Steffensen’s method is 
, the same as that of Newton’s method.
In this section we consider a family of derivative free two-point methods without memory of order four. Its variant with memory is studied in Chapter 6. Some of the presented results are studied in Petković et al. (2010c). In general, derivative free methods are useful for finding zeros of a function f when the calculation of derivatives of f is complicated and expensive.
Let
where 
is an arbitrary real constant. Upon expanding 
into Taylor’s series about x, we arrive at
Hence, we obtain an approximation to the derivative 
in the form
(2.88)
studied many years ago in Traub (1964, p. 178).
To construct derivative free two-point methods of optimal order, let us start from the double Newton’s method (2.48). It is well-known that the iterative scheme (2.48) is inefficient and our primary aim is to improve its computational efficiency. We also wish to substitute derivatives 
and 
in (2.48) by convenient approximations. This replacement can be carried out at the first step using the approximation (2.88) to 
. The derivative 
in the second step of (2.48) will be approximated by 
, where 
is a differentiable function that depends on two real variables
Therefore,
(2.89)
(2.90)
Starting from the iterative scheme (2.48) and using (2.89) and (2.90), we construct the following family of two-point methods (Petković et al., 2010c)
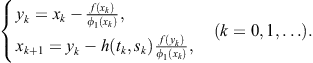(2.91)
The weight function h should be determined in such a way to provide the fourth order of convergence of the two-point method (2.91).
Let 
denote the error of approximation calculated in the kth iteration. In our convergence analysis we will omit sometimes the iteration index k for simplicity. A new approximation 
to the root 
will be denoted with 
. Let us introduce the errors
We will use Taylor’s expansion about the root 
to express 
, and 
as series in 
. Then we represent 
and 
by Taylor’s polynomials in 
.
Assume that x is sufficiently close to the zero 
of f, then s and t are very small quantities in magnitude. Let us represent a real function of two variables h appearing in (2.91) by Taylor’s series about (0, 0) in a linear form,
(2.92)
where 
and 
denote partial derivatives of h with respect to t and s. It can be proved that the use of partial derivatives of higher order does not provide faster convergence (greater than four) of two-point methods without memory.
Expressions of Taylor’s polynomials (in 
) of functions involved in (2.91) are cumbersome and lead to tedious calculations, which requires the use of a computer. If a computer is employed anyway, it is reasonable to perform all calculations necessary in finding the convergence rate using symbolic computation, as done in what follows. Such an approach was used in Thukral and Petković (2010) and later papers. Therefore, instead of presenting explicit expressions in the convergence analysis we use symbolic computation in Mathematica to find candidates for h. If necessary, intermediate expressions can always be displayed during this computation using the program given below, although their presentation is most frequently of academic interest.
We will find the coefficients 
of the expansion (2.92) using a simple program in Mathematica and an interactive approach explained by the comments C1, C2, and C3. First, let us introduce abbreviations used in this program.
, 
, 
, 
,
, 
, 
,
, 
, 
, 
, 
.Program (written in Mathematica)
fx = f1a∗(e + c2∗eˆ2 + c3∗eˆ3 + c4∗eˆ4);
fxi = f1a∗((e + g∗fx)+c2∗(e + g∗fx)ˆ2 + c3∗(e + g∗fx)ˆ3);
fi = Series[(fxi-fx)/(g∗fx),{e,0,2}];
ey = e-g∗fxˆ2∗Series[1/(fxi-fx),{e,0,2}];
fy = f1a∗(ey + c2∗eyˆ2 + c3∗eyˆ3);
e1 = ey-(h0 + ht∗t + hs∗s)∗Series[fy/fi,{e,0,3}]//Simplify;
Out[A2]= c2(1 + g f1a)(1-h0)
h0 = 1; A3 = Coefficient[e1,eˆ3]//Simplify
Out[A3]=
(2+
(1-ht)-ht-hs-g f1a (-3 + 2ht + hs))
ht = 1; hs = 1; A4 = Coefficient[e1,eˆ4]//Simplify
Out[A4]=
Comment C1: From the expression for the error 
we observe that 
is of the form
(2.93)
The iterative two-point method (2.91) will have order four if the coefficients of the expansion (2.92) are chosen so that 
and 
(in (2.93)) vanish. We find these coefficients equating shaded expressions in the boxed formulae to 0. First, from Out[A2] we set 
and then calculate 
.
Comment C2: From Out[A3] we see that the term 
can be eliminated only if we choose 
. With this value the coefficient 
will vanish if we take 
.
Comment C3: Substituting the entries 
in the expression of e1 (
), we obtain
or, using the iteration index,
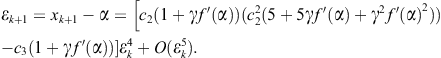(2.94)
Therefore, to provide the fourth-order of convergence of the two-point methods (2.91), it is necessary to choose the function of two variables h so that its truncated expansion (2.92) satisfies
(2.95)
According to the above analysis we can formulate the following convergence theorem.
Theorem 2.6
Let 
be a differentiable function of two variables that satisfies the conditions 
. If an initial approximation 
is sufficiently close to a zero 
of a function f, then the order of the family of two-point methods (2.91) is equal to four.
Let us study the choice of the weight function h in (2.91). Considering (2.95), we see that the simplest form of h is obviously
(2.96)
Note that any function of the form 
, where g is a differentiable function such that 
, satisfies the condition (2.95). For example, we can take 
(
is a parameter), 
, and so on. The two-parameter function 
also satisfies the condition (2.95).
Other examples of usable functions are as follows:
(2.97)
(2.98)
(2.99)
(2.100)
It is easy to check that these functions satisfy the conditions (2.95).
Remark 2.8
The family of two-point methods (2.91) requires three F.E. and has order of convergence four. Therefore, this family is optimal in the sense of the Kung-Traub conjecture and possesses the computational efficiency 
.
Remark 2.9
According to (2.94), we find the asymptotic error constant
However, this expression is valid if the Taylor series of h is truncated to the polynomial form (2.96). For any other particular function h, the asymptotic error constant takes a specific expression. For example, choosing 
(formula (2.97)) we find the asymptotic error constant
Remark 2.10
We speak about the family (2.91) since the choice of the free parameter 
and various weight functions h, satisfying the conditions (2.95), provides a variety of two-point methods.
Remark 2.11
Peng et al. (2011) displayed (without derivation) the following derivative free two-point method of fourth order,
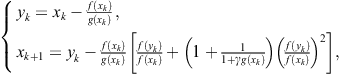
where 
coincides with 
given by (2.88) and 
is a real parameter. It is easy to show that this method is a special case of the family (2.91) with the basic choice
Remark 2.12
Sharma and Goyal (2006) have shown that the derivative free two-point method
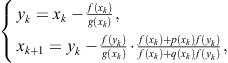
where
has order four. To avoid any additional calculations, it is preferable to choose 
as a constant. Therefore, without loss of generality, we can adopt that 
The Sharma-Goyal method can be obtained from the family (2.91) taking
and 
in (2.88), providing 
. Moreover, the family (2.91), with 
chosen as above, can deal with arbitrary 
, that is, we may replace 
by 
given by (2.88).
Now we will present a derivative free two-point method of optimal order four related to the family (2.91). Starting from the Steffensen-Newton scheme
(2.101)
of fourth order, Ren et al. (2009) eliminated 
using only available information. In this way, they derived a two-point method of order four costing three function evaluations. Using an interpolating polynomial
and the conditions
(2.102)
where 
, the following approximation is obtained:
(2.103)
Here 
is an arbitrary parameter. Substituting (2.103) into (2.101), the derivative free two-point method of the form
(2.104)
was stated and the following theorem was proved in Ren et al. (2009).
Theorem 2.7
(Ren et al., 2009) Let 
be a simple zero of a sufficiently differentiable function 
for an open interval 
. If 
is sufficiently close to 
, then the class of methods defined by (2.104) is of fourth order, and satisfies the error relation
(2.105)
Observe from the error relation (2.105) that the parameter a does not influence the order of convergence considering (2.104) as a method without memory. This is also clear from the estimations
Namely, the term 
in the denominator of (2.104) is of higher order and can be neglected. This is equivalent to the choice 
in the iterative scheme (2.104). Practical examples justify such conclusion. Finally, note that the approximation (2.103) with 
can be obtained using Newtonian interpolation, see (2.107).
Remark 2.13
Regarding (2.105), a modified method with slightly improved convergence order could be constructed calculating 
. It is assumed that 
, and 
are approximated using data from the previous and current iteration. However, this approach is rather artificial and awkward and gives only slight acceleration of convergence. More efficient accelerating methods are studied in Chapter 6.
Let us compare the Ren-Wu-Bi method (2.104) with 
and the family (2.91) with 
. The first step for both methods is the Steffensen method (2.87). The second step of (2.104)a=0 may be written in the form
where 
is the already mentioned function (2.99) and 
is given by (2.88) for 
. Therefore, the Ren-Wu-Bi method (2.104) for 
can be derived from the family (2.91) as a special case for
This also means that a simpler interpolation function of the form
and the conditions (2.102) can be used for the approximation of 
in (2.103). It is easy to check that the two-point method (2.104)a=0 is obtained in this manner.
Cordero and Torregrosa (2011) approximated the derivative 
in the Steffensen-Newton scheme (2.101) in the following way,
where 
, and 
are real parameters. They proved that the obtained derivative free family of two-point methods is of order four if 
and 
and the error relation
holds. However, it is easy to show that this method is only a special case of Ren-Wu-Bi’s family (2.104) for 
. Consequently, the above error relation reduces to (2.105) for 
.
An additional observation about the Ren-Wu-Bi method (2.104) for 
. This special case has appeared as a starting point in developing a new method in the paper of Liu et al. (2010). Namely, having in mind that
Liu et al. (2010) use a simple approximation of the form 
(for small 
) and find
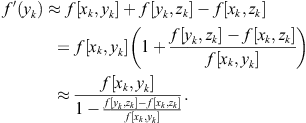
Returning back into 
yields the derivative free two-point fourth-order method,
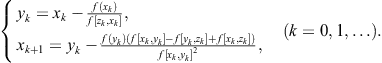
From the previous consideration we can observe that several methods for constructing two-point methods have been used: interpolation by bilinear function, Hermite’s interpolation, approximation of the derivative, interpolating polynomials. We shall deal with inverse interpolation in Section 2.5. Now we demonstrate another approach based on Newton’s interpolation with divided differences. Let the first step in (2.48) be represented by Steffensen’s method (2.87). We calculate the next approximation by
(2.106)
is Newton’s interpolating polynomial of second degree that satisfies the conditions
where 
. Hence
(2.107)
Using (2.87) and (2.107), the following two-point method is stated
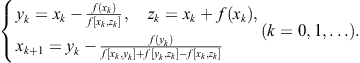(2.108)
In this manner we derived the Ren-Wu-Bi method (2.104) for 
. The iterative method (2.108) can also be obtained as a special case of the family (2.91) for 
and 
.
2.5 Kung-Traub’s multipoint methods
A fundamental and one of the most influential papers in the topic of multipoint methods for solving nonlinear equations is certainly Kung-Traub’s paper (Kung and Traub, 1974). Aside from the famous conjecture on the upper bound of the order of convergence of multipoint methods with fixed number of F.E. (see Section 1.3), this paper presents two optimal multipoint families of iterative methods of arbitrary order. These general families will be studied in later chapters together with their convergence analysis. However, frequent use and citation of these families, called K-T family for brevity, imposes their short introduction. We present Kung-Traub’s families in the form given in Kung and Traub (1974).
K-T (2.109): For any m, define iteration function 
as follows: 
and for 
,
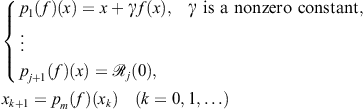(2.109)
for 
, where 
is the inverse interpolating polynomial of degree at most j such that
Let us note that the family K-T (2.109) requires no evaluation of derivatives of f. The order of convergence of the family K-T (2.109), consisting of 
steps, is 
.
K-T (2.110): For any m, define iteration function 
as follows: 
, and for 
,
(2.110)
for 
, where 
is the inverse interpolating polynomial of degree at most j such that
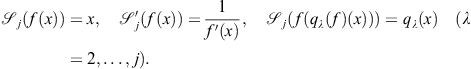
The order of convergence of the family K-T (2.110), consisting of 
steps, is 
.
Remark 2.14
in (2.109) and 
in (2.110) are only initializing steps and they do not make the first step of the described iterations.
In this chapter we study two-point methods so that it is of interest to present two-point methods obtained as special cases of the Kung-Traub families (2.109) and (2.110). First, for 
we obtain from (2.109) the derivative free two-point method
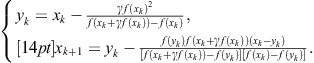(2.111)
The two-point method (2.111) is of fourth order and requires three F.E. so that it belongs to the class 
of optimal methods.
The iterative scheme (2.111) can be rewritten in the form
(2.112)
where 
and 
. Comparing (2.112) to (2.91) with h given by (2.98), we observe that the family (2.91) is a generalization of the Kung-Traub two-point method (2.111).
Taking 
in (2.110), we obtain Kung-Traub’s two-point method of fourth order,
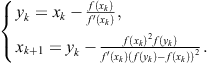(2.113)
Note that the family (2.74) is a generalization of Kung-Traub’s method (2.113), which follows from this family taking 
in (2.80) or 
in (2.83).
Example 2.6
We have applied some of the presented two-point methods of fourth order to the function
to approximate its zero 
. In this test we have used the common initial approximation 
. The absolute values of the errors of approximations 
in the first four iterations are displayed in Table 2.3.
Table 2.3 Example 2.6 – 
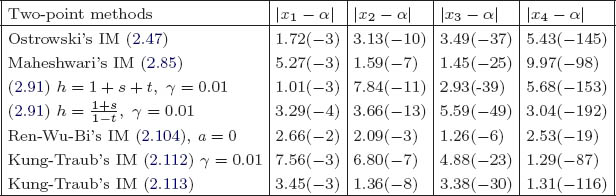
2.6 Optimal two-point methods of Jarratt’s type
Most of the multipoint methods presented in this book use two or more evaluations of a given function f at different points and only one evaluation of 
. After Ostrowski’s two-point method (2.47) of optimal order four (Ostrowski, 1960), constructed in 1960, the next two-point method of fourth order was derived by Jarratt (1966). Jarratt’s approach relies on an extended Traub’s form investigated in Traub (1964) and uses one function and two derivative evaluations per iteration. For this reason, optimal two-point methods with such a model of evaluation are often called methods of Jarratt’s type. It is worth noting that, among two-point methods, only Jarratt’s model possesses (at present) the feature to generate two-point methods of optimal order four for finding multiple roots (see Section 2.7).
2.6.1 Jarratt’s two-step methods
Let us define the functions
Traub showed in Traub (1964, pp. 197–204) that iterative formulae of the type
(2.114)
can reach cubic order of convergence by suitable choices of the parameters 
, and 
, costing one evaluation of 
and two of 
per iteration. Further acceleration of convergence of (2.114) is not possible without increasing the number of F.E.
In his paper (Jarratt, 1966) Jarratt examined a similar class of iterative methods of the form
(2.115)
where
Jarratt succeeded in increasing the order of convergence of (2.115) from three to four without additional F.E., contrary to Traub’s iterative formulae (2.114) of third order.
Let 
be a zero of f and let 
be the error in the kth iteration. Sometimes we will write 
instead of 
and omit the argument of u for simplicity. Using the Taylor expansions of 
and 
about the zero 
, we find
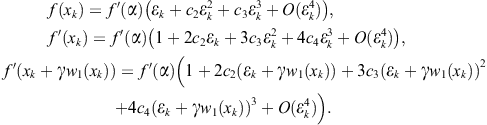
Since
(2.116)
(2.117)
After tedious but elementary calculations, from (2.116) and (2.117) one obtains
(2.118)
and
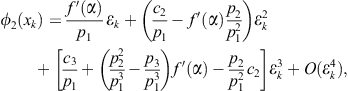(2.119)
where the abbreviations
are used. Now we substitute (2.118) and (2.119) into (2.115) and after collecting terms in 
, the error relation of the form
is obtained.
The coefficients 
, and 
depend on 
, and 
. The expressions for these coefficients are rather lengthy and will not be given explicitly. The iterative method (2.115) will reach fourth order only if 
. To satisfy these conditions, the following system of equations must be fulfilled (see Jarratt, 1966):
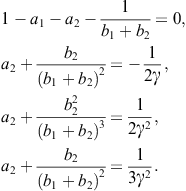
For consistency of the second and last equation we must choose 
so that the above system reduces to
(2.120)
(2.121)
(2.122)
where we set 
for convenience. The restrictions 
are necessary since 
gives 
while 
leads to 
. In both cases (2.115) degenerate to (2.114) and the fourth order cannot be achieved.
Assuming that 
, the general solution of the system (2.122) in terms of 
is
In this way Jarratt constructed a general family of fourth-order two-point methods requiring only one function and two derivative evaluations per iteration,
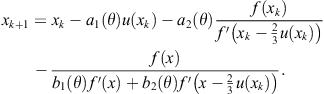(2.123)
Therefore, Jarratt’s family (2.123) is optimal in the sense of the Kung-Traub conjecture.
The parameter 
in (2.123) should be chosen so that the form of (2.123) is as simple as possible. The following three particular methods were presented in Jarratt’s paper (Jarratt, 1966) putting 
for short:
(2.124)
(2.125)
(2.126)
Jarratt applied a similar approach in Jarratt (1969) to construct a two-point method of fourth order consuming one function and two derivative evaluations per iteration. He searched for efficient I.F. in the form
(2.127)
where 
and 
are given by (2.116) and (2.117). To determine the coefficients 
, and 
in (2.127), Jarratt used the Schröder basic sequence (1.27). Recall that two iterative methods of order p can only differ by terms proportional to 
or higher, see Theorem 1.7. By comparing 
and the fifth-order method 
given by (2.56), Jarratt arrived at the following difference (with the parameter 
renamed to 
)
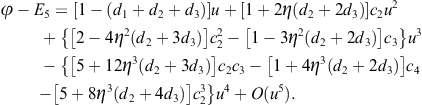(2.128)
The I.F. 
will reach fourth order if the coefficients of 
, and 
all vanish for arbitrary function 
. These conditions lead to the following system of equations obtained from (2.128):
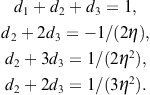(2.129)
Similarly as in the case of Jarratt’s family (2.123), the second and last equations will be consistent only if 
. With this value, the system (2.129) reduces to
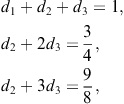
with the solution 
. In view of (2.127), the two-point method gets the simple form
(2.130)
Let us return to Jarratt’s method (2.124) and rewrite it in the form
(2.131)
where
If x is sufficiently close to a zero of f, then 
is small and we have 
. Then the expansion in geometric series gives
Substituting this into (2.131) yields the iterative formula of order four
(2.132)
This two-point method is often called inverse-free Jarratt’s method, see, e.g., Amat et al. (2004) and Varona (2002). These cited papers present the convergence behavior of the inverse-free Jarratt method (2.132) and several other methods from a dynamical point of view, using a graphic visualization by fractal pictures. Comparing the iterative formulae (2.124) and (2.132) it might look at first glance that the inverse has been eliminated. However, this is not quite correct since 
contains 
, which is a drawback if (2.132) is applied to systems of nonlinear equations.
Remark 2.15
Note that the methods (2.123), (2.130), and (2.132) of Jarratt’s type use in the first step a specific approximation 
(with 
), contrary to most multi-step methods that employ Newton’s approximation 
(with 
). The former will be called Jarratt’s step to differ from the latter Newton’s step.
A family of two-point methods of fourth order, which also uses one function and two derivative evaluations as Jarratt’s methods (2.123), (2.130), and (2.132), has been proposed in Chun and Ham (2008a). The base for constructing this family is the third-order method
(2.133)
often called super-Halley’s method, where
The second derivative can be eliminated using a finite difference quotient
(2.134)
where
and h is a suitably chosen real-valued function. Then 
is approximated by
(2.135)
Substituting 
by 
into (2.133), the following modification of the super-Halley method is obtained:
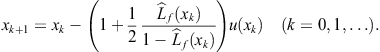(2.136)
The following theorem was proved in Chun and Ham (2008a).
Theorem 2.8
Let 
be a simple zero of a sufficiently differentiable function 
on an open interval 
and let h be any function satisfying 
and 
. If 
is sufficiently close to 
, then the family of two-point methods defined by (2.136) has order four, and its error relation is given by
(2.137)
Several choices of the function h have been considered in Chun and Ham (2008a), for example 
and 
, but the choice 
is both the simplest and cheapest from the computational point of view. This value of h gives the predictor 
of Jarratt’s methods (2.123) and (2.130).
A similar approach has been applied in Kou et al. (2007b) for constructing the following multi-parametric family of two-point methods
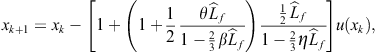(2.138)
where 
is defined by (2.135) and the predictor 
is calculated by
(2.139)
It is obvious that the choice 
reduces (2.138) to the previous family (2.136).
It was proved in Kou et al. (2007b) that the family (2.138) has order four if 
. Then the iterative formula (2.138) becomes (after short rearrangement)
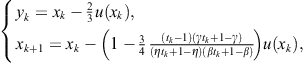(2.140)
where
Although the iterative formula (2.140) is more complicated than (2.136), it gives some interesting special cases. For example, taking 
in (2.140), a particular method (2.124) from Jarratt’s family (2.123) is obtained, written in somewhat different form,
Other two-point methods based on Jarratt’s step (2.139) and the approximation (2.134) of the second derivative 
were developed by Kou (2007). The third-order Euler-Cauchy method
(2.141)
has served as the basic method, where 
is defined as above. Taking
from (2.135) there follows
(2.142)
Replacing this approximation into (2.141), Kou derived the following two-point method of fourth order
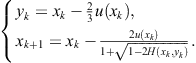(2.143)
Using Taylor’s expansion and (2.142), in the same paper (Kou, 2007) Kou proposed the following root-free methods of fourth order:
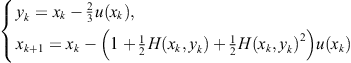(2.144)
and
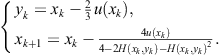(2.145)
Note that the Euler-Cauchy method (2.141) (a special case of Hansen-Patrick’s method (1.25)) was also applied in Sharma et al. (2009) for the construction of the two-point method of fourth order
(2.146)
where 
.
Jarratt’s step (2.139) was applied in Basu’s paper (Basu, 2008) for constructing two methods of optimal fourth order:
(I) Starting from Traub’s method (2.16), Basu obtained the two-point method
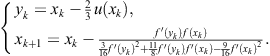(2.147)
(II) The second two-point method
(2.148)
was constructed using Traub’s method (2.14). Note that (2.148) is equivalent to Jarratt’s method (2.124).
2.6.2 Jarratt-like family of two-point methods
Now we will construct a family of Jarratt’s type of two-point methods which, among others, includes the methods (2.147) and (2.148). Let
Consider a two-point method in the form
(2.149)
where 
is a weight function to be determined such that the method (2.149) has fourth order. As in Section 2.3, we approximate the weight function 
by its Taylor’s polynomial of third degree
We use the Taylor expansion about the point 
since
Using symbolic computation we find the error relation of (2.149)
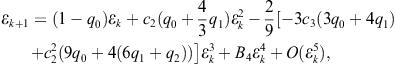
where the expression of 
is rather lengthy and will be given explicitly after its simplification. Hence, the two-point method (2.149) will be of order four if the coefficients of 
, and 
all vanish. These conditions are satisfied if we take the weight function 
in (2.149) with the properties
(2.150)
The above error relation now becomes
(2.151)
According to (2.150) and (2.151) we can state the following theorem.
Theorem 2.9
Let 
be a sufficiently differentiable function having a simple zero 
in an open interval 
. If 
is close enough to 
and the conditions (2.150) hold, then the family (2.149) is of order four.
A number of Jarratt-like methods can be constructed for various choices of 
. A rather general two-parameter family is obtained using the rational function
(2.152)
For example, taking 
in (2.149), we obtain Jarratt’s method (2.148) (rediscovered by Basu (2008)). Note that Basu’s method (2.147) is obtained from (2.149) for 
. Here are two other examples arising from (2.152):
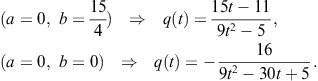
More generally, choosing
(for 
in (2.152), 
), the Jarratt family (2.123) follows from (2.149).
Using a different approach, Chun et al. (2012) derived a generalized family of Jarratt’s type, which is essentially the same to (2.149) and has the form
(2.153)
where
It was shown in Chun et al. (2012) that the family (2.153) is of order four if
It is easy to show that these conditions are equivalent to (2.150) since 
.
A lot of new and old methods of Jarratt’s type can be generated from (2.153). For example, taking
in (2.153), where 
, we obtain (2.140).
Remark 2.16
Observe that most multipoint methods considered in this book do not use more than one derivative evaluation. On the other hand, the methods presented in this section use two evaluations of the derivative, which is computationally attractive in problems where the evaluation of 
is rapid compared to 
. As noted by Jarratt (1966), such cases arise when f is defined by an integral.
2.7 Two-point methods for multiple roots
In Section 1.6 we gave a short review of one-point iterative methods for finding multiple zeros of a given real function f with a known order of multiplicity m. Those formulae can also be applied for finding an isolated complex zero. The presented formulae of third order depend on 
, and 
. Studying one-point methods, authors have concentrated mainly on the construction of (i) new methods of third order with the known multiplicity m, see, e.g., Chun et al. (2009), Chun and Neta (2009a), and Osada (1994), or (ii) new methods with the unknown multiplicity, for instance, King (1977), Parida and Gupta (2008), Wu and Fu (2001), Wu et al. (2001), and Yun (2009, 2010, 2011).
Since the main goal of this book is to investigate multipoint methods, in what follows we will consider only two-point methods for finding multiple zeros of known multiplicities. The basic idea in almost all methods relies on the elimination of the second derivative. At present, n-point methods (
) for multiple zeros are not of interest because of their low-computational efficiency.
2.7.1 Non-optimal two-point methods for multiple zeros
We start with a review of non-optimal two-point methods for multiple zeros. Using two evaluations of f and one evaluation of 
, Dong (1982) has constructed two methods of third order,
and
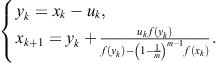(2.154)
Employing the same information, Victory and Neta (1983) have stated the following third-order method
(2.155)
where
By a composition of the third-order methods (2.154) and (2.155), Chun et al. (2009) have developed a one-parameter two-point method of third order,
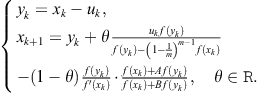
This method also requires three F.E.
A one-parameter family of third order for multiple zeros,
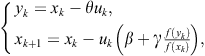(2.156)
has been given by Neta (2008), where
As in the case of the previous methods, the family (2.156) also uses two evaluations of f and one evaluation of 
per iteration.
Two other two-point methods of third order have been developed in Dong (1987) requiring one evaluation of f and two evaluations of 
,
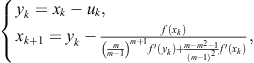
and
Homeier (2009) has proposed the following third-order method
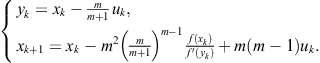
Li et al. (2009a) have constructed two families of third order methods, the first of which is given by
where 
and 
is a real parameter. The second family is defined by
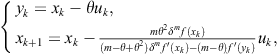
where 
.
Neta and Johnson (2008) have proposed a two-point method of fourth order requiring one function and three derivative evaluations per iteration. This method is based on the Jarratt method (Jarratt, 1966) and given by the iterative formula
where
(2.157)
A table of values of the parameters 
is given in Neta and Johnson (2008) for several values of m.
Another fourth-order method, which also uses one function and three derivative evaluations per iteration, has been given by Neta (2010). This method is based on Murakami’s method (Murakami, 1978) and reads
where 
, and 
are given by (2.157) and
A table of values of the parameters 
is given in Neta (2010) for several values of m. Li et al. (2010) got closed form formulae for several methods based on the work in Neta (2010) and Neta and Johnson (2008).
The presented list does not exhaust all two-point non-optimal methods for multiple zeros. However, our primary goal is to present two-point methods of optimal order four for multiple zeros, which is the topic discussed in what follows.
2.7.2 Optimal two-point methods for multiple zeros
The first optimal two-point method for multiple zeros was developed by Li et al. (2009b). Surprisingly enough, it happened almost one half of century after constructing the first optimal two-point method for simple zeros (Ostrowski, 1960). They have started with the iterative scheme of Jarratt’s type
(2.158)
where 
, and 
are parameters to be determined so that the method (2.158) has fourth order. Setting 
, and 
in (2.158), one gets the fourth-order Jarratt method (2.124) proposed in Jarratt (1966) (for simple zeros).
The determination of the parameters 
can be carried out using Taylor’s series with the help of symbolic computation by using computer algebra system such as Mathematica or Maple. Complete procedure is given in Li et al. (2009b) and we present only a part of that presentation.
Let 
be a zero of f with multiplicity m and let
Using Taylor’s series of 
, and 
about the zero 
of f, the following error relation is obtained from (2.158)
(2.159)
where
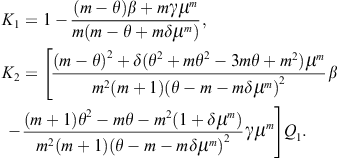
The expressions of 
and 
are very lengthy and will be listed after some simplification performed by a suitable choice of 
and 
.
To annihilate 
and 
it is necessary to take
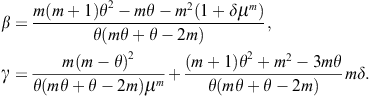
(2.160)
where
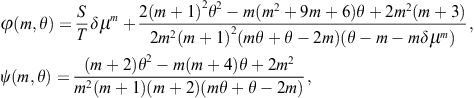
with the abbreviations
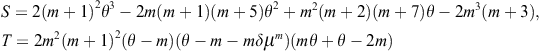
(see Li et al., 2009b).
To obtain fourth order it is necessary that 
and 
in (2.160) vanish. From the relations 
and 
we obtain
(2.161)
Substituting 
and 
into the expressions for 
and 
we get
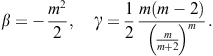(2.162)
Returning to the iterative scheme (2.158) with the values given by (2.161) and (2.162) we obtain the following fourth order method
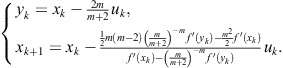(2.163)
Since the coefficients 
, and 
are annihilated, from (2.159) we obtain the error relation
where
The two-point method (2.163) has order four and requires three F.E. per iteration. Therefore, it is optimal in the sense of the Kung-Traub conjecture. Its efficiency index is 
, higher than the efficiency index of any iterative (one-point or multi-point) method for multiple zeros constructed before this method.
Li et al. (2010) derived later the iterative method (2.163) as a special case. It was done in a different way starting from the iterative scheme
Taking 
(that is, 
), the following two-point fourth-order method is obtained
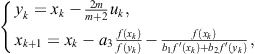(2.164)
where
In a special case when 
, the iterative method (2.164) reduces to Li-Liao-Cheng’s method (2.163).
Zhou et al. (2011) have generalized the two-point method (2.163) beginning from the two-point scheme
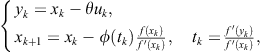(2.165)
where 
is a real parameter and 
is at least twice differentiable. The parameter 
and the function 
have to be determined so that the two-point method (2.165) reaches fourth order. This task is considered in the following theorem proved in Zhou et al. (2011).
Theorem 2.10
Let 
be a multiple zero of multiplicity m of a function 
for an open interval 
. If an initial approximation 
is sufficiently close to 
, then the order of convergence of the method (2.165) is at least four when the following conditions are satisfied:
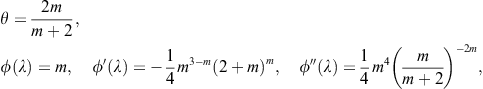
where 
.
Several special cases of the function 
are given in Zhou et al. (2011):
,
,
,
,
,
To develop an iterative two-point method of optimal order four for finding multiple zeros, Sharma and Sharma (2010a) have utilized Jarratt’s multipoint iterative scheme for simple zeros (Jarratt, 1969)
(2.166)
where
Taking 
, the fourth-order method (2.130) of Jarratt is obtained. The following theorem proved in Sharma and Sharma (2010a) shows that a suitable choice of parameters in (2.166) can lead to a fourth-order method for multiple zeros.
Theorem 2.11
Let 
be a multiple zero of multiplicity m of a sufficiently differentiable function 
for an open interval 
. If 
is close enough to 
, then the iterative method (2.166) is of order four if
Remark 2.17
The family of two-point methods (2.165) contains as special cases Li-Liao-Cheng’s fourth-order method (2.163) (variant 3) and Sharma-Sharma’s fourth-order method (2.166) (variant 4).
We do not give numerical examples for two-point methods for multiple zeros since, having in mind Remark 2.17 and special cases of (2.165), there are no other methods for comparison.
References
1. Amat S, Busquier S, Plaza S. Review of some iterative root-finding methods from a dynamical point of view. Sci Ser A Math Sci (N.S.). 2004;10:3–35.
2. Basu D. From third to fourth order variant of Newton’s method for simple roots. Appl Math Comput. 2008;202:886–892.
3. Chun C. A family of composite fourth-order iterative methods for solving nonlinear equations. Appl Math Comput. 2007a;187:951–956.
4. Chun C. On the construction of iterative methods with at least cubic convergence. Appl Math Comput. 2007b;189(1384–1392):b0025.
5. Chun C. Some variants of King’s fourth-order family of methods for nonlinear equations. Appl Math Comput. 2007c;190:57–62.
6. Chun C. Some variants of Chebyshev-Halley methods free from second derivative. Appl Math Comput. 2007e;191:193–198.
7. Chun C. Some fourth-order iterative methods for solving nonlinear equations. Appl Math Comput. 2008;195:454–459.
8. Chun C, Ham Y. A one-parameter fourth-order family of iterative methods for nonlinear equations. Appl Math Comput. 2007a;189:610–614.
9. Chun C, Ham Y. Some fourth-order modifications of Newton’s method. Appl Math Comput. 2008b;197:654–658.
10. Chun C, Ham Y. Some second-derivative-free variants of super-Halley method with fourth-order convergence. Appl Math Comput. 2008a;195:537–541.
11. Chun C, Kim YI. Several new third-order iterative methods for solving nonlinear equations. Acta Appl Math. 2010;109:1053–1063.
12. Chun C, Neta B. A third-order modification of Newton’s method for multiple roots. Appl Math Comput. 2009a;211:474–479.
13. Chun C, Neta B. Certain improvements of Newton’s method with fourth-order convergence. Appl Math Comput. 2009b;215:821–828.
14. Chun C, Bae HJ, Neta B. New families of nonlinear third-order solvers for finding multiple roots. Comput Math Appl. 2009;57:1574–1582.
15. Chun C, Lee MY, Neta B, Džunić J. On optimal fourth-order iterative methods free from second derivative and their dynamics. Appl Math Comput. 2012;218:6427–6438.
16. Cordero A, Torregrosa JR. A class of Steffensen type methods with optimal order of convergence. Appl Math Comput. 2011;217:7653–7659.
17. Cordero A, Hueso JL, Martı´nez E, Torregrosa JR. New modifications of Potra-Pták’s method with optimal fourth and eighth orders of convergence. J Comput Appl Math. 2010;234:2969–2976.
18. Dong C. A basic theorem of constructing an iterative formula of the higher order for computing multiple roots of an equation. Math Numer Sinica. 1982;11:445–450.
19. Dong C. A family of multipoint iterative functions for finding multiple roots of equations. Int J Comput Math. 1987;21:363–367.
20. Frontini M, Sormani E. Some variant of Newton’s method with third-order convergence. Appl Math Comput. 2003;140:419–426.
21. Hansen E, Patrick M. A family of root finding methods. Numer Math. 1977;27(257–269):b0110.
22. Homeier HHH. A modified Newton method for rootfinding with cubic convergence. J Comput Appl Math. 2003;157:227–230.
23. Homeier HHH. On Newton-type methods with cubic convergence. J Comput Appl Math. 2005;176:425–432.
24. Homeier HHH. On Newton-type methods for multiple roots with cubic convergence. J Comput Appl Math. 2009;231:249–254.
25. Jarratt P. Some fourth order multipoint methods for solving equations. Math Comp. 1966;20:434–437.
26. Jarratt P. Some efficient fourth-order multipoint methods for solving equations. BIT. 1969;9:119–124.
27. King RF. A family of fourth order methods for nonlinear equations. SIAM J Numer Anal. 1973a;10:876–879.
28. King RF. A secant method for multiple roots. BIT. 1977;17:321–328.
29. Kou J. Fourth-order variants of Cauchy’s method for solving nonlinear equations. Appl Math Comput. 2007;192:113–119.
30. Kou J, Li Y, Wang X. A composite fourth-order iterative method for solving nonlinear equations. Appl Math Comput. 2007a;184:471–475.
31. Kou J, Li Y, Wang X. Fourth-order iterative methods free from second derivative. Appl Math Comput. 2007b;184:880–885.
32. Kou J, Li Y, Wang X. A family of fourth-order methods for solving nonlinear equations. Appl Math Comput. 2007c;188:1031–1036.
33. Kung HT, Traub JF. Optimal order of one-point and multipoint iteration. J ACM. 1974;21:643–651.
34. Li S, Liao X, Cheng L. A new fourth-order iterative method for finding multiple roots of nonlinear equations. Appl Math Comput. 2009a;215:1288–1292.
35. Li S, Li H, Cheng L. Some second-derivative-free variants of Halley’s method for multiple roots. Appl Math Comput. 2009b;215:2192–2198.
36. Li S, Cheng L, Neta B. Some fourth-order nonlinear solvers with closed formulae for multiple roots. Comput Math Appl. 2010;59:126–135.
37. Liu Z, Zheng Q, Zhao P. A variant of Steffensen’s method of fourth-order convergence and its applications. Appl Math Comput. 2010;216:1978–1983.
38. Maheshwari AK. A fourth-order iterative method for solving nonlinear equations. Appl Math Comput. 2009;211(383–391):b0195.
39. Kanwar V. Mamta, Kukreja VK, Singh S. On a class of quadratically convergent iteration formulae. Appl Math Comput. 2005;166:633–637.
40. Murakami T. Some fifth order multipoint iterative formulae for solving equations. J Inform Process. 1978;1:138–139.
41. Neta B. New third order nonlinear solvers for multiple roots. Appl Math Comput. 2008;202:162–170.
42. Neta B. Extension of Murakami’s high order nonlinear solver to multiple roots. Int J Comput Math. 2010;87:1023–1031.
43. Neta B, Johnson AN. High-order nonlinear solver for multiple roots. Comput Math Appl. 2008;55:2012–2017.
44. Osada N. An optimal multiple root-finding method of order three. J Comput Appl Math. 1994;51:131–133.
45. Ostrowski AM. Solution of Equations and Systems of Equations. New York: Academic Press; 1960.
46. Ostrowski AM. Solution of Equations and Systems of Equations. New York: Academic Press; 2004.
47. Özban AY. Some new variants of Newton’s method. Appl Math Lett. 2004;17:677–682.
48. Parida PK, Gupta DK. An improved method for finding multiple root and it’s multiplicity of nonlinear equations in R. Appl Math Comput. 2008;202:498–503.
49. Peng Y, Feng H, Li Q, Zhang X. A fourth-order derivative-free algorithm for nonlinear equations. J Comput Appl Math. 2011;235:2551–2559.
50. Petković LD, Petković MS. A note on some recent methods for solving nonlinear equations. Appl Math Comput. 2007;185:368–374.
51. Petković MS, Petković LD. A one parameter square root family of two-step root-finders. Appl Math Comput. 2007c;188:339–344.
52. Petković MS, Petković LD. Families of optimal multipoint methods for solving nonlinear equations: a survey. Appl Anal Discrete Math. 2010;4:1–22.
53. Petković MS, Triv cković S, Herceg Ð. On Euler-like methods for the simultaneous approximation of polynomial zeros. Japan J Idustr Appl Math. 1998;15:295–315.
54. Petković MS, Ilić S, Džunić J. Derivative free two-point methods with and without memory for solving nonlinear equations. Appl Math Comput. 2010a;217:1887–1895.
55. Potra FA, Pták V. Nondiscrete Induction and Iterative Processes. Research Notes in Mathematics vol 103 Boston: Pitman; 1984.
56. Ren H, Wu Q, Bi W. A class of two-step Steffensen type methods with fourth-order convergence. Appl Math Comput. 2009;209:206–210.
57. Salehov GS. On the convergence of the process of tangent hyperbolas. Dokl Akad Nauk SSSR. 1952;82:525–528 (in Russian).
58. Sharma JR. A composite third order Newton-Steffensen method for solving nonlinear equations. Appl Math Comput. 2005;169:242–246.
59. Sharma JR, Goyal RK. Fourth-order derivative-free methods for solving nonlinear equations. Int J Comput Math. 2006;83:101–106.
60. Sharma JR, Guha RK. Second-derivative free methods of third and fourth order for solving nonlinear equations. Int J Comput Math. 2011;88:163–170.
61. Sharma JR, Sharma R. Modified Jarratt method for computing multiple roots. Appl Math Comput. 2010a;217:878–881.
62. Sharma JR, Guha RK, Sharma R. Some variants of Hansen-Patrick method with third and fourth order convergence. Appl Math Comput. 2009;214:171–177.
63. Steffensen IF. Remarks on iteration Skand Aktuarietidskr. 1933;16:64–72.
64. Thukral R, Petković MS. Family of three-point methods of optimal order for solving nonlinear equations. J Comput Appl Math. 2010;233:2278–2284.
65. Traub JF. Iterative Methods for the Solution of Equations. Englewood Cliffs, New Jersey: Prentice-Hall; 1964.
66. Varona L. Graphic and numerical comparison between iterative methods. Math Intelligencer. 2002;24:37–46.
67. Victory HD, Neta B. A higher order method for multiple zeros of nonlinear functions. Int J Comput Math. 1983;12:329–335.
68. Weerakoon S, Fernando TGI. A variant of Newton’s method with accelerated third-order convergence. Appl Math Lett. 2000;13:87–93.
69. Wu XY, Fu DS. New higher-order convergence iteration methods without employing derivatives for solving nonlinear equations. Comput Math Appl. 2001;41:489–495.
70. Wu XY, Xia JL, Shao R. Quadratically convergent multiple roots finding method without derivatives. Comput Math Appl. 2001;42:115–119.
71. Yun BI. A non-iterative method for solving nonlinear equations. Appl Math Comput. 2008;198:691–699.
72. Yun BI. A derivative free iterative method for finding multiple roots of nonlinear equations. Appl Math Lett. 2009;22(1859–1863):b0360.
73. Yun BI. New higher order methods for solving nonlinear equations with multiple roots. J Comput Appl Math. 2011;235:1553–1555.
74. Yun BI, Petković MS. Iterative methods based on the signum function approach for solving nonlinear equations. Numer Algorithms. 2009;52:649–662.
75. Zhou X, Chen X, Song Y. Construction of higher order methods for multiple roots of nonlinear equations. J Comput Appl Math. 2011;235:4199–4206.