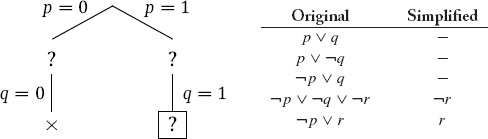Satisfiability
5.1 INTRODUCTION
The propositional satisfiability problem (often called SAT) is the problem of determining whether a set of sentences in propositional logic is satisfiable. The problem is significant both because the question of satisfiability is important in its own right and because many other questions in propositional logic can be reduced to that of propositional satisfiability. In practice, many automated reasoning problems in propositional logic are first reduced to satisfiability problems and then solved by using a satisfiability solver. Today, SAT solvers are commonly used in hardware design, software analysis, planning, mathematics, computer security analysis, and many other areas.
In this chapter, we look at several basic methods for solving SAT problems. Many modern SAT solvers are highly optimized variants of these basic methods.
5.2 TRUTH TABLE METHOD
We have seen in chapter 4 how to use truth tables to determine the satisfiability of a single sentence. It is a simple extension to use truth tables to determine the satisfiability of a set of sentences. Let’s look at a example here. Let Φ = {p ∨ q, p ∨¬q, ¬p ∨ q, ¬p ∨¬q ∨¬r, ¬p ∨ r}. To determine whether is satisfiable, we build the truth table below.

There is one row for each possible truth assignment. For each truth assignment, each of the sentences Φ in is evaluated. If any sentence evaluates to 0, then Φ as a whole is not satisfied by the truth assignment. If a satisfying truth assignment is found, then Φ is determined to be satisfiable. If no satisfying truth assignment is found, then ϕ is unsatisfiable. In this example, every row ends with Φ not satisfied. So the truth table method concludes that Φ is unsatisfiable.
The truth table method is complete because every truth assignment is checked. However, the method is impractical for all but very small problem instances. In our example with 3 propositions, there are 23 = 8 rows. For a problem instance with 10 propositions, there are 210 = 1024 rows—still quite small for a modern computer. But as the number of propositions grow, the number of rows quickly overwhelm even the fastest computers. A more efficient method is needed.
5.3 BASIC BACKTRACKING SEARCH
Looking at the example in the preceding section, we can observe that, often times, a partial truth assignment is all that is required to determine whether the input Φ is satisfied.
For example, let’s consider the partial assignment {p = 1, q = 0}. Even without the truth value for r, we can see that ¬p ∨ q evaluates to 0 and therefore Φ is not satisfied. Furthermore, we can conclude that no truth assignment that extends this partial assignment can satisfy Φ because the sentence ¬p ∨ q would always evaluate to 0 in every extension. So by determining whether the input in satisfied by a partial assignment, we can save the work of checking all extensions of the partial assignment. In this case, we can conclude that neither the truth assignment {p = 1, q = 0, r = 0} nor the assignment {p = 1, q = 0, r = 1} satisfies Φ. The saving is small in this case; but, as the number of propositions increase, the technique can eliminate many more truth assignments from consideration. Basic backtracking search is a method that allows us to realize these savings by systematically searching partial assignments.
To search the space of truth assignments systematically, both partial and complete, we can set the propositions one at a time. The process can be visualized as a tree search where each branch sets the truth value of a proposition, each interior node is a partial truth assignment, and each leaf node is a complete truth assignment. Below is a tree whose fringe represents all complete truth assignments.

In basic backtracking search, we start at the root of the tree (the empty assignment where nothing is known) and work our way down a branch. At each node, we check whether the input Φ is satisfied. If Φ is satisfied, we move down the branch by choosing a truth value for a currently unassigned proposition. If Φ is falsified, then, knowing that all the (partial) truth assignments further down the branch also falsify Φ, we backtrack to the most recent decision point and proceed down a different branch. At some point, we will either find a truth assignment that satisfies all the sentences of or determine that none exists.
Let’s look at an example. At each step, we show the part of the tree explored so far. A boxed node is the current node. An × mark at a node indicates that the truth assignment at that node falsifies at least one sentence in Φ. A ![]() indicates that the truth assignment at that node satisfies all the sentences in Φ. A? indicates that the partial truth assignment at the node neither satisfies nor falsifies Φ.
indicates that the truth assignment at that node satisfies all the sentences in Φ. A? indicates that the partial truth assignment at the node neither satisfies nor falsifies Φ.
Let’s start with the assumption that p is false. This leads to the partial tree shown below.
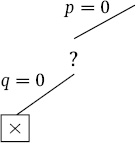
Now, let’s assume that q is false. In this case, Φ is falsified, and the current branch is closed.

Since the current branch is closed, we backtrack to the most recent choice point where another branch can be taken. This time, let’s assume that q is true.
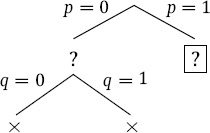
Again, Φ is falsified, and the current branch is closed. Again we backtrack to the most recent choice point where another branch can be taken. Let p be true.

Let q be false.
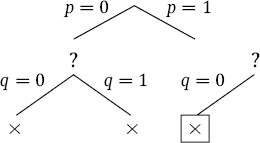
Again, our sentences are falsified, and we backtrack. Let q be true.

Let r be false.
Our sentences are falsified by this assignment, and we backtrack one last time. Let r be true.
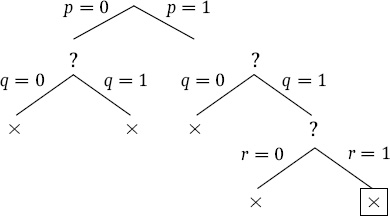
Once again, our sentences are falsified. Since all branches have been explored and closed, the method determines that Φ is unsatisfiable.
Looking at the full search tree compared to the portion explored by the basic backtracking search, we can see that the greyed out subtrees are all pruned from the search space. In this particular example, the savings are not spectacular. But in a bigger example with more propositions, the pruned subtrees can be much bigger.
5.4 SIMPLIFICATION AND UNIT PROPAGATION
In this section, we consider two optimizations of basic backtracking search—simplification and unit propagation. In order for these methods to work, we assume that our sentences have been transformed into disjunctions (using a method like the one described in the preceding chapter). As we choose the truth values of some propositions in a partial truth assignment for these disjunctions, there are opportunities to simplify the set of sentences that need to be checked.
Suppose, for example, a proposition p has been assigned the truth value 1. (1) Each disjunction containing a disjunct p may be ignored because it must already be satisfied by the current partial assignment. (2) Each disjunction ϕ containing a disjunct ¬p may be modified (call the result ϕ’) by removing from it all occurrences of the disjunct ¬p because under all truth assignments with p = 1, ϕ holds if and only if ϕ’ holds.
If a proposition p has been assigned the truth value 0, we can simplify our sentences analogously. (1) Each disjunction containing a disjunct ¬p may be ignored because it must already be satisfied by the current partial assignment. (2) Each disjunction ϕ containing a disjunct p may be modified by removing from it all occurrences of the disjunct p.
Consider once again the example in the preceding section. Under the partial assignment p = 1, we can simplify our sentences as shown below. The first two sentences are dropped, and the literal ¬p is dropped from the other three sentences.
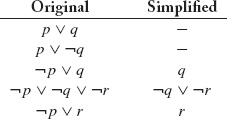
While simplifying sentences is helpful in and of itself, the real value of simplification is that it enables a further optimization that can drastically decrease the search space.
In the course of the backtracking search, if we see a sentence that consists of single atom, say p, we know that the only possible satisfying assignments further down the branch must set p to true. In this case, we can fix p to be true and ignore the subbranch that sets p to false. Similarly, when we encounter a sentence that consists of a single negated atom, say ¬p, we can fix p to be false and ignore the other subbranch. This optimization is called unit propagation because sentences of the form p or ¬p (a simple sentence or the negation of a simple sentence) are called units.
Let’s redo example 1 with formula simplification and unit propagation. As we proceed through this example, we illustrate each step with the search tree on that step (on the left) and the simplified sentence set (in the table on the right).
To start, let p be false.
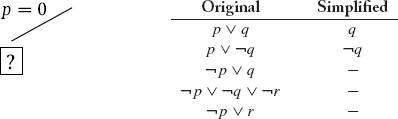
In the simplified set of sentences, we have the unit ¬q, so we fix q to be false (unit propagation). (We also have the unit q, so we could have fixed q to true. The final result is the same in either case.)
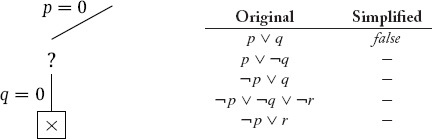
Φ is falsified, so we backtrack to the most recent decision point, all the way back at the root. Let p be true.
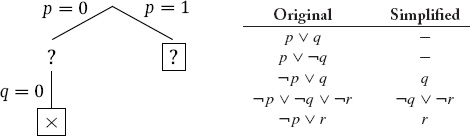
In the simplified set of sentences, we have the unit q so we do unit propagation, fixing q to be true. (We could also have performed unit propagation using the other unit r.)
In the simplified set of sentences, we have the unit ¬r so we do unit propagation, fixing r to be false.
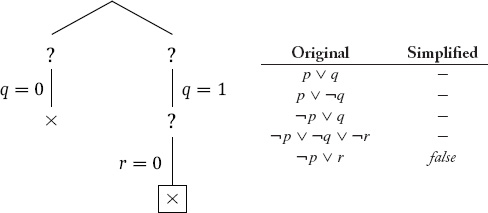
ϕ is falsified on this branch, so the branch is closed. All branches are closed, so the method determines that is Φ unsatisfiable.
Compared to the tree explored by the basic backtracking search, we see that the greyed out subtrees are pruned away from the search space.
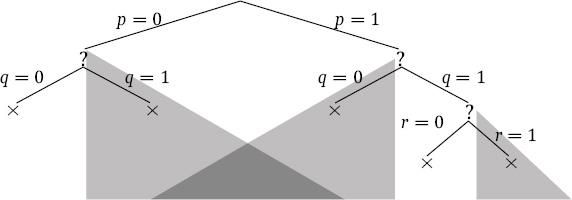
5.5 DPLL
The Davis-Putnam-Logemann-Loveland method (DPLL) is a classic method for SAT solving. It is essentially backtracking search along with unit propagation and pure literal elimination (described in Chapter 8). Most modern, complete SAT solvers are based on DPLL, with additional optimizations not discussed here. These SAT solvers are routinely used to solve SAT problems with large numbers of propositions.
5.6 GSAT
Many practical SAT solvers based on complete search for models are routinely used to solve satisfiability problems of significant size. However, some problem instances are still impractical to solve using complete search for models.
In these problem instances, it is impractical to exhaustively eliminate every truth assignment as a possible model. In such situations, one may consider incomplete search methods: search methods that answers correctly when it can, but sometimes fail to answer. The basic idea is to sample a subset of truth assignments. If a satisfying assignment is found, then we can conclude that the input is satisfiable. If no satisfying assignment is found, then we don’t know whether the input is satisfiable. In practice, modern incomplete SAT solvers tend to be very good at finding the satisfying assignments in a reasonable amount of time when they exists, but they still lack the ability to answer definitively that an input is unsatisfiable.
The first idea may be to uniformly sample a number of truth assignments from the space of all truth assignments. However, in large problem instances with few satisfying assignments, one would expect to take a very long time before happening upon a satisfying assignment.
What enables incomplete SAT solvers to work efficiently is the use of heuristics that frequently steer the search toward satisfying assignments.
One family of incomplete SAT solvers uses local search heuristics to look for a truth assignment that maximizes the number of sentences it satisfies. Clearly, a set of sentences is satisfiable if and only if it is satisfied by an optimal truth assignment (optimal in terms of maximizing the number of sentences satisfied).
We look at one particular method called GSAT in more detail. The GSAT method starts with an arbitrary truth assignment. Then GSAT moves from one truth assignment to the next by flipping one of the propositions to achieve the greatest increase in the number of sentences satisfied. The search stops when it reaches a truth assignment such that the number of sentences satisfied cannot be increased by flipping the truth value of one proposition (in other words, a locally optimal truth assignment is reached).
Consider the set of sentences {p∨q∨r, ¬p, ¬q, ¬r}. This set is clearly unsatisfiable. What follows is one possible execution of GSAT on this case. For each step, we show the truth assignment for the proposition constants; we show the truth values for the sentences in our set; and we show how many sentences are satisfied. (In this case, we need this number to be 4 in order for the set as a whole to be satisfied.) We start with an arbitrary assignment in which all proposition constants are true.
Only one sentence is satisfied by this assignment. However, we can improve matters by flipping the value of p.
![]()
Still not satisfied, but we can improve matters by flipping the value of q.
![]()
At this point, we are stuck. No flipping of a proposition value can increase the number of sentences satisfied. The search terminates without finding a satisfying assignment. Indeed, the input set of sentences is unsatisfiable.
Now, let’s see what happens when we apply the method to a set or sentences that is satisfiable. Our set in this case is {p, ¬p ∨ q, ¬p ∨ r}. As before, we start with an arbitrary assignment.
![]()
Flipping the value of q improves matters.
![]()
Flipping the value of r improves matters further.
![]()
Since all three sentences are satisfied, the search terminates, concluding that the set is satisfiable.
Unfortunately, local search of this sort is not guaranteed to be complete—the search may fail to find a satisfying assignment even when one exists. Depending on the starting assignment and the arbitrary choices in breaking ties between flipping one proposition vs. another, the GSAT method may fail to find a satisfying assignment for a satisfiable set of input sentences.
To see an example of incompleteness, let’s look a different execution of GSAT on the same set of sentences as above. We begin with the same initial assignment as before.
![]()
This time, instead of flipping the value of q, let’s flip the value of p.
Unfortunately, at this point, we are stuck. No flipping of a proposition value can increase the number of sentences satisfied. Although a satisfying assignment exists, the search terminates without finding it.
To avoid becoming stuck without finding a satisfying assignment, one can modify the search procedure by allowing some combination of the following.
• Restarting at a random truth assignment (randomized restarts).
• Flipping a proposition to move to a truth assignment that satisfies the same number of sentences (plateau moves).
• Flipping a random proposition regardless of whether the move increases the number of satisfied sentences (noisy move).
Active research and engineering efforts continue in developing search methods that can find a satisfying assignment more quickly (when one exists).
RECAP
The propositional satisfiability problem (often called SAT) is the problem of determining whether a set of sentences in propositional logic is satisfiable. Many other questions in propositional logic (such as logical entailment) can be reduced to that of propositional satisfiability. The truth table method for testing satisfiability checks every truth assignment one by one to see whether any truth assignment satisfies the input sentences. The method is straightforward but prohibitively expensive for all but the smallest problems. The basic backtracking search explores the partial truth assignments using a systematic tree search. When a partial assignment is found to falsify at least one input sentence, all extensions of the partial assignment can be eliminated from the search space. Simplification is a technique that simplifies the input set of sentences based on the current partial truth assignment. Unit propagation eliminates from the search space truth assignments that disagree with units—a simple sentence or the negation of a simple sentence—in the simplified set of input sentences. Backtracking search with simplification and unit propagation is a practical method for testing satisfiability. The method is complete in the sense that it is guaranteed to terminate with the correct answer. Most modern, complete SAT solvers are highly optimized versions of this basic method. Another class of SAT solvers are the incomplete SAT solvers. Instead of exhausting the space of truth assignments, incomplete SAT solvers use heuristics to quickly identify satisfying assignments. In practice, incomplete SAT solvers tend to be very good at quickly finding satisfying assignments, but lack the ability to answer definitely that an input is unsatisfiable.