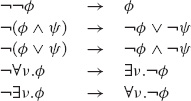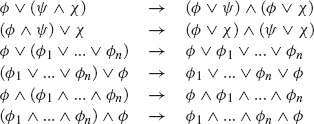Resolution
8.1 INTRODUCTION
The (general) Resolution Principle is a rule of inference for Herbrand Logic analogous to the Propositional Resolution Principle for Propositional Logic. Using the Resolution Principle alone (without axiom schemata or other rules of inference), it is possible to arrive at a proof method that proves the same consequences as the Fitch system given in Chapter 7. The search space using the Resolution Principle is smaller than the search space for generating Fitch proofs.
In our tour of Resolution, we look first at unification, which allows us to unify expressions by substituting terms for variables. We then move on to a definition of clausal form extended to handle variables. The Resolution Principle follows. We then look at some applications. Finally, we examine strategies for making the procedure more efficient.
8.2 CLAUSAL FORM
As with Propositional Resolution, (general) Resolution works only on expressions in clausal form. The definitions here are analogous. A literal is either a relational sentence or a negation of a relational sentence. A clause is a set of literals and, as in Propositional Logic, represents a disjunction of the literals in the set. A clause set is a set of clauses and represents a conjunction of the clauses in the set.
The procedure for converting Herbrand Logic sentences to clausal form is similar to that for Propositional Logic. Some of the rules are the same. However, there are a few additional rules to deal with the presence of variables and quantifiers. The conversion rules are summarized below and should be applied in order. The conversion process assumes that the input sentences have no free variables.
In the first step (Implications out), we eliminate all occurrences of the ⇒, ⇐, and ⇔ operators by substituting equivalent sentences involving only the ∧, ∨, and ¬ operators.

In the second step (Negations in), negations are distributed over other logical operators and quantifiers until each such operator applies to a single atomic sentence. The following replacement rules do the job.
In the third step (Standardize variables), we rename variables so that each quantifier has a unique variable, i.e., the same variable is not quantified more than once within the same sentence. The following transformation is an example.
∀x.(p(x) ⇒∃x.q(x)) → ∀x.(p(x) ⇒∃y.q(y))
In the fourth step (Existentials out), we eliminate all existential quantifiers. The method for doing this is a little complicated, and we describe it in two stages.
If an existential quantifier does not occur within the scope of a universal quantifier, we simply drop the quantifier and replace all occurrences of the quantified variable by a new object constant; i.e., one that is not in our current language and hence is not used anywhere in our set of sentences. The object constant used to replace the existential variable in this case is called a Skolem constant. The following example assumes that a is not in the language. The conversion produces clauses in an expanded language with new object constants.
∃x.p(x) → p(a)
If an existential quantifier is within the scope of any universal quantifiers, there is the possibility that the value of the existential variable depends on the values of the associated universal variables. Consequently, we cannot replace the existential variable with an object constant. Instead, the general rule is to drop the existential quantifier and to replace the associated variable by a term formed from a new function symbol applied to the variables associated with the enclosing universal quantifiers. Any function defined in this way is called a Skolem function. The following example illustrates this transformation. It assumes that f is not in the current language. The conversion produces clauses in an expanded language with new function constants.
∀x.(p(x) ∧∃z.q(x, y, z)) → ∀x.(p(x) ∧ q(x, y, f (x, y)))
In the fifth step (Alls out), we drop all universal quantifiers. Because the remaining variables at this point are universally quantified, this does not introduce any ambiguities.
∀x.(p(x) ∧ q(x, y, f (x, y))) → p(x) ∧ q(x, y, f (x, y))
In the sixth step (Disjunctions in), we put the expression into conjunctive normal form, i.e., a conjunction of disjunctions of literals. This can be accomplished by repeated use of the following rules.
In the seventh step (Operators out), we eliminate operators by separating any conjunctions into its conjuncts and writing each disjunction as a separate clause.
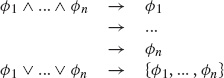
As an example of this conversion process, consider the problem of transforming the following expression to clausal form. The initial expression appears on the top line, and the expressions on the labeled lines are the results of the corresponding steps of the conversion procedure.

Here is another example. In this case, the starting sentence is almost the same. The only difference is the leading ¬, but the result looks quite different.
In Propositional Logic, the clause set corresponding to any sentence is logically equivalent to that sentence. In Herbrand Logic, this is not necessarily the case. For example, the clausal form of the sentence ∃x.p(x) is {p(a)}. These are not logically equivalent to each other. They are not even in the same language.
On the other hand, the converted clause set has a special relationship to the original set of sentences—over the expanded language, the clause set satisfiable if and only if the original sentence is satisfiable (also over the expanded language). As we shall see, in resolution, this equivalence of satisfiability is all we need to obtain a proof method as powerful as the Fitch system presented in Chapter 7.
8.3 UNIFICATION
Unification is the process of determining whether two expressions can be unified, i.e., made identical by appropriate substitutions for their variables. As we shall see, making this determination is an essential part of Resolution.
A substitution is a finite mapping of variables to terms. In what follows, we write substitutions as sets of replacement rules, like the one shown below. In each rule, the variable to which the arrow is pointing is to be replaced by the term from which the arrow is pointing. In this case, x is to be replaced by a, y is to be replaced by f (b), and z is to be replaced by v.
{x←a, y←f (b), z←v}
The variables being replaced together constitute the domain of the substitution, and the terms replacing them constitute the range. For example, in the preceding substitution, the domain is {x, y, z}, and the range is {a, b, v}.
A substitution is pure if and only if all replacement terms in the range are free of the variables in the domain of the substitution. Otherwise, the substitution is impure. The substitution shown above is pure whereas the one shown below is impure.
The result of applying a substitution σ to an expression ϕ is the expression ϕσ obtained from the original expression by replacing every occurrence of every variable in the domain of the substitution by the term with which it is associated.

Note that, if a substitution is pure, application is idempotent, i.e., applying a substitution a second time has no effect.
![]()
However, this is not the case for impure substitutions, as illustrated by the following example. Applying the substitution once leads to an expression with an x, allowing for a different answer when the substitution is applied a second time.
![]()
Given two or more substitutions, it is possible to define a single substitution that has the same effect as applying those substitutions in sequence. For example, the substitutions {x←a, y←f (u), z ←v} and {u←d, v←e} can be combined to form the single substitution {x←a, y←f (d), z←e, u ←d, v←e}, which has the same effect as the first two substitutions when applied to any expression whatsoever.
Computing the composition of a substitution σ and a substitution τ is easy. There are two steps. (1) First, we apply τ to the range of σ Δ. (2) Then we adjoin to σ all pairs from τ with different domain variables.
As an example, consider the composition shown below. In the right-hand side of the first equation, we have applied the second substitution to the replacements in the first substitution. In the second equation, we have combined the rules from this new substitution with the non-conflicting rules from the second substitution.

It is noteworthy that composition does not necessarily preserve substitutional purity. The composition of two impure substitutions may be pure, and the composition of two pure substitutions may be impure.
This problem does not occur if the substitutions are composable. A substitution σ and a substitution τ are composable if and only if the domain of σ and the range of τ are disjoint. Otherwise, they are noncomposable.
{x←a, y←b, z←v}{x←u, v←b}
By contrast, the following substitutions are noncomposable. Here, x occurs in both the domain of the first substitution and the range of the second substitution, violating the definition of composability.
{x←a, y←b, z←v}{x←u, v←x}
The importance of composability is that it ensures preservation of purity. The composition of composable pure substitutions must be pure. In the sequel, we look only at compositions of composable pure substitutions.
A substitution σ is a unifier for an expression ϕ and an expression ψ if and only if ϕσ =ψσ, i.e., the result of applying σ to ϕ is the same as the result of applying σ to ψ. If two expressions have a unifier, they are said to be unifiable. Otherwise, they are nonunifiable.
The expressions p(x, y) and p(a,v) have a unifier, e.g., {x←a, y←b, v←b} and are, therefore, unifiable. The results of applying this substitution to the two expressions are shown below.
p(x, y){x←a, y←b, v←b}=p(a, b)
p(a, v){x←a, y←b, v←b}=p(a, b)
Note that, although this substitution unifies the two expressions, it is not the only unifier. We do not have to substitute b for y and v to unify the two expressions. We can equally well substitute c or d or f (c) or f (w). In fact, we can unify the expressions without changing v at all by simply replacing y by v.
In considering these alternatives, it should be clear that some substitutions are more general than others are. We say that a substitution σ is as general as or more general than a substitution τ if and only if there is another substitution δ such that σδ=τ. For example, the substitution {x←a, y ←v} is more general than {x←a, y←f (c), v←f (c)} since there is a substitution {v←f (c)} that, when applied to the former, gives the latter.
{x←a, y←v}{v←f (c)}={x←a, y←f (c), v←f (c)}
In Resolution, we are interested only in unifiers with maximum generality. A most general unifier, or mgu, σ of two expressions has the property that it as general as or more general than any other unifier.
Although it is possible for two expressions to have more than one most general unifier, all of these most general unifiers are structurally the same, i.e., they are unique up to variable renaming. For example, p(x) and p(y) can be unified by either the substitution {x←y} or the substitution {y←x}; and either of these substitutions can be obtained from the other by applying a third substitution. This is not true of the unifiers mentioned earlier.
One good thing about our language is that there is a simple and inexpensive procedure for computing a most general unifier of any two expressions if it exists.
The procedure assumes a representation of expressions as sequences of subexpressions. For example, the expression p(a, f (b),z) can be thought of as a sequence with four elements, viz. the relation constant p, the object constant a, the term f (b), and the variable z. The term f (b) can in turn be thought of as a sequence of two elements, viz. the function constant f and the object constant b.
We start the procedure with two expression and a substitution, which is initially the empty substitution. We then recursively process the two expressions, comparing the subexpressions at each point. Along the way, we expand the substitution with variable assignments as described below. If, we fail to unify any pair of subexpression at any point in this process, the procedure as a whole fails. If we finish this recursive comparison of the expressions, the procedure as a whole succeeds, and the accumulated substitution at that point is the most general unifier.
The processing of subexpressions goes as follows.
1. If two expressions being compared are identical, then nothing more needs to be done.
2. If two expressions are not identical and both expressions are constants, then we fail, since there is no way to make them look alike.
3. If one of the expressions is a variable, we first check whether the variable has a binding in the current substitution. If so, we try to unify the binding with the second expression. If there is no binding, we check whether the second expression contains the variable. If the variable occurs within the expression, we fail; otherwise, we set the substitution to the composition of the old substitution and a new substitution in which we bind the variable to the second expression.
4. The only remaining possibility is that the two expressions are both sequences. In this case, we simply iterate across the expressions, comparing as described above.
As an example, consider the computation of the most general unifier for the expressions p(x,b) and p(a,y) with the initial substitution { }. A trace of the execution of the procedure for this case is shown below. We show the beginning of a comparison with a line labelled Compare together with the expressions being compared and the input substitution. We show the result of each comparison with a line labelled Result. The indentation shows the depth of recursion of the procedure.

As another example, consider the process of unifying the expression p(x,x) and the expression p(a,y). A trace is shown below. The main interest in this example comes in the step involving x and y. At this point, x has a binding, so we recursively compare the replacement a to y, which results in binding of y to a.

One important part of the unification procedure is the test for whether a variable occurs within an expression before the variable is bound to that expression. This test is called an occur check since it is used to check whether or not the variable occurs within the term with which it is being unified. For example, p(x) is not unifiable with p(f (x)). When the algorithm tries to unify the two expressions using the substitution x ← f(x), it performs the occur check. Upon finding that the variable x occurs in the term f(x), the algorithm fails, concluding that no unifier can be found. Without this check, the algorithm would incorrectly find that expressions such as p(x) and p(f (x)) are unifiable, even though there is no substitution for x that, when applied to both, makes them look alike.
8.4 RESOLUTION PRINCIPLE
The Resolution Principle is analogous to that of Propositional Resolution. The only difference is the use of unification to unify literals before applying the rule.
A simple version of the Resolution Principle is shown below. Given a clause with a literal ϕ and a second clause with a literal ¬ψ such that ϕ and ψ have a most general unifier σ, we can derive a conclusion by applying σ to the clause consisting of the remaining literals from the two original clauses.

Consider the example shown below. The first clause contains the positive literal p(a,y) and the second clause contains a negative occurrence of p(x, f (x)). The substitution {x←a, y←f (a)} is a most general unifier of these two expressions. Consequently, we can collect the remaining literals r(y) and q(g(x)) into a clause and apply the substitution to produce a conclusion.
Unfortunately, this simple version of the Resolution Principle is not quite good enough. Consider the two clauses shown below. Given the meaning of these two clauses, it should be possible to resolve them to produce the empty clause. However, the two atomic sentences do not unify. The variable x must be bound to a and b at the same time.
![]()
Fortunately, this problem can easily be fixed by extending the Resolution Principle slightly as shown below. Before trying to resolve two clauses, we select one of the clauses and rename any variables the clause has in common with the other clause.

Renaming solves this problem. Unfortunately, we are still not quite done. There is one more technicality that must be addressed to finish the story. As stated, even with the extension mentioned above, the rule is not quite good enough. Given the clauses shown below, we should be able to infer the empty clause { }; however, this is not possible with the preceding definition. The clauses can be resolved in various ways, but the result is never the empty clause.
![]()
The good news is that we can solve this additional problem with one last modification to our definition of the Resolution Principle. If a subset of the literals in a clause Φ has a most general unifier γ, then the clause Φ’ obtained by applying γ to Φ is called a factor of Φ. For example, the literals p(x) and p(f (y)) have a most general unifier {x←f (y)}, so the clause {p(f (y)), r(f (y), y)} is a factor of {p(x), p(f (y)),r(x, y)}. Obviously, any clause is a trivial factor of itself.
Using the notion of factors, we can give a complete definition for the Resolution Principle. Suppose that Φ and Ψ are two clauses. If there is a literal ϕ in some factor of Φ and a literal ¬ψ in some factor of Ψ, then we say that the two clauses Φ and Ψ resolve and that the new clause ((Φ′ −{ϕ}) ∪ (Ψ′ −{¬ψ}))σ is a resolvent of the two clauses.
Using this enhanced definition of Resolution, we can solve the problem mentioned above. Once again, consider the premises {p(x), p(y)} and {¬p(u), ¬p(v)}. The first premise has the factor {p(x)}, and the second has the factor {¬p(u)}, and these two factors resolve to the empty clause in a single step.
8.5 RESOLUTION REASONING
Reasoning with the (general) Resolution Principle is analogous to reasoning with the Propositional Resolution Principle. We start with premises; we apply the Resolution Principle to those premises; we apply the rule to the results of those applications; and so forth until we get to our desired conclusion or until we run out of things to do.
As with Propositional Resolution, we define a Resolution derivation of a conclusion from a set of premises to be a finite sequence of clauses terminating in the conclusion in which each clause is either a premise or the result of applying the Resolution Principle to earlier members of the sequence. And, as with Propositional Resolution, we do not use the word proof, because we reserve that word for a slightly different concept, which is discussed in the next section.
As an example, consider a problem in the area kinship relations. Suppose we know that Art is the parent of Bob and Bud; suppose that Bob is the parent of Cal; and suppose that Bud is the parent of Coe. Suppose we also know that grandparents are parents of parents. Starting with these premises, we can use Resolution to conclude that Art is the grandparent of Coe. The derivation is shown below. We start with our five premises—four simple clauses for the four facts about the parent relation p and one more complex clause capturing the definition of the grandparent relation g. We start by resolving the clause on line 1 with the clause on line 5 to produce the clause on line 6. We then resolve the clause on line 3 with this result to derive that conclusion that Art is the grandparent of Cal. Interesting but not what we set out to prove; so we continue the process. We next resolve the clause on line 2 with the clause on line 5 to produce the clause on line 8. Then we resolve the clause on line 5 with this result to produce the clause on line 9, which is exactly what we set out to prove.
One thing to notice about this derivation is that there are some dead-ends. We first tried resolving the fact about Art and Bob before getting around to trying the fact about Art and Bud. Resolution does not eliminate all search. However, at no time did we ever have to make an arbitrary assumption or an arbitrary choice of a binding for a variable. The absence of such arbitrary choices is why Resolution is so much more focussed than natural deduction systems like Fitch.
Another worthwhile observation about Resolution is that, unlike Fitch, Resolution frequently terminates even when there is no derivation of the desired result. Suppose, for example, we were interested in deriving the clause {g(cal,art)} from the premises in this case. This sentence, of course, does not follow from the premises. And Resolution is sound, so we would never generate this result. The interesting thing is that, in this case, the attempt to derive this result would eventually terminate. With the premises given, there are a few more Resolutions we could do, e.g., resolving the clause on line 1 with the second literal in the clause on line 5. However, having done these additional Resolutions, we would find ourselves with nothing left to do; and, unlike Fitch, the process would terminate.
Unfortunately, like Propositional Resolution, general Resolution is not generatively complete, i.e., it is not possible to find Resolution derivations for all clauses that are logically entailed by a set of premise clauses. For example, the clause {p(a), ¬p(a)} is always true, and so it is logically entailed by any set of premises, including the empty set of premises. Resolution requires some premises to have any effect. Given an empty set of premises, we would not be able to derive any conclusions, including this valid clause.
Although Resolution is not generatively complete, problems like this one are solved by negating the goal and demonstrating that the resulting set of sentences is unsatisfiable.
8.6 UNSATISFIABILITY
One common use of Resolution is in demonstrating unsatisfiability. In clausal form, a contradiction takes the form of the empty clause, which is equivalent to a disjunction of no literals. Thus, to automate the determination of unsatisfiability, all we need do is to use Resolution to derive consequences from the set to be tested, terminating whenever the empty clause is generated.
Let’s start with a simple example. See the derivation below. We have four premises. The derivation in this case is particularly easy. We resolve the first clause with the second to get the clause shown on line 5. Next, we resolve the result with the third clause to get the unit clause on line 6. Note that r(a) is the remaining literal from clause 3 after the Resolution, and r(a) is also the remaining literal from clause 5 after the Resolution. Since these two literals are identical, they appear only once in the result. Finally, we resolve this result with the clause on 4 to produce the empty clause.

Here is a more complicated derivation, one that illustrates renaming and factoring. Again, we have four premises. Line 5 results from Resolution between the clauses on lines 1 and 3. This one is easy. Line 6 results from Resolution between the clauses on lines 2 and 4. In this case, renaming is necessary in order for the unification to take place. Line 7 results from renaming and factoring the clause on line 5 and resolving with the clause on line 6. Finally, line 8 results from factoring line 5 again and resolving with the clause on line 7. Note that we cannot just factor 5 and factor 6 and resolve the results in one step. Try it and see what happens.

In demonstrating unsatisfiability, Resolution and Fitch (as given in Chapter 7) are equally powerful. Given a set of sentences, Resolution can derive the empty clause from the clausal form of the sentences if and only if Fitch can find a proof of a sentence of the form ψ ∧¬ψ. The benefit of using Resolution is that the search space is smaller.
8.7 LOGICAL ENTAILMENT
As with Propositional Logic, we can use a test for unsatisfiability to test logical entailment as well. Suppose we wish to show that the set of sentences Δ logically entails the formula ϕ. We can do this by finding a proof of ϕ from Δ, i.e., by establishing Δ ![]() ϕ. One version of the refutation theorem states that Δ
ϕ. One version of the refutation theorem states that Δ ![]() ϕ if and only if there is a sentence α of the form ψ ∧¬ψ such that Δ ∪{¬ϕ}
ϕ if and only if there is a sentence α of the form ψ ∧¬ψ such that Δ ∪{¬ϕ} ![]() α. In addition, recall that Resolution and Fitch are equally powerful in demonstrating unsatisfiability. Thus, if we show using Resolution that the set of formulas Δ ∪{¬ϕ} is unsatisfiable, we have demonstrated that Δ
α. In addition, recall that Resolution and Fitch are equally powerful in demonstrating unsatisfiability. Thus, if we show using Resolution that the set of formulas Δ ∪{¬ϕ} is unsatisfiable, we have demonstrated that Δ ![]() ϕ and hence Δ logically entails ϕ.
ϕ and hence Δ logically entails ϕ.
To apply this technique of establishing logical entailment by establishing unsatisfiability using Resolution, we first negate ϕ and add it to Δ to yield Δ’. We then convert Δ’ to clausal form and apply Resolution. If the empty clause is produced, the original Δ was unsatisfiable, and we have demonstrated that Δ logically entails ϕ. This process is called a Resolution refutation; it is illustrated by examples in the following sections.
As an example of using Resolution to determine logical entailment, let’s consider a case we saw earlier. The premises are shown below. We know that everybody loves somebody and everybody loves a lover.
![]()
Our goal is to show that everybody loves everybody.
∀x.∀y.loves(x,y)
In order to solve this problem, we add the negation of our desired conclusion to the premises and convert to clausal form, leading to the clauses shown below. Note the use of a Skolem function in the first clause and the use of Skolem constants in the clause derived from the negated goal.

Starting from these initial clauses, we can use Resolution to derive the empty clause and thus prove the result.
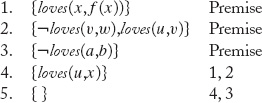
As another example of Resolution, once again consider the problem of Harry and Ralph introduced in the preceding chapter. We know that every horse can outrun every dog. Some greyhounds can outrun every rabbit. Greyhounds are dogs. The relationship of being faster is transitive. Harry is a horse. Ralph is a rabbit.

We desire to prove that Harry is faster than Ralph. In order to do this, we negate the desired conclusion.
¬f (harry, ralph)
To do the proof, we take the premises and the negated conclusion and convert to clausal form. The resulting clauses are shown below. Note that the second premise has turned into two clauses. Note also that the Skolem constant gary is introduced.

From these clauses, we can derive the empty clause, as shown in the following derivation.

Don’t be misled by the simplicity of these examples. Resolution can and has been used in proving complex mathematical theorems, in proving the correctness of programs, and in many other applications.
8.8 ANSWER EXTRACTION
In a previous section, we saw how to use Resolution in answering true-or-false questions (e.g., Is Art a grandparent of Coe?). In this section, we show how Resolution can be used to answer fill-in-the-blank questions as well (e.g., Who is a grandparent of Coe?).
A fill-in-the-blank question is a sentence with free variables specifying the blanks to be filled in. The goal is to find bindings for the free variables such that the set of premises logically entails the sentence obtained by substituting the bindings into the original question. For example, consider the following premises:

To ask about Jon’s parent, we would write the question p(x,jon). Using the premises above, we see that art is an answer to this question, since the sentence p(art, jon) is logically entailed by the premises.
An answer literal for a fill-in-the-blank question ϕ is a sentence goal (ν1,…, νn), where ν1,…, νn are the free variables in ϕ. To answer ϕ, we form an implication from ϕ and its answer literal and convert to clausal form. For example, the literal p(x, jon)is combined with its answer literal goal (x) to form the rule (p(x, jon) ⇒ goal (x)), which leads to the clause {¬p(x, jon), goal (x)}.
We then use Resolution as described above, except that we change the termination test. Rather than waiting for the empty clause to be produced, the procedure halts as soon as it derives a clause consisting of only answer literals. The following Resolution derivation shows how we compute the answer to Who is Jon’s parent?
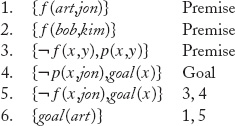
If this procedure produces only one answer literal, the terms it contains constitute the only answer to the question. In some cases, the result of a fill-in-the-blank Resolution depends on the refutation by which it is produced. In general, several different refutations can result from the same query, leading to multiple answers.
Suppose, for example, that we knew the identities of both the father and mother of Jon and that we asked Who is a parent of Jon? The following Resolution trace shows that we can derive two answers to this question.

Unfortunately, we have no way of knowing whether or not the answer statement from a given refutation exhausts the possibilities. We can continue to search for answers until we find enough of them. However, due to the undecidability of logical entailment, we can never know in general whether we have found all the possible answers.
Another interesting aspect of fill-in-the-blank Resolution is that in some cases the procedure can result in a clause containing more than one answer literal. The significance of this is that no one answer is guaranteed to work, but one of the answers must be correct.
The following Resolution trace illustrates this fact. Suppose we have a disjunction asserting that Art or Bob is the father of Jon, but we do not know which man is. The goal is to find a parent of John. After resolving the goal clause with the sentence about fathers and parents, we resolve the result with the premise disjunction, obtaining a clause that can be resolved a second time yielding a clause with two answer literals. This answers indicates not two answers but rather uncertainty as to which is the correct answer.

In such situations, we can continue searching in hope of finding a more specific answer. However, given the undecidability of logical entailment, we can never know in general whether we can stop and say that no more specific answer exists.
8.9 STRATEGIES
One of the disadvantages of using the Resolution rule in an unconstrained manner is that it leads to many unnecessary inferences. Some inferences are redundant in that their conclusions can be derived in other ways. Some inferences are irrelevant in that they do not lead to derivations of the desired result.
This section presents a number of strategies for eliminating unnecessary work. In reading this material, it is important to bear in mind that we are concerned here not with the order in which inferences are done, but only with the size of a Resolution graph and with ways of decreasing that size by eliminating unnecessary deductions.
PURE LITERAL ELIMINATION
A literal occurring in a clause set is pure if and only if it has no instance that is complementary to an instance of another literal in the clause set. A clause that contains a pure literal is redundant for the purposes of refutation, since the literal can never be resolved away. Consequently, we can safely remove such a clause. Removing clauses with pure literals defines a deletion strategy known as pure-literal elimination.
The clause set that follows is unsatisfiable. However, in proving this we can ignore the second and third clauses, since they both contain the pure literal s. The example in this case involves clauses in Propositional Logic, but it applies equally well to Herbrand Logic.
Note that, if a set of clauses contains no pure literals, there is no way we can derive any clauses with pure literals using Resolution. The upshot is that we need to apply pure-literal elimination only once to the starting set of premise clauses; we do not have to check each clause as it is generated.
TAUTOLOGY ELIMINATION
A tautology is a clause containing a pair of complementary literals. For example, the clause {p(f (a)), ¬p(f (a))} is a tautology. The clause {p(x), q(y), ¬q(y), r(z)} also is a tautology, even though it contains additional literals.
As it turns out, the presence of tautologies in a set of clauses has no effect on that set’s satisfiability. A satisfiable set of clauses remains satisfiable, no matter what tautologies we add. An unsatisfiable set of clauses remains unsatisfiable, even if we remove all tautologies. Therefore, we can remove tautologies from a set of clauses, because we need never use them in subsequent inferences. The corresponding deletion strategy is called tautology elimination.
Note that the literals in a clause must be exact complements for tautology elimination to apply. We cannot remove non-identical literals, just because they are complements under unification. For example, the set of clauses {¬p(a), p(x)}, {p(a)}, and {¬p(b)} is unsatisfiable. However, if we were to remove the first clause (by an incorrect application of tautology elimination), the remaining clauses would be satisfiable.
SUBSUMPTION ELIMINATION
In subsumption elimination, the deletion criterion depends on a relationship between two clauses in a database. A clause Φ subsumes a clause Ψ if and only if there exists a substitution σ such that Φσ ⊆ Ψ. For example, {p(x), q(y)} subsumes {p(a), q(v), r(w)}, since there is a substitution {x←a, y ←v} that makes the former clause a subset of the latter.
If one member in a set of clauses subsumes another member, then the set remaining after eliminating the subsumed clause is satisfiable if and only if the original set is satisfiable. Therefore, subsumed clauses can be eliminated. Since the Resolution process itself can produce tautologies and subsuming clauses, we need to check for tautologies and subsumptions as we perform Resolutions.
UNIT RESOLUTION
A unit resolvent is one in which at least one of the parent clauses is a unit clause, i.e., one containing a single literal. A unit derivation is one in which all derived clauses are unit resolvents. A unit refutation is a unit derivation of the empty clause.
As an example of a unit refutation, consider the following proof. In the first two inferences, unit clauses from the initial set are resolved with binary clauses to produce two new unit clauses. These are resolved with the first clause to produce two additional unit clauses. The elements in these two sets of results are then resolved with each other to produce the contradiction.

Note that the proof contains only a subset of the possible uses of the Resolution rule. For example, clauses 1 and 2 can be resolved to derive the conclusion {q, r}. However, this conclusion and its descendants are never generated, since neither of its parents is a unit clause.
Inference procedures based on Unit Resolution are easy to implement and are usually quite efficient. It is worth noting that, whenever a clause is resolved with a unit clause, the conclusion has fewer literals than the parent does. This helps to focus the search toward producing the empty clause and thereby improves efficiency.
Unfortunately, inference procedures based on Unit Resolution generally are not complete. For example, the clauses {p, q}, {¬p, q}, {p, ¬q}, and {¬p, ¬q} are inconsistent. Using unconstrained Resolution, it is easy to derive the empty clause. However, Unit Resolution fails in this case, since none of the initial clauses contains just one literal.
On the other hand, if we restrict our attention to Horn clauses (i.e., clauses with at most one positive literal), the situation is much better. In fact, it can be shown that there is a unit refutation of a set of Horn clauses if and only if there is a (unconstrained) Resolution refutation.
INPUT RESOLUTION
An input resolvent is one in which at least one of the two parent clauses is a member of the initial (i.e., input) set of clauses. An input deduction is one in which all derived clauses are input resolvents. An input refutation is an input deduction of the empty clause.
It can be shown that Unit Resolution and Input Resolution are equivalent in inferential power in that there is a unit refutation from a set of clauses if and only if there is an input refutation from the same set of clauses.
One consequence of this fact is that Input Resolution is complete for Horn clauses but incomplete in general. The unsatisfiable set of clauses {p, q}, {¬p, q}, {p, ¬q}, and {¬p, ¬q} provides an example of a deduction on which Input Resolution fails. An input refutation must (in particular) have one of the parents of { } be a member of the initial set of clauses. However, to produce the empty clause in this case, we must resolve either two single literal clauses or two clauses having single-literal factors. None of the members of the base set meet either of these criteria, so there cannot be an input refutation for this set.
LINEAR RESOLUTION
Linear Resolution (also called Ancestry-filtered Resolution) is a slight generalization of Input Resolution. A linear resolvent is one in which at least one of the parents is either in the initial set of clauses or is an ancestor of the other parent. A linear deduction is one in which each derived clause is a linear resolvent. A linear refutation is a linear deduction of the empty clause.
Linear Resolution takes its name from the linear shape of the proofs it generates. A linear deduction starts with a clause in the initial set of clauses (called the top clause) and produces a linear chain of Resolution. Each resolvent after the first one is obtained from the last resolvent (called the near parent) and some other clause (called the far parent). In Linear Resolution, the far parent must either be in the initial set of clauses or be an ancestor of the near parent.
Much of the redundancy in unconstrained Resolution derives from the Resolution of intermediate conclusions with other intermediate conclusions. The advantage of Linear Resolution is that it avoids many useless inferences by focusing deduction at each point on the ancestors of each clause and on the elements of the initial set of clauses.
Linear Resolution is known to be refutation complete. Furthermore, it is not necessary to try every clause in the initial database as top clause. It can be shown that, if a set of clauses Δ is satisfiable and Δ∪{Φ} is unsatisfiable, then there is a linear refutation with Φ as top clause. So, if we know that a particular subset of our input clauses is consistent, we need not attempt refutations with the elements of that subset as top clauses.
A merge is a resolvent that inherits a literal from each parent such that this literal is collapsed to a singleton by the most general unifier. The completeness of Linear Resolution is preserved even if the ancestors that are used are limited to merges. resolvent (i.e., clause {q}) is a merge.
SET OF SUPPORT RESOLUTION
If we examine Resolution traces, we notice that many conclusions come from Resolutions between clauses contained in a portion of the clauses that we know to be satisfiable. For example, in many cases, the set of premises is satisfiable, yet many of the resolvents are obtained by resolving premises with other premises rather than the negated conclusion. As it turns out, we can eliminate these Resolutions without affecting the refutation completeness of Resolution.
A subset Γ of a set Δ is called a set of support for Δ if and only if Δ − Γ is satisfiable. Given a set of clauses Δ with set of support Γ, a set of support resolvent is one in which at least one parent is selected from Γ or is a descendant of Γ. A set of support deduction is one in which each derived clause is a set of support resolvent. A set of support refutation is a set of support deduction of the empty clause.
The following derivation is a set of support refutation, using as set of support the singleton set consisting of the clause {¬r}. The clause {¬r} resolves with {¬p, r} and {¬q, r} to produce {¬p} and {¬q}. These then resolve with clause 1 to produce {q} and {p}. Finally, {q} resolves with {¬q} to produce the empty clause.

Obviously, this strategy would be of little use if there were no easy way of selecting the set of support. Fortunately, there are several ways this can be done at negligible expense. For example, in situations where we are trying to prove conclusions from a consistent set of premises, the natural choice is to use the clauses derived from the negated goal as the set of support. This set satisfies the definition as long as the set of premises itself is satisfiable. With this choice of set of support, each Resolution must have a connection to the overall goal, so the procedure can be viewed as working backward from the goal. This is especially useful for premises in which the number of conclusions possible by working forward is larger. Furthermore, the goal-oriented character of such refutations often makes them more understandable than refutations using other strategies.
RECAP
The (general) Resolution Principle is a rule of inference for Herbrand Logic analogous to the Propositional Resolution Principle for Propositional Logic. As with Propositional Resolution, (general) Resolution works only on expressions in clausal form.
Unification is the process of determining whether two expressions can be unified, i.e., made identical by appropriate substitutions for their variables. A substitution is a finite mapping of variables to terms. The variables being replaced together constitute the domain of the substitution, and the terms replacing them constitute the range. A substitution is pure if and only if all replacement terms in the range are free of the variables in the domain of the substitution. Otherwise, the substitution is impure. The result of applying a substitution σ to an expression ϕ is the expression ϕσ obtained from the original expression by replacing every occurrence of every variable in the domain of the substitution by the term with which it is associated. The composition of two substitutions is a single substitution that has the same effect as applying those substitutions in sequence. A substitution σ is a unifier for an expression ϕ and an expression ψ if and only if ϕσ = ψσ, i.e., the result of applying σ to ϕ is the same as the result of applying σ to ψ. If two expressions have a unifier, they are said to be unifiable. Otherwise, they are nonunifiable. A most general unifier, or mgu, σ of two expressions has the property that it as general as or more general than any other unifier. Although it is possible for two expressions to have more than one most general unifier, all of these most general unifiers are structurally the same, i.e., they are unique up to variable renaming.
The (general) Resolution Principle is a generalization of Propositional Resolution. The main difference is the use of unification to unify literals before applying the rule. A Resolution derivation of a conclusion from a set of premises is a finite sequence of clauses terminating in the conclusion in which each clause is either a premise or the result of applying the Resolution Principle to earlier members of the sequence. Resolution and Fitch are equally powerful. Given a set of sentences, Resolution can derive the empty clause from the clausal form of the sentences if and only if Fitch can find a proof of a contradiction. The benefit of using Resolution is that the search space is smaller.