Chapter 10
Structural Design Using Finite Elements
10.8 INTRODUCTION
Finite element analysis is concerned with determining the response (displacements and stresses) of a given structure for a given set of loads and boundary conditions. It is an analysis procedure in which the structural configuration—its geometry, material properties, boundary conditions and loads—is well defined, and the goal is to determine its response. On the other hand, engineering design is a process of synthesis in which parts are put together to build a structure that will perform a required set of functions satisfactorily. Analysis is very systematic and can be taught easily. Design is an intuitive and iterative process. Clearly, analysis is one of the several steps in the design process because we use analysis to evaluate the adequacy of the design. In this chapter, we will briefly discuss the basic steps in structural design and the use of finite element analysis (FEA) in the process of designing a structure.
There are two general approaches to design: creative design and adaptive design. The former is concerned with creating a new structure or machine that does not exist, whereas the latter is concerned with modifying an existing design to perform better. Although analysis techniques such as FEA play a crucial role, the designer’s experience and creative ideas are important for the former. Adaptive design is an evolutionary process and is encountered much more frequently in practice. For example, how many times does an automotive company design a new car from scratch? The majority of engineers’ work concentrates on improving the existing vehicle so that the new car will be more comfortable, more durable, safer, and more fuel efficient. In this chapter, we will discuss the role of FEA in the adaptive design process.
Structural design is a procedure to improve or enhance the performance of a structure by changing its parameters. Performances can be quite general in engineering fields and can include the weight, stiffness, or compliance; the fatigue life; noise and vibration levels; safety, and so forth. However, the performance does not include such aesthetic measures as attractiveness. The performances are measurable quantities. Especially, we are interested in the performance measures that can be computed by finite element analysis.
In structural design, two different types of performances are often considered. The first type is related to the criteria that the system must satisfy. As long as the performance satisfies the criteria, its level is not important. In engineering design, this type of performance is called a constraint. For example, the allowable strength is often used as a constraint in structural design so that the stresses are less than the allowable strength. The second type, called goal, is the performance that the engineer wants to improve as much as possible. The total weight of the structure or cost of manufacturing is an example of a goal. Since a goal is a function of design, it is often referred to as the objective function.
System parameters are variables that the engineer can change during the design process. For example, the thickness of a vehicle body panel can be changed to improve the stiffness of a vehicle. The cross section of a beam can be changed in designing a bridge structure. System parameters that can be changed during the design process are called design variables. The design variables can include the plate thickness, cross‐sectional dimensions, location and size of cutouts, shape of the structure, and so forth. In this chapter, we will learn how to change the design variables to improve the goal, while satisfying system constraints.
A set of design variables that satisfies the constraints is called a feasible design, while a set that does not satisfy constraints is called an infeasible design. It is difficult to determine whether a current design is feasible unless the structural problem is analyzed. For complicated structural problems, it may not be easy to choose appropriate design constraints so that the feasible region is not empty.
In the process of structural design, finite element analysis is used to calculate the objective function and constraints. For example, if a design problem has a stress constraint, it is necessary to use finite element analysis to calculate the stress constraint. That is, a new finite element model is defined for a given set of design variables, from which the objective function and constraints are evaluated. In addition to the function values, the design process often requires the gradients (i.e., derivatives) of these functions with respect to design variables, which is called sensitivity. It is possible to calculate this sensitivity information using a variation of finite element analysis. A brief introduction of sensitivity analysis will also be provided in this chapter.
Since this is only an introduction to structural design, we will first present conventional design approaches using safety margin and intuitive design in the first two sections. Design parameterization in section 10.4 deals with the definition of design variables. The topics of parametric study and sensitivity analysis in section 10.5 investigate the effect of a change in design variables on the performance. Section 10.6 introduces structural optimization, which is a mathematical tool to find the best design.
10.2 CONSERVATISM IN STRUCTURAL DESIGN
Structural design anticipates various sources of uncertainty. For example, material properties show variability even if they are manufactured under the same process. In addition, it is difficult to accurately estimate the maximum load applied to an airplane wing under a gust wind environment. As we discussed in chapter 9, finite element analysis results may have an error in stress calculation. Therefore, it is important to make sure that the designed structure is safe under such uncertain material properties, environment, and calculation errors1. In this section, various ways of making the structure safe under uncertainty are discussed. In structural design, the major sources of uncertainty come from material properties, applied loads, and calculation errors.
10.2.1 Allowable Strength
The common approach to make the designed structure to be safe under uncertainty is to design based on conservative values. For example, when the failure strength of a material shows a statistical distribution, engineers are allowed to design a structure with a smaller strength than the nominal strength, which is called an allowable strength or stress allowables. In the design community, the allowable strength is sometimes included in the calculation of the factor of safety, but in this text, the allowable strength is not included in the calculation of the factor of safety.
Before defining the allowable strength, it is necessary to define the failure strength first, as the former is based on the latter. For ductile materials (e.g., most metals), the failure strength means either the yield or ultimate strength, depending on the definition of structural failure. The yield strength is when the material starts to plastically deform, while the ultimate strength is when the material fracture occurs. Therefore, if the structure is considered to be failed when a permanent deformation occurs, then the yield strength is used for the failure strength. On the other hand, if the structure is not considered failed until fracture, then the ultimate strength can be used for the failure strength. On brittle materials, however, these two values are often so close as to be indistinguishable. Therefore, it is usually acceptable to use the ultimate strength as the failure strength.
In the aircraft structural design, for example, the Federal Aviation Administration (FAA) requires aircraft structure to be designed using either A‐basis or B‐basis allowable strength (MIL‐HDBK‐17 Vol. 1, FAR 25.613). In order to maintain safety, these allowable strengths are lower than the average failure strength of the material. The A‐basis allowable strength is used when the failure of a structural component can lead to a catastrophic failure. On the other hand, the B‐basis allowable strength is used when structural redundancy exists such that when a structural component fails, another component(s) can redistribute the load. In this chapter, we will use σallowable to represent the allowable strength of the material.
In general, the allowable strength is calculated using coupon tests. A coupon represents a specimen for testing material properties, such as a tensile test specimen of metallic materials. A set of coupons is tested to estimate the statistical distribution of the material’s failure strengths. Let us assume that N number of coupons are used, from which the average failure strength is ![]() and the standard deviation is s. Then, the allowable strength can be calculated based on the statistical distribution of failure strengths, whose histogram is shown in figure 10.1. The A‐basis is the lowest first percentile of the distribution, while the B‐basis is the lowest tenth percentile. That is, if 100 coupons are used, then at the A‐basis allowable stress less than 1% of the coupons fail, while at the B‐basis allowable stress a tenth of the coupons fail. From the assumption that the failure strength shows a normal distribution, these allowable strengths can be calculated by
and the standard deviation is s. Then, the allowable strength can be calculated based on the statistical distribution of failure strengths, whose histogram is shown in figure 10.1. The A‐basis is the lowest first percentile of the distribution, while the B‐basis is the lowest tenth percentile. That is, if 100 coupons are used, then at the A‐basis allowable stress less than 1% of the coupons fail, while at the B‐basis allowable stress a tenth of the coupons fail. From the assumption that the failure strength shows a normal distribution, these allowable strengths can be calculated by
The allowable strength will be low when the coupon tests show a wide distribution, that is, a large standard deviation. That means, even if the average strength of a material is high, the allowable strength can be low when the coupon test results are scattered.

Figure 10.1 Histogram of failure strengths and allowable strengths
If infinitely many coupons are used, then the average and the standard deviation are the true average and the true standard deviation of the material’s strength. However, since N number of coupons are used, the calculated average and standard deviation are different from the true ones. Therefore, an additional knockdown factorkB is used to reduce the allowable strength further, which can compensate for inaccuracy caused by the limited number of coupons. Therefore, using the coupon test results, the allowable strength can be defined as
where kB is also called a tolerance limit factor.
It is obvious that the knockdown factor in eq. (10.2) depends on the number of coupons. When a small number of coupons are used, the errors in the calculated mean and standard deviation can be large, and therefore, a large value of the knockdown factor should be used. The knockdown factor will converge to the exact factor in eq. (10.1) as the number of coupons increases. Figure 10.2 shows the trend of the knockdown factor for the B‐basis allowable strength as a function of the number of coupons. In fact, the knockdown factors in this figure are obtained from the 95% confidence of the tenth percentile of a normal distribution.

Figure 10.2 Knockdown factor for the B‐basis allowable strength
Unlike the allowable strength, other types of performance measures do not have the concept of allowable values and do not have a specific method to establish it. In the case of displacement, for example, the allowable displacement is determined based on geometry or interference with other components. Although the design engineers can determine the allowable displacement with a certain margin, there is no randomness or uncertainty in the allowable displacement. Therefore, there is no need to apply additional conservatism to it.
10.2.2 Factor of Safety
In chapter 5, we defined the concept of a factor of safety and its application in determining whether a structure is safe or not. For a given loading condition, the structural analysis determines the stresses, and the ratio between the failure strength and the actual stress is defined as the factor of safety. In this section, the concept of the factor of safety is redefined in the perspective of structural design; that is, we want to design a structure that has a given level of the safety factor.
As we mentioned in the previous section, the randomness in material strength is taken into account by calculating a conservative allowable strength. In addition to the variability in material strength, however, many different factors need to be considered in order to make the structure safe, such as an error in stress calculation, unexpected loads, misuse, or degradation as time goes by. Many structural systems are purposefully built much stronger than needed for normal usage to take into account these factors. In structural design, the effect of all these factors is translated into a load carrying capacity of the structural system.
Factors of safety, also known as a safety factor, is a term describing the load carrying capacity of a system beyond the expected or actual loads. Essentially, the factor of safety is how much stronger the system is than it usually needs to be for an intended load. In order to consider the factor of safety in the design process, it is required to determine the maximum applied load that the system can experience during its normal operation. The maximum applied load can be measured from an existing similar system or can be estimated from experience. If the system is operated under a constant loading condition, such as gas turbine engines, the maximum load is the nominal operating load. Under the variable loading condition, on the other hand, it is the maximum load that the system can experience during its lifecycle. For example, the maximum load on the airplane wing is calculated when the airplane meets an extreme gust wind. Of course, the extreme condition can be subjective. The maximum load is often determined by government regulations.
Once the maximum applied load is determined, the design load can be determined using the factor of safety, SF, as
It is beneficial to emphasize two aspects that are different here from the definition of the factor of safety in chapter 5. First, the factor of safety is defined here in terms of loads, not stresses. Therefore, it is a global quantity, not local. This is because the factor of safety is used to measure the load carrying capacity of the entire structural system. Second, eq. (10.3) is not for calculating the factor of safety but for calculating the design load. Once the factor of safety is defined based on regulation or experience, the design load can be calculated by multiplying it with the maximum load. Therefore, the factor of safety is related to how much the structure can carry the load beyond the maximum load. In aircraft structural design, for example, the FAA requires designing the structure with SF = 1.5, which means that the aircraft structure can support a load that is 1.5 times larger than the maximum load. In fact, during the certification of the airplane, the design load is applied on the structure, and no major failure should happen for it to pass the certification test.
Once the design load is determined for a given safety factor, the stress constraint can be defined as
where σdesign is the calculated stress under the design load, and σmax is the calculated stress under the maximum load. If the design load is used to calculate stress, there is no need to multiply the safety factor because the design load already includes it. On the other hand, if the maximum applied load is used, then the stress should be multiplied by the safety factor before comparing with the allowable strength.
The structure is considered to be failed when any part of the structure reaches its allowable strength. Due to the safety factor and the allowable strength, however, it is unlikely that the structure actually fails. Conservatism is the main difference between analysis and design. This level of conservatism is required to compensate for various factors in the design process. For example, the stress calculated from finite element analysis may differ from the actual stress due to various errors and also various assumptions made in the model, and the failure strength might be beyond the linear region of the material behavior.
Although we explained the factor of safety using the strength constraint, the above safety constraint can be applied to other types of performance measures. The above safety constraint can be restated as: the response (Ri) of a member under the maximum operating condition should be less than the capacity (Ci) of the member material. In the case of strength constraint, the calculated stress under the maximum load is the response, while the allowable strength is the capacity. Then, we can extend eq. (10.4) to general performance measures as
When multiple loads are applied simultaneously, the response Ri should be the combination of the effects of all loads. Typically,

where Fj is the j‐th load and NL is the total number of applied loads.
Note that the safety constraint in eq. (10.5) is applied to a point x of the i‐th member, and it must be satisfied everywhere. In practice, the location at which the response is critical is considered.
An alternative and useful measure of safety is the safety margin, which measures the excess capacity compared with the response; thus
In the case of the strength constraint, the member can afford additional Zi stress before it fails.
From a different viewpoint, we can define a sufficiency factorSi as a ratio of the allowable capacity to the response. Then, the safety constraint can be restated as
For example, a sufficiency factor 0.8 means that Ri has to be multiplied by 0.8, or Ci is divided by 0.8 so that the sufficiency factor increases to one. In other words, this means that Ri has to be decreased by 20% (1 − 0.8), or Ci has to be increased by 25% ((1/0.8) − 1) in order to achieve the required safety. The sufficiency factor is automatically normalized with respect to the capacity. The sufficiency factor is useful in estimating the resources needed to achieve the required safety factor. For example, if the current design has the sufficiency factor of 0.8, then this indicates that maximum stresses must be lowered by 20% to meet the safety. This permits the engineers to readily estimate the load to reduce stresses to a given level.
10.2.3 Load Factor
Instead of reducing the capacity by the factor of safety, it is possible to increase the applied loads, which is basic idea of the load factor. The load factorλ is the minimum factor by which a set of loads acting on the structure must be multiplied to cause the structure to fail. Commonly, the loads are taken as those acting on the structure during service conditions. For ductile materials, the strength of the structure is determined from the yield stress in the idealized elastic‐plastic material model. For brittle materials, the tensile strength is used as the allowable strength.
Let us assume that a set of working loads Fj are applied to the structure, and the structure is safe. For a given failure mode (i.e., for a given ultimate strength), the structure is considered to have failed or collapsed when the capacity Ci are related to the factored load λFj by
where F is the vector of all applied loads. The load factor is the scale of the applied loads such that the response becomes equal to the capacity. If proportional loading is assumed, Ri is a linear function, and the load factor can be taken out of parentheses. Then, eq. (10.9) can be written in the following form:
In the structural analysis viewpoint, the load factor is the ratio between capacity and response. From the design viewpoint, the structure should be designed in order to satisfy a given level of load factor.
Clearly, there is much similarity in formulation between the factor of safety and the load factor as measures of structural safety. The difference is the reference level at which the two measures operate: the first at the level of working loads, while the second, at the level of collapse loads.

Figure 10.3 Cantilevered beam design
10.3 INTUITIVE DESIGN: FULLY STRESSED DESIGN
In example 10.2, we were able to determine the height of the beam that satisfies the stress or deflection constraint because the constraint was explicitly written in terms of the design variable. It is unlikely that we will have such an explicit relationship for more complex structures. Instead, we can evaluate the performance measures at a given set of values for the design variables. In such a case, an iterative process can be used to find the best design. Starting from the initial values of the design variables, we can update the design variables according to the calculated performances. In the case of the beam design problem, for example, if the stress is too high, we increase the height gradually. We can repeat this process until the stress becomes just right. The above‐mentioned process is called intuitive design.
When structures are subject only to stress and minimum gauge constraints, the fully stressed design (FSD) is the best design. The basic concept can be used to design the structure as follows:
This implies that we should remove material from members that are not fully stressed unless prevented by minimum gauge constraints. This appears reasonable but it is based on an implicit assumption that the primary effect of adding or removing material from a structural member is to change the stresses in that member. If this assumption is not true, that is, if adding material to one part of the structure can have large effects on the stresses in other parts of the structure, we may want to have members that are not fully stressed because they help to relieve stresses in other members.
For statically determinate structures, the assumption that adding material to a member influences primarily the stresses in that member is correct. In fact, without an inertia or thermal load, there is no effect at all on stresses in other members. Therefore, we can expect that the FSD criterion will hold at the minimum weight design of such structures. However, for statically indeterminate structures, the minimum weight design may not be fully stressed. In most structures made of a single material, there is a fully stressed design near the optimum design, and so the method has been extensively used for metal structures. The FSD method may not do as well when several materials are used.
The FSD technique is usually complemented by a resizing algorithm based on the assumption that the load distribution in the structure is independent of member sizes. That is, the stress in each member is calculated, and then the member is resized to bring the stresses to their allowable values assuming that the loads carried by members remained constant (this is logical since the FSD criterion is based on a similar assumption). For example, for truss structures, where the design variables are often cross‐sectional areas, the force in any member is σ⋅A, where σ is the axial stress and A is the cross‐sectional area. Assuming that σ⋅A is constant leads to the following stress ratio resizing technique:
which gives the resized area Anew in terms of the current area Aold, the current stress σ, and the allowable stress σallowable. For a statically determinate truss, the assumption that member forces are constant is valid, and therefore eq. (10.13) will bring the stress in each member to its allowable value. If the structure is not statically determinate, eq. (10.13) has to be applied repeatedly until convergence to any desired tolerance is achieved. Also, if Anew obtained by eq. (10.13) is smaller than the minimum gauge, the minimum gauge is selected rather than the value given by eq. (10.13).
Equation (10.13) works well for truss structures and under the assumption that the member force does not change significantly as the cross sections change. In the case of beam element, we can obtain a similar stress ratio resizing technique. In that case, we use the section modulus. The maximum stress in the beam occurs at the top or bottom of the cross section. Thus,
where S is the section modulus. Assuming that the bending moment remains constant during the design process, we can obtain the following stress ratio resizing technique:
Note that the difference compared to the truss structure is the use of section modulus rather than cross‐sectional area. Again, if the bending moment remains constant (i.e., statically determinate), then eq. (10.15) will yield the fully stress design in one iteration.

Figure 10.4 Three‐bar truss for fully stressed design
10.4 DESIGN PARAMETERIZATION
In the previous sections, we discussed simple design processes that can be applied to design variables that are related to cross‐sectional geometry. However, when more complicated structures, such as plane solids or three‐dimensional solids, are considered, it may not be trivial to define design variables. In this section, we discuss various types of design variables and procedures to define them.
Selecting design variables is called design parameterization. The design variables are assumed to vary during the design process. In some cases, it is relatively simple to choose them from analysis parameters and to vary their values. In other cases, however, it may not be easy because changing the design variables involves modifying finite element mesh. Based on their role in finite element analysis, we will discuss three different types of design variables.
Material property design variables: In structural analysis, material properties are used as a parameter. Young’s modulus and Poisson’s ratio, for example, are required in the analysis of an isotropic material. If these material properties are subject to change, then they are called material propertydesign variables. These kinds of design variables do not appear in regular design problems since in most cases material properties are presumed to be constant. Analysis using constant material properties is called a deterministic approach. On the other hand, a probabilistic approach assumes that material properties are not constant but randomly distributed within certain ranges. This approach is more practical because if multiple specimens from the same material batch are tested, they will show different material properties. This happens because of the randomness in the microstructures during the manufacturing process. In this case, material properties are no longer considered to be constant and can, therefore, be used as design variables.
Sizing design variables: Sizing design variables are related to geometric parameters of a structure, and they are often called parametric design variables. For example, most automotive and airplane parts are made from plate/shell components. It is natural that engineers want to vary the thicknesses (or gauge) of the plate/shell in order to reduce the weight of the vehicle. In that case, the plate thicknesses are sizing design variables. During structural analysis, the thicknesses are considered as variable parameters. The sizing design variables are similar to the material property design variables in the sense that both types of variables change analysis parameters, not the overall shape and layout of the structure.
Another important type of sizing design variable is the cross‐sectional geometry of bars and beams. Figure 10.5 provides some examples of the shapes and parameters that define these cross sections. In the structural analysis of bars, for example, the cross‐sectional area is required to determine the axial rigidity. If a rectangular cross section is used, then the area would be defined as A = b × h. Thus, the two parameters, b and h, can be considered design variables. Note that these variables contribute to the cross‐sectional area for bars and the moment of inertia for beams.

Figure 10.5 Sizing design variables for cross sections of bars and beams; (a) Solid circular cross section; (b) Rectangular cross section; (c) Circular tube; (d) Rectangular tube; (e) I–section
Shape design variables: While material properties and sizing design variables are related to the parameters of structural analysis, shape design variables are related to the structure’s geometry. Difficulty in this approach is that the shape of the structure does not explicitly appear as a parameter. Although the design variables in figure 10.5 determine the cross‐sectional shape, they are not shape design variables, since these cross‐sectional shapes are considered parameters in structural analysis. However, the length of bars or beams should be treated as a shape design variable. Usually, the shape design variable defines the domain of integration in structural analysis. Thus, it is not convenient to extract shape design variables from a structural model and to use them as sizing design variables.
Consider a rectangular block with a hole, as shown in figure 10.6. The location and size of the hole are determined by the geometric values of Cx, Cy, and r, which are shape design variables. Different values of shape design variables yield different structural shapes. However, these shape design variables do not explicitly appear in structural analysis. If finite element analysis is used to perform structural analysis, then the shape design variables change the mesh, as shown in figure 10.6. Note that the mesh remains constant in the case of material properties and sizing design variables. Thus, the shape design problem is more difficult to solve than the sizing design problem.
It is important to note that inappropriate parameterization can lead to unacceptable shapes. This includes not only design variables but also the range of designs. For example, the ranges in Cx, Cy, and r should be limited such that the hole remains inside of the rectangle in figure 10.6.

Figure 10.6 Shape design variables in a plate with a hole
Shape design parameterization describes the boundary shape of a structure as a function of design variables. There are many different methods, but we will only discuss two methods: isoparametric mapping method and solid model‐based parameterization. Both methods have advantages and disadvantages. The first method works well with the mapped mesh in which the topological mesh remains constant throughout the design process. Only the physical mesh changes according to shape designs. For example, let us consider changing the radius of the structure shown in figure 10.7. The initial mesh is generated using the mapped mesh. Then when the radius is changed, the topology of the mesh remains unchanged, but due to change in physical dimension, the geometries of elements change accordingly. This type of parameterization is convenient because the number of elements and nodes will not change during the design process. For example, if the user specifies the performance as displacement at a node or stress at an element, it is easy to track the location and value of the performance. However, mesh distortion will be the bottleneck of this method when the changes in design variables are large. Initially, well‐shaped elements will eventually be distorted as design variables change from their initial values.

Figure 10.7 Design perturbation using isoparametric mapping method
The second method parameterizes the shape dimensions on the solid model. This method assumes that the preprocessing program has solid modeling and automatic mesh generation capabilities. When a solid model is generated, the user provides dimensions to geometric features, such as fillets, holes, cutouts, and so forth. It is also assumed that the preprocessing has a capability of automatically updating the solid model when the values of dimensions are changed. Most CAD software programs have these capabilities. As shown in figure 10.6, dimensions of solid models are usually selected as shape designs. It is unnecessary to select all dimensions. Only those dimensions that are supposed to change are considered as design variables. For a given design, the dimensions of the solid model are fixed, and the mesh is automatically generated on the solid model (refer to figure 10.7(a)). When design variables are changed, the solid model is updated to reflect the new designs, and the mesh is regenerated on the new model (refer to figure 10.7(b)). This type of parameterization can reduce mesh distortion problems because the preprocessing program will generate a free mesh for the given designs. However, a small change in design may end up in a completely different mesh. Thus, it is difficult to track the performance value at a particular location. Especially, numerical/discretization errors may dominate in finding the trend of performance.
10.5 PARAMETRIC STUDY – SENSITIVITY ANALYSIS
10.5.1 Parameter Study
Once the design variables are determined, structural analysis (i.e., finite element analysis) can be carried out to calculate performances. When the design variables are changed, we expect different values of the performance measures. Often we can estimate if a performance will increase or decrease based on our knowledge of mechanics. However, it would be nontrivial to estimate how much the performance will change. The parameter study investigates the effect of design variables on the performance. Usually, one design variable is changed at a time and the performance changes are plotted in a graph.
Table 10.1 Parametric study of a cantilevered beam
| w (in) | h (in) | σmax (ksi) |
| 2.0 | 4.0 | 37.5 |
| 2.0 | 4.5 | 29.6 |
| 2.0 | 5.0 | 24.0 |
| 2.5 | 4.0 | 30.0 |
| 2.5 | 4.5 | 23.7 |
| 2.5 | 5.0 | 19.2 |
| 3.0 | 4.0 | 25.0 |
| 3.0 | 4.5 | 19.8 |
| 3.0 | 5.0 | 16.0 |

Figure 10.8 Parametric study plot for the cantilevered beam
For example, the cantilevered beam in example 10.2 has two design variables: w (width) and h (height) of the cross section. Let each design variable (or parameter) have three levels. Then, table 10.1 shows nine cases for the parametric study. Since there are only two parameters, it is possible to plot the results as a three‐dimensional surface as shown in figure 10.8. Note that the maximum stress decreases as both the width and height of the beam increase. In addition, the maximum stress is higher than the allowable stress when the height and width are small. Thus, a valid design can be chosen from the acceptable region.
10.5.2 Sensitivity Analysis
The parametric study is a useful tool to provide quantitative behavior of the performance as the design changes. However, when the number of design variables becomes large, the parameter study can be expensive. In the case of two design variables with three levels, nine analyses were required. Sometimes, multiple parameters are varied simultaneously in order to reduce the number of analyses, but still, this can be expensive. In addition, when the performance changes rapidly, the parametric study cannot capture the local change unless the interval is small enough.
In many cases, we cannot afford to perform the parametric study with all variables. In addition, we do not need to find the performance changes throughout the entire range. It is often enough to find the effect of design variables in the vicinity of the current design point. In such a case, design sensitivity analysis can be used to effectively find it. Design sensitivity analysiscomputes the rate of performance change with respect to design variables. In conjunction with structural analysis, design sensitivity analysis generates a critical information, the gradient, for design optimization. Obviously, the performance is presumed to be a continuous function of the design, at least in the neighborhood of the current design point.
Explicit dependency on design: In general, a structural performance depends on the design. For example, a change in the cross‐sectional area of a beam would affect the structural weight. This type of dependence is simple if the expression of weight in terms of the design variables is known. For example, the weight of a beam with a circular cross section can be expressed as
where r is the radius, and l is the length of the beam. If the radius is a design variable, then the design sensitivity of W with respect to r would be
This type of function is explicitly dependent on the design variable since the function can be explicitly written in terms of that design. Consequently, only algebraic manipulation is involved, and no finite element analysis is required to obtain the design sensitivity of an explicitly dependent performance.
Implicit dependence on design: However, in most cases, a structural performance does not explicitly depend on the design. For example, when the stress in a beam is considered as a performance, there is no simple way to express the design sensitivity of stress explicitly in terms of the design variable r. In the linear elastic problem, the stress of the structure is determined from the displacement, which is a solution to the finite element analysis. Thus, the sensitivity of stress σ(q) can be written as
where q is the vector of nodal DOFs of the beam element. Since the expression of stress as a function of displacement is known, dσ/dq can easily be obtained. The only difficulty is the computation of dq/dr, which is the displacement sensitivity with respect to the design variable r.
When a design engineer wants to compute the design sensitivity of performance such as stress σ(q) in eq. (10.20), structural analysis (finite element analysis, for example) has presumably already been carried out. We will use the symbol b for generic design variable, and the nodal DOFs q is a part of the global DOF vector {Q}. Assume that the structural problem is governed by the following linear algebraic equation
Equation (10.21) is a matrix equation of finite elements. Suppose the explicit expressions of [K(b)] and {F(b)} are known and differentiable with respect to design variable b. Since the stiffness matrix [K(b)] and load vector {F(b)} depend on the design b, solution {Q} also depends on the design b. However, it is important to note that this dependency is implicit, which is why we need to develop a design sensitivity analysis methodology. As shown in eq. (10.20), dq/db must be computed using the governing equation of eq. (10.21). This can be achieved by differentiating eq. (10.21) with respect to b as
Assuming that the explicit expressions of [K(b)] and {F(b)} are known, [dK/db] and {dF/db} can be evaluated. Thus, if solution {Q} in eq. (10.21) is known, then {dQ/db} can be computed from eq. (10.22), which can then be substituted into eq. (10.20) to compute dσ/db. Note that the stress is implicitly dependent on the design through nodal DOFs q.
When more than one design variable is defined, the above sensitivity equation must be solved for each design variable. Thus, the sensitivity analysis can be expensive when the problem has a large number of design variables. However, the sensitivity equation (10.22) uses the same stiffness matrix as the original finite element analysis. The difference is on the RHS. As we discussed in chapter 9, eq. (10.22) is similar to the finite element analysis with multiple load cases. The RHS of eq. (10.22) can be considered as a pseudo‐force vector. The best way of solving eq. (10.22) might be to construct the RHS of eq. (10.22) for different design variables and to use the restart procedure. Then, the sensitivity equation can be solved with the stiffness matrix that is already factorized during the finite element analysis. Thus, the computational cost in solving eq. (10.22) is usually less than 5% of that of finite element analysis.
In general, it can be assumed that a general performance measure H depends on the design explicitly and implicitly. That is, the performance measure H is presumed to be a function of design b, and nodal DOFs q(b) as
The sensitivity of H can thus be expressed as
The only unknown term in eq. (10.24) is dq/db, which can be obtained from eq. (10.22). When [dK/db] and {dF/db} are not available, we can calculate the sensitivity using a finite difference method as follows.
Finite difference method: The easiest way to compute sensitivity information of the performance is by using the finite difference method. Different designs yield different analysis results and, thus, different performance values. The finite difference method actually computes design sensitivity of performance by evaluating performance at different stages in the design process. If b is the current design, then the analysis results provide the value of performance measure H(b). In addition, if the design is perturbed to b + Δb, where Δb represents a small change in the design, then the sensitivity of H(b) can be approximated as
Equation (10.25) is called the forward difference method since the design is perturbed in the direction of + Δb. If –Δb is substituted in eq. (10.25) for Δb, then the equation is defined as the backward difference method. Additionally, if the design is perturbed in both directions, such that the design sensitivity is approximated by
then the equation is defined as the central difference method.
The advantage of the finite difference method is obvious. If structural analysis can be performed and the performance measure can be computed as a result of the structural analysis, then the expressions in eqs. (10.25) and (10.26) are virtually independent of the problem types considered. Consequently, this method is still popular in engineering design.
However, sensitivity computation costs become the dominant concern in the design process if the finite difference method is used. If n represents the number of designs, then n + 1 analyses have to be carried out for the forward and backward difference methods, and 2n + 1 analyses are required for the central difference method. Unlike the sensitivity analysis in eq. (10.22), we cannot use the restart procedure in the finite difference method because the stiffness matrix at the perturbed design is different from that of the original design. For practical engineering applications using the finite element method, the cost of structural analysis is rather expensive. Hence, this method is not feasible for large‐scale problems containing many design variables.

Figure 10.9 Influence of step size in the forward finite difference method
Another major disadvantage of the finite difference method is the accuracy of its sensitivity results. In eq. (10.25), accurate results can be expected when Δb approaches zero. Figure 10.9 shows some sensitivity results using the finite difference method. The tangential slope of the curve at b0 is the exact sensitivity value. Depending on perturbation size, we can see that sensitivity results are quite different. For a mildly nonlinear performance measure, relatively large perturbation provides a reasonable estimation of sensitivity results. However, for highly nonlinear performance measures, a large perturbation yields completely inaccurate results. Thus, the determination of perturbation size greatly affects the sensitivity result. And even though it may be necessary to choose a very small perturbation, numerical noise becomes dominant for a too‐small perturbation size. That is, with a too‐small perturbation, no reliable difference can be found in the analysis results. For example, if up to five digits of significant numbers are valid in a structural analysis, then any design perturbation in the finite difference that is smaller than the first five significant digits cannot provide meaningful results. As a consequence, it is very difficult to determine design perturbation sizes that work for all problems
10.6 STRUCTURAL OPTIMIZATION
The purpose of many structural design problems is to find the best design among many possible candidates. As will be discussed in this section, at least one possible candidate should exist within a feasible design region that satisfies problem constraints. Every design in the feasible region is an acceptable design, even if it is not the best one. The best design is usually the one that minimizes (or maximizes) the objective function (goal) of the design problem. Thus, the goal of the design optimization problem is to find the design that minimizes the objective function among all feasible designs. Unfortunately, there is no mathematical theory that can find the global optimum design for general nonlinear functions. In this section, simple optimization methods are briefly introduced. However, this brief discussion is by no means the complete treatment of optimization methods. For a more detailed treatment, refer to Haftka and Gurdal2 or Arora3.
Most gradient‐based optimization algorithms are based on mathematical programming methods, which require performance and sensitivity information for given values of the design variables. For a given design that defines the structural model, the structural analysis provides the values of the objective and constraint functions to the algorithm. Gradients (design sensitivities) of the objective and constraint functions must also be supplied to the optimization algorithm. Then, the optimization algorithm calculates the best possible design of the problem. In this section, we will introduce how the optimization problem can be formulated and how it can be solved using graphical and mathematical programming methods.
10.6.1 Optimization Problem Formulation
An important step in optimization is to transcribe the verbal statement of the optimization problem into a well‐defined mathematical statement. In the verbal statement, the goal of the optimization problem is to find the best design that minimizes (or maximizes) the objective function (or cost function) under the given constraints by changing design parameters. Examples of the objective function in structural analysis are the weight, stiffness or compliance; the fatigue life; the noise level; amplitude and frequency of vibration; safety, and so forth. Constraints are similar to objective functions, but they are given as limits so that a design must satisfy them in order to be a candidate. Therefore, as long as a constraint satisfies the limit, the magnitude of the constraint is not important. However, the design that can yield a smaller value of the objective function is better than other designs with larger values of the objective function. Design variables are parameters or geometry of the structure that can be varied during design. Figure 10.10 shows the flow chart of the design optimization process.

Figure 10.10 Structural design optimization procedure
Three‐step problem formulation: In order to formulate the optimization problem, it is important to properly define three components—design variables, objective, and constraint functions.
- Identification and precise definition of design variables. As we discussed in section 10.4, different types of design variables are available. Some designs only change some parameters in the finite element analysis, but some designs change the finite element model itself. It is important to make sure that the finite element model, including properties and parameters, must completely be defined with a given set of design variables. For example, the cross section in figure 10.11(a) requires four parameters to define it: w, h, t1, and t2. Of course, it is unnecessary to choose all four as design variables. We can fix t1 and t2 and define w and h as design variables. The important thing is that once the values of design variables are given, the model should be defined uniquely. In addition, it is important to provide the lower and upper bounds of design variables and to make sure that the finite element analysis can be carried out successfully over the entire range of design variables. When finite element analysis cannot be carried out for a given design, the objective function or constraint is often assigned with very large values so that the optimum design occurs somewhere else. Another important aspect of selecting design variables is independence. All design variables must be independent of each other. If design variables are dependent, it may not be possible to generate the model, and the optimization algorithm may fail. Figure 10.11(b) shows an example of improperly defined design variables. If w, h, b, t1, and t2 are defined as design variables, then the following relation exists: h = b + 2 t1. It is possible to define six design variables and provide this relation as a constraint, but it will make the optimization problem unnecessarily complicated. In addition, selection of design variables is not unique. In figure 10.11(b), for example, we can choose w, h, t1, and t2 as independent design variables, or w, b, t1, and t2.
- Defining an objective function (cost function): Once design variables are defined, the next step is to define the objective function of the problem. The objective function defines the ranking of different designs. The goal of optimization is to find the design that has the best ranking in terms of the objective function. It is obvious that the objective function must depend on design variables. The absolute magnitude of the objective function is not important. A constant can be added or multiplied to the objective function without changing the optimization result. When more than one objective functions are involved, it is possible to combine them using weights as(10.38)

where fI(b) is an individual objective function, and wI is the corresponding weight. The weights must be chosen based on the importance of each objective function. Different optimum designs will be expected for a different set of weights. When one is unclear about the weights, the multi‐objective optimization problem can be solved, which will provide all possible sets of optimum designs4.
- Identification and definition of constraints. Unlike the objective functions, constraints do not rank the designs, but they validate whether the design is feasible or not. Once the design is determined to be usable, it is not important how much safety margin the design has. In general, there are two types of constraints: equality and inequality. Equality constraints provide relations between design variables or impose conditions that a usable design must satisfy. When the relation is linear, it is possible to remove one design variable for each equality constraint. Because of that, they are considered as strong constraints. In general, however, it is not easy to remove a design variable when the equality constraint is nonlinear. Inequality constraints are more popular in structural problems, and they provide limits on performances. For example, the maximum stress of usable design should be less than the allowable strength of the material. As long as the maximum stress is lower than the allowable strength, it is not important how low the stress is. Some constraints limit the lower or upper bounds of design variables. These constraints are called side constraints. Since it is relatively easy to impose the lower or upper bounds of design variables, these constraints are often treated separately.
Usually, an optimization problem has one objective function with many constraints. In general, there is no limit on the number of inequality constraints. For example, one can choose stresses of all elements and make them less than the allowable stress. In such a case, many elements will have stress much less than the allowable stress, and those elements will be ignored during optimization until their values become close to the allowable stress. However, the number of equality constraints should be less than that of design variables. This is obvious from the fact that we can theoretically remove one design variable for each equality constraint.

Figure 10.11 Design parameters for beam cross section
Standard form: The above description of three components in optimization needs to be written in mathematical form so that there will be no ambiguity in the problem definition. The standard form of design optimization problem can be written as
where b = {b1, b2, …, bK}T is the vector of design variables, f(b) is the objective function, gi(b) (i = 1, …, N) are inequality constraints, hj(b) (j = 1, …, M) are equality constraints, and ![]() and
and ![]() are, respectively, the lower and upper bounds of design variables. Note that the objective function is minimized, and the inequality constraints are written in “less than or equal to” form.
are, respectively, the lower and upper bounds of design variables. Note that the objective function is minimized, and the inequality constraints are written in “less than or equal to” form.
The standard form in eq. (10.39) is to find the minimum value of the objective function within the region that satisfies constraints. Thus, it is convenient to define the following feasible set S:
Then, the optimization problem is to find the minimum f(b) in the feasible set S. Once an optimization problem is written in the standard form, solving the optimization problem is independent of applications. Whether it is a structural or financial problem, the same optimization technique can be used to solve it.

Figure 10.12 Design of a beer can
It is important to distinguish two different types of minima in order to understand the nature of optimum design that we can obtain using practical methods.
Global minimum: In an optimization problem, the best design is the one that yields the smallest value of the objective function within the feasible set, which is called a global minimum. Formally, a point b* is called a global minimum for f(b) if
for all b∈S. The global minimum is the eventual goal of optimization. It is easy to define the global minimum, but unfortunately, it is not trivial to find one. If f(b) is continuous, and the set S is closed and bounded, then there is a global minimum. However, there is no mathematical method to find it. In addition, it is possible that the problem may have multiple global minima. Figure 10.13 shows an objective function f as a function of design b. The point b3 corresponds to the global minimum because f(b3) is smallest within the feasible set. In this case, a unique global minimum exists.
Local minimum: Unlike the global minimum, a local minimum is easier to find. There are many mathematical theories to find it. Formally, a point b* is called a local minimum for f(b) if
for all b∈S in a small neighborhood of b*. In the case of a single design variable, a small neighborhood is ![]() for an arbitrarily small Δ. If we can find any Δ such that f satisfies eq. (10.43), then it is a local minimum. In figure 10.13, b1, b3, and b5 are local minima. Note that b3 is a local minimum as well as a global minimum.
for an arbitrarily small Δ. If we can find any Δ such that f satisfies eq. (10.43), then it is a local minimum. In figure 10.13, b1, b3, and b5 are local minima. Note that b3 is a local minimum as well as a global minimum.

Figure 10.13 Local and global minima of a function
10.6.2 Graphical Optimization
After the optimization problem is written in the standard form, it can be solved using numerical methods. Before we discuss the various numerical methods to solve the optimization problem, let us consider simple cases in which we can solve the optimization problem graphically. When the optimization problem has only one or two design variables, graphical methods can be used to solve the problem. Graphical methods are often more expensive than other numerical methods because they require a large number of evaluations of the objective functions and constraints. However, they help engineers to visualize the design space and to understand the nature of design problem.
The first step in graphical optimization is to set up the graphical domain using the side constraints. The range of design variables defines all possible combinations of the two design variables. Since any design outside the side constraints is not feasible, it is unnecessary to plot functions in the infeasible region. The feasible region is typically referred to as the design space. The next step is to plot the objective function and constraints on the graph. In the case of constraints, it is possible to draw a boundary curve for each of the constraints. An inequality constraint will define the feasible region as one side (i.e., constraint is negative) of the curve, while an equality constraint will define the feasible region along the curve of the constraint. The difference between the equality and inequality constraints is in the interpretation of the design space.
Once the feasible set is clearly defined using constraints, the next step is to plot the objective function. Unlike the constraints, the objective function does not have a fixed value. One way of representing the objective function is to plot contour lines. They are similar to equal‐temperature or equal‐pressure curves in weather maps. They can be created by setting the objective function equal to a constant. This will provide an equation for one of the curves. Along this curve, the objective function has the same value. By gradually increasing or decreasing the constant, we can plot other contour curves. Sometimes, different colors are used for different constant values so that the values of the objective function can be easily found.
The final step of graphical optimization is to inspect the optimal solution. The optimal solution is the point in the feasible set that has the smallest value of the objective function. The optimal design may be located on the constraint curves or inside the feasible set. The latter is rarely encountered in structural optimization because most problems have important constraints that limit the objective function. If the lowest contour line intersects the boundary of one or more inequality constraints, then some or all of these constraints dictate the location of the optimal solution and are called active constraints.
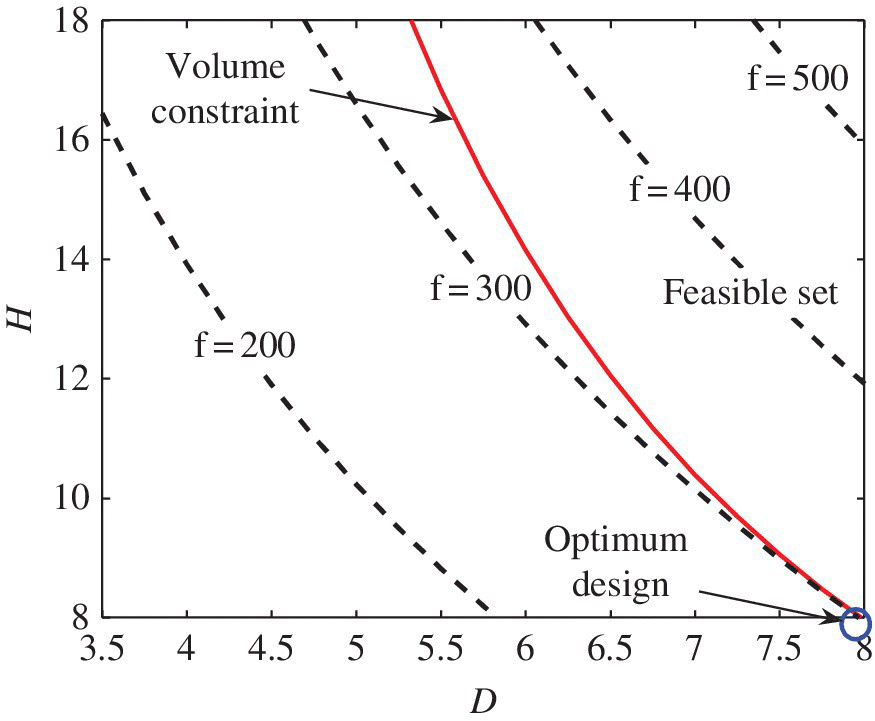
Figure 10.14 Graphical optimization of the beer can problem
10.6.3 Numerical Methods
As we discussed before, there is no mathematical method to find a global minimum, except for very simple cases. Almost all numerical methods provide a local minimum. They are basically, starting from an initial design, finding a new design that reduces the objective function while satisfying all constraints. The method repeats until there is no design in the vicinity that can reduce the objective function further.
Basic algorithm: Most of gradient‐based optimization algorithms take the following steps:
- Start with b(0) and K = 0.
- Evaluate function values and their gradients.
- Using information from step 2, determine ∆b(K).
- Check for termination.
- Update design(10.44)

- Increase K = K + 1 and go to step 2.
Change in design: In the above algorithm, the change in design is further decomposed into two steps. First, the direction of design change is found, and then the amount of design change in that direction is determined. Thus, the change in design can be written as
where αK is called the step size, and d(K) is called the search direction vector. Since the search direction also reduces the objective function, it is also called the descent direction. Various algorithms have different methods to calculate the search direction so that the optimization problem can converge fast. In this introductory chapter, we will not present any algorithms in detail. Interested users are referred to advanced optimization textbooks by Haftka and Gurdal6.
10.6.4 Optimization Using Excel™ Solver
There are many commercially available optimization programs. Some of them are based on mathematical programming, while others are based on heuristic approaches. However, in this section, we demonstrate the optimization process using Microsoft® Excel spreadsheet. We explain the process using a simple structural example.
Problem definition: Consider the minimum weight design of the four‐bar truss shown in figure 10.15. For the sake of simplicity, we assume that members 1 through 3 have the same area A1 and member 4 has an area A2. The constraints are limits on the stresses in the members and on the vertical displacement at the right end of the truss. Under the specified loading, the member forces and the vertical displacement δ at the end are found to be

We assume the allowable stresses in tension and compression to be 8.74 × 10−4E and 4.83 × 10−4E, respectively, and limit the displacement to be no greater than 3 × 10−3L. First, convert the design variables into non‐dimensional ones as
Then, the minimum weight design subject to stress and displacement constraints can be formulated as


Figure 10.15 Minimum weight design of four‐bar truss
Loading the Solver add‐in: Before using Solver, the user must first load the Solver add‐in into the memory. When installing Excel, the user was given the option of installing the add‐ins that ship with Excel. If the add‐ins were installed, Solver can be loaded into the memory using Add‐ins menu in File → Options. If add‐ins is not installed, it must be installed first in order to use Solver. To load Solver into the memory, follow these steps:
- Select File → Options on the main menu. Figure 10.16 shows Excel Options window.
- If Solver Add‐in is shown in Excel Options window, then Solver is already loaded into the memory. Skip next steps.
- If Solver Add‐in is not shown, click Go… button at the bottom to open Add‐In window. Figure 10.17 shows the currently installed Add‐ins.
- From the list of installed add‐ins, check Solver Add‐In.
- Choose OK or press Enter. Now, Solver Add‐in should appear in Excel Options window as shown in figure 10.16. The Solver command is located in the main menu Data → Solver.

Figure 10.16 List of the submenu in Tools menu (Solver appears in Tools menu)

Figure 10.17 Add‐in dialog box with installed Solver add‐in
Setting up the example problem: To use Solver in Excel worksheets, the optimization problem must be defined first. The user must specify the cells corresponding to design variables, objective function, and constraints. With Solver, the objective and constraint cells should be based on formulas in terms of design variable cells. Thus, if the values of design variables cells are changed, the objective and constraints are changed accordingly. Therefore, to set up the problem, determine which of the cells will be used as the objective and constraints and make sure that they contain formulas. The worksheet shown in figure 10.18 illustrates the example problem that the Solver will use.
In figure 10.18, cells C4 and C5 are selected for design variables b1 and b2, respectively (Changing Cell in Solver Parameters dialog box). The objective function is formulated in cell C7 (Target Cell in Solver Parameters dialog box). The constraint equation g1, g2, and g3 are formulated in cell C10, C11, and C12, respectively.
- Type text in cells A1, A3, A7, A9, B4, B5, B10, B11, and B12, as shown in figure 10.18. These are unnecessary for Solver but can help the user understand the meaning of each cell.
- Select cell C4 and type 10. This is an arbitrary initial value of design variable b1.
- Select cell C5 and type 10. This is an arbitrary initial value of design variable b2.
- Click C7 and key in objective function formulas as follows
=3*C4+sqrt(3)*C5 - Click C10 and key in constraint equation formulas g1 as follows
=18/C4+6*sqrt(3)/C5‐3 - Click C11 and key in constraint equation formulas g2 as follows
=5.73‐C4 - Click C12 and type constraint equation formulas g3 as follows
=7.17‐C5

Figure 10.18 Excel worksheet for minimum weight design of the four‐bar truss and Solver Parameters dialog box
Running Solver: After the locations and formulas of design variables, objective, and constraints are set up, follow these steps to run Solver:
- Select Solver in Data menu to start the solver add‐in. The Solver Parameter dialog box will be displayed as shown in figure 10.18.
- Indicate the cell that contains the objective function formula in the Set Objective text box. The objective cell can directly type in as $C$7 or can be selected using the cell selection method in Excel.
- In the To section of the dialog box, select Min button as the objective function will be minimized.
- In the By Changing Variable Cells text box, indicate the cell or range of cells that will be used as design variables. In this case, choose C4 and C5.
- To specify constraints, select the Add button to add each constraint to the problem. Figure 10.19 shows the Add Constraint dialog box.
- To create a constraint, specify the cell containing the formula on which the constraint is based on the Cell Reference text box (for example, C10 for the first constraint). Click the drop‐down arrow to display the list of constraint operators, and select the appropriate operator (choose < = symbol). In the final text box, enter the value the constraint must meet (type in 0). Choose the Add button to add the current constraint to the problem and create another, or choose OK to add the constraint and return to the Solver Parameters dialog box. The three constraints should appear in the Subject to the Constraints list box in the Solver Parameters dialog box (See figure 10.18).
- Choose Options button in the Solver Parameters dialog box to control maximum computing time, iteration, convergence, etc. The Options dialog box will be displayed as shown in figure 10.20. Choose appropriate settings in the Options dialog box. Check Show Iteration Results buttons and click OK button. The Solver Parameters dialog box in figure 10.18 will be redisplayed.
- Click Solve button to start the Solver. The Solver begins calculating the optimal solutions. Intermediate solution values are displayed on the worksheet and Show Trial Solution dialog box as shown in figure 10.21 will appear.
- The intermediate solution can be stored by selecting Save Scenario button in Show Trial Solution dialog box. In order to continue the optimization, click Continue button. When Solver finds a solution, the Solver Results dialog box appears, as shown in figure 10.22. Note that the values of the objective function, design variables, and constraints are changed. Select Keep Solver Solution to use the offered solutions. If the Restore Original Values button is selected, then the worksheet will return to the original values. Figure 10.22 also shows the worksheet after the Solver has found the solutions for the problem.

Figure 10.19 Add Constraint dialog box

Figure 10.20 Solver Options dialog box

Figure 10.21 Show Trial Solution dialog box

Figure 10.22 Solver Results dialog box
Creating Solver Reports: Solver can generate reports summarizing the results of its solutions. There are three types of reports: Answer, Sensitivity, and Limit report. The Answer report shows the original and final values for the target cell (objective function) and the adjustable cells (design variables), as well as the status of each constraint. The Sensitivity report shows the sensitivity of each element of the solution to changes in input cells or constraints. The Limits report shows the upper and lower values of the design variables within the specified constraints. To create a report, select the reports from the list that appears in the Solver Results dialog box, and choose OK. Excel creates the reports in a separate sheet. Figure 10.23 shows Answer Report of the four bar truss example.

Figure 10.23 Answer Report worksheet
10.7 PROJECTS
Table 10.2 Input data for ten‐bar truss
| Parameters | Values |
| Dimension, b | 360 inches |
| Safety factor, SF | 1.5 |
| Load, P1 | 66.67 kips |
| Load, P2 | 66.67 kips |
| Density, ρ | 0.1 lb/in3 |
| Modulus of elasticity, E | 104 ksi |
| Allowable stress, σallowable | 25 ksi* |
| Initial area Ai | 1.0 in2 |
| Minimum cross‐sectional area | 0.1 in2 |
*Member 9 has the allowable strength of 75 ksi

Figure 10.24 Ten‐bar truss

Figure 10.25 Geometry of a bracket (unit mm)
Table 10.3 Lower and upper bounds of design parameters (unit mm)
| Design | Name | Lower Bound | Initial Value | Upper Bound |
| b1 | Slot height | 54 | 55 | 120 |
| b2 | Slot Vr 1 | 9 | 20 | 21 |
| b3 | Slot Vr 2 | 9 | 20 | 21 |
| b4 | Slot Hr 1 | 9 | 10 | 30 |
| b5 | Slot Hr 2 | 9 | 10 | 30 |
| b6 | Out Hr 1 | 17 | 31 | 32 |
| b7 | Out Hr 2 | 17 | 31 | 32 |
| b8 | Out Hr 3 | 43 | 62 | 63 |
| b9 | Out Hr 4 | 43 | 62 | 63 |
| b10 | Bottom 1 | 1 | 19 | 21 |
| b11 | Bottom 2 | 1 | 19 | 21 |
10.8 EXERCISES
- Answer the following descriptive questions.
- Explain the relationship between performance, objective, and constraints in design optimization.
- Explain the usage of a knockdown factor in calculating allowable strength.
- Based on 10 coupon tests, the strength of material A is normally distributed by N(500, 402), while material B is by N(480, 202). Which material has a higher B‐basis allowable strength?
- In structural design, why do we need to consider both the allowable strength and the safety factor simultaneously?
- When a truss is statically determinate, how many iterations would be necessary to obtain the fully stressed design? Explain why.
- If a beam structure is modeled using 3D solid elements and if the cross‐sectional geometry is design, is it sizing design or shape design?
- What are the three steps of optimization formulation?
- Write the standard form of an optimization problem.
- At an optimum design, the gradient of the objective may not be zero. Explain in what situation that will happen.
- Calculate the B‐basis allowable strengths with 5, 10, 20, and 30 coupons, and show the calculated allowable strengths converge to the true allowable strength in example 10.1. The coupon test results can be simulated by generating random numbers from a normal distribution with mean = 310 MPa and standard deviation = 25 MPa. The true tenth percentile of the distribution is 278 MPa. Plot a graph of the allowable strength versus the number of coupons, and show that the curve converges to 278 MPa.
- Determine the height of the beam in example 10.2 when the load factor of λ = 2.0 is used with the failure stress of 40 ksi.
- Determine the height of the beam in example 10.2 so that the safety margin is 10 ksi with the failure stress of 40 ksi.
- A two‐dimensional truss shown in the figure is made of aluminum with Young’s modulus E = 80 GPa and failure stress σY = 150 MPa. Determine the minimum cross‐sectional area of each member so that the truss is safe with safety factor 1.5.

- Consider a stepped beam structure modeled using two beam elements. The cross‐sections are circular. Use Young’s modulus E = 80 GPa, yield stress σY = 250 MPa, and L = 1 m. When F2 = F3 = 1,000 N, calculate the minimum diameters of two sections so that the beam does not fail with a safety margin of 100 MPa.

- A cantilever beam of length 1 m is subjected to a uniformly distributed load p(x) = p0 = 12,000 N/m and a clockwise couple 5,000 N⋅m at the tip. The load factors for the distributed load and couple are, respectively, 1.5 and 2.0. When the cross section is circular, calculate the minimum diameter. Use Young’s modulus 80 GPa and yield strength 250 MPa.

- The frame shown in the figure is clamped at the left end and supported on a hinged roller at the right end. An axial force P and a couple C act at the right end. The load factor for the axial force is 1.5 and that of the couple is 2.0. Determine the radius of the circular cross section. Assume the following numerical values: L = 1 m, E = 80 GPa, P = 15,000 N, C = 1,000 Nm.

- All members of the truss shown in the figure initially have a circular cross section with a diameter of 2″. Using a commercial finite element analysis program, calculate the minimum diameter of each member using fully stressed design. Assume that Young’s modulus is 104 psi.

- Consider a two‐bar structure in the figure with Young’s modulus E = 100 GPa, yield stress σY = 250 MPa, and F = 10,000 N. Design variables are b1 = area of section AB and b2 = area of section BC. Starting from the initial design of b1 = 1 × 10−4 m2 and b2 = 2 × 10−4 m2, perform fully stressed design to obtain minimum cross‐sectional areas.

- Repeat problem 10 with the initial design of b1 = 2 × 10−4 m2 and b2 = 1 × 10−4 m2. Discuss the results with that of problem 10.
- For the clamped beam shown in the figure, two design variables are defined, as I1 = b1 and I2 = b2. Using the finite element method and sensitivity analysis, calculate the sensitivity of the vertical displacement v2 with respect to b1 and b2. Use the following values for the current design: E = 30 × 106 psi, b1 = 0.1 in4, and b2 = 0.05 in4. Compare the results with the exact sensitivity.

- Calculate the sensitivity of the vertical displacement v2 in problem 12 using forward finite difference method with perturbation size 1%. Compare the results with the exact sensitivity.
- Consider a simply supported beam of length L = 1 m subjected to a uniformly distributed transverse load p0 = 100 N/m. The cross section is rectangular with width w = 0.01 m and height h = 0.02 m. Calculate the sensitivity of the vertical displacement at the center with respect to h. Use one finite element with Young’s modulus = 80 GPa. Compare the sensitivity against the finite difference method with perturbation size 1%.

- Repeat problem 14 to calculate the sensitivity of maximum tensile stress with respect to h.
- A cantilevered beam shown in the figure is under a couple of 500 lb.⋅in. at the end. The optimization problem is to find a design that minimizes the cross‐sectional area, while the maximum stress is less than 2,000 psi. The thicknesses of the flange and the web of the cross section are fixed with t = 0.1 in. The design variables are the width w and the height h of the cross section. Determine graphically the optimal design. The width and the height are constrained to remain in the range
 and
and  .
.






