CHAPTER 16
Cryptography
Cryptography is the study of methods for secure communication in the presence of adversaries who want to intercept information. Early cryptography, which was simply writing, worked because only a few people could read. Later forms of cryptography used special alphabets known only to the message sender and recipient. One of the earliest known instances of this form of cryptography used nonstandard hieroglyphics carved on monuments in Egypt circa 1900 BCE.
Another form of cryptography used by the ancient Greeks and Spartans used a wooden rod called a scytale (rhymes with “Italy”). A strip of parchment was wrapped in a spiral around the rod, and words were written on it. When the parchment was unwrapped, the letters were out of order. To read the message, the recipient would wrap the parchment around a rod with the same diameter.
These forms of cryptography are sometimes called security through obscurity, because they rely on the fact that the adversary doesn't know the trick. If the adversary knows the secret alphabet or knows that the message was written on a scytale, it's easy to reproduce the message.
More modern cryptographic techniques assume that the adversary knows all about how the message was encrypted but doesn't know some small, crucial piece of information called the key. The message's sender uses the key to encrypt the message, and the recipient uses the key to decrypt it. Because the method of encryption is known, an attacker who can find the key can also decrypt the message.
This form of encryption, in which the attacker knows the encryption method, is more powerful than security through obscurity, because even an attacker who knows the encryption method cannot decrypt the message. This model is also more realistic in the modern world because sooner or later the attacker will discover the encryption method.
This chapter describes some interesting and useful cryptographic techniques. It starts out by describing some classical cryptographic methods. These are no longer considered secure, but they are interesting and demonstrate a few useful concepts such as frequency analysis.
Cryptanalysis, the study of how to break encryptions to recover a message, has been around as long as cryptography. The following sections that describe classical methods also explain the cryptanalysis that lets you break those methods.
The later sections describe more secure techniques, such as permutation networks and public-key encryption. A complete discussion of the latest encryption methods, such as Advanced Encryption Standard (AES) and Blowfish, is beyond the scope of this book, but the later sections should give you a general idea of how modern approaches work.
Terminology
Before starting the study of cryptography, you should know a few basic terms.
In cryptography, the goal is for a sender to send a message to a receiver without a third party, usually called an adversary or attacker, understanding the message. It is assumed that the attacker will intercept the encrypted message, so only the encryption stands between the attacker and understanding the message.
The unencrypted message is called plaintext. The encrypted message is called ciphertext. Turning plaintext into ciphertext is called encrypting or enciphering the plaintext. Recovering the plaintext from the ciphertext is called decrypting or deciphering the ciphertext.
Technically, a cipher is a pair of algorithms used to encrypt and decrypt messages.
Cryptanalysis is an attacker's study of methods for breaking an encryption.
To make working with smaller messages easier, they are usually encrypted in all capital letters without spaces or punctuation. That means the sender and receiver don't need to consider more characters than necessary—an important consideration if you're encrypting and decrypting messages by hand. This also removes clues that spaces and punctuation might give to an attacker.
To make encrypted messages a bit easier to read, they usually are written in five-character chunks in a fixed-width font so that characters line up nicely. For example, the message “This is a secret message” would be written as
, and it might be encrypted as something like THISI SASEC RETME SSAGE
. The receiver may need to spend a little extra time figuring out where to insert spaces and punctuation.TSRSH AESIS TASEM GICEE
Modern cryptographic algorithms encrypt and decrypt byte streams. Therefore, they can include uppercase and lowercase letters, spaces, punctuation, and even Unicode characters or images, depending on the type of message. Those algorithms are good enough that the attacker shouldn't be able to tell the spaces and punctuation apart from other characters to get extra information about the message.
Transposition Ciphers
In a transposition cipher, the plaintext's letters are rearranged in some specific way to create the ciphertext. The recipient puts the letters back in their original positions to read the message.
These ciphers work partly with security through obscurity if the attacker doesn't know what kind of transposition is being used. For example, the scytale method described at the beginning of the chapter uses a transposition caused by winding the parchment around a rod. It relies solely on the fact that the attacker doesn't know that it was the method used to encrypt the message.
Most of transposition ciphers also provide a key that gives some information about the transposition. For example, the row/column transposition cipher described in the next section uses the number of columns as a key. These keys tend to allow a fairly limited set of values, however, so it isn't hard to guess the key and break the encryption, particularly if you use a computer.
These ciphers are fairly easy to work through with paper and pencil and can be a fun exercise. (If they're too easy, try working them out in your head.)
Row/Column Transposition
In a row/column transposition cipher, the plaintext message is written into an array by rows. Then the ciphertext is read from the array by columns. For example, Figure 16.1 shows the plaintext “THIS IS A SECRET MESSAGE” written by rows into a four-row, five-column array. (Normally, if the message doesn't fit exactly, you pad it with X's or random characters to make it fit.)

Figure 16.1: In a row/column transposition cipher, you write the plaintext into an array by rows and then read the ciphertext by columns.
To get the cipher text, you read down each column. In this example, that gives the ciphertext TSRSH AESIS TASEM GICEE. The key is the number of columns used in the transposition.
To decode a ciphertext message, you basically undo the encryption operation. You build the array, write the ciphertext characters into it by columns, and then read the decoded message by rows.
If you're implementing this in a program, you don't really need to write the text into an array. Instead, if the number of columns is
, you can simply read the characters from the plaintext string, skipping num_columns
between each character. The following pseudocode shows this approach:num_columns
String: ciphertext = ""For col = 0 Tonum_columns- 1Integer: index = colFor row = 0 To num_rows - 1ciphertext = ciphertext + plaintext[index]index +=num_columnsNext rowNext col
To decipher a message in a program, notice that decoding a message that was originally written in an array that has R rows and C columns is the same as encrypting a message with an array that has C rows and R columns.
The preceding example writes a message into a ![]() array. Figure 16.2 shows the ciphertext TSRSH AESIS TASEM GICEE written into a
array. Figure 16.2 shows the ciphertext TSRSH AESIS TASEM GICEE written into a ![]() array by rows. If you look at the figure, you'll see that you can read the plaintext by columns.
array by rows. If you look at the figure, you'll see that you can read the plaintext by columns.

Figure 16.2: Decrypting with an  array is equivalent to encrypting with a
array is equivalent to encrypting with a  array.
array.
Row/column transposition is easy and makes for a fun exercise, but it's a relatively easy system to break. The secret key is the number of columns in the array. If you factor the length of the ciphertext, you can come up with a few choices for the key.
For instance, the previous ciphertext contains 20 characters. The factors of 20 are 1, 2, 4, 5, 10, and 20, so those are the possibilities for the number of columns. The ![]() and
and ![]() arrays make the ciphertext the same as the plaintext, so there are really only two possibilities to check. If you simply try each value, you'll see that the characters spell gibberish when you use four columns, but they spell words when you use five columns.
arrays make the ciphertext the same as the plaintext, so there are really only two possibilities to check. If you simply try each value, you'll see that the characters spell gibberish when you use four columns, but they spell words when you use five columns.
The sender can try to make the attacker's life a little harder by adding some extra random characters to the end of the ciphertext so that the array's size isn't exactly determined by the message's length. For example, you could add nine characters to the previous ciphertext to get a message that is 29 characters long. Then it wouldn't be as obvious that the array must have four or five columns.
Even so, you can easily make a program that tries every possible number of columns between 2 and 1 less than the length of the ciphertext. When the program sees that the corresponding decrypted text contains words, it finds the key.
Column Transposition
In a column transposition cipher, the plaintext message is written into an array by rows much as it is in a row/column transposition cipher. The columns are then rearranged, and the message is read out by rows.
Figure 16.3 shows the plaintext “THIS IS A SECRET MESSAGE” written by rows into a four-row, five-column array on the left. The columns are then rearranged. The numbers above the array on the left show the ordering of the columns in the rearranged array on the right. Reading the message by rows from the array on the right gives the ciphertext HTIIS ASSCE ERTEM SSAEG.

Figure 16.3: In a column transposition cipher, you write the plaintext into an array by rows, rearrange the columns, and read the ciphertext by rows.
In this case, the encryption's key is the number of columns in the array plus the permutation of the columns. You could write the key for this example as 21354.
A key that would be easier to remember would be a word with a length equal to the number of columns and with letters whose alphabetical order gives the column permutation. For this example, the key could be CARTS. In this word, the letter A comes first alphabetically, so its value is 1, the letter C comes second alphabetically, so its value is 2, the letter R comes third alphabetically, so its value is 3, and so on. Putting the letters' alphabetical values in the order in which they appear in the word gives the numeric key 21354, and that gives the ordering of the columns. (In practice, you pick the word first and then use it to determine the column ordering. You don't pick an ordering and then try to come up with a word to match.)
To decrypt a message, you write the ciphertext into an array that has as many columns as the keyword has letters. You then find the inverse mapping defined by the letters' alphabetical ordering. In this example, the numeric key 21354 means that the columns move as follows:
- Column 1 moves to position 2.
- Column 2 moves to position 1.
- Column 3 moves to position 3.
- Column 4 moves to position 5.
- Column 5 moves to position 4.
Simply reverse that mapping so that:
- Column 2 moves to position 1.
- Column 1 moves to position 2.
- Column 3 moves to position 3.
- Column 5 moves to position 4.
- Column 4 moves to position 5.
Now you can rearrange the columns and read the plaintext by rows.
As is the case with a row/column transposition cipher, a program that performs row transposition doesn't really need to write values into an array; it just needs to keep careful track of where the characters need to move. In fact, a program can use the inverse mapping described in the preceding paragraphs to figure out which character goes in which position of the ciphertext.
Suppose that
is an array of integers that gives the column transposition. For example, if column number 2 moves to position 1, then mapping
mapping[2]
. Similarly, suppose = 1
is an array that gives the inverse mapping, so for this example, inverse_mapping
. Then the following pseudocode shows how the program can encrypt the plaintext:inverse_mapping[1] = 2
String: ciphertext = ""For row = 0 to num_rows - 1// Read this row in permuted order.For col = 0 to num_columns - 1Integer: index = row * num_columns + inverse_mapping[col]ciphertext = ciphertext + plaintext[index]Next colNext row
Notice that this pseudocode uses the inverse mapping to encrypt the plaintext. To find the character that maps to a particular column number in the ciphertext, it must use the inverse mapping to find the column from which the character came.
You can use the forward mapping to decrypt the ciphertext.
To attack a column transposition cipher, an attacker would write the message into an array that has the number of columns given by the length of the keyword. The attacker would then swap columns to try to guess the proper ordering. If the array has C columns, then there are C! possible orderings of the columns, so this could require looking at a lot of combinations. For example, 10 columns would result in 3,628,800 possible arrangements of columns.
That seems like a lot of possibilities, particularly if the attacker isn't using a computer, but the attacker may be able to decrypt the message incrementally. The attacker could start by trying to find the first five columns in the plaintext. If the first five columns are correct, then the first row will show five characters of valid words. It may show a complete word or at least a prefix of a word. The other rows may begin with partial words, but after that they will also contain words or prefixes. There are only ![]() possible arrangements of five columns chosen from 10, so this is a lot fewer combinations to check, although it would still be a daunting task.
possible arrangements of five columns chosen from 10, so this is a lot fewer combinations to check, although it would still be a daunting task.
Route Ciphers
In a route cipher, the plaintext is written into an array or some other arrangement and then is read in an order determined by a route through the arrangement.
For example, Figure 16.4 shows a plaintext message written into an array by rows. The ciphertext is read by following the array's diagonals, starting with the lower-left diagonal, so the ciphertext is SRSSE ATATG HSMEI EESCI.

Figure 16.4: In a route cipher, you write the plaintext into an array by rows and then read the ciphertext in some other order.
In theory, the number of possible routes through the array is enormous. If the array holds N entries, then there are N! possible routes. The example shown in Figure 16.4 has ![]() possible routes.
possible routes.
However, a good route should be reasonably simple so that the receiver can remember it. The diagonal route shown in Figure 16.4 is easy to remember, but if the route jumps randomly all over the array, then the receiver would need to write it down, basically making the key as long as the message. (Later in this chapter you'll see that a one-time pad also has a key as long as the message, and that it also changes the message's letters, so the attacker cannot get extra information such as the frequency of the different letters in the message.)
Some routes also leave large pieces of the message intact or reversed. For example, an inward clockwise spiral starting in the upper-left corner is easy to remember, but the first row of the message appears unscrambled in the ciphertext. These sorts of routes give the attacker extra information and may make it easier to figure out the route.
If you eliminate routes that cannot be easily remembered and routes that include large sections of unscrambled plaintext, then the number of available routes is much smaller than the theoretical maximum.
Substitution Ciphers
In a substitution cipher, the letters in the plaintext are replaced with other letters. The following sections describe four common substitution ciphers.
Caesar Substitution
About 2,100 years ago, Julius Caesar (100 BC–44 BCE) used a technique that is now called a Caesar substitution cipher to encrypt messages he sent to his officers. In his version of this cipher, he shifted each character in the message by three letters in the alphabet. A became D, B became E, and so on. To decrypt a message, the receiver subtracted 3 from each letter, so Z became W, Y became V, and so on.
For example, the message “This is a secret message” with a shift of 3 becomes WKLVL VDVHF UHWPH VVDJH.
Julius Caesar's nephew Augustus used a similar cipher with a shift of 1 instead of 3. More generally, you can shift the letters in the plaintext by any number of characters.
An attacker can try to decipher a message encrypted using this method by examining the frequencies of the letters in the ciphertext. In English, the letter E occurs much more often than the other letters. It occurs about 12.7 percent of the time. The next most common letter, T, occurs 9.1 percent of the time. If the attacker counts the number of times each letter is used in the ciphertext, the one that occurs most is probably an encrypted E. Finding the number of characters between the ciphertext letter and E gives the shift used to encrypt the message.
This attack works best with long messages, because short ones may not have a typical distribution of letters.
Table 16.1 shows the number of occurrences of the letters in the ciphertext WKLVL VDVHF UHWPH VVDJH.
Table 16.1: Number of Occurrences of the Letters in the Example Ciphertext
| LETTER | D | F | H | J | K | L | P | U | V | W |
| Occurrences | 2 | 1 | 4 | 1 | 1 | 2 | 1 | 1 | 5 | 2 |
If you assume V is the encryption of the letter E, then the shift must be 17. Decrypting the message with that shift gives you FTUEU EMEQO DQFYQ EEMSQ, which does not contain valid words.
If you assume the second-most-used character H is the encryption of E, you get a shift of 3, and now you can decode the original message.
Vigenère Cipher
One problem with the Caesar substitution cipher is that it uses only 26 keys. An attacker could easily try all 26 possible shift values to see which one produces valid words. The Vigenère cipher improves on the Caesar substitution cipher by using different shift values for different letters in the message.
In the Vigenère cipher, a keyword specifies the shifts for different letters in the message. Each letter in the keyword specifies a shift based on its position in the alphabet. A indicates a shift of 0, B represents a shift of 1, and so on.
To encrypt a message, you write the plaintext below a copy of the keyword repeated as many times as necessary to have the same length as the message. Figure 16.5 shows a message below the keyword ZEBRAS repeated several times.

Figure 16.5: In a Vigenère cipher, repeat the keyword as many times as necessary over the plaintext.
Now you can use the corresponding letters to produce the ciphertext. For example, key letter Z represents a shift of 25, so you shift the plaintext letter T by 25 to get S.
To make shifting the letters easier, you can use a “multiplication table” like the one shown in Figure 16.6. To encrypt the plaintext letter T with the key letter Z, you look in row T, column Z.

Figure 16.6: This table makes it easier to shift letters in a Vigenère cipher.
To decrypt a ciphertext letter, you look down the key letter's column until you find the ciphertext letter. The row tells you the plaintext letter.
The simple frequency analysis that you can use to attack a Caesar substitution cipher doesn't work with a Vigenère cipher because the letters don't all have the same shift. However, you can use the ciphertext's letter frequencies to attack a Vigenère cipher in a different way.
Suppose the keyword is K letters long. In that case, every Kth letter has the same offset. For example, the letters in positions 1, ![]() ,
, ![]() , and so forth have the same offset. Those letters are not the same as the plaintext letters, but their relative frequencies are the same.
, and so forth have the same offset. Those letters are not the same as the plaintext letters, but their relative frequencies are the same.
To begin the attack, you try guessing the key's length. You then look at the letters that have the same offset. For example, suppose that you try a key length of 2. You then examine the letters in the ciphertext in positions 0, 2, 4, 6, and so forth. If the key's length actually is 2, then the letters' frequencies should look like those in normal English (or whatever language you're using). In particular, a few letters corresponding to plaintext letters such as E, S, and T should occur much more often than other letters corresponding to plaintext letters such as X and Q.
If the key's length is not 2, the letters' frequencies should be fairly uniform, with no letters occurring much more often than the others. In that case, you guess a new key length and try again.
When you find a key length that gives a frequency distribution that looks something like the one for English, you look at the specific frequencies, as you did for a Caesar substitution cipher. The letter that occurs most often is probably an encrypted E.
Similarly, you look at the other letters with the same offsets to figure out what their offset is. For example, if the key has length 5, then you first look at the group of letters in positions 0, 5, 10, and so on. Next, you look at the group of letters in positions 1, 6, 11, and so on. Different groups will have different offsets, but all of the letters in each group will have the same offset.
Basically, in this step you decrypt a Caesar substitution cipher for each letter in the key.
When you're finished, you should have the offset for each letter in the key. This is more work than the Caesar substitution cipher, but it is still possible.
Simple Substitution
In a simple substitution cipher, each letter has a fixed replacement letter. For example, you might replace A with H, B with J, C with X, and so forth.
In this cipher, the key is the mapping of plaintext letters to ciphertext letters. If the message can contain only the letters A through Z, then there are ![]() possible mappings.
possible mappings.
If you're encrypting and decrypting messages by hand, you'll need to write down the mapping.
If you're using a computer, you may be able to use a pseudorandom number generator to re-create the mapping. The sender picks a number K, uses it to initialize the pseudorandom number generator, and then uses the generator to randomize the letters A through Z and produce the mapping. The value K becomes the key. The receiver follows the same steps, using K to initialize the random-number generator and generate the same mapping the sender used.
It's easier to remember a single number than the entire mapping, but most random-number generators have far fewer possible internal states than ![]() . For example, if the number you use to initialize the random-number generator is a signed 32-bit integer, then the key can have only about 2 billion values. That's still a lot, but a computer can easily try all possible 2 billion values to see which one produces valid words.
. For example, if the number you use to initialize the random-number generator is a signed 32-bit integer, then the key can have only about 2 billion values. That's still a lot, but a computer can easily try all possible 2 billion values to see which one produces valid words.
You can also use letter frequencies to make the process a little easier. If the letter W appears most often in the ciphertext, then it is probably an encrypted E.
One-Time Pads
A one-time pad cipher is sort of like a Vigenère cipher where the key is as long as the message. Every letter has its own offset, so you cannot use the letters' frequencies in the ciphertext to find the offsets.
Because any ciphertext letter can have any offset, the corresponding plaintext letter could be anything, so an attacker cannot get any information from the ciphertext (except the message's length, and you can even disguise that by adding extra characters to the message).
In a manual system, the sender and receiver each have a copy of a notepad containing random letters. To encrypt a message, the sender uses the pad's letters to encrypt the message, crossing out the pad's letters as they are used so that they are never used again. To decrypt the message, the receiver uses the same letters in the pad to decrypt the message, also crossing out the letters as they are used.
Because each letter essentially has its own offset, this cipher is unbreakable as long as the attacker doesn't get hold of a copy of the one-time pad.
One drawback of the one-time pad cipher is that the sender and receiver must have identical copies of the pad, and sending a copy securely to the receiver can be as hard as sending a secure message. Historically, pads were sent by couriers. If an attacker intercepted a courier, then the pad was discarded, and a new one was sent.
Block Ciphers
In a block cipher, the message is broken into blocks, each block is encrypted separately, and the encrypted blocks are combined to form the encrypted message.
Many block ciphers also encrypt blocks by applying some sort of transformation to the data many times in rounds. The transformation must be invertible so that you can later decrypt the ciphertext. Giving the blocks a fixed size means that you can design the transformation to work with a block of that size.
Block ciphers also have the useful feature that they let cryptographic software work with messages in relatively small pieces. For example, suppose that you want to encrypt a very large message, perhaps a few gigabytes. If you use a column transposition cipher, the program needs to jump throughout the message's location in memory. That can cause paging, which slows down the program greatly.
In contrast, a block cipher can consider the message in pieces, each of which fits easily in memory. The program may still need to page, but it needs to load each piece of the message into memory only once instead of many times.
The following sections describe some of the most common types of block ciphers.
Substitution-Permutation Networks
A substitution-permutation network cipher repeatedly applies rounds consisting of a substitution stage and a permutation stage. It helps to visualize the stages being performed by machines in boxes that are called substitution boxes (S-boxes) and permutation boxes (P-boxes).
An S-box takes a small part of the block and combines it with part of the key to make an obfuscated result. To obscure the result as much as possible, changing a single bit in the key should ideally change about half of the bits in the result. For example, if an S-box works with 1 byte, then it might use the XOR operation to combine the first bit in the key with bits 1, 3, 4, and 7 in the plaintext byte. The S-box would combine other key bits with the message bits in different patterns. You could use different S-boxes for different parts of the block.
A P-box rearranges the bits in the entire block and sends them to different S-boxes. For example, bit 1 from the first S-box might go to the next stage's bit 7 in the third S-box.
Figure 16.7 shows a schematic for a three-round substitution-permutation network cipher. The S-boxes ![]() ,
, ![]() ,
, ![]() , and
, and ![]() combine the key with pieces of the message. (Note that each round could use different key information.) The P-boxes all use the same permutation to send the outputs of the S-boxes into the next round of S-boxes.
combine the key with pieces of the message. (Note that each round could use different key information.) The P-boxes all use the same permutation to send the outputs of the S-boxes into the next round of S-boxes.

Figure 16.7: In a substitution-permutation network cipher, substitution stages alternate with permutation stages.
To decrypt a message, you perform the same steps in reverse. You run the ciphertext through the inverted S-boxes, pass the results through the inverted P-box, and repeat the necessary number of rounds.
One drawback of this method is that the S-boxes and P-boxes must be invertible so that you can decrypt messages. The code that performs encryption and decryption is also different, so you have more code to write, debug, and maintain.
Feistel Ciphers
In a Feistel cipher, named after cryptographer Horst Feistel, the message is split into left and right halves, ![]() and
and ![]() . A function is applied to the right half, and the XOR operation is used to combine the result with the left half. The two halves are swapped, and the process is repeated for some number of rounds.
. A function is applied to the right half, and the XOR operation is used to combine the result with the left half. The two halves are swapped, and the process is repeated for some number of rounds.
The following steps describe the algorithm at a high level:
- Split the plaintext into two halves,
 and
and  .
. - Repeat:
- Set
 .
. - Set
 .
.
- Set
Here ![]() is a subkey used for round i. This is a series of values generated by using the message's key. For example, a simple approach would be to split the key into pieces and then use the pieces in order, repeating them as necessary. (You can think of a Vigenère cipher as doing this because it uses each letter in the key to encrypt a single message character and then repeats the key letters as needed.)
is a subkey used for round i. This is a series of values generated by using the message's key. For example, a simple approach would be to split the key into pieces and then use the pieces in order, repeating them as necessary. (You can think of a Vigenère cipher as doing this because it uses each letter in the key to encrypt a single message character and then repeats the key letters as needed.)
After you have finished the desired number of rounds, the ciphertext is ![]() .
.
To decrypt a message, you split the ciphertext into two halves to get the final values ![]() and
and ![]() . If you look at the preceding steps, you'll see that
. If you look at the preceding steps, you'll see that ![]() is
is ![]() . Therefore, because you already know
. Therefore, because you already know ![]() , you already know
, you already know ![]() .
.
To recover ![]() , substitute
, substitute ![]() for
for ![]() in the equation used in step 2b to get this:
in the equation used in step 2b to get this:
At this point you know ![]() , so you can calculate
, so you can calculate ![]() . If you combine that with
. If you combine that with ![]() , then the
, then the ![]() terms cancel, leaving only
terms cancel, leaving only ![]() , so you have recovered
, so you have recovered ![]() .
.
The following steps describe the decryption algorithm:
- Split the ciphertext into two halves,
 and
and  .
. - Repeat:
- Set
 .
. - Set
 .
.
- Set
One advantage to Feistel ciphers is that decryption doesn't require you to invert the function F. That means you can use any function for F, even functions that are not easily invertible.
Another advantage of Feistel ciphers is that the code for encryption and decryption is basically the same. The only real difference is that you use the subkeys in reverse order to decrypt the ciphertext. This means that you need only one piece of code for encryption and decryption.
Public-Key Encryption and RSA
Public-key encryption uses two separate keys: a public key and a private key. The public key is published, so everyone (including the attacker) knows it. The private key is known only to the receiver.
A sender uses the public key to encrypt the message and sends the result to the receiver. Note that even the sender doesn't know the private key. Only the receiver knows that key, so only the receiver can decrypt the message.
In contrast, other forms of encryption are sometimes called symmetric-key encryption because you use the same key to encrypt and decrypt messages.
One of the best-known public-key algorithms is RSA, which is named after those who first described it: Ron Rivest, Adi Shamir, and Leonard Adleman.
You follow these steps to generate the public and private keys for the algorithm:
- Pick two large prime numbers p and q.
- Compute
 . Release this as the public key modulus.
. Release this as the public key modulus. - Compute
 , where φ is Euler's totient function. (I'll say more about this shortly.)
, where φ is Euler's totient function. (I'll say more about this shortly.) - Pick an integer e where
 and e and
and e and  are relatively prime. (In other words, they have no common factors.) Release this as the public key exponent.
are relatively prime. (In other words, they have no common factors.) Release this as the public key exponent. - Find d, the multiplicative inverse of e modulo
 . In other words,
. In other words,  . (I'll also say more about this shortly.) The value d is the private key.
. (I'll also say more about this shortly.) The value d is the private key.
The public key consists of the values n and e. To encrypt a numeric message M, the sender uses the formula ![]() .
.
To decrypt a message, the receiver simply calculates ![]() .
.
The strength of RSA relies on the fact that it is hard to factor very large numbers. An attacker who can factor the public modulus n can recover the primes p and q. From p and q, plus the public exponent e, the attacker can then figure out the private key and break the cipher.
This is why the primes p and q must be large—to prevent an attacker from easily factoring n.
Euler's Totient Function
Step 3 of the RSA key-generating algorithm requires you to calculate Euler's totient function ![]() . The totient function, which is also called the phi function, is a function that gives the number of positive integers less than a particular number that are relatively prime to that number. For example,
. The totient function, which is also called the phi function, is a function that gives the number of positive integers less than a particular number that are relatively prime to that number. For example, ![]() is 4 because there are four numbers less than 12 that are relatively prime to it: 1, 5, 7, and 11.
is 4 because there are four numbers less than 12 that are relatively prime to it: 1, 5, 7, and 11.
Because a prime number is relatively prime to every positive integer less than itself, ![]() if p is prime.
if p is prime.
It turns out that, if p and q are relatively prime, then ![]() . If p and q are both primes, then they are relatively prime, so in step 3,
. If p and q are both primes, then they are relatively prime, so in step 3, ![]() . If you know p and q, then this is easy to compute.
. If you know p and q, then this is easy to compute.
For example, suppose ![]() and
and ![]() . Then
. Then ![]()
![]() . This is true because the positive integers smaller than 15 that are relatively prime to 15 are the eight values 1, 2, 4, 7, 8, 11, 13, and 14.
. This is true because the positive integers smaller than 15 that are relatively prime to 15 are the eight values 1, 2, 4, 7, 8, 11, 13, and 14.
Multiplicative Inverses
Step 5 of the key-generating algorithm requires you to find the multiplicative inverse d of e modulo ![]() . In other words, find d so that
. In other words, find d so that ![]() .
.
For example, suppose ![]() and
and ![]() . The question now is, “What is the multiplicative inverse of 7 modulo 40?” In this example,
. The question now is, “What is the multiplicative inverse of 7 modulo 40?” In this example, ![]() , so 23 is the multiplicative inverse of 7 modulo 40.
, so 23 is the multiplicative inverse of 7 modulo 40.
One simple way to find the inverse is to compute ![]() ,
, ![]() ,
, ![]() , and so on, until you discover a value that makes the result 1.
, and so on, until you discover a value that makes the result 1.
You can also use the extended GCD algorithm described in Chapter 2 to find the value e more efficiently. See the section “Extending Greatest Common Divisors” in Chapter 2 for more information on the extended GCD algorithm. See the following web page for information on using that algorithm to calculate inverses:
An RSA Example
First, consider this example of picking the public and private keys:
- Pick two large prime numbers p and q.
For this example, let
 and
and  . In a real application, these values should be much larger, such as 128-bit numbers when written in binary, so they would have an order of magnitude of about
. In a real application, these values should be much larger, such as 128-bit numbers when written in binary, so they would have an order of magnitude of about  .
. - Compute
 . Release this as the public key modulus.
. Release this as the public key modulus.
The public key modulus n is
 .
. - Compute
 where φ is Euler's totient function.
where φ is Euler's totient function.
The value
 .
. - Pick an integer e where
 and e and
and e and  are relatively prime.
are relatively prime.
For this example, you need to pick e where
 and e and 448 are relatively prime. The prime factorization of 448 is
and e and 448 are relatively prime. The prime factorization of 448 is  , so e cannot include the factors 2 or 7. For this example, let
, so e cannot include the factors 2 or 7. For this example, let  .
. - Find d, the multiplicative inverse of e modulo
 . In other words, find d such that
. In other words, find d such that  .
.
For this example, you must find the multiplicative inverse of 165 mod 448. In other words, find d such that
 . In this example,
. In this example,  , so the inverse is 429. (Example program MultiplicativeInverse, which is included in the downloads for this chapter, exhaustively finds inverses such as this one. It tried values until it discovered that 429 worked.)
, so the inverse is 429. (Example program MultiplicativeInverse, which is included in the downloads for this chapter, exhaustively finds inverses such as this one. It tried values until it discovered that 429 worked.)
So, the public exponent ![]() , the public modulus
, the public modulus ![]() , and the secret key
, and the secret key ![]() .
.
Now suppose that you want to encrypt the message value 321. The encrypted value C would be ![]() . The ExponentiateMod program, which is available for download on the book's website as part of the solution to Chapter 2, Exercise 12, calculates large exponentials quickly. That program calculates that
. The ExponentiateMod program, which is available for download on the book's website as part of the solution to Chapter 2, Exercise 12, calculates large exponentials quickly. That program calculates that ![]() , so the encrypted value is 359.
, so the encrypted value is 359.
To decrypt the value 359, the receiver calculates ![]() mod n. For this example, that's
mod n. For this example, that's ![]() . The ExponentiateMod program from Chapter 2 calculates that
. The ExponentiateMod program from Chapter 2 calculates that ![]() , so the decrypted message is 321 as it should be.
, so the decrypted message is 321 as it should be.
Practical Considerations
Generating good private keys and calculating big exponents can take some time even if you use fast modular exponentiation. Remember that p and q are very large numbers, so using private-key cryptography to encrypt a long message in blocks small enough to be represented as numbers could take quite a while.
To save time, some cryptographic systems use public-key encryption to allow a sender and receiver to exchange a private key for use with symmetric-key encryption.
Other Uses for Cryptography
The algorithms described in this chapter focus on encrypting and decrypting messages, but cryptography has other uses as well.
For example, a cryptographic hash function takes as an input a block of data such as a file and returns a hash value that identifies the data. You then can make the file and hash value available publicly.
A receiver who wants to use the file can perform the same hashing function to see if the new hash value matches the published one. If someone has tampered with the file, then the hash values will probably not match, and the receiver knows that the file is not in its original form.
A good hash function should have the following properties:
- It should be easy to compute.
- It should be prohibitively difficult for an attacker to create a file with a given hash value (so the attacker cannot replace the true file with a fake one).
- It should be prohibitively difficult to modify the file without changing its hash value.
- It should be prohibitively difficult to find two files with the same hash value.
One application of cryptographic hashing is password verification. You create a password, and the system stores its hash value. The system doesn't store the actual password, so an attacker who breaks into the system cannot steal the password.
Later, when you want to log into the system, you enter your password again. The system hashes it and verifies that the new hash value matches the one that is saved.
A digital signature is a cryptographic tool that is somewhat similar to cryptographic hashing. If you want to prove that you wrote a particular document, you sign it. Later, someone else can examine the document to verify that you have signed it. If someone else modifies the document, that person cannot sign it in your name.
Typically, a digital signature system includes three parts:
- A key-generation algorithm that creates private and public keys
- A signing algorithm that uses the private key to sign a document
- A verification algorithm that uses a public key that you publish to verify that you did sign the document
In a sense, a digital signature is the opposite of a private-key encryption system. In a private-key encryption system, any number of senders can use a public key to encrypt a message, and a single receiver uses a private key to decrypt the message. In a digital signature, a single sender uses a private key to sign a message and then any number of receivers can use a public key to verify the signature.
Summary
This chapter explained a few cryptographic algorithms. The simpler forms, such as transposition and substitution ciphers, are not cryptographically secure, but they provide some interesting exercises. Any student of algorithms should also have some experience with these, particularly Caesar and Vigenère ciphers.
The algorithms described later in the chapter explained how some of the current state-of-the-art cryptographic algorithms work. AES, which uses substitution-permutation networks, and RSA, which uses public-key encryption, are two of the most commonly used algorithms today. Although DES is no longer considered completely secure, it uses a Feistel cipher, which is still interesting and can produce secure encryption schemes such as triple DES.
This chapter covered only a tiny fraction of the cryptographic algorithms that have been invented. For more information, search online or consult a book on cryptography. Two places where you can start your search online include https://en.wikipedia.org/wiki/Cryptography and http://mathworld.wolfram.com/Cryptography.html. If you prefer a book, I highly recommend Applied Cryptography: Protocols, Algorithms, and Source Code in C, Second Edition by Bruce Schneier (Wiley, 1996). It describes a huge number of algorithms for encryption and decryption, digital signatures, authentication, secure elections, and digital money. It does not cover the most recent algorithms (and apparently more recent editions do not either), but it contains excellent background information.
All of these encryption algorithms rely on the fact that you can perform some calculations relatively easily if you know the key and an attacker cannot perform the same operation without knowing the key. For example, in RSA, the receiver can easily decrypt messages, but an attacker cannot without factoring the product of two large prime numbers. It is believed that factoring large numbers is difficult, so an attacker cannot break an RSA encryption.
In the study of algorithms, there are two extremely important sets: P and NP. The first set includes problems that are relatively easy to solve, such as multiplying two numbers or searching a binary tree for a piece of information. The second set includes much harder problems, such as solving the bin packing, knapsack, and traveling salesman problems described in Chapter 12.
The next chapter discusses P and NP and explains some of the interesting questions about these important classes of problems that remain unanswered.
Exercises
You can find the answers to these exercises in Appendix B. Asterisks indicate particularly difficult problems.
- Write a program that uses a row/column transposition cipher to encrypt and decrypt messages.
- Write a program that uses a column transposition cipher to encrypt and decrypt messages.
- A column transposition cipher uses the relative alphabetic order of its key's letters to determine the column mapping. What happens if a key contains duplicated letters, as in PIZZA or BOOKWORM? How can you solve that problem? Does this approach have any benefits?
- A column transposition cipher swaps the columns in a message written into an array. Would you gain extra security by swapping both columns and rows?
- Write a program similar to a column transposition cipher that swaps both columns and rows.
- Write a program that uses a Caesar substitution cipher to encrypt and decrypt messages. What is the encryption of “Nothing but gibberish” with a shift of 13?
- *Write a program that displays the frequencies of occurrence of the letters in a message. Sort the results by frequency, and for each letter, display the offset that would map E to that letter.
Then use that program and the program you wrote for Exercise 6 to decipher the message KYVIV NRJRK ZDVNY VETRV JRIJL SJKZK LKZFE NRJKY VJKRK VFWKY VRIK. What is the encryption's offset?
- Write a program that uses a Vigenère cipher to encrypt and decrypt messages. Use the program to decrypt the ciphertext VDOKR RVVZK OTUII MNUUV RGFQK TOGNX VHOPG RPEVW VZYYO WKMOC ZMBR with the key VIGENERE.
- After you have used all of the letters in a one-time pad, why can't you start over and use the letters again?
- Suppose that you're using a large one-time pad to send and receive many messages with another person, and one of the messages you receive decrypts into gibberish. What might have happened, and what can you do about it?
- When using a one-time pad, suppose you send ciphertext messages together with the index of the first letter used to encrypt them. Would that compromise the encryption?
- Write a program that uses a one-time pad. Rather than making a truly random one-time pad, hard-code a string of random characters into the program. You can generate the characters by hand, use a pseudorandom number generator, or use some other source of randomness such as
http://www.dave-reed.com/Nifty/randSeq.html.As you encrypt and decrypt messages, make the program keep track of the characters that have been used for encryption and decryption.
- Explain how a perfectly secure cryptographic random-number generator is equivalent to an unbreakable encryption scheme. In other words, if you have a cryptographically secure random-number generator, how could you use it to create an unbreakable encryption scheme and vice versa?
- The lengths and timing of messages can sometimes give information to an attacker. For example, an attacker might notice that you always send a long message before an important event such as a dignitary visiting or a large stock purchase. How you can avoid giving that sort of information to an attacker?
- Suppose you're using RSA with the primes
 ,
, 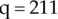 , and
, and  . In that case, what are n,
. In that case, what are n,  , and d? What is the encryption of the value 1,337? What is the decryption of 19,905? (You may want to use the ExponentiateMod program from Chapter 2. You may also want to write a program to find inverses in a modulus, or you can use the MultiplicativeInverse program included in this chapter's downloads.)
, and d? What is the encryption of the value 1,337? What is the decryption of 19,905? (You may want to use the ExponentiateMod program from Chapter 2. You may also want to write a program to find inverses in a modulus, or you can use the MultiplicativeInverse program included in this chapter's downloads.)
