Reinforcement learning introduces new terminologies as listed here, which are quite different from that of older machine learning techniques:

The key component in reinforcement learning is a decision-making agent that reacts to its environment by selecting and executing the best course of actions and being rewarded or penalized for it [11:3]. You can visualize these agents as robots navigating through an unfamiliar terrain or a maze. Robots use reinforcement learning as part of their reasoning process after all. The following diagram gives the overview architecture of the reinforcement learning agent:

The four state transitions of reinforcement learning

The agent collects the state of the environment, selects, and then executes the most appropriate action. The environment responds to the action by changing its state and rewarding or punishing the agent for the action.

The four steps of an episode or learning cycle are as follows:

The action of the agent modifies the state of the system, which in turn notifies the agent of the new operational condition. Although not every action will trigger a change in the state of the environment, the agent collects the reward or penalty nevertheless. At its core, the agent has to design and execute a sequence of actions to reach its goal. This sequence of actions is modeled using the ubiquitous Markov decision process (refer to the Markov decision processes section in Chapter 7, Sequential Data Models).

A good metaphor for such a scenario is the rollback of the action. However, not all environments support such a dummy action, and the agent may have to run Monte-Carlo simulations to try out an action.

Reinforcement learning is particularly suited to problems for which long-term rewards can be balanced against short-term rewards. A policy enforces the trade-off between short-term and long-term rewards. It guides the behavior of the agent by mapping the state of the environment to its actions. Each policy is evaluated through a variable known as the value of a policy.

Intuitively, the value of a policy is the sum of all the rewards collected as a result of the sequence of actions taken by the agent. In practice, an action over the policy farther in the future obviously has a lesser impact than the next action from a state S_t to a state S_t+1. In other words, the impact of future actions on the current state has to be discounted by a factor, known as the discount coefficient for future rewards < 1.

The optimum policy π* is the agent's sequence of actions that maximizes the future reward discounted to the current time.

The following table introduces the mathematical notation of each component of reinforcement learning:

The purpose is to compute the maximum expected reward R_t from any starting state s_k as the sum of all discounted rewards to reach the current state s_t. The value V^π of a policy π at the state s_t is the maximum expected reward R_t given the state s_t.

Note

M1: The cumulative reward R_t and value function V^π(st) for the state st given a policy π and a discount rate γ is defined as:

The problem of finding the optimal policies is indeed a nonlinear optimization problem whose solution is iterative (dynamic programming). The expression of the value function V^π of a policy π can be formulated using the Markovian state transition probabilities p_t.

Note

M2: The value function V^π(s_t) for a state st and future state s_k with a reward r_k using the transition probability p_k, given a policy π and a discount rate γ is defined as:

V*(s_t) is the optimal value of the state st across all the policies. The equations are known as the Bellman optimality equations.

If the environment model, state, action, and rewards, as well as transition between states, are completely defined, the reinforcement learning technique is known as model-based learning. In this case, there is no need to explore a new sequence of actions or state transitions. Model-based learning is similar to playing a board game in which all combinations of steps that are necessary to win are completely known.

However, most practical applications using sequential data do not have a complete, definitive model. Learning techniques that do not depend on a fully defined and available model are known as model-free techniques. These techniques require exploration to find the best policy for any given state. The remaining sections in this chapter deal with model-free learning techniques, and more specifically, the temporal difference algorithm.

Temporal difference is a model-free learning technique that samples the environment. It is a commonly used approach to solve the Bellman equations iteratively. The absence of a model requires a discovery or exploration of the environment. The simplest form of exploration is to use the value of the next state and the reward defined from the action to update the value of the current state, as described in the following diagram:

An illustration of the temporal difference algorithm

The iterative feedback loop used to adjust the value action on the state plays a role similar to the backpropagation of errors in artificial neural networks or minimization of the loss function in supervised learning. The adjustment algorithm has to:

The iterative formulation of the first Bellman equation predicts V^π(st), the value function of state st from the value function of the next state s_t+1. The difference between the predicted value and the actual value is known as the temporal difference error abbreviated as δt.

Note

M3: The formula for tabular temporal difference δ_t for a value function V(s_t) at state s_t, a learning rate α, a reward r_t, and a discount rate γ is defined as:

An alternative to evaluating a policy using the value of the state V^π(s_t) is to use the value of taking an action on a state s_t known as the value of action (or action-value) Q^π(s_t, a_t).

Note

M4: The definition of the value Q of action at a state st as the expectation of a reward R_t for an action a_t on a state s_t is defined as:

There are two methods to implement the temporal difference algorithm:

Let's consider the temporal difference algorithm using an off-policy method and its most commonly used implementation: Q-learning.

Q-learning is a model-free learning technique using an off-policy method. It optimizes the action-selection policy by learning an action-value function. Like any machine learning technique that relies on convex optimization, the Q-learning algorithm iterates through actions and states using the quality function, as described in the following mathematical formulation.

The algorithm predicts and discounts the optimum value of action max{Q_t} for the current state st and action at on the environment to transition to the state s_t+1.

Similar to genetic algorithms that reuse the population of chromosomes in the previous reproduction cycle to produce offspring, the Q-learning technique strikes a balance between the new value of the quality function Q_t+1 and the old value Q_t using the learning rate α. Q-learning applies temporal difference techniques to the Bellman equation for an off-policy methodology.

Note

M5: The Q-learning action-value updating formula for a given policy π, set of states {s_t}, a set of actions {a_t} associated with each state s_t, a learning rate α, and a discount rate γ is given by:

Q-learning estimates the cumulative reward discounted for future actions.

Let's apply our hard-earned knowledge of reinforcement learning to management and optimization of a portfolio of exchange-traded funds.

The key components of the implementation of the Q-learning algorithm are defined as follows:

The following diagram shows the key components of the Q-learning algorithm:

The UML components diagram of the Q-learning algorithm

The QLAction class specifies the transition of one state with a from identifier to another state with the to identifier, as shown here:

class QLAction(val from: Int, val to: Int)

Actions have a Q value (or action-value), a reward, and a probability. The implementation defines these three values in three separate matrices: Q for the action values, R for rewards, and P for probabilities, in order to stay consistent with the mathematical formulation.

A state of the QLState type is fully defined by its identifier, id, the list of actions to transition to some other states, and a prop property of the parameterized type, as shown in the following code:

class QLState[T](val id: Int, 
  val actions: List[QLAction] = List.empty, 
  val instance: T])

The state might not have any actions. This is usually the case of the goal or absorbing state. In this case, the list is empty. The parameterized instance is a reference to the object for which the state is computed.

The next step consists of creating the graph or search space.

The search space is the container responsible for any sequence of states. The QLSpace class takes the following parameters:

The QLSpace class is implemented as follows:

class QLSpace[T](states: Seq[QLState[T]], goals: Array[Int]) {
  val statesMap = states.map(st =>(st.id, st)) //1
  val goalStates = new HashSet[Int]() ++ goals //2
  
  def maxQ(state: QLState[T], 
      policy: QLPolicy): Double   //3
  def init(state0: Int)  //4
  def nextStates(st: QLState[T]): Seq[QLState[T]]  //5
   …
}

The constructor of the QLSpace class generates a map, statesMap. It retrieves the state using its id value (line 1) and the array of goals, goalStates (line 2). Furthermore, the maxQ method computes the maximum action-value, maxQ, for a state given a policy (line 3). The implementation of the maxQ method is described in the next section.

The init method selects an initial state for training episodes (line 4). The state is randomly selected if the state0 argument is invalid:

def init(state0: Int): QLState[T] = 
  if(state0 < 0) {
    val seed = System.currentTimeMillis+Random.nextLong
      states((new Random(seed)).nextInt(states.size-1))
  }
  else states(state0)

Finally, the nextStates method retrieves the list of states resulting from the execution of all the actions associated with the st state (line 5).

The QLSpace search space is actually created by the apply factory method defined in the QLSpace companion object, as shown here:

def apply[T](goals: Array[Int], instances: Seq[T],
    constraints: Option[Int =>List[Int]): QLSpace[T] ={ //6

  val r = Range(n, instances.size)  

  val states = instances.zipWithIndex.map{ case(x, n) => {
    val validStates = constraints.map( _(n)).getOrElse(r)
    val actions = validStates.view
          .map(new QLAction(n, _)).filter(n != _.to) //7
    QLState[T](n, actions, x)
  }}
  new QLSpace[T](states, goals) 
}

The apply method creates a list of states using the instances set, the goals, and the constraints constraining function as inputs (line 6). Each state creates its list of actions. The actions are generated from this state to any other states (line 7).

The search space of states is illustrated in the following diagram:

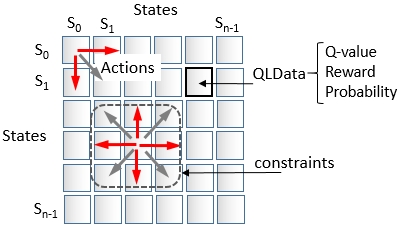
The state transition matrix with QLData (Q-value, reward, and probability)

The constraints function limits the scope of the actions that can be triggered from any given state, as illustrated in the preceding diagram.

Each action has an action-value, a reward, and a potentially probability. The probability variable is introduced to simply model the hindrance or adverse condition for an action to be executed. If the action does not have any external constraint, the probability is 1. If the action is not allowed, the probability is 0.

The QLData class is a container for three values: reward, probability, and a value variable for the Q-value, as shown here:

class QLData(val reward: Double, val probability: Double) {
  var value: Double = 0.0
  def estimate: Double = value*probability
}

The estimate method adjusts the Q-value, value, with the probability to reflect any external condition that can impede the action.

Next, let's create a simple schema or class, QLInput, to initialize the reward and probability associated with each action as follows:

class QLInput(val from: Int, val to: Int, 
    val reward: Double, val probability: Double = 1.0)

The first two arguments are the identifiers for the from source state and the to target state for this specific action. The last two arguments are the reward, collected at the completion of the action, and its probability. There is no need to provide an entire matrix. Actions have a reward of 1 and a probability of 1 by default. You only need to create an input for actions that have either a higher reward or a lower probability.

The number of states and a sequence of input define the policy of the QLPolicy type. It is merely a data container, as shown here:

class QLPolicy(input: Seq[QLInput]) { 
  val numStates = Math.sqrt(input.size).toInt  //8
  
  val qlData = input.map(qlIn => 
new QLData(qlIn.reward, qlIn.prob))  //9
  
  def setQ(from: Int, to: Int, value: Double): Unit =
     qlData(from*numStates + to).value = value //10

  def Q(from: Int, to: Int): Double = 
    qlData(from*numStates + to).value  //11
  def EQ(from: Int, to: Int): Double = 
    qlData(from*numStates + to).estimate //12
  def R(from: Int, to: Int): Double = 
    qlData(from*numStates + to).reward //13
  def P(from: Int, to: Int): Double = 
    qlData(from*numStates + to).probability //14
}

The number of states, numStates, is the square root of the number of elements of the initial input matrix, input (line 8). The constructor initializes the qlData matrix of the QLData type with the input data, reward, and probability (line 9). The QLPolicy class defines the shortcut methods to update (line 10) and retrieve (line 11) the value, the estimate (line 12), the reward (line 13), and the probability (line 14).

The QLearning class encapsulates the Q-learning algorithm, and more specifically, the action-value updating equation. It is a data transformation of the ETransform type with an explicit configuration of the QLConfig type (line 16) (refer to the Monadic data transformation section in Chapter 2, Hello World!):

class QLearning[T](conf: QLConfig, 
    qlSpace: QLSpace[T], qlPolicy: QLPolicy) //15
    extends ETransform[QLConfig](conf) { //16

  type U = QLState[T] //17
  type V = QLState[T] //18

  val model: Option[QLModel] = train //19
  def train: Option[QLModel]
  def nextState(iSt: QLIndexedState[T]): QLIndexedState[T]

  override def |> : PartialFunction[U, Try[V]]
  …
}

The constructor takes the following parameters (line 15):

The model is generated or trained during the instantiation of the class (refer to the Design template for classifier section in the Appendix A, Basic Concepts) (line 19). The Q-learning algorithm is implemented as an explicit data transformation; therefore, the U type of the input element and the V type of the output element to the |> predictor are initialized as QLState (lines 17 and 18).

The configuration of the Q-learning algorithm, QLConfig, specifies the learning rate, alpha, the discount rate, gamma, the maximum number of states (or length) of an episode, episodeLength, the number of episodes (or epochs) used in training, numEpisodes, and the minimum coverage, minCoverage, required to select the best policy as follows:

case class QLConfig(val alpha: Double, 
  val gamma: Double, 
  val episodeLength: Int, 
  val numEpisodes: Int, 
  val minCoverage: Double) extends Config

The QLearning class has two constructors defined in its companion object that initializes the policy either from an input matrix of states or from a function that compute the reward and probabilities:

The first constructor for the QLearning class passes the initialization of states => Seq[QLInput], the sequence of references of instances associated with the states, and the constraints scope constraining function as an argument, besides the configuration and the goals (line 20):

def apply[T](config: QLConfig,  //20
   goals: Array[Int], 
   input: => Seq[QLInput], 
   instances: Seq[T],
   constraints: Option[Int =>List[Int]] =None): QLearning[T]={
     
   new QLearning[T](config, 
     QLSpace[T](goals, instances, constraints),
     new QLPolicy(input))
}

The second constructor passes the input data, xt (line 21), the reward function (line 22), and the probability function (line 23) as well as the sequence of references of instances associated with the states and the constraints scope constraining function as arguments:

def apply[T](config: QLConfig, 
   goals: Array[Int],
   xt: DblVector,  //21
   reward: (Double, Double) => Double, //22
   probability: (Double, Double) => Double, //23
   instances: Seq[T].
   constraints: Option[Int =>List[Int]] =None): QLearning[T] ={

  val r = Range(0, xt.size)
  val input = new ArrayBuffer[QLInput] //24
  r.foreach(i => 
    r.foreach(j => 
     input.append(QLInput(i, j, reward(xt(i), xt(j)), 
          probability(xt(i), xt(j))))
    )
  )
  new QLearning[T](config, 
    QLSpace[T](goals, instances, constraints), 
    new QLPolicy(input))
}

The reward and probability matrices are used to initialize the input state (line 24).

Let's take a look at the computation of the best policy during training. First, we need to define a QLModel model class with the bestPolicy optimum policy (or path) and its coverage as parameters:

class QLModel(val bestPolicy: QLPolicy, 
    val coverage: Double) extends Model

The creation of model consists of executing multiple episodes to extract the best policy. The training is executed in the train method: Each episode starts with a randomly selected state, as shown in the following code:

def train: Option[QLModel] = Try {
  val completions = Range(0, config.numEpisodes)
     .map(epoch => if(train(-1)) 1 else 0).sum  //25
  completions.toDouble/config.numEpisodes //26
}
.map( coverage => {
  if(coverage > config.minCoverage) 
    Some(new QLModel(qlPolicy, coverage))  //27
  else None
}).get

The train method iterates through the generation of the best policy starting from a randomly selected state config.numEpisodes times (line 25). The state coverage is calculated as the percentage of times the search ends with the goal state (line 26). The training succeeds only if the coverage exceeds a threshold value, config.minAccuracy, specified in the configuration.

The train(state0: Int) method does the heavy lifting at each episode (or epoch). It triggers the search by selecting either the state0 initial state or a r random generator with a new seed, if state0 is < 0, as shown in the following code:

case class QLIndexedState[T](val state: QLState[T], 
  val iter: Int)

The QLIndexedState utility class keeps track of the state at a specific iteration, iter, within an episode or epoch:

def train(state0: Int): Boolean = {
  @tailrec
  def search(iSt: QLIndexedState[T]): QLIndexedState[T]

    val finalState = search(
       QLIndexedState(qlSpace.init(state0), 0)
    )
  if( finalState.index == -1) false //28
  else qlSpace.isGoal(finalState.state) //29
}

The implementation of search for the goal state(s) from a state0 predefined or random is a textbook implementation of the Scala tail recursion. Either the recursive search ends if there are no more states to consider (line 28) or the goal state is reached (line 29).

Tail recursion is a very effective construct to apply an operation to every item of a collection [11:5]. It optimizes the management of the function stack frame during the recursion. The annotation triggers a validation of the condition necessary for the compiler to optimize the function calls, as shown here:

@tailrec
def search(iSt: QLIndexedState[T]): QLIndexedState[T] = {
  val states = qlSpace.nextStates(iSt.state) //30 

  if( states.isEmpty || iSt.iter >= config.episodeLength) //31 
    QLIndexedState(iSt.state, -1)

  else {
    val state = states.maxBy(s => 
       qlPolicy.R(iSt.state.id, s.id)) //32
    if( qlSpace.isGoal(state) ) 
       QLIndexedState(state, iSt.iter)  //33
    
    else {
      val fromId = iSt.state.id
      val r = qlPolicy.R(fromId, state.id)   
      val q = qlPolicy.Q(fromId, state.id) //34

      val nq = q + config.alpha*(r + 
         config.gamma * qlSpace.maxQ(state, qlPolicy)-q) //35
      qlPolicy.setQ(fromId, state.id,  nq) //36
      search(QLIndexedState(state, iSt.iter+1))
    }
  }
}

Let's dive into the implementation for the Q action-value updating equation. The search method implements the M5 mathematical expression for each recursion.

The recursion uses the QLIndexedState utility class (state, iteration number in the episode) as an argument. First, the recursion invokes the nextStates method of QLSpace (line 30) to retrieve all the states associated with the st current state through its actions, as shown here:

def nextStates(st: QLState[T]): Seq[QLState[T]] = 
  if( st.actions.isEmpty )
    Seq.empty[QLState[T]]
  else
    st.actions.map(ac => statesMap.get(ac.to) )

The search completes and returns the current state if the length of the episode (maximum number of states visited) is reached or the goal is reached or there is no further state to transition to (line 31). Otherwise, the recursion computes the state to which the transition generates the higher reward R from the current policy (line 32). The recursion returns the state with the highest reward if it is one of the goal states (line 33). The method retrieves the current q action-value (line 34) and r reward matrices from the policy, and then applies the equation to update the action-value (line 35). The method updates the action-value Q with the new value nq (line 36).

The action-value updating equation requires the computation of the maximum action-value associated with the current state, which is performed by the maxQ method of the QLSpace class:

def maxQ(state: QLState[T], policy: QLPolicy): Double = {
   val best = states.filter( _ != state)  //37
      .maxBy(st => policy.EQ(state.id, st.id))  //38
   policy.EQ(state.id, best.id)
}

The maxQ method filters out the current state (line 37) and then extracts the best state, which maximizes the policy (line 38).

A commercial application may require multiple types of validation mechanisms regarding the states transition, reward, probability, and Q-value matrices.

One critical validation is to verify that the user-defined constraints function does not create a dead end in the search or training of Q-learning. The constraints function establishes the list of states that can be accessed from a given state through actions. If the constraints are too tight, some of the possible search paths may not reach the goal state. Here is a simple validation of the constraints function:

def validateConstraints(numStates: Int, 
    constraints: Int => List[Int]): Boolean = 
  Range(0, numStates).exists( constraints(_).isEmpty )

The last functionality of the QLearning class is the prediction using the model created during training. The |> method predicts the optimum state transition (or action) from a given state, state0:

override def |> : PartialFunction[U, Try[V]] = {
  case state0: U if(isModel) =>  Try {
    if(state0.isGoal) state0  //39
    else nextState(QLIndexedState[T](state0, 0)).state) //40
  }
}

The |> data transformation returns itself if the state0 input state is the goal (line 39) or computes the best outcome, nextState, (line 40) using another tail recursion, as follows:

@tailrec
def nextState(iSt: QLIndexedState[T]): QLIndexedState[T] =  {
  val states = qlSpace.nextStates(iSt.state) //41

  if( states.isEmpty || iSt.iter >=config.episodeLength) 
     iSt  //42
  else {
    val fromId = iSt.state.id
    val qState = states.maxBy(s =>  //43
       model.map(_.bestPolicy.R(fromId, s.id)).getOrElse(-1.0))
    nextState(QLIndexedState[T](qState, iSt.iter+1)) //44
  }
}

The nextState method executes the following sequence of invocations:

The |> prediction method returns either the best possible state or None if the model cannot be created during training.

Let's select N = 2 as the number of days in the future for our prediction. Any longer-term prediction is quite unreliable because it falls outside the constraint of the discrete Markov model. Therefore, the price of the option two days in the future is the value of the reward—profit or loss.

The OptionProperty class encapsulates the four attributes of an option (line 45) as follows:

class OptionProperty(timeToExp: Double, volatility: Double, 
     vltyByVol: Double, priceToStrike: Double) { //45

  val toArray = Array[Double](
     timeToExp, volatility, vltyByVol, priceToStrike
  )
}

The OptionModel class is a container and a factory for the properties of the option. It creates the list of propsList option properties by accessing the data source of the four features introduced earlier. It takes the following parameters:

The implementation of the OptionModel class is as follows:

class OptionModel(symbol: String,  strikePrice: Double, 
   src: DataSource, minExpT: Int, nSteps: Int) {

  val propsList = (for {
    price <- src.get(adjClose)
    volatility <- src.get(volatility)
    nVolatility <- normalize(volatility)
    vltyByVol <- src.get(volatilityByVol)
    nVltyByVol <- normalize(vltyByVol)
    priceToStrike <- normalize(price.map(p => 
       (1.0 - strikePrice/p)))
  } yield {
    nVolatility.zipWithIndex./:(List[OptionProperty]()){ //46
      case(xs, (v,n)) => {
         val normDecay = (n + minExpT).toDouble/
            (price.size + minExpT) //47
         new OptionProperty(normDecay, v, nVltyByVol(n), 
           priceToStrike(n)) :: xs
      }
    }.drop(2).reverse  //48
   })
  .getOrElse(List.empty[OptionProperty].)

  def quantize(o: DblArray): Map[Array[Int], Double] 
}

The factory uses the zipWithIndex Scala method to represent the index of the trading sessions (line 46). All feature values are normalized over the interval [0, 1], including the time decay (or time to expiration) of the normDecay option (line 47). The instantiation of the OptionModel class generates a list of OptionProperty elements if the constructor succeeds (line 48), an empty list otherwise.

The four properties of the option are continuous values, normalized as a probability [0, 1]. The states in the Q-learning algorithm are discrete and require a quantization or categorization known as a function approximation; although a function approximation scheme can be quite elaborate [11:9]. Let's settle for a simple linear categorization, as illustrated in the following diagram:

Quantization of the state of a traded option

The function approximation defines the number of states. In this example, a function approximation that converts a normalized value into three intervals or buckets generates 3⁴ = 81 states or potentially 3⁸-3⁴ = 6480 actions! The maximum number of states for l buckets function approximation and n features is lⁿ with a maximum number of l²ⁿ-lⁿ actions.

The quantize method of the OptionModel class converts the normalized value of each option property of features into an array of bucket indices. It returns a map of profit and loss for each bucket keyed on the array of bucket indices, as shown in the following code:

def quantize(o: DblArray): Map[Array[Int], Double] = {
  val mapper = new mutable.HashMap[Int, Array[Int]] //49
  val _acc = new NumericAccumulator[Int] //50
   
  val acc = propsList.view.map( _.toArray)
       .map( toArrayInt( _ )) //51
       .map(ar => { 
          val enc = encode(ar)  //52
          mapper.put(enc, ar)
          enc
       }).zip(o)
       ./:(_acc){ 
          case (acc, (t,y)) => { //53
          acc += (t, y)
          acc 
       }}
   acc.map {case (k, (v,w)) => (k, v/w) }  //54
     .map {case( k,v) => (mapper(k), v) }.toMap
}

The method creates a mapper instance to index the array of buckets (line 49). An acc accumulator of the NumericAccumulator type extends Map[Int, (Int, Double)] and computes the tuple (number of occurrences of features on each buckets and the sum of increase or decrease of the option price) (line 50). The toArrayInt method converts the value of each option property (timeToExp, volatility, and so on) into the index of the appropriate bucket (line 51). The array of indices is then encoded (line 52) to generate the id or index of a state. The method updates the accumulator with the number of occurrences and the total profit and loss for a trading session for the option (line 53). It finally computes the reward on each action by averaging the profit and loss on each bucket (line 54).

A view is used in the generation of the list of OptionProperty to avoid unnecessary object creation.

The source code for the toArrayInt and encode methods and NumericAccumulator is documented and available online.