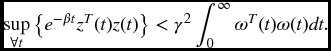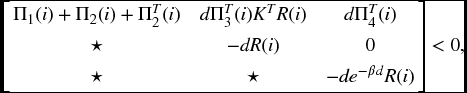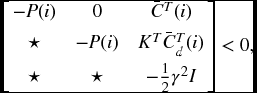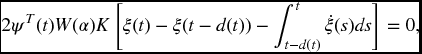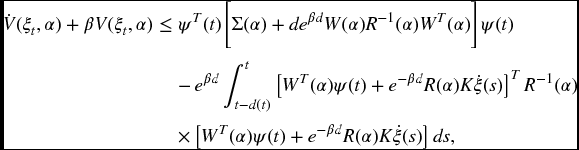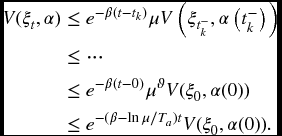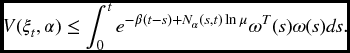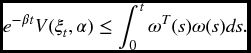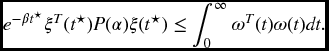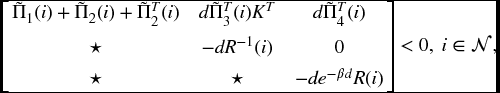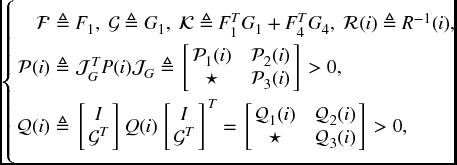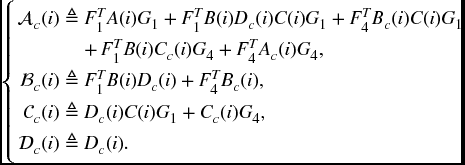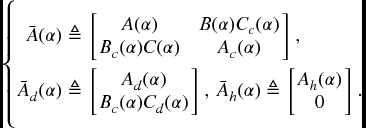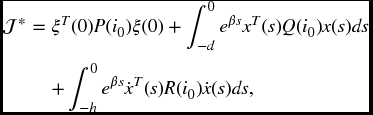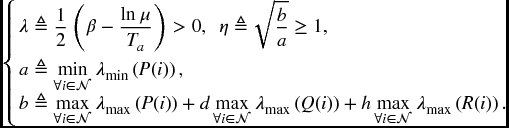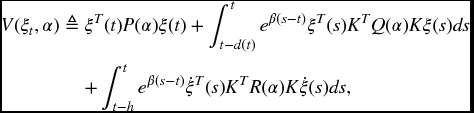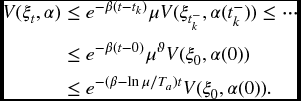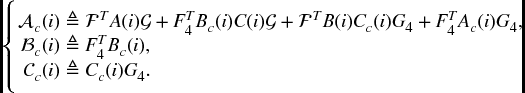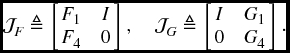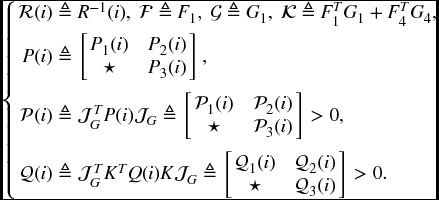6.2.1 System Description and Preliminaries

Consider a class of switched state-delayed hybrid systems of the form:

(6.1a)

(6.1b)

(6.1c)

(6.1d)

where x(t) ∈ Rⁿ is the system state vector; u(t) ∈ R^m is the control input; y(t) ∈ R^p is the measured output; z(t) ∈ R^q is the controlled output; ω(t) ∈ R^l is the disturbance input which belongs to . {(A(α), A_d(α), B(α), B₁(α), C(α), C_d(α), is a family of matrices parameterized by an index set , and (denoted by α for simplicity) is the switching signal defined as the same in Chapter 5. d(t) denotes the time-varying delays satisfying 0 ≤ d(t) ≤ d and for known constants d and τ and φ(t) is a differentiable vector-valued initial function on [ − d, 0]. For each possible value , we will denote the system matrices associated with mode i by A(i) = A(α), A_d(i) = A_d(α), B(i) = B(α), B₁(i) = B₁(α), C(i) = C(α), C_d(i) = C_d(α), D₁(i) = D₁(α), E(i) = E(α), and E_d(i) = E_d(α).

Assuming that some state components of system (6.1a) are not available, we now seek to design a DOF controller of general structure described by

(6.2a)

(6.2b)

where x_c(t) ∈ Rⁿ is the DOF controller state vector; A_c(α), B_c(α), C_c(α), and D_c(α) are appropriately dimensioned matrices to be determined.

Augmenting the model of (6.1a)–(6.1d) to include the states of the DOF controller dynamics in (6.2a)–(6.2b), we obtain the following closed-loop system:

(6.3a)

(6.3b)

(6.3c)

where , and

(6.4)

Before proceeding, we give the following definitions.

Definition 6.2.1 The closed-loop system in (6.3a)–(6.3c) with ω(t) = 0 is said to be exponentially stable under α if its solution ξ(t) satisfies

where η ≥ 1 and λ > 0 are two real constants, and

Definition 6.2.2 For β > 0 and γ > 0, the closed-loop system in (6.3a)–(6.3c) is said to be exponentially stable with a weighted - performance γ, if under α it is exponentially stable with ω(t) = 0, and under zero initial condition, that is, ϕ(t) = 0, t ∈ [ − d, 0], for any nonzero , it holds that

(6.5)

Therefore, the - DOF control problem can be formulated as follows: for switched state-delayed hybrid systems (6.1a)–(6.1d) and a prescribed performance level γ > 0, determine DOF controllers in the form of (6.2a)–(6.2b) such that the resulting closed-loop system in (6.3a)–(6.3c) is exponentially stable with a weighted - performance level γ.

6.2.2 Main Results

First, we will investigate the exponential stability and the weighted - performance for the closed-loop system (6.3a)–(6.3c), and give the following result.

Theorem 6.2.3 Given constants β > 0 and γ > 0, suppose that there exist matrices P(i) > 0, Q(i) > 0, R(i) > 0, X(i), Y(i), and Z(i) such that for ,

(6.6a)

(6.6b)

where and

Then, the closed-loop system in (6.3a)–(6.3c) is exponentially stable with a weighted - performance level γ for any switching signal with average dwell time satisfying , where μ ≥ 1 satisfies

(6.7)

Moreover, an estimate of the state decay is given by

(6.8)

where

(6.9)

Proof. Choose a Lyapunov function of the following form:

(6.10)

where P(α) > 0, Q(α) > 0, and R(α) > 0, are to be determined. Then, as with the solution of system (6.3a)–(6.3c) for a fixed α, it follows that

(6.11)

On the other hand, Newton–Leibniz formula gives

Then for any appropriately dimensioned matrices , we have

(6.12)

where .

First, we will show the stability of the closed-loop system (6.3a)–(6.3c) with ω(t) = 0. By (6.11)–(6.12), we have

(6.13)

where

By Schur complement, LMI (6.6) implies

(6.14)

and noting

(6.15)

Thus considering (6.13)–(6.15), we have

(6.16)

For an arbitrary piecewise constant switching signal α, and for any t > 0, we let 0 = t₀ < t₁ < ⋅⋅⋅ < t_k < ⋅⋅⋅, k = 1, 2, …, denote the switching points of α over the interval (0, t). As mentioned earlier, the i_kth subsystem is activated when t ∈ [t_k, t_{k + 1}). Integrating (6.16) from t_k to t gives

(6.17)

Using (6.7) and (6.10), at switching instant t_k, we have

(6.18)

where t⁻_k denotes the left limitation of t_k. Therefore, it follows from (6.17)–(6.18), and noting ϑ = N_α(0, t) ≤ (t − 0)/T_a, that

(6.19)

Notice from (6.10) that V(ξ_t, α) ≥ a‖ξ(t)‖² and V(ξ₀, α(0)) ≤ b‖ξ(0)‖_C², where a and b are defined in (6.9). Considering (6.19) yields

which implies (6.8). By Definition 6.2.1 with t₀ = 0, we know that the closed-loop system (6.3a)–(6.3c) with ω(t) = 0 is exponentially stable.

Now, we will establish the weight - performance for the closed-loop system in (6.3a)–(6.3c). For any appropriately dimensioned matrix , we have

(6.20)

where and . Considering (6.11) and (6.20), we have

(6.21)

where Π(α)≜Π₁(α) + Π₂(α) + Π^T₂(α) + dΠ^T₃(α)K^TR(α)KΠ₃(α) with Π₁(α), Π₂(α) and Π₃(α) defined in (6.6). Note that

(6.22)

By Schur complement, LMI (6.6) implies

(6.23)

Thus, considering (6.21)–(6.23), we have

(6.24)

Let Γ(t)≜ − ω^T(t)ω(t), then (6.24) can be rewritten as

(6.25)

As in the proof of stability above, integrating (6.25) from t_k to t gives

(6.26)

Therefore, it follows from (6.18) and (6.26) and the relationship ϑ = N_α(0, t) ≤ (t − 0)/T_a that

(6.27)

Under zero initial condition, (6.27) implies

(6.28)

Multiplying both sides of (6.28) by yields

(6.29)

Notice that N_α(0, t) ≤ t/T_a and T_a > T*_a = ln μ/β, we have N_α(0, t)ln μ ≤ βt. Thus, (6.29) implies

(6.30)

Moreover, according to (6.10) and (6.30), we have

Thus, for any time t = t^⋆ ≥ 0, we have

(6.31)

Since t^⋆ denotes any time, it is also true that

(6.32)

From inequalities (6.31) and (6.32), we have

(6.33)

Using Schur complement again, LMI (6.6) yields

(6.34)

Combining (6.33) with (6.34) gives

that is, for any t^⋆ ≥ 0,

Taking the supremum over t^⋆ ≥ 0 yields (6.5), thus the weight - performance has been established. The proof is completed. ▀

Now, we are in a position to present a solution to the - DOF control problem.

Theorem 6.2.4 Consider the switched state-delayed hybrid systems in (6.1a)–(6.1d). For given constants β > 0 and γ > 0, suppose that there exist matrices , , , , , R(i) > 0, , , , , , , , , , , , , and such that for ,

(6.35a)

(6.35b)

(6.35c)

(6.35d)

(6.35e)

Then there exists a DOF controller in the form of (6.2a)–(6.2b), such that the closed-loop system in (6.3a)–(6.3c) is exponentially stable with a weighted - performance γ for any switching signal with average dwell time satisfying , where μ ≥ 1 satisfies

(6.36)

Moreover, a desired - DOF controller realization is given by

(6.37)

where

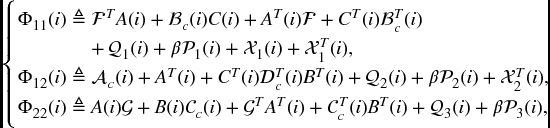
and

Proof. Introducing a slack matrix F, it is not difficult to see that the conditions in Theorem 6.2.3 are satisfied if there exist matrices P(i) > 0, Q(i) > 0, R(i) > 0 X(i), Y(i), Z(i), and F such that (6.6b) and the following conditions hold:

(6.38)

where

The condition in (6.38) implies (6.6a) in Theorem 6.2.3. To show this, we perform a projection transformation to (6.38) by diag{Λ(i), R(i), I} with

and thus imply (6.6a). Notice that if the condition in (6.38) holds, then matrix F is nonsingular, so we can let the matrix F be partitioned as

(6.39)

As we are considering a full-order DOF controller, F₄ and G₄ are both square. Without loss of generality, we assume that F₄ and G₄ are nonsingular (if not, F₄ and G₄ may be perturbed respectively by matrices ΔF₄ and ΔG₄ with sufficiently small norms such that F₄ + ΔF₄ and G₄ + ΔG₄ are nonsingular and satisfy (6.38)). Then, we can define the following matrices, which are also nonsingular,

(6.40)

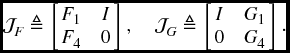
Notice that

(6.41)

Performing a congruence transformation on (6.38) by matrix with , we have

(6.42)

where

(6.43)

Define the following matrices:

(6.44)

and

(6.45)

LMI (6.42) implies (6.35a) by considering (6.4), (6.39)–(6.41), and (6.43)–(6.45). Moreover, performing a congruence transformation on (6.6b) by matrix , we have

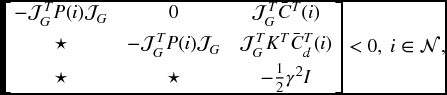
which is (6.35b) by noting (6.4) and (6.44). In addition, considering the conditions in (6.7) together (6.44) implies (6.36). Finally, considering (6.45) together with (6.44) yields (6.37). This completes the proof. ▀

Remark 6.1 In the proof of Theorem 6.2.4, we used conditions (6.38) and (6.6b), and not (6.6a)–(6.6b), to solve the - DOF control problem. The reason is that there is no product term between the parameter-dependent Lyapunov matrices and the system dynamic matrices in (6.38); this separation is crucial to solving the - DOF control problem. ♦

Remark 6.2 To solve the parameters of the DOF controller in (6.37), matrices F₄ and G₄ should be available in advance, and they can be obtained by taking any full rank factorization of (derived from ). ♦

Note that the obtained conditions in Theorem 6.2.4 are not all of LMI form because of (6.35e), which can not be solved directly using LMI procedures. Now, using the CCL method [66], we suggest the following minimization problem involving LMI conditions instead of the original nonconvex feasibility problem formulated in Theorem 6.2.4.

Problem DOFC-SDS (DOF control of switched delayed systems):

(6.46)

If the solution of the aforesaid minimization problem is Nn, then the conditions in Theorem 6.2.4 are solvable. We suggest the following algorithm to solve Problem DOFC-SDS.

Algorithm DOFC-SDS

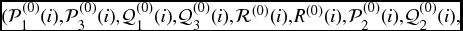
• Step 1. Find a feasible set satisfying (6.35a)–(6.35d), (6.36), and (6.46). Set κ = 0.
• Step 2. Solve the following optimization problem:
  
  and denote f* as the optimized value.
• Step 3. Substitute the obtained matrix variables into (6.42). If (6.42) is satisfied, with
  
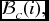
  for a sufficiently small scalar δ > 0, then output the feasible solutions , and EXIT.
• Step 4. If where is the maximum number of iterations allowed, so EXIT.
• Step 5. S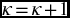et . Let , and go to Step 2.

6.2.3 Illustrative Example

Example 6.2.5 Consider system (6.1a)–(6.1d) with N = 2 and the following parameters:

and d(t) = 0.9 + 0.3sin (t), β = 0.5. A straightforward calculation gives d = 1.2 and τ = 0.3. It can be checked that the switched state-delayed hybrid system in (6.1a)–(6.1d) with u(t) = 0 and the above parameters is unstable for switching signal given in Figure 6.1 (which is generated randomly; here, ‘1’ and ‘2’ represent the first and second subsystems, respectively) – the states of open-loop system are shown in Figure 6.2 with the initial condition given by , t ∈ [ − 1.2, 0].

Our aim is to design an - DOF controller in the form of (6.2a)–(6.2b), such that the closed-loop system is exponentially stable with a weighted - performance. Setting μ = 1.01 (in this case, , thus we can choose T_a ≥ 0.02) and solving Problem DOFC-SDS using Algorithm DOFC-SDS, it follows that the minimized feasible γ is γ* = 1.1726, and

Setting F₄ = I, then from in Remark 6.2.3. Therefore, by (6.37) we have

To show the effectiveness of the designed - DOF controller through simulation, let the exogenous disturbance input be ω(t) = exp ( − t)sin (t). Figure 6.3 gives the states of the closed-loop system, and Figure 6.4 depicts the states of the DOF controller.

6.3.1 System Description and Preliminaries

Consider a class of switched neutral delay systems of the form

(6.47a)

(6.47b)

(6.47c)

where x(t) ∈ Rⁿ is the system state vector, y(t) ∈ R^p is the measured output, and u(t) ∈ R^m is the control input. (denoted by α for simplicity) is the switching signal defined as the same in the previous section. h ≥ 0 is the constant neutral delay and d(t) denotes the time-varying delays satisfying 0 ≤ d(t) ≤ d and , where d and τ are two known constants. φ(t) is a differentiable vector-valued initial function on with .

For each possible value α = i , we denote the system matrices associated with mode i by A(i) = A(α), A_d(i) = A_d(α), A_h(i) = A_h(α), B(i) = B(α), C(i) = C(α), and C_d(i) = C_d(α), where A(i), A_d(i), A_h(i), B(i), C(i), and C_d(i) are constant matrices. Corresponding to the switching signal α, we have the switching sequence with t₀ = 0, which means that the i_kth subsystem is activated when t ∈ [t_k, t_{k + 1}).

Here, we are interested in designing a DOF controller of a general structure described by

(6.48a)

(6.48b)

where x_c(t) ∈ Rⁿ is the controller state vector; A_c(α), B_c(α), and C_c(α) are appropriately dimensioned constant matrices to be determined later.

Augmenting the model of (6.47a)–(6.47c) to include the states of the DOF controller in (6.48a)–(6.48b), we obtain the following closed-loop system:

(6.49a)

(6.49b)

where 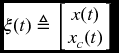, and

(6.50)

Associated with the closed-loop system (6.49a)–(6.49b) is the following cost function:

(6.51)

where U > 0 and W > 0 are given matrices.

We now introduce the following definitions before presenting our main results in this section.

Definition 6.3.2 The closed-loop system in (6.49a)–(6.49b) is said to be exponentially stable under α if its solution ξ(t) satisfies

where η ≥ 1 and λ > 0 are two real constants, and

Therefore, the problem to be addressed can be formulated as follows: for system (6.47a)–(6.47c), develop a procedure to design a DOF controller u(t) in the form of (6.48a)–(6.48b) such that the closed-loop system in (6.49a)–(6.49b) is exponentially stable and the specified linear integral-quadratic cost function in (6.51) has an upper bound.

6.3.2 Main Results

We will first present a sufficient condition for the existence of the DOF controller in (6.48a)–(6.48b), then give a parameterized representation of the controller in terms of the feasible solutions to a certain set of LMIs.

Theorem 6.3.3 Consider the closed-loop system in (6.49a)–(6.49b). For a given constant β > 0, suppose there exist matrices P(i) > 0, Q(i) > 0, and R(i) > 0 such that for ,

(6.52)

where

Then the closed-loop system in (6.49a)–(6.49b) is exponentially stable and the cost function (6.51) has the bound of

(6.53)

for any switching signal with average dwell time satisfying , where μ ≥ 1 satisfies

(6.54)

Moreover, an estimate of the state decay is given by

(6.55)

where

(6.56)

Proof. Choose a Lyapunov function of the following form:

(6.57)

where P(α) > 0, Q(α) > 0, and R(α) > 0 () are to be determined. Then, as with the solution of the closed-loop system in (6.49a)–(6.49b) for a fixed α, we have

Thus,

where 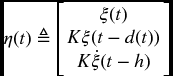and

with Π₁₁(α) defined in (6.52). It can be seen from (6.52) that Π(α) < 0, which implies

(6.58)

Now, for an arbitrary piecewise constant switching signal α, and for any t > 0, we let 0 = t₀ < t₁ < ⋅⋅⋅ < t_k < ⋅⋅⋅, k = 1, …, denote the switching points of α over the interval (0, t). As mentioned earlier, the i_kth subsystem is activated when t ∈ [t_k, t_{k + 1}). Integrating (6.58) from t_k to t gives

(6.59)

Using (6.54) and (6.57), at switching instant t_k, we have

(6.60)

Therefore, it follows from (6.59)–(6.60) and the fact ϑ = N_α(0, t) ≤ (t − 0)/T_a that

(6.61)

It can be shown from (6.57) that there exist scalars a > 0 and b > 0 such that the following holds:

(6.62)

where a and b are defined in (6.56). Combining (6.61) and (6.62) yields

which implies (6.55). By Definition 6.3.2 with t₀ = 0, the closed-loop system in (6.49a)–(6.49b) is exponentially stable.

However, it can be seen from (6.52) that

where Ψ(α) is as defined previously. The above inequality implies

Thus, we have

(6.63)

Moreover, by integrating both sides of (6.63) from 0 to ∞ and using the initial condition, we obtain

The desired result follows Definition 6.3.1, thus the proof is completed. ▀

Now, we present a solution to the guaranteed cost DOF control problem for the switched neutral delay system in (6.47a)–(6.47c).

Theorem 6.3.4 Consider the switched neutral delay system in (6.47a)–(6.47c). For a given constant β > 0, suppose there exist matrices , , , , , R(i) > 0, , , , , , , , and such that for ,

(6.64a)

(6.64b)

(6.64c)

(6.64d)

where

Then there exists a DOF controller in the form of (6.48a)–(6.48b), such that the closed-loop system in (6.49a)–(6.49b) is exponentially stable and the cost function (6.51) has the bound of

(6.65)

for any switching signal with average dwell time satisfying , where μ ≥ 1 satisfies

(6.66)

Moreover, if the above conditions are feasible, then a desired DOF controller realization is given by

(6.67)

Proof. By Theorem 6.3.3 and introducing a slack matrix F, it is not difficult to see that the conditions in Theorem 6.3.3 are satisfied if there exist matrices P(i) > 0, Q(i) > 0, R(i) > 0, and F such that the following LMI condition holds:

(6.68)

where

The above can be verified by performing a projection transformation on (6.68) by

and we can obtained (6.52).

In what follows, we will use (6.68), rather than (6.52), to solve the DOF control problem because there is no product term between the parameter-dependent Lyapunov matrix and the system dynamic matrix in (6.68), which is crucial to solving the present problem.

Notice that if the condition in (6.68) holds, then matrix F is nonsingular. Let the matrix F and its inverse matrix be partitioned respectively as

(6.69)

Without loss of generality, we assume that F₄ and G₄ are nonsingular – if not, F₄ and G₄ may be perturbed respectively by matrices ΔF₄ and ΔG₄ with sufficiently small norms such that F₄ + ΔF₄ and G₄ + ΔG₄ are nonsingular and satisfy (6.68).

Define the following matrices that are also nonsingular:

(6.70)

Noticing that , , and F₁G₁ + F₂G₄ = I, and performing a congruence transformation on (6.68) by , we obtain

(6.71)

where

Define the following matrices:

(6.72)

It can be easily seen from (6.72) that and . Also, we define

(6.73)

Thus, by considering (6.50), (6.69)–(6.70) and (6.72)–(6.73), we have

(6.74)

Substituting (6.74) into (6.71) implies (6.64a).

Moreover, considering (6.54) together with (6.72), gives (6.66), and considering (6.73) together with (6.72), yields (6.67). Finally, considering the zero initial condition of x_c(t), that is, x_c(0) = 0, we have

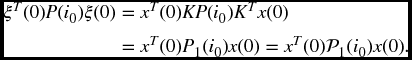
Therefore, replacing ξ^T(0)P(i₀)ξ(0) and Q(i₀) with and in (6.53) of Theorem 6.3.3, respectively, supplies (6.65). This completes the proof. ▀

The following theorem presents a method of selecting an optimal DOF controller minimizing the upper bound of the guaranteed cost (6.65).

Theorem 6.3.5 Consider the switched neutral delay system in (6.47a)–(6.47c) and cost function (6.51). For a given constant β > 0, suppose the following optimal problem:

(6.75)

subject to (6.64a)–(6.64d), (6.66) and

(6.76a)

(6.76b)

(6.76c)

has a feasible solution for , , , , , R(i) > 0, , , , , , , , , , (), and a scalar ϵ > 0, where

(6.77)

with E and F being given constant matrices with appropriate dimensions. Then, the corresponding DOF controller in the form of (6.48a)–(6.48b) with (6.67) is an optimal DOF controller with a guaranteed cost in the sense that the upper bound on the closed-loop cost function (6.65) is minimized under this controller.

Proof. The proof of this theorem is along the same lines as that of Theorem 6.3.4. By Schur complement, LMI (6.76a) is equivalent to . However, noting (6.77), we have

Moreover, it follows from (6.77) and that

Thus, according to (6.65), we have , and the minimization of implies the minimization of the guaranteed cost for the switched neutral delay system in (6.47a)–(6.47c). The optimality of the solution to the optimization problem (6.75) follows from the convexity of the objective function as well as the constraints. This completes the proof. ▀

Notice that the conditions in Theorem 6.3.5 are not all of LMI form because of (6.64d), hence they can not be solved directly using LMI procedures. Now, by using the CCL method again, we suggest the following minimization problem involving LMI conditions instead of the original nonconvex feasibility problem formulated in Theorem 6.3.5.

Problem DOFC-SNDS-GC (DOF control of switched neutral delay systems with a guaranteed cost):

(6.78)

The following algorithm is suggested to solve the Problem DOFC-SNDS-GC.

Algorithm DOFC-SNDS-GC

• Step 1. Find a feasible set 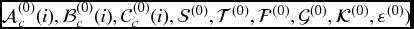satisfying (6.64a)–(6.64c), (6.66), (6.76a)–(6.76c), and (6.78). Set κ = 0.
• Step 2. Solve the following optimization problem:
  
  and denote f* as the optimized value.
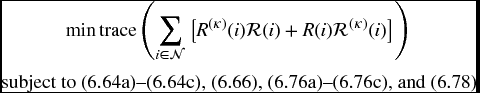
• Step 3. Substitute the obtained matrix variables into (6.71). If (6.71) is satisfied, with
  
  for a sufficiently small scalar δ > 0, then output the feasible solutions , so EXIT.
• Step 4. If where is the maximum number of iterations allowed, so EXIT.
• Step 5. Set κ = κ + 1, , and go to Step 2.

6.3.3 Illustrative Example

Example 6.3.6 Consider system (6.47a)–(6.47c) with N = 2 (that is, there are two subsystems) and the related parameters are given as follows:

with d(t) = 0.7 + 0.3sin (t) and β = 0.5. A straightforward calculation gives d = 1.0 and τ = 0.3. It can be checked that the system in (6.47a)–(6.47c) with u(t) = 0 and the above parameters is unstable for switching signal given in Figure 6.5 (which is generated randomly; here, ‘1’ and ‘2’ represent the first and second subsystems, respectively), and the states of open-loop system are shown in Figure 6.6 with the initial condition given by , θ ∈ [ − 1, 0]. In view of this, our aim is to design a DOF controller u(t) in the form of (6.48a)–(6.48b), such that the closed-loop system is exponentially stable and the specified linear integral-quadratic cost function in (6.51) has an upper bound.

Setting μ = 1.01 (thus ) and U = diag{0.1, 0.1, 0.1}, W = 0.5, i₀ = 1, we solve Problem DOFC-SNDS-GC by Algorithm DOFC-SNDS-GC, and obtain

Setting F₄ = I, we have by Remark 6.4. Therefore, it follows from (6.67) that

Consequently, the optimal guaranteed cost of the closed-loop system is . The states of the closed-loop system are given in Figure 6.7 and the DOF control input is shown in Figure 6.8.