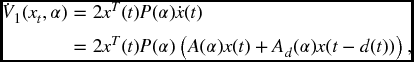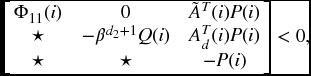5.2.1 System Description

Consider the continuous-time switched state-delayed hybrid systems described by

(5.1a)

(5.1b)

where x(t) ∈ Rⁿ is the state vector; u(t) ∈ R^m is the control input; φ(t) ∈ C_{n, d} is a differentiable vector-valued initial function on [ − d, 0] for a known constant d > 0; d(t) denotes the time-varying delay satisfying either (A1) 0 ≤ d(t) ≤ d ; and or (A2) 0 ≤ d(t) ≤ d.

In system (5.1a), is a family of matrices parameterized by an index set , and is a piecewise constant function of time t called a switching signal. At a given time t, the value of α(t), denoted by α for simplicity, might depend on t or x(t), or both, or may be generated by any other hybrid scheme. Therefore, the switched delayed hybrid system effectively switches among N subsystems with the switching sequence controlled by α. We assume that the value of α is unknown, but its instantaneous value is available in real time.

For each , we will denote the system matrices associated with mode i by A(i) = A(α), A_d(i) = A_d(α), and B(i) = B(α), where A(i), A_d(i), and B(i) are constant matrices. Corresponding to the switching signal α, we have the switching sequence with t₀ = 0, which means that the i_kth subsystem is activated when t ∈ [t_k, t_{k + 1}).

For the switching signal α, we revisit the average dwell time property from the following definition.

Definition 5.2.1 [129] For any T₂ > T₁ ≥ 0, let N_α(T₁, T₂) denote the number of switching of α over (T₁, T₂). If N_α(T₁, T₂) ≤ N₀ + (T₂ − T₁)/T_a holds for T_a > 0, N₀ ≥ 0, then T_a is called an average dwell time.

Assumption 5.1 The switching signal α(t) has an average dwell time.

Definition 5.2.2 The continuous-time switched state-delayed hybrid system in (5.1a)–(5.1b) with u(t) = 0 is said to be exponentially stable under α(t) if the solution x(t) of the system satisfies

for constants η ≥ 1 and λ > 0, and

Remark 5.1 By the average dwell time switching, we mean a class of switching signals such that the average time interval between consecutive switchings is at least T_a. Then, a basic problem for such systems is how to specify the minimal T_a and thereby get the admissible switching signals such that the system is stable and satisfies a prescribed performance if the system dynamics meets some conditions. As commonly used in the literature, we choose N₀ = 0 in Definition 5.2.1. ♦

5.2.2 Main Results

In this section, we will establish an exponential stability condition for system (5.1a)–(5.1b) with u(t) = 0 by applying the average dwell time approach and the piecewise Lyapunov function technique, and give the following result.

Theorem 5.2.3 For a given constant β > 0, suppose (A1) holds and there exist matrices P(i) > 0, Q(i) > 0, R(i) > 0, and X(i), Y(i) such that for ,

(5.2)

where

Then the switched system in (5.1a)–(5.1b) with u(t) = 0 is exponentially stable for any switching signal with average dwell time satisfying , where μ ≥ 1 and satisfies

(5.3)

Moreover, an estimate of the state decay is given by

(5.4)

where

(5.5)

Proof Choose a Lyapunov function of the following form:

with

(5.6)

where P(α) > 0, Q(α) > 0, and R(α) > 0 are to be determined. Then, as with the solution of (5.1a)–(5.1b) for a fixed α, we have

(5.7)

(5.8)

(5.9)

However, the Newton–Leibniz formula gives

Then, for any appropriately dimensioned matrices , we have

(5.10)

where . Considering (5.7)–(5.10), it follows that

(5.11)

where

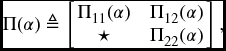
with

Notice that, in (5.11),

(5.12)

Performing a congruence transformation on (5.2) by diag{I, I, I, e^βdI} and considering , , by Schur complement, (5.2) implies

(5.13)

Thus, it follows from (5.11)–(5.13) that

(5.14)

Now, for an arbitrary piecewise constant switching signal α, and for any t > 0, we let 0 < t₁ < ⋅⋅⋅ < t_k < ⋅⋅⋅, k = 0, 1, …, denote the switching points of α over the interval (0, t). As mentioned earlier, the i_kth subsystem is activated when t ∈ [t_k, t_{k + 1}). Integrating (5.14) from t_k to t gives

(5.15)

Using (5.3) and (5.6), at switching instant t_k, we have

(5.16)

Therefore, it follows from (5.15)–(5.16) and the relationship ϑ = N_α(0, t) ≤ (t − 0)/T_a that

(5.17)

Notice from (5.6) that

(5.18)

where a and b are defined in (5.5). Combining (5.17)–(5.18) yields

which implies (5.4). By Definition 5.2.1 with t₀ = 0, system (5.1a)–(5.1b) is exponentially stable. This completes the proof. ▀

Remark 5.2 Notice that Theorem 5.2.3 gives a delay-dependent sufficient condition for the exponential stability of system (5.1a)–(5.1b) with u(t) = 0. In the derivation of the delay-dependent result in Theorem 5.2.3, no model transformation was performed to system (5.1a)–(5.1b). Moreover, we introduced slack variables and , which helps avoid using bounding techniques and hence the possible conservativenes. ♦

Remark 5.3 Notice that there exist constraints P(i) ≤ μP(j), Q(i) ≤ μQ(j), and R(i) ≤ μR(j), in (5.3) of Theorem 5.2.3. So μ( > 1) is only dependent upon (5.3), and it is independent of (5.2). In fact, μ can be found to have very many solutions, for example,

and any value larger than μ* can also be considered as a solution of μ. ♦

Remark 5.4 When μ = 1 in , we have T_a > T*_a = 0, which means that the switching signal α can be arbitrary. In this case, (5.3) turns out to be P(i) ≤ P(j), Q(i) ≤ Q(j), and R(i) ≤ R(j), . Thus the only possibility is P(i) = P(j) = P, Q(i) = Q(j) = Q, and R(i) = R(j) = R, , which implies that a common (that is, mode-independent) Lyapunov function is required for all subsystems. ♦

Remark 5.5 When μ > 1 and β → 0 in , we have T_a → ∞, that is, there is no switching. Switched system (5.1a)–(5.1b) is effectively operating at one of the subsystems all the time. In this case, according to the proof of Theorem 5.2.3, the asymptotic stability result of system (5.1a)–(5.1b) coincides with Theorem 1 in [243] when delay d(t) = d is constant. ♦

Remark 5.6 It should be pointed out that the methods used in this chapter for deriving the stability condition in Theorem 5.2.3 are different from that in [188], thus the obtained results are different. Since it introduced more slack matrices in Theorem 1 of [188], the condition becomes hard to apply to stabilization and controller synthesis problems. Our result in Theorem 5.2.3 overcomes the above difficulty, and this can be verified by the SMC problem presented in Chapter 7. ♦

The result in Theorem 5.2.3 is based on (A1), but when considering (A2), we have the following theorem. The result can be obtained by employing the same techniques used as in the proof of Theorem 5.2.3, thus we omit the proof.

Theorem 5.2.4 For a given constant β > 0, suppose (A2) holds and there exist matrices P(i) > 0, R(i) > 0, and X(i), Y(i) such that for ,

where

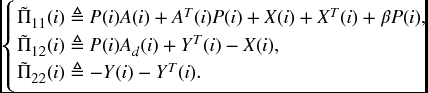
Then the switched system in (5.1a)–(5.1b) with u(t) = 0 is exponentially stable for any switching signal with average dwell time satisfying , where μ ≥ 1 and satisfies

Moreover, an estimate of state decay is given by

where

Remark 5.7 Comparing the results in Theorems 5.2.3 and 5.2.4, we found that the result in Theorem 5.2.4 requires a weaker condition on the time-varying delay when compared with Theorem 5.2.3. To obtain Theorem 5.2.4, a Lyapunov function is chosen as follows:

Notice that the derivative of the functional does not require bounding of the rate of delay d(t). In particular, the delay in Theorem 5.2.3 is required to be differentiable, but the one in Theorem 5.2.4 may be non-differentiable with arbitrarily fast time-varying behavior. ♦

5.2.3 Illustrative Example

Example 5.2.5 Consider the switched delay system in (5.1a)–(5.1b) with N = 2 and the following system parameters:

and d = 1.2, β = 0.5, τ = 0.3. It can be checked by using Theorem 1 of [243] that the above two subsystems are both asymptotically stable. We consider the average dwell time scheme, and set μ = 1.2 > 1, thus by (5.3). Solving LMIs (5.2)–(5.3), it follows that

which means that the above switched system is exponentially stable. Taking T_a = 1 > T*_a, and considering (5.4)–(5.5) yield a = 2.6702, b = 6.6340, η = 1.5762 and λ = 0.1588, thus

5.3.1 System Description

Consider a discrete-time switched system with time delays, which can be described by the following dynamical equations:

(5.19a)

(5.19b)

where x(k) ∈ Rⁿ is the system state vector; u(k) ∈ R^m represents the control input; φ(k) is the initial condition; is a family of matrices parameterized by an index set ; and is a piecewise constant function of time, called a switching signal, which takes its values in the finite set . At an arbitrary discrete time k, the value of α(k), denoted by α for simplicity, might depend on k or x(k), or both, or may be generated by any other hybrid scheme. We assume that the sequence of subsystems in switching signal α is unknown a priori, but its instantaneous value is available in real time. For the switching time sequence k₀ < k₁ < k₂ < ⋅⋅⋅ of switching signal α, the holding time between [k_l, k_{l + 1}] is called the dwell time of the currently engaged subsystem, where . The delay d(k) satisfies 1 ≤ d₁ ≤ d(k) ≤ d₂, where d₁ and d₂ are constant positive scalars representing the minimum and maximum delays, respectively.

Remark 5.8 For each possible value α = i, , we will denote the system matrices associated with mode i by A(i) = A(α), A_d(i) = A_d(α), and B(i) = B(α), where A(i), A_d(i), and B(i) are constant matrices. Corresponding to the switching signal α, we have the switching sequence with k₀ = 0, which means that the i_lth subsystem is activated when k ∈ [k_l, k_{l + 1}). ♦

For the switching signal α, we introduce the following definition.

Definition 5.3.1 For a switching signal and any k_i > k_j > k₀, let N_α(k_j, k_i) be the switching numbers of α_k over the interval [k_j, k_i]. If for any given N₀ > 0 and T_a > 0, we have N_α(k_j, k_i) ≤ N₀ + (k_i − k_j)/T_a, then T_a and N₀ are called average dwell time and the chatter bound, respectively.

Here, we assume N₀ = 0 for simplicity as commonly used in the literature.

Assumption 5.2 The switching signal α(k) has an average dwell time.

Design a stabilization controller with the following general structure:

(5.20)

where K(α) ∈ R^{m × n} are parameter matrices to be designed.

Substituting the stabilization controller in (5.20) into system (5.19a)–(5.19b), we obtain the closed-loop system as

(5.21a)

(5.21b)

where

Definition 5.3.2 The discrete-time switched time-delay hybrid system in (5.19a)–(5.19b) with u(k) = 0 is said to be exponentially stable under α if the solution x(k) satisfies

for constants η ≥ 1 and 0 < ρ < 1, and

where ξ(θ)≜x(θ + 1) − x(θ).

Remark 5.9 Notice that the phrase ‘under α’ appears in Definition 5.3.2. This serves to emphasize that all results obtained subsequently in this chapter are dependent on the switching signal α, and α is not an arbitrary switching signal but a restricted one having an average dwell time. ♦

5.3.2 Main Results

First, we will use the piecewise Lyapunov technique and the average dwell time approach to propose a sufficient condition for the exponential stability of the discrete-time switched time-delay system in (5.19a)–(5.19b) with u(k) = 0. We have the following theorem.

Theorem 5.3.3 Given a constant 0 < β < 1, suppose that there exist matrices P(i) > 0, Q(i) > 0, R(i) > 0, S₁(i) > 0, and S₂(i) > 0, and matrices L(i), M(i), and N(i) such that for ,

(5.22)

where

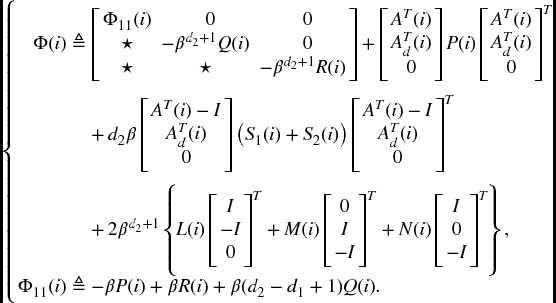
Then the discrete-time switched time-delay system in (5.19a)–(5.19b) with u(k) = 0 is exponentially stable for any switching signal with average dwell time satisfying , where μ ≥ 1 satisfies

(5.23)

Proof Choose a Lyapunov function of the following form:

(5.24)

where ξ(k)≜x(k + 1) − x(k), S(α)≜S₁(α) + S₂(α), and P(α) > 0, Q(α) > 0, R(α) > 0, S₁(α) > 0, and S₂(α) > 0 are real matrices. For k ∈ [k_l, k_{l + 1}), we define

thus with

(5.25)

(5.26)

(5.27)

(5.28)

(5.29)

Moreover, for and any appropriately dimensioned matrices L(α), M(α), and N(α), the following equations are true:

(5.30)

Considering (5.25)–(5.29) and (5.30), we have

where Φ(α) is defined in (5.22) and

Moreover, it can be seen from (5.22) that

Then we have

(5.31)

Now, for an arbitrary piecewise constant switching signal α_k, and for any k > 0, we let k₀ < k₁ < ⋅⋅⋅ < k_l < ⋅⋅⋅, l = 1, …, denote the switching points of α_k over the interval (0, k). As mentioned earlier, the i_lth subsystem is activated when k ∈ [k_l, k_{l + 1}). Therefore, for k ∈ [k_l, k_{l + 1}), it holds from (5.31) that

(5.32)

Using (5.23) and (5.24), at switching instant t_k, we have

(5.33)

Therefore, it follows from (5.32)–(5.33) and the relationship ϑ = N_α(0, k) ≤ (k − k₀)/T_a that

(5.34)

Note from (5.24) that there exist two positive constants a and b (a ≤ b) such that

(5.35)

Combining (5.34) and (5.35) yields

Furthermore, letting , it follows that

By Definition 5.3.2, we know that if 0 < ρ < 1, that is, , the discrete-time switched time-delay system in (5.19a)–(5.19b) with u(k) = 0 is exponentially stable, where function ceil(h) represents rounding real number h to the nearest integer greater than or equal to h. The proof is completed.

Remark 5.10 In Theorem 5.3.3, the parameter β plays a key role in controlling the lower bound of the average dwell time, which can be seen from . Specifically, if β is given a smaller value, the lower bound of the average dwell time becomes smaller with a fixed μ, which may result in the instability of the system. ♦

Remark 5.11 Note that when μ = 1 in we have T_a > T*_a = 0, which means that the switching signal α(k) can be arbitrary. In this case, (5.23) turns out to be P(i) = P(j) = P, Q(i) = Q(j) = P, R(i) = R(j) = P, S₁(i) = S₁(j) = S₁, S₂(i) = S₂(j) = S₂, , and the proposed approach becomes a quadratic one thus conservative. In this case, the system in (5.19a)–(5.19b) with u(k) = 0 turns out to be

(5.36a)

(5.36b)

and we have the following result for the system in (5.36a)–(5.36b). ♦

Corollary 5.3.4 The discrete-time time-delay system in (5.36a)–(5.36b) is asymptotically stable if there exist matrices P > 0, Q > 0, R > 0, S₁ > 0, and S₂ > 0, and matrices L, M, and N such that

where

Proof To prove the above result, we choose the following Lyapunov function:

where ξ(k)≜x(k + 1) − x(k), and P > 0, Q > 0, R > 0, S₁ > 0, and S₂ > 0 are real matrices to be determined. The remaining processes can be followed along the same lines as for the proof of Theorem 5.3.3, and we omit the details.

Notice that there exist two product terms between the Lyapunov matrices (i.e. P(i) and S₁(i) + S₂(i)) and the system matrices A(i) in the condition of Theorem 5.3.3, which will cause some problems with the solution of the stabilization control synthesis problem. In the following, a subsequent result is given in order to facilitate the control design procedure.

Corollary 5.3.5 Given a constant 0 < β < 1, suppose that there exist matrices P(i) > 0 and Q(i) > 0 such that for ,

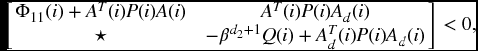
where

Then the discrete-time switched time-delay system in (5.19a)–(5.19b) with u(k) = 0 is exponentially stable for any switching signal with average dwell time satisfying , where μ ≥ 1 satisfies

Now, based on the above corollary, we consider the stabilization problem for system (5.19a)–(5.19b).

Theorem 5.3.6 Given a constant 0 < β < 1, the system in (5.19a)–(5.19b) is stabilizable, that is, the closed-loop system in (5.21a)–(5.21b) is exponentially stable under the control input u(k) in (5.20), if there exist matrices , , and such that for ,

(5.37)

where

Then the discrete-time switched time-delay system in (5.19a)–(5.19b) is exponentially stabilizable for any switching signal with average dwell time satisfying , where μ ≥ 1 satisfies

(5.38)

In this case, a stabilizing state feedback controller can be chosen by

(5.39)

Proof By Schur complement, it can be seen from Corollary 5.3.5 that the closed-loop system in (5.21a)–(5.21b) is exponentially stable if there matrices P(i) > 0 and Q(i) > 0 such that for ,

(5.40)

where the switching signal has an average dwell time satisfying , where μ ≥ 1 satisfies

Performing a congruence transformation on (5.40) by (where ) and letting , we have

where is defined in (5.37). Moreover, we define , we have (5.37), and we know that . The proof is completed.▀

5.3.3 Illustrative Example

Example 5.3.8 (Stability analysis) Consider the system in (5.19a)–(5.19b) with N = 2, and its parameters are given as follows:

and d₁ = 1, d₂ = 2, β = 0.8. We consider the average dwell time approach proposed in this chapter, and set μ = 1.5 > 1, thus . Solving LMI (5.22) with (5.23), we can obtain a feasible solution of (P(1), P(2), Q(1), Q(2), R(1), R(2), S₁(1), S₁(2), . .S₂(1), S₂(2), L(1), L(2), M(1), M(2), N(1), N(2)). Therefore, we can conclude that the above discrete-time switched system is exponentially stable.

In addition, for d₁ = 1, μ = 1.5, and τ = 0.6, considering different β, the upper bound of d₂ for different cases are listed in Table 5.1.

5.3.8 Example (Stabilization problem) Consider the system in (5.19a)–(5.19b) with N = 2, and the system parameters are given as follows:

with d(k) = 2.5 + ( − 1)^k/2 (thus d₁ = 1, d₂ = 3), and suppose that μ = 1.5, β = 0.9, and .

The switching signal is given in Figure 5.1 (which is generated randomly; here, ‘1’ and ‘2’ represent the first and second subsystems, respectively). The state trajectories of the open-loop system are shown in Figure 5.2, from which we can see that the open-loop system is not stable. In this situation, we will design a state feedback stabilization controller such that the closed-loop system is stable. To this end, by solving the LMI conditions in Theorem 5.3.6, we obtain

The state trajectories of the closed-loop system are shown in Figure 5.3.

β	0.5	0.6	0.7	0.8	0.9
	1.3344	1.7345	2.2247	2.9278	4.1299