Chapter 10

Letting Operational Amplifiers Do the Tough Math Fast

In This Chapter

Performing hand calculations electronically with operational amplifiers

Modeling secrets of operational amplifiers with dependent sources

Taking a look at op-amp circuits

Putting together some systems

The operational amplifier (op amp) is a powerful tool when you’re working with active devices in modern-day circuit applications. Because op amps can do calculations electronically, they perform mathematical operations (like addition, subtraction, multiplication, division, integration, and derivatives) fast. You can put together basic op-amp circuits to build accurate mathematical models that predict complex and real-world behavior — like when the breakfast pastry in your toaster will turn into a flaming torch.

This chapter introduces op-amp circuits, demonstrates how to use them to perform certain mathematical operations, and gives you a peek at the more complex processing actions that op amps serve as the building blocks for.

The Ins and Outs of Op-Amp Circuits

Commercial op amps first entered the market as integrated circuits in the mid-1960s, and by the early 1970s, they dominated the active device market in analog circuits. The op amp itself consists of a complex arrangement of transistors, diodes, resistors, and capacitors put together and built on a tiny silicon chip called an integrated circuit.

You can model the op amp with simple equations with little concern for what’s going on inside the chip. You just need some basic knowledge of the constraints on the voltages and currents at the external terminals of the device.

In the following sections, you discover typical diagrams of op-amp circuits, the characteristics of ideal op amps and op amps with dependent sources, and the two equations necessary for analyzing these special circuits.

Discovering how to draw op amps

Unlike capacitors, inductors, and resistors, op amps require power to work. Op amps have the following five key terminals (see their symbols in Figure 10-1):

The positive terminal, called the noninverting input vP

The negative terminal, called the inverting input vN

The output terminal, resulting from the voltage applied between noninverting and inverting inputs: vO = A(vP – vN)

Positive and negative power supply terminals, usually labeled as +VCC and –VCC and required for the op amp to operate correctly

Illustration by Wiley, Composition Services Graphics

Figure 10-1: The circuit symbol of the op amp and its five terminals.

Although many op amps have more than five terminals, those terminals aren’t normally shown symbolically. Also, to reduce the clutter when you’re investigating an op-amp circuit, the power supplies aren’t usually shown, either.

When the power supplies aren’t shown in a diagram of an op-amp circuit, don’t forget that the power supplies provide upper and lower limits of the output voltage, restricting its voltage range. Barring otherworldly powers, you can’t get more power output than you supply.

Looking at the ideal op amp and its transfer characteristics

You can model the op amp with a dependent source if you need accurate results, but the ideal op amp is good enough for most applications.

The op amp amplifies the difference between the two inputs, vP and vN, by a gain A to give you a voltage output vO:

The voltage gain A for an op amp is very large — greater than 105.

When the output voltage exceeds the supplied power, the op-amp saturates. This means that the output is clipped or maxed out at the supplied voltages and can increase no further. When this happens, the op-amp behavior is no longer linear but operates in the nonlinear region.

You can see this idea in Figure 10-2. The left diagram shows the transfer characteristic, whereas the right diagram shows the ideal transfer characteristic of an op amp with an infinite gain. The graph shows three modes of operation for the op amp. You have positive and negative saturated regions, showing the nonlinear and linear regions. If you want to make signals bigger, you need to operate in the linear region. You can describe the three regions mathematically as follows

To perform math functions (such as addition and subtraction), the op amp must work in linear mode. All op-amp circuits given in this chapter operate in the linear active region.

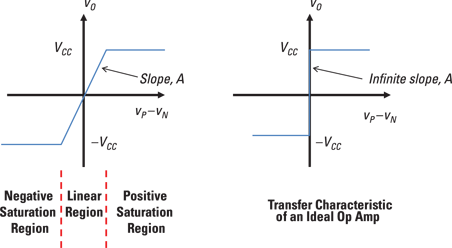
Illustration by Wiley, Composition Services Graphics

Figure 10-2: Practical and ideal op-amp properties and a linear dependent source model.

Modeling an op amp with a dependent source

If you need accurate results, you can model the op amp with a voltage-controlled dependent source, like the one in Figure 10-3. This model consists of a large gain A, a large input resistance RI, and a small output resistance RO. The table in Figure 10-3 shows ideal and typical values of these op-amp properties.

High amplification (or gain) makes the analysis simpler, allowing you not to worry about what’s going on inside the op amp. As long as the op amp has high gain, the op-amp math circuits will work. High-input resistance draws little current from the input source circuit, increasing battery life for portable applications. Low- or no-output resistance delivers maximum voltage to the output load.

Illustration by Wiley, Composition Services Graphics

Figure 10-3: Dependent source model of an op amp.

The dependent voltage-controlled current source is shown in Figure 10-3. The output is restricted between the positive and negative voltages when the op amp is operating in the linear region.

Examining the essential equations for analyzing ideal op-amp circuits

The ideal properties of an op amp produce two important equations:

These equations make analyzing op amps a snap and provide you with valuable insight into circuit behavior. Why? Because feedback from the output terminals to one or both inputs ensures that vP and vN are equal.

To get the first constraint, consider that the linear region of an op amp is governed by when the output is restricted by the supply voltages as follows:

You can rearrange the equation to limit the input to vP – vN:

For an ideal op amp, the gain A is infinity, so the inequality becomes

Therefore, the ideal op amp (with infinite gain) must have this constraint:

An op amp with infinite gain will always have the noninverting and inverting voltages equal. This equation becomes useful when you analyze a number of op-amp circuits, such as the op-amp noninverter, inverter, summer, and subtractor.

The other important op amp equation takes a look at the input resistance RI. An ideal op amp has infinite resistance. This implies that no input currents can enter the op amp:

The equation says that the op-amp input terminals act as open circuits.

You need to connect the output terminal to the inverting terminal to provide negative feedback in order to make the op amp work. If you connect the output to the positive side, you’re providing positive feedback, which isn’t good for linear operation. With positive feedback, the op amp would either saturate or cause its output to undergo oscillations.

Looking at Op-Amp Circuits

The mathematical uses for signal processing include noninverting and inverting amplification, addition, and subtraction. Doing these math operations simply requires resistors and op amps. (As a gentle reminder to some students who are troubleshooting their circuits, you also need power.) In the following sections, you analyze several op-amp configurations using the op-amp equations: vP = vN and iP = iN = 0.

Analyzing a noninverting op amp

One of the most important signal-processing applications of op amps is to make weak signals louder and bigger. The following example shows how the feedback affects the input-output behavior of an op-amp circuit. Consider Figure 10-4, which first shows the input connected to the noninverting input. You have a feedback path from the output circuit leading to the inverting input.

The voltage source vS connects to the noninverting input vP:

You gotta first find the voltage at the inverting input so you can figure out how the input and output voltages are related. Apply Kirchhoff’s current law (KCL) at Node A between resistors R1 and R2. (Remember that KCL says the sum of incoming currents is equal to the outgoing currents.) Applying KCL gives you

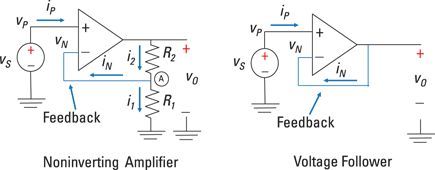
Illustration by Wiley, Composition Services Graphics

Figure 10-4: Noninvert-ing amplifier op amp and voltage follower.

At the output side of the op amp, the inverting current iN is equal to zero because you have infinite resistance at the inverting input. This means that all the current going through resistor R2 must go through resistor R1. If the current is the same, R1 and R2 must be connected in series, giving you

Because resistors R1 and R2 are connected in series, you can use voltage division (see Chapter 4 for details). Voltage division gives you the voltage relationship between the inverting input vN and output vO:

The inverting input vN and noninverting input vP are equal for ideal op amps. So here’s the link between the input source voltage vS and output voltage vO:

You now have the ratio of the voltage output to the input source:

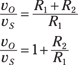
You just made the input voltage vS larger by making sure the ratio of the two resistors is greater than 1. You read right: To make the input signal louder, the feedback resistor R2 should have a larger value than input resistor R1. Piece of cake! For example, if R2 = 9 kΩ and R1 = 1 kΩ, then you have the following output voltage:

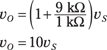
You’ve amplified the input voltage by ten. Awesome!

Following the leader with the voltage follower

A special case of the noninverting amplifier is the voltage follower, in which the output voltage follows in lock step with whatever the input signal is. In the voltage follower (pictured in Figure 10-4), vS is connected to the noninverting terminal. You can express this idea as

You also see that the output vO is connected to the inverting terminal, so

An ideal op amp has equal noninverting and inverting voltage. This means that the preceding two equations are equal. In other words

You can also view the voltage follower as a special case of the noninverting amplifier with a gain of 1, because the feedback resistor R2 is zero (a short circuit) and resistor R1 is infinite (open circuit):

The output voltage vO is equal to the input source voltage vS. The voltage gain is 1 where the output voltage follows the input voltage. But a piece of wire gives a gain of 1, too, so what good is this circuit? Well, the voltage follower provides a way to put together two separate circuits without having them affect each other. When they do affect each other in a bad way, that’s called loading. A voltage follower solves the loading problem.

Turning things around with the inverting amplifier

An inverting amplifier takes an input signal and turns it upside down at the op-amp output. When the value of the input signal is positive, the output of the inverting amplifier is negative, and vice versa.

Figure 10-5 shows an inverting op amp. The op amp has a feedback resistor R2 and an input resistor R1 with one end connected to the voltage source. The other end of the input resistor is connected to the inverting terminal, and the noninverting terminal is grounded at 0 volts. The amount of amplification depends on the ratio between the feedback and input resistor values.

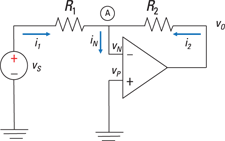
Illustration by Wiley, Composition Services Graphics

Figure 10-5: A standard inverting amplifier.

Because the noninverting input is grounded to 0 volts, you have

For ideal op amps, the voltages at the inverting and noninverting terminals are equal and set to zero. The inverting terminal is connected to a virtual ground because it’s indirectly connected to ground by vP.

Apply Kirchhoff’s current law (KCL) to Node A to get the following:

Simplify the equation with the following constraints for an ideal op amp:

The constraints make the KCL equation simpler:

You wind up with the following relationship between the input and output voltages:

Again, the amplification of the signal depends on the ratio of the feedback resistor R2 and input resistor R1. You need only external components of the op amp to make the signal way bigger. The negative sign means the output voltage is an amplified but inverted (or upside down) version of the input signal.

For a numerical example, let R2 = 10 kΩ and R1 = 1 kΩ. In that case, the inverted output voltage vO is ten times as big as the input voltage vS. In nothing flat, you just made a weak signal stronger. Nice work — you deserve a raise!

Resistors should be around the 1 kΩ to 100 kΩ range to minimize the effects of variation in the op-amp characteristics and voltage sources.

Adding it all up with the summer

You can extend the inverting amplifier to more than one input to form a summer, or summing amplifier. Figure 10-6 shows an inverting op amp with two inputs. The two inputs connected at Node A (called a summing point) are connected to an inverting terminal.

Because the noninverting input is grounded, Node A is also connected as a virtual ground. Applying the KCL equation at Node A, you wind up with

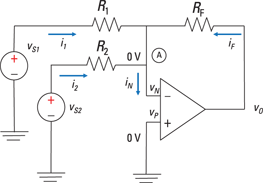
Illustration by Wiley, Composition Services Graphics

Figure 10-6: An inverting op-amp summer.

Replace the input currents in the KCL equation with node voltages and Ohm’s law (i = v/R):

Because iN = 0 for an ideal op amp, you can solve for the output voltage in terms of the input source voltages:

The output voltage is a weighted sum of the two input voltages. The ratios of the feedback resistance to the input resistances determine the gains, G1 and G2, for this op-amp configuration.

To form a summing amplifier (or inverting summer), you need to set the input resistors equal with the following constraint:

Applying this constraint gives you the output voltage:

This shows that the output is proportional to the sum of the two inputs. You can easily extend the summer to more than two inputs.

Plug in the following values for Figure 10-6 to test this mumbo jumbo: vS1 = 0.7 volts, v2 = 0.3 volts, R1 = 7 kΩ, R2 = 3 kΩ, and RF = 21 kΩ. Then calculate the output voltage vo:

The signals are bigger — mission accomplished. If signals are changing in time, the summer adds these signals instantly with no problem.

What’s the difference? Using the op-amp subtractor

You can view the next op-amp circuit — which is a differential amplifier, or subtractor — as a combination of a noninverting amplifier and inverting amplifier (see the earlier related sections for the scoop on these amplifiers). Figure 10-7 shows an op-amp subtractor.

Illustration by Wiley, Composition Services Graphics

Figure 10-7: An op-amp subtractor.

You use superposition to determine the input and the output relationship. As I explain in Chapter 7, the superposition technique involves the following steps:

1. Turn on one source and turn off the others.

2. Determine the output of the source that’s on.

3. Repeat for each input, taking the sources one at a time.

4. Algebraically add up all the output contributions for each input to get the total output.

For Figure 10-7, first turn off voltage source vS2 so that there’s no input at the noninverting terminal (vP = 0). With the noninverting input grounded, the circuit acts like an inverting amplifier. You wind up with output contribution vO1 due to vS1:

You next turn off voltage source vS1 (vN = 0) and turn vS2 back on. The circuit now acts like a noninverting amplifier. Because this is an ideal op amp, no current (iP = 0) is drawn from the series connection of resistors R3 and R4, so you can use the voltage divider equation to determine vP. The voltage at the noninverting input is given by

The noninverting input vP is amplified to give you an output vO2:

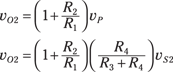
You then add up the outputs vO1 and vO2 to get the total output voltage:

Here, –G1 is the inverting gain and G2 is the noninverting gain. You need the following constraint to form a subtractor:

Applying the constraint simplifies the output voltage, giving you

There you have it! You now have the output proportional to the difference between the two inputs.

Increasing the Complexity of What You Can Do with Op Amps

If you’ve already read the earlier section “Looking at Op-Amp Circuits,” then you have the basic building blocks of op-amp circuits and are ready to tackle the complex processing actions I describe next.

Analyzing the instrumentation amplifier

The instrumentation amplifier is a differential amplifier suited for measurement and test equipment. Figure 10-8 shows the input stage of an instrumentation amplifier. Your goal is to find the voltage output vO proportional to the difference of the two inputs, v1 and v2. Getting the desired output requires some algebraic gymnastics, but you can handle it.

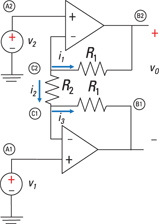
Illustration by Wiley, Composition Services Graphics

Figure 10-8: Input stage of an instrumentation amplifier.

At Node C2, you apply KCL (i1 + i2 = 0) and Ohm’s law (i = v/R) and wind up with

At Node C1, the KCL equation (–i2 + i3 = 0) with Ohm’s law leads you to

Figure 10-8 shows the noninverting input connected to independent voltages v1 and v2. Use the op-amp voltage constraint vP = vN to get the following:

Substitute v1 and v2 into KCL equations, which gives you

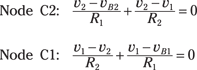
Now solve for vB2 and vB1, because the output voltage vO depends on these two values:

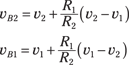
The output voltage vO is the difference between the vB1 and vB2:

Cool! Resistor R2 can be used to amplify the difference v2 – v1. After all, it’s easier to change the value of one resistor R2 than of two resistors R1.

Implementing mathematical equations electronically

As an example of how op amps can solve equations, consider a single output and three voltage input signals:

You can rewrite the equation in many ways to determine which op-amp circuits you need to perform the math. Here’s one way:

The equation suggests that you have an inverting summer with three inputs: –v1, –v2, and v3. You need an inverting amplifier with a gain of –1 for v1 and v2. Input v1 has a summing gain of –10, input v2 has a summing gain of –5, and input v3 has a summing gain of –4. You can see one of many possible op-amp circuits in the top diagram of Figure 10-9. The dashed boxes indicate the two inverting amplifiers and the inverting summer.

The outputs of the two inverting amplifiers are –v1 and –v2, and they’re inputs to the inverting summer. The third input to the summer is v3. Adding up the three inputs with required gains entails an inverting summer, which you see in Figure 10-9.

For input v1, the ratio of the inverting summer’s feedback resistor of 200 kΩ to its input resistor of 20 kΩ provides a gain of –10. Similarly, for input v2, the ratio of the feedback resistor of 200 kΩ to its input resistor of 40 kΩ gives you a gain of –5. Finally, for input v3, the ratio of the feedback resistor of 200 kΩ to its input resistor of 50 kΩ provides a gain of –4. You can use other possible resistor values as long as the ratio of resistors provides the correct gains for each input.

Reducing the number of op amps during the design process helps lower costs. And with some creativity, you can reduce the number of op amps in the circuit by rewriting the math equation of the input-output relationship:

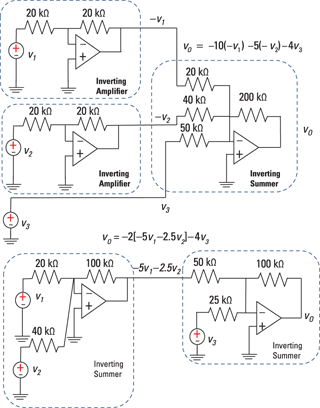
Illustration by Wiley, Composition Services Graphics

Figure 10-9: Doing calculations with op amps.

This suggests you need two op amps. One input is a combination of inputs v1 and v2 formed by an inverting summer. When you take the output of the first summer and feed it and another input to a second inverting summer, the result is proportional to v3 with gain –4. The bottom diagram of Figure 10-9 shows one way to implement this equation.

For v1, the ratio of the feedback resistor of 100 kΩ to the input resistor of 20 kΩ produces a gain of –5. For v2, the input resistor of 40 kΩ gives you a gain of –2.5. The output of the first summer is then multiplied by –2 because of the ratio of the second inverting summer’s feedback resistor of 100 kΩ to the input resistor of 50 kΩ. The input v3 to the second summer is multiplied by –4 because of the ratio between the 100-kΩ feedback resistor to the 25-kΩ resistor.

Creating systems with op amps

Op-amp circuits are basic building blocks for many applications in signal processing, instrumentation, process control, filtering, digital-to-analog conversion, and analog-to-digital conversion.

For example, you can do a digital-to-analog conversion (DAC) using the inverting summer. The primary purpose of this common device is to convert a digital signal consisting of binary 1s and 0s (perhaps coming from your personal computer) to an analog and continuous signal (to run your DC motor in your remote-control toy). The device has extensive applications in robotics, high-definition televisions, and cellphones.

To simplify the example, I focus on 3-bit devices (even though most applications use 8- to 24-bit DACs). DACs have one output voltage vo with a number of digital inputs (b0, b1, b2), along with a reference voltage VREF. You see a block diagram of a 3-bit input in Figure 10-10.

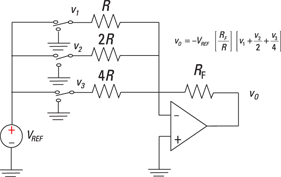
Illustration by Wiley, Composition Services Graphics

Figure 10-10: A digital-to-analog converter.

The following equation gives you the relationship between the digital input and analog output:

Bit b2 is the most significant bit (MSB) because it’s weighted with the largest weight in the sum; bit b0 is the least significant bit (LSB) because it has the smallest weight.

To implement a DAC, you can use an inverting summer, as in Figure 10-10. Also shown are the digital inputs that can have only one of two voltage values: A digital 1 is equal to VREF, and a digital 0 is equal to 0 volts. The inputs v1, v2, and v3 to the summer are weighted appropriately to give you the voltage output vO based on the three inputs. Input v1 has the most weight, and input v3 has the least. That’s my two bits on making DACs.