Chapter 4

Simplifying Circuit Analysis with Source Transformation and Division Techniques

In This Chapter

Recognizing equivalent circuits

Transforming circuits into equivalent series and parallel circuits

Analyzing circuits with voltage and current divider techniques

Using Kirchhoff’s laws and Ohm’s laws (see Chapter 3) can get pretty laborious when you’re analyzing complex circuits. Fortunately, you can make analyzing circuits easier by replacing part of the circuit with a simpler but equivalent circuit.

Through a makeover or transformation technique, you modify a complex circuit so that in the transformed circuit, the devices are all connected in series or in parallel. After the transformation, you no longer need to systematically apply Kirchhoff’s laws, because you can use shortcuts: the current divider technique and the voltage divider technique.

In this chapter, I explain how to make the transformation and apply both types of divider techniques. Rest assured that the info in this chapter can make your life a little easier when you start analyzing more-complex circuits.

Equivalent Circuits: Preparing for the Transformation

When you’re analyzing a complex circuit, you can simplify the math by replacing part of the circuit with a simpler, equivalent circuit. Two circuits are said to be equivalent if they have the same i-v characteristics at a pair of terminal connections. (You can find information about the i-v characteristics of various electrical devices in Chapter 2.)

You find the i-v characteristic for each circuit by using Kirchhoff’s laws and Ohm’s law, which give you the equations that relate the current i and voltage v across two terminals (see Chapter 3 for details). Then you compare the i-v relationships associated with the pair of terminals to find out in which conditions the circuits are equivalent. Even better, after you understand how to do source transformations, you no longer need to rely completely on Kirchhoff’s and Ohm’s laws to complete your analysis.

Take a look at the practical models of independent voltage and current sources in Figure 4-1. Circuit A depicts an ideal voltage source connected in series with a resistor, and Circuit B depicts an ideal current source connected in parallel with a resistor. In the following example, I show you that these two circuits are considered equivalent because they have the same i-v characteristics at the terminal pair A and B.

Illustration by Wiley, Composition Services Graphics

Figure 4-1: Models of equivalent circuits with voltage and current sources.

To find the i-v characteristic of Circuit A, you have to develop the relationship between the current i and voltage v for Terminals A and B. You do this by using Kirchhoff’s and Ohm’s laws.

Kirchhoff’s voltage law (KVL) says that the sum of the voltage drops and rises around a loop is zero. In other words, the voltage source has to equal the voltage drops across the resistors. Therefore, using KVL for Circuit A produces

Using Ohm’s law for resistor R1 gives you the following voltage:

Substituting the value of vR into yields

One way to get the i-v characteristic for Circuit A is to solve for v, which yields the following:

The resulting equation relates the voltage v and the current i at Terminals A and B in Circuit A of Figure 4-1. If you know the current and voltage from the input voltage source, you can find the voltage output.

An alternate form of the i-v characteristic requires manipulating

by solving for current i to obtain . When you do this, knowing the

voltage input provides you with the current output at Terminals A and B.

Look at Circuit B in Figure 4-1 to find a similar i-v relationship at Terminals A and B. You use Kirchhoff’s current law (KCL), which states that the sum of the incoming currents is equal to the sum of the outgoing currents at any node or terminal — here, at Terminal A or Terminal B. KCL yields

Using Ohm’s law for R2 gives you the following:

When you substitute the value of iR into , you get

Solving for v gives you the following i-v characteristic:

This equation relates the voltage v and the current i at Terminals A and B for Circuit B.

Now you can compare the result for Circuit B, , with the result for Circuit A, , to find the conditions for equivalent circuits. One way of doing so is to equate v between the two circuits. For this example, this approach gives you:

If you rearrange these equations to group the independent sources and collect like terms for the current i, you wind up with the following conditions:

The first expression in parentheses deals with the independent sources, and the second collects like terms with current i. For this equation to be equal to zero, you set the terms in parentheses equal to zero, which gives you the following two equations:

Because R1 and R2 are equal to each other, removing their subscripts yields a general resistor value of R for the two circuits. These are the conditions in which the two circuits are said to be equivalent.

Transforming Sources in Circuits

Each device in a series circuit has the same current, and each device in a parallel circuit has the same voltage. Therefore, finding the current in each device in a circuit is easier when the devices are all connected in parallel, and finding the voltage is easier when they’re all connected in series. Through a circuit transformation, or makeover, you can treat a complex circuit as though all its devices were arranged the same way — in parallel or in series — by appropriately changing the independent source to either a current or voltage source.

Changing the practical voltage source to an equivalent current source (or vice versa) requires the following conditions (see the preceding section to find out why these conditions characterize equivalent circuits):

The resistors must be equal in both circuits.

The source transformation must be constrained by .

The constraining equation, , looks like Ohm’s law, which should help you remember what to do when transforming between independent voltage and current sources.

In this section, I show you how to transform a circuit.

Converting to a parallel circuit with a current source

Transformation techniques let you convert a practical voltage source with a resistor connected in series to a current source with a resistor connected in parallel. Therefore, you can convert a relatively complex circuit to an equivalent circuit if all the devices in the external circuit are connected in parallel. You can then find the current of individual devices by applying the current divider techniques that I discuss later in “Cutting to the Chase Using the Current Divider Technique.”

When switching from a voltage source to a current source, the resistors have to be equal in both circuits, and the source transformation must be constrained by . Solving the constraint equation for is allows you to algebraically convert the practical voltage source into a current source:

Figure 4-2 illustrates the conversion of a voltage source, in Circuit A, into an equivalent current source, in Circuit B. The resistors, R, are equal, and the constraint equation was applied to change the voltage source into a current source.

Illustration by Wiley, Composition Services Graphics

Figure 4-2: Transforming a voltage source into a current source.

Figure 4-3 shows the conversion with some numbers plugged in. Both circuits contain the same 3-kΩ resistor, and the source voltage in Circuit A is 15 volts. With this information, you can find the source current, is, for the transformed Circuit B.

Illustration by Wiley, Composition Services Graphics

Figure 4-3: A numerical example of transforming a voltage source into a current source.

Use the constraint equation to find the source current in Circuit B. Here’s what you get when you plug in the numbers:

Changing to a series circuit with a voltage source

You can convert a current source connected in parallel with a resistor to a voltage source connected in series with a resistor. You use this technique to form an equivalent circuit when the external circuit has devices connected in series.

Converting a practical current source connected with a resistor in parallel to a voltage source connected with a resistor in series follows the conditions for equivalent circuits:

The resistors must be equal in both circuits.

The source transformation must be constrained by .

Figure 4-4 illustrates how to convert a current source into a voltage source.

Illustration by Wiley, Composition Services Graphics

Figure 4-4: Transforming a current source into a voltage source.

Figure 4-5 depicts the same transformation of a current source to a voltage source with some numbers plugged in. Both circuits contain the same 3-kΩ resistor, and the current source in Circuit A is 5 mA.

Illustration by Wiley, Composition Services Graphics

Figure 4-5: Numerical example of transforming a current source into a voltage source.

You can use the constraint equation to find the source voltage for Circuit B. Plugging in the numbers produces the following:

Suppose you have a complex circuit that has a current source, a resistor connected in parallel, and an external circuit with multiple resistors connected in series. You can transform the circuit so that it has a voltage source connected with all the resistors in series.

Consider Circuit A in Figure 4-6, where the right side of Terminals A and B consists of two resistors connected in series. On the left side of Terminals A and B is a practical current source modeled as an ideal current source in parallel with a resistor.

You want all the devices to be connected in series, so you need to move R when you transform the circuit. To transform the circuit, change the current source to a voltage source and move R so that it’s connected in series rather than in parallel. When you use the constraint equation vs = isR to find the source voltage, remember that R is the resistor you moved.

Circuit B is a series circuit where all the devices share the same current. You can find the voltage through R, R1, and R2 using voltage divider techniques, which I discuss in the next section.

Illustration by Wiley, Composition Services Graphics

Figure 4-6: Transforming a complex circuit into a series circuit.

Divvying It Up with the Voltage Divider

The voltage divider technique allows you to calculate the voltage for each device connected in series with an input voltage source. In the preceding section, I show you how to transform a circuit to a series circuit with a voltage source. This section shows you how to formulate the voltage divider equation. Then you see the voltage divider equation at work.

If a circuit problem with a current source asks you to find the voltage for a particular device, you may find it easier to convert the circuit to a series circuit first. Then you can find voltage using the voltage divider technique.

Getting a voltage divider equation for a series circuit

You use the voltage divider when the device in the circuit is connected in series and is driven by a voltage source. The input voltage source is divided proportionally according to the resistor values.

To get the voltage divider equation, you start with the fact that for a series circuit, the same current flows through each resistor. With this current, you use Kirchhoff’s voltage law (KVL) and Ohm’s law to obtain the voltage across a particular resistor. You can solve for (or eliminate) the current in the expression. In the resulting equation, the desired voltage across the resistor is proportional to the input source voltage. Because the voltage source is multiplied by a ratio of resistors having a value of less than 1, the desired output and device voltage are always less than the input source voltage.

Look at Circuit B of Figure 4-6, which has a voltage source and three resistors connected in series. You want to calculate the voltage across the resistors.

KVL says that the sum of the voltage rises and drops around a loop is equal to zero. So applying KVL to Circuit B produces the following:

Because the circuit is connected in series, the same current i flows through each of the resistors. Using Ohm’s law for each resistor yields

Substituting vR, v1, and v2 into and factoring out the current i gives you

When you divide the voltage across Resistor 1, which is , by , you get one form of the desired voltage divider equation:

This form of the voltage divider is often referred as a voltage transfer function, which relates the output voltage (voltage v1 for this example) to the input voltage source (which is vs in this case). You can find the output voltage if you know the input voltage source.

Solving for v1 yields the following voltage divider equation:

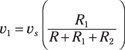
You can find similar voltage divider relationships for v2 and vR:

These divider equations show that to find the voltage across a particular resistor, you simply multiply the input source voltage by the desired resistor and divide by the total resistance of the series circuit. That is, the voltage of each device of Figure 4-6 depends on the ratio of resistors multiplied by the source voltage.

The voltage across each resistor is always less than and proportional to the supplied independent source voltage because the ratio of resistors is always less than 1. This idea offers a handy check of your calculations. The largest voltage goes across the largest resistor, and the lowest voltage goes across the smallest resistor.

Figuring out voltages for a series circuit with two or more resistors

Voltage divider techniques work well for a series circuit that has two or more resistors. You calculate the output voltage by multiplying the input source voltage by the desired resistor and dividing by the total resistance in the circuit.

I use Figure 4-7 to illustrate the voltage divider technique numerically. The given Circuit A has a source current of 5 milliamps as well as a 4-kΩ resistor arranged in parallel with a series combination of 6-kΩ and 10-kΩ resistors. To find the voltage across the resistors, you first transform Circuit A so that it has a voltage source and all three resistors in series.

Start by finding the source voltage in the transformed circuit, Circuit B. The transformation must be constrained by , so here’s the source voltage:

Illustration by Wiley, Composition Services Graphics

Figure 4-7: Numerical example of the voltage divider method.

According to the voltage divider equation, you find the voltage across a resistor by multiplying the source voltage by the desired resistor and then dividing by the total resistance of the series circuit (see the preceding section for details). Try calculating the voltage for each resistor shown. Use the voltage divider shortcut and plug in the numbers:

Finding voltages when you have multiple current sources

Analyzing a circuit that has multiple current sources and parallel resistors would be tedious if you could only use Kirchhoff’s laws and Ohm’s law. However, thanks to the power of source transformation and the voltage divider technique, the analysis is relatively straightforward.

Circuit A in Figure 4-8 has two current sources and two parallel resistors. What’s the voltage, v1, through resistor R1?

You transform this circuit in two stages. First transform the circuit so that it has two voltage sources and all the resistors arranged in series. Then combine the voltage sources to get one equivalent voltage source. After that, you can find v1, the voltage across R1, using the voltage divider technique.

Illustration by Wiley, Composition Services Graphics

Figure 4-8: Circuit analysis with multiple current sources.

Circuit B of Figure 4-8 is the transformation of Circuit A using several operations. On the right side of Circuit A, you want to move both R2 and R3 so that they’re connected in series. These resistors are connected in parallel, so find their equivalent resistance, Req:

Next, transform the two current sources by converting them to voltage sources:

Circuit C of Figure 4-8 completes the transformation. The two voltage sources connected in series are combined, forming one equivalent voltage source. Observing the voltage polarities results in one voltage source, as follows:

For a numerical example, check out the circuit in Figure 4-9. Your goal is to find v1, the voltage of the 11-kΩ resistor. Start the circuit transformation by putting the resistors in series and switching to voltage sources.

Illustration by Wiley, Composition Services Graphics

Figure 4-9: Numerical example with multiple current sources.

Here’s the equivalent total resistance for two parallel resistors of 6 kΩ and 12 kΩ:

Use the transformation equations and to convert the two current sources to two voltage sources:

You can see the source transformations and equivalent resistance in Circuit B of Figure 4-9.

The voltage sources are connected in series, so combine them, noting their polarities:

Circuit C of Figure 4-9 shows the completed and simplified transformation. Now you can use the voltage divider equation to find v1:

Even though the voltage divider shortcut for series circuits lets you find an unknown voltage without using Kirchhoff’s and Ohm’s laws, this technique was developed from the foundational equations of Kirchhoff’s and Ohm’s laws.

Using the voltage divider technique repeatedly

When a part of a circuit has a combination of series and parallel resistors, you can use the voltage divider technique repeatedly. For example, you may use this approach when resistors are connected in parallel and one of the parallel branches has a series combination.

Consider Circuit A in Figure 4-10. You could find all the components’ voltages and currents using Kirchhoff’s voltage and current laws. But if all you want is the voltage across a specific device, you can take a shortcut with source transformation and the voltage divider technique. You can find the voltage vx across the 3-kΩ resistor using the voltage divider technique repeatedly.

Illustration by Wiley, Composition Services Graphics

Figure 4-10: Circuit analysis using voltage divider methods repeatedly.

On the right side of Circuit A, you have a resistor series combination of 3 kΩ and 1 kΩ connected in parallel with the 4-kΩ resistor. The total resistance for this combination is

I tell you how to find equivalent resistance in Chapter 3.

Circuit B shows the circuit after you combine these resistors. Calculate the voltage across Req using the voltage divider method:

However, the 6 volts also go across the resistor series combination of 3 kΩ and 1 kΩ, as depicted in Circuit C of Figure 4-10. Use the voltage divider method once again to find vx:

Cutting to the Chase Using the Current Divider Technique

The current divider technique lets you easily calculate the current for each device connected in parallel when the devices are driven by an input current source. Earlier in “Converting to a parallel circuit with a current source,” I show you how to transform your circuit. This section shows you where the current divider equation comes from and how to apply it.

Getting a current divider equation for a parallel circuit

For devices connected in parallel with a current source, the current divider technique allows you to find the current through each device. Basically, you’re looking at how the current source distributes its supplied current to each device, depending on the ratio of conductances (or resistances) in the circuit.

The current divider shortcut replaces using Kirchhoff’s current law and Ohm’s law in finding the current through each device. Of course, the shortcut works only because it’s based on these fundamental laws. To see where the current divider equation comes from, look at Figure 4-11. Circuit A is a complex circuit with a voltage source. You want to find an equation to calculate the current through each resistor.

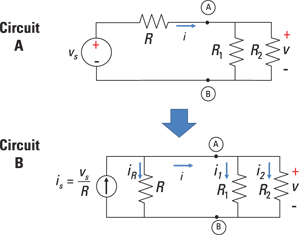
Illustration by Wiley, Composition Services Graphics

Figure 4-11: Source transformation of a complex circuit into a parallel circuit.

Start by transforming the circuit. Circuit B is Circuit A transformed into a parallel circuit with a current source. Kirchhoff’s current law (KCL) says that the sum of the incoming currents is equal to the sum of the outgoing currents. Applying KCL to Circuit B of Figure 4-11 gives you the following:

Because Circuit B shows devices connected in parallel, the voltage v is the same across each resistor. Using Ohm’s law for each resistor and using the definition of conductance G (found in Chapter 3) yields the following expressions for the currents:

where G = 1/R, G1 = 1/R1, and G2 = 1/R2.

Substituting the values of iR, i1, and i2 into and factoring out the voltage v gives you

When you divide by , you wind up with the following form of the desired current divider equation:

This form of the current divider equation is often referred to as a current transfer function, and it relates the ratio output current (current i1 for this example) to the input source current (is in this example). With this equation, you can find the output current going through any device for a given input source current.

Algebraically solving for i1 yields the following form of the current divider equation:

You can find similar relationships for i2 and iR:

These equations show that to find the current through a desired conductance, you simply multiply the input source current by the desired conductance divided by the total conductance of the parallel combination in the circuit. Thus, in Figure 4-11, the current through each resistor depends on the ratio of resistors multiplied by the input source current.

The current through each resistor is always less than and proportional to the supplied independent source current because the ratio of conductance is always less than 1. That idea offers a neat way to check your answer: For a parallel combination of resistors, the largest current goes through the smallest resistor because it has the least resistance, and the smallest current goes through the largest resistor.

Figuring out currents for parallel circuits

The current divider method provides a shortcut in finding the current through each device when all the devices are connected in parallel.

Try using current divider techniques to calculate the current through each resistor in Circuit A of Figure 4-12. Circuit A is a complex circuit with a voltage source, so first transform it into an equivalent circuit that has a current source and all the resistors connected in parallel, as in Circuit B.

Start by finding the source current in Circuit B. The transformation must be constrained by , where V = 24 volts and vs = 6 Ω, so the source current for Circuit B, is, is 4 amps.

Illustration by Wiley, Composition Services Graphics

Figure 4-12: Numerical example to convert a complex circuit to a parallel circuit.

After you know the source current, is, you can use the current divider equation for each resistor. Using the current divider method yields the following (see the preceding section for the derivation of this equation):

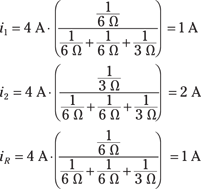
These results show how easy it is to use the current divider method after you’ve transformed the circuit into a parallel circuit driven by a practical current source.

Finding currents when you have multiple voltage sources

Circuit A of Figure 4-13 has multiple voltage sources. What is i1, the current through R1? You can find the answer by transforming the circuit and using the current divider technique.

Transforming this circuit involves two stages. The first is converting the voltage sources to current sources and connecting all resistors in parallel. The second is combining the two current sources. You can then apply the current divider technique to find i1.

Illustration by Wiley, Composition Services Graphics

Figure 4-13: Circuit analysis with multiple voltage sources.

Circuit B shows the first part of the transformation of Circuit A: switching from voltage to current sources. For the transformed circuit to be equivalent to the original, the following equations have to hold true (see the earlier section “Converting to a parallel circuit with a current source” for these constraint equations):

Circuit C of Figure 4-13 completes the transformation. The two current sources are connected in parallel and combined to form one equivalent current source. The current sources point in the same direction, so you can add them up to get the following:

Figure 4-14 provides a numerical example for the circuit shown in Figure 4-13. Start by switching to current sources.

Illustration by Wiley, Composition Services Graphics

Figure 4-14: Numerical example of a circuit with multiple voltage sources.

The transformation of the two voltage sources to two current sources yields

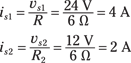
You can see the results of the source transformations and equivalent resistance in Circuit B of Figure 4-14.

The current sources are connected in parallel and point in the same direction, so add them together:

Circuit C of Figure 4-14 shows the completed and simplified transformation that you use to calculate i1. Use the current divider technique to find the current through the 3-Ω resistor:

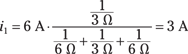
Using the current divider technique repeatedly

When you see parts of a circuit with resistor combinations connected in parallel within other combinations of devices connected in parallel, you can use current divider techniques repeatedly. To see how this works, consider Circuit A in Figure 4-15. You can use current divider shortcuts repeatedly to find the current ix through the 8-kΩ resistor.

Illustration by Wiley, Composition Services Graphics

Figure 4-15: Finding current in a complex circuit using current divider techniques repeatedly.

The circuit includes a resistor series combination of 6 kΩ and 2 kΩ connected in parallel with the 8-kΩ resistor. For this resistor combination, total resistance yields

Circuit B shows the equivalent resistance. Calculate the current through Req using the current divider equation:

However, the 4-milliamp current is split between the 4-kΩ resistor and the series resistor combination of 6 kΩ and 2 kΩ, as in Circuit C of Figure 4-15. Use the current divider method once again to find the current through the 8-kΩ resistor:

Even though the current divider shortcut for parallel circuits makes it so you don’t have to use Kirchhoff’s laws and Ohm’s laws to find an unknown current, this technique was developed from the foundational equations of Kirchhoff’s laws and Ohm’s law.