Chapter 5

Giving the Nod to Node-Voltage Analysis

In This Chapter

Describing node-voltage analysis

Applying Kirchhoff’s current law to node-voltage analysis

Putting node-voltage equations in matrix form

You can describe voltages across each device in a circuit by using node-voltage analysis (NVA), one of the major techniques in circuit analysis. Better yet, NVA reduces the number of equations you have to deal with. I tell you all about the key ingredients of NVA — node voltages and reference nodes — in this chapter. I also walk you through the technique, first with a basic example and then with more-complex ones.

Getting Acquainted with Node Voltages and Reference Nodes

A node is a particular junction or point on a circuit. To use node voltages, you need to select a reference point (or ground point) defined as 0 volts. Node voltages are voltages at circuit nodes measured with respect to that reference node.

Figure 5-1 shows you the notation for node voltage variables as well as the voltage across each device. The voltages VA and VB are the node voltages measured with respect to a reference node, which is identified by the ground symbol. These node voltages can describe the voltages v1, v2, and v3 for the three devices in the circuit.

Illustration by Wiley, Composition Services Graphics

Figure 5-1: Definition and notation for node voltages.

You calculate device voltage as the difference between two node voltages. Take the node voltage at the device’s positive terminal minus the node voltage at the device’s negative terminal.

Look at Figure 5-1. Because it takes two points to define a voltage, the device voltage v1 is the difference between the node voltage VA and the voltage of the reference node, 0 volts. Device 1 has its positive terminal connected to Node A and its negative terminal connected to the reference node, so here’s the device voltage:

Device 2 has its positive terminal connected to Node A and its negative terminal connected to Node B. Device 2’s voltage v2 is

Device 3 has its positive terminal connected to Node B and its negative terminal connected to the reference node. Because Device 3 is connected to a reference node, its voltage v3 is

Testing the Waters with Node-Voltage Analysis

With node-voltage analysis, or NVA, the goal is to find the voltages across the devices in a circuit. You first apply Kirchhoff’s current law (KCL), which states that the sum of incoming currents is equal to the sum of the outgoing currents at any node in the circuit. (See Chapter 3 for more on KCL.) With KCL, you can find a set of equations to determine the unknown node voltages. And when you know all the node voltages in the circuit, you can find the voltages across each device in terms of the node voltages.

In other words, node-voltage analysis involves the following steps:

1. Select a reference (ground) node.

The reference node doesn’t have to be actually connected to ground. You simply identify the node that way for the analysis.

Because a reference node has 0 volts, you can simplify the analysis by choosing a node where a large number of devices are connected as your reference node.

2. Formulate a KCL equation for each nonreference node.

3. Express the device currents in terms of node voltages by using device relationships such as Ohm’s law.

4. Substitute the device equations from Step 3 into the KCL equations of Step 2.

Simplify the equations to put them in standard form.

5. Solve the system of equations to find the unknown node voltages.

Rearrange the standard-form equations into matrix form and use matrix software to solve for the node voltages (or solve very simple systems of equations using other techniques from linear algebra).

Because Step 1 is easy, the next sections walk you through the rest of the steps of node-voltage analysis.

What goes in must come out: Starting with KCL at the nodes

After you choose a reference node, the first step in finding node voltage equations is to set up the Kirchhoff’s current law (KCL) equations for a given circuit. I use the circuit in Figure 5-2 to show you how to develop these equations. The ground symbol at the bottom of the figure tells you which node is the reference node (the node having 0 volts).

This circuit has two node voltages, VA and VB, and four element currents, is, i1, i2, and i3.

Illustration by Wiley, Composition Services Graphics

Figure 5-2: A circuit with a reference node and two node voltages.

At Node A, the source current is splits into i1 and i2. Here’s the KCL equation for the device currents at Node A:

And here’s the KCL equation for Node B:

So now you know about the currents at play in Figure 5-2. How do you get the voltages? By applying Ohm’s law, as I explain next.

Describing device currents in terms of node voltages with Ohm’s law

Ohm’s law expresses a linear relationship between voltage and current when the device in question is a resistor. You need Ohm’s law to describe a device’s current in terms of its node voltages. First, you determine what the node voltages are and find the device voltages. Then you substitute the node voltage expressions of the device currents into KCL and get the set of node voltage equations to be solved.

Look at the node voltages on either side of resistor R1 in Figure 5-2. The device voltage is the difference in node voltages. Because the negative terminal is connected to a reference node, the voltage v1 across resistor R1 is

The voltage v2 for Device 2 is the difference between the node voltages at Nodes A and B. The device’s positive terminal is connected to Node A, and its negative terminal is connected to Node B, so

The negative terminal for Device 3 is connected to a reference node, so the voltage v3 is simply

Now apply Ohm’s law (i = v/R) to express the device currents through R1, R2, and R3 in terms of the node voltages. Using Ohm’s law produces the following device currents:

You can now substitute these device-current expressions into the KCL equations at Nodes A and B (see the preceding section for the KCL equations). You wind up with:

Collect like terms and rearrange these two node equations to get the following:

These two node voltage equations are said to be in standard form, but you can easily put this set of equations into matrix form.

Putting a system of node voltage equations in matrix form

The node voltage equations (see the preceding section) give you a system of linear equations, which you can solve using matrices. Of course, you can skip the matrices if the system is simple and you want to use other techniques from linear algebra, such as back substitution, to find the answers. But in most cases, using matrices is faster and easier, especially if you have a large and complicated circuit.

Here’s how to transform node voltage equations from standard form to matrix form:

1. Take the coefficients (of resistors or conductances) of the node voltages to form a square matrix.

Make sure the variable terms are in the same order in all your node voltage equations before setting up the matrix.

A square matrix has the same number of columns and rows. Each column holds all the coefficients on a particular variable, and each row holds all the coefficients from a particular equation.

2. Multiply the coefficient matrix from Step 1 by a column vector of the node voltages (the variables you want to solve for).

A column vector is a single-column matrix. The number of rows in the column vector should equal the number of columns in the square matrix.

In the column vector, write the variables in the order in which they appear in your node voltage equations.

3. Write the right side of each node equation as a vector element to form a column vector of current sources when combining the system of node equations.

The column vector of current sources should have the same number of rows as the column vector of node voltages.

In this column vector, write the current sources that appear to the right of the equal signs in your node voltage equations.

When you translate the set of node voltage equations from the preceding section into matrix form, you wind up with the following description of the circuit:

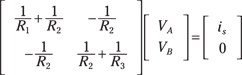
This matrix equation follows the form of Ax = b, where A consists of a matrix of coefficients of resistors or conductances, x is a vector of unknown node voltages, and b is vector of independent current sources.

Confirming diagonal symmetry in the square matrix is a useful way to check that your node voltage equations are right. For circuits with independent sources, you should see positive values along one diagonal and negative values along the opposite diagonal (the off-diagonal elements).

Solving for unknown node voltages

After you have your system of node voltage equations in matrix form, you’re ready to solve for the unknown node voltages. You could solve simple matrices for the node voltages using Cramer’s rule or other techniques from linear algebra. But for circuits with a large number of elements, use matrix software or a graphing calculator. For instance, you can find node voltages by multiplying the inverse of the coefficient matrix by the answer matrix (the column vector of current sources) on your graphing calculator: A–1b = x.

Matrix software is great for doing calculations, but it doesn’t develop the node voltage equations for you. Make sure you know how to set up the matrix problem to help you solve for the node voltages. Fortunately, some circuit analysis software does solve for the unknown voltages. You need to build the circuit graphically (depending on the software), and the software performs the required calculations.

Applying the NVA Technique

If you’ve reviewed the earlier sections in this chapter, then you’re ready to set up some node voltage equations with numerical examples. When you have a voltage source with one of its terminals connected to a reference node, the node voltage is simply equal to the voltage source. Although doing so requires a little more work, if you’re comfortable with current sources, you can always transform a voltage source into a current source. (If you’re wondering what NVA and node voltage equations are, spend some time with the first part of this chapter before moving on.)

Solving for unknown node voltageswith a current source

Formulating the node voltage equations leads to a linear system of equations. You can see what I mean by working through the NVA process I outline in the earlier section “Testing the Waters with Node-Voltage Analysis.” Try finding the voltages and currents for the devices in the circuit in Figure 5-3. (Note that Figure 5-3 is the same as Figure 5-2 but with numbers given for R1, R2, and R3.)

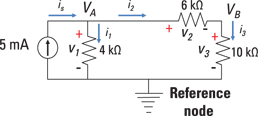
Illustration by Wiley, Composition Services Graphics

Figure 5-3: Numerical example of node-voltage analysis.

Start by identifying your reference node. I marked my chosen reference node with the ground symbol in Figure 5-3. Now you can form the KCL equations for Nodes A and B:

Next, express the device currents in terms of node voltages by using Ohm’s law (see the earlier section “Getting Acquainted with Node Voltages and Reference Nodes” for help writing the device currents). You wind up with the following equations:

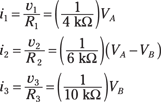
Go ahead and substitute these current values into the KCL equations. Then rearrange the equations to put them in standard form. Here’s the equation for Node A:

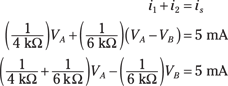
And here’s the equation for Node B:

You now have a system of linear equations for Node A and Node B — two equations with two variables. Write this system of equations in matrix form (for details, see the earlier section “Putting a system of node voltage equations in matrix form”). The resulting matrix looks like this:

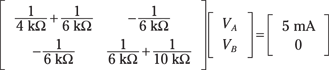
Use your calculator or matrix software to solve for VA­ and VB. You wind up with the following node voltages:

Now calculate the device voltages by finding the difference between two node voltages (see the first section in this chapter for details). Given these node voltages, the voltages across the resistors are

To complete the analysis, use Ohm’s law to calculate the current for each resistor:

After you finish the calculations, check whether your answers make sense. You can verify your results by applying Kirchhoff’s and Ohm’s laws. You can also verify that devices connected in series have the same current and that devices connected in parallel have the same voltage.

The answers make sense for this problem because the outgoing currents i1 and i2 at Node A add up to 5 milliamps. Also, resistor R1, with a resistance of 4 kΩ, has four times the current of the series combination of R2 and R3, whose resistance totals 16 kΩ. And R2 and R3 have the same current, as is true for any series combination.

Dealing with three or more node equations

The node voltage approach is most useful when the circuit has three or more node voltages. You can use the same step-by-step process you use for circuits with two nodes, which I show you earlier in “Testing the Waters with Node-Voltage Analysis.”

The circuit in Figure 5-4 has four nodes: A, B, C, and a reference node of 0 volts marked with a ground symbol. You want to find the voltage across each device in the circuit.

Illustration by Wiley, Composition Services Graphics

Figure 5-4: A circuit with three nonreference nodes.

At Node A, you have incoming current is and outgoing currents i1 and i2. At Node B, you have incoming current i1 and outgoing currents i3 and i4. And at Node C, you have incoming currents i2 and i3 and outgoing current i5. By applying the KCL equations at Nodes A, B, and C, you wind up with the following:

Next, express the device currents in terms of node voltages using Ohm’s law (see the earlier section “Getting Acquainted with Node Voltages and Reference Nodes” for info on writing the device currents):

Substitute these device-current equations into the KCL equations. Then algebraically rearrange the equations to put them in standard form. Here’s the equation for Node A:

Here’s the equation for Node B:

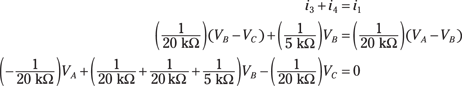
And here’s the equation for Node C:

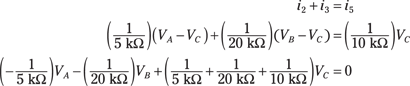
Simplifying the coefficients gives you the following set of node voltage equations for Nodes A, B, and C:

Now put this system of node voltage equations in matrix form. (I explain how to do this earlier in “Putting a system of node-voltage equations in matrix form.”)

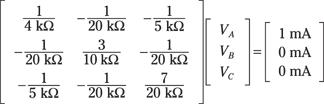
The preceding matrix equation is of the form Ax = b. Notice that the square matrix is symmetrical along the diagonal the diagonal terms are positive, and the off-diagonal terms are negative, all of which suggests that you’ve converted to matrix form correctly.

Plug the matrix equation into your calculator or matrix software, giving you

Now that you know the voltages for Nodes A, B, and C, you can determine the voltages across Devices 1 through 5:

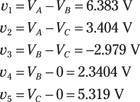
To complete the analysis, find the current through each device:

These results make sense because they satisfy the KCL equations at each of the three nodes.

Working with Voltage Sources in Node-Voltage Analysis

When a voltage source is connected to a node, you end up with fewer unknown node voltage equations because one of the node voltages is given in terms of the known voltage source. Here’s how the node voltages compare if you have a voltage source:

If the negative terminal of the voltage source is connected to a reference node, then the voltage of the node connected to the positive terminal of the voltage source has to be equal to the source voltage.

If the voltage source terminals are connected to two nonreference nodes, then the difference between the two node voltages is simply the source voltage. So if you know one node voltage, you get the other by adding or subtracting the source voltage to or from the known node voltage.

If you’re more comfortable dealing with current sources, you can perform a source transformation by replacing the voltage source and resistors connected in series with an equivalent current source and resistors connected in parallel. I show you how to transform independent sources in Chapter 4.

Figure 5-5 shows that the negative terminal of a voltage source is usually given as 0 volts. As you can see, Circuit A has two voltage sources and three nonzero nodes. Through source transformation, you can transform the circuit into Circuit B, which has only one nonreference node.

Illustration by Wiley, Composition Services Graphics

Figure 5-5: Using source transformation of voltage sources for NVA.

When you apply node-voltage analysis in Circuit B, you wind up with the following equation:

You get the same result using source transformation by noting that VA = Vs1 and VC = vs2. The next example illustrates the technique by relating the node voltages to the voltage source.

Sometimes you encounter circuits with two voltage sources that don’t have a common node. One voltage source is connected to a reference node, and the other voltage source has terminals connected to nonreference nodes, as in Figure 5-6.

Illustration by Wiley, Composition Services Graphics

Figure 5-6: Dealing with ungrounded voltage source for NVA.

Consider the voltage source at the top of Figure 5-6. Currents i1 through i4 leave and enter through the negative and positive terminals of vs2, which leads to the following KCL equation:

You can express these node voltages in the KCL equation in the following expression:

The source voltage vs1 at Node B is connected to a reference node, which means that

Because vs2 is connected at Nodes A and C, the voltage across vs2 is the difference between the node voltages at these nodes:

Replace VB and VC in the KCL equation to get the following expression:

Put the source voltages on one side of the equation, which gives you

This equation now has one node voltage term.

Now, suppose the desired output voltage is the voltage across resistor R4, connected to VC. Substitute VC + vs2 for VA into the preceding equation:

Now simplify the equation:

Now you have one equation with the node voltage VC. This equation is easily solvable using algebra after you plug in some numbers for the resistors and voltage sources.