2.1.1 Complete-Case Methods

As the name suggests, the complete-case method (also known as list-wise deletion) makes use of cases with complete data on all variables of interest in the analysis. Cases with incomplete data on one or more variables are discarded. This approach is easiest to implement since standard full data analysis can be applied without modification, and is the default in many statistical software packages (i.e., cases with any missing values are automatically ignored). The disadvantages include loss of precision due to a smaller sample size and bias in complete-data summaries when the cases with 17 missing data differ systematically from the completely observed cases (i.e., when data are not missing completely at random).

In practice, when the loss of precision and the bias are small, we may opt for this approach for its simplicity. Unfortunately, the loss of precision and the bias are difficult to quantify since both depend not only on the fraction of complete cases but also on the extent to which complete and incomplete cases differ on the parameters of interest. So there is no universal rule of thumb, such as a certain percentage of missing data, for deciding whether this is an appropriate method.

2.1.2 Weighted Complete-Case Methods

The earlier complete-case strategy can potentially lead to biased summaries because the sample of observed cases may not be representative of the full sample. Another strategy reweights the sample to make it more representative. For example, if the response rate is twice as likely among men as women, data from each man in the sample could receive a weight of 2 in order to make the data more representative. This strategy is commonly used in sample surveys, especially in the case of unit nonresponse, where all the survey items are missing for cases in the sample that did not participate. For example, if only one variable is missing, this method first creates a model to predict nonresponse in one variable as a function of the rest of the variables in the data. The inverse of the predicted probabilities of response from this model could then be used as survey weights to make the complete-case sample more representative. If more than one variable is missing, this method becomes more complicated, and there will be problems with standard errors if predicted response probabilities are close to 0.

We give an example to illustrate this method more formally. Let Y be the outcome of interest and R be the indicator of whether Y was observed. We also let X denote the set of variables that were observed for both respondents and nonrespondents. Suppose that the MAR (missing at random) assumption holds, that is, Pr (R|X, Y) = Pr (R|X). Then the response probability of the ith subject is denoted by

If π(X_i) values are known for all n subjects in the sample, we could use

to estimate the marginal mean of Y, which is the so-called inverse probability weighted estimator (Cassel et al., 1983; Skinner and D'arrigo, 2011. If the parameter θ is interest, which satisfies E[g(Y, X; θ)] = 0, we could solve the following estimating equation to find an estimate of θ:

In many practical applications, the response probability π(X) is unknown. In this case, we may assume a parametric model for it, that is, π(X) is known up to some parameters. Or we can estimate π(X) nonparametrically if X does not contain many variables. In some applications, we may group the values of π(X) into four to six categories and create a new variable C, which is used to adjust weights in the analysis. This might be required because directly weighting by [π(X)]⁻¹ places more reliance on correct model specification of the regression of R on X than adjusting for C (Little and Rubin, 1987).

2.1.3 Removing Variables with Large Amounts of Missing Values

This approach drops variables from the analysis that have a large proportion of missing values. This is not recommended since it may exclude important variables in the regression model, required for causal interpretation, and may lead to bias and unnecessarily large standard errors. For important variables with more than trivial amounts of missing data, the explicit model-based methods in the next sections are suggested.

2.2.1 Maximum Likelihood

Many procedures arise from defining a model for the variables with missing values and making statistical inferences based on maximum likelihood (ML) methods. The fundamental idea behind the ML methods is conveyed by their name: find the values of the parameters that are most probable, or most likely, for the data that have actually been observed.

Denote D_obs as the observed data, which have the probability density p(D_obs|θ). Here θ is a set of parameters of interest. Then, the likelihood function L(θ|D_obs) is equal to p(D_obs|θ), that is, L(θ|x) = p(D_obs|θ), and is thought of as a function of θ, where the data D_obs are fixed. The log-likelihood l(θ|D_obs) is equal to log (L(θ|x) and is, in general, easier to be maximized.

The next step is to deduce a numerical value for θ using our knowledge of L(θ|x). The ML principle says we should choose an estimate of θ that maximizes the log-likelihood function. In other words, we choose a value of the parameter that best explains the observed data, and this value is called the ML estimate of θ.

Finding the maximum can be easy or hard, depending on the form of p(D_obs|θ). For the normal (Gaussian) distribution, θ consists of the mean μ and variance σ², and we can find the derivative of l(θ|D_obs), set it equal to zero, and solve directly for μ and σ². But for most problems, these analytic expressions are hard to come by, and we will have to use more elaborate techniques. One might use the Newton–Raphson or quasi-Newton algorithms to maximize directly the likelihood of the observed data. One of the most popular techniques for maximizing the likelihood function is the expectation–maximization (EM) algorithm of Dempster et al. 1977. We briefly discuss the EM algorithm in Section 2.2.1.1 and readers may find the theoretical details in Little and Rubin (1987).

2.3.1 Single Imputation Methods

2.3.2 Multiple Imputation

While imputation may solve the missing data problem, naive or unprincipled imputation methods may create more problems than they solve, by distorting estimates and standard errors. Rubin (1987) addressed the question of how to obtain valid inference from imputed data by using multiple imputation, a technique where missing data are replaced by m values drawn from the posterior predictive distribution of the missing data, resulting in m complete data sets. Standard full data methods are then used on each of the m complete data sets to estimate the parameters of interest, resulting in m estimated parameters and their corresponding standard errors. These estimates are then combined, or averaged, to produce estimates and confidence intervals that incorporate the missing data uncertainty. This averaging will, in general, lower the variance of the combined estimate. In particular, this method recognizes two sources of uncertainty: the uncertainty caused by sampling the subjects from a source population, and the uncertainty in estimating underlying distributions of the variables with missing values. A simple method is used to combine both sources of uncertainty, resulting in a single corrected standard error of the estimated association.

The multiple imputation method was originally developed in the setting of large public-use data sets from sample surveys and censuses. However, with advances in computational methods and software for creating multiple imputations, the technique has become attractive to researchers in most fields where missing data cause a problem, as documented in Schafer (1997b).

Software most readily available to implement multiple imputation assumes that the missing data are MAR, although the paradigm certainly does not require MAR nonresponse. In principle, multiple imputations can be created in any kind of model for the missing data mechanism, and resulting data will be valid under that mechanism (Rubin, 1987). But methods that assume MAR have the advantage of avoiding explicit modeling of nonresponse, although unfortunately the observed data cannot provide enough information on the validity of the MAR assumption.

Usually the imputed values are drawn from an imputation model. If only one variable is subject to missingness, it is easy to construct the imputation model. For example, we can use logistic regression to model a binary variable, and a linear Gaussian model for a continuous variable. If there are multiple variables subject to missingness, the imputation model can be constructed jointly or conditionally.

The joint modeling approach assumes that given the other observed variables, the variables subject to missingness follow a multivariate normal distribution. However, in practice, the variables subject to missingness may involve different types such as binary, categorical, and ordinal variables. In this case, it would be computationally implausible to simulate the posterior predictive distribution simultaneously for all the missing variables. The multiple imputation with chained equations is proposed. The idea of chained equations is to update the missing variables one by one, based on a series of full conditional distributions, as proposed by van Buuren and Groothuis-Oudshoorn (2011).

Denote Y = (Y₁, ..., Y_p)′ the set of p variables in the data set that are subject to missingness, which include both response variables and covariates. Let Y_−j = (Y₁, ..., Y_j−1, Y_j+1, ..., Y_p)′ be the collection of all variables in Y but Y_j. The model assumptions are made for each variable Y_j fully conditional on all other variables Y_−j:

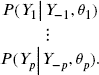
This model framework is called “chained equations”. It specifies p univariate regression models, and avoids the hassle of jointly model the multivariate distributions for all the missing variables.

With a sample of size n, the observed data on Y_j is a vector of observations from n subjects, denoted by y_j. Hence we can partition y_j into the missing part and the observed part , indicating a pool of subjects with observed or missing Y_j. It should be noted that this is a partition of subjects for each variable, whereas the partition of variables for a subject will be introduced in later chapters. The iteration procedures are described as follows:

where is the imputed data vector of y_j after the tth iteration. The draws for the parameters are just a full Bayesian regression analysis. Note that for drawing , the condition is on rather than . In other words, only subjects with observed response (Y_j) are included in the regression; the covariates (Y_−j) are all imputed based on the previous iteration. The draws for the missing data are performed sequentially for each variable on the subjects with missing values, which is based on the p univariate regression models. This procedure has been implemented in the R package mice.

In practice, the chained equation approach can be briefly broken down into the following steps, and we will illustrate these with examples in the later chapters.

1. Examine the missing data patterns and identify key variables with missing values that require imputation. Decide on the sequence of the imputation, usually based on amount of missingness and quality of the variables used to impute them.
2. Initialize all missing values with a simple imputation, such as mean imputation or last-value-carry-forward.
3. Construct an imputation model (typically a regression model) for the first variable (Y₁) requiring imputation. For example, if Y₁ is a binary variable, a logistic regression model may be constructed with Y₁ being the dependent variable, and other variables as covariates. For other types of variables, linear, Poisson or other generalized linear regression models may be employed.
4. The missing values for Y₁ are then replaced with predictions (imputations), using either predictive mean matching method or direct sampling from predictive posterior distributions. Note the latter method may require Gibbs sampling for intractable distributions. When Y₁ is used in subsequent imputation models for other variables, the observed values and imputed values for Y₁ will be combined to form a complete data vector.
5. Steps 3 and 4 are repeated for each variable that has missing values, Y₂, ..., Y_p. The cycling through each of the variables constitutes one iteration. At the end of each iteration all of the missing values have been replaced with imputed values from regressions that are assumed to reflect relationships among these variables. The number of iterations to be performed can be decided by the researchers. Though it is suggested that 10 iterations are usually sufficient, nowadays with the increasing computing power, we recommend performing iterations many more times to ensure convergence of the algorithm. The imputed data set in the last iteration is taken to be one imputed data set.
6. Iterate steps 2 through 5 to obtain multiple imputed datasets. The number of imputations should depend on the missing information of the data set. In most cases, 10-20 imputations would be sufficient.
7. With each imputed complete dataset, we then proceed with parameter estimation. The results are pooled together over all imputed datasets for the final inference.

The chained equation is able to handle flexible type of missing variables, and is usually simple to implement. Although the convergence of the algorithm is not proved rigorously, its performance in practice is stable in most circumstances, as long as the missing data proportion is not too high. One important limitation of the chained equation approach is that there is no guarantee that the imputed sample is indeed drawn from the posterior predicted distribution because there may not exist a joint distribution that yields the specified conditional distributions.