Chapter 9. Beams on Elastic Foundations

9.1. Introduction

In the problems involving beams previously considered, support was provided at a number of discrete locations, and the beam was usually assumed to suffer no deflection at these points of support. We now explore the case of a prismatic beam supported continuously along its length by a foundation, itself assumed to experience elastic deformation. We shall take the reaction forces of the elastic foundation to be linearly proportional to the beam deflection at any point. This simplest analytical model of a continuous elastic foundation is often referred to as the Winkler model.

The foregoing assumption not only leads to equations amenable to solution, but represents an idealization closely approximating many real situations. Examples include a railroad track, where the elastic support consists of the cross ties, the ballast, and the subgrade; concrete footings on an earth foundation; long steel pipes resting on earth or on a series of elastic springs; ship hulls; or a bridgedeck or floor structure consisting of a network of closely spaced bars.

9.2. General Theory

Let us consider a beam on elastic foundation subject to a variable loading, as depicted in Fig. 9.1. The force q per unit length, resisting the displacement of the beam, is equal to –kυ. Here υ is the beam deflection, positive downward as in the figure. The quantity k represents a constant, usually referred to as the modulus of the foundation, possessing the dimensions of force per unit length of beam per unit of deflection (for example, newtons per square meter or pascals).

Figure 9.1. Beam on elastic (Winkler) foundation.

The analysis of a beam whose length is very much greater than its depth and width serves as the basis of the treatment of all beams on elastic foundations. Referring again to Fig. 9.1, which shows a beam of constant section supported by an elastic foundation, the x axis passes through the centroid and the y axis is a principal axis of the cross section. The deflection υ, subject to reaction q and applied load per unit length p, for a condition of small slope, must satisfy the beam equation:

(9.1)

For those parts of the beam on which no distributed load acts, p = 0, and Eq. (9.1) takes the form

(9.2)

It will suffice to consider the general solution of Eq. (9.2) only, requiring the addition of a particular integral to satisfy Eq. (9.1) as well. Selecting υ = e^ax as a trial solution, it is found that Eq. (9.2) is satisfied if

requiring that

α = ± β(1 ± i)

where

(9.3)

The general solution of Eq. (9.2) may now be written as

(9.4)

where A, B, C, and D are the constants of integration.

In the developments that follow, the case of a single load acting on an infinitely long beam will be treated first. The solution of problems involving a variety of loading combinations will then rely on the principle of superposition.

9.3 Infinite Beams

Consider an infinitely long beam resting on a continuous elastic foundation, loaded by a concentrated force P (Fig. 9.2). The variation of the reaction kυ is unknown, and the equations of static equilibrium are not sufficient for its determination. The problem is therefore statically indeterminate and requires additional formulation, which is available from the equation of the deflection curve of the beam. Owing to beam symmetry, only that portion to the right of the load P need be considered. The two boundary conditions for this segment are deduced from the fact that as x → ∞ the deflection and all derivatives of ν with respect to x must vanish. On this basis, it is clear that the constants A and B in Eq. (9.4) must equal zero. What remains is

Figure 9.2. Infinite beam on an elastic foundation and loaded at the origin.

(9.5)

The conditions applicable a very small distance to the right of P are

(a)

where the minus sign is consistent with the general convention adopted in Sec. 1.3. Substitution of Eq. (a) into Eq. (9.5) yields

Introduction of the expressions for the constants into Eq. (9.5) provides the following equation, applicable to an infinite beam subject to a concentrated force P at midlength:

(9.6a)

or

(9.6b)

Equation (9.6b) indicates clearly that the characteristic of the deflection is an exponential decay of a sine wave of wavelength

To simplify the equations for deflection, rotation, moment, and shear, the following notations and relations are introduced:

(9.7)

Table 9.1 lists numerical values of the foregoing functions for various values of the argument βx. The solution of Eq. (9.5) for specific problems is facilitated by this table and the graphs of the functions of βx [Ref. 9.1]. Equation (9.6) and its derivatives, together with Eq. (9.7), yield the following expressions for deflection, slope, moment, and shearing force:

(9.8)

Table 9.1. Selected Values of the Functions Defined by Eqs. (9.7)

These expressions are valid for x ≥ 0.

Example 9.1

A very long rectangular beam of width 0.1 m and depth 0.15 m (Fig. 9.3) is subject to a uniform loading over 4 m of its length of p = 175 kN/m. The beam is supported on an elastic foundation having a modulus k = 14 MPa. Derive an expression for the deflection at an arbitrary point Q within length L. Calculate the maximum deflection and the maximum force per unit length between beam and foundation. Use E = 200 GPa.

Figure 9.3. Example 9.1.

Solution The deflection Δυ at point Q due to the load P_x = p dx is, from Eq. (9.8);

The deflection at point Q resulting from the entire distributed load is then

or

(b)

Although the algebraic sign of the distance a in Eq. (b) is negative, in accordance with the placement of the origin in Fig. 9.3, we shall treat it as a positive number because Eq. (9.8) gives the deflection for positive x only. This is justified on the basis that the beam deflection under a concentrated load is the same at equal distances from the load, whether these distances are positive or negative. By the use of Eq. (9.3),

From this value of β, βL = (0.888) (4) = 3.552 = β(a + b). We are interested in the maximum deflection and therefore locate the origin at point Q, the center of the distributed loading. Now a and b represent equal lengths, so βa = βb = 1.776, and Eq. (b) gives

The maximum force per unit of length between beam and foundation is then kυ_max = 14 × 10⁶(0.0129) = 180.6 kN/m.

Example 9.2

A very long beam is supported on an elastic foundation and is subjected to a concentrated moment M_o (Fig. 9.4). Determine the equations describing the deflection, slope, moment, and shear.

Figure 9.4. Example 9.2.

Solution Observe that the couple P · e is equivalent to M_o for the case in which e approaches zero (indicated by the dashed lines in the figure). Applying Eq. (9.8), we have therefore

Successive differentiation yields

(9.9)

which are the deflection, slope, moment, and shear, respectively.

9.4 Semi-Infinite Beams

The theory of Sec. 9.3 is now applied to a semi-infinite beam, having one end at the origin and the other extending indefinitely in a positive x direction, as in Fig. 9.5. At x = 0, the beam is subjected to a concentrated load P and a moment M_A. The constants C and D of Eq. (9.5) can be ascertained by applying the following conditions at the left end of the beam:

The results are

Figure 9.5. Semi-infinite end-loaded beam on elastic foundation.

The deflection is now found by substituting C and D into Eq. (9.5) as

(9.10)

At x = 0,

(9.11)

Finally, successively differentiating Eq. (9.10) yields expressions for slope, moment, and shear:

(9.12)

Application of these equations together with the principle of superposition permits the solution of more complex problems, as is illustrated next.

Example 9.3

Determine the equation of the deflection curve of a semi-infinite beam on an elastic foundation loaded by concentrated force P a distance c from the free end (Fig. 9.6a).

Figure 9.6. Example 9.3.

Solution The problem may be restated as the sum of the cases shown in Figs. 9.6b and c. Applying Eqs. (9.8) and the conditions of symmetry, the reactions appropriate to the infinite beam of Fig. 9.6b are

(a)

Superposition of the deflections of Fig. 9.6b and c [see Eqs. (9.8) and (9.12)] results in

Introducing Eqs. (a) into this, the following expression for deflection, applicable for positive x, is obtained:

This is clearly applicable for negative x as well, provided that x is replaced by |x|.

Example 9.4

A 2-m-long steel bar (E = 210 GPa) of 75-mm by 75-mm square cross section rests with a side on a rubber foundation (k = 24 MPa). If a concentrated load P = 20 kN is applied at the left end of the beam (Fig. 9.5), determine (a) the maximum deflection and (b) the maximum bending stress.

Solution Applying Eq. (9.3), we have

Inasmuch as pL = 1.814(2) = 3.638 > 3, the beam can be considered to be a long beam (see Sec. 9.4); Eqs. (9.12) with M_A = 0 thus apply.

a. The maximum deflection occurs at the left end for which f₄(βx) is a maximum or βx = 0. The first of Eqs. (9.12) is therefore

b. Referring to Table 9.1, f₂(βx) has its maximum of 0.3224 at βx = π/4. Using the third of Eqs. (9.12),

The maximum stress in the beam is obtained from the flexure formula:

The location of this stress is at x = π/4β = 433 mm from the left end.

9.5. Finite Beams: Classification of Beams

The bending of a finite beam on elastic foundation may also be treated by application of the general solution, Eq. (9.4). In this instance, four constants of integration must be evaluated. To accomplish this, two boundary conditions at each end may be applied, usually resulting in rather lengthy formulations. Results have been obtained applying this approach and are tabulated for numerous cases.^*

^* For a detailed presentation of a number of practical problems, see Refs. 9.1 through 9.3.

An alternative approach to the solution of problems of finite beams with simply supported and clamped ends employs equations derived for infinite and semi-infinite beams, together with the principle of superposition. The use of this method was demonstrated in connection with semi-inverse beams in Example 9.3. Energy methods can also be employed in the analysis of beams whose ends are subjected to any type of support conditions [Ref. 9.4]. Solution by trigonometric series results in formulas that are particularly simple, as will be seen in Example 10.12. Design tables for short beams with free ends on elastic foundation have been provided by Iyengar and Ramu [Ref. 9.5].

To permit the establishment of a stiffness criterion for beams, it serves well to consider a finite beam on an elastic foundation, centrally loaded by a concentrated force P (Fig. 9.7), and to compare the deflections occurring at the center and end of the beam. Note that the beam deflection is symmetrical with respect to C. The appropriate boundary conditions are, for x ≥ 0, υ′(L/2) = 0, EIυ′″(L/2) = P/2, EIυ″(0) = 0, and EIυ′″(0) = 0. Substituting these into the proper derivatives of Eq. (9.4) leads to four equations with unknown constants A, B, C, and D. After routine but somewhat lengthy algebraic manipulation, the following expressions are determined:

(9.13)

(9.14)

From Eqs. (9.13) and (9.14), we have

(9.15)

Figure 9.7. Comparison of the center and end deflections of a finite beam on an elastic foundation subjected to a concentrated center load.

Figure 9.7, a plot of Eq. (9.15), enables us to readily discern a rationale for the classification of beams:

1. Short beams, βL < 1: Inasmuch as the end deflection is essentially equal to that at the center, the deflection of the foundation can be determined to good accuracy by regarding the beam as infinitely rigid.

2. Intermediate beams, 1 < βL < 3: In this region, the influence of the central force at the ends of the beam is substantial, and the beam must be treated as finite in length.

3. Long beams, βL > 3: It is clear from the figure that the ends are not affected appreciably by the central loading. Therefore, if we are concerned with one end of the beam, the other end or the middle may be regarded as being an infinite distance away; that is, the beam may be treated as infinite in length.

The foregoing groups do not relate only to the special case of loading shown in Fig. 9.7, but are quite general. Should greater accuracy be required, the upper limit of group 1 may be placed at βL = 0.6 and the lower limit of group 3 at βL = 5.

9.6 Beams Supported by Equally Spaced Elastic Elements

In the event that a long beam is supported by individual elastic elements, as in Fig. 9.8a, the problem is simplified if the separate supports are replaced by an equivalent continuous elastic foundation. To accomplish this, it is assumed that the distance a between each support and the next is small, and that the concentrated reactions R_i = Kυ_i are replaced by equivalent uniform or stepped distributed forces shown by the dashed lines of Fig. 9.8b.

Figure 9.8. Infinite beam supported by equally spaced elastic springs. Loading diagram: (a) with concentrated reactions; (b) with average continuous reaction force distribution.

For practical calculations, the usual limitation is a ≤ π/4β. Here K represents a spring constant (for example, newtons per meter). The average continuous reaction force distribution is shown by the solid line in the figure. The intensity of the latter distribution is ascertained as follows:

or

(a)

where the foundation modulus of the equivalent continuous elastic support is

(9.16)

The solution for the case of a beam on individual elastic support is then obtained through the use of Eq. 9.2, in which the value of k is that given by Eq. (9.16).

Example 9.5

A series of springs, spaced so that a = 1.5 m, supports a long thin-walled steel tube having E = 206.8 GPa. A weight of 6.7 kN acts down at midlength of the tube. The average diameter of the tube is 0.1 m, and the moment of inertia of its section is 6 × 10^-6 m⁴. Take the spring constant of each support to be K = 10 kN/m. Find the maximum moment and the maximum deflection, assuming negligible tube weight.

Solution Applying Eqs. (9.3) and (9.16), we obtain

From Eq. (9.8),

9.7 Simplified Solutions for Relatively Stiff Beams

Examination of the analyses of the previous sections and of Fig. 9.7 leads us to conclude that the distribution of force acting on the beam by the foundation is, in general, a nonlinear function of the beam length coordinate. This distribution approaches linearity as the beam length decreases or as the beam becomes stiffer. Reasonably good results can be expected, therefore, by assuming a linearized elastic foundation pressure for stiff beams. The foundation pressure is then predicated on beam displacement in the manner of a rigid body [Ref. 9.6] and the reaction is, as a consequence, statically determinate.

To illustrate the approach, consider once more the beam of Fig. 9.7, this time with a linearized foundation pressure (Fig. 9.9). Because of loading symmetry, the foundation pressure is, in this case, not only linear but constant as well. We shall compare the results thus obtained with those found earlier.

Figure 9.9. Relatively stiff finite beam on elastic foundation and loaded at the center.

The exact theory states that points E and C deflect in accordance with Eqs. (9.13) and (9.14). The relative deflection of these points is simply

(a)

For the simplified load configuration shown in Fig. 9.9, the relative beam deflection may be determined by considering the elementary solution for a beam subjected to a uniformly distributed loading and a concentrated force. For this case, we label the relative deflection υ₁ as follows:

(b)

The ratio of the relative deflections obtained by the exact and approximate analyses now serves to indicate the validity of the approximations. Consider

(c)

where υ and υ₁ are given by Eqs. (a) and (b). The trigonometric and hyperbolic functions may be expanded as follows:

(d)

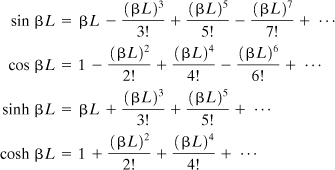
Introducing these into Eq. (c), we obtain

(e)

Substituting various values of βL into Eq. (e) discloses that, for βL < 1.0, υ/υ₁ differs from unity by no more than 1%, and the linearization is seen to yield good results. It can be shown that for values of βL < 1 the ratio of the moment (or slope) obtained by the linearized analysis to that obtained from the exact analysis differs from unity by less than 1%.

Analysis of a finite beam, centrally loaded by a concentrated moment, also reveals results similar to those given here. We conclude, therefore, that when βL is small (< 1.0) no significant error is introduced by assuming a linear distribution of foundation pressure.

9.8 Solution by Finite Differences

Because of the considerable time and effort required in the analytical solution of practical problems involving beams on elastic foundations, approximate methods employing numerical analysis are frequently applied. A solution utilizing the method of finite differences is illustrated in the next example.

Example 9.6

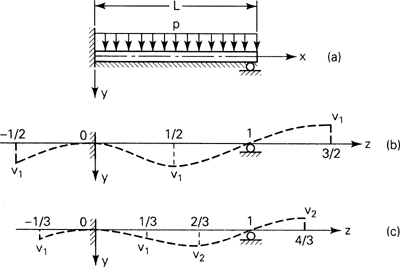
Determine the deflection of the built-in beam on an elastic foundation shown in Fig. 9.10a. The beam is subjected to a uniformly distributed loading p and is simply supported at x = L.

Figure 9.10. Example 9.6.

Solution The deflection is governed by Eq. (9.1), for which the applicable boundary conditions are

(a)

The solution will be obtained by replacing Eqs. (9.1) and (a) by a system of finite difference equations. It is convenient to first transform Eq. (9.1) into dimensionless form through the introduction of the following quantities:

The deflection equation is therefore

(b)

We next divide the interval of z(0,1) into n equal parts of length h = 1/m, where m represents an integer. Multiplying Eq. (b) by h⁴ = 1/m⁴, we have

(c)

Employing Eq. (7.23), Eq. (c) assumes the following finite difference form:

(d)

Upon setting C = kL⁴/EI, this becomes

(e)

The boundary conditions, Eqs. (a), are transformed into difference conditions by employing Eq. (7.4):

(f)

Equations (e) and (f) represent the set required for a solution, with the degree of accuracy increased as the magnitude of m is increased. Any desired accuracy can thus be attained.

For purposes of illustration, let k = 2.1 MPa, E = 200 GPa, I = 3.5 × 10^-4 m⁴, L = 3.8 m, and p = 540 kN/m. Determine the deflections for m = 2, m = 3, and m = 4. Equation (e) thus becomes

(g)

For m = 2, the deflection curve, satisfying Eq. (f), is sketched in Fig. 9.10b. At z = we have υ_n = υ₁. Equation (g) then yields

from which υ₁ = 16 mm.

For m = 3, the deflection curve satisfying Eq. (f) is now as in Fig. 9.10c. Hence, Eq. (g) at z = (by setting υ_n = υ₁) and at z = (by setting υ_n = υ₂) leads to

from which υ₁ = 9 mm and υ₂ = 11 mm.

For m = 4, a similar procedure yields υ₁ = 5.3 mm, υ₂ = 9.7 mm, and υ₃ = 7.5 mm.

9.9 Applications

The theory of beams on elastic foundation is applicable to many problems of practical importance, of which one is discussed next. The concept of a beam on elastic foundation may also be employed to approximate stress and deflection in axisymmetrically loaded cylindrical shells. The governing equations of the two problems are of the same form. This means that solutions of one problem become solutions of the other problem through a simple change of constants [Ref. 9.7].

Grid Configurations of Beams

The ability of a floor to sustain extreme loads without undue deflection, as in a machine shop, is significantly enhanced by combining the floor beams in a particular array or grid configuration. Such a design is illustrated in the ensuing problem.

Example 9.7

A single concentrated load P acts at the center of a machine room floor composed of 79 transverse beams (spaced a = 0.3 m apart) and one longitudinal beam, as shown in Fig. 9.11. If all beams have the same modulus of rigidity EI, determine the deflection and the distribution of load over the various transverse beams supporting the longitudinal beam. Assume that the transverse and longitudinal beams are attached so that they deform together.

Figure 9.11. Example 9.7. Long beam supported by several identical and equally spaced crossbeams. All beams are simply supported at their ends.

Solution The spring constant K of an individual elastic support such as beam AA is

where υ_c is the central deflection of a simply supported beam of length L_t carrying a center load R_c. From Eq. (9.16), the modulus k of the equivalent continuous elastic foundation is found to be

Thus,

and

In accordance with the criteria discussed in Secs. 9.4 and 9.5, the longitudinal beam may be classified as a long beam resting on a continuous elastic support of modulus k. Consequently, from Eqs. (9.8), the deflection at midspan is

The deflection of a transverse beam depends on its distance x from the center of the longitudinal beam, as shown in the following tabulation:

We are now in a position to calculate the load R_cc supported by the central transverse beam. Since the midspan deflection υ_M of the central transverse beam is equal to υ_p, we have

and

The remaining transverse beam loads are now readily calculated on the basis of the deflections in the previous tabulation, recalling that the loads are linearly proportional to the deflections.

We observe that, beyond beam 11, it is possible for a transverse beam to be pulled up as a result of the central loading. This is indicated by the negative value of the deflection. The longitudinal beam thus serves to decrease transverse beam deflection only if it is sufficiently rigid.

Problems

Secs. 9.1 through 9.4

9.1. A very long S127 × 15 steel 1-beam, 0.127 m deep, resting on a foundation for which k = 1.4 MPa, is subjected to a concentrated load at midlength. The flange is 0.0762 m wide, and the cross-sectional moment of inertia is 5.04 × 10^-6 m⁴. What is the maximum load that can be applied to the beam without causing the elastic limit to be exceeded? Assume that E = 200 GPa and σ_yp = 210 MPa.

9.2. A long steel beam (E = 200 GPa) of depth 2.5b and width b is to rest on an elastic foundation (k = 20 MPa) and support a 40-kN load at its center (Fig. 9.2). Design the beam (compute b) if the bending stress is not to exceed 250 MPa.

9.3. A long beam on an elastic foundation is subjected to a sinusoidal loading p = P₁ sin (2πx/L), where p₁ and L are the peak intensity and wavelength of loading, respectively. Determine the equation of the elastic deflection curve in terms of k and β.

9.4. If point Q is taken to the right of the loaded portion of the beam shown in Fig. 9.3, what is the deflection at this point?

9.5. A single train wheel exerts a load of 135 kN on a rail assumed to be supported by an elastic foundation. For a modulus of foundation k = 16.8 MPa, determine the maximum deflection and maximum bending stress in the rail. The respective values of the section modulus and modulus of rigidity are S = 3.9 × 10^-4 m³ and EI = 8.437 MN · m².

9.6. A long rail is subjected to a concentrated load at its center (Fig. 9.2). Determine the effect on maximum deflection and maximum stress of overestimating the modulus of foundation k by (a) 25% and (b) 40%.

9.7. Calculate the maximum resultant bending moment and deflection in the rail of Prob. 9.5 if two wheel loads spaced 1.66 m apart act on the rail. The remaining conditions of the problem are unchanged.

9.8. Determine the deflection at any point Q under the triangular loading acting on an infinite beam on an elastic foundation (Fig. P9.8).

Figure P9.8.

9.9. What are the reactions acting on a semi-infinite beam built in at the left end and subjected to a uniformly distributed loading p? Use the method of superposition. [Hint: At a large distance from the left end, the deflection is p/k.]

9.10. A semi-infinite beam on elastic foundation is subjected to a moment M_A at its end (Fig. 9.5 with P = 0). Determine (a) the ratio of the maximum upward and maximum downward deflections; (b) the ratio of the maximum and minimum moments.

9.11. A semi-infinite beam on an elastic foundation is hinged at the left end and subjected to a moment M_L at that end. Determine the equation of the deflection curve, slope, moment, and shear force.

Secs. 9.5 through 9.9

9.12. A machine base consists partly of a 5.4-m-long S127 × 15 steel I-beam supported by coil springs spaced a = 0.625 m apart. The constant for each spring is K = 180 kN/m. The moment of inertia of the I-section is 5.4 × 10^-6 m⁴, the depth is 0.127 m, and the flange width is 0.0762 m. Assuming that a concentrated force of 6.75 kN transmitted from the machine acts at midspan, determine the maximum deflection, maximum bending moment, and maximum stress in the beam.

9.13. A steel beam of 0.75-m length and 0.05-m square cross section is supported on three coil springs spaced a = 0.375 m apart. For each spring, K = 18 kN/m. Determine (a) the deflection of the beam if a load P = 540 N is applied at midspan and (b) the deflection at the ends of the beam if a load P = 540 N acts 0.25 m from the left end.

9.14. A finite beam with EI = 8.4 MN · m² rests on an elastic foundation for which k = 14 MPa. The length L of the beam is 0.6 m. If the beam is subjected to a concentrated load P = 4.5 kN at its midpoint, determine the maximum deflection.

9.15. A finite beam is subjected to a concentrated force P = 9 kN at its mid-length and a uniform loading p = 7.5 kN/m. Determine the maximum deflection and slope if L = 0.15 m, EI = 8.4 MN · m², and k = 14 MPa.

9.16. Redo Example 9.6 for the case in which both ends of the beam are simply supported.

9.17. Assume that all the data of Example 9.7 are unchanged except that a uniformly distributed load p replaces the concentrated force on the longitudinal beam. Compute the load R_CC supported by the central transverse beam.