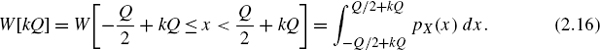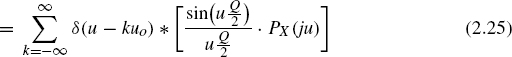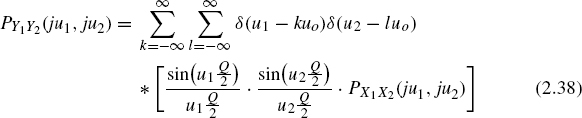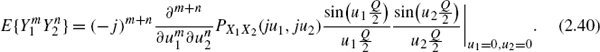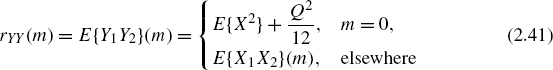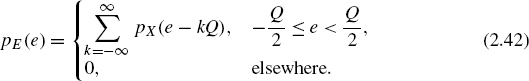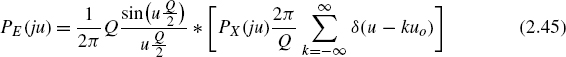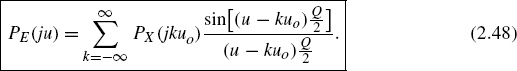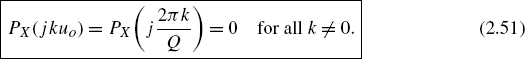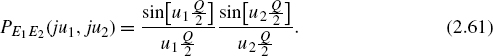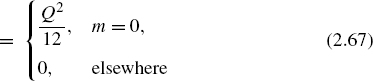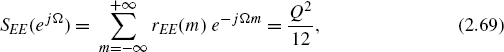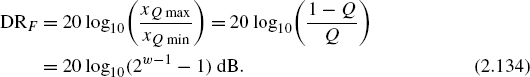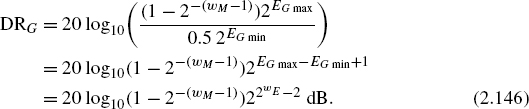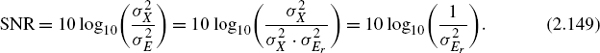Chapter 2

Quantization

Basic operations for AD conversion of a continuous-time signal x(t) are the sampling and quantization of x(n) yielding the quantized sequence x_Q(n) (see Fig. 2.1). Before discussing AD/DA conversion techniques and the choice of the sampling frequency f_S = 1/T_S in Chapter 3 we will introduce the quantization of the samples x(n) with finite number of bits. The digitization of a sampled signal with continuous amplitude is called quantization. The effects of quantization starting with the classical quantization model are discussed in Section 2.1. In Section 2.2 dither techniques are presented which, for low-level signals, linearize the process of quantization. In Section 2.3 spectral shaping of quantization errors is described. Section 2.4 deals with number representation for digital audio signals and their effects on algorithms.

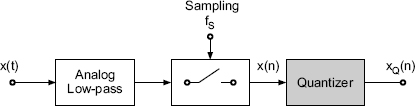
Figure 2.1 AD conversion and quantization.

2.1 Signal Quantization

2.1.1 Classical Quantization Model

Quantization is described by Widrow's quantization theorem [Wid61]. This says that a quantizer can be modeled (see Fig. 2.2) as the addition of a uniform distributed random signal e(n) to the original signal x(n) (see Fig. 2.2, [Wid61]). This additive model,

is based on the difference between quantized output and input according to the error signal

Figure 2.2 Quantization.

This linear model of the output x_Q(n) is only then valid when the input amplitude has a wide dynamic range and the quantization error e(n) is not correlated with the signal x(n). Owing to the statistical independence of consecutive quantization errors the autocorrelation of the error signal is given by , yielding a power density spectrum .

The nonlinear process of quantization is described by a nonlinear characteristic curve as shown in Fig. 2.3a, where Q denotes the quantization step. The difference between output and input of the quantizer provides the quantization error e(n) = x_Q(n) − x(n), which is shown in Fig. 2.3b. The uniform probability density function (PDF) of the quantization error is given (see Fig. 2.3b) by

Figure 2.3 (a) Nonlinear characteristic curve of a quantizer. (b) Quantization error e and its probability density function (PDF) _pE(e).

The mth moment of a random variable E with a PDF _pE(e) is defined as the expected value of E^m:

For a uniform distributed random process, as in (2.3), the first two moments are given by

The signal-to-noise ratio

is defined as the ratio of signal power to error power .

For a quantizer with input range ±x_max and word-length w, the quantization step size can be expressed as

By defining a peak factor,

the variances of the input and the quantization error can be written as

The signal-to-noise ratio is then given by

A sinusoidal signal (PDF as in Fig. 2.4) with gives

For a signal with uniform PDF (see Fig. 2.4) and we can write

and for a Gaussian distributed signal (probability of overload <10⁻⁵ leads to P_F = 4.61, see Fig. 2.5), it follows that

It is obvious that the signal-to-noise ratio depends on the PDF of the input. For digital audio signals that exhibit nearly Gaussian distribution, the maximum signal-to-noise ratio for given word-length w is 8.5 dB lower than the rule-of-thumb formula (2.14) for the signal-to-noise ratio.

Figure 2.4 Probability density function (sinusoidal signal and signal with uniform PDF).

Figure 2.5 Probability density function (signal with Gaussian PDF).

2.1.2 Quantization Theorem

The statement of the quantization theorem for amplitude sampling (digitizing the amplitude) of signals was given by Widrow [Wid61]. The analogy for digitizing the time axis is the sampling theorem due to Shannon [Sha48]. Figure 2.6 shows the amplitude quantization and the time quantization. First of all, the PDF of the output signal of a quantizer is determined in terms of the PDF of the input signal. Both probability density functions are shown in Fig. 2.7. The respective characteristic functions (Fourier transform of a PDF) of the input and output signals form the basis for Widrow's quantization theorem.

Figure 2.6 Amplitude and time quantization.

Figure 2.7 Probability density function of signal x(n) and quantized signal x_Q(n).

First-order Statistics of the Quantizer Output

Quantization of a continuous-amplitude signal x with PDF_pX(x) leads to a discrete-amplitude signal y with PDF_pY(y) (see Fig. 2.8). The continuous PDF of the input is sampled by integrating over all quantization intervals (zone sampling). This leads to a discrete PDF of the output.

In the quantization intervals, the discrete PDF of the output is determined by the probability

Figure 2.8 Zone sampling of the PDF.

For the intervals k = 0, 1, 2, it follows that

The summation over all intervals gives the PDF of the output

where

Using

the PDF of the output is given by

The PDF of the output can hence be determined by convolution of a rect function [Lip92] with the PDF of the input. This is followed by an amplitude sampling with resolution Q as described in (2.23) (see Fig. 2.9).

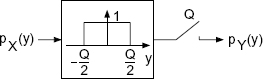
Figure 2.9 Determining PDF of the output.

Using , the characteristic function (Fourier transform of PY(y)) can be written, with u_o = 2π/Q, as

Equation (2.26) describes the sampling of the continuous PDF of the input. If the quantization frequency u_o = 2π/Q is twice the highest frequency of the characteristic function P_X(ju) then periodically recurring spectra do not overlap. Hence, a reconstruction of the PDF of the input _pX(x) from the quantized PDF of the output _pY(y) is possible (see Fig. 2.10). This is known as Widrow's quantization theorem. Contrary to the first sampling theorem (Shannon's sampling theorem, ideal amplitude sampling in the time domain) , it can be observed that there is an additional multiplication of the periodically characteristic function with (see (2.26)).

If the base-band of the characteristic function (k = 0)

is considered, it is observed that it is a product of two characteristic functions. The multiplication of characteristic functions leads to the convolution of PDFs from which the addition of two statistically independent signals can be concluded. The characteristic function of the quantization error is thus

Figure 2.10 Spectral representation.

and the PDF

(see Fig. 2.11).

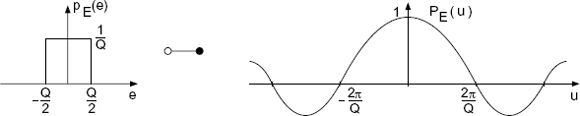
Figure 2.11 PDF and characteristic function of quantization error.

The modeling of the quantization process as an addition of a statistically independent noise signal to the input signal leads to a continuous PDF of the output (see Fig. 2.12, convolution of PDFs and sampling in the interval Q gives the discrete PDF of the output). The PDF of the discrete-valued output comprises Dirac pulses at distance Q with values equal to the continuous PDF (see (2.23)). Only if the quantization theorem is valid can the continuous PDF be reconstructed from the discrete PDF.

Figure 2.12 PDF of model.

In many cases, it is not necessary to reconstruct the PDF of the input. It is sufficient to calculate the moments of the input from the output. The mth moment can be expressed in terms of the PDF or the characteristic function:

If the quantization theorem is satisfied then the periodic terms in (2.26) do not overlap and the mth derivative of P_Y(ju) is solely determined by the base-band¹ so that, with (2.26),

With (2.32), the first two moments can be determined as

Second-order Statistics of Quantizer Output

In order to describe the properties of the output in the frequency domain, two output values Y₁ (at time n₁) and Y₂ (at time n₂) are considered [Lip92]. For the joint density function,

with

and

For the two-dimensional Fourier transform, it follows that

Similar to the one-dimensional quantization theorem, a two-dimensional theorem [Wid61] can be formulated: the joint density function of the input can be reconstructed from the joint density function of the output, if P_X1X2(ju₁, ju₂) = 0 for u₁ ≥ u_o/2 and u₂ ≥ u_o/2. Here again, the moments of the joint density function can be calculated as follows:

From this, the autocorrelation function with m = n₂ − n₁ can be written as

(for m = 0 we obtain (2.34)).

2.1.3 Statistics of Quantization Error

First-order Statistics of Quantization Error

The PDF of the quantization error depends on the PDF of the input and is dealt with in the following. The quantization error e = x_Q − x is restricted to the interval . It depends linearly on the input (see Fig. 2.13). If the input value lies in the interval then the error is e = 0 − x. For the PDF we obtain _pE(e) = _pX(e). If the input value lies in the interval then the quantization error is and is again restricted to . The PDF of the quantization error is consequently _pE(e) = _pX(e + Q) and is added to the first term. For the sum over all intervals we can write

Figure 2.13 Probability density function and quantization error.

Because of the restricted values of the variable of the PDF, we can write

The PDF of the quantization error is determined by the PDF of the input and can be computed by shifting and windowing a zone. All individual zones are summed up for calculating the PDF of the quantization error [Lip92]. A simple graphical interpretation of this overlapping is shown in Fig. 2.14. The overlapping leads to a uniform distribution of the quantization error if the input PDF _pX(x) is spread over a sufficient number of quantization intervals.

Figure 2.14 Probability density function of the quantization error.

For the Fourier transform of the PDF from (2.44) it follows that

If the quantization theorem is satisfied, i.e. if P_X(ju) = 0 for u > u_o/2, then there is only one non-zero term (k = 0 in (2.48)). The characteristic function of the quantization error is reduced, with P_X(0) = 1, to

Hence, the PDF of the quantization error is

Sripad and Snyder [Sri77] have modified the sufficient condition of Widrow (band-limited characteristic function of input) for a quantization error of uniform PDF by the weaker condition

The uniform distribution of the input PDF,

with characteristic function

does not satisfy Widrow's condition for a band-limited characteristic function, but instead the weaker condition,

is fulfilled. From this follows the uniform PDF (2.49) of the quantization error. The weaker condition from Sripad and Snyder extends the class of input signals for which a uniform PDF of the quantization error can be assumed.

In order to show the deviation from the uniform PDF of the quantization error as a function of the PDF of the input, (2.48) can be written as

The inverse Fourier transform yields

Equation (2.56) shows the effect of the input PDF on the deviation from a uniform PDF.

Second-order Statistics of Quantization Error

To describe the spectral properties of the error signal, two values E₁ (at time n₁) and E₂ (at time n₂) are considered [Lip92]. The joint PDF is given by

Here δ_QQ(e₁, e₂) = δ_Q(e₁) · δ_Q(e₂) and rect(e₁/Q, e₂/Q) = rect(e₁/Q) · rect(e₂/Q). For the Fourier transform of the joint PDF, a similar procedure to that shown by (2.45)–(2.48) leads to

If the quantization theorem and/or the Sripad–Snyder condition

are satisfied then

Thus, for the joint PDF of the quantization error,

Due to the statistical independence of quantization errors (2.63),

For the moments of the joint PDF,

From this, it follows for the autocorrelation function with m = n₂ − n₁ that

The power density spectrum of the quantization error is then given by

which is equal to the variance of the quantization error (see Fig. 2.15).

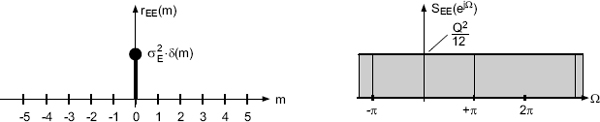
Figure 2.15 Autocorrelation r_EE(m) and power density spectrum S_EE(e^jΩ) of quantization error e(n).

Correlation of Signal and Quantization Error

To describe the correlation of the signal and the quantization error [Sri77], the second moment of the output with (2.26) is derived as follows:

With the quantization error e(n) = y(n) − x(n),

where the term E{X · E }, with (2.72), is written as

With the assumption of a Gaussian PDF of the input we obtain

with the characteristic function

Using (2.57), the PDF of the quantization error is then given by

Figure 2.16a shows the PDF (2.77) of the quantization error for different variances of the input.

Figure 2.16 (a) PDF of quantization error for different standard deviations of a Gaussian PDF input. (b) Variance of quantization error for different standard deviations of a Gaussian PDF input.

For the mean value and the variance of a quantization error, it follows using (2.77) that E{E} = 0 and

Figure 2.16b shows the variance of the quantization error (2.78) for different variances of the input.

For a Gaussian PDF input as given by (2.75) and (2.76), the correlation (see (2.74)) between input and quantization error is expressed as

The correlation is negligible for large values of σ/Q.

2.2 Dither

2.2.1 Basics

The requantization (renewed quantization of already quantized signals) to limited word-lengths occurs repeatedly during storage, format conversion and signal processing algorithms. Here, small signal levels lead to error signals which depend on the input. Owing to quantization, nonlinear distortion occurs for low-level signals. The conditions for the classical quantization model are not satisfied anymore. To reduce these effects for signals of small amplitude, a linearization of the nonlinear characteristic curve of the quantizer is performed. This is done by adding a random sequence d(n) to the quantized signal x(n) (see Fig. 2.17) before the actual quantization process. The specification of the word-length is shown in Fig. 2.18. This random signal is called dither. The statistical independence of the error signal from the input is not achieved, but the conditional moments of the error signal can be affected [Lip92, Ger89, Wan92, Wan00].

Figure 2.17 Addition of a random sequence before a quantizer.

Figure 2.18 Specification of the word-length.

The sequence d(n), with amplitude range (−Q/2 ≤ d(n) ≤ Q/2), is generated with the help of a random number generator and is added to the input. For a dither value with Q = 2^−(w−1):

The index k of the random number d_k characterizes the value from the set of N = 2^s possible numbers with the probability

With the mean value , the variance and the quadratic mean , we can rewrite the variance as .

For a static input amplitude V and the dither value d_k the rounding operation [Lip86] is expressed as

For the mean of the output as a function of the input V, we can write

The quadratic mean of the output for input V is given by

For the variance for input V,

The above equations have the input V as a parameter. Figures 2.19 and 2.20 illustrate the mean output and the standard deviation d_R(V) within a quantization step size, given by (2.83), (2.84) and (2.85). The examples of rounding and truncation demonstrate the linearization of the characteristic curve of the quantizer. The coarse step size is replaced by a finer one. The quadratic deviation from the mean output is termed noise modulation. For a uniform PDF dither, this noise modulation depends on the amplitude (see Figs. 2.19 and 2.20). It is maximum in the middle of the quantization step size and approaches zero toward the end. The linearization and the suppression of the noise modulation can be achieved by a triangular PDF dither with bipolar characteristic [Van89] and rounding operation (see Fig. 2.20). Triangular PDF dither is obtained by adding two statistically independent dither signals with uniform PDF (convolution of PDFs). A dither signal with higher-order PDF is not necessary for audio signals [Lip92, Wan00].

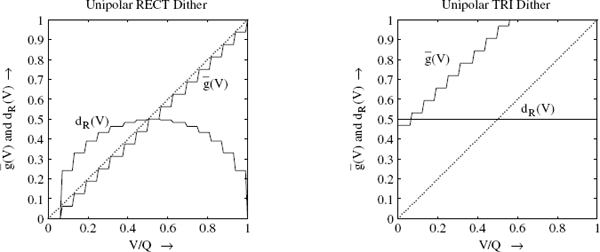
Figure 2.19 Truncation – linearizing and suppression of noise modulation (s = 4, m = 0).

The total noise power for this quantization technique consists of the dither power and the power of the quantization error [Lip86]. The following noise powers are obtained by integration with respect to V.

Figure 2.20 Rounding – linearizing and suppression of noise modulation (s = 4, m = 1).

1. Mean dither power d²:

   

   

   (This is equal to the deviation from mean output in accordance with (2.83).)

2. Mean of total noise power :

   

   (This is equal to the deviation from an ideal straight line.)

In order to derive a relationship between and d², the quantization error given by

is used to rewrite (2.88) as

The integrals in (2.91) are independent of d_k. Moreover, Σ_k P(d_k) = 1. With the mean value of the quantization error

and the quadratic mean error

it is possible to rewrite (2.91) as

With , (2.94) can be written as

Equations (2.94) and (2.95) describe the total noise power as a function of the quantization and the dither addition . It can be seen that for zero-mean quantization, the middle term in (2.95) results in . The acoustically perceptible part of the total error power is represented by and .

2.2.2 Implementation

The random sequence d(n) is generated with the help of a random number generator with uniform PDF. For generating a triangular PDF random sequence, two independent uniform PDF random sequences d₁(n) and d₂(n) can be added. In order to generate a triangular high-pass dither, the dither value d₁(n) is added to −d₁(n − 1). Thus, only one random number generator is required. In conclusion, the following dither sequences can be implemented:

The power density spectra of triangular PDF dither and triangular PDF HP dither are shown in Fig. 2.21. Figure 2.22 shows histograms of a uniform PDF dither and a triangular PDF high-pass dither together with their respective power density spectra. The amplitude range of a uniform PDF dither lies between ±Q/2, whereas it lies between ±Q for triangular PDF dither. The total noise power for triangular PDF dither is doubled.

2.2.3 Examples

The effect of the input amplitude of the quantizer is shown in Fig. 2.23 for a 16-bit quantizer (Q = 2⁻¹⁵). A quantized sinusoidal signal with amplitude 2⁻¹⁵ (1-bit amplitude) and frequency f/fS = 64/1024 is shown in Fig. 2.23a, b for rounding and truncation. Figure 2.23c, d shows their corresponding spectra. For truncation, Fig. 2.23c shows the spectral line of the signal and the spectral distribution of the quantization error with the harmonics of the input signal. For rounding (Fig. 2.23d with special signal frequency f/fS = 64/1024), the quantization error is concentrated in uneven harmonics.

Figure 2.21 Normalized power density spectrum for triangular PDF dither (TRI) with d₁(n) + d₂(n) and triangular PDF high-pass dither (HP) with d₁(n) − d₁(n − 1).

In the following, only the rounding operation is used. By adding a uniform PDF random signal to the actual signal before quantization, the quantized signal shown in Fig. 2.24a results. The corresponding power density spectrum is illustrated in Fig. 2.24c. In the time domain, it is observed that the 1-bit amplitudes approach zero so that the regular pattern of the quantized signal is affected. The resulting power density spectrum in Fig. 2.24c shows that the harmonics do not occur anymore and the noise power is uniformly distributed over the frequencies. For triangular PDF dither, the quantized signal is shown in Fig. 2.24b. Owing to triangular PDF, amplitudes ±2Q occur besides the signal values ±Q and zero. Figure 2.24d shows the increase of the total noise power.

In order to illustrate the noise modulation for uniform PDF dither, the amplitude of the input is reduced to A = 2⁻¹⁸ and the frequency is chosen as f/fS = 14/1024. This means that input amplitude to the quantizer is 0.25 bit. For a quantizer without additive dither, the quantized output signal is zero. For RECT dither, the quantized signal is shown in Fig. 2.25a. The input signal with amplitude 0.25Q is also shown. The power density spectrum of the quantized signal is shown in Fig. 2.25c. The spectral line of the signal and the uniform distribution of the quantization error can be seen. But in the time domain, a correlation between positive and negative amplitudes of the input and the quantized positive and negative values of the output can be observed. In hearing tests this noise modulation occurs if the amplitude of the input is decreased continuously and falls below the amplitude of the quantization step. This process occurs for all fade-out processes that occur in speech and music signals. For positive low-amplitude signals, two output states, zero and Q, occur, and for negative low-amplitude signals, the output states zero and −Q, occur. This is observed as a disturbing rattle which is overlapped to the actual signal. If the input level is further reduced the quantized output approaches zero.

Figure 2.22 (a, b) Histogram and (c, d) power density spectrum of uniform PDF dither (RECT) with d₁(n) and triangular PDF high-pass dither (HP) with d₁(n) − d₁(n − 1).

In order to reduce this noise modulation at low levels, a triangular PDF dither is used. Figure 2.25b shows the quantized signal and Fig. 2.25d shows the power density spectrum. It can be observed that the quantized signal has an irregular pattern. Hence a direct association of positive half-waves with the positive output values as well as vice versa is not possible. The power density spectrum shows that spectral line of the signal along with an increase in noise power owing to triangular PDF dither. In acoustic hearing tests, the use of triangular PDF dither results in a constant noise floor even if the input level is reduced to zero.

Figure 2.23 One-bit amplitude – quantizer with truncation (a, c) and rounding (b, d).

2.3 Spectrum Shaping of Quantization – Noise Shaping

Using the linear model of a quantizer in Fig. 2.26 and the relations

the quantization error e(n) may be isolated and fed back through a transfer function H(z) as shown in Fig. 2.27. This leads to the spectral shaping of the quantization error as given by

Figure 2.24 One-bit amplitude – rounding with RECT dither (a, c) and TRI dither (b, d).

and the corresponding Z-transforms

A simple spectrum shaping of the quantization error e(n) is achieved by feeding back with H(z) = z⁻¹ as shown in Fig. 2.28, and leads to

and the Z-transforms

Figure 2.25 0.25-bit amplitude – rounding with RECT dither (a, c) and TRI dither (b, d).

Figure 2.26 Linear model of quantizer.

Equation (2.113) shows a high-pass weighting of the original error signal e(n). By choosing H(z) = z⁻¹(−2 +z⁻¹), second-order high-pass weighting given by

can be achieved. The power density spectrum of the error signal for the two cases is given by

Figure 2.29 shows the weighting of power density spectrum by this noise shaping technique.

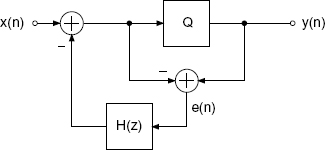
Figure 2.27 Spectrum shaping of quantization error.

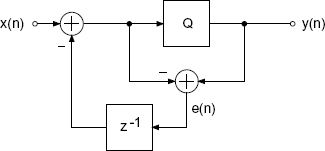
Figure 2.28 High-pass spectrum shaping of quantization error.

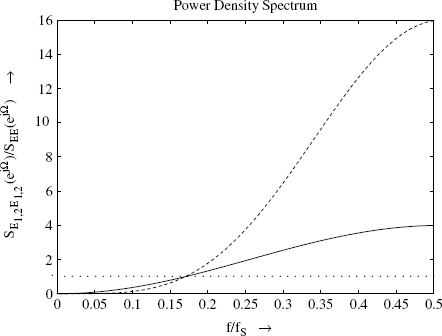
Figure 2.29 Spectrum shaping (S_EE(e^jΩ) …, S_E1E1(e^jΩ)—, S_E2E2(e^jΩ)---).

By adding a dither signal d(n) (see Fig. 2.30), the output and the error are given by

and

For the Z-transforms we write

The modified error signal e₁(n) consists of the dither and the high-pass shaped quantization error.

Figure 2.30 Dither and spectrum shaping.

By moving the addition (Fig. 2.31) of the dither directly before the quantizer, a high-pass spectrum shaping is obtained for both the error signal and the dither. Here the following relationships hold:

with the Z-transforms given by

Apart from the discussed feedback structures which are easy to implement on a digital signal processor and which lead to high-pass noise shaping, psychoacoustic-based noise shaping methods have been proposed in the literature [Ger89, Wan92, Hel07]. These methods use special approximations of the hearing threshold (threshold in quiet, absolute threshold) for the feedback structure 1 − H(z). Figure 2.32a shows several hearing threshold models as a function of frequency [ISO389, Ter79, Wan92]. It can be seen that the sensitivity of human hearing is high for frequencies between 2 and 6 kHz and sharply decreases for high and low frequencies. Figure 2.32b also shows the inverse ISO 389-7 threshold curve which represents an approximation of the filtering operation in our perception. The feedback filter of the noise shaper should affect the quantization error with the inverse ISO 389 weighting curve. Hence, the noise power in the frequency range with high sensitivity should be reduced and shifted toward lower and higher frequencies. Figure 2.33a shows the unweighted power density spectra of the quantization error for three special filters H(z) [Wan92, Hel07]. Figure 2.33b depicts the same three power density spectra, weighted by the inverse ISO 389 threshold of Fig. 2.32b. These weighted power density spectra show that the perceived noise power is reduced by all three noise shapers versus the frequency axis. Figure 2.34 shows a sinusoid with amplitude Q = 2⁻¹⁵, which is quantized to w = 16 bits with psychoacoustic noise shaping. The quantized signal x_Q(n) consists of different amplitudes reflecting the low-level signal. The power density spectrum of the quantized signal reflects the psychoacoustic weighting of the noise shaper with a fixed filter. A time-variant psychoacoustic noise shaping is described in [DeK03, Hel07], where the instantaneous masking threshold is used for adaptation of a time-variant filter.

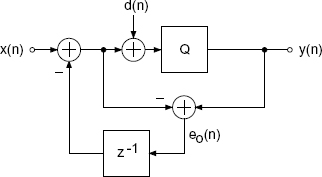
Figure 2.31 Modified dither and spectrum shaping.

2.4 Number Representation

The different applications in digital signal processing and transmission of audio signals leads to the question of the type of number representation for digital audio signals. In this section, basic properties of fixed-point and floating-point number representation in the context of digital audio signal processing are presented.

2.4.1 Fixed-point Number Representation

In general, an arbitrary real number x can be approximated by a finite summation

where the possible values for b_i are 0 and 1.

The fixed-point number representation with a finite number w of binary places leads to four different interpretations of the number range (see Table 2.1 and Fig. 2.35).

Figure 2.32 (a) Hearing thresholds in quiet. (b) Inverse ISO 389-7 threshold curve.

Table 2.1 Bit location and range of values.

The signed fractional representation (2's complement) is the usual format for digital audio signals and for algorithms in fixed-point arithmetic. For address and modulo operation, the unsigned integer is used. Owing to finite word-length w, overflow occurs as shown in Fig. 2.36. These curves have to be taken into consideration while carrying out operations, especially additions in 2's complement arithmetic.

Quantization is carried out with techniques as shown in Table 2.2 for rounding and truncation. The quantization step size is characterized by Q = 2^−(w−1) and the symbol denotes the biggest integer smaller than or equal to x. Figure 2.37 shows the rounding and truncation curves for 2's complement number representation. The absolute error shown in Fig. 2.37 is given by e = x_Q − x.

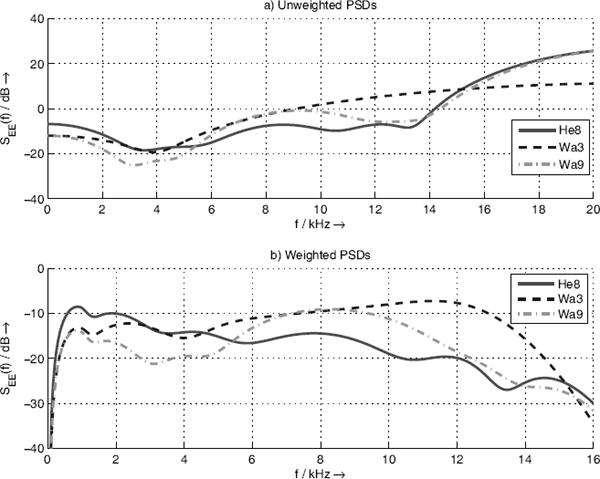
Figure 2.33 Power density spectrum of three filter approximations (Wa3 third-order filter, Wa9 ninthorder filter, He8 eighth-order filter [Wan92, Hel07]): (a) unweighted PSDs, (b) inverse ISO 389-7 weighted PSDs.

Table 2.2 Rounding and truncation of 2s complement numbers.

Digital audio signals are coded in the 2's complement number representation. For 2's complement representation, the range of values from − X_max to +X_max is normalized to the range −1 to +1 and is represented by the weighted finite sum x_Q = −b₀ + b₁ · 0.5 + b₂ · 0.25 + b₃ · 0.125 +…+ b_w−1 · 2^−(w−1). The variables b₀ to b_w−1 are called bits and can take the values 1 or 0. The bit b₀ is called the MSB (most significant bit) and b_w−1 is called the LSB (least significant bit). For positive numbers, b₀ is equal to 0 and for negative numbers b₀ equals 1. For a 3-bit quantization (see Fig. 2.38), a quantized value can be represented by x_Q = −b₀ + b₁ · 0.5 + b₂ · 0.25. The smallest quantization step size is 0.25. For a positive number 0.75 it follows that 0.75 = −0 + 1 · 0.5 + 1 · 0.25. The binary coding for 0.75 is 011.

Figure 2.34 Psychoacoustic noise shaping: signal x(n), quantized signal x_Q(n) and power density spectrum of quantized signal.

Figure 2.35 Fixed-point formats.

Figure 2.36 Number range.

Figure 2.37 Rounding and truncation curves.

Figure 2.38 Rounding curve and error signal for w = 3 bits.

Dynamic Range. The dynamic range of a number representation is defined as the ratio of maximum to minimum number. For fixed-point representation with

the dynamic range is given by

Multiplication and Addition of Fixed-point Numbers. For the multiplication of two fixed-point numbers in the range from −1 to +1, the result is always less than 1. For the addition of two fixed-point numbers, care must be taken for the result to remain in the range from −1 to +1. An addition of 0.6 + 0.7 = 1.3 must be carried out in the form 0.5(0.6 + 0.7) = 0.65. This multiplication with the factor 0.5 or generally 2^−s is called scaling. An integer in the range from 1 to, for instance, 8 is chosen for the scaling coefficient s.

Error Model. The quantization process for fixed-point numbers can be approximated as an the addition of an error signal e(n) to the signal x(n) (see Fig. 2.39). The error signal is a random signal with white power density spectrum.

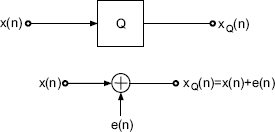
Figure 2.39 Model of a fixed-point quantizer.

Signal-to-noise Ratio. The signal-to-noise ratio for a fixed-point quantizer is defined by

where is the signal power and is the noise power.

2.4.2 Floating-point Number Representation

The representation of a floating-point number is given by

with

where M_G denotes the normalized mantissa and E_G the exponent. The normalized standard format (IEEE) is shown in Fig. 2.40 and special cases are given in Table 2.3. The mantissa M is implemented with a word-length of w_M bits and is in fixed-point number representation. The exponent E is implemented with a word-length of w_E bits and is an integer in the range from −2^w_E−1 + 2 to 2^w_E−1 − 1. For an exponent word-length of w_E = 8 bits, its range of values lies between −126 and +127. The range of values of the mantissa lies between 0.5 and 1. This is referred to as the normalized mantissa and is responsible for the unique representation of a number. For a fixed-point number in the range between 0.5 and 1, it follows that the exponent of the floating-point number representation is E = 0. To represent a fixed-point number in the range between 0.25 and 0.5 in floating-point form, the range of values of the normalized mantissa M lies between 0.5 and 1, and for the exponent it follows that E = −1. As an example, for a fixed-point number 0.75 the floating-point number 0.75 · 2⁰ results. The fixed-point number 0.375 is not represented as the floating-point number 0.375 · 2⁰. With the normalized mantissa, the floating-point number is expressed as 0.75 · 2⁻¹. Owing to normalization, the ambiguity of floating-point number representation is avoided. Numbers greater than 1 can be represented. For example, 1.5 becomes 0.75 · 2¹ in floating-point number representation.

Figure 2.41 shows the rounding and truncations curves for floating-point representation and the absolute error e = x_Q − x. The curves for floating-point quantization show that for small amplitudes small quantization step sizes occur. In contrast to fixed-point representation, the absolute error is dependent on the input signal.

Figure 2.40 Floating-point number representation.

Table 2.3 Special cases of floating-point number representation.

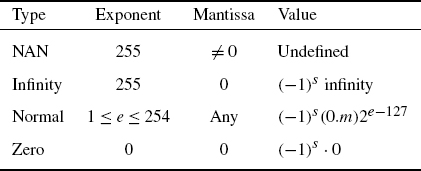
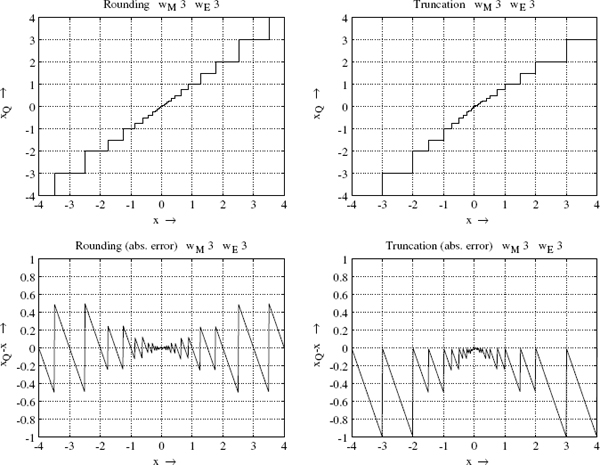
Figure 2.41 Rounding and truncation curves for floating-point representation.

In the interval

the quantization step is given by

For the relative error

of the floating-point representation, a constant upper limit can be stated as

Dynamic Range. With the maximum and minimum numbers given by

and

the dynamic range for floating-point representation is given by

Multiplication and Addition of Floating-point Numbers. For multiplications with floating-point numbers, the exponents of both numbers x_Q1 = M₁2^E₁ and x_Q2 = M₂2^E₂ are added and the mantissas are multiplied. The resulting exponent E_G = E₁ + E₂ is adjusted so that M_G = M₁ M₂ lies in the interval 0.5 ≤ M_G < 1. For additions the smaller number is denormalized to get the same exponent. Then both mantissa are added and the result is normalized.

Error Model. With the definition of the relative error e_r(n) = [x_Q(n) − x(n) ]/x(n) the quantized signal can be written as

Floating-point quantization can be modeled as an additive error signal e(n) = x(n) · e_r(n) to the signal x(n) (see Fig. 2.42).

Signal-to-noise Ratio. Under the assumption that the relative error is independent of the input x, the noise power of the floating-point quantizer can be written as

Figure 2.42 Model of a floating-point quantizer.

For the signal-to-noise-ratio, we can derive

Equation (2.149) shows that the signal-to-noise ratio is independent of the level of the input. It is only dependent on the noise power which, in turn, is only dependent on the word-length w_M of the mantissa of the floating-point representation.

2.4.3 Effects on Format Conversion and Algorithms

First, a comparison of signal-to-noise ratios is made for the fixed-point and floating-point number representation. Figure 2.43 shows the signal-to-noise ratio as a function of input level for both number representations. The fixed-point word-length is w = 16 bits. The word-length of the mantissa in floating-point representation is also w_M = 16 bits, whereas that of the exponent is w_E = 4 bits. The signal-to-noise ratio for floating-point representation shows that it is independent of input level and varies as a sawtooth curve in a 6 dB grid. If the input level is so low that a normalization of the mantissa due to finite number representation is not possible, then the signal-to-noise ratio is comparable to fixed-point representation. While using the full range, both fixed-point and floating-point result in the same signal-to-noise ratio. It can be observed that the signal-to-noise ratio for fixed-point representation depends on the input level. This signal-to-noise ratio in the digital domain is an exact image of the level-dependent signal-to-noise ratio of an analog signal in the analog domain. A floating-point representation cannot improve this signal-to-noise ratio. Rather, the floating-point curve is vertically shifted downwards to the value of signal-to-noise ratio of an analog signal.

AD/DA Conversion. Before processing, storing and transmission of audio signals, the analog audio signal is converted into a digital signal. The precision of this conversion depends on the word-length w of the AD converter. The resulting signal-to-noise ratio is 6w dB for uniform PDF inputs. The signal-to-noise ratio in the analog domain depends on the level. This linear dependence of signal-to-noise ratio on level is preserved after AD conversion with subsequent fixed-point representation.

Digital Audio Formats. The basis for established digital audio transmission formats is provided in the previous section on AD/DA conversion. The digital two-channel AES/EBU interface [AES92] and 56-channel MADI interface [AES91] both operate with fixed-point representation with a word-length of at most 24 bits per channel.

Figure 2.43 Signal-to-noise ratio for an input level.

Storage and Transmission. Besides the established storage media like compact disc and DAT which were exclusively developed for audio application, there are storage systems like hard discs in computers. These are based on magnetic or magneto-optic principles. The systems operate with fixed-point number representation. With regard to the transmission of digital audio signals for band-limited transmission channels like satellite broadcasting (Digital Satellite Radio, DSR) or terrestrial broadcasting, it is necessary to reduce bit rates. For this, a conversion of a block of linearly coded samples is carried out in a so-called block floating-point representation in DSR. In the context of DAB, a data reduction of linear coded samples is carried out based on psychoacoustic criteria.

Equalizers. While implementing equalizers with recursive digital filters, the signal-to-noise ratio depends on the choice of the recursive filter structure. By a suitable choice of a filter structure and methods to spectrally shape the quantization errors, optimal signal-to-noise ratios are obtained for a given word-length. The signal-to-noise ratio for fixed-point representation depends on the word-length and for floating-point representation on the word-length of the mantissa. For filter implementations with fixed-point arithmetic, boost filters have to be implemented with a scaling within the filter algorithm. The properties of floating-point representation take care of automatic scaling in boost filters. If an insert I/O in fixed-point representation follows a boost filter in floating-point representation then the same scaling as in fixed-point arithmetic has to be done.

Dynamic Range Control. Dynamic range control is performed by a simple multiplicative weighting of the input signal with a control factor. The latter follows from calculating the peak and RMS value (root mean square) of the input signal. The number representation of the signal has no influence on the properties of the algorithm. Owing to the normalized mantissa in floating-point representation, some simplifications are produced while determining the control factor.

Mixing/Summation. While mixing signals into a stereo image, only multiplications and additions occur. Under the assumption of incoherent signals, an overload reserve can be estimated. This implies a reserve of 20/30 dB for 48/96 sources. For fixed-point representation the overload reserve is provided by a number of overflow bits in the accumulator of a DSP (Digital Signal Processor). The properties of automatic scaling in floating-point arithmetic provide for overload reserves. For both number representations, the summation signal must be matched with the number representation of the output. While dealing with AES/EBU outputs or MADI outputs, both number representations are adjusted to fixed-point format. Similarly, within heterogeneous system solutions, it is logical to make heterogeneous use of both number representations, though corresponding number representations have to be converted.

Since the signal-to-noise ratio in fixed-point representation depends on the input level, a conversion from fixed-point to floating-point representation does not lead to a change of signal-to-noise ratio, i.e. the conversion does not improve the signal-to-noise ratio. Further signal processing with floating-point or fixed-point arithmetic does not alter the signal-to-noise ratio as long as the algorithms are chosen and programmed accordingly. Reconversion from floating-point to fixed-point representation again leads to a level-dependent signal-to-noise ratio.

As a consequence, for two-channel DSP systems which operate with AES/EBU or with analog inputs and outputs, and which are used for equalization, dynamic range control, room simulation etc., the above-mentioned discussion holds. These conclusions are also valid for digital mixing consoles for which digital inputs from AD converters or from multitrack machines are represented in fixed-point format (AES/EBU or MADI). The number representation for inserts and auxiliaries is specific to a system. Digital AES/EBU (or MADI) inputs and outputs are realized in fixed-point number representation.

2.5 Java Applet – Quantization, Dither, and Noise Shaping

This applet shown in Fig. 2.44 demonstrates audio effects resulting from quantization. It is designed for a first insight into the perceptual effects of quantizing an audio signal.

The following functions can be selected on the lower right of the graphical user interface:

• Quantizer
  • – word-length w leads to quantization step size Q = 2^w−1.
• Dither
  • – rect dither – uniform probability density function
  • – tri dither – triangular probability density function
  • – high-pass dither – triangular probability density function and high-pass power spectral density.
• Noise shaping
  • – first-order H(z) = z⁻¹
  • – second-order H(z) = −2z⁻¹ + z⁻²
  • – psychoacoustic noise shaping.

You can choose between two predefined audio files from our web server (audio1.wav or audio2.wav) or your own local wav file to be processed [Gui05].

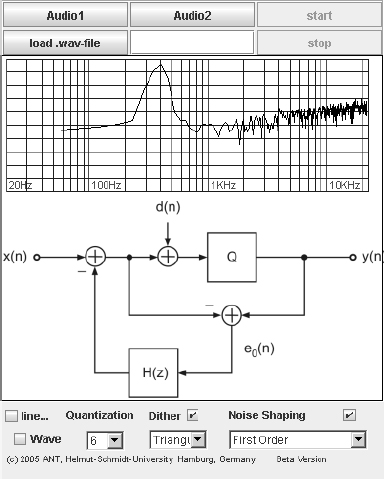
Figure 2.44 Java applet – quantization, dither, and noise shaping.

2.6 Exercises

1. Quantization

1. Consider a 100 Hz sine wave x(n) sampled with f_S = 44.1 kHz, N = 1024 samples and w = 3 bits (word-length). What is the number of quantization levels? What is the quantization step Q when the signal is normalized to −1 ≤ x(n) < 1. Show graphically how quantization is performed. What is the maximum error for this 3-bit quantizer? Write Matlab code for quantization with rounding and truncation.
2. Derive the mean value, the variance and the peak factor P_F of sequence e(n), if the signal has a uniform probability density function in the range −Q/2 < e(n) < −Q/2. Derive the signal-to-noise ratio for this case. What will happen if we increase our word-length by one bit?
3. As the input signal level decreases from maximum amplitude to very low amplitudes, the error signal becomes more audible. Describe the error calculated above when w decreases to 1 bit? Is the classical quantization model still valid? What can be done to avoid this distortion?
4. Write Matlab code for a quantizer with w = 16 bits with rounding and truncation.
   • Plot the nonlinear transfer characteristic and the error signal when the input signal covers the range 3Q < x(n) < 3Q.
   • Consider the sine wave x(n) = A sin (2π(f/fS)n), n = 0,…, N − 1, with A = Q, f/fS = 64/N and N = 1024. Plot the output signal (n = 0,…, 99) of a quantizer with rounding and truncation in the time domain and the frequency domain.
   • Compute for both quantization types the quantization error and the signal-to-noise ratio.

2. Dither

1. What is dither and when do we have to use it?
2. How do we perform dither and what kinds of dither are there?
3. How do we obtain a triangular high-pass dither and why do we prefer it to other dithers?
4. Matlab: Generate corresponding dither signals for rectangular, triangular and triangular high-pass.
5. Plot the amplitude distribution and the spectrum of the output x_Q(n) of a quantizer for every dither type.

3. Noise Shaping

1. What is noise shaping and when do we do it?
2. Why is it necessary to dither during noise shaping and how do we do this?
3. Matlab: The first noise shaper used is without dither and assumes that the transfer function in the feedback structure can be first-order H(z) = z⁻¹ or second-order H(z) = −2z⁻¹ + z⁻². Plot the output x_Q(n) and the error signal e(n) and its spectrum. Show with a plot the shape of the error signal.
4. The same noise shaper is now used with a dither signal. Is it really necessary to dither with noise shaping? Where would you add your dither in the flow graph to achieve better results?
5. In the feedback structure we now use a psychoacoustic-based noise shaper which uses the Wannamaker filter coefficients

   

   Show with a Matlab plot the shape of the error with this filter.

References

[DeK03] D. De Koning, W. Verhelst: On Psychoacoustic Noise Shaping for Audio Requantization, Proc. ICASSP-03, Vol. 5, pp. 453–456, April 2003.

[Ger89] M. A. Gerzon, P. G. Craven: Optimal Noise Shaping and Dither of Digital Signals, Proc. 87th AES Convention, Preprint No. 2822, New York, October 1989.

[Gui05] M. Guillemard, C. Ruwwe, U. Zölzer: J-DAFx – Digital Audio Effects in Java, Proc. 8th Int. Conference on Digital Audio Effects (DAFx-05), pp. 161–166, Madrid, 2005.

[Hel07] C. R. Helmrich, M. Holters, U. Zölzer: Improved Psychoacoustic Noise Shaping for Requantization of High-Resolution Digital Audio, AES 31st International Conference, London, June 2007.

[ISO389] ISO 389-7:2005: Acoustics – Reference Zero for the Calibration of Audiometric Equipment – Part 7: Reference Threshold of Hearing Under Free-Field and Diffuse-Field Listening Conditions, Geneva, 2005.

[Lip86] S. P. Lipshitz, J. Vanderkoy: Digital Dither, Proc. 81st AES Convention, Preprint No. 2412, Los Angeles, November 1986.

[Lip92] S. P. Lipshitz, R. A. Wannamaker, J. Vanderkoy: Quantization and Dither: A Theoretical Survey, J. Audio Eng. Soc., Vol. 40, No. 5, pp. 355–375, May 1992.

[Lip93] S. P. Lipshitz, R. A. Wannamaker, J. Vanderkooy: Dithered Noise Shapers and Recursive Digital Filters, Proc 94th AES Convention, Preprint No. 3515, Berlin, March 1993.

[Sha48] C. E. Shannon: A Mathematical Theory of Communication, Bell Systems, Techn. J., pp. 379–423, 623–656, 1948.

[Sri77] A. B. Sripad, D. L. Snyder: A Necessary and Sufficient Condition for Quantization Errors to be Uniform and White, IEEE Trans. ASSP, Vol. 25, pp. 442–448, October 1977.

[Ter79] E. Terhardt: Calculating Virtual Pitch, Hearing Res., Vol. 1, pp. 155–182, 1979.

[Van89] J. Vanderkooy, S. P. Lipshitz: Digital Dither: Signal Processing with Resolution Far Below the Least Significant Bit, Proc. AES Int. Conf. on Audio in Digital Times, pp. 87–96, May 1989.

[Wan92] R. A. Wannamaker: Psychoacoustically Optimal Noise Shaping, J. Audio Eng. Soc., Vol. 40, No. 7/8, pp. 611–620, July/August 1992.

[Wan00] R. A. Wannamaker, S. P. Lipshitz, J. Vanderkooy, J. N. Wright: A Theory of Nonsubtractive Dither, IEEE Trans. Signal Processing, Vol. 48, No. 2, pp. 499–516, 2000.

[Wid61] B. Widrow: Statistical Analysis of Amplitude-Quantized Sampled-Data Systems, Trans. AIEE, Pt. II, Vol. 79, pp. 555–568, January 1961.