We will now discuss why, with central projection, we can use linear interpolation of 1/z, called zi in Chapter 7, and not simply z. For example, with two points P1(x′1, y′1, zi1 and P2(x′2, y′2, zi2), where x′1, y′1, x′2 and y′2 are logical screen coordinates, while zi1 = 1/z1 and zi2 = 1/z2, we can compute similar coordinates of the midpoint M(xM, yM, ziM) by using
| x′M = 0.5 (x′1 + x′2) |
| y′M = 0.5 (y′1 + y′2) |
| ziM = 0.5(zi1 + zi2) |
In general we have
Figure A.1 shows the eye-coordinate axes x and z and the screen z = −d. For simplicity, we ignore the y-axis. Recall that the position E of the eye is the origin of this coordinate system and that the negative z-axis points towards the center of the object. Point P lies on line l, which has the following equation:
The ray of light PE intersects the screen in P′(x′, −d). Then all points (x, z) of this ray of light satisfy the equation
or
To compute the point of intersection of this ray of light and line l, we substitute this result in (A.1), finding
Dividing the left- and right-hand sides of this equation by z and swapping them, we obtain
which shows that 1/z is a linear function of x′.
This is useful because it enables us to perform linear interpolation. This term is used to indicate that, with a linear function
| f(x) = mx + c |
and three values xA, xB and xI satisfying
| xI = xA + λ(xB − xA) |
we can express f(xI) in f(xA) and f(xB) in the same way as xI is expressed in xA and xB, that is,
| f(xI) = f(xA) + λ{f(xB) − f(xA)} |
Although this sounds very plausible, here is a proof for the sake of completeness:
As we have seen in Equation (A.2) that 1/z is a linear function of x′, it follows that we can find the z-coordinate of a point I on a line AB in 3D space by using
where λ indicates the position of the projection I′ relative to A′ and B′:
| xI′ = xA′ + λ(xB′ − xA′) |
| yI′ = yA′ + λ(yB′ − yA′) |
We have used Equation (A.3) in Chapters 6 and 7 to compute the z-coordinate of an unknown 3D point that is the original of a given 2D image point.
A different notation
In the preceding discussion we have written equations of the form
| xI′ = xA′ + λ(xB′ − xA′) |
in which the variable xA′ occurs twice. We can instead use a different equation, in which each of the variables xA′ and xB′ occurs only once, at the price of using two occurrences of the parameter λ:
| xI′ = (1 − λ)xA′ + λxB′ |
An example
Using λ = 0.5 in the above formulas, we obtain
| xI′ = 0.5 (xA′ + xB′) |
| yI′ = 0.5 (yA′ + yB′) |

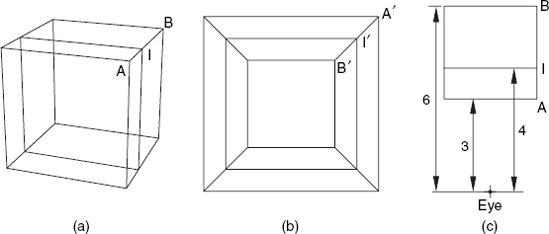
Figure A.2 illustrates this. The object shown in (a) is a wire-frame model of a cube, containing an extra square between the front and back faces and passing through point I. The viewpoint indicated in (c) as Eye is used to obtain the perspective view (b). Here the projection I′ is the midpoint of A′B′, so that the first and second of the above three equations clearly apply. In 3D space, I is not the midpoint of AB, but BI = 2AI, as (a) and (c) show. Since the negative ze-axis points from the eye to the center of the object, the distances shown in (c) imply that
| zA = −3 |
| zI = −4 |
| zB = −6 |
These values satisfy the third of the above three equations.