7

Measures of Central Tendency and Dispersion

This is where you finally get to start analyzing data! For better or worse, there are some calculations that you will have to be able to perform in the actual exam. This is a part that a lot of people get stuck on because these aren’t things that data analysts calculate manually, but you do need to know them for the exam. Online testing centers should have a simple calculator built into the calculation questions, and an online document for taking notes. However, you will not be provided with the equations you are expected to know. Time to dust off some of those old math skills!

Before we jump into the equations, we will start by going over what a distribution is and some common distributions you might come across. Next, we will start with the simplest math, talking about measures of central tendency, how to calculate them, and when to use which. Then, we will go over measures of dispersion. We will focus on ranges and quartiles first. Then, we will move on to variance and finish up with standard deviation. There is a lot to cover, so let’s get started!

In this chapter, we’re going to cover the following main topics:

• Discovering distributions
• Understanding measures of central tendency
• Calculating range and quartiles
• Finding variance and standard deviation

Discovering distributions

Distributions are often discussed when statistics come up; they have even been mentioned earlier in this book. The question is, what are they? A statistics class will tell you something like the following: a distribution is a function that describes a line that depicts the probabilities of any theoretical outcome that occurs, based on the evidence of a study. Is this easily understood and actionable information? Not really.

Effectively, you can think of a distribution as a model of historical data. It tells you how likely a specific value is when compared to everything you have collected before. This has all kinds of uses. You can predict the probability that a new entry will be a specific value, or in a range of values. You can take a value and see how it compares to the rest of your information. It even turns out that the shape of your distribution can tell you all kinds of things. Additionally, several statistical methods require a specific distribution as one of their assumptions.

There are specific methods for finding the exact distribution of your data, but you can get away with making a histogram and eyeballing it most of the time. Is this the ideal approach? Can you tell whether something is perfectly within the allowable range of variables, which will tell you whether it is a specific distribution or not? No, but this is not a book on statistical rigor for research methodology. Data analysts will rarely have to do more than make a histogram.

This is all pretty theoretical, so let’s look at an example. You follow a soccer team, the Fighting Goldfish, and write down the number of goals they make for 100 games: 10 they didn’t score at all, 20 they scored 1 goal, 50 times they scored 2 goals, 20 times they scored 3 goals, and 10 they scored 4 goals. First, let’s try to visualize this through the following diagram:

Figure 7.1 – Histogram of Fighting Goldfish goals

In Figure 7.1 here, we see this data displayed as a histogram. Technically, the distribution is the function describing the line.

Figure 7.2 – Distribution of Fighting Goldfish goals

In Figure 7.2, we see that while the curve of the line describes the distribution, if you point to any specific point on that line, you can find the probability of a given value. However, you will notice that the histogram does a pretty good job of telling us what the shape of the distribution is. Now that we have this data set up, one way or another, we can answer all kinds of questions. What is the probability of the Fighting Goldfish scoring two goals in their next game? 50%. In their last game, the Fighting Goldfish scored four goals; how does that compare to their other games? That is higher than 70% of their other games. There are all kinds of things that you can learn from a probability distribution, including how much variance there is and how reliable your data is.

Earlier, we mentioned that you can learn some things from the shape of the line. Some shapes naturally come up more often than others and are considered common distributions. Depending on what sort of data you are using, some distributions may be more common than others. Let’s go over a few that you might run into.

Normal distribution

Gaussian – does it ring a bell? If you didn’t get that joke, trust me, it’s hilarious. A Gaussian distribution, often called a normal distribution, looks like a bell and is often described as a bell curve. In Figure 7.3 here, we get a rough idea of the shape:

Figure 7.3 – Normal distribution

Many statistical analyses require this distribution because it is the most common and pops up all the time. If you’re curious, the formula for the function can take many forms, but is often roughly something like this:

The basic idea behind this distribution is that, ideally, the mean, median, and mode are all in the center and that is the highest point in the curve. As you move away from the mean, left or right, the probability decreases evenly on both sides, so both sides are equal. This is what gives it the characteristic bell shape.

Uniform distribution

A uniform distribution is very boring. It is, quite literally, a flat line. If you were to create a histogram of a dataset of 1, 2, and 3, you would get a uniform distribution.

Figure 7.4 – Uniform distribution

In Figure 7.4 here, we can see what a uniform distribution looks like. What does this tell us? That every value has the exact same chance of happening. There is a maximum value and a minimum value, but everything between has happened roughly the same number of times in the past. When you have a uniform distribution, there is not a lot to do besides watch to make sure it doesn’t break. If you suddenly get a value above your maximum or below your minimum, or if you suddenly start getting the value in the middle more than the others, it means something has drastically changed your data and it will probably impact your other variables as well.

Poisson distribution

Poisson is a pretty specialized distribution. This is the number of times an event happens over a fixed, repeating period. It’s usually time but does not have to be. When I originally taught this, the example used was counting every occurrence of roadkill for every mile down a certain road. With this, you can give the probability of the number of occurrences of roadkill down the next mile of the road. Neat, huh?

Perhaps a more relevant example: you are looking at how many hits a website gets every hour, or how many products are sold a day. These are all based on a count over a repeating interval, usually time.

That said, the shape of a Poisson distribution depends on Lambda (λ), which is defined by the rate, which is, in turn, defined by the average. Long story short, this one can have different shapes:

Figure 7.5 – Possible Poisson distributions

In Figure 7.5 here, we can see that this is a tricky one, and it is defined more by what the variables are than by the shape.

Exponential distribution

Exponential distributions are, as the name suggests, distributions that increase or decrease exponentially. These are often described as being related to Poisson distribution because they are used to describe the waiting time between events. However, they do exist on their own. If you see any variable that changes with a sharp curve, it might be exponential:

Figure 7.6 – Exponential distributions

In Figure 7.6 here, we can see that this does have multiple shapes, but they are all the same basic shape with different orientations.

Bernoulli distribution

Bernoulli distributions are another specialized distribution, but they are very simple and easy to identify. Just remember that Bernoulli distributions are Booleans. There are only two possible outcomes: true or false. You can call these outcomes whatever you want: pass or fail, success or failure, 1 or 0, yes or no, and so on. It doesn’t matter what you use as long as it is a binary variable and all values are either one thing or the other. This is used, quite simply, to give the probability of one of the outcomes. This is also only run once.

Let’s say you are a fan of model rockets. For those of you who don’t know, a model rocket is a cardboard tube with a plastic tip that you stuff with explosives to send flying in the air. If stuffed improperly, there is a chance that the rocket will just sit there, catch fire, explode, or some combination of any of these things. Any outcome that does not involve the rocket safely being launched into the air in one piece is considered a failed launch. Hypothetically, for someone without experience, there is a 50% chance that your rocket will successfully launch and a 50% chance that it will explosively fail on any one launch!

Figure 7.7 – Bernoulli distribution

In Figure 7.7 here, we get a general idea of what this looks like as a distribution. It is probably safest to not stand too close to the rocket when you try to launch it.

Binomial distribution

A binomial distribution is like a Bernoulli distribution, but the experiment is repeated. Instead of launching one rocket, you launch ten! This changes things a little. For example, instead of looking at success and failure, you are now only looking at the probability of success. To be more accurate, you are looking at the probability of a specific number of successes.

Figure 7.8 – Binomial distribution of rocket launches

In Figure 7.8 here, we can see our binomial distribution. If we launch 10 rockets and each one has a 50% chance of success, what is the probability that we will have exactly 5 successful launches? Roughly 25%.

Note that binomial distributions do not have a set shape. If we look at Figure 7.7, we can see that this is normally distributed, but that is only because we have a success rate of exactly 50%. The shape of this distribution changes based on the probability that any one run is successful.

Skew and kurtosis

Skew is a measure of crookedness. If a distribution leans to the left or to the right, it is skewed. If it leans too far, then the distribution can no longer be considered normal. This makes sense since one of the defining characteristics of a normal distribution is that the sides are equal, so if one side is longer than the other, it no longer meets this criterion.

Figure 7.9 – Negative or left skew

In Figure 7.9 here, we can see a distribution that is skewed to the left. This is also called a negative skew. You can remember the name because the long tail points toward the skew. The tail is pointing to the left or toward the negative numbers, so it is a left or negative skew:

Figure 7.10 – Positive or right skew

In Figure 7.10 here, we can see, you guessed it, a distribution that is right-skewed, or positively skewed. Again, the long tail points to the right or toward the positive numbers. Lots of things can cause a skew, including, but not limited to, outliers that pull the probability to one side or the other.

If skew describes your distribution being crooked to the left or right, kurtosis is it being crooked up or down. To be more precise, it is looking at the difference in the tails from a normal distribution:

Figure 7.11 – Leptokurtic distribution

In Figure 7.11 here, we can see a leptokurtic distribution. That means it is tall and skinny, with tails smaller than a normal distribution. It also means that all of the values are closely packed at the center line. You can remember this name because the distribution “lept” into the air! Like “leaped?” It’s a pun.

Figure 7.12 – Platykurtic distribution

In Figure 7.12 here, we see a platykurtic distribution. This is a short, wide distribution, with larger tails than a normal distribution. In this case, the data is much more spread out and is only slightly more likely to be near the center line. You can remember this name because it is short and flat like a plate. As a side note, a normal distribution is said to be mesokurtic, which you can remember because meso literally means middle.

You now have a rough understanding of skew and kurtosis. Does the distribution lean left or right? Is it tall or squat? That said, the ideal data may not actually exist in the wild. Your data is allowed to lean a little bit, or be a little tall, and still be considered normal. There are actually tests that will give you specific numbers for skew and kurtosis and an acceptable range for what is considered normal, but at the end of the day, it is a judgment call. Does it look like a bell curve or is it so deformed in any direction that it is no longer normal? That’s up to you.

To be perfectly clear, you should be familiar with the concepts of skew and kurtosis for the exam, but you will not be asked whether a specific skew value is too high or how to normalize a distribution that is skewed.

Understanding measures of central tendency

A measure of central tendency is a summary of a dataset in a single number. The name comes from the fact that these values should be in the center of your distribution and should be the value with the highest probability of occurring. Overall, because they are useful summaries, they are often used as variables in other statistical analyses. You can use them by themselves. It is easiest to compare two averages than to compare every value in two datasets.

There are a few different ones, but in common practice, you will only come across three:

• Mean
• Median
• Mode

You may have heard of these before, but let’s go over them briefly.

Mean

The mean is also called the average. To find the average, you take the sum of the values and divide them by the number of values. This may be simple, but let’s break it into steps:

1. Find the sum of the values.
2. Divide the sum by the number of values.

Let’s try a quick example. You have three puppies. The puppies weigh 22 lb, 26 lb, and 24 lb:

1. Find the sum of the values.

For our example, we will add together 22, 26, and 24:

22 + 26 + 24 = 72

So, our sum is 72.

2. Divide the sum by the number of values.

We have three puppies, so we have three values:

72 / 3 = 24

The mean weight of our puppies is 24 lb.

You can practice this process on your own with the following dataset: 12, 7, 11, 6, 9.

Median

The median is the middle of your data. Aren’t they all? Well, yes, but the median is literally, if you put all of your values in ascending order, the value that falls in the exact middle. The steps are as follows:

1. Arrange values in ascending or descending order.
2. Find the value that is in the exact middle.
3. If your dataset has an even number of values, find the mean of the two in the middle.

Let’s go back to our puppies. As you may recall, their weights (lb) are 22, 26, and 24:

1. Arrange values in ascending or descending order.

If we put them in ascending order, we get 22, 24, 26.

2. Find the value in the exact middle:

22, 24, 26

24 is in the middle.

Because we had an odd number of values, that is the end and 24 is our median. Let’s try this process again with the addition of a fourth puppy who weighs 25 lb, so our new dataset is 22, 26, 24, 25:

1. Arrange values in ascending or descending order.

If we put them in ascending order, we get 22, 24, 25, 26.

2. Find the value in the exact middle:

22, 24, 25, 26

Now, 24 and 25 are both in the middle, so we continue to the next step.

3. If your dataset has an even number of values, find the mean of the two in the middle.

So, we have to find the average of 24 and 25:

24 + 25 = 49

49 / 2 = 24.5

The median for this dataset is 24.5 lb.

You can practice this process on your own with the following dataset: 6, 12, 8, 72, 1, 15.

Mode

Mode is all about frequency. It is literally whatever number occurs most often in your dataset. This one is a little different from the others. You can have no mode if no value is repeated, or you can have multiple modes if two values happen the same number of times. The steps are as follows:

1. Arrange values in ascending or descending order.
2. Count the occurrences of all repeating values.
3. Compare the number of occurrences for every repeated value.

We will use the puppy data again, because everyone loves puppies. However, we will add a few more puppies! Our puppy data is now 22, 26, 24, 25, 25, 24, 23, 25, 22. Whew! That is a lot of puppies:

1. Arrange values in ascending or descending order:

22, 22, 23, 24, 24, 25, 25, 25, 26

2. Count the occurrences of all repeating values:

22	23	24	25	26
2	1	2	3	1

3. Compare the number of occurrences for every repeating value.

25 has the highest number of occurrences.

Our mode is 25 lb.

Hypothetically, if we had 1 fewer 25, then 22, 24, and 25 would all be modes because they would all be tied for the highest frequency.

You can practice this process on your own with the following dataset: 7, 3, 2, 4, 3, 4, 5.

When to use which

Okay, so what is the point of having different measures? Do you have to find all of them every time? The answer is no. Some of them work better with certain kinds of data. Let’s look at each in turn.

When to use the mean

Mean is the default; when in doubt, it is a safe bet. It works with normal distributions perfectly. It can work with other distributions but is easily pulled in the wrong direction by outliers, so skewed data or asymmetrical data can give you incorrect values.

When to use the median

The median is an underrated metric, and some people use it for everything because it is immune to outliers. It doesn’t matter whether there is a value at the end that is 1,000 times higher than any other value; it still only counts as 1 value above. This makes it ideal for working with skewed or asymmetrical data, where a mean can’t. Medians are also great for working with ordinal variables. If you recall, an ordinal variable is a scale that uses regular intervals, so medians naturally work well with finding the middle.

When to use the mode

The mode is not very popular, but it can do something that others can’t. It can work with nominal variables. Recall that nominal variables are categorical variables that have no inherent order. You could try to take the average or the median of colors, but it would be a very silly thing to do. However, since the mode works with frequencies, it is ideal for handling nominal variables.

Calculating ranges and quartiles

Range and quartiles, as well as variance and standard deviation, are considered measures of dispersion. As the name suggests, these are all ways to find out how dispersed or spread out your data is. Is your data random and widely spread, or are the points tightly clustered around the mean? Not only are these values used in more advanced calculations but they are also very useful in and of themselves. If you recall, several of these were common in EDA because it is basic information that has many uses.

Ranges

A range is the simplest measure of dispersion. The idea is simply to know how far spread your dataset is. This is designed to be quick and easy, but not the most useful measure. The steps are as follows:

1. Arrange values in ascending or descending order.
2. Identify the minimum and maximum values.
3. Subtract the minimum from the maximum.

Let’s look at an example. You are hired by a small chicken farm and you are tracking the number of eggs produced every day for 10 days. The dataset is as follows: 12, 18, 10, 22, 15, 25, 16, 17, 14, and 19:

1. Arrange values in ascending or descending order:

10, 12, 14, 15, 16, 17, 18, 19, 22, 25

2. Identify the minimum and maximum values.

Luckily, now that we have ordered them, these are the values on the far left and the far right:

10, 12, 14, 15, 16, 17, 18, 19, 22, 25

3. Subtract the minimum from the maximum:

25 – 10 = 15

Just like that, we have a range of 15.

You can practice this process on your own with the following dataset: 4, 6, 5, 2, 6, 8, 4, 6, 1, 4.

Quartiles

Quartiles divide your data into quarters. To divide your data up into four pieces means that you have three points of division as seen in Figure 7.13 here:

Figure 7.13 – Quartiles

These points of division are called the lower quartile (Q1), the middle quartile (Q2), and the upper quartile (Q3). Normally, when this is taught, you learn a slightly different equation for each quartile that will give you the position in an ordered dataset of each quartile. Then, you can look up each value by its position. This isn’t a bad method, but there is an easier way that I will teach you:

1. Arrange values in ascending or descending order.
2. Find the median – Q2.
3. Split the dataset at the median.
4. Find the median of the lower dataset – Q1.
5. Find the median of the upper dataset – Q3.

You already know how to find the median, so let’s jump right in with our egg data – or is it chicken data? Which came first? The dataset is as follows: 12, 18, 10, 22, 15, 25, 16, 17, 14, and 19:

1. Arrange values in ascending or descending order:

10, 12, 14, 15, 16, 17, 18, 19, 22, 25

2. Find the median:

The median is 16.5, so Q2 is 16.5.

3. Split the dataset at the median:

Lower dataset: 10, 12, 14, 15, 16

Upper dataset: 17, 18, 19, 22, 25

4. Find the median of the lower dataset:

Lower dataset: 10, 12, 14, 15, 16

Q1 is 14.

5. Find the median of the upper dataset:

Upper dataset: 17, 18, 19, 22, 25

Q3 is 19.

Therefore, our lower quartile is 14, our middle quartile is 16.5, and our upper quartile is 19.

You can practice this process on your own with the following dataset: 3, 8, 4, 9, 2, 6, 5, 9, 4, 7.

Interquartile range

An interquartile range is a measure of dispersion that combines the two techniques you just learned. You are literally just finding the range of the quartiles. This should be a quick one:

1. Find the quartiles.
2. Subtract Q1 from Q3.

Since we just found the quartiles of our dataset in the last example, this should be easy:

1. Find the quartiles:

Q1 = 14, Q2 = 16.5, Q3 = 19

2. Subtract Q1 from Q3:

19 – 14 =5

The interquartile range is 5.

You can practice this process on your own with the following dataset: 6, 4, 2, 5, 6, 3, 4, 1, 4, 6.

Finding variance and standard deviation

Variance and standard deviation are very popular. They are a little bit more complicated to perform by hand, not that you would ever perform them by hand if you didn’t have to for the exam, but they are a much better measure of how dispersed your data is. Instead of giving you a rough idea based on the range, these tell you the average distance of every point from your mean.

Variance

Variance is a measure of dispersion that looks at the squared deviation of a random variable from the mean of that variable. This equation looks a little scary, but we will break it down step by step:

=

It should be noted that this denominator (n-1) is used for samples. If you are using an entire population, then the denominator is just (). Let’s go over this briefly. is the sample variance, represents the value of each observation, represents the mean of the sample, and is the number of data points in your dataset. Let’s go ahead and go through the steps:

1. Find the mean of the dataset.
2. Subtract the mean from each data point.
3. Square the results from the previous step.
4. Find the sum of the previous step.
5. Divide that sum by the number of data points minus 1.

Some of these steps may not sound clear, so let’s jump right into the example. Now, you work for a website that sells specialized boats. The values represent how many boats are sold in a week: 3, 6, 4, 7, 5, 1, 9, 5, 4, and 6:

1. Find the mean of the dataset:

The mean is 5.

2. Subtract the mean from each data point:

( 3 – 5 ), ( 6 – 5 ), ( 4 – 5 ), ( 7 – 5 ), ( 5 – 5 ), ( 1 – 5 ), ( 9 – 5), ( 5 – 5), ( 4 – 5 ),

( 6 – 5)

becomes

( -2 ), ( -1 ), ( 1 ), ( 2 ), ( 0 ), ( -4 ), ( 4 ), ( 0 ), ( -1 ), ( 1 )

3. Square the results from the previous step:

, , , , , , , , ,

becomes

4, 1, 1, 4, 0, 16, 16, 0, 1, 1

4. Find the sum of the previous step:

4 + 1 + 1 + 4 + 0 + 16 + 16 + 0 + 1 + 1 = 44

The sum is 44.

5. Divide that sum by the number of data points minus 1:

The variance for this dataset is 4.9.

You can practice this process on your own with the following dataset: 10, 8, 12, 11, 9, 9, 8, 12, 11, 10.

Standard deviation

You may have noticed that variance is represented by . You will be happy to know that standard deviation is just s. That’s right – standard deviation is a measure of dispersion that is the square root of the variance. The steps are the same, but you take the square root at the very end. Why is this important? Because it puts the standard deviation in the same units as your dataset and you can apply it to your distribution.

Let’s take a step back. The coolest thing about standard deviation is what happens when you apply it to a normal distribution. One standard deviation above the mean will always include 34.1% of your data points as seen in Figure 7.14 here:

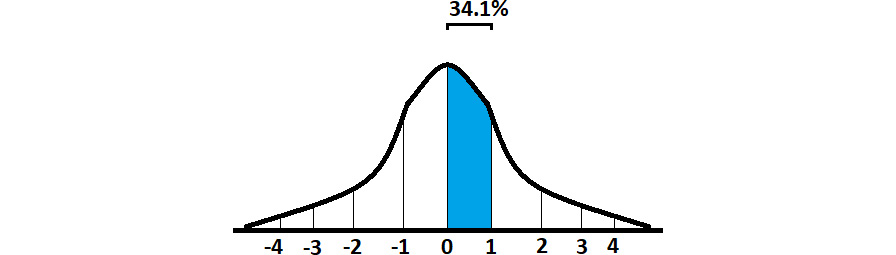
Figure 7.14 – One standard deviation

Because both sides are the same in a normal distribution, that means that one standard deviation below also includes 34.1% of your data points. Together, that means that 68.2% of your data points are within one standard deviation of your mean as seen in Figure 7.15 here:

Figure 7.15 – One standard deviation above and below the mean

This keeps going, with 95.4% of all of your data points within two standard deviations and 99.6% of your population within three standard deviations, as seen in Figure 7.16 here:

Figure 7.16 – Standard deviation percentages

This is pretty nifty and you can see why many data analysts use three standard deviations as a cutoff for outliers. If you delete every data point that is more than three standard deviations away from your mean, you are only losing 0.4% of your data and removing any outliers while you are at it.

There are many things to learn about standard deviation, but they will not be on the test – so let’s go ahead and focus back on what will be. The steps are the same as we had for variance, but we are adding one more to the end:

1. Find the mean of the dataset.
2. Subtract the mean from each data point.
3. Square the results from the previous step.
4. Find the sum of the previous step.
5. Divide that sum by the number of data points minus 1.
6. Take the square root of the previous step.

For our example, we will stick to the boat data, but we will go ahead and collect another sample of 10 days: 4, 5, 3, 4, 2, 2, 6, 4, 6, and 4:

1. Find the mean of the dataset:

The mean is 4.

2. Subtract the mean from each datapoint:

( 4 – 4 ), ( 5 – 4 ), ( 3 – 4 ), ( 4 – 4 ), ( 2 – 4 ), ( 2 – 4 ), ( 6 – 4 ), ( 4 – 4), ( 6 – 4 ),

( 4 – 4 )

becomes

( 0 ), ( 1 ), (- 1 ), ( 0 ), ( -2 ), ( -2 ), ( 2 ), ( 0 ), ( 2 ), ( 0 )

3. Square the results from the previous step:

, , , , , , , , ,

becomes

0, 1, 1, 0, 4, 4, 4, 0, 4, 0

4. Find the sum of the previous step:

0 + 1 + 1 + 0 + 4 + 4 + 4 + 0 + 4 + 0 = 18

The sum is 18.

5. Divide that sum by the number of data points minus 1:

The variance for this dataset is 2.

6. Take the square root of the previous step:

The standard deviation is 1.41. Note that if the square root is not obvious, as here, the answer may be displayed as .

You can practice this process on your own with the following dataset: 7, 4, 10, 8, 6, 7, 6, 5, 8, 9.

Summary

This chapter covered a lot of information, with a heavy focus on calculations. Just a reminder – while we have spent a fair amount of time learning about these calculations, there will only be a few of these questions on the test. Don’t panic, you can get a couple of these wrong and still pass the test if you do well on the other sections.

Distributions show the shape of your data and can tell you a lot about how it is distributed. Common distributions include normal, uniform, Poisson, exponential, Bernoulli, and binomial. Skew is how your data is distorted left or right (negative skew or positive skew). Kurtosis is how your data is distorted up or down (leptokurtic or platykurtic).

Measures of central tendency summarize your data with a single metric. Common forms include the mean, median, and mode. Each measure is best used on specific types of data.

Measures of dispersion include simpler methods such as range and quartiles, as well as slightly more complicated methods such as variance and standard deviation. Ranges, quartiles, and interquartile ranges are all focused on the extent to which your dataset is spread. Variance and standard deviation are more accurate measures that give the average distance of every point from the mean. Standard deviation has an even greater number of uses when applied to a normal distribution because it can break it down into standardized chunks.

If you are not comfortable with arithmetic, you may want to practice the steps covered in this chapter. You can even make up your own datasets and give them a go. The datasets used on the exam will be pretty small and simple and you can use the datasets in the examples of this chapter as a guide.

Practice questions

Let’s try to practice the material in this chapter with a few example questions.

Questions

1. The following distribution is considered:

1. Uniform
2. Normal
3. Poisson
4. Exponential

2. What is the mode(s) of the following dataset?

24, 18, 36, 51, 24, 48, 18

1. 18
2. 24
3. 18 and 24
4. None of the above

3. What is the range of the following dataset?

15, 615, 46, 73, 45, 80, 46

1. 131
2. 46
3. 73
4. 600

4. What is the middle quartile (Q2) of the following dataset?

10, 24, 13, 9, 15, 7, 19

1. 9
2. 13
3. 19
4. 15

5. What is the standard deviation of the following sample dataset?

9, 11, 7, 8, 9, 10

1. 2
2. 9
3. 
4. 

Answers

Now, we will briefly go over the answers to the questions. If you got one wrong, make sure to review the topic in this chapter before continuing:

1. The answer is: Normal

The distribution is the distinctive bell curve of a normal distribution.

2. The answer is: 18 and 24

Both 18 and 24 are repeated twice, meaning they are both modes.

3. The answer is: 600

Make sure you identify the minimum and maximum to calculate the range.

4. The answer is: 13

Remember that the middle quartile (Q2) is the same as the median.

5. The answer is:

Make sure to take your time and go through the steps one by one.