4.24. Finite lossy tubes
A two-port network for a finite tube of any length [13]
We have already introduced two-port networks for transducers using z-parameters in Section 3.10. Here we shall apply the theory to a tube with viscous and thermal losses. A general equivalent circuit for passive two-port networks is shown in Fig. 4.43. Because of
the reciprocity of the tube, or in other words, the fact that it does not matter at which end there is a transmitter or receiver, we obtain z
22
=
z
11 and z
21
=
z
12.
From Eq. (3.64), we write
 (4.218)
(4.218)
The equations for the tube with losses take on the same form as those without losses which we have already derived in Chapter 2. From Eqs. (2.58) to (2.59) for the pressure and velocity in a finite tube, the following z-parameters are obtained:
 (4.219)
(4.219)
 (4.220)
(4.220)
where we have replaced ρ
0
c with Z
s
for a tube with viscous and thermal losses. This is equivalent to using a piston to apply a velocity u(l) at z
=
l while the other end (at z
=
0) is blocked (hence z
T
=
∞) and using a probe microphone to measure the pressure at z
=
l and z
=
0. The pressures
 (l) and
(l) and
 (0) are then divided by
(0) are then divided by
 (l) to determine z
11 and z
12, respectively. The wave number k and characteristic impedance Z
s
with losses are given by Eqs. (4.215) and (4.217), respectively. The trigonometrical functions in Eqs. (4.219) and (4.220) can be conveniently calculated to within 1% using Eqs. (A2.42) and (A2.43) from Appendix II with the expansion limits set to 20(1
+
|x|)/arg x. Using the relationships of Eqs. (3.74)–(3.77), we can write the following equations for the transmission parameters
(l) to determine z
11 and z
12, respectively. The wave number k and characteristic impedance Z
s
with losses are given by Eqs. (4.215) and (4.217), respectively. The trigonometrical functions in Eqs. (4.219) and (4.220) can be conveniently calculated to within 1% using Eqs. (A2.42) and (A2.43) from Appendix II with the expansion limits set to 20(1
+
|x|)/arg x. Using the relationships of Eqs. (3.74)–(3.77), we can write the following equations for the transmission parameters
 (4.221)
(4.221)
where
 (4.222)
(4.222)
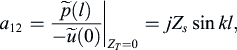 (4.223)
(4.223)
 (4.224)
(4.224)
 (4.225)
(4.225)
If the tube is blocked at the far end, the impedance Z
in
at the entrance is simply
 (4.226)
(4.226)
If the far end is open, then
 (4.227)
(4.227)
The tangent, cotangent, and cosecant functions may be conveniently calculated using Eqs. (A2.42), (A2.43), and (A2.43a), respectively, from Appendix II.
A two-port network for a short finite tube
When the wavelength is about six times greater than the length l of the tube or greater, we can take just the first two terms of the equivalent series forms for the cotangent and cosecant so that Eqs. (4.219) and (4.220) reduce to
where
C
s
=
Cl is a lossy specific compliance and
M
s
=
ρl is a lossy specific mass. The bold typeface indicates that these are not pure reactances but also contain resistive components due to losses. The compliance
C
s
contains thermal losses and
M
s
contains viscous losses. The dynamic compressibility C and dynamic density ρ are given by Eqs. (4.214) and (4.211), respectively. The compliance and mass are shown in Fig. 4.44 as an equivalent electrical circuit. It is valid so long as the radius a is greater than the molecular mean free path length λ
m. When one end of the tube is open and the radiation load is negligible, the corresponding pair of terminals is effectively shorted and, at low frequencies, the two upper mass elements ½
M
s
dominate so that the total mass is
M
s
.
When one end is closed, the corresponding pair of terminals is open-circuited and, at low frequencies, the compliance element
C
s
dominates. The mass is now due to one upper element and the negative middle element, which gives
The fact that the mass of a blocked tube is one-third of that of an open tube can be verified by expanding the tangent function of Eq. (4.227), as we did in Section 4.2.
A two-port network for a short finite tube using approximate discrete elements
Let us now shorten the equivalent series forms of the Bessel functions in the function Q(x) of Eq. (4.198) to just their first two terms:
We now apply this to the dynamic density from Eq. (4.211) to obtain
For small values of k
V
a, this simplifies to
We also apply Eq. (4.230) to the dynamic compressibility from Eq. (4.214) to obtain
For small values of k
T
a, this simplifies to
By substituting Eqs. (4.233) and (4.235) into Eqs. (4.215) and (4.217), we obtain the asymptotic wave number and characteristic impedance for a short very narrow tube
 (4.237)
(4.237)
To separate out the reactive and resistive elements of Fig. 4.44, we have to include the second-order terms of Eqs. (4.215) and (4.217). However, the approximation is not optimum because the singularity of the polynomial approximation of Q(x) in Eq. (4.230) does not match that of the Bessel function expression. Hence, we will modify Eq. (4.230) to align the singularities
where α
=
2.4048 is the first zero of J
0(x). In other words, J
0(α)
=
0. The numerator part of this approximation has been determined to lead to the same asymptotic expressions for ρ, C, k, and Z
s
as Eq. (4.230). We now apply this to the dynamic density from Eq. (4.211) to obtain
 (4.239)
(4.239)
The impedance because of the complex mass
M
s
is then given by
We see that the first term represents the resistance because of viscous flow losses while the second term represents the mass reactance. We also apply Eq. (4.238) to the dynamic compressibility from Eq. (4.214) to obtain
 (4.242)
(4.242)
Ignoring the fourth-order terms and substituting k
T
from Eqs. (4.177), (4.182), (4.192), and (4.206) yields
 (4.243)
(4.243)
We will use the approximation that
The impedance because of the complex compliance
C
s
is then given by
 (4.244)
(4.244)
where
 (4.247)
(4.247)
where
These elements are shown on the equivalent electrical circuit of Fig. 4.45 and are known as lumped elements as opposed to the distributed ones of Eqs. (4.219) and (4.220) because the mass, compliance, and resistance elements have been separated out into discrete elements, whereas in reality they are evenly distributed over the length of the tube. However, the distributed parameter model may be considered as an infinite number of lumped parameter sections coupled together, where each one is infinitesimally short. At low frequencies, the impedance because of C
T
is larger than R
T
so that the total compliance is effectively C
0
+
C
T
=
1/P
0. The low-frequency pressure fluctuations are isothermal because of heat transfer to and from the wall of the tube. At higher frequencies, R
T
represents energy loss because of the time taken for the heat to flow back and forth. At even higher frequencies, R
T
is greater than the impedance because of C
T, so very little heat is transferred, making the pressure fluctuations adiabatic in nature. The total compliance is then effectively C
0
=
1/(γP
0). Hence, the compliance at low frequencies is greater than that at high frequencies by a factor of γ (that is, around 40% greater).
Regimes for an open-ended tube
The real and imaginary impedances at the entrance of the tube with the far end open, that is, with one pair of terminals of the two-port network shorted, are shown in Figs. 4.46 and 4.47, respectively. In each case, a number of different curves are plotted. For the exact curves (black), Eq. (4.227) is used together with the exact wave number and
characteristic impedance of Eqs. (4.215) and (4.217), respectively. These are valid for a > λ
m
. Real and imaginary approximate curves are also shown for the three following regimes:


-
1. For the very narrow radius or asymptotic curves (medium gray dashed), Eq. (4.227) is also used but with the asymptotic wave number and characteristic impedance of Eqs. (4.236) and (4.237), respectively. The real curve is valid for
 and the imaginary curve for
and the imaginary curve for
 . We ignore the compliance elements of the analogous circuit of Fig. 4.45, which has the output terminals shorted in
the case of an open tube, so that the input impedance reduces to Z
in
=
R
V
+
jωM
0, where R
V
is given by Eq. (4.249) and M
0 becomes a negative mass given by
. We ignore the compliance elements of the analogous circuit of Fig. 4.45, which has the output terminals shorted in
the case of an open tube, so that the input impedance reduces to Z
in
=
R
V
+
jωM
0, where R
V
is given by Eq. (4.249) and M
0 becomes a negative mass given by -

Figure 4.47 Imaginary impedance at the entrance of an open-ended tube at a frequency of 100 Hz plotted against its radius a where the length l of the tube is 10 mm. The exact solution is given by Eq. (4.227) together with Eqs. (4.215) and (4.217). For medium, narrow and very narrow tubes, Z in = R V + jωM 0 where R V and M 0 are given by Eqs. (4.251) and (4.252) for medium tubes, Eqs. (4.249) and (4.250) for narrow tubes, and Eqs. (4.249) and (4.250a) for very narrow tubes. The ultra narrow solution is given by Eq. (4.237). -
 (4.250a)
(4.250a)
- Hence, there is a null in the black curve of Fig. 4.47 where the sign of the mass changes. The negative mass is derived from the property of the tangent function in Eq. (4.227) whereby
 Also,
Also,
 .
.
-
2. At low frequencies, we can ignore the compliance elements of Fig. 4.45 for an open tube. Hence, the input impedance reduces to Z
in
=
R
V
+
jωM
0 where R
V
and M
0 are given by Eqs. (4.249) and (4.250), respectively, and these are used for the narrow radius curves (medium gray), commonly known as the Poisseulle flow. The real curve is valid for
 and the imaginary curve for
and the imaginary curve for
 .
. -
3. For medium radius tubes (light gray), that is for
 , we again ignore the compliance elements of Fig. 4.45 and use the expression Z
in
=
R
V
+
jωM
0, but this time apply the expressions developed by Ingard for R
V
and M
0 as follows:
, we again ignore the compliance elements of Fig. 4.45 and use the expression Z
in
=
R
V
+
jωM
0, but this time apply the expressions developed by Ingard for R
V
and M
0 as follows:
The fact that the resistance in Eq. (4.251) varies with frequency does not really matter much in practice. In a resonant system, such as where the acoustic mass of the tube is combined with the acoustic compliance of a cavity, the resistance only dominates over a small range of frequencies either side of the resonant frequency, especially as the resistance of a medium tube is relatively small and so the Q value is likely to be high. Hence, we can simply use the value of the resistance at the resonant frequency for all frequency values.
Let us now examine the elements R
V
and M
0 of Fig. 4.45. Using Eqs. (4.249) and (4.250) but with zero slip (B
u
=
0), the frequency at which their impedances are equal is given by
 (4.253)
(4.253)
It turns out that an effective viscous boundary layer thickness δ
visc
can be defined by
 (4.254)
(4.254)
This can be obtained by letting tan kl
≈
kl in Eq. (4.227) for a short tube, while letting Q(x)
≈
− 2j/x in Eq. (4.211) for a medium radius as well as ignoring boundary slip and only keeping the higher powers of (
 ) in the resulting expression for Z
in
.
) in the resulting expression for Z
in
.
In other words, at ω
=
ω
V
, we have a
=
 δ
Visc
so that the radius is about 1.73 times greater than the effective boundary layer thickness when the mass reactance and resistance are equal. Above this frequency, the mass reactance of the air in the tube
dominates and below it the viscous resistance dominates. If we insert the values μ
=
1.86
×
10
−5
N·s/m2 and ρ
0
=
1.18
kg/m3 into Eq. (4.253) we also obtain
δ
Visc
so that the radius is about 1.73 times greater than the effective boundary layer thickness when the mass reactance and resistance are equal. Above this frequency, the mass reactance of the air in the tube
dominates and below it the viscous resistance dominates. If we insert the values μ
=
1.86
×
10
−5
N·s/m2 and ρ
0
=
1.18
kg/m3 into Eq. (4.253) we also obtain
 , which is the demarcation between narrow and medium radius tubes above. Hence, in a narrow tube, the frequency-invariant resistance dominates, and in a medium diameter one the mass reactance dominates and the resistance is proportional to the square root of frequency. This can be clearly seen from Figs. 4.46 and 4.47 where he mass reactance and resistance are both approximately 10 rayls at a
=
0.4
mm.
, which is the demarcation between narrow and medium radius tubes above. Hence, in a narrow tube, the frequency-invariant resistance dominates, and in a medium diameter one the mass reactance dominates and the resistance is proportional to the square root of frequency. This can be clearly seen from Figs. 4.46 and 4.47 where he mass reactance and resistance are both approximately 10 rayls at a
=
0.4
mm.
Ultra-narrow tube
At high frequencies in narrow tubes, we encounter a fourth regime which is distinct from those already discussed (very narrow, narrow, and medium) and where the lumped parameter model of Fig. 4.45 no longer applies. Let us now examine some properties of the tangent function in Eq. (4.227) for the impedance of an open tube. The argument kl and Z
s
can be expressed in terms of lumped parameters using the wave number from Eq. (4.215) together with jωρl
=
jω
M
s
=
Z
V
and jωCl
=
jω
C
s
=
1/Z
T
so that
We can see that for small arguments of the tangent function, where tan kl
≈
kl, the impedance of the open tube is just Z
in
=
Z
V
. Using similar arguments with Eq. (4.226), where cot kl
≈
1/(kl), we find that the impedance of a blocked tube is Z
in
=
Z
T
. From Eq. (4.248), Z
V
=
R
V
+
jωM
0. From Eq. (4.244), we will use the approximation Z
T
=
1/(jωC
0). Putting these into Eq. (4.255), we obtain
If ω
<<
ω
V
, then this simplifies to
From Eq. (A2.48) of Appendix II, one property of the tangent function is that tan(x
−
jy)
≈
−
j for virtually any value of x provided that y is greater than about 2. Hence, we can define a transition frequency ω
T
by
Below the transition frequency, the tube regimes are those for an open-ended tube above. Above it, the impedance is given by
where the asymptotic expression for Z
s
is given by Eq. (4.237). In this regime, the impedance is proportional to the inverse square root of frequency and the real and imaginary parts are equal, as can be seen in Figs. 4.48 and 4.49 where the transition frequency according to Eq. (4.258) is 1.45
kHz. Above this frequency, the dashed curves for Z
s
from Eq. (4.237) match very closely with the black curves for the exact
expression of Eq. (4.227). At low frequencies, the dark gray curves representing the lumped parameter model of Fig. 4.45 with one pair of terminals shorted appear to be a good approximation for the black exact curves. Although there is up to 25% error in the imaginary lumped impedance at low frequencies, it is less than 10% of the total impedance, which is mainly resistive and so the impedance modulus is fairly accurate.


Interestingly, above the transition frequency of 1.45
kHz, the real and imaginary impedances of the closed tube shown in Figs. 4.50 and 4.51, respectively, are virtually identical to those of the open tube shown in Figs. 4.48 and 4.49, respectively. This is not so surprising considering that if the tangent function in Eq. (4.227) converges toward −
j, then the cotangent function in Eq. (4.226) must converge toward j. Together with the fact that the input impedance is the characteristic impedance Z
s
, this suggests that the tube under this regime behaves as an infinitely long one in which no sound is transmitted to the far end or reflected back from it because of full internal absorption. This can be confirmed if we take a look at the two-port model of Fig. 4.43.
The z-parameters are described by Eqs. (4.219) and (4.220), which under this regime reduce to


because cotan(x
−
jy)
→
j and cosec(x
−
jy)
→
0 for y
>
2 for any x. As stated above, the existence of this regime is conditional that ω
T
<< ω
V
where ω
V
and ω
T
are given by Eqs. (4.253) and (4.258), respectively. Hence,
Now let us define a Q value by
In practice, the regime only exists for highly damped tubes where Q
<
0.05 or l
>
(6
×
106)a
2. According to Eq. (4.258), it describes the asymptotic curves in Fig. 4.46 and Fig. 4.47 for a
<
3
μm and hence can be regarded as an “ultra-narrow” tube regime.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.


