Generalizing PACK and UNPACK
This appendix shows how the PACK and UNPACK operators can usefully be generalized to deal not just with sets of intervals as such but also with other kinds of sets—in particular, sets of relations, sets of sets, and sets of bags. The important special case of packing a relation on a relation valued attribute is considered in some detail.
Keywords: gneralized UNPACK; generalized PACK; unpacked form; packed form
All generalizations are dangerous (often quoted in the form All generalizations are false).
—Alexandre Dumas fils (attrib.)
In Chapter 8, we introduced the operators EXPAND and COLLAPSE and considered their effect on sets of intervals specifically. But we did also note the point in passing that there’s no reason why those operators shouldn’t be generalized to work on other kinds of sets, and indeed there might be good reasons to do so. In this appendix, we briefly investigate this possibility. Recall from Chapter 10, however, that EXPAND and COLLAPSE—meaning, specifically, the unary relation versions of those operators—are really special cases of UNPACK and PACK, respectively; thus, the discussions in this appendix can and will be framed in terms of UNPACK and PACK instead of EXPAND and COLLAPSE as such. For simplicity, however, we’ll pretend as we did throughout most of Chapter 8—barring explicit statements to the contrary—that the operands to those operators are just sets and not, as they really ought to be, unary relations. Among other things, this pretense should help make the pictures we’ll be drawing to illustrate the ideas a little easier to understand.
Sets of Relations
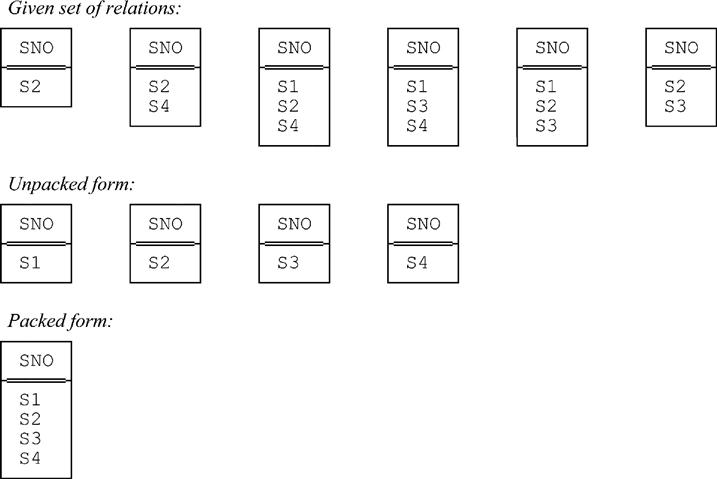
Let X be a set of relations all of the same type RT. Then we define UNPACK (X) and PACK (X) as follows:
■ UNPACK (X) returns a set Y of relations of type RT, such that (a) each relation in Y is of cardinality one and (b) a relation containing tuple t appears in Y if and only if a relation containing tuple t appears in X. Note in particular, therefore, that if X is empty, then Y is empty also. (What happens if X contains just one relation and that relation is empty?)
■ PACK (X) returns a set Y containing exactly one relation of type RT: namely, the union of all of the relations in X.1 Note in particular, therefore, that if X is empty, then Y contains just the empty relation of type RT, and if X contains just one relation r, then Y also contains just that one relation r. (Refer to Chapter 2 if you need to refresh your memory regarding unions of just one relation and unions of no relations at all.)
Fig. C.1 shows a sample set of relations and the corresponding unpacked and packed forms of that set.
Sets of Sets
In similar fashion we can define UNPACK and PACK for sets of sets. Let ST be some set type,2 and let X be a set of sets all of type ST. Then:
■ UNPACK (X) returns a set Y of sets of type ST, such that (a) each set in Y is of cardinality one and (b) a set containing the value v appears in Y if and only if a set containing the value v appears in X. Note: If X is empty, then Y is empty also. What happens if X contains just one set and that set is empty?
■ PACK (X) returns a set Y containing exactly one set of type ST: namely, the union of all of the sets in X. (If X is empty, then Y contains just the empty set of type ST, and if X contains just one set s, then Y also contains just that one set s.)
Sets of Bags
We can also, albeit somewhat less satisfactorily, define UNPACK and PACK for sets of bags.3 Let X be a set of bags all of the same type BT. Then:
■ UNPACK (X) returns a set Y of bags of type BT, such that (a) each bag in Y is of cardinality one and (b) a bag containing the value v appears in Y if and only if a bag containing the value v appears in X. Note carefully that each bag in Y is in fact a set, and furthermore that (by definition, since Y is a set) no bag in Y appears more than once.
■ PACK (X) returns a set Y containing exactly one bag of type BT: namely, the union of all of the bags in X.
At this point, however, we run into a problem. What exactly do we mean by “the union of all of the bags in X”? It turns out that if A and B are bags, then there are three different interpretations that might be given to the natural language expression “the union of A and B”—i.e., there are three different union operators that can apply to bags [39]:
■ The first is the regular set union operator, which returns a result—in fact, a set—in which the value v appears exactly once if and only if it appears in A or B or both at least once. In SQL terms, this is the UNION DISTINCT operator (more or less).
■ The second is what might be called the union plus operator, which returns a result—a bag—in which the value v appears exactly n times if and only if it appears exactly a times in A and exactly b times in B and n = a+b. In SQL terms, this is the UNION ALL operator (again, more or less).
■ The third is the true bag union operator as such [39], which returns a result—again a bag—in which the value v appears exactly n times if and only if it appears exactly a times in A and exactly b times in B and n = MAX {a,b}. SQL doesn’t support this operator.
So which union should we use in “bag PACK”?
■ If it’s the regular set union, the resulting bag will contain no duplicates (in fact, it’ll be a set). In a sense, therefore, information—specifically, “amount of duplication” information—represented by the original set of bags will be lost (in general).
■ On the other hand, if it’s one of the other two unions, then one unfortunate consequence is that the expressions PACK (X) and PACK (UNPACK (X)) will produce different results (again in general).
To illustrate these matters, let X contain just two bags, one containing just one occurrence of the supplier number S1 and nothing else, and the other containing just two occurrences of the supplier number S1 and nothing else. Then:
■ UNPACK (X) returns a set containing just one bag (actually a set) containing just one occurrence of S1.
■ PACK (UNPACK (X)) thus also returns a set containing just one bag (actually a set) containing just one occurrence of S1—and we get this same result no matter which union we use in the definition of PACK.
■ However, PACK (X) returns three different results, depending on which kind of union we use:
■ (Set union) PACK (X) returns the same result as PACK (UNPACK (X)): namely, a set containing just one bag containing just one occurrence of S1. (But therefore the “amount of duplication” information—i.e., the fact that S1 appeared once in one bag and twice in the other in the original set of bags X—has been lost. Of course, the same observation applies to UNPACK (X) also in this example.)
■ (Unionplus) PACK (X) returns a set containing just one bag containing three occurrences of S1. This result is different from the result of PACK (UNPACK (X)) (see above).
■ (Bag union) PACK (X) returns a set containing just one bag containing two occurrences of S1. This result is also different from the result of PACK (UNPACK (X)) (see above).
From the foregoing analysis, it follows that, while we certainly can define UNPACK and PACK operators for sets of bags if we want to, on the whole it looks as if it might not be a good idea to do so. Moreover, analogous remarks apply to sets of lists and sets of arrays and, more generally, to sets involving any kind of “collection,” if individual collections of the kind in question can contain distinct elements with the same value.
Bags: A Digression
This appendix overall is concerned primarily with various kinds of sets; however, the discussions of the previous section (“Sets of Bags”) remind us that some languages—SQL among them—support bags in addition to or in place of sets, and the case of bags as opposed to sets is thus perhaps worth some brief consideration as well. Now, bags can of course contain elements of many different kinds (integers, tuples, intervals, relations, and so on). In this appendix, however, we limit our attention to the cases of (a) bags whose contained elements are sets—the inverse, in a sense, of the case examined in the previous section—and (b) bags whose contained elements are themselves bags in turn.
Bags of Sets
Let X be a bag of sets, all of the same type ST. Then:
■ UNPACK (X) returns a bag Y of sets of type ST, such that (a) each set in Y is of cardinality one and (b) a set containing the value v appears in Y exactly n times if and only if that value v appears in exactly n sets in X.
■ PACK (X) returns a bag Y containing exactly one set of type ST: namely, the set union of all of the sets in X. (Since by definition the elements in X are sets specifically, the only kind of union that makes sense here is, of course, regular set union.)
By way of illustration, let X contain just three sets, one containing just the supplier number S1, one containing just the supplier numbers S1 and S2, and one being empty. Then:
■ UNPACK (X) returns a bag containing just three sets, two containing just S1 and one containing just S2.
■ PACK (UNPACK (X)) returns a bag (actually a set) containing just one set, containing just S1 and S2.
It follows that if we support bags at all, we can certainly define PACK and UNPACK for the particular case of bags whose contained elements are sets, if we want to.
Bags of Bags
Now we turn our attention to the case of bags whose contained elements are bags themselves—despite the fact that (in accordance with the remarks at the end of the section “Sets of Bags”) it’s our belief that support for UNPACK and PACK on such a construct might be a little unwise. Be that as it may, let X be a bag of bags all of the same type BT. Then:
■ UNPACK (X) returns a bag Y of bags of type ST, such that (a) each bag in Y is of cardinality one and (b) a bag containing the value v appears in Y exactly n times if and only if that value v appears a total of n times in the “union plus” of all of the bags in X.
■ PACK (X) returns a set Y containing exactly one bag of type BT: namely, the union of all of the bags in X—but again, as in the section “Sets of Bags,” we have three choices as to what might be meant by the term “union” here.
Development of examples to illustrate the foregoing definitions is left as an exercise.
Other Kinds of Sets
What about sets (or possibly bags) of values that aren’t collections?—for example, a set of integers or a set of tuples? Without going into details, suffice it to say that we’ve investigated this question, and we believe PACK and UNPACK should both be defined just to return their input in such cases.
Effect on “PACK and UNPACK ON”
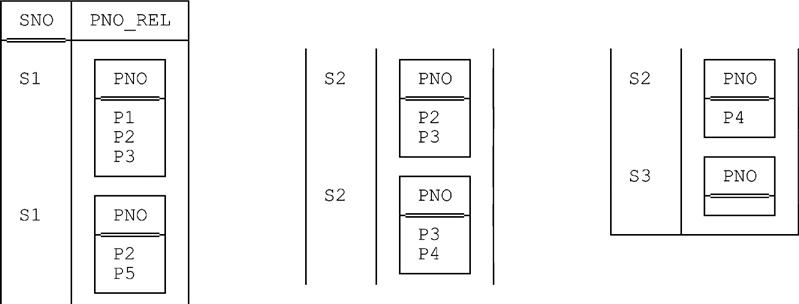
Chapters 9 and 10 described in great detail what we might call “the PACK and UNPACK ON” operators—i.e., versions of PACK and UNPACK that pack or unpack a given relation on the basis of some interval attribute (Chapter 9), or more generally on the basis of some number of such attributes (Chapter 10). So what about packing or unpacking a relation on the basis of an attribute of some other type? In this section, we consider just one example of this possibility; to be specific, we show what’s involved in packing a relation on a single attribute, but one that’s relation valued instead of interval valued (an unpack analog of the example is left as an exercise). Fig. C.3 shows such a relation; let’s call it r. Note the redundancy in that relation—for example, it shows supplier S2 paired with part P3 twice. Note that it also shows supplier S3 paired with no parts at all.
From the definition of the PACK operator in Chapter 9, we have the following as the expansion for the expression PACK r ON (PNO_REL):4
WITH ( r1 := r GROUP { PNO_REL } AS X , r2 := EXTEND r1 : { X := COLLAPSE ( X ) } ) :r2 UNGROUP X
Let’s consider this expansion one step at a time.
1. First, we evaluate the expression
r GROUP { PNO_REL } AS X
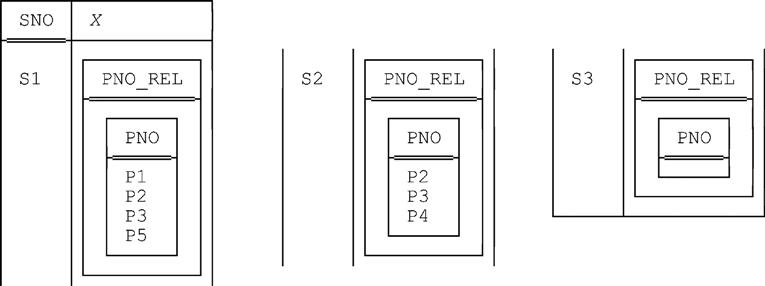
The result is shown in Fig. C.4. Observe that not only does that result have an attribute, X, that’s relation valued (as is always the case with the result of a GROUP operation), but the relations that are values of that attribute have a single attribute, PNO_REL, that’s relation valued in turn. In other words, there’s a kind of “double nesting” going on here—the result is a relation that contains relations that contain relations.
2. Next, we evaluate the expression
EXTEND r1 : { X := COLLAPSE ( X ) }
The result, r2, is shown in Fig. C.5.
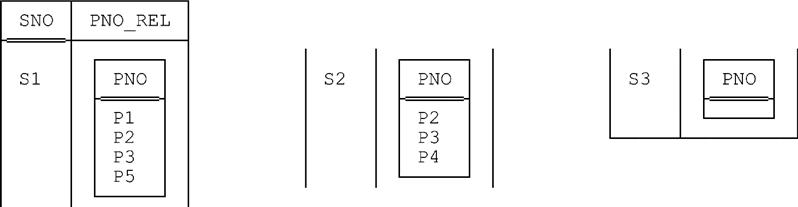
3. Finally, we evaluate the expression
r2 UNGROUP X
The result is shown in Fig. C.6. Note that the net effect is to eliminate all of the redundancies that were present in the original relation r. The parallels with packing a relation on an interval valued attribute should be obvious.