9
Functional Criteria
Given a program p and a specification R whose domain is X, we are interested to generate test data T as a subset of X in such a way that when we execute the candidate program p on all the elements of set T and observe its behavior, we can make meaningful inference on the functional properties of program p. In Chapter 8, we have discussed the requirements that set T must satisfy, depending on the goal of testing, and we have analyzed possible generation criteria that yield such data sets. The generation of test data may proceed either by analyzing the specification of the program or by analyzing the source code of the program. In this chapter, we focus on the first approach.
9.1 DOMAIN PARTITIONING
The criterion of domain partitioning is based on the premise that the input space X of the specification can be partitioned into equivalence classes such that in each class, candidate programs either runs successfully on all the states in the class or fails on all the states in the class; this criterion may be rationalized if we define equivalence classes to include all the input data that are processed the same way. Under such a condition, we can let T be a subset of S that includes a single element of each equivalence class. The selection criterion on a test set T can be formulated as follows:
The first condition means that all equivalence classes are represented in T; the second condition means that each equivalence class is represented by no more than one element in T.
A special example of equivalence relation arises when the specification of the program is deterministic (in particular, when the specification used is the intended function of the program); hence the following heuristic:
This relation has as many equivalence classes as F has elements in its range; hence for functions F with a finite and small range, this produces a small test data set T. The rationale for this criterion may be that all the inputs that are mapped to the same output are processed using the same sequence of operations; hence if the sequence is correct, it will work correctly for all the inputs in the same class, and if it is incorrect, it will fail for all the inputs in the same class. This criterion is as good as the assumption it is based on.
As an illustration, we consider the following example: We let the input space be defined by three real positive variables x, y, and z, which we assume to represent the sides of a triangle, and we consider the following specification, which analyzes the properties of the triangle represented by the input variables: Given that x, y, and z represent the sides of a triangle, place in t the class of the triangle represented by x, y, and z from the set {scalene, isosceles, equilateral, rightisosceles, right}. We assume that the label “isosceles” is reserved for triangles that are isosceles but not equilateral and that the label “right” is reserved for triangles that are right but not isosceles.
This specification can be written by means of the following predicates:
-
 .
. -
 .
. -
 .
.
Using these predicates, we define the following relations:
-
 .
. -
 .
. -
 .
. -
 .
. -
 .
.
Using these relations, we form the relational specification of the triangle classification problem:
We leave it to the reader to check that T is a function; clearly, relation ![]() is an equivalence relation on the domain of T. Its equivalence classes are:
is an equivalence relation on the domain of T. Its equivalence classes are:
-
 .
. -
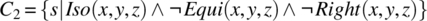 .
. -
 .
. -
 .
. -
 .
.
This partition is illustrated in Figure 9.1 (where it is superimposed on the division of space S into the set of right triangles, the set of isosceles triangles, the set of equilateral triangles, and the set of scalene triangles).

Figure 9.1 Partitioning the set of triangles.
From this partition of S, we derive an arbitrary set of test data:
| Partition | Test data | |||||
| Name | Definition | x | y | z | ||
| C1 | Equi(x, y, z) | 2 | 2 | 2 | ||
| C2 |
|
2 | 2 | 1 | ||
| C3 |
|
2 | 2 |
|
||
| C4 |
|
3 | 4 | 5 | ||
| C5 |
|
2 | 3 | 4 | ||
The rationale of space partitioning is that any program that runs successfully on these five test data triplets will run successfully on any triplet of positive reals. We have no reason to subscribe to this rationale, except for the fact that, in all likelihood, candidate programs operate by comparing the relative values of x, y, and z; hence any two states s and s’ whose x-, y-, and z-components are in the same relations relative to each other are processed the same way by the program; therefore the program succeeds for both or fails for both. Notice that, because this test generation method is functional, then (by definition) we generate the test data without ever looking at the program that we are supposed to test with this data.
Now that the data has been generated, let us now look at a possible implementation of the specification presented above:
#include <iostream>#include <cmath>using namespace std;/* constants */float eps = 0.000001;/* state variables */float x, y, z;/* functions */bool equal(float a, float b);bool equi(float x, float y, float z);bool iso(float x, float y, float z);bool right(float x, float y, float z);int main (){cout << “enter the triangle sides on one line” << endl;cin >> x >> y >> z;if (equi(x,y,z)){cout << “equilateral” << endl;}else{if (iso(x,y,z)){if (right(x,y,z)){cout << “isosceles right” << endl;}else {cout << “isosceles” <<endl;}}else{if (right(x,y,z)) {cout << “right” << endl;}else {cout << “scalene” << endl;}}}}bool equal (float a, float b){return abs(a-b)<eps;}bool equi(float x, float y, float z){return (equal(x,y) && equal(y,z));}bool iso(float x, float y, float z){return (equal(x,y) || equal(y,z) || equal(x,z));}bool right(float x, float y, float z){return (equal(x*x+y*y,z*z) || equal(x*x+z*z,y*y) || equal(y*y+z*z,x*x));}
Execution of this program on the proposed test data yields the following results:
| Input variables | Output | ||
| x | y | z | |
| 2 | 2 | 2 | Equilateral |
| 2 | 2 | 1 | Isosceles |
| 2 | 2 |
|
Right isosceles |
| 3 | 4 | 5 | Right |
| 2 | 3 | 4 | Scalene |
The behavior of the program on the selected test data is correct; according to the heuristic of space partitioning, and to the extent that it is valid, we can infer from this test that the program will behave correctly for any triplet of positive real numbers that define a triangle.
So far we have assumed that the input values x, y, and z define a triangle and have focused on the correctness of candidate programs with respect to a relation whose domain is the set of triangles; but assume that, for the sake of robustness, we wish to lift this assumption and consider cases where the input does not define a triangle (e.g., the triplet (3,3,10) does not define a triangle). We introduce the following predicate:
-
 .
.
Using this predicate, we define a new specification T′ in terms of the previous specification T, according to the following formula:
To make our program robust (i.e., able to handle any triplet of real numbers), we modify it to be correct with respect to specification T′. We obtain the following program:
#include <iostream>#include <cmath>using namespace std;/* constants */float eps = 0.000001;/* state variables */float x, y, z;/* functions */Bool tri(float x, float y, float z);bool equal(float a, float b);bool equi(float x, float y, float z);bool iso(float x, float y, float z);bool right(float x, float y, float z);int main (){cout << “enter the triangle sides on one line” << endl;cin >> x >> y >> z;if (!tri(x,y,z)){cout << “not a triangle” << endl;}else{if (equi(x,y,z)){cout << “equilateral” << endl;}elseif (iso(x,y,z)){if (right(x,y,z)){cout << “isosceles right” << endl;}else {cout << “isosceles” <<endl;}else{if (right(x,y,z)) {cout << “right” << endl;}else {cout << “scalene” << endl;}}}}bool tri (float x, float y, float z){return ((x<=y+z) && (y<=x+z) && (z<=x+y));}bool equal (float a, float b){return abs(a-b)<eps;}bool equi(float x, float y, float z){return (equal(x,y) && equal(y,z));}bool iso(float x, float y, float z){return (equal(x,y) || equal(y,z) || equal(x,z));}bool right(float x, float y, float z){return (equal(x*x+y*y,z*z) || equal(x*x+z*z,y*y) ||equal(y*y+z*z,x*x));}
From the viewpoint of test data generation, this adds a new output value, hence a new equivalence class in the domain of the specification, for which we must select a representative. We choose (3,3,10), yielding the following table:
| Input variables | Output | ||
| x | y | z | |
| 2 | 2 | 2 | Equilateral |
| 2 | 2 | 1 | Isosceles |
| 2 | 2 |
|
Right isosceles |
| 3 | 4 | 5 | Right |
| 2 | 3 | 4 | Scalene |
| 3 | 3 | 10 | Not a triangle |
Remember that for our purposes, if it weren’t for the fact that it is impractical, X is the most effective test data set; selecting the test data set T = X would enable us, if it were feasible, to run the program exhaustively on all its possible inputs. Notice that the criterion of domain partitioning enables us, in effect, to run the program exhaustively on all its possible outputs, instead.
9.2 TEST DATA GENERATION FROM TABULAR EXPRESSIONS
In the previous section, we have analyzed a criterion for test data selection that applies to deterministic specifications and partitions the domain of the specification (say F) using the nucleus of F as the equivalence relation ![]() . In this section, we see instances where the nucleus of F is either too coarse-grained or too fine-rained for our purposes, and we choose a different equivalence relation.
. In this section, we see instances where the nucleus of F is either too coarse-grained or too fine-rained for our purposes, and we choose a different equivalence relation.
Tabular specifications are a form of formal specifications where complex functions that take different expressions according to many parameters can be represented in a way that highlights their dependencies and facilitates their analysis and their understanding. As an example, consider a table that specifies the tax rates of individual taxpayers in a particular jurisdiction, as a function of their income, their marital status, and their number of dependents.
| Function: Tax(X, d, t) | ||||||||
| t: Marital status |
d: Number of dependents |
X: Income bracket (in $K) |
||||||
| X ≤ 20 | 20 < X ≤ 60 | 60 < X ≤ 150 | 150 < X ≤ 250 | 250 < X | ||||
| Single | 1 | 0.08 × X | 1.6 +0.10×(X − 20) | 5.6 +0.15 × (X − 60) | 19.1 +0.20 × (X − 150) | 39.1 + 0.25 × (X − 250) | ||
| 2 | 0.07 × X | 1.4 + 0.09(X − 20) | 5.0 +0.14 × (X − 60) | 17.6 +0.19 × (X − 150) | 36.6 + 0.24 × (X − 250) | |||
| 3 or more | 0.06 × X | 1.2 + 0.08(X − 20) | 4.4 +0.13 × (X − 60) | 16.1 +0.18 × (X − 150) | 34.1 + 0.23 × (X − 250) | |||
| Married/filing singly | 1 | 0.07 × X | 1.4 + 0.09(X − 20) | 5.0 +0.14 × (X − 60) | 17.6 +0.19 × (X − 150) | 36.6 + 0.24 × (X − 250) | ||
| 2 | 0.06 × X | 1.2 + 0.08(X − 20) | 4.4 +0.13 × (X − 60) | 16.1 +0.18 × (X − 150) | 34.1 + 0.23 × (X − 250) | |||
| 3 | 0.05 × X | 1.0 + 0.07(X − 20) | 3.8 +0.12 × (X − 60) | 14.6 +0.17 × (X − 150) | 31.6 + 0.22 × (X − 250) | |||
| 4 or more | 0.04 × X | 0.8 + 0.06(X − 20) | 3.2 +0.11 × (X − 60) | 13.1 +0.16 × (X − 150) | 29.1 + 0.21 × (X − 250) | |||
We let X, d, and t be variables that represent, respectively, the taxpayer’s income, his/her number of dependents, and his/her marital status (filing status). The input space of this specification is defined by the set of values that these three variables take, where X is a real number, d is an integer, and t is a binary value (single, married). If we assume, for the sake of argument, that incomes of interest range between 0 and 1000,000, and that taxes are rounded to the nearest dollar figure, then the output of this function ranges between 0 and 186,600. If we were to apply the criterion of domain partitioning strictly, we would find that this function partitions its domain into 186,601 equivalence classes, hence T would have to have that many elements.
Yet, without knowing how candidate programs compute this function, we can assume with some level of confidence that each entry in this tabular expression corresponds to a distinct execution path; hence if we generated one test datum for each entry rather than one test datum for each tax value, we would get a much smaller test data set (35 elements rather than 186,601) without perhaps much loss of effectiveness. To this effect, we apply domain partitioning to a function Tax′ derived from Tax by replacing each expression in the tabular representation of Tax by a (distinct) constant. The rationale for this substitution is the assumption that if and only if an expression in the table of Tax produces a correct value for one element within its domain of application, then it produces a correct value for all elements within its domain of application. This yields the following function.
| Function: Tax '(X, d, t) | ||||||||
| t:Marital status | d: Number of dependents |
X:Income bracket (in $K) | ||||||
| X ≤ 20 | 20 < X ≤ 60 | 60 < X ≤ 150 | 150 < X ≤ 250 | 250 < X | ||||
| t = Single | d = 1 | C1,1,1 | C1,1,2 | C1,1,3 | C1,1,4 | C1,1,5 | ||
| d = 2 | C1,2,1 | C1,2,2 | C1,2,3 | C1,2,4 | C1,2,5 | |||
| d ≥ 3 | C1,3,1 | C1,3,2 | C1,3,3 | C1,3,4 | C1,3,5 | |||
| t = Married | d = 1 | C2,1,1 | C2,1,2 | C2,1,3 | C2,1,4 | C2,1,5 | ||
| d = 2 | C2,2,1 | C2,2,2 | C2,2,3 | C2,2,4 | C2,2,5 | |||
| d = 3 | C2,3,1 | C2,3,2 | C2,3,3 | C2,3,4 | C2,3,5 | |||
| d ≥ 4 | C2,4,1 | C2,4,2 | C2,4,3 | C2,4,4 | C2,4,5 | |||
Applying space partitioning to function Tax′ using the nucleus of this function, we find the following test data.
| Marital status/Taxpayer status | Number of dependents | Income bracket (X, in $K) | ||||||
| X ≤ 20 | 20 < X ≤ 60 | 60 < X ≤ 150 | 150 < X ≤ 250 | 250 < X | ||||
| t = Single | d = 1 | (10, 1, S) | (40, 1, S) | (100, 1, S) | (200, 1, S) | (300, 1, S) | ||
| d = 2 | (10, 2, S) | (40, 2, S) | (100, 2, S) | (200, 2, S) | (300, 2, S) | |||
| d ≥ 3 | (10, 4, S) | (40, 4, S) | (100, 4, S) | (200, 4, S) | (300, 4, S) | |||
| t = Married | d = 1 | (10, 1, M) | (40, 1, M) | (100, 1, M) | (200, 1, M) | (300, 1, M) | ||
| d = 2 | (10, 2, M) | (40, 2, M) | (100, 2, M) | (200, 2, M) | (300, 2, M) | |||
| d = 3 | (10, 3, M) | (40, 3, M) | (100, 3, M) | (200, 3, M) | (300, 3, M) | |||
| d ≥ 4 | (10, 5, M) | (40, 5, M) | (100, 5, M) | (200, 5, M) | (300, 5, M) | |||
To check that the boundaries between the various income brackets are processed properly by candidate programs, we may also want to duplicate this table for all boundary values of X, namely X=20, 60, 150, 250, and 1000 (assuming that 1M is the maximum income under consideration). This yields the following test data.
| Marital status/Taxpayer status | Number of dependents | Income bracket (X, in $K) | ||||||
| X ≤ 20 | 20 < X ≤ 60 | 60 < X ≤ 150 | 150 < X ≤ 250 | 250 < X | ||||
| t = Single | d = 1 | (10, 1, S) | (40, 1, S) | (100, 1, S) | (200, 1, S) | (300, 1, S) | ||
| (20, 1, S) | (60, 1, S) | (150, 1, S) | (250, 1, S) | (1000, 1, S) | ||||
| d = 2 | (10, 2, S) | (40, 2, S) | (100, 2, S) | (200, 2, S) | (300, 2, S) | |||
| (20, 2, S) | (60, 2, S) | (150, 2, S) | (250, 2, S) | (1000, 2, S) | ||||
| d ≥ 3 | (10, 4, S) | (40, 4, S) | (100, 4, S) | (200, 4, S) | (300, 4, S) | |||
| (20, 4, S) | (60, 4, S) | (150, 4, S) | (250, 4, S) | (1000, 4, S) | ||||
| t = Married | d = 1 | (10, 1, M) | (40, 1, M) | (100, 1, M) | (200, 1, M) | (300, 1, M) | ||
| (20, 1, M) | (60, 1, M) | (150, 1, M) | (250, 1, M) | (1000, 1, M) | ||||
| d = 2 | (10, 2, M) | (40, 2, M) | (100, 2, M) | (200, 2, M) | (300, 2, M) | |||
| (20, 2, M) | (60, 2, M) | (150, 2, M) | (250, 2, M) | (1000, 2, M) | ||||
| d = 3 | (10, 3, M) | (40, 3, M) | (100, 3, M) | (200, 3, M) | (300, 3, M) | |||
| (20, 3, M) | (60, 3, M) | (150, 3, M) | (250, 3, M) | (1000, 3, M) | ||||
| d ≥ 4 | (10, 5, M) | (40, 5, M) | (100, 5, M) | (200, 5, M) | (300, 5, M) | |||
| (20, 5, M) | (60, 5, M) | (150, 5, M) | (250, 5, M) | (1000, 5, M) | ||||
Assuming that the specification is valid (is not in question) and a candidate program p computes taxes as a linear function of income within each partition of the input space, it is highly unlikely that program p runs successfully on all the test data presented above, yet fail on any other valid input.
We consider a second example, where we show that the important criterion for space partitioning is not the nucleus of the function, but rather how the specification is represented in tabular form. We consider a (fictitious) tabular specification that represents the graduate admissions criteria at a university, depending on standard graduate record examination (GRE) scores for quantitative reasoning (G) and grade point average (GPA) (A); also the admissions committee lends different levels of credibility to different institutions and hence interprets the GPA with different levels of confidence, according to whether the candidate did his undergraduate degree in the same institution, in another North American institution, or elsewhere, as shown by the table below. We assume that the specification provides three distinct outcomes and they are admission (Ad), rejection (Re), and conditional acceptance (Cond), where the latter outcome places the application on hold until an admitted student declines the admission, thereby freeing up a spot for admission.
| Admission criteria | |||||||
| Institution, I | GPA, A | GRE score, G | |||||
| G < 155 | 155 ≤ G < 160 | 160 ≤ G < 165 | 165 ≤ G | ||||
| Same Institution | 2.9 ≤ A | Ad | Ad | Ad | Ad | ||
| 2.3 ≤ A < 2.9 | Cond | Cond | Ad | Ad | |||
| A < 2.3 | Re | Re | Cond | Cond | |||
| Another North American Institution | 2.9 ≤ A | Cond | Ad | Ad | Ad | ||
| 2.3 ≤ A < 2.9 | Re | Cond | Ad | Ad | |||
| A < 2.3 | Re | Re | Cond | Cond | |||
| Overseas | 2.9 ≤ A | Re | Cond | Ad | Ad | ||
| 2.3 ≤ A < 2.9 | Re | Re | Cond | Ad | |||
| A < 2.3 | Re | Re | Re | Cond | |||
The input space for this function is the Cartesian product of three variables, namely G, A, and I. If we apply space partitioning using the nucleus of this function, we find three equivalence classes, corresponding to the three possible outputs. But in practice, any candidate program most likely proceeds by combining the conditions shown above; hence it makes more sense to partition the input space by combining these conditions, which gives 36 classes rather than 3. If for each class we select a test datum in the middle of the interval and at the boundary, we find the following test data set.
| Admission criteria | |||||
| Institution, I | GPA, A | GRE score, G | |||
| G < 155 | 155 ≤ G < 160 | 160 ≤ G < 165 | 165 ≤ G | ||
| Same Institution (S) | 2.9 ≤ A | (120,S,3.5)(0,S,2.9) | (158,S,3.5)(155,S,2.9) | (162,S,3.5)(160,S,2.9) | (168,S,3.5)(165,S,2.9) |
| 2.3 ≤ A < 2.9 | (120,S,2.5)(0,S,2.3) | (158,S,2.5)(155,S,2.3) | (162,S,2.5)(160,S,2.3) | (168,S,2.5)(165,S,2.3) | |
| A < 2.3 | (120,S,2.0)(0,S,.0) | (158,S,2.0)(155,S,.0) | (162,S,2.0)(160,S,.0) | (168,S,2.0)(165,S,.0) | |
| Another North American Institution (N) | 2.9 ≤ A | (120,N,3.5)(0,N,2.9) | (158,N,3.5)(155,N,2.9) | (162,N,3.5)(160,N,2.9) | (168,N,3.5)(165,N,2.9) |
| 2.3 ≤ A < 2.9 | (120,N,2.5)(0,N,2.9) | (158,N,2.5)(155,N,2.9) | (162,N,2.5)(160,N,2.9) | (168,N,2.5)(165,N,2.9) | |
| A < 2.3 | (120,N,2.0)(0,N,.0) | (158,N,2.0)(155,N,.0) | (162,N,2.0)(160,N,.0) | (168,N,2.0)(165,N,.0) | |
| Overseas (O) | 2.9 ≤ A | (120,O,3.5)(0,O,2.9) | (158,O,3.5)(155,O,2.9) | (162,O,3.5)(160,O,2.9) | (168,O,3.5)(165,O,2.9) |
| 2.3 ≤ A <2.9 | (120,O,2.5)(0,O,2.9) | (158,O,2.5)(155,O,2.9) | (162,O,2.5)(160,O,2.9) | (168,O,2.5)(165,O,2.9) | |
| A < 2.3 | (120,O,2.0)(0,O,.0) | (158,O,2.0)(155,O,.0) | (162,O,2.0)(160,O,.0) | (168,O,2.0)(165,O,.0) | |
For completeness, we could enrich the data set by combining normal values with boundary values.
9.3 TEST GENERATION FOR STATE BASED SYSTEMS
A state-based system is a system whose output depends not only on its (current) input but also on an internal state, which is itself dependent on past inputs. As we discussed in Chapter 4, such systems can be specified in relational form by means of the following artifacts:
- An input space X, from which we derive a set H of sequences of X
- An output space Y
- A relation R from H to Y.
It is common to specify such systems in a way that makes their internal state explicit, by means of the following artifacts:
- An input space X
- An output space Y
- An internal state space, ∑
- An output function, ω from X × ∑ to Y
- A state transition function, θ from X × ∑ to ∑.
We argue that it is possible to map a specification of the form (X,Y,R) into a specification of the form (X,Y,∑,ω,θ), as follows:
- X and Y are preserved.
-
We define the equivalence relation E on H (=X*) by:
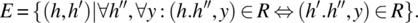
In other words, the pair (h, h′) is in E if and only if they are equivalent histories, in the sense that they produce the same output now (for h″ empty) and in the future (for h″ not empty). Using this equivalence relation, we define the internal state space of the system as the quotient (H/E), that is, the set of equivalence classes of H modulo E. Whereas the output of the system depends on its input history, this does not mean that the system must remember its input history in all its detail; rather it must only remember the equivalence class of its input history; this is exactly the internal state of the system.
- The output function is defined as follows:Given a current internal state σ and a current input symbol x, we let h be an arbitrary element of σ, and we let y be an image of (h. x) by R. Because σ is an equivalence class of H modulo E, the choice of h within σ is immaterial, by definition.
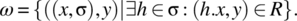
- The state transition function is defined as follows:where E(h. x) designates the set of images of (h. x) by relation E, which is the equivalence class of (h. x) modulo E.
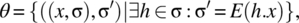
We have made the observation that even software systems that carry an internal state can, in theory, be modeled by a mere relation from an input set (structured as the set of lists formed from the input space) to an output space. This observation is important because it means that we can, in theory, select test data for such a system in the same way as we do for a system that has no internal state, except for considering the special structure of the input set.
As an illustration of the mapping between the (X, Y, R) model of specification and the (X, Y, ∑, ω, θ) model, we consider the specification of the stack given in Chapter 4 in the (X, Y, R) format and we discuss (informally) the terms of its (X, Y, ∑, ω, θ) specification.
- X: The input space of the stack is defined aswhere itemtype is the data type of the items we envision to store in the stack. We distinguish, in set X, between inputs that affect the state of the stack (namely:

 and inputs that merely report on it (namely:
and inputs that merely report on it (namely:  ).
).- From the set of inputs X, we build the set of input histories, H, defined as,
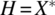 .
.
- From the set of inputs X, we build the set of input histories, H, defined as,
-
Y: The output space includes all the values returned by all the inputs of VX, namely:

- ∑: The equivalence relation E includes two histories h and h′ if and only if any subsequent history h″ produces the same outcomes. Examples of histories that are equivalent modulo relation E include, for instance:
- pop.top.init.pop.push(a).
- init.push(a).
- init.pop.top.size.push(a).empty.push(b).top.pop.
- init.push(a).push(b).push(c).push(d).top.pop.pop.pop.
- init.push(a).
- ω: The output function of the stack maps an internal state σ and a current input x into an output y by virtue of the equation:

where h is an element of σ. If we consider the internal state σ that is the equivalence class of init.push(a), and we let h = init.push(a) be a representative element of state σ, then the output of the stack for internal state σ and input x is characterized by the following equation:

For
 ,
,  .
.For
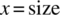 ,
, 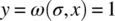
For
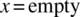 ,
,  .
.For x = pop, push(_), or init,
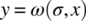 is arbitrary (an arbitrary element of Y), since these are elements of AX that change the state of the stack but generate no output.
is arbitrary (an arbitrary element of Y), since these are elements of AX that change the state of the stack but generate no output. - θ: The state transition function of the stack maps an internal state σ and a current input x into a new internal state σ′ by virtue of the equation:where h is an element of σ. If we consider the internal state σ that is the equivalence class of init.push(a), and we let h = init.push(a) be a representative element of state σ, then the next state of the stack for internal state σ and input x is characterized by the following equation:

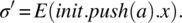
The following table shows the result of applying function θ to the init.push(a)
and to the input sympols of AX.
| x | θ (init.push(a), x) |
| init | init |
| push(b) | init.push(a).push(b) |
| pop | init |
Because formally, state-based systems can be specified by binary relations, then in theory we can apply to them any criterion that we apply to simple input/output systems which are also specified by (homogeneous) binary relations. But in recognition of the special structure that implementations of state-based systems have (in terms of an input space, an internal space, and an output space), it makes sense to formulate test data selection criteria accordingly. Among the test data selection criteria that we may adopt, we mention the following:
- Select Test Data to Visit Every State. The question that arises with this criterion is that the specification of the product is defined in terms of input sequences and outputs and has no cognizance of internal states; also, even if we derive the states from the trace specifications as we have discussed above, the implementation does not have to adopt these very states. We obviate this dilemma by considering that, for an outside observer, a state is characterized by the values of all the VX operations at that state. In other words, to check that the software product is in the right state (without looking at the internal data of the product) with respect to the specification, we generate the sequence of operations that leads us to that state, and then we append to it in turn all the VX operations of the specification. The procedure that generates data according to this criterion proceeds as follows:
- Partition the set of histories into equivalence classes modulo the equivalence relation E defined above.
- Choose an element of each equivalence class, and add to it, in turn, all the VX operations of the specification.
- Select Test Data to Perform Every State Transition. We perform state transitions by appending AX operations to existing sequences for all the AX operations of the specification, then appending in turn all the VX operations to identify the new state, and check its validity with respect to the specification. This criterion is illustrated in the Figure 9.3, where the quadrants represent equivalence classes of H* modulo E, h1, h2, …, h8 represent the elements of the equivalence classes, and v1, v2, …, vi represent the VX operations of the specification, and a1, a2, …, aj represent its AX operations.
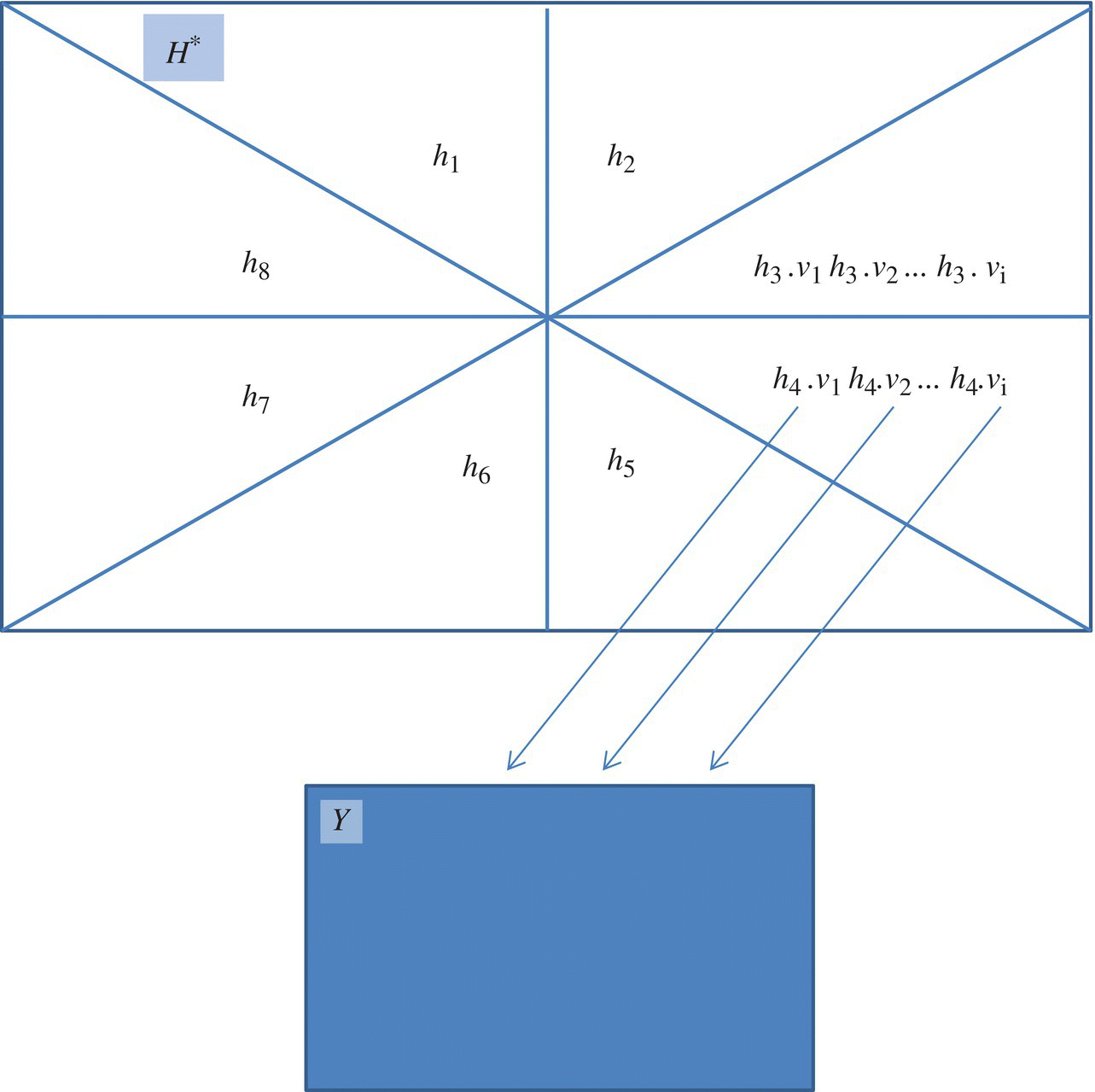
Figure 9.2 Visiting each state.

Figure 9.3 Visiting each state transition.
From this discussion we infer that the set of test data that we ought to generate to visit all the states and traverse all the state transitions is the union of two terms:
-
 (by virtue of the criterion of visiting all the states) and
(by virtue of the criterion of visiting all the states) and -
 (by virtue of traversing all the state transitions).
(by virtue of traversing all the state transitions).
Whence the following test data generation criterion:
Whereas the formula of T (above) provides for composing sets (X*/E), AX, and VX by means of the Cartesian product, we in fact mean to obtain a set of sequences constructed by concatenation of elements of these sets; this is illustrated in the example below.
While AX and VX are usually small, (X*/E) is usually infinite, requiring some additional assumptions to replace it by a finite/small subset. As an illustration, we consider again the stack specification, and we argue that two input sequences of this specification are equivalent if and only if they are reducible to the same sequence of the form:
This set of states is clearly infinite, given that k can be arbitrarily large, and t1, t2, t3, …, tk, can take arbitrary values. If we assume that the success or failure of a stack implementation will not depend, perhaps, on the value that we store in the stack at any position, then we can represent states as follows, where ![]() represents a sequence of n instances of push() for arbitrary values on the stack, then we can write the states of the stack as:
represents a sequence of n instances of push() for arbitrary values on the stack, then we can write the states of the stack as:
This set is also infinite, since k may take arbitrary natural values; hence further assumptions are needed. We may assume (with some risk) that any implementation of the stack that works for stacks of size 3 works for stacks greater than 3, provided we have assurances that overflow is not an issue (either because our stack size is bounded or because our supply of memory is unbounded). Hence (X*/E) can be approximated with the following set:
This gives the following test data, which we present in two different tables that correspond to the two terms of the union in the formula of T:
| (X*/E) | |||||||
| init | init.push(–) | init.push( ). push( ) | init.push( ). push( ). push( ) | ||||
| VX | top | init.top | init.push(a).top | init.push(–).push(a).top | init.push(–).push(–).push(a).top | ||
| size | init.size | init.push(a).size | init.push(–).push(a).size | init.push(–).push(–).push(a).size | |||
| empty | init.empty | init.push(a).empty | init.push(–).push(a).empty | init.push(–).push(–).push(a).empty | |||
| AX | VX |
|
|||||
| init | init.push(–) | init.push( ). push( ) | init.push( ). push( ). push( ) | ||||
| init | top | init.init.top | init.push(a).init.top | init.push(–).push(a).init.top | init.push(–).push(–).push(a).init.top | ||
| size | init.init.size | init.push(a).init.size | init.push(–).push(a).init.size | init.push(–).push(–).push(a).init.size | |||
| empty | init.init.empty | init.push(a).init.empty | init.push(–).push(a).init.empty | init.push(–).push(–).push(a).init.empty | |||
| push | top | init.push(b).top | init.push(a).push(b).top | init.push(–).push(a).push(b).top | init.push(–).push(–).push(a).push(b).top | ||
| size | init
push(b).size |
init.push(a).push(b).size | init.push(–).push(a).push(b).size | init.push(–).push(–).push(a).push(b).size | |||
| empty | init.push(b).empty | init.push(a).push(b).empty | init.push(–).push(a).push(b).empty | init.push(–).push(–).push(a).push(b).empty | |||
| pop | top | init.pop.top | init.push(a).pop.top | init.push(–).push(a).pop.top | init.push(–).push(–).push(a).pop.top | ||
| size | init.pop.size | init.push(a).pop.size | init.push(–).push(a).pop.size | init.push(–).push(–).push(a).pop.size | |||
| empty | init.pop.empty | init.push(a).pop.empty | init.push(–).push(a).pop.empty | init.push(–).push(–).push(a).pop.empty | |||
How do we test an implementation using this test data? Simply by declaring an instance of the class that implements the specification R and by writing sequences of method calls that represent the data shown in this table. For example,
#include <iostream>#include “stack.cpp”using namespace std;/* state variables */stack s;itemtype t; int z; bool e; // to store outputs of VX operationsint main (){s.init(); t=s.top(); cout << t; // test datum: init.top// … … …s.init(); s.push(c); s.push(d); s.push(a); s.push(b);// test datum: init.push(_).push(_).push(a).pop.empty}
As for the question of whether these executions took place according to the specification, it will be addressed when we discuss oracle design, in Chapter 11.
9.4 RANDOM TEST DATA GENERATION
Test data generation is a difficult, labor-intensive, time-consuming and error-prone activity. Like all such activities, it raises the question of whether it can be automated. To automate the generation of specific test data that meet specific generation criteria using specifications is very difficult, especially if one considers that very often the specification is not available in the form and with the precision that is required for this purpose. What is possible, however, is to generate great volumes of random test data, according to arbitrary probability distributions; there are many cases where this approach provides an excellent return on investment, in terms of test effectiveness versus testing effort. Random number generators are widely available, in conjunction with common programming languages, or as part of mathematical packages; they can be used to generate a wide range of probability laws. Also, because they operate automatically, they can be used to generate arbitrarily large volumes of data and provide arbitrary levels of test thoroughness at relatively little cost and little risk.
- Using the package
“rand.cpp”, we can generate random numbers between 0 (inclusive) and 1 (non-inclusive) by calling the functionNextRand()as many times as we need; prior to the first call, we must initialize the random generation process by calling the functionSetSeed()with an arbitrary numeric parameter. - Using function
NextRand(), we can generate random real numbers that range uniformly 0.0 inclusive and M (non-inclusive) for an arbitrary value of real number M.float function randomReal(float M){return M*NextRand();} - Using function
NextRand(), we can generate random integers that range uniformly between 1 (inclusive) and N (inclusive), for an arbitrary positive integer N.int function randomInt(int N){return 1+ int(N*NextRand());} - Using function
NextRand(), we can generate a Boolean function that returns true with a given probability (and false otherwise); the following function returns true with probability p.bool function randomBool(float p){return (NextRand() <= p);} - Using function
randomBool(), we can generate a Boolean function that returns true, on average, once every N times that it is called.bool function randomEvent(int N){return (randomBool(1.0/N));} - Using function
randomInt(), we can generate an integer function that ranges uniformly between two values N1 and N2, where .
.int function randomInterval(int N1, int N2){return (N1-1+randomInt(N2-N1+1));} - Using function
randomInterval(), we can generate an integer function that ranges uniformly between –N and N, for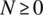 .
.int function randomSym(int N){return (randomInterval(-N,N));} - Using function
NextRand(), we can generate a function that produces a set of discrete outcomes with a specific probability distribution.
itemtype randomItems (itemtype items[],float distribution[]){float cumul[nbitems];for (int i=0; i<nbitems; i++){cumul[i]=0;for (int j=0; j<=i; j++) {cumul[i]=cumul[i]+distribution[j];}}float p; p=NextRand(); int i; i=0; while (p>cumul[i]){i++;}return (items[i]);}
This function proceeds by taking the array that represents the probability distribution and building an array of cumulative probability distributions, as follows:
| index | 0 | 1 | 2 | 3 | … | nbitems-1 |
| items | a0 | a1 | a2 | a3 | … |
|
| distribution. | p0 | p1 | p2 | p3 | … |
|
| cumul | p0 |
|
|
|
… | 1.0 |
Once the cumulative array is loaded, the function draws a random number p between 0.0 (inclusive) and 1.0 (exclusive) and returns the first item ai for which p is less than or equal to cumul[i]. Such a value i satisfies the following condition:
The length of this interval is the difference between ![]() and cumul[i], which is pi. The bigger the value of pi, the more likely p is to fall in this interval, the more ai is to be selected. To test this function, we invoke a large number of times and show that the distribution with which it generates the various items mimics the given probability distribution. To this effect, we execute the following program on a set of five items (which we represent by 0, 1, 2, 3, 4) with a probability distribution of (0, 0.1, 0.2, 0.3, and 0.4). The program that runs this experiment is given below:
and cumul[i], which is pi. The bigger the value of pi, the more likely p is to fall in this interval, the more ai is to be selected. To test this function, we invoke a large number of times and show that the distribution with which it generates the various items mimics the given probability distribution. To this effect, we execute the following program on a set of five items (which we represent by 0, 1, 2, 3, 4) with a probability distribution of (0, 0.1, 0.2, 0.3, and 0.4). The program that runs this experiment is given below:
#include <iostream>#include “rand.cpp”using namespace std;// constantsint nbitems = 5;// type defstypedef int itemtype;// functionsitemtype randomItems (itemtype items[], float distribution[]);int main (){SetSeed(684);int stats[5];itemtype items[5]; float distribution[5];for (int k=0; k<5; k++){items[k]=k; distribution[k]=k/10.0;stats[k]=0;}for (int k=0; k<100000; k++){stats[randomItems(items,distribution)]++;}for (int i=0; i<5; i++){cout << stats[i] << “ ”;}cout << endl;}
Execution of this program yields the following outcome, which reflects a very consistent behavior with respect to our original distribution.
0 100749 199899 300003 399349
As a simple illustration of this toolbox of functions for random test data generation, we consider that we must generate test data for a small function that searches an item in an array, where:
- Arrays vary in size between 1 and 100.
- The contents of arrays are integers that vary between −20 and 80.
- The item to be searched in the array is an element of the array in 34% of the cases
To this effect, we write the following program:
#include <iostream>#include “rand.cpp”using namespace std;// constantsint maxN = 100; // max array sizeint N1=-20; int N2=80; // range of array valuesint maxX=200000;float prob=0.34;// type defstypedef int itemtype;// functionsint randomInt (int maxval);int randomInterval (int N1, int N2);int randomSym (int N);bool randomBool (float p);int main (){itemtype a[maxN]; itemtype X; SetSeed(684);int N; N=randomInt(maxN); cout << “array a: ” << endl;for (int i=0; i<N; i++){a[i]=randomInterval(N1,N2); cout << a[i] << “ ”;}cout << endl << “item to search, X: ” ;if (randomBool(prob)){int i; i=randomInt(N); X=a[i];} // assured to be in aelse {X=randomSym(maxX);} // unlikely to be in acout << X << endl;}
If we iterate the sequence of code given in the main program an arbitrary number of times, we get as many test data samples as we wish.
9.5 TOURISM AS A METAPHOR FOR TEST DATA SELECTION
In his book titled Exploratory Software Testing, Jim Whittaker, test engineering director at Google, discusses strategies for functional test data selection that equate testing a software product to exploring its various recesses, nooks and crannies so as to expose all its faults. Because these strategies are widely applicable, and cut across most existing techniques, we briefly present them in this section. The software product is mapped into districts (just like a city), and the tours are partitioned by district (just like city tours). Specifically, six districts are identified:
- The business district, which is the code that performs the core functionality of the product.
- The historic district, which is the legacy code on which the application may have been built.
- The tourist district, which is the code that delivers elementary functionality for novice system users.
- The entertainment district, which is the code that delivers supportive features of the product.
- The hotel district, which is the code that is active when the software is at rest.
- The seedy district, which is the code that few users ever activate, but that may contain product vulnerabilities.
Many tours are scheduled for each one of these districts; we cite a few, referring the interested reader to the original source.
- Tours of the Business District
- The guidebook tour: This tour advocates reading the user manual in detail and exercising the product’s functionalities according to the manual’s guidelines. This tour tests the system’s ability to deliver its advertised function, as well as the user manual’s precision in describing the system’s function.
- The skeptical customer tour: This tour advocates running the software product through a demo used by salespeople, but constantly interrupting the sequence of the demo to try variations that an end-user may be interested in, such as the following: What if I wanted to do this? How would I do that?
- Tours through the Historical District
- The bad neighborhood tour: This tour advocates running the software product in such a way as to exercise parts of its codes that are likely to have faults; the assumption is that faults tend to congregate in a software product, and the more faults one finds in a part of the product, the more likely other faults are to be found therein.
- The museum tour: This tour advocates running the software product in such a way as to exercise parts of it that stems from legacy code; the rationale of this tour is to expose any faults that may exist in the interface between legacy code and new code.
- Tours through the Entertainment District
- The supporting actor tour: This tour advocates exercising features of the software product that share the screen with core features that most users typically use; they may be less visited than typical functions, but equally likely to have faults.
- The back alley tour: This tour advocates exercising features that are at the low end of the feature table of the software product, on the grounds that they may also correspond to the least covered code of the product.
- Tours through the Tourist District
- The collector’s tour: This tour advocates running the application on a sufficiently broad set of inputs and under a sufficiently diverse set of circumstances that you can generate all the possible outcomes that the product is designed to deliver.
- The supermodel tour. This tour advocates to test the application, not on the basis of its functionality, but on the basis of its appearance.
- Tours through the Hotel District
- The rained out tour: This tour advocates initiating actions by the software product and then canceling them as the earliest convenience offered by the application, to check whether the product resets its state properly and diligently.
- The couch potato tour: This tour advocates running the software product in such a way as to provide as little data as possible, to check the product’s ability to proceed with incomplete information or by using default values.
- Tours through the Seedy District
- The saboteur tour: This tour advocates initiating operations by the software product and then interfering with the proper execution of these operations (e.g., launching an I/O operation and disconnecting the relevant device); the purpose of this tour is to test the product’s ability to handle exceptions.
- The obsessive compulsive tour: This tour advocates initiating the same operation with the same input data over and over again and observing whether the behavior of the system (in terms of whether the successive operations are interpreted as multiple queries, whether they are properly separated from each other, whether they override each other, etc.) is consistent with its requirements.
9.6 CHAPTER SUMMARY
The focus of this chapter is generating test data by considering the specification of the software product for inspiration. We have reviewed a few criteria for test data generation, namely:
- Generating test data by recognizing, or assuming (on the basis of some rationale), that some attributes of input test data are irrelevant from the standpoint of testing: they have no effect on whether candidate programs succeed or fail on an input data. By abstracting away the irrelevant attributes, we find an equivalence relation that places in the same equivalence class all the inputs that have the same effectiveness in exposing faults in candidate programs. Once such an equivalence relation is defined, we test candidate programs by selecting a single element in each equivalence class.
- When the specification of the software requirements is structured in tabular form, it is sensible to use the tabular structure as a guideline to generate test data.
- State-based systems can be specified by relations, albeit heterogeneous relations defined on structured spaces, from which we can derive a theoretical state space, which may or may not be the state space adopted by candidate implementations; regardless, we can generate test data for such implementation using coverage criteria of (theoretical) states and state transitions.
- It is possible to automatically generate random test data for a wide range of purposes using elementary random data generators that are standard features of common programming languages.
9.7 EXERCISES
- 9.1. Let F be a function. Compute the relation
 . Show that this is an equivalence relation and define its equivalence classes. These are called the level sets of function F; explain.
. Show that this is an equivalence relation and define its equivalence classes. These are called the level sets of function F; explain. - 9.2. Show that the domains of relations T1, T2, T3, T4, and T5 form a partition of the domain of
 .
. - 9.3. Consider the specification of the Tax application given in Section 9.2, and write a program that meets this specification.
- Consider the test data generated for this program and use the specification to record the expected output for each test datum.
- Check that your program meets the specification, and correct it as needed.
- Introduce five different faults in the program (in conditions, or assignments, or structured statements, etc.); check whether the generated test data can detect the fault.
- 9.4. Same exercise as above, for the admissions specification.
- 9.5. Consider a system that computes the tuition and fees for students at a university, as a function of the following parameters:
- The number of credits taken by the student for the current term, according to some sliding scale.
- Whether the student is graduate or undergraduate.
- Whether the student is resident in the state, an out-of-state national, or an international student.Give a tabular specification of this function and generate test data accordingly.
- 9.5. Consider a system that checks whether a date, given by a month, day, and year is legitimate. The year is an arbitrary positive number, the month is an integer between 1 and 12, and the day is an integer between 1 and 31 whose value varies according to the month and (for February) according to the year. Write a tabular specification of this system and generate test data accordingly. Discuss the rationale of your test generation criterion.
- 9.6. Consider the specification of a queue ADT given in Chapter 4.
- List the states of this ADT according to the formula presented in this chapter.
- Generate test data to visit all the states and all the transitions of this ADT.
- 9.7. Consider the specification of a set ADT given in Chapter 4.
- List the states of this ADT according to the formula presented in this chapter.
- Generate test data to visit all the states and all the transitions of this ADT.
- 9.8. Consider the sample stack implementations discussed in Section 4.10.1, that use an integer rather than an array and index. Run them on the test data generated in this chapter.
- 9.10. In the English language, the letters of the alphabet do not appear with the same frequency. The following table shows their frequency of appearance:
a 0.082 b 0.015 c 0.028 d 0.042 e 0.126 f 0.022 g 0.020 h 0.061 i 0.070 j 0.002 k 0.008 l 0.040 m 0.024 n 0.067 o 0.075 p 0.019 q 0.001 r 0.060 s 0.063 t 0.091 u 0.028 v 0.010 w 0.024 x 0.001 y 0.020 z 0.001 Generate a function that produces characters of the alphabet with the given frequency. Run a large number of times and estimate the frequency of appearance of each letter; compare it with the table given above.
- 9.11. Generate a random sorted array whose values are included between a lower bound Low and a higher value High.
9.8 BIBLIOGRAPHIC NOTES
For more details on tabular specifications and their semantics, consult (Janicki et al., 1997 ; Janicki and Khedhri, 2001). The criterion of test data generation for state-based software product, which provides for visiting all states and exercising all state transitions, is due to Mathur (2008). Whereas in this chapter we used a simple random number generator that produces a uniform distribution over a unitary interval, specialized environments such as MATLAB (©Mathworks) offer functions for a wide range of probability laws. For a detailed discussion of James Whittaker’s criteria for exploratory software testing, consult (Whittaker, 2010).
