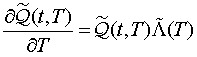Chapter 5. Migration Matrices and the Markov Chain Approach

Jarrow et al. (1997) (hereafter JLT) were the first to model default and transition probabilities by using a Markov chain on a finite state space The model and its relevance for determining risk-neutral migration matrices will be descibed in more detail in Chapter 8. Here we will concentrate on the definition and properties of discrete and continuous-time transition matrices.

5.1. The Markov Chain Approach

The state space S represents the different rating classes. Hereby, state S = 1 denotes the best credit rating; state K represents the default case. Hence, in the discrete case, the (K × K) one-period transition matrix looks as follows:

(5.1)

where for all and for all i. The variable P^ij represents the actual probability of going to state j from initial rating state i in one time step.

Thus, rating based models can be seen as a special case of the intensity model framework; see, e.g., Duffie and Singleton, 1999 where randomness in the default arrival is simply modeled via a Markov chain.

Alternatively, credit migration can also be modeled by a continuous-time Markov chain. Therefore, we will also introduce the idea of generator matrices and continuous-time modeling of rating transitions.^[1]

¹ Some of the results of this section were originally published in Trueck and Özturkmen (2004). The structure of the section follows the original publication.

5.1.1. Generator Matrices

A continuous-time time-homogeneous Markov chain is specified via a K × K generator matrix of the following form:

(5.2)

where for all i, j and , for The off-diagonal elements represent the intensities of jumping from rating i to rating j. The default K is an absorbing state.

Definition 5.1 Noris (1998): A generator of a time-continuous Markov chain is given by a matrix satisfying the following properties:

1. 
2. 
3. 

Further, see Noris (1998), the following theorem holds:

Theorem 5.2 The following two properties are equivalent for matrix satisfying the following properties:

1. Λ satisfies the properties in Definition 5.1.
2. is a transition matrix for every

Hence, the K × K t-period transition matrix is then given by

(5.3)

On the other hand, under certain conditions that will be investigated in more detail in the next section, given a discrete-time one-year transition matrix, the corresponding generator matrix can be calculated using the following expression:

(5.4)

For example, consider the transition matrix P

 

P	A	B	D
A	0.90	0.08	0.02
B	0.1	0.80	0.1
D	0	0	1

where the corresponding generator matrix is of the form

 

Λ	A	B	D
A	−0.1107	0.0946	0.0162
B	0.1182	−0.2289	0.1107
D	0	0	0

The use of generator matrices in credit risk is manifold. A main issue is, for example, the construction of so-called credit curves, giving information about cumulative default rates; see, e.g., Jarrow et al. (1997). For a given generator matrix Λ the cumulative default rate for rating class i is given by the Kth entry of the vector:

(5.5)

where denotes the row of the corresponding transition matrix to the given rating R. Figure 5.1 shows a chart of the credit curves to the corresponding matrix P on our example.

FIGURE 5.1. Credit curves for exemplary transition matrix with three rating states. Cumulative PDs for exemplary rating classes A (solid line) and B (dashed line).

Similar to the discrete-time framework, JLT transform the empirical generator matrix into a risk-neutral generator matrix by multiplying it with a matrix of risk premiums. This corresponds to an adjustment in order to transform the actual probabilities into the risk-neutral probabilities for valuation purposes:

(5.6)

where is a diagonal matrix with strictly positive entries for as deterministic functions of t.

The t-period transition matrix under the martingale measure can then be computed by the Kolmogorov forward and backward equations:

(5.7)

(5.8)

Assuming constant risk premiums the risk-neutral transition matrix under the martingale measure is the solution of

JLT define a methodology to value risky bonds as well as credit derivatives that is based on ratings that allow for changes in credit quality before default. In the following section we will give a brief outline of the advantages of continuous- versus discrete-time models.

5.2. Discrete Versus Continuous-Time Modeling

Lando and Skødeberg (2002)as well as Christensen et al. (2004) focus on the advantages of the continuous-time modeling over the discrete-time approach used by rating agencies in order to analyze rating transition data. Generally, rating agencies estimate transition probabilities using the multinomial method by computing

(5.9)

for Where Nⁱ is the number of firms in rating class i at the beginning of the year and N^ij is the number of firms that migrated from class i to rating class j.

The authors argue that these transition probabilities do not capture rare events such as a transition from rating AAA to default as they may not be observed. However, it is possible that a firm reaches default through subsequent downgrades from AAA—even within one year and the probability of moving from AAA to default must be non-zero. Following Küchler and Sorensen (1997) a maximum-likelihood estimator for the continuous-time method is proposed:

(5.10)

The variable denotes the number of firms in rating class i at time s and is the total number of transitions over the period from i to j, where i ≠ j. Under the assumption of time homogeneity over the considered period, the transition matrix for a time interval t can be computed by the formula .

Following Lando and Skødeberg (2002), we consider now an example with three rating classes A, B, and D for default. It is assumed that at the beginning of the year there are 10 firms in A, 10 in B, and none in default. Now one A-rated company is downgraded to B after one month and stays there for the rest of the year; a B-rated company is upgraded to A after two months and remains there for the rest of the period, and a B-rated company defaults after six months. The discrete-time multinomial method then estimates the following one-year transition matrix:

 

P	A	B	D
A	0.90	0.10	0
B	0.1	0.80	0.1
D	0	0	1

The maximum-likelihood estimator for the continuous-time approach computes the following generator matrix:

 

	A	B	D
A	-0.10084	0.10084	0
B	0.10909	-0.21818	0.10909
D	0	0	0

For instance, the nondiagonal element equals

The diagonal element is computed such that the row sums to zero. Exponentiating the generator gives the following one-year transition matrix:

 

P	A	B	D
A	0.90887	0.08618	0.00495
B	0.09323	0.80858	0.09819
D	0	0	1

Thus, we have a strictly positive default probability for class A although there have been no observations from A to default in this period. However, this makes sense as the migration probability from A to B and from B to default is non-zero. Hence, it could happen within one year that a company is downgraded from rating state A to B and then defaults from rating state B within one year.

For the time-inhomogeneous case, the Nelson-Aalen estimator [see, e.g., Küchler and Sorensen (1997)] can be used:

where are the observed times of transitions from state h to j and counts the number of firms in rating class h at a time just prior to t. The transition matrix is then computed by

(5.11)

where is the identity matrix, Tⁱ is a jump time in the interval (s, t], and

The diagonal elements count the total number of transitions from class i to another rating state divided by the number of exposed firms. The off-diagonal elements count the number of migrations to the corresponding class also divided by the number of exposed firms. This estimator can be interpreted as a cohort method applied to very short time intervals.

Applying this approach to our example, we obtain the following matrices:

Using equation (5.2), we get

As in the time-homogeneous case, we obtain a strictly positive default probability for class A, although the entries in the matrix above are slightly different than in the time-homogeneous case. However, Lando and Skødeberg (2002) indicate that in most cases the results are not dramatically different for large data sets. Compared to the estimator for the transition matrix using the discrete multinomial estimator, we obtain obvious deviations.

Summarizing the key advantages of the continuous-time approach, we find that we get more realistic non-zero estimates for probabilities of rare events, whereas the multinomial method leads to estimates that are zero. Further, using generator matrices, it is also possible to obtain transition matrices for arbitrary time horizons. We will see in later chapters that the continuous time framework also permits us to generate confidence sets for default probabilities in higher rating classes. Finally, in the continous-time approach we do not have to worry which yearly periods we consider. Using a discrete-time approach may lead to quite different results depending on the starting point of our consideration.

However, the last issue is also a critical point for the estimation of generator matrices. In internal rating systems it is often the case that rating changes are reported only once a year and that the exact time of the change is not provided. Then it is not appropriate to use the maximum-likelihood or the Nelson-Aalen estimator for estimation of the transition matrix.

So far we have described the basic ideas of rating based credit risk evaluation methods and the advantages of continuous-time transition modeling over the discrete-time case. Despite these advantages of continuous-time modeling, there are also some problems to deal with, like the existence, uniqueness, or adjustment of the generator matrix to the corresponding discrete transition matrix.

In many cases in the internal rating system of a bank, only discrete-time historical transition matrices are reported. To benefit from the advantages of continuous-time modeling, the bank might still be interested in finding the correspondent generator matrix. In this case an important issue is whether for a given discrete one-year transition matrix a so-called “true” generator exists. For some discrete transition matrices, there is no generator matrix at all, while for some there exists a generator that has negative off-diagonal elements. This would mean that, considering short time intervals, transition probabilities may be negative, which is not acceptable from a practical point of view. Examining the question of existence and suggesting numerical methods for finding true generators, or approximations for true generators, we will follow an approach by Israel et al. (2000).

In their paper they first identify conditions under which a true generator does or does not exist. Then they provide a numerical method for finding the true generator once its existence is proved and show how to obtain an approximate one in case of the absence of a true generator. The authors define two issues concerning transition matrices: embeddability, which is to determine if an empirical transition matrix is compatible with a true generator or with a Markov process; and identification, which is to search for the true generator once its existence is known.

Given the one-year N × N transition matrix P, we are interested in finding a generator matrix Λ such that

(5.12)

Dealing with the question if there exists a generator matrix, we can use the following theorem (Noris, 1998):

Theorem 5.3 If a migration matrix is strictly diagonal dominant, i.e., for every i, then the log-expansion

(5.13)

converges to a matrix satisfying

1. (5.14)
2. (5.15)

The convergence is geometrically fast and denotes an N × N matrix having row-sums of zero and satisfying exactly. For the proof, see Israel et al. (2000).

However, it is important to note that even if the series Λ^* does not converge or converges to a matrix that cannot be a true generator, P may still have a true generator.

There is also a simpler way to check if S < 1, namely if the transition matrix consists of diagonal elements that are greater than 0.5. In this case we get S < 1 and the convergence of (5.3) is guaranteed. In practice, for historical transition matrices of the major rating agencies, this will be true, so we can assume that generators having row-sums of zero and satisfying can be found.

For the existence of an exact generator matrix, Israel et al. (2000) state the following proposition.

Proposition 5.4 Let P be a transition matrix. If one of the following three conditions holds

• 
• 
• there are states i and j such that j is accessible from i, but then there does not exist an exact generator matrix for P.

However, often there remains another problem: the main disadvantage of (5.3) is that Λⁿ may converge but does not have to be a true generator matrix in economic sense; it is particularly possible that some off-diagonal elements are negative.

We will illustrate this with an example. Consider the one-year transition matrix:

 

P	A	B	C	D
A	0.9	0.08	0.0199	0.0001
B	0.050	0.850	0.090	0.010
C	0.010	0.090	0.800	0.100
D	0	0	0	1

Calculating the generator that exactly matches by using (5.3), we get

 

Λ	A	B	C	D
A	-0.1080	0.0907	0.0185	-0.0013
B	0.0569	-0.1710	0.1091	0.0051
C	0.0087	0.1092	-0.2293	0.1114
D	0	0	0	0

having a negative entry in the off-diagonal element .

From an economic viewpoint, this is not acceptable because a negative entry in the generator may lead to negative transition probabilities for very short time intervals. Israel et al. (2000) show that it is possible that sometimes there exists more than one generator. They provide conditions for the existence or nonexistence of a valid generator matrix and further a numerical algorithm for finding this matrix.

5.2.1. Some Conditions for the Existence of a Valid Generator

In this section we will examine conditions for the existence and nonexistence of a valid generator matrix. We will first define the conditions to conclude the uniqueness of a generator matrix.

Since a transition matrix P sometimes has more than one valid generator, there is also the problem of its uniqueness. Following Singer and Spilerman (1976), we provide the following theorem.

A theorem for the uniqueness of the generator is as follows:

Theorem 5.5 Let P be a transition matrix.

• If det(P) > 0.5, then P has at most one generator.
• If det(P) > 0.5 and then the only possible generator for P is the one obtained by (5.3).
• If P has distinct eigenvalues and , then the only possible generator is the one obtained by (5.3).

For the proofs of the above conditions and further material, we refer to the original article (Singer and Spilerman, 1976).

If there exists more than one valid generator matrix, the question is which one to choose. Since it is unlikely for a firm to migrate to a “far” rating from its current rating, Israel et al. (2000) suggest to choose among valid generators the one with the lowest value of

which ensures that the chance of jumping too far is minimized.

Investigating the existence or nonexistence of a valid generator matrix with only positive off-diagonal elements, we start with another result obtained by Singer and Spilerman (1976):

Proposition 5.6 Let P be a transition matrix that has real distinct eigenvalues.

• If all eigenvalues of P are positive, then the matrix obtained by (5.3) is the only real matrix Λ such that exp (Λ) = p.
• If P has any negative eigenvalues, then there exists no real matrix Λ such that exp (Λ) = p.

Using the conditions above, we can conclude for the nonexistence of a valid generator.

Proposition 5.7 Let P be a transition matrix such that the (5.3) converges to a matrix Λ with negative off-diagonal elements. If at least one of the following three conditions hold

• 
• P has distinct eigenvalues and or
• P has distinct real eigenvalues

then there does not exist a valid generator for P.

For the considered example

we get the following results:

• 
• P has the distinct positive eigenvalues 0.9702, 0.8529, 0.7269, and 1.0000 and .
• P has distinct real eigenvalues.

So we conclude that the conditions in proposition 5.5 for the uniqueness of a generator hold. Since (5.3) converges to

we find with proposition 5.7 that there exists no true generator for the transition matrix P. Israel et al. (2000) also suggest a search algorithm for a valid generator if the series (5.3) fails to converge or converges to a matrix that has some off-diagonal terms but is not unique. For a further description we refer to the original publication. In the following we will provide some approximation methods for generator matrices that are useful in the case of negative off-diagonal elements.

5.3. Approximation of Generator Matrices

In the preceding section we saw that despite the manifold advantages of continuous-time transition modeling there is a chance of the nonexistence of a valid generator matrix to a given discrete-time transition. This may lead to some difficulties in practical implementations. Especially for matrices having rows with several zeros (e.g., no transitions to default states), often no valid generator matrix exists. In this case, some approximation methods can be used to determine an adequate generator matrix that will be discussed in the following.

If we find a generator matrix with negative off-diagonal entries in a row, we will have to correct this. The result may lead to a generator not providing exactly but only an approximation, though ensuring that from an economic viewpoint the necessary condition that all off-diagonal row entries in the generator are nonnegative is guaranteed. The literature suggests different methods to deal with this problem; see, e.g., Jarrow et al. (1997),; Israel et al. (2000),; Araten and Angbazo (1997),; Kreinin and Sidelnikova (2001). In this section we will describe the approaches suggested in Jarrow et al. (1997) and Israel et al. (2000). For approaches using regularization algorithms that approximate the root of the annual transition matrix, we refer to the original publiations by Araten and Angbazo (1997) and Kreinin and Sidelnikova (2001).

5.3.1. The Method Proposed by Jarrow, Lando, and Turnbull (1997)

The first apporach to deal with off-diagonal row entries in the generator was initially suggested by Jarrow et al. (1997). Note that we will describe this in more detail in Chapter 8, which focuses on risk-neutral migration matrices. In this section we restrict ourselves to a review of their suggestion of how to adjust a generator matrix. In their approach every firm is assumed to have either zero or only one transition throughout the year. Under this hypothesis it can be shown that for for i = 1, …, K – 1

(5.16)

the estimates of can be obtained by solving the system

JLT provide the solution to this system as

This leads only to an approximate generator matrix; however, it is guaranteed that the generator will have no nonnegative entries except the diagonal elements.

For our example, the JLT method gives the associated approximate generator

 

Λ	A	B	C	D
A	−0.1054	0.0843	0.0210	0.0001
B	0.0542	−0.1625	0.0975	0.0108
C	0.0112	0.1004	−0.2231	0.1116
D	0	0	0	0
.

with nonegative entries; however, exp(Λ) is only close to the original transition matrix P:

 

PJLT	A	B	C	D
A	0.9021	0.0748	0.0213	0.0017
B	0.0480	0.8561	0.0811	0.0148
C	0.0118	0.0834	0.8041	0.1006
D	0	0	0	1

Especially in the last column, high deviations (from 0.0001 to 0.0017 in the first row or 0.0148 instead of 0.010 in the second) for low default probabilities have to be considered as a rather rough approximation. We conclude that the method suggested by JLT in 1997 solves the problem of negative entries in the generator matrix, though we get an approximation that is not really close enough to the “real” transition matrix.

5.3.2. Methods Suggested by Israel, Rosenthal, and Wei (2000)

Due to the deficiencies of the method suggested by JLT, in their paper Israel et al. (2000) suggest a different approach to finding an approximate true generator. They suggest to using (5.3) to calculate the associated generator and then adjust this matrix using one of the following methods:

• Replace the negative entries with zero and add the appropriate value back in the corresponding diagonal entry to guarantee that row-sums are zero. Mathematically,The new matrix will not exactly satisfy .
• Replace the negative entries with zero and add the appropriate value back into all entries of the corresponding row proportional to their absolute values. Let Gⁱ be the sum of the absolute values of the diagonal and nonnegative off-diagonal elements and Bⁱ the sum of the absolute values of the negative off-diagonal elements:Then set the modified entries

In our example where the associated generator was

 

Λ	A	B	C	D
A	−0.1080	0.0907	0.0185	−0.0013
B	0.0569	−0.1710	0.1091	0.0051
C	0.0087	0.1092	−0.2293	0.1114
D	0	0	0	0

applying the first method and setting to zero and adding –0.0013 to the diagonal element , we would get for the adjusted generator matrix Λ^*

 

Λ*	A	B	C	D
A	−0.1093	0.0907	0.0185	0
B	0.0569	−0.1710	0.1091	0.0051
C	0.0087	0.1092	−0.2293	0.1114
D	0	0	0	0

which gives us for the approximate one-year transition matrix

 

PIRW1	A	B	C	D
A	0.8989	0.0799	0.0199	0.0013
B	0.0500	0.8500	0.0900	0.0100
C	0.0100	0.0900	0.8000	0.1000
D	0	0	0	1
.

Obviously the transition matrix P^IRW1 is much closer to the “real” one-year transition than the result for the method by Jarrow et al. (1997). Especially for the second and third row, we get almost exactly the same transition probabilities than for the “real” transition matrix. Also the deviation for the critical default probability is clearly reduced compared to the JLT method described above.

Applying the second suggested method and again replacing the negative entries with zero but redistributing the appropriate value to all entries of the corresponding row proportional to their absolute values gives us the adjusted generator

 

Λ*	A	B	C	D
A	−0.1086	0.0902	0.0184	0
B	0.0569	−0.1710	0.1091	0.0051
C	0.0087	0.1092	−0.2293	0.1114
D	0	0	0	0

and the associated one-year transition matrix

 

PIRW1	A	B	C	D
A	0.8994	0.0795	0.0198	0.0013
B	0.0500	0.8500	0.0900	0.0100
C	0.0100	0.0900	0.8000	0.1000
D	0	0	0	1
.

Again we get results that are very similar to the ones using the first method by Israel et al. (2000). The authors state that generally by testing various matrices, they found similar results. To compare the goodness of the approximation, they used different distance matrix norms.

While the approximation of the method suggested by JLT in their 1997 seminal paper is rather rough, the methods suggested by Israel et al. (2000) give better approximations of the true transition matrix. Note, IRW give better approximations if the true transition matrix. Note, however, that these results are rather qualitative at the moment. For different measures to compare the goodness of the approximation, we refer to Chapter 7.

5.4. Simulating Credit Migrations

In this section we will review some techniques that can be used to simulate credit migration matrices. Simulation results from migration matrices are of particular interest when it comes to calculations of Value-at-Risk or expected shortfall for a credit or loan portfolio. This section provides a quick guide to different simulation techniques and presents algorithms for the time-discrete, time-continuous, and a nonparametric approach.

5.4.1. Time-Discrete Case

In the time-discrete case the simulation procedure is straightforward and can be conducted the following way: depending on the initial rating i of the firm, the interval [0, 1] is divided into subintervals according to the migration probabilities P^ij for j = 1, …, K. For example, for each rating class i, the intervals can be determined according to the following procedure:

(5.17)

Then a uniform distributed random variable u^t between 0 and 1 is drawn. Depending on which subinterval the random variable lies in, the company stays in the same rating class i or migrates to rating class j. The migration process for a company or loan in rating class i is determined by the following function :

(5.18)

If more than one time-period is considered and a migration to rating state j occurs, new subintervals have to be calculated based on the migration probabilities P^jk for k = 1,…, K and a new random number is drawn for the following period. The procedure is either going to be repeated for periods or terminated, if the company migrates to the absorbing default state.

5.4.2. Time-Continuous Case

Recall that a continuous-time, time-homogeneous Markov chain is specified via the a K × K generator matrix of the following form:

(5.19)

where , for all i, j and for The off-diagonal elements represent the intensities of jumping from rating i to rating j. The default state K is considered to be absorbing.

In the following we will illustrate two different techniques that might be used to simulate credit migrations from a continuous-time Markov chain. The first one is applied, for example, in Christensen et al. (2004) or Trueck and Rachev (2005).

As the waiting time for leaving state i has an exponential distribution with the mean we draw an exponentially distributed random variable t¹ with the density function

for each company with initial rating i. Depending on the considered time horizon T for , the company stays in its current class during the entire period T. If we get t¹ < T, we have to determine to which rating class the company migrates.

Hence, similar to the discrete-time approach the interval [0, 1] is divided into subintervals according to the migration intensities calculated via Then a uniform distributed random variable between 0 and 1 is drawn. Depending on which subinterval the random variable lies in, we determine the new rating class j the company migrates to. Then we draw again from an exponentially distributed random variable t²—this time with parameter from the generator matrix. If we find that , the considered company stays in the new rating class and the simulation is completed for this firm. If , we have to determine the new rating class. The procedure is repeated until we get or the company migrates to the absorbing default state where it will remain for the rest of the considered time period.

An alternative procedure that could be used follows an algorithm that is, e.g., described in Glasserman (1992). Recall that the waiting times for leaving state i to any other rating state j have exponential distributions with mean . Therefore, we draw for each of the companies with initial rating i k – 1 exponentially distributed random variables t^ij with density functions

(5.20)

We then determine the minimum of the drawn waiting times for . Depending on the time horizon T, if , the company stays in its current rating state i for the entire period T. If , the company migrates to the rating class j with the smallest drawn waiting time t^ij. In the case of migration we again draw seven exponentially distributed random variables t^jk with density functions and determine . If , the company stays in the new rating class j and the simulation for this firm is completed. If , the company migrates to the rating class k with the smallest drawn waiting time t^jk. The procedure is repeated until or the company migrates to default state.

5.4.3. Nonparametric Approach

Finally, we will describe the underlying idea of nonparametric simulation of credit migrations. For an empirical application, see, e.g., Schuermann and Hanson (2004). The authors use a nonparametric simulation procedure to estimate confidence intervals for probabilities of default. Note that for this approach the estimated discrete or continuous-time migration matrix will not be sufficient. To apply a nonparametric approach, the actual individual migrations of the loans or bonds need to be available. Based on the observed migrations, for each of the rating classes, a data table can be constructed containing the duration times and the rating class the corresponding company migrated to.

The simulation procedure can be described as follows: for each of the companies we draw randomly a row in the corresponding duration time data table. If the duration time t in the drawn row is greater than the considered time horizon T, the company stays in the initial rating class. For t < T we have to differentiate between two cases. If the initial rating and the end rating of the drawn row coincide, the company stays, of course, in the initial rating. We then have to randomly draw another row from the same duration time data table, whereas the considered time horizon T has to be reduced by t. If the end rating j and the initial rating i of the drawn row vary, a migration to rating j occurs. In this case we have to randomly draw a row from the duration time data table of the new rating class j. The procedure is repeated until either a default occurs or the sum of the drawn duration times exceed the simulated time horizon T.

The following example may help to illustrate the procedure. Table 5.1 gives an exemplary representation for hypothetical duration times in rating class AA. Assume that for each of the other rating classes a similar table was constructed. Hereby, also the duration records of companies which remained in the initial rating class for the considered time period were included. The simulation is then conducted according to the algorithm described above. Depending on the drawn random number, the corresponding row in the table is considered to simulate the duration time in the rating class and the migration.

TABLE 5.1. Parts of the Duration Time Table for Rating Class AA

Row	Duration Time t (in months)	Initial Rating i	End Rating j
1	36	AA	AA
2	4	AA	AAA
3	71	AA	AA
4	17	AA	BBB
…	…	…	…

Note that in this section we assumed that all individual migrations are independent. For approaches that can also be used to simulate dependent credit migrations, we refer to Section 10.5.