Chapter 5

How to Solve a Game II

Sequential Games

The early bird gets the worm, but the early worm gets eaten.
—Proverb

Now we will look at games similar to the ones discussed already, but change the important assumption that the players move simultaneously. We will be looking to predict how players should make choices, and the key is to anticipate the other player’s reaction. We will discuss what the outcome will be, and whether it is better to go first, go second, or whether it does not matter.

5.1 Backward Induction and “Subgame Perfect” ­Equilibria

Let us first turn our attention to the Dating Game from Table 3.4. Here we are going to allow Bob to go first, and then, after seeing Bob’s choice, Suzy will make her decision. What will happen?

First we need to familiarize ourselves with a common way to represent such a game, called an “extensive form game,” or “game tree.” On the left we see Bob, making the first choice between going to the opera or the wrestling match. Next we see Suzy twice, on the top making her choice after Bob goes to the opera, and on the bottom making her choice after seeing Bob go to the wrestling match. We have made Bob’s choices and payoffs bold to help clarify.

At the end of each of the four paths we see the same payoffs for the four outcomes as in the simultaneous game. For example, if Bob goes to the opera and then Suzy goes to the opera, Bob will get 6 and Suzy will get 10.

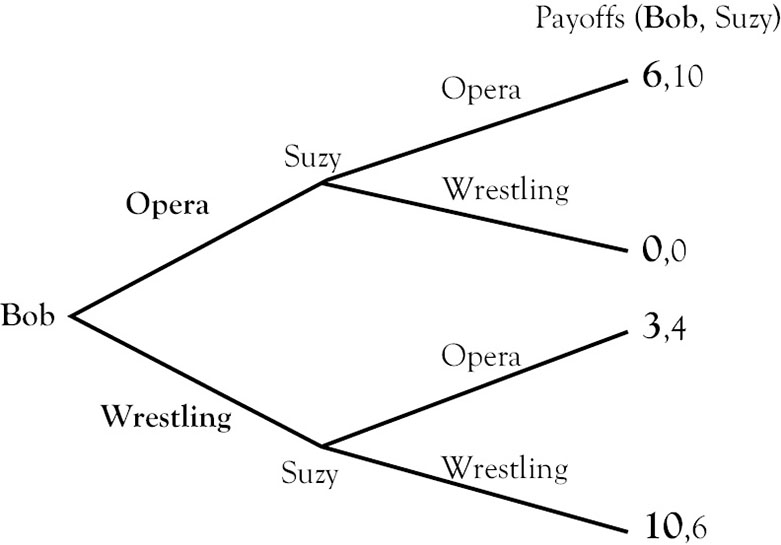
Since Bob has to make his decision first, we use the Game Theorist’s Number One Rule: Anticipate the other player’s reaction in order to make your best choice. Here is how it can be done: Bob says to himself “What is Suzy’s best response if she saw me go to the opera?” She has two possible choices: to follow him to the opera for 10 or to go alone to the wrestling match for 0. Of course, she will follow him to the opera. Then Bob says: “What is Suzy’s best response if she saw me go to the wrestling match?” She has two possible choices: to follow him to the wrestling match for 6 or to go alone to the opera for 4. Of course, she will follow him to the wrestling match. I draw boxes around these two outcomes. Now that Bob has anticipated Suzy’s reaction to each of his choices, he has to make his decision: “Should I go to the opera, where I know Suzy will follow and I will get 6, or do I go to the wrestling match, where I know Suzy will ­follow and I will get 10?” Our prediction should be that Bob will go to the wrestling match, Suzy will follow, and Bob will get 10, Suzy will get 6. This outcome is marked with **.

A few definitions: The process of looking ahead to anticipate the other player’s reactions we call “Backward Induction,” because we start at the end of the game (Suzy’s reactions) and work backward to logically determine Bob’s best choice. The answer or prediction of how the players will behave is called a “Subgame Perfect Equilibrium.” In this game, there are two “subgames”; a subgame is a small part of the whole game. Here the subgames are where Suzy might get the chance to make her choices, after seeing what Bob has done. In a “subgame perfect” equilibrium, we must observe Suzy making rational choices when she is asked to. For example, even though Suzy might threaten to “go alone to the opera if you go to the wrestling match,” we know that she will come around in the end and make the choice that truly makes her happier. Once again, we are assuming that Suzy is rational!

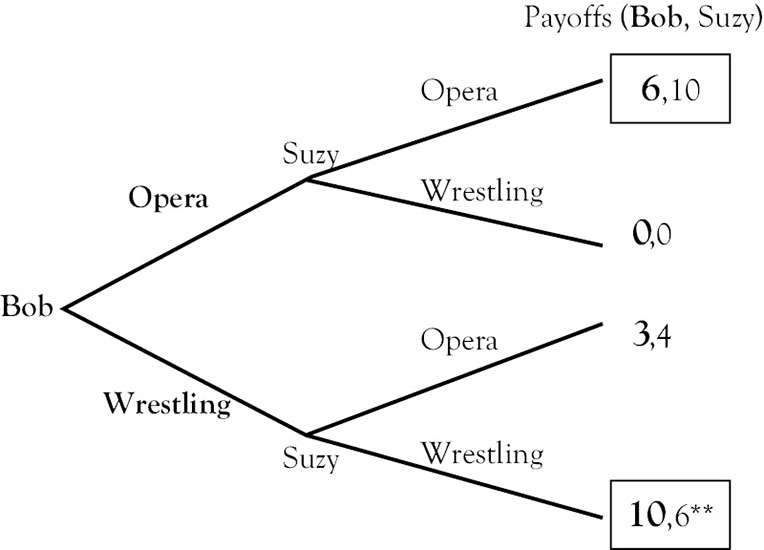
Now, what can we say about Suzy if we allow her to go first in this game? Below is the game tree, where you should notice that even though it looks very similar to the previous one, there are two critical differences. First, Suzy’s choice is on the far left, indicating that she is going first. Second, note that the payoffs in the middle have switched places (the (0,0) and (3,4)) because the (3,4) must be at the place where Bob is at the wrestling match and Suzy is at the opera, and that outcome is now in the second position from the top, rather than the third.

What should Suzy do? Suzy knows that if she goes to the opera, Bob will follow her, and she will end up with 10. She also knows that if she goes to the wrestling match, Bob will follow her, and she will end up with 6. Being rational, she will go to the opera, Bob will follow, and she will get 10, while Bob ends up with 6.

Now comes the important question: Would you rather go first, or ­second in this game? Does the answer depend on whether we ask Bob or Suzy?

5.2 First and Second Mover Advantages

In the Dating Game, Bob and Suzy would both prefer to be the one who goes first. When Bob goes first he gets 10, when he goes second he gets 6; Suzy’s answers are the same. The player that goes first gets to determine which of the two Nash equilibria the couple will end up playing. Thus, there is an incentive for each of them to try to take steps to be the first mover.

Let us take a look back at many of the simultaneous games we investigated earlier in the book and see what happens when it becomes a sequential game, though we have alluded to some of the answers earlier. The Dating Game, Hawk–Dove Game, and Chicken all have a first mover advantage. To repeat, these games have two Nash equilibria, and the two players prefer different ones of those two equilibria. So, to go first means to commit to one of those two Nash equilibria.

However, having two Nash equilibria does not necessarily mean that there will be a first mover advantage. The cooperative coordination games in Section 3.3 also had two Nash equilibria. In the Stag Hunt Game, allowing one player to go first determines that we will end up at the “good” equilibrium where both hunt the Stag. Let us think this through:

Suppose Hunter 1 (H1) has to make his move first. He wants to anticipate how Hunter 2 would react if he went after the Stag. Hunter 2 could go after the Stag as well for a payoff of 2, or spear his rabbit for a payoff of only 1. Of course, Hunter 2 would also participate in the Stag hunt for a higher payoff, and each Hunter will receive 2. If Hunter 1 instead chooses to spear his hare, then Hunter 2 will as well, and each will receive a payoff of 1. Because it is rational for Hunter 2 to “join in the hunt” with Hunter 1, then it is rational for Hunter 1 to lead the charge to the Stag.

The same logic applies, no matter who goes first in this game. Since both players prefer the same outcome, in the sequential Stag hunt there is no first mover or second mover advantage. However, as there is no incentive to be the first mover, it does take a certain amount of guts or trust in the other hunter, to be the first to take off chasing the Stag before the opportunity slips by. Using a somewhat similar logic, we can see that in Section 4.3 on “Teenage Angst” that the one Nash equilibrium that is preferred by both girls should be the result no matter who goes first.

Similarly, in the two player, two choice games, we have been investigating games where there is only one Nash equilibrium, the order of play will not matter for the outcome. In order for there to be a Nash equilibrium in these games, at least one player must have a dominant strategy.

So we see that in some games that have two Nash equilibria, one of these equilibria gets “weeded out” in a sequential game. What about games where the only equilibrium is to randomize? In Matching Pennies and Rock, Paper, Scissors we had zero-sum games with no pure strategy Nash equilibria. We discussed a way that some people try to win in Rock, Paper, Scissors is to hesitate just long enough to become a second mover. Once you know what your opponent has played, it is easy to win every time. Thus, in these games there is a second mover advantage.

Let us revisit Sarah and Paul from Table 2.6, a positive sum game with no Nash equilibrium. Recall that Paul wants to follow Sarah, but Sarah doesn’t want to be around Paul. The two extensive form games are here:

Here we see that when Sarah goes first, they both end up at the football game giving Sarah 6 and Paul 13. However, when Paul goes first, he will go to the football game, and Sarah will go skating; Sarah will get 9 and Paul gets 8. Once again, we see a second mover advantage which should make sense in this game. The second mover can avoid, follow the other, or both, depending on their preferences.

To sum up our experience so far, in some games it is best to act first, but in others it pays to wait and react. Let us take a step back and look at the real world for a bit. After you have determined that a game you are playing has either a first or second mover advantage, what can one do in order to make sure they are in the preferred position?

In a game with a first mover advantage, you want to work fast to make a choice first, announce that choice to the other player(s), and make sure that your choice is clearly irreversible. In the Dating Game, Suzy should buy nonrefundable tickets to the opera earlier in the week, or send a text message to Bob saying that she will meet him at the opera, and then cut off all communication (say, her phone died) to make it irreversible. Similarly, earlier we pointed out that the first person in Chicken who rips off their steering wheel would be the winner. We must make clear that not only is being first important, but (at least the appearance of) irreversibility is critical.

In games with a second mover advantage, securing the second position could be trickier. Simply waiting for the other person to move could leave everyone waiting around forever! And of course, wasting time has its own costs so this is not a good outcome, either. In this kind of game, ­spying, subterfuge, and misinformation come into play, which we will discuss more in Chapter 7. However, the real-world players often make plans over long periods of time. Becoming the “second mover” only requires that you somehow learn information about what your opponent is planning, and while keeping your own plans secret.

5.3 A Game Where Order Matters, and Players Can Agree on the Best Order of Play

All of the games without pure strategy Nash equilibria we have looked at so far have had a second mover advantage, but this does not always have to be the case. Look at this game (Table 5.1).

A distinguishing feature of this game is that while there is no predictable outcome in the simultaneous game (our prediction would be for players to randomize their choices), the Row player has a strong preference about what he wishes Column to do—the outcome for Row is much better when ­Column chooses left. Of course, in a simultaneous game Row has no control over what Column does; let us see how a sequential game would play out.

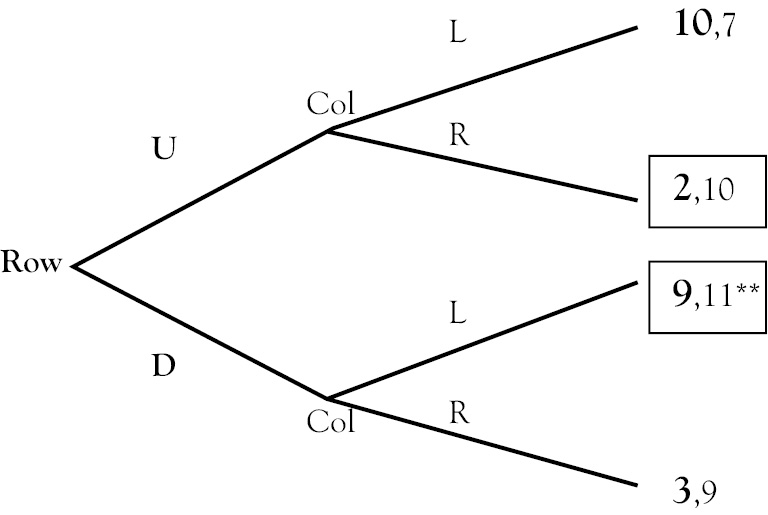
When Row goes first, he knows that if he goes up, Column will go right leaving him with 2, but if he goes down, Column will respond by going left, leaving him with 9. So, Down, Left would be the outcome. However if Column goes first, he knows that if he goes left, Row will respond with up giving Column 7, but if he chooses to go right, Row’s best response is to go down, leaving Column with 9. Therefore, in this case Right, Down would be the outcome.

So far, so good. However, answer the following question: Is there a first mover advantage or a second mover advantage in this game? The not-so-straightforward answer is that both players prefer for Row to go first and Column to go second. By “serving up” Column’s best possible outcome (11) by choosing up, this induces Column to choose left, giving Row a pretty good outcome of 9 in the process. However, if Column goes first, he will not choose left—which is devastating to Row, and also takes Column’s best payoff off of the table. So, in this game, even though the players disagree about the best outcome, they can agree on who should go first, which decreases the amount of real-world conflict significantly.

5.4 Larger Sequential Games

Of course, we can use the same logic to solve games with more than two choices, and as we will see below, we can analyze games with a long sequence of choices. First, let’s analyze the “Extra-Large Game” from Chapter 4, Table 4.4 as a sequential game. In the simultaneous game we found one logical prediction (B, Z) using “iterated dominance.” In the sequential game, we arrive at the same result regardless of who goes first. Here is the game tree where Player 1 goes first, choosing A–E, and Player 2’s best responses are highlighted. After finding Player 2’s best response to Player 1’s choices A–E, Player 1 picks his best choice, which is B for a payoff of 3 when Player 2 chooses Z.

Next we will analyze a sequential game with a different structure. We will analyze the “Centipede” game, so called because there is a version of it where there are 100 choices to be made, creating 100 “feet” on the game tree. Here we have two players, A and B. A makes the first choice, and can choose right or down. If he chooses down, the game is over. If he chooses right, then B gets a choice.

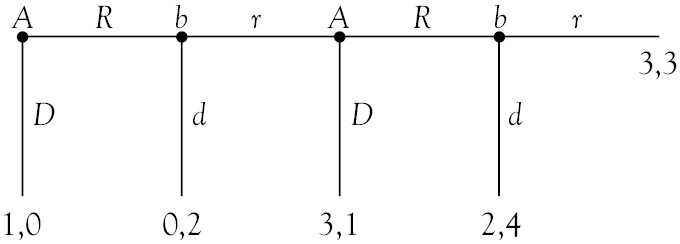
In order to solve this game, of course we need to use backward induction again. Starting at the end of the game, we see that B gets a choice between r or d. He prefers d for a payoff of 4. At the previous step of the game, it is A’s choice. If he chooses R then he knows that B is going to choose d, leaving him with 2. However, we also have the opportunity to choose D for a payoff of 3, so A will not give B the chance to make that last decision; instead he will end the game here, taking the payoff of 3 and leaving B a payoff of 1.

So, what will B do in the second stage of the game? If he allows A the chance to make a move after him, he will end up with only 1. But by ­ending the game now he could get 2, and leave A with 0.

Which takes us back to the very first decision that A must make. If he chooses R, he knows that he will end up with 0 but by ending the game before it even gets started, he can assure himself a payoff of 1. So, our prediction for the Centipede game is that A will end it in the very first move and get a payoff of 1, leaving B with 0.

What is intriguing about this game is that it is somewhat analogous to a Prisoner’s Dilemma: If the two players could cooperate, then they could both earn payoffs of 3. However, by pursuing their individually selfish choices they are both worse off than if they could cooperate. The same thing holds even if this Centipede game had 100, or 1000, or one million choices to make. As long as there is a definite end, the fact that each player is certain of what the other player will do to them in the very last stage makes them want to do it in the next to the last stage, which unravels cooperation still further. However, there are some ways to achieve cooperation, and these will be discussed in Chapter 6.

5.5 What If Your Opponent Is Irrational? Be Prudent

As we have discussed before, in most of game theory we assume that both players are rational and want the best outcome for themselves. However, sometimes you might be forced to play a game against an irrational player. Recent examples include negotiations between Europe and the United States on one side, and Iran and North Korea on the other. It makes perfect sense to Europe and the United States that imposing sanctions on a poor country should cause an obvious reaction: that these countries give up their nuclear bomb-making programs. However, time after time Western leaders seem confounded by the “irrational” decisions made by these countries.

Another common example is the typical path of divorce proceedings in the United States. During a divorce, parties are often irrational and rather than looking out for their best interests, seek to inflict as much punishment on the other party as possible. It is common in a divorce to spend so much money battling over dividing “the pie” that in the end, there is no pie left.

Now, it is important when we discuss irrationality to recognize that this could mean many different things. For example, the player could be simply insane or incompetent, making decisions at random, or based on something strange such as the sound of a word rather than on the implications of the choice. Or, as in the case of divorce, a player may simply be “out to get us.”

In these cases, using solution concepts that assume that both players are rational is ill-advised. A different kind of strategy, sometimes described as “Prudent” may be useful here. “Prudent” means cautious, wary, and careful. If you think that the other player is out to get you, then this kind of thinking may be your best bet. Let me introduce a technical term:

Maximin: Make choices that Maximize the minimum payoff your opponent could leave you with.

Rather than focusing on maximizing your payoff, our mindset switches to limiting our vulnerabilities. Some describe maximin as ­finding the option that has the “best worst payoff.”

What is often lost in discussions of irrationality is how players can gain by playing the part of the irrational (crazy like a fox!). If there is a chance that I am crazy, or might go crazy if you make some sort of choice, then I cause my opponents to act differently. Take the game between Row and Column in Section 5.3.

Suppose Column was forced to go first for some reason and Row has a tendency to go crazy when players who go first “insult” him by playing right, thus forcing him into a low payoff situation. Thus we might think of Row as having three possibilities in response to Column’s right: up, down, and “hand grenade” (doing something that is reckless and crazy, normally not an option for rational players). Thus, by being (or at least having a reputation for being) a little crazy Row can force Column to play left, giving Row his highest payoff of 10.

However, gaining a reputation for being crazy has its costs, and must be acquired through repeated interactions with other players, which we have avoided discussing up until now. In the next chapter, we focus on repeated games and how cooperation can evolve.